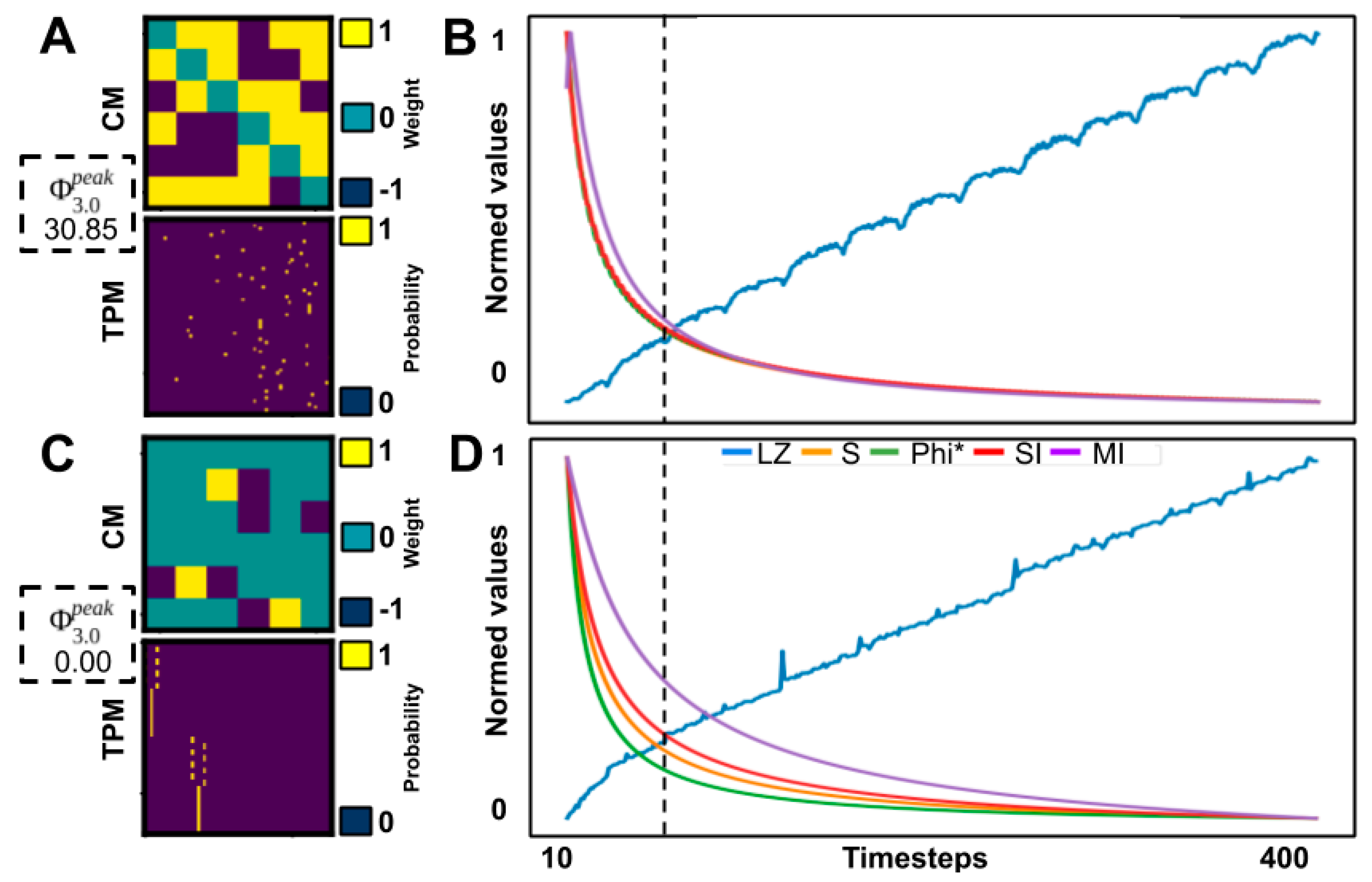
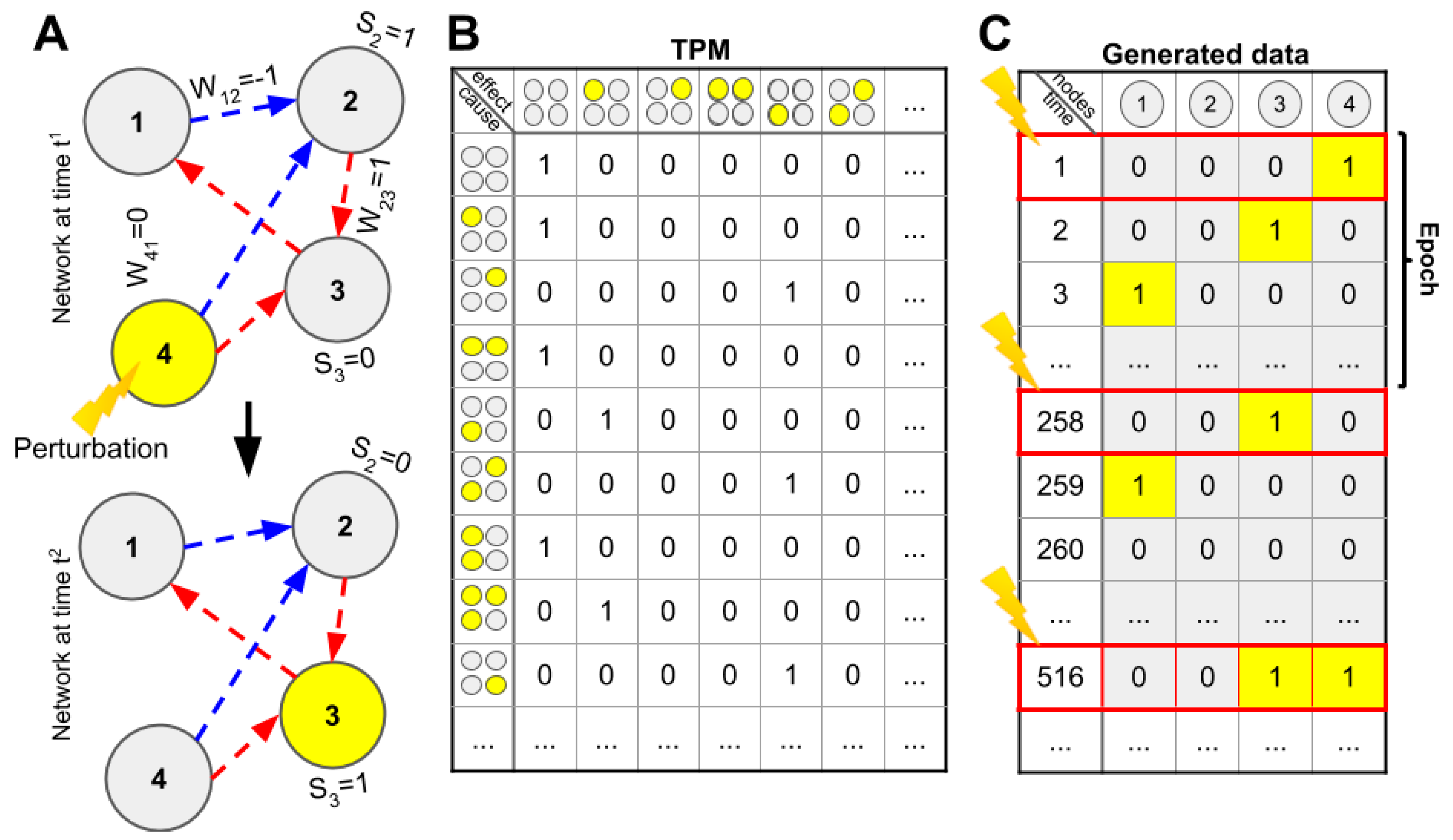
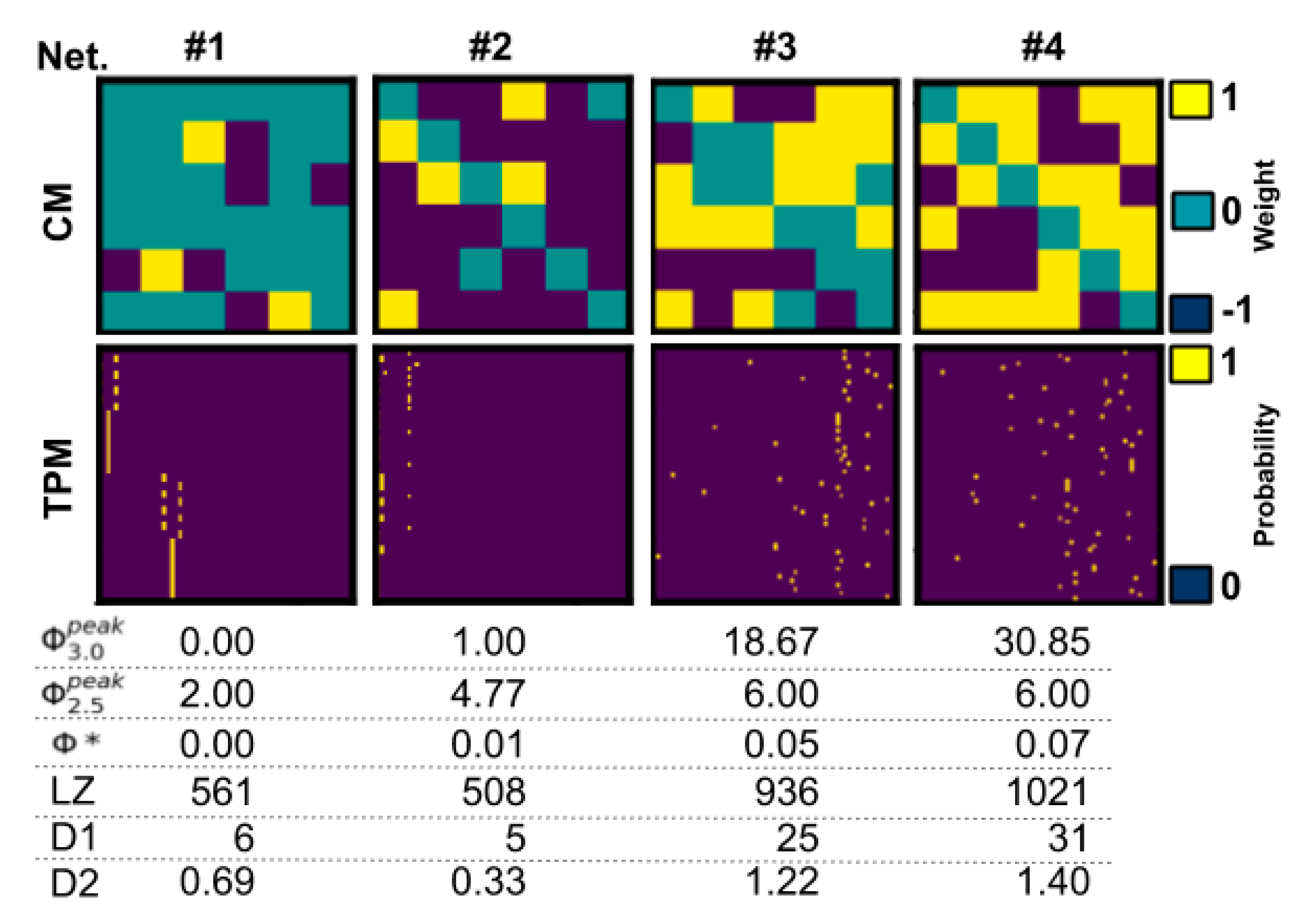
We randomly generated a population of small networks (three to six nodes) with linear threshold logic and both excitatory and inhibitory connections. We evaluated several approximations and heuristic measures of integrated information based on how well they corresponded to the Φ
3.0, according to the definition proposed by integrated information theory. The purpose of the work was to determine which methods, if any, might be used to test the theory. Since the accuracy of these methods cannot be evaluated for large networks of the size typically of interest for consciousness studies, we considered success in the current study—correspondence in small networks where Φ
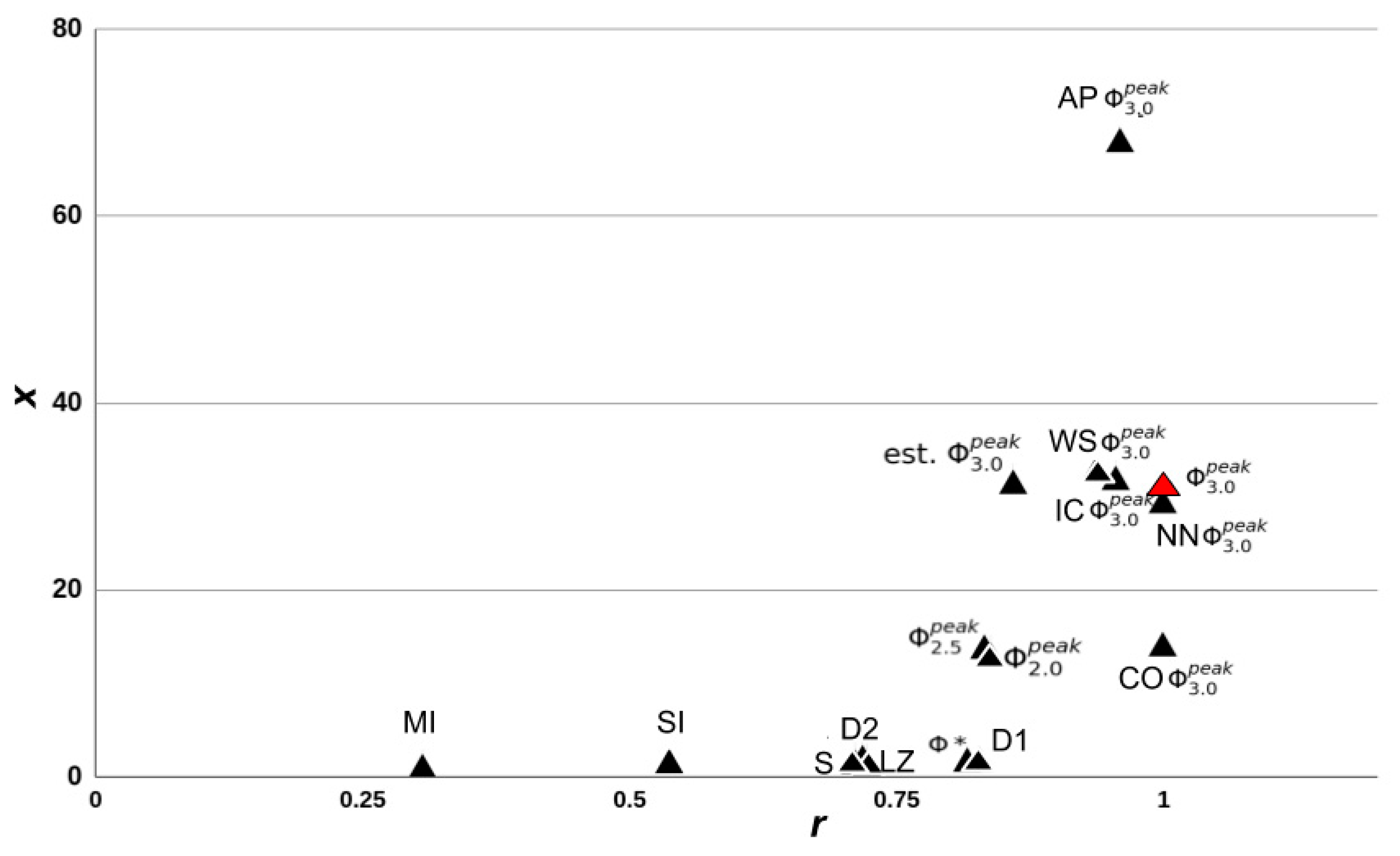
3.0 can be computed—as a minimal requirement for any such measure. In summary, we observed that the computational approximations were strong predictors (as defined in
Section 2.4) of both Φ
3.0 and
, while heuristic measures were only able to capture
. The approximation measures were still computationally intensive and required full knowledge of the systems TPM, meaning they only provided a marginal increase to the size of the systems that can be studied. Heuristic measures on the other hand, provided greater reductions in computation and knowledge requirements and can be applied to much larger systems, but only in a coarser state-independent manner.
4.1. Approximation Measures
The approximation measures we tested were developed by starting from the definition of Φ3.0 and then making assumptions to simplify the computations. Although they did not reduce computation enough to substantially increase the applicability of Φ3.0, their success provides a blueprint for future approximations. We discuss two aspects of Φ3.0 computation that should be investigated in future work: finding the MC of a network and finding the MIP of a mechanism–purview combination.
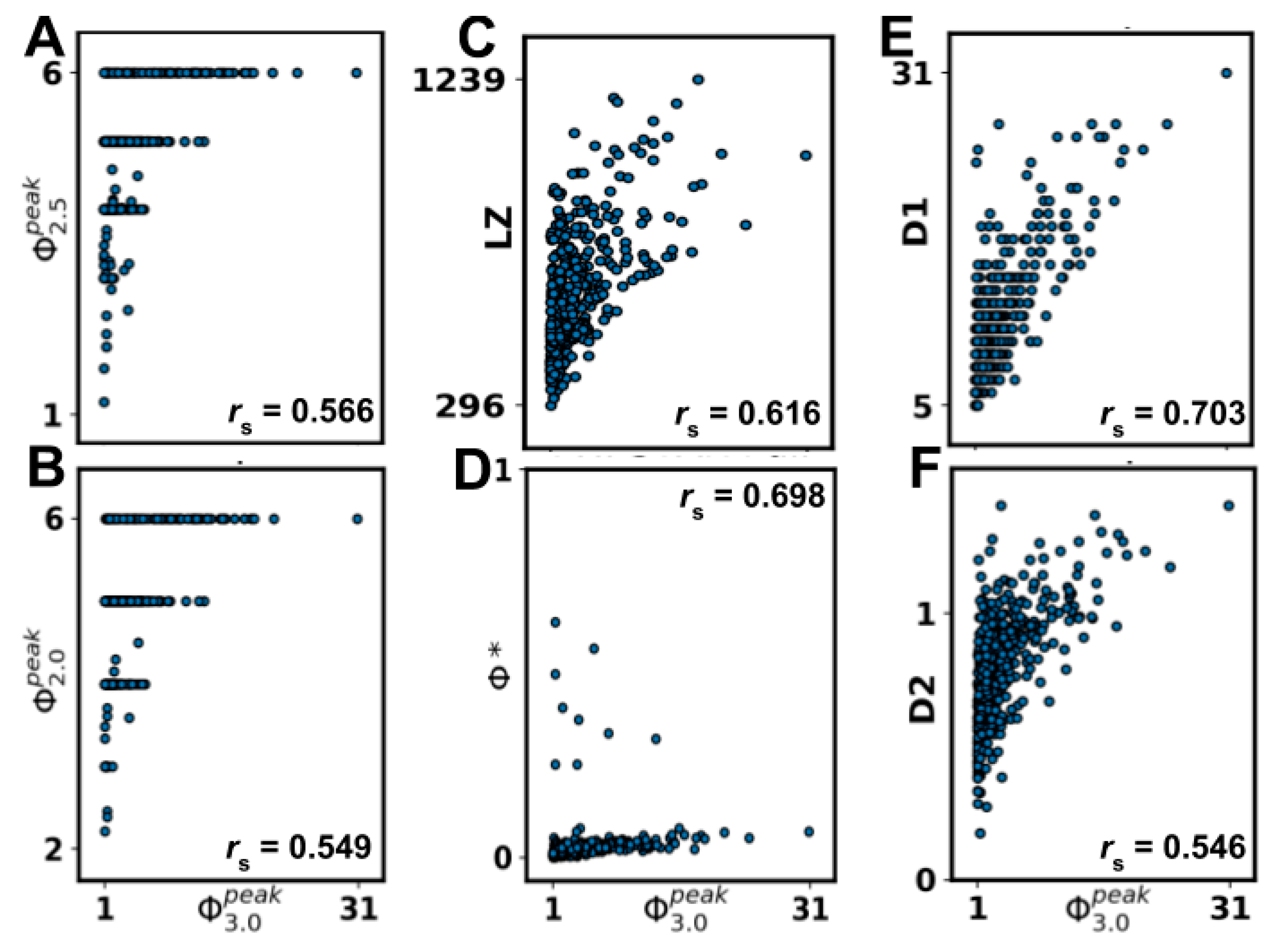
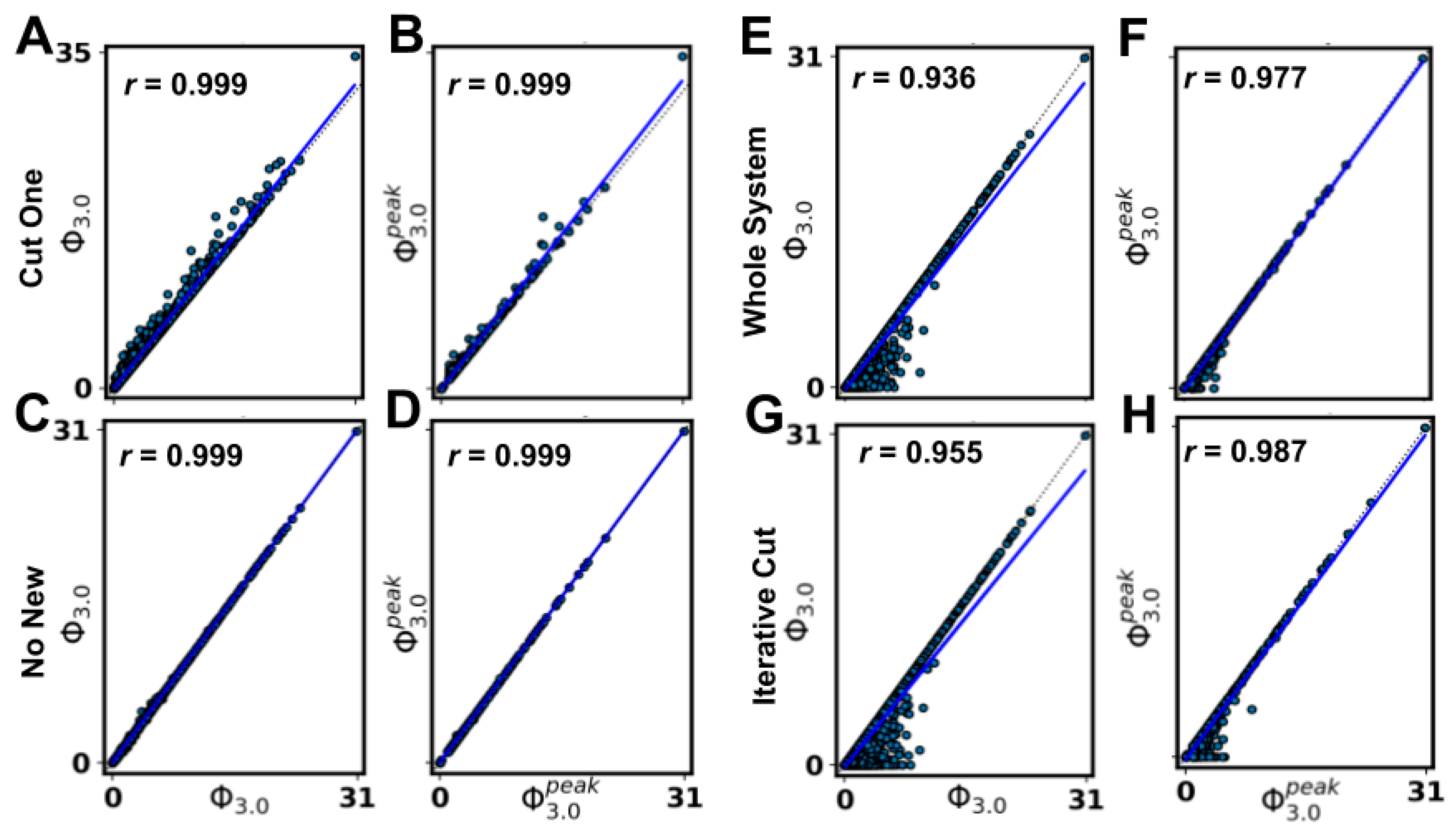
Regarding the estimates of the MC, the Φ
3.0 value of any subsystem within a network is a lower bound on the Φ
3.0 of the MC of that network. Moreover, the WS approximation (assuming the MC is the whole system) and the IC approximation (assuming the MC is the whole system after removing nodes without inputs or without outputs and inactive nodes) were both highly predictive of Φ
3.0 (and of
). Estimating the MC provided computational savings by eliminating the need to compute Φ
3.0 for all possible subsets of elements. However, the computational cost of computing Φ
3.0 for an individual subsystem still grows exponentially with the size of the subsystem. Any MC estimate close to the full size of the network will still require substantial computation. Therefore, finding a minimal MC that still accurately estimates Φ
3.0 would be most efficient for reducing the computational demands. While this may limit the usability of MC estimates (for highly integrated systems, the MC is more likely to be the whole system), such methods could be used to investigate questions regarding which part of a system is conscious (e.g., cortical location of consciousness [
27]).
Using the CO approximation (assuming that at the system level, the MIP results from partitioning a single node), we observed very strong correlations with Φ
3.0 (and
). Usually, the number of partitions to check grows exponentially with the number of nodes in the system, but with the CO approximation it grew linearly, providing a substantial computational savings. Extending the CO approximation (or some variant of it, see [
28,
29,
30]) from the system-level MIP to the mechanism-level MIPs could provide even greater computational savings. While only a single system-level MIP needs to be found to compute Φ
3.0, a mechanism-level MIP must be found for every mechanism–purview combination (the number of which grows exponentially with the system size).
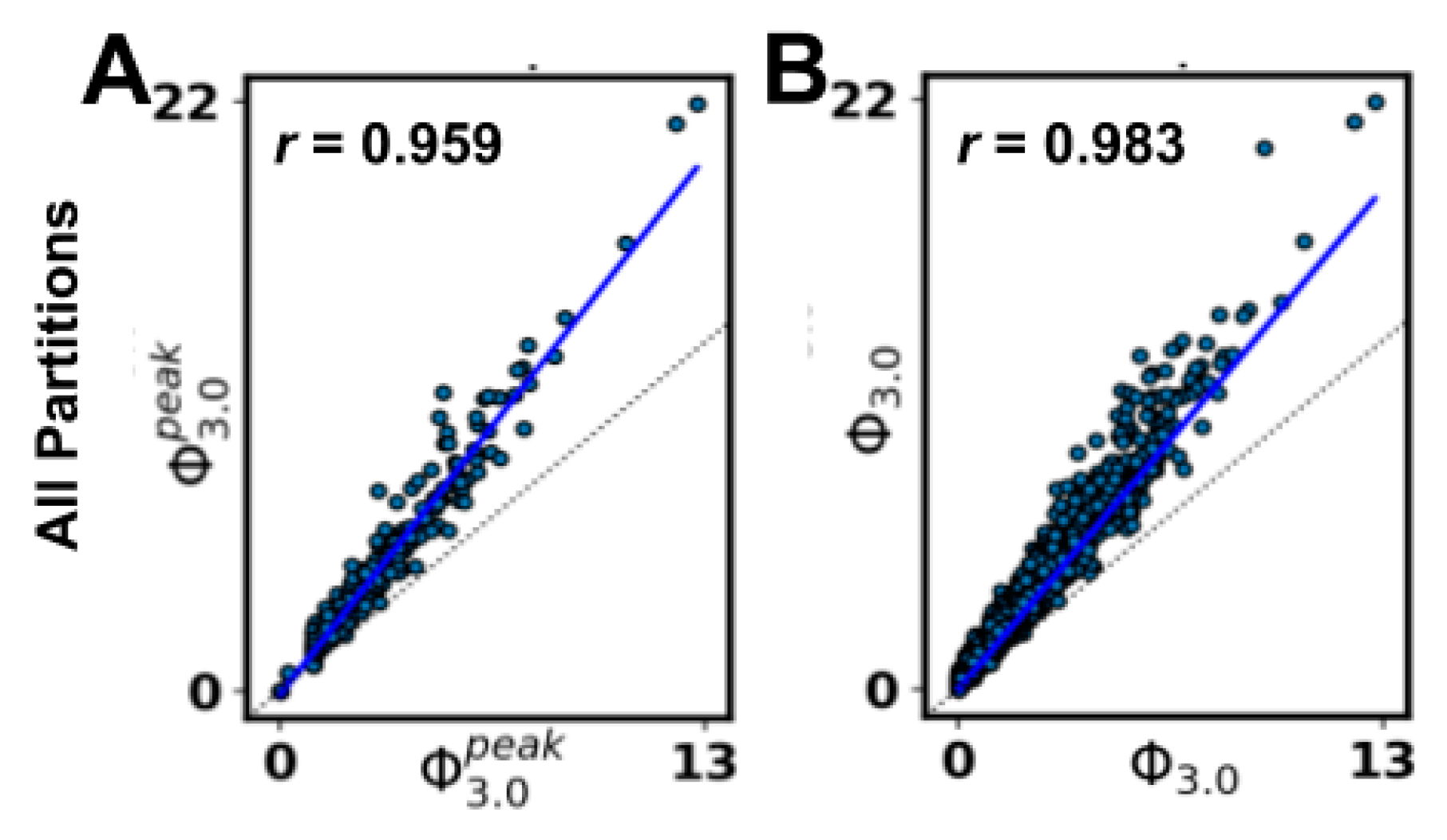
As an aside, the IIT
3.0 formalism only considers bipartitions of nodes when searching for the MIP, presumably on the basis that further partitioning a mechanism (or system) could cause additional information loss (and, thus, never be a
minimum information partition). To explore this, we employed an alternative definition of the MIP requiring a search over all partitions (AP, as opposed to bipartitions) for a subset of our networks. While we observed a very high correlation between all the partitions and bipartitions schemes (S.I.
R
2 = 0.966; S.D. Φ
3.0 R
2 = 0.921; see
Appendix A.7), the correspondence was not exact. Note that the definition of a partition used for the ‘all partitions’ option is slightly different than the definition for ‘bipartitions’, so the set of partitions in the AP option is not strictly a superset of the set of bipartitions (see PyPhi v1.0 and its documentation [
6] or
Appendix A.7 for more details). Despite this difference, we saw a very strong correlation between the methods, suggesting that different rules for permissible cuts could be considered as potential approximations.
4.2. Heuristic Measures
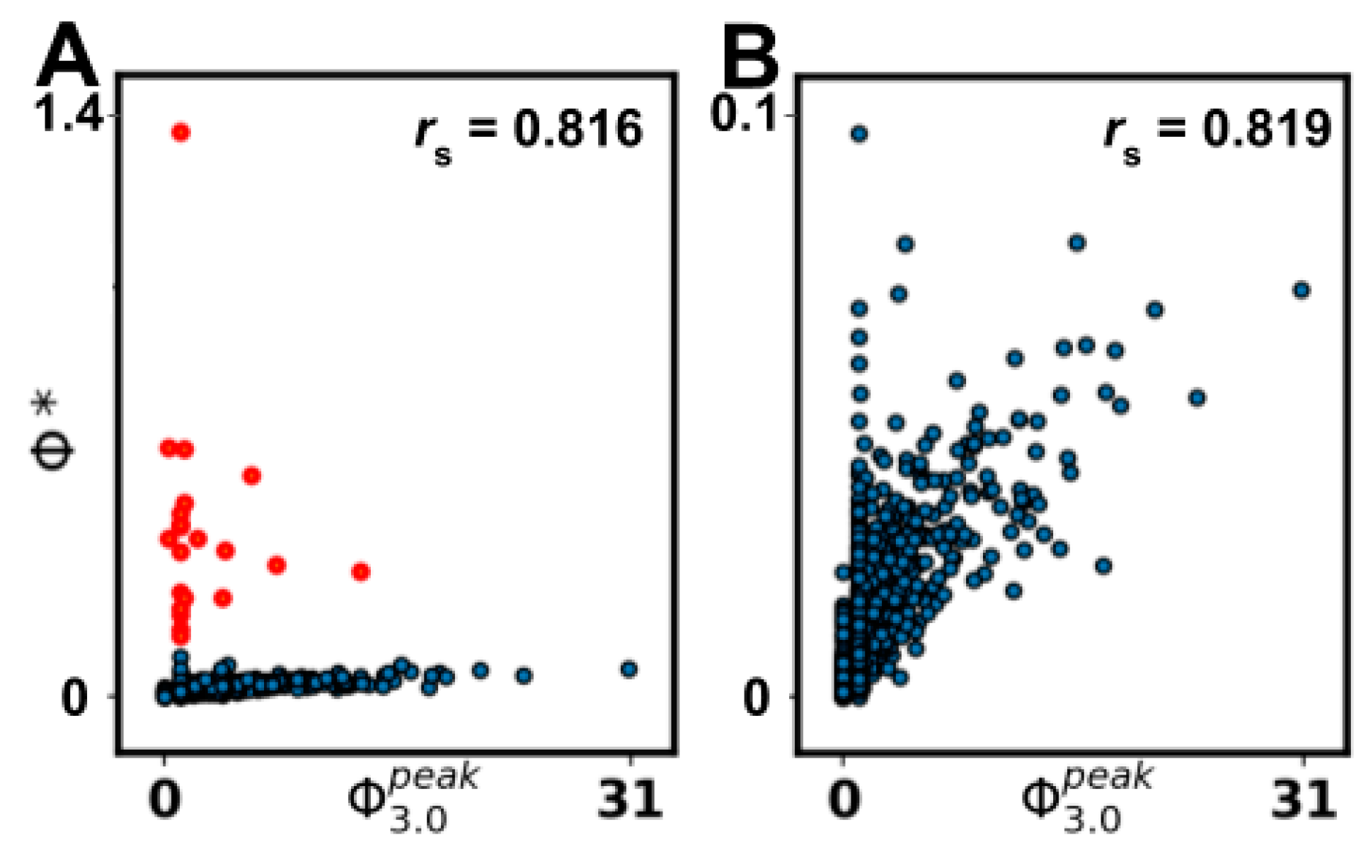
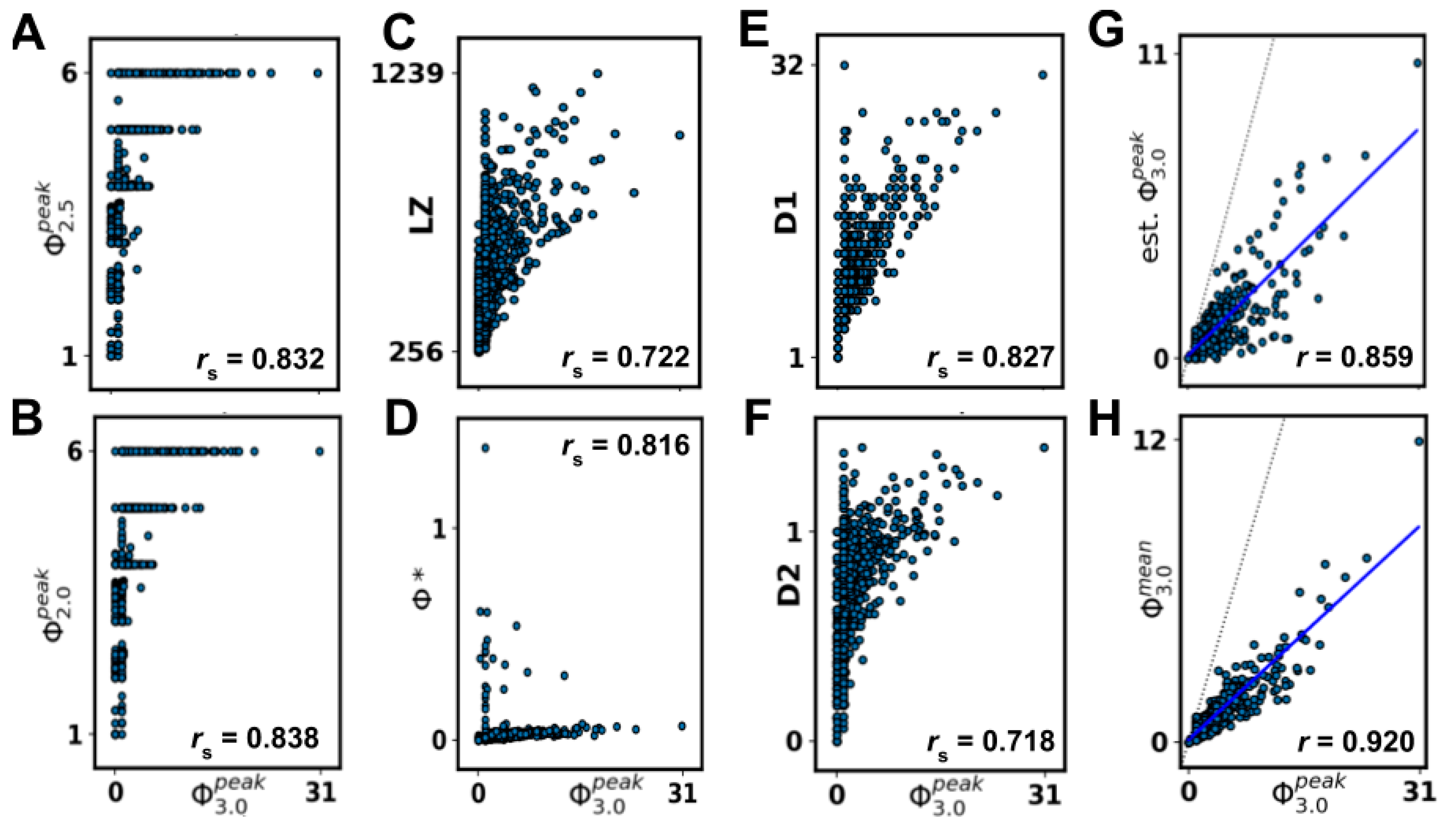
Although heuristic measures did not capture state-dependent Φ3.0, most were rank-correlated with state-independent . However, all heuristic measures were negatively impacted by removing networks with = 0‖1, indicating that reducible ( = 0) or circular ( = 1) networks can confound comparisons, as a majority of networks fall in this range. The heuristics that showed the strongest correlation after removal of = 0‖1 networks were measures of state differentiation (D1), integrated information (Φ*), and complexity (LZ). Together, these results suggest that D1, Φ*, and, to a lesser degree, LZ could be useful heuristics for at the group level, although unreliable at the individual level.
The heuristic D1 measures the number of states accessible by a system [
15], and the strong correlation we observed indicates that systems with a large repertoire of available states are also likely to have high
(assuming the systems are irreducible, i.e.,
> 0). This finding is interesting because clinical results also corroborate state differentiation as a factor in unconsciousness, where it has been observed that the state repertoire of the brain is reduced during anesthesia [
31]. While D1 is computationally tractable, it requires full knowledge of the system (i.e., a TPM with 2
2n bits of information), that the system is integrated, and that transitions are relatively noise-free. As such, unfortunately, D1 cannot be applied to larger artificial or biological systems of interest (such as the brain). The second measure that correlated well with
can also be seen to quantify state differentiation to some extent. LZ is a measure of signal complexity [
32], offering a concrete algorithm to quantify the number of unique patterns in a signal. While LZ has been used to differentiate conscious and unconscious states [
13,
33], it cannot distinguish between a noisy system and an integrated but complex one from observed data alone. Thus, some knowledge of the structure of the system in question is required for its interpretation. In addition, while LZ allows for analysis of real systems based on time-series data, it is also the measure that is the furthest removed from IIT (but see [
14]). It is highly dependent on the size of the input and is hard to interpret without normalization, which makes it difficult to compare systems of varying size. Finally, the measure Φ* is aimed at providing a tractable measure of integrated information using mismatched decoding and is applicable to time-series data, both discrete and continuous [
10]. Φ* is relatively fast to compute and can also be applied to continuous time series like EEG. However, while we observed a high correlation with
, a cluster of high Φ* values with corresponding low
values limited the interpretation. This suggests that Φ* might not be reliable for low
networks, but the analysis of larger networks is needed to draw a conclusion. While the results did not suggest a clear tractable alternative to Φ
3.0, several of the measures could be useful in statistical comparisons of groups of networks.
Prior work directly comparing Φ
3.0 with measures of differentiation (e.g., D1, LZ) reported lower correlations than those observed here for Φ
3.0 [
15]. There are at least three possible reasons for this: (a) the current work considered only linear nodes instead of nodes implementing general logic, (b) we compared against
and not
, and (c) we considered only the whole system as a basis for the heuristics, and not the subset of elements that constitutes the MC. For (b), we reran the analysis replacing
with
, producing negligible deviances in the results (see
Appendix A.5). For (c), the results of the WS (whole-system approximation) suggested that using the whole system to approximate the MC does not make a substantial difference (at least for networks of this size). This leaves (a), the types of network studied, as the likely reason for the differences in the strength of the correlations.
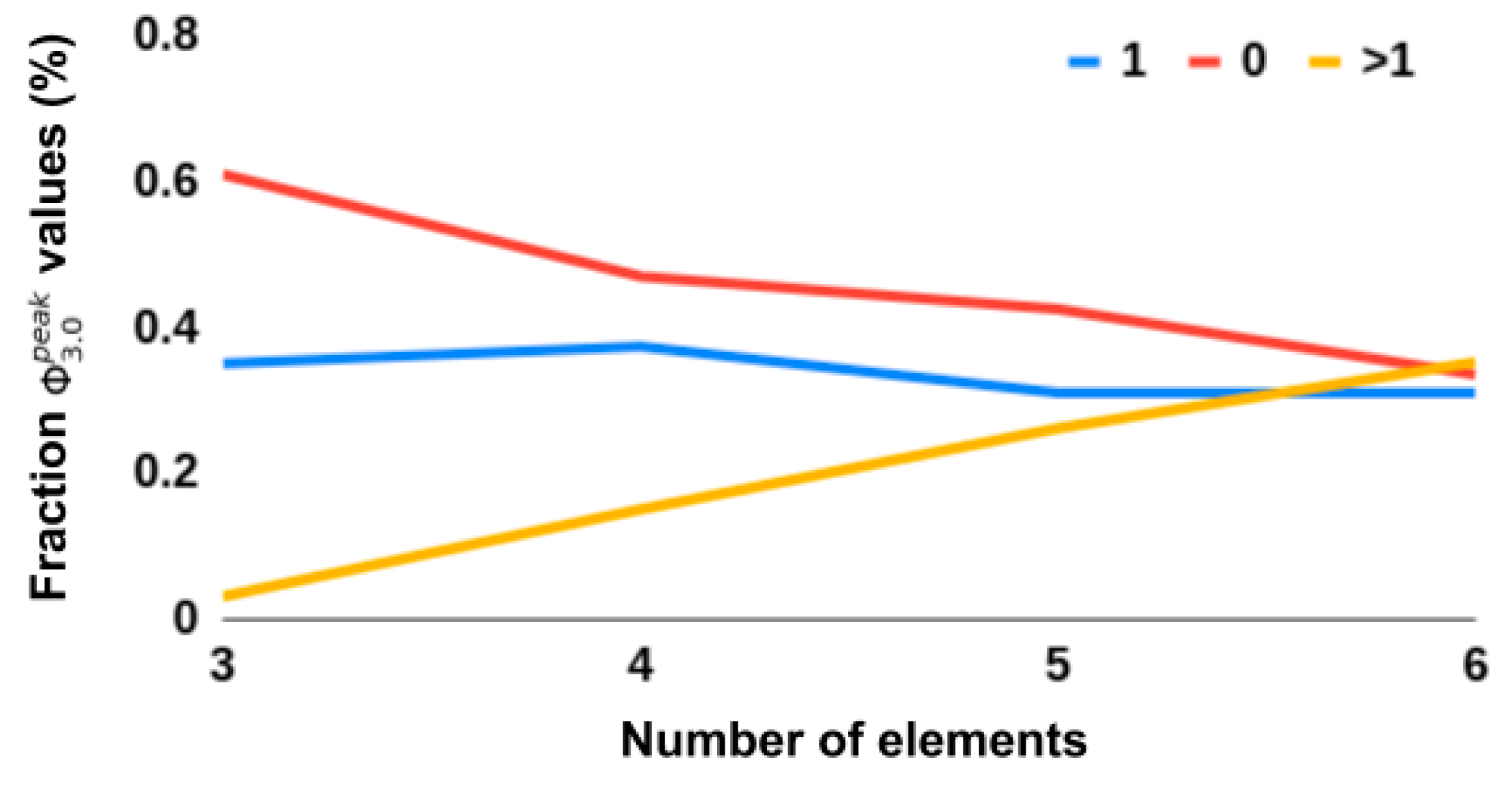
All heuristic measures’ rank correlations with
were negatively impacted by removing networks with
= 0‖1. This suggests that such networks are indeed relevant to consider and that finding a tractable measure that seperates
= 0 and
networks would be useful in its own right. Evident in the results was that all heuristics, except S, SI, and MI, showed an inverse predictability with
, i.e., low scores on a given heuristic corresponded to a low score on
but the higher the scores, the larger the spread of
(see
Figure 5). This could explain why the correlations drop when removing networks with
= 0‖1. This inverse predictability indicates two things. First, that the tested measures could be useful as negative markers, that is, low scores on measures can indicate low
networks, but not the converse. Secondly, it suggests
has dependencies on aspects of the underlying network that are not captured by any of the heuristic measures.
4.3. Future Outlook
Finally, we discuss several topics that we consider to be relevant for future work. First, there are several conceptual aspects of Φ
3.0 that are worth considering when developing future methods.
Composition: One of the major changes in IIT
3.0 from previous iterations of the theory is the role of all possible mechanisms (subsets of nodes) in the integration of the system as a whole. To our knowledge, all existing heuristic measures of integrated information are wholistic, always looking at the system as a whole. Future heuristics could take a compositional approach, combining integration values from subsets of measurements, rather than using all measurements at once.
State dependence: We report that heuristic measures do not correlate with state-dependent Φ
3.0 (see
Appendix A.6 for a perturbation-based approach), but a more accurate statement is that there are no (data-based) state-dependent heuristics; the nature of heuristic measures does not naturally accommodate state-dependence.
Cut directionality: Φ
3.0 uses unidirectional cuts, i.e., separating one directed connection, while other heuristics use bidirectional cuts (Φ
2.0, Φ
2.5) or even total cuts, separating system elements (Φ*, SI, MI). This leads, in effect, to an overestimation of integrated information, even for feedforward and ring-shaped networks (see
Figure 2). This could potentially partially explain the inverse predictability noted above.
Secondly, there are differences in the data used for the different measures. Only the approximations (and D1/D2/Φ
2.0/Φ
2.5) were calculated on the full TPM, the other heuristics were calculated on the basis of the generated time-series data. However, while deterministic networks such as those considered here can be fully described by both time-series data and TPM, given that the system was initialized to all possible states at least once, data from deterministic systems might be “insufficient” as a time series, as they often converge on a few cyclical states and, as such, need to be regularly perturbed. One solution to this could be to add noise to the system to avoid fixed points. In addition, as all heuristics considered here (except D1/D2/Φ
2.0/Φ
2.5) were dependent on the size of the generated time series (see
Appendix A.1), future work should control for the number of samples and discuss the impact of non-self-sustainable activity (convergence on a set of attractor states).
Thirdly, studies comparing measures of information integration, differentiation, and complexity, have also observed both qualitative and quantitative differences between the measures, even for simple systems [
19,
20]. Thus, there might be a large number of networks where the tested heuristics would correspond to Φ
3.0 if only certain prerequisites are met, such as a certain degree of irreducibility or small-worldness. One could, for example, imagine systems that have evolved to become highly integrated through interacting with an environment [
34]. Such evolved networks might have further qualities than being integrated, such as state differentiation that serves distinctive roles for the system, i.e., differences that make a behavioral difference to an organism, which is an important concept in IIT (although considered from an internal perspective in the theory) [
5]. While it is still an open question what Φ
3.0 captures of the underlying network above that of the heuristics considered here, investigation into structural and functional aspects that lead to systems with high Φ
3.0 could point to avenues for developing new measures inspired by IIT. Further, while estimates of the upper bound of Φ
3.0, given a system size, have been proposed (e.g., see [
15]), not much is known about the actual distribution of Φ
3.0 over different network types and topologies. Here, we explored a variety of network topologies, but the system properties, such as weight, noise, thresholds, element types, and so on, were omitted because of the limited scope of the paper. Investigating the relation between such network properties and Φ
3.0 would be an interesting research project moving forward. This could be useful as a testbed for future IIT-inspired measures and be informative about what kind of properties could be important for high Φ
3.0 in biological systems and the properties to aim for in artificial systems to produce “consciousness”.
Finally, there are several approximations and heuristics not included in the present study [
11,
12,
19,
28,
35,
36,
37,
38,
39,
40], some of which are specifically applicable to time-series data [
10,
11,
12,
19,
21,
28,
40]. Accordingly, the present work should not be considered an exhaustive exploration of Φ
3.0 correlates.