Studying Lexical Dynamics and Language Change via Generalized Entropies: The Problem of Sample Size
Abstract
:1. Introduction
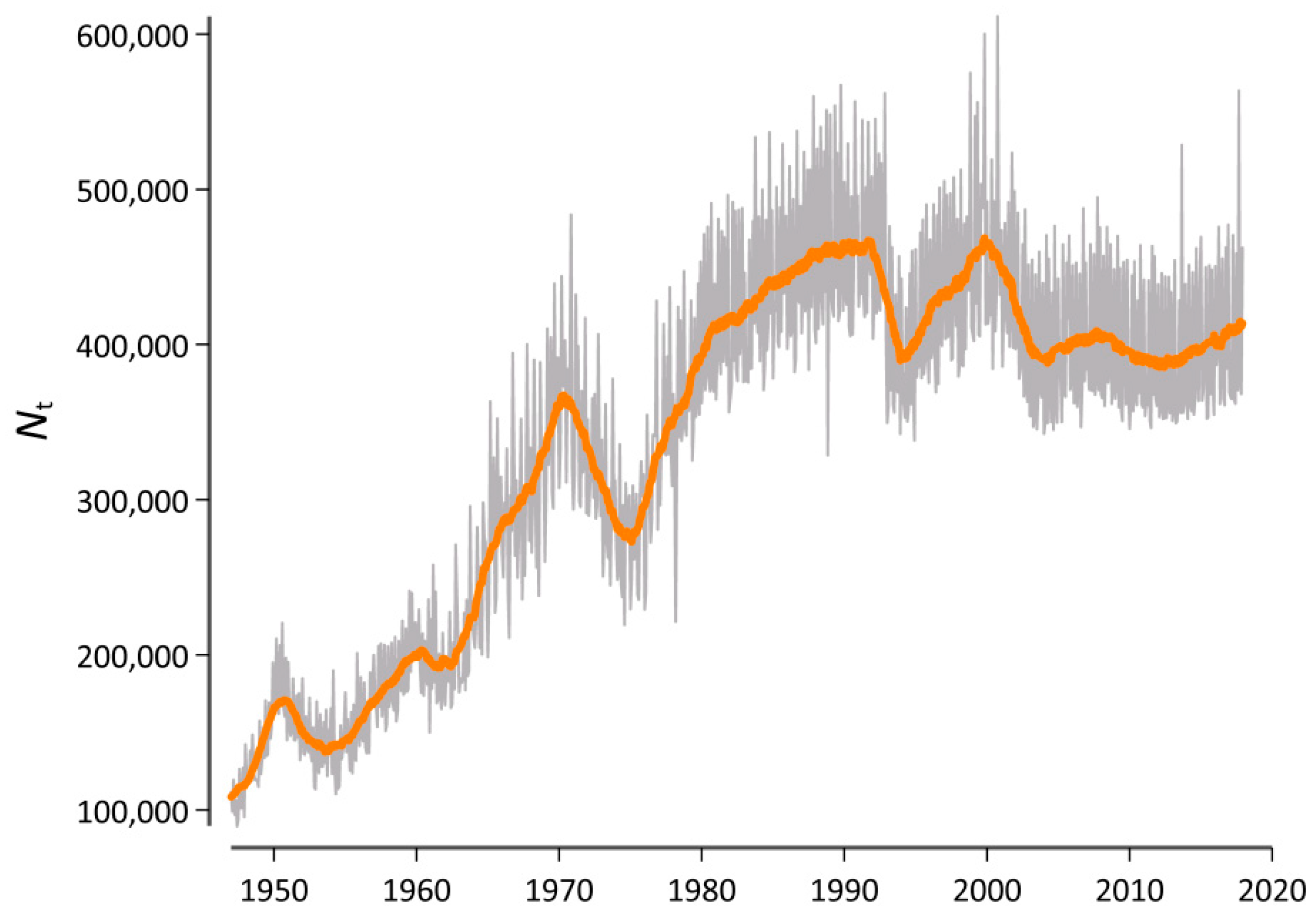
2. Materials and Methods
3. Results
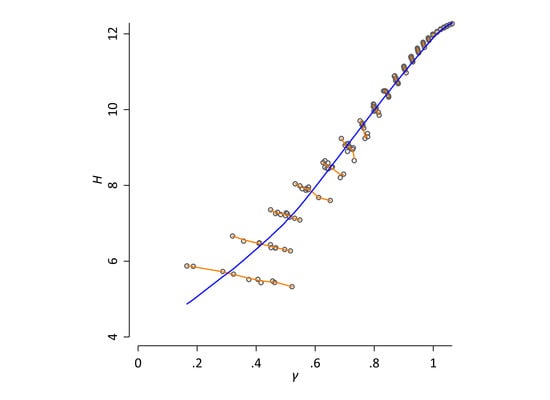
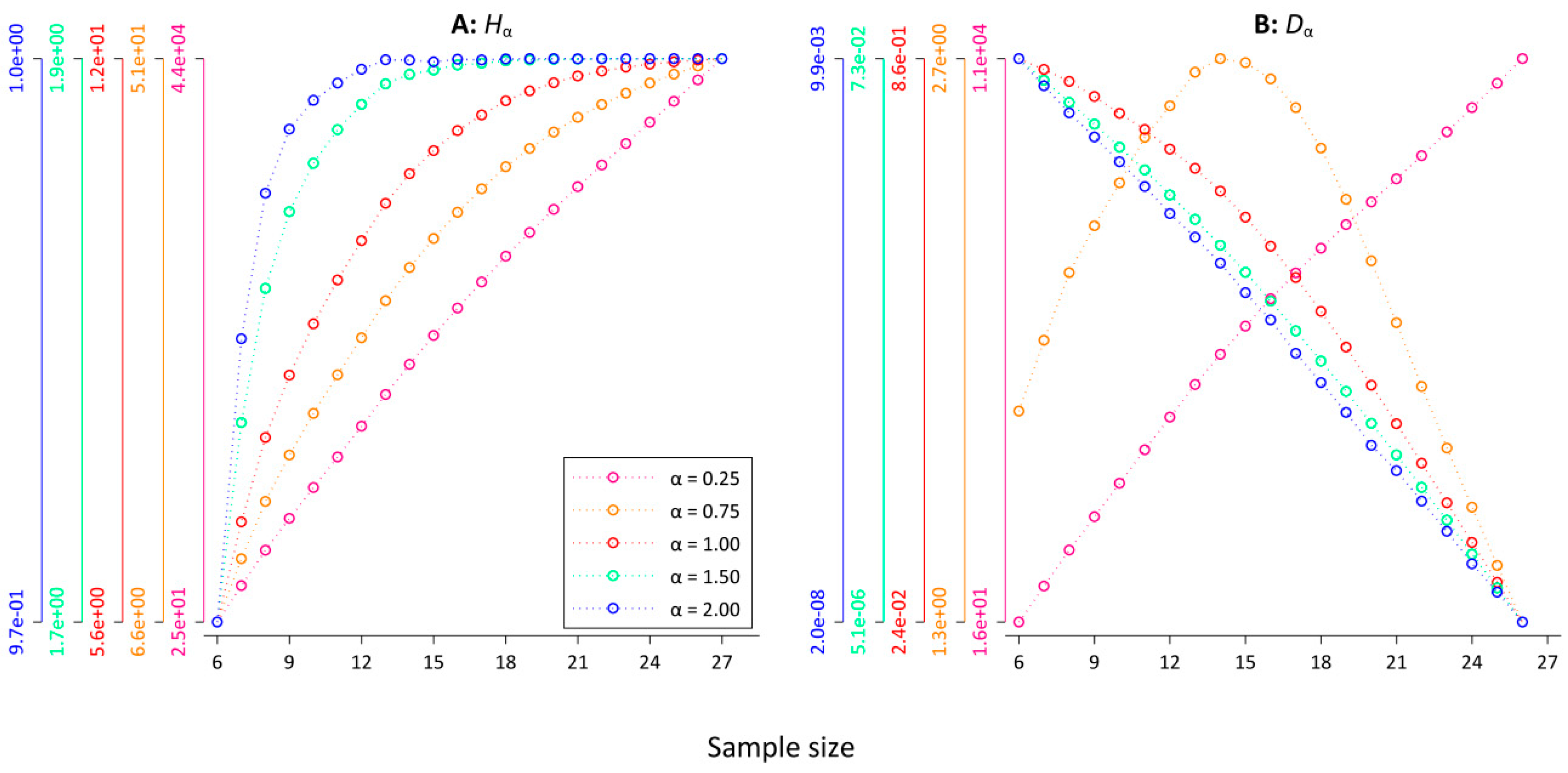
3.1. Entropy Hα
3.2. Divergence Dα
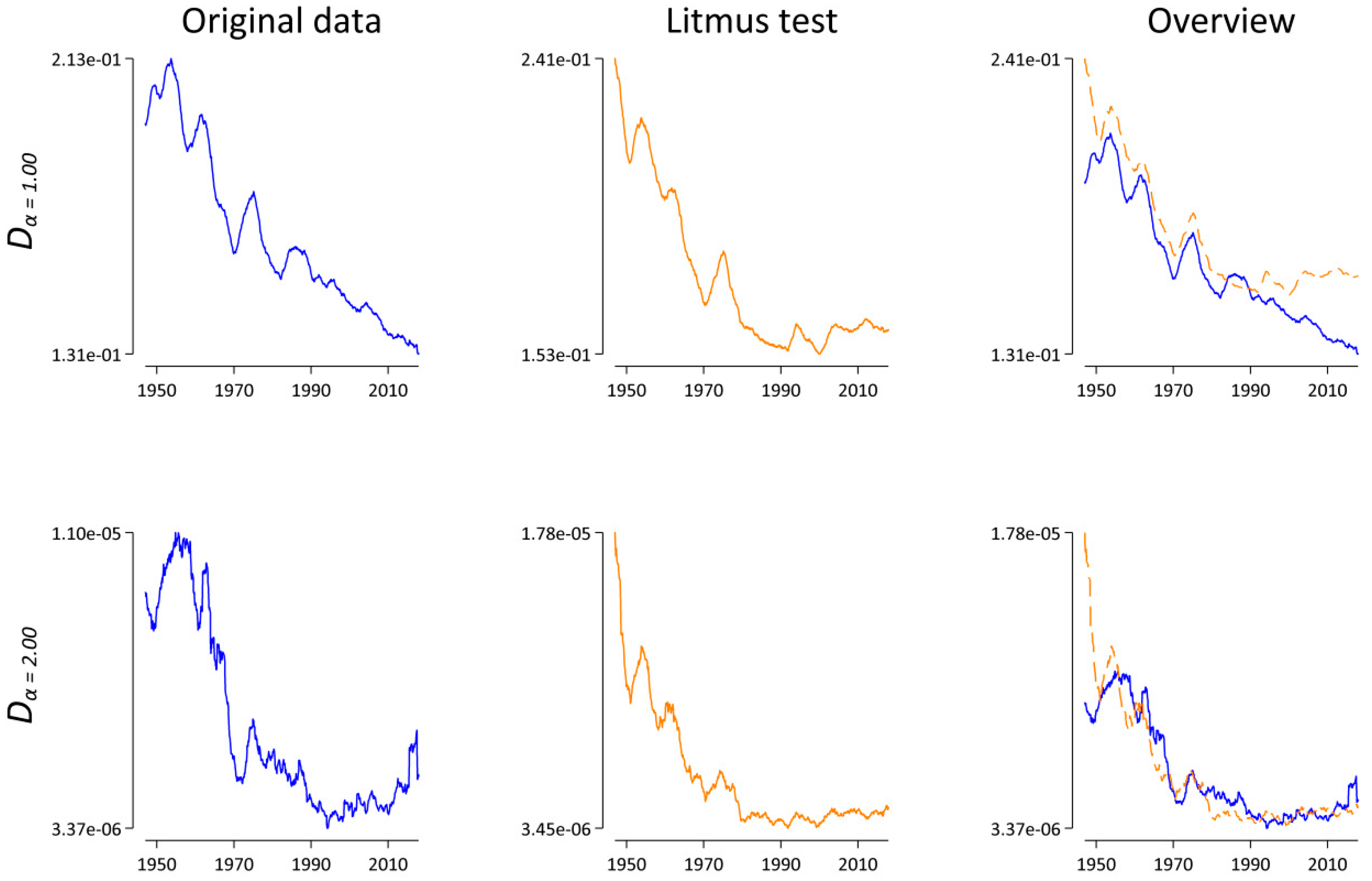
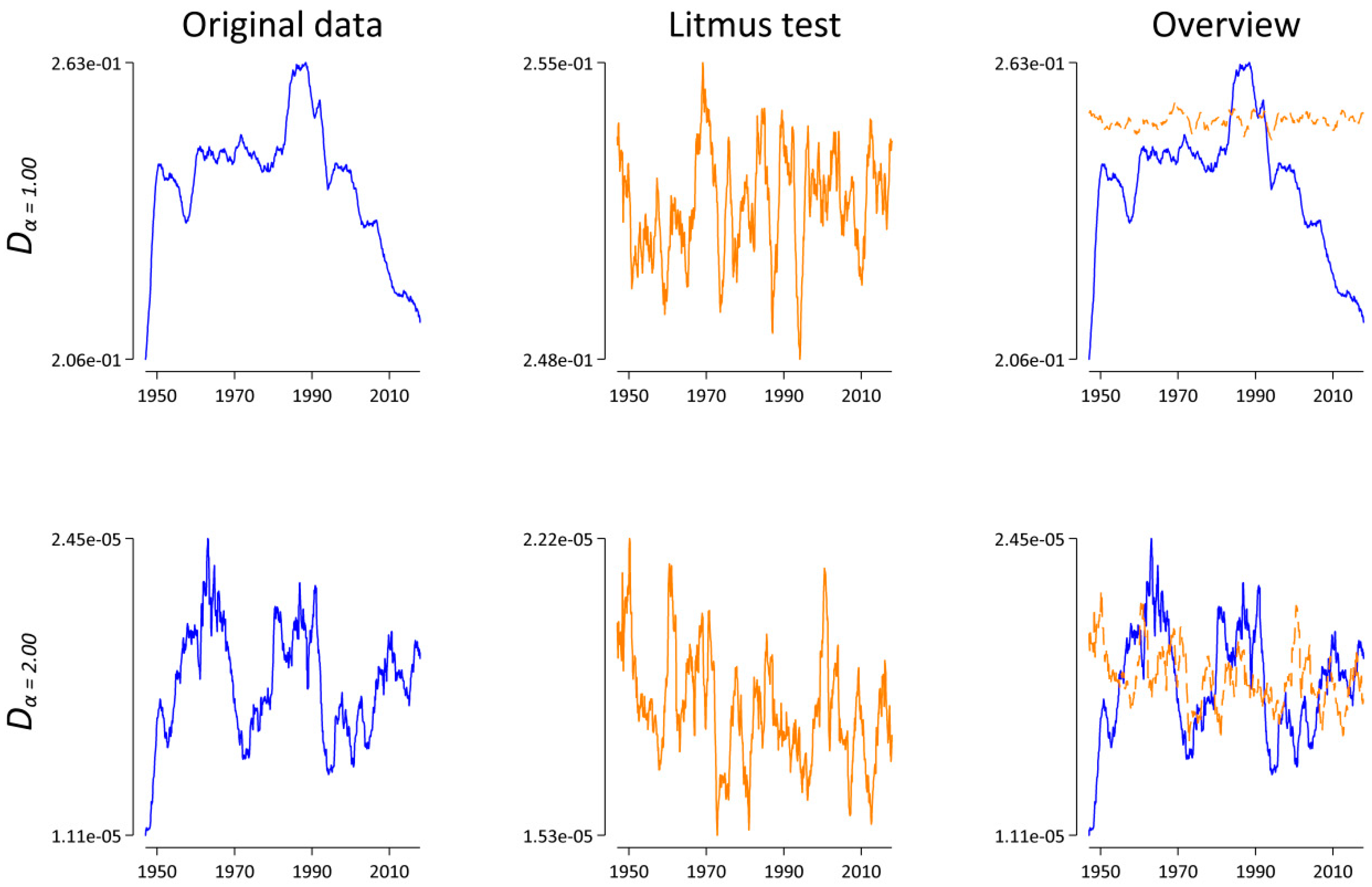
3.3. Case Study
4. Discussion
The sample size crucially determines a great many measures that have been proposed as characteristic text constants. However, the values of these measures change systematically as a function of the sample size. Similarly, the parameters of many models for word frequency distribution [sic!] are highly dependent on the sample size. This property sets lexical statistics apart from most other areas in statistics, where an increase in the sample size leads to enhanced accuracy and not to systematic changes in basic measures and parameters.… The second issue concerns the theoretical assumption […] that words occur randomly in texts. This assumption is an obvious simplification that, however, offers the possibility of deriving useful formulae for text characteristics. The crucial question, however, is to what extent this simplifying assumption affects the reliability of the formulae when applied to actual texts and corpora.(p.1)
- (i)
- In [12], an exploratory data-driven method was presented that extracts word-types from diachronic corpora that have undergone the most pronounced change in frequency of occurrence in a given period of time. To this end, a measure that is approximately equivalent to the Jensen–Shannon divergence is computed and period-to-period changes are calculated as in Section 3.3.
- (ii)
- In [15], the parameters of the Zipf–Mandelbrot law were used to quantify and visualize diachronic lexical, syntactical, and stylistic changes, as well as aspects of linguistic change for different languages.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Inclusion of Punctuation and Cardinal Numbers.
| Token Frequency | Number of Cases | Examples | α = 0.25 | α = 0.75 | α = 1.00 | α = 1.50 | α = 2.00 |
|---|---|---|---|---|---|---|---|
| 1 | 2,511,837 | paragraphenplantage penicillinhaltigen partei-patt | 48.51 | 8.94 | 2.16 | 0.00 | 0.00 |
| 2–10 | 1,148,295 | koberten optimis-datenbank gazprom-zentrale | 29.82 | 10.46 | 3.32 | 0.00 | 0.00 |
| 11–100 | 303,049 | dunkelgraue stirlings drollig | 13.26 | 13.57 | 6.54 | 0.02 | 0.00 |
| 101–1000 | 76,049 | abgemagert irakern aufzugehen | 5.86 | 18.56 | 13.50 | 0.15 | 0.00 |
| 1001–10,000 | 14,710 | nord- selbstbestimmung alexandra | 1.99 | 19.35 | 20.60 | 0.83 | 0.02 |
| 10,001-100,000 | 1966 | parteien banken entscheidungen | 0.46 | 13.24 | 19.57 | 2.86 | 0.22 |
| 100,001-1,000,000 | 183 | wurde würde dieses | 0.08 | 7.47 | 14.89 | 10.05 | 2.66 |
| 1,000,001 + | 33 | auf wie , | 0.03 | 8.40 | 19.42 | 86.09 | 97.09 |
| 4,056,122 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 |
| Minimum Sample Size | Number of Datapoints | α = 0.25 | α = 0.75 | α = 1.00 | α = 1.50 | α = 2.00 |
|---|---|---|---|---|---|---|
| 26 | 23 | 1.00 * | 1.00 * | 1.00 * | 0.99 * | 0.49 |
| 27 | 22 | 1.00 * | 1.00 * | 1.00 * | 0.99 * | 0.41 |
| 28 | 21 | 1.00 * | 1.00 * | 1.00 * | 0.99 * | 0.32 |
| 29 | 20 | 1.00 * | 1.00 * | 1.00 * | 0.99 * | 0.22 |
| 210 | 19 | 1.00 * | 1.00 * | 1.00 * | 0.99 * | 0.09 |
| 211 | 18 | 1.00 * | 1.00 * | 1.00 * | 0.99 * | −0.08 |
| 212 | 17 | 1.00 * | 1.00 * | 1.00 * | 0.98 * | −0.28 |
| 213 | 16 | 1.00 * | 1.00 * | 1.00 * | 0.98 * | −0.53 |
| 214 | 15 | 1.00 * | 1.00 * | 1.00 * | 0.97 * | −0.50 |
| 215 | 14 | 1.00 * | 1.00 * | 1.00 * | 0.97 * | −0.45 |
| 216 | 13 | 1.00 * | 1.00 * | 1.00 * | 0.96 * | −0.81 |
| 217 | 12 | 1.00 * | 1.00 * | 1.00 * | 0.95 * | −0.76 |
| 218 | 11 | 1.00 * | 1.00 * | 1.00 * | 0.94 * | −0.71 |
| 219 | 10 | 1.00 * | 1.00 * | 1.00 * | 0.95 * | −0.61 |
| 220 | 9 | 1.00 * | 1.00 * | 1.00 * | 0.95 * | −0.47 |
| 221 | 8 | 1.00 * | 1.00 * | 1.00 * | 0.93 | −0.31 |
| 222 | 7 | 1.00 * | 1.00 * | 1.00 * | 0.89 | 0.04 |
| 223 | 6 | 1.00 * | 1.00 * | 1.00 * | 0.83 | 0.66 |
| 224 | 5 | 1.00 * | 1.00 * | 1.00 * | 1.00 * | 1.00 * |
| Minimum Sample Size | Number of Datapoints | α = 0.25 | α = 0.75 | α = 1.00 | α = 1.50 | α = 2.00 |
|---|---|---|---|---|---|---|
| 26 | 22 | 1.00 * | −0.51 | −1.00 * | −1.00 * | −1.00 * |
| 27 | 21 | 1.00 * | −0.59 | −1.00 * | −1.00 * | −1.00 * |
| 28 | 20 | 1.00 * | −0.68 * | −1.00 * | −1.00 * | −1.00 * |
| 29 | 19 | 1.00 * | −0.76 * | −1.00 * | −1.00 * | −1.00 * |
| 210 | 18 | 1.00 * | −0.84 * | −1.00 * | −1.00 * | −1.00 * |
| 211 | 17 | 1.00 * | −0.89 * | −1.00 * | −1.00 * | −1.00 * |
| 212 | 16 | 1.00 * | −0.94 * | −1.00 * | −1.00 * | −1.00 * |
| 213 | 15 | 1.00 * | −0.97 * | −1.00 * | −1.00 * | −1.00 * |
| 214 | 14 | 1.00 * | −1.00 * | −1.00 * | −1.00 * | −1.00 * |
| 215 | 13 | 1.00 * | −1.00 * | −1.00 * | −1.00 * | −1.00 * |
| 216 | 12 | 1.00 * | −1.00 * | −1.00 * | −1.00 * | −1.00 * |
| 217 | 11 | 1.00 * | −1.00 * | −1.00 * | −1.00 * | −1.00 * |
| 218 | 10 | 1.00 * | −1.00 * | −1.00 * | −1.00 * | −1.00 * |
| 219 | 9 | 1.00 * | −1.00 * | −1.00 * | −1.00 * | −1.00 * |
| 220 | 8 | 1.00 * | −1.00 * | −1.00 * | −1.00 * | −1.00 * |
| 221 | 7 | 1.00 * | −1.00 * | −1.00 * | −1.00 * | −1.00 * |
| 222 | 6 | 1.00 * | −1.00 * | −1.00 * | −1.00 * | −1.00 * |
| 223 | 5 | 1.00 * | −1.00 * | −1.00 * | −1.00 * | −1.00 * |
| 224 | 4 | 1.00 * | −1.00 * | −1.00 * | −1.00 * | −1.00 * |
| Row | Scenario | α | Number of Cases | Original Data | Litmus Test |
|---|---|---|---|---|---|
| 1 | Original | 1.00 | 851 | −0.77 * | −0.91 * |
| 2.00 | 851 | −0.63 * | −0.70 * | ||
| 2 | Natural weights | 1.00 | 851 | −0.77 * | −0.91 * |
| 2.00 | 851 | −0.63 * | −0.70 * | ||
| 3 | Yearly data | 1.00 | 70 | −0.74 * | −0.98 * |
| 2.00 | 70 | −0.39 | −0.83 * | ||
| 4 | Random draw | 1.00 | 851 | −0.29 * | −0.69 * |
| 2.00 | 851 | −0.45 * | −0.56 * | ||
| 5 | Cut-off | 1.00 | 851 | 0.07 | 0.05 |
| 2.00 | 851 | 0.11 | −0.07 |
Appendix B. Replication of Table 2 for a Different Formulation of Generalized Entropy.
| Minimum Sample Size | Number of Datapoints | α = 0.25 | α = 0.75 | α = 1.00 | α = 1.50 | α = 2.00 |
|---|---|---|---|---|---|---|
| 26 | 22 | 1.00 * | 1.00 * | 1.00 * | 1.00 * | 0.92 * |
| 27 | 21 | 1.00 * | 1.00 * | 1.00 * | 1.00 * | 0.90 * |
| 28 | 20 | 1.00 * | 1.00 * | 1.00 * | 1.00 * | 0.89 * |
| 29 | 19 | 1.00 * | 1.00 * | 1.00 * | 1.00 * | 0.87 * |
| 210 | 18 | 1.00 * | 1.00 * | 1.00 * | 1.00 * | 0.85 * |
| 211 | 17 | 1.00 * | 1.00 * | 1.00 * | 1.00 * | 0.82 * |
| 212 | 16 | 1.00 * | 1.00 * | 1.00 * | 1.00 * | 0.78 |
| 213 | 15 | 1.00 * | 1.00 * | 1.00 * | 1.00 * | 0.73 |
| 214 | 14 | 1.00 * | 1.00 * | 1.00 * | 1.00 * | 0.70 |
| 215 | 13 | 1.00 * | 1.00 * | 1.00 * | 0.99 * | 0.65 |
| 216 | 12 | 1.00 * | 1.00 * | 1.00 * | 0.99 * | 0.55 |
| 217 | 11 | 1.00 * | 1.00 * | 1.00 * | 0.99 * | 0.43 |
| 218 | 10 | 1.00 * | 1.00 * | 1.00 * | 0.99 * | 0.24 |
| 219 | 9 | 1.00 * | 1.00 * | 1.00 * | 0.98 * | −0.05 |
| 220 | 8 | 1.00 * | 1.00 * | 1.00 * | 0.98 * | −0.17 |
| 221 | 7 | 1.00 * | 1.00 * | 1.00 * | 0.96 * | 0.25 |
| 222 | 6 | 1.00 * | 1.00 * | 1.00 * | 0.94 | −0.20 |
| 223 | 5 | 1.00 * | 1.00 * | 1.00 * | 0.90 | 0.10 |
| 224 | 4 | 1.00 * | 1.00 * | 1.00 * | 0.80 | −0.80 |
References
- Manning, C.D.; Schütze, H. Foundations of Statistical Natural Language Processing; MIT Press: Cambridge, MA, USA, 1999; ISBN 978-0-262-13360-9. [Google Scholar]
- Jurafsky, D.; Martin, J.H. Speech and Language Processing: An Introduction to Natural Language Processing, Computational Linguistics, and Speech Recognition; Pearson Education (US): Upper Saddle River, NJ, USA, 2009; ISBN 978-0-13-504196-3. [Google Scholar]
- Adami, C. What is information? Philos. Trans. R. Soc. A 2016, 374, 20150230. [Google Scholar] [CrossRef] [PubMed]
- Cover, T.M.; Thomas, J.A. Elements of information theory, 2nd ed.; Wiley-Interscience: Hoboken, NJ, USA, 2006; ISBN 978-0-471-24195-9. [Google Scholar]
- Bentz, C.; Alikaniotis, D.; Cysouw, M.; Ferrer-i-Cancho, R. The Entropy of Words—Learnability and Expressivity across More than 1000 Languages. Entropy 2017, 19, 275. [Google Scholar] [CrossRef]
- Lin, J. Divergence measures based on the Shannon entropy. IEEE Trans. Inf. Theory 1991, 37, 145–151. [Google Scholar] [CrossRef]
- Endres, D.M.; Schindelin, J.E. A new metric for probability distributions. IEEE Trans. Inf. Theory 2003, 49, 1858–1860. [Google Scholar] [CrossRef]
- Hughes, J.M.; Foti, N.J.; Krakauer, D.C.; Rockmore, D.N. Quantitative patterns of stylistic influence in the evolution of literature. Proc. Natl. Acad. Sci. USA 2012, 109, 7682–7686. [Google Scholar] [CrossRef] [PubMed]
- Klingenstein, S.; Hitchcock, T.; DeDeo, S. The civilizing process in London’s Old Bailey. Proc. Natl. Acad. Sci. USA 2014, 111, 9419–9424. [Google Scholar] [CrossRef]
- DeDeo, S.; Hawkins, R.; Klingenstein, S.; Hitchcock, T. Bootstrap Methods for the Empirical Study of Decision-Making and Information Flows in Social Systems. Entropy 2013, 15, 2246–2276. [Google Scholar] [CrossRef]
- Bochkarev, V.; Solovyev, V.; Wichmann, S. Universals versus historical contingencies in lexical evolution. J. R. Soc. Interface 2014, 11, 20140841. [Google Scholar] [CrossRef] [PubMed]
- Koplenig, A. A Data-Driven Method to Identify (Correlated) Changes in Chronological Corpora. J. Quant. Linguist. 2017, 24, 289–318. [Google Scholar] [CrossRef]
- Pechenick, E.A.; Danforth, C.M.; Dodds, P.S. Characterizing the Google Books corpus: Strong limits to inferences of socio-cultural and linguistic evolution. PLOS ONE 2015. [Google Scholar] [CrossRef]
- Zipf, G.K. The Psycho-biology of Language. An Introduction to Dynamic Philology; Houghton Mifflin Company: Boston, MA, USA, 1935. [Google Scholar]
- Koplenig, A. Using the parameters of the Zipf–Mandelbrot law to measure diachronic lexical, syntactical and stylistic changes–a large-scale corpus analysis. Corpus Linguist. Linguist. Theory 2018, 14, 1–34. [Google Scholar] [CrossRef]
- Baayen, R.H. Word Frequency Distributions; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2001. [Google Scholar]
- Tweedie, F.J.; Baayen, R.H. How Variable May a Constant be? Measures of Lexical Richness in Perspective. Comput. Hum. 1998, 32, 323–352. [Google Scholar] [CrossRef]
- Simpson, E.H. The Interpretation of Interaction in Contingency Tables. J. R. Stat. Soc. Series B 1951, 13, 238–241. [Google Scholar] [CrossRef]
- Gerlach, M.; Altmann, E.G. Stochastic Model for the Vocabulary Growth in Natural Languages. Phys. Rev. X 2013, 3, 021006. [Google Scholar] [CrossRef]
- Briët, J.; Harremoës, P. Properties of classical and quantum Jensen-Shannon divergence. Phys. Rev. A 2009, 79, 052311. [Google Scholar] [CrossRef]
- Altmann, E.G.; Dias, L.; Gerlach, M. Generalized entropies and the similarity of texts. J. Stat. Mech. Theory Exp. 2017, 2017, 014002. [Google Scholar] [CrossRef]
- Gerlach, M.; Font-Clos, F.; Altmann, E.G. Similarity of Symbol Frequency Distributions with Heavy Tails. Phys. Rev. X 2016, 6, 021009. [Google Scholar] [CrossRef]
- Tanaka-Ishii, K.; Aihara, S. Computational Constancy Measures of Texts—Yule’s K and Rényi’s Entropy. Comput. Linguist. 2015, 41, 481–502. [Google Scholar] [CrossRef]
- Rényi, A. On Measures of Entropy and Information. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Volume 1: Contributions to the Theory of Statistics, Berkeley, CA, USA, 20 June–30 July 1960; University of California Press: Berkeley, CA, USA, 1961; pp. 547–561. [Google Scholar]
- He, Y.; Hamza, A.B.; Krim, H. A generalized divergence measure for robust image registration. IEEE Trans. Signal Process. 2003, 51, 1211–1220. [Google Scholar]
- Schmid, H. Probabilistic Part-of-Speech Tagging Using Decision Trees. In Proceedings of the International Conference on New Methods in Language Processing, Manchester, UK, 1994; pp. 44–49. [Google Scholar]
- Köhler, R.; Galle, M. Dynamic aspects of text characteristics. In Quantitative Text Analysis; Hřebíček, L., Altmann, G., Eds.; Quantitative linguistics; WVT Wissenschaftlicher Verlag Trier: Trier, Germany, 1993; pp. 46–53. ISBN 978-3-88476-080-2. [Google Scholar]
- Popescu, I.-I.; Altmann, G. Word Frequency Studies; Quantitative linguistics; Mouton de Gruyter: Berlin, Germany, 2009; ISBN 978-3-11-021852-7. [Google Scholar]
- Wimmer, G.; Altmann, G. Review Article: On Vocabulary Richness. J. Quant. Linguist. 1999, 6, 1–9. [Google Scholar] [CrossRef]
- Michel, J.-B.; Shen, Y.K.; Aiden, A.P.; Verses, A.; Gray, M.K.; Google Books Team; Pickett, J.P.; Hoiberg, D.; Clancy, D.; Norvig, P.; et al. Quantitative Analysis of Culture Using Millions of Digitized Books. Science 2010, 331, 176–182. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.; Michel, J.-B.; Aiden, L.E.; Orwant, J.; Brockmann, W.; Petrov, S. Syntactic Annotations for the Google Books Ngram Corpus. In Proceedings of the 50th Annual Meeting of the Association for Computational Linguistics, Jeju Island, Korea, 8–14 July 2012; pp. 169–174. [Google Scholar]
- Kupietz, M.; Lüngen, H.; Kamocki, P.; Witt, A. The German Reference Corpus DeReKo: New Developments–New Opportunities. In Proceedings of the Eleventh International Conference on Language Resources and Evaluation (LREC 2018), Miyazaki, Japan, 7–12 May 2018; Choukri, K., Cieri, C., Declerck, T., Goggi, S., Hasida, K., Isahara, H., Maegaard, B., Mariani, J., Mazo, H., Moreno, A., et al., Eds.; European Language Resources Association (ELRA): Miyazaki, Japan, 2018. [Google Scholar]
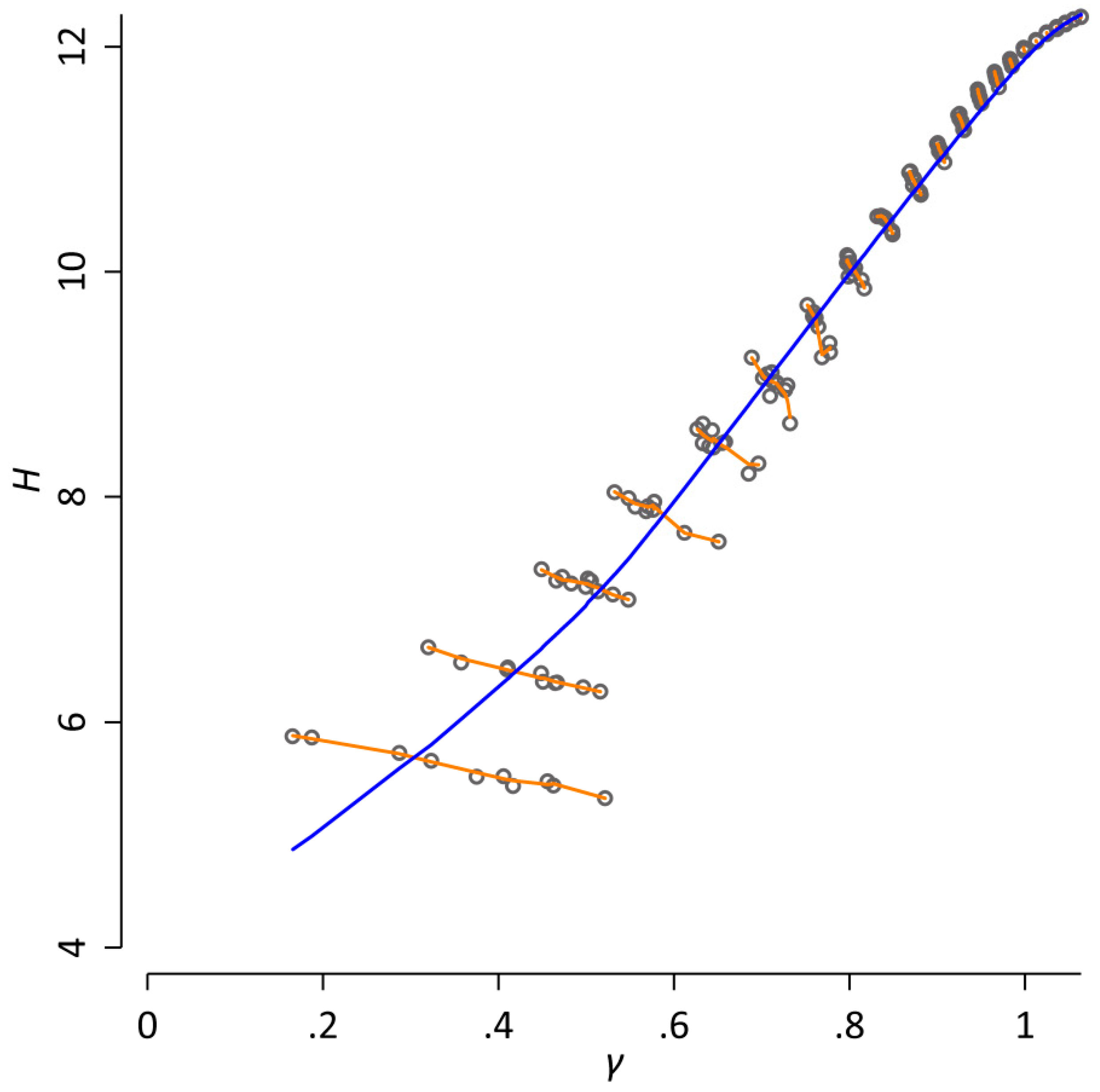
| Token Frequency | Number of Cases | Examples | α = 0.25 | α = 0.75 | α = 1.00 | α = 1.50 | α = 2.00 |
|---|---|---|---|---|---|---|---|
| 1 | 2,486,393 | koalitionsbündnisse nr.6/1962 bruckner-breitklang | 48.65 | 9.32 | 2.38 | 0.00 | 0.00 |
| 2–10 | 1,135,102 | geschlechterschulung unal wiedervereinigungs-prozedur | 29.86 | 10.89 | 3.65 | 0.01 | 0.00 |
| 11–100 | 296,573 | hotpants lánský planwirtschaftlichen | 13.16 | 14.03 | 7.13 | 0.04 | 0.00 |
| 101–1000 | 74,791 | wanda verbannte mitschnitt | 5.83 | 19.21 | 14.69 | 0.28 | 0.00 |
| 1001–10,000 | 14,388 | schüren ablesen vollmachten | 1.96 | 19.81 | 22.07 | 1.53 | 0.06 |
| 10,001–100,000 | 1871 | london sitzen beginnen | 0.44 | 13.38 | 20.68 | 5.31 | 0.64 |
| 100,001–1,000,000 | 173 | mark frau kaum | 0.07 | 7.38 | 15.21 | 17.83 | 7.12 |
| 1,000,001 + | 27 | es die er | 0.02 | 5.98 | 14.19 | 75.02 | 92.18 |
| 4,009,318 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 |
| Minimum Sample Size | Number of Datapoints | α = 0.25 | α = 0.75 | α = 1.00 | α = 1.50 | α = 2.00 |
|---|---|---|---|---|---|---|
| 26 | 22 | 1.00 * | 1.00 * | 1.00 * | 1.00 * | 0.92 * |
| 27 | 21 | 1.00 * | 1.00 * | 1.00 * | 1.00 * | 0.91 * |
| 28 | 20 | 1.00 * | 1.00 * | 1.00 * | 1.00 * | 0.89 * |
| 29 | 19 | 1.00 * | 1.00 * | 1.00 * | 1.00 * | 0.87 * |
| 210 | 18 | 1.00 * | 1.00 * | 1.00 * | 1.00 * | 0.85 * |
| 211 | 17 | 1.00 * | 1.00 * | 1.00 * | 1.00 * | 0.82 * |
| 212 | 16 | 1.00 * | 1.00 * | 1.00 * | 1.00 * | 0.79 * |
| 213 | 15 | 1.00 * | 1.00 * | 1.00 * | 1.00 * | 0.74 |
| 214 | 14 | 1.00 * | 1.00 * | 1.00 * | 1.00 * | 0.71 |
| 215 | 13 | 1.00 * | 1.00 * | 1.00 * | 0.99 * | 0.65 |
| 216 | 12 | 1.00 * | 1.00 * | 1.00 * | 0.99 * | 0.55 |
| 217 | 11 | 1.00 * | 1.00 * | 1.00 * | 0.99 * | 0.43 |
| 218 | 10 | 1.00 * | 1.00 * | 1.00 * | 0.99 * | 0.24 |
| 219 | 9 | 1.00 * | 1.00 * | 1.00 * | 0.98 * | −0.05 |
| 220 | 8 | 1.00 * | 1.00 * | 1.00 * | 0.98 * | −0.17 |
| 221 | 7 | 1.00 * | 1.00 * | 1.00 * | 0.96 * | 0.25 |
| 222 | 6 | 1.00 * | 1.00 * | 1.00 * | 0.94 | −0.20 |
| 223 | 5 | 1.00 * | 1.00 * | 1.00 * | 0.90 | 0.10 |
| 224 | 4 | 1.00 * | 1.00 * | 1.00 * | 0.80 | −0.80 |
| Minimum Sample Size | Number of Datapoints | α = 0.25 | α = 0.75 | α = 1.00 | α = 1.50 | α = 2.00 |
|---|---|---|---|---|---|---|
| 26 | 21 | 1.00 * | −0.42 | −1.00 * | −1.00 * | −1.00 * |
| 27 | 20 | 1.00 * | −0.54 | −1.00 * | −1.00 * | −1.00 * |
| 28 | 19 | 1.00 * | −0.64 | −1.00 * | −1.00 * | −1.00 * |
| 29 | 18 | 1.00 * | −0.74 | −1.00 * | −1.00 * | −1.00 * |
| 210 | 17 | 1.00 * | −0.83 * | −1.00 * | −1.00 * | −1.00 * |
| 211 | 16 | 1.00 * | −0.90 * | −1.00 * | −1.00 * | −1.00 * |
| 212 | 15 | 1.00 * | −0.95 * | −1.00 * | −1.00 * | −1.00 * |
| 213 | 14 | 1.00 * | −0.99 * | −1.00 * | −1.00 * | −1.00 * |
| 214 | 13 | 1.00 * | −1.00 * | −1.00 * | −1.00 * | −1.00 * |
| 215 | 12 | 1.00 * | −1.00 * | −1.00 * | −1.00 * | −1.00 * |
| 216 | 11 | 1.00 * | −1.00 * | −1.00 * | −1.00 * | −1.00 * |
| 217 | 10 | 1.00 * | −1.00 * | −1.00 * | −1.00 * | −1.00 * |
| 218 | 9 | 1.00 * | −1.00 * | −1.00 * | −1.00 * | −1.00 * |
| 219 | 8 | 1.00 * | −1.00 * | −1.00 * | −1.00 * | −1.00 * |
| 220 | 7 | 1.00 * | −1.00 * | −1.00 * | −1.00 * | −1.00 * |
| 221 | 6 | 1.00 * | −1.00 * | −1.00 * | −1.00 * | −1.00 * |
| 222 | 5 | 1.00 * | −1.00 * | −1.00 * | −1.00 * | −1.00 * |
| 223 | 4 | 1.00 * | −1.00 * | −1.00 * | −1.00 * | −1.00 * |
| 224 | 3 | 1.00 * | −1.00 * | −1.00 * | −1.00 * | −1.00 * |
| Row | Scenario | α | Number of Cases | Original Data | Litmus Test |
|---|---|---|---|---|---|
| 1 | Original | 1.00 | 851 | −0.76 * | −0.91 * |
| 2.00 | 851 | −0.70 * | −0.79 * | ||
| 2 | Natural weights | 1.00 | 851 | −0.77 * | −0.90 * |
| 2.00 | 851 | −0.70 * | −0.79 * | ||
| 3 | Yearly data | 1.00 | 70 | −0.74 * | −0.97 * |
| 2.00 | 70 | −0.46 * | −0.87 * | ||
| 4 | Random draw | 1.00 | 851 | −0.16 * | −0.69 * |
| 2.00 | 851 | −0.50 * | −0.61 * | ||
| 5 | Cut-off | 1.00 | 851 | 0.12 * | 0.08 |
| 2.00 | 851 | 0.08 | −0.10 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koplenig, A.; Wolfer, S.; Müller-Spitzer, C. Studying Lexical Dynamics and Language Change via Generalized Entropies: The Problem of Sample Size. Entropy 2019, 21, 464. https://doi.org/10.3390/e21050464
Koplenig A, Wolfer S, Müller-Spitzer C. Studying Lexical Dynamics and Language Change via Generalized Entropies: The Problem of Sample Size. Entropy. 2019; 21(5):464. https://doi.org/10.3390/e21050464
Chicago/Turabian StyleKoplenig, Alexander, Sascha Wolfer, and Carolin Müller-Spitzer. 2019. "Studying Lexical Dynamics and Language Change via Generalized Entropies: The Problem of Sample Size" Entropy 21, no. 5: 464. https://doi.org/10.3390/e21050464
APA StyleKoplenig, A., Wolfer, S., & Müller-Spitzer, C. (2019). Studying Lexical Dynamics and Language Change via Generalized Entropies: The Problem of Sample Size. Entropy, 21(5), 464. https://doi.org/10.3390/e21050464