Bounded Rational Decision-Making from Elementary Computations That Reduce Uncertainty
Abstract
:1. Introduction
- (i)
- Based on a fundamental concept of probability transfers related to the Pigou–Dalton principle of welfare economics [26], we promote a generalized notion of uncertainty reduction of a probability distribution that we call elementary computation. This leads to a natural definition of cost functions that quantify the resource costs for uncertainty reduction necessary for decision-making. We generalize these concepts to arbitrary reference distributions. In particular, we define Pigou–Dalton-type transfers for probability distributions relative to a reference or prior distribution, which induce a preorder that is slightly stronger than Kullback-Leibler divergence, but is equivalent to the notion of divergence given by all f-divergences combined. We prove several new characterizations of the underlying concept, known as relative majorization.
- (ii)
- An interesting property of cost functions is their behavior under coarse-graining, which plays an important role in decision-making and formalizes the general notion of making abstractions. More precisely, if a decision in a set is split up into two steps by partitioning and first deciding in the set of (coarse-grained) partitions and secondly choosing a fine-grained option inside the selected partition , then it is an important question how the cost for the total decision-making process differs from the sum of the costs in each step. We show that f-divergences are superadditive with respect to coarse-graining, which means that decision-making costs can potentially be reduced by splitting up the decision into multiple steps. In this regard, we find evidence that the well-known property of Kullback-Leibler divergence of being additive under coarse-graining might be viewed as describing the minimal amount of processing cost that cannot be reduced by a more intelligent decision-making strategy.
- (iii)
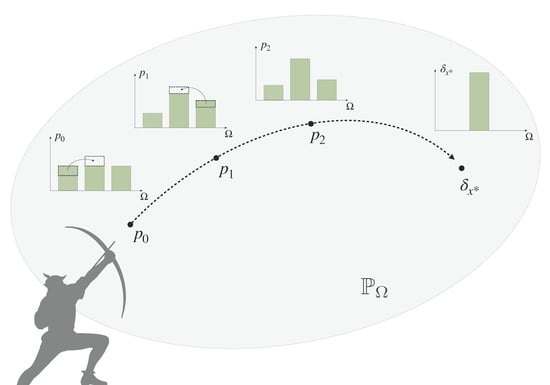
- We define bounded rational decision-makers as decision-making processes that are optimizing a given utility function under a constraint on the cost function, or minimizing the cost function under a minimal requirement on expected utility. As a special case for Shannon-type information costs, we arrive at information-theoretic bounded rationality, which may form a normative baseline for bounded-optimal decision-making in the absence of process-dependent constraints. We show that bounded-optimal posteriors with informational costs trace a path through probability space that can itself be seen as an anytime decision-making process, where each step optimally trades off utility and processing costs.
- (iv)
- We show that Bayesian inference can be seen as a decision-making process with limited resources given by the number of available datapoints.
Notation
2. Decision-Making with Limited Resources
- (i)
- reduces uncertainty
- (ii)
- by spending resources.
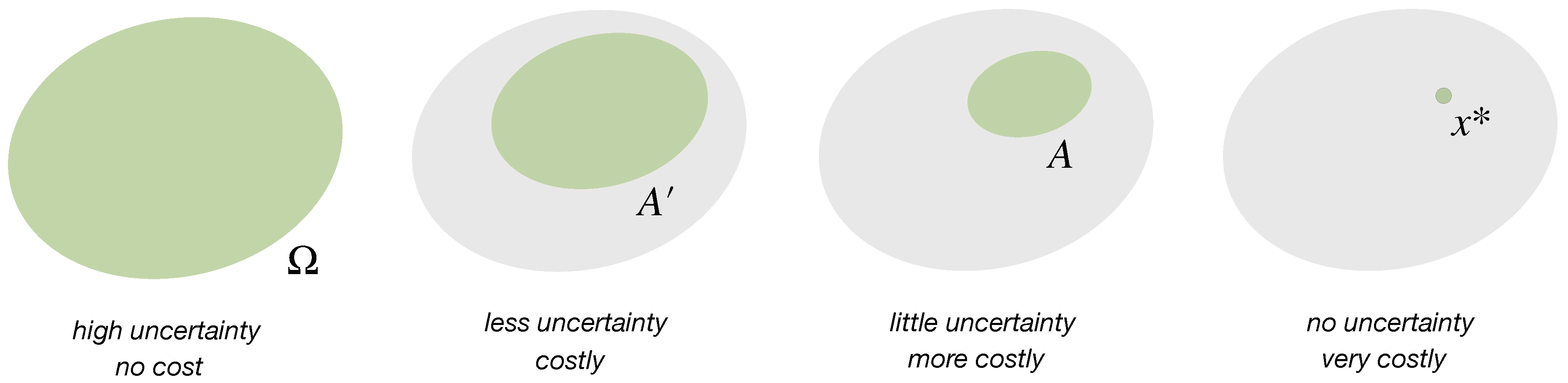
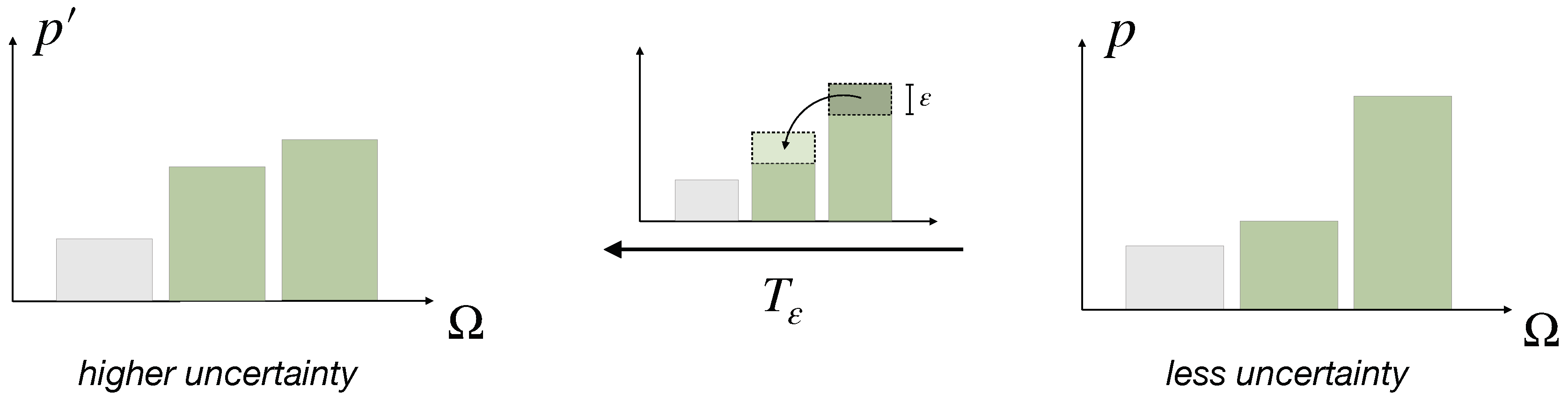
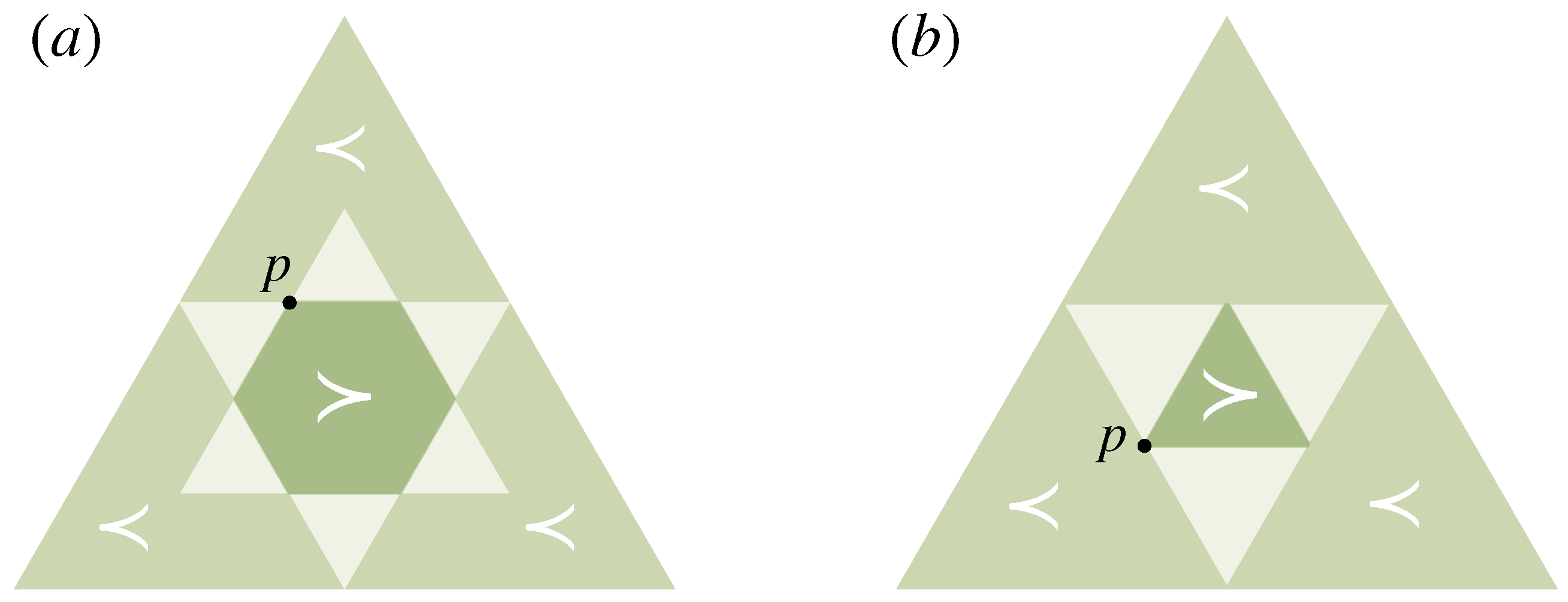
2.1. Uncertainty Reduction by Eliminating Options
2.2. Probabilistic Decision-Making
- (i)
- , i.e., contains more uncertainty than p (Definition 2)
- (ii)
- is the result of finitely many T-transforms applied to p
- (iii)
- for a doubly stochastic matrix A
- (iv)
- where , , , and is a permutation for all
- (v)
- for all continuous convex functions f
- (vi)
- for all , where denotes the decreasing rearrangement of p
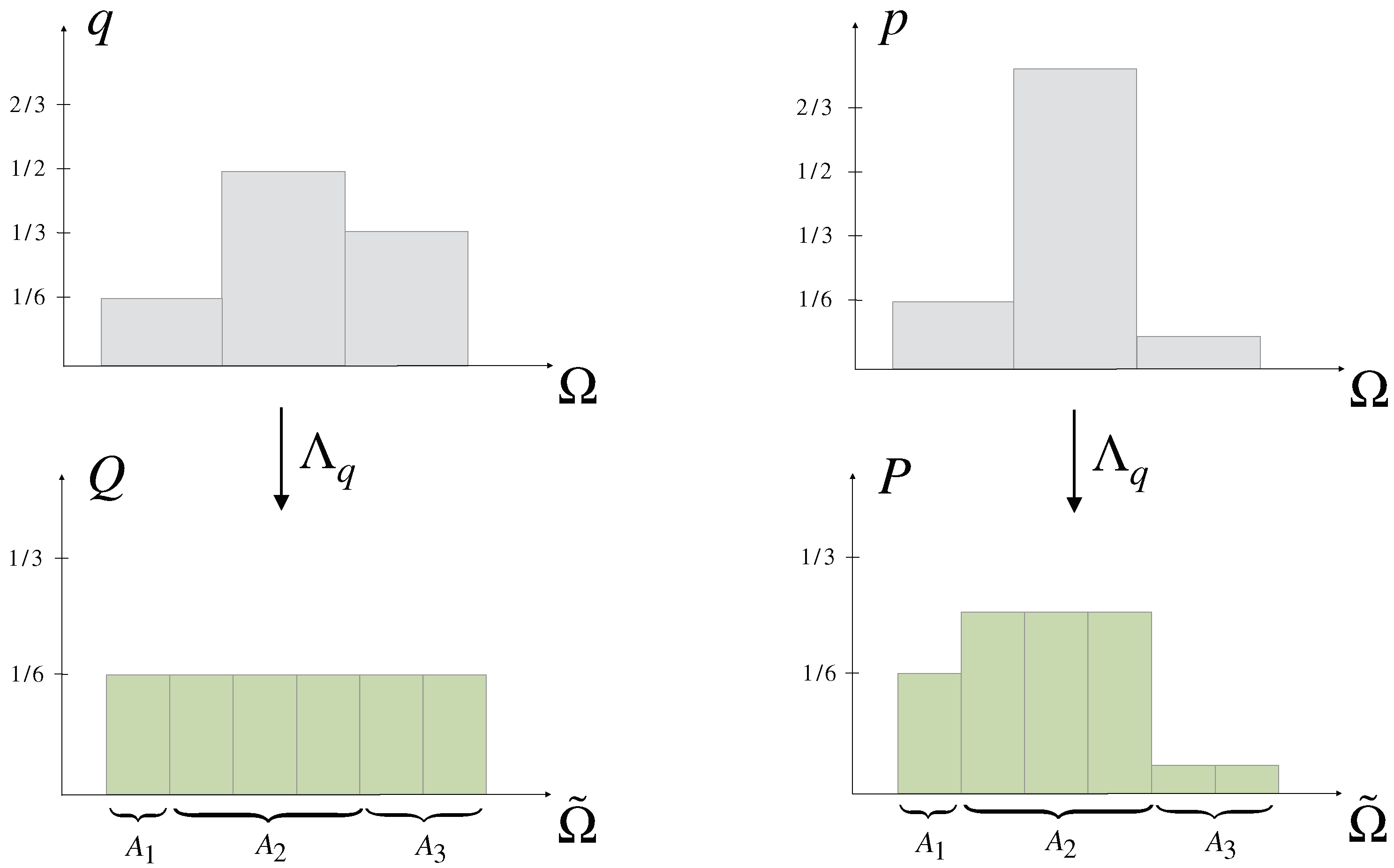
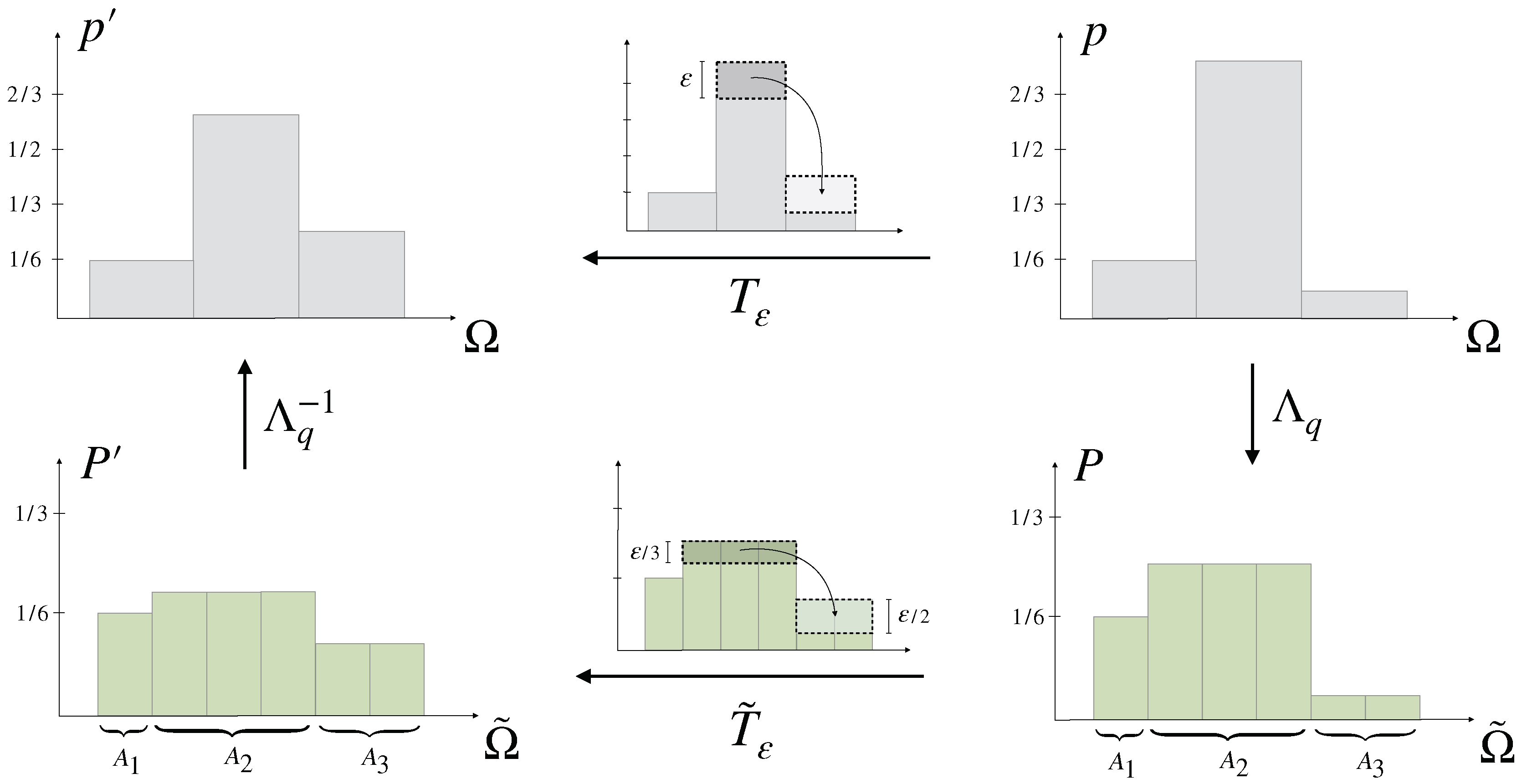
2.3. Decision-Making with Prior Knowledge
- (i)
- , i.e., contains more uncertainty relative to q than p (Definition 4).
- (ii)
- can be obtained from by a finite number of elementary computations and permutations on .
- (iii)
- for a q-stochastic matrix A, i.e., and .
- (iv)
- for all continuous convex functions f.
- (v)
- for all and , where , and the arrows indicate that is ordered decreasingly.
3. Bounded Rationality
3.1. Bounded Rational Decision-Making
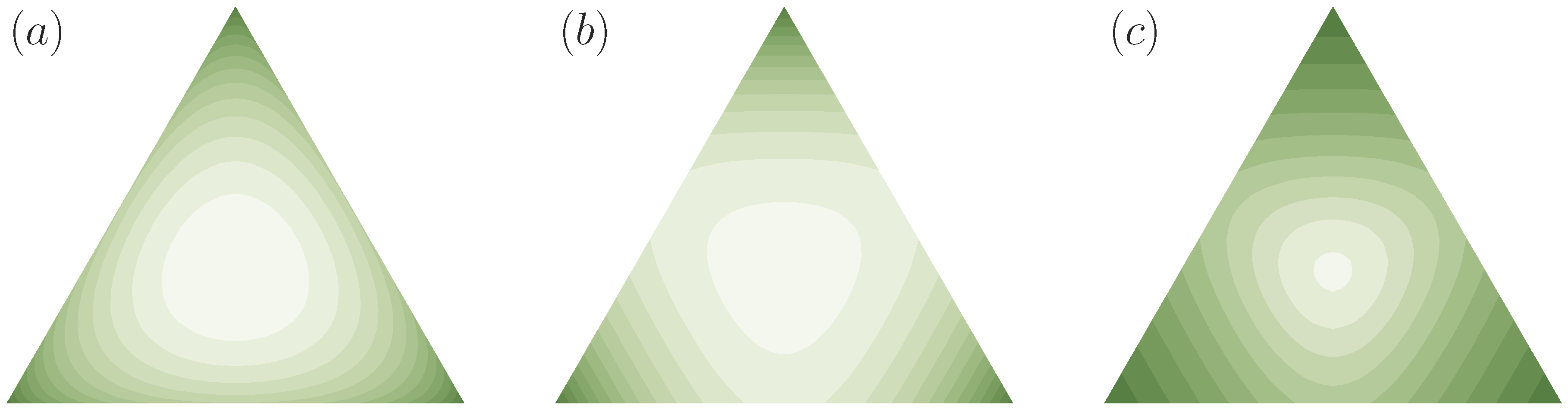
3.2. Information-Theoretic Bounded Rationality
3.3. The Recursivity of and the Value of a Decision Problem
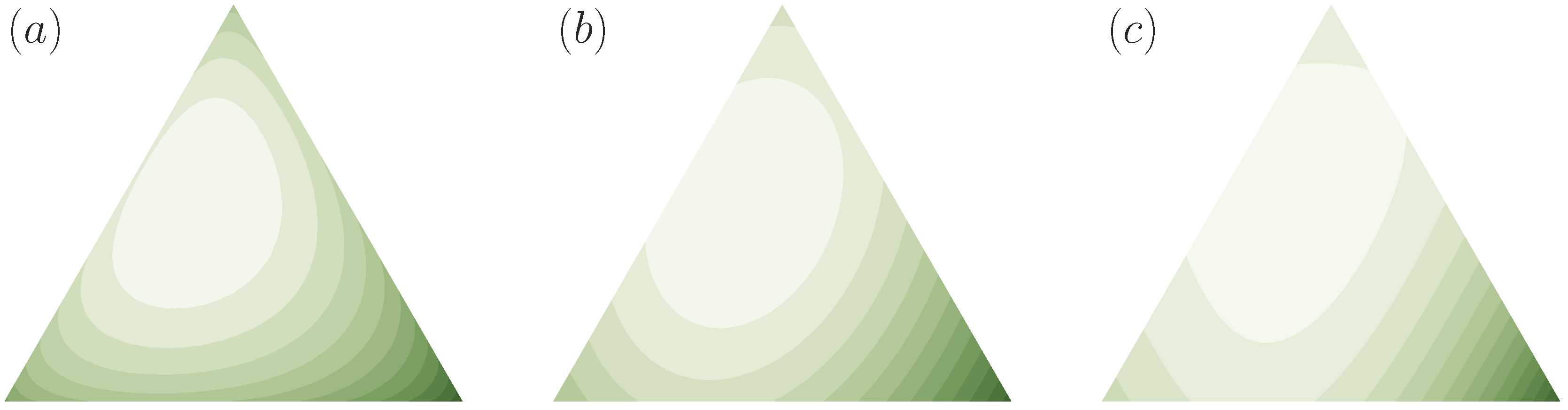
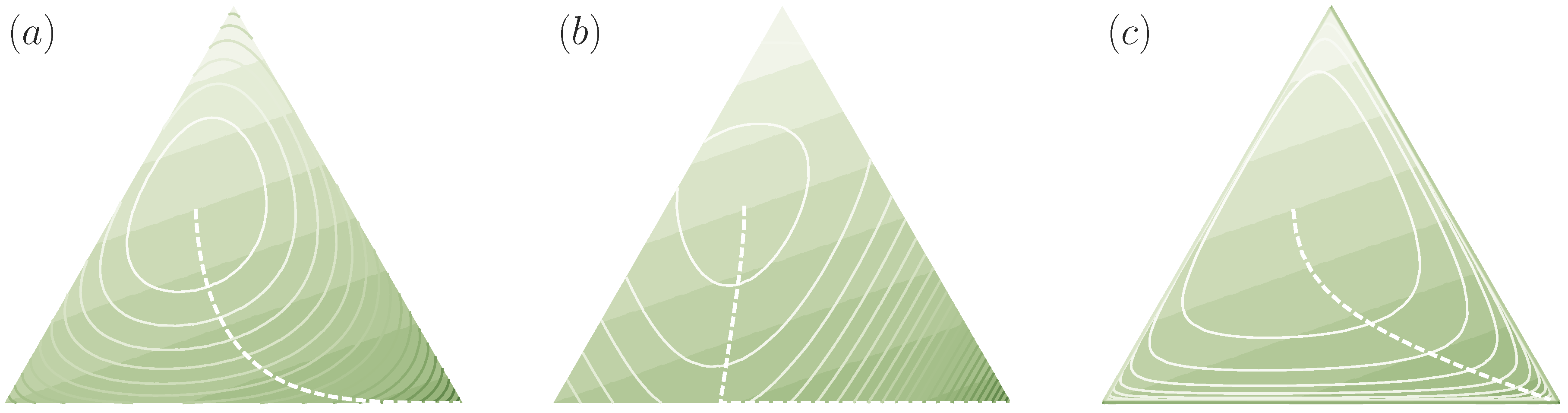
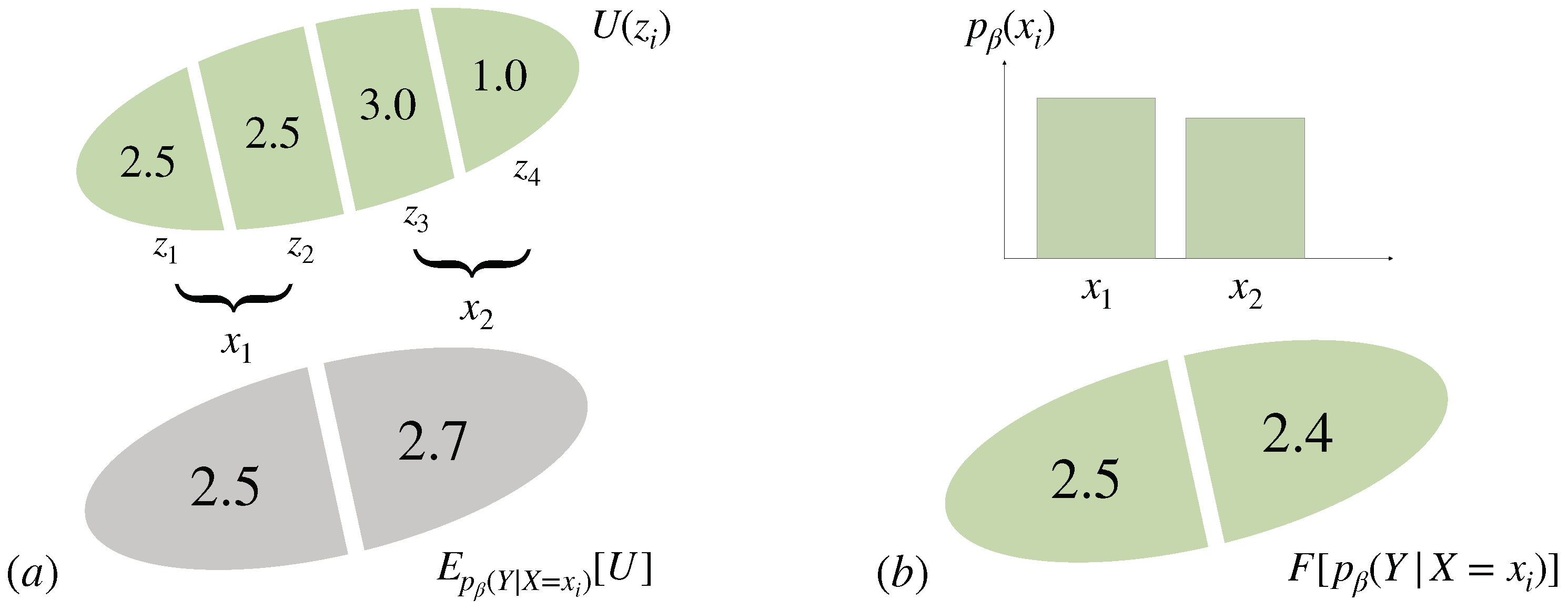
3.4. Multi-Task Decision-Making and the Optimal Prior
3.5. Multi-Task Decision-Making with Unknown World State Distribution
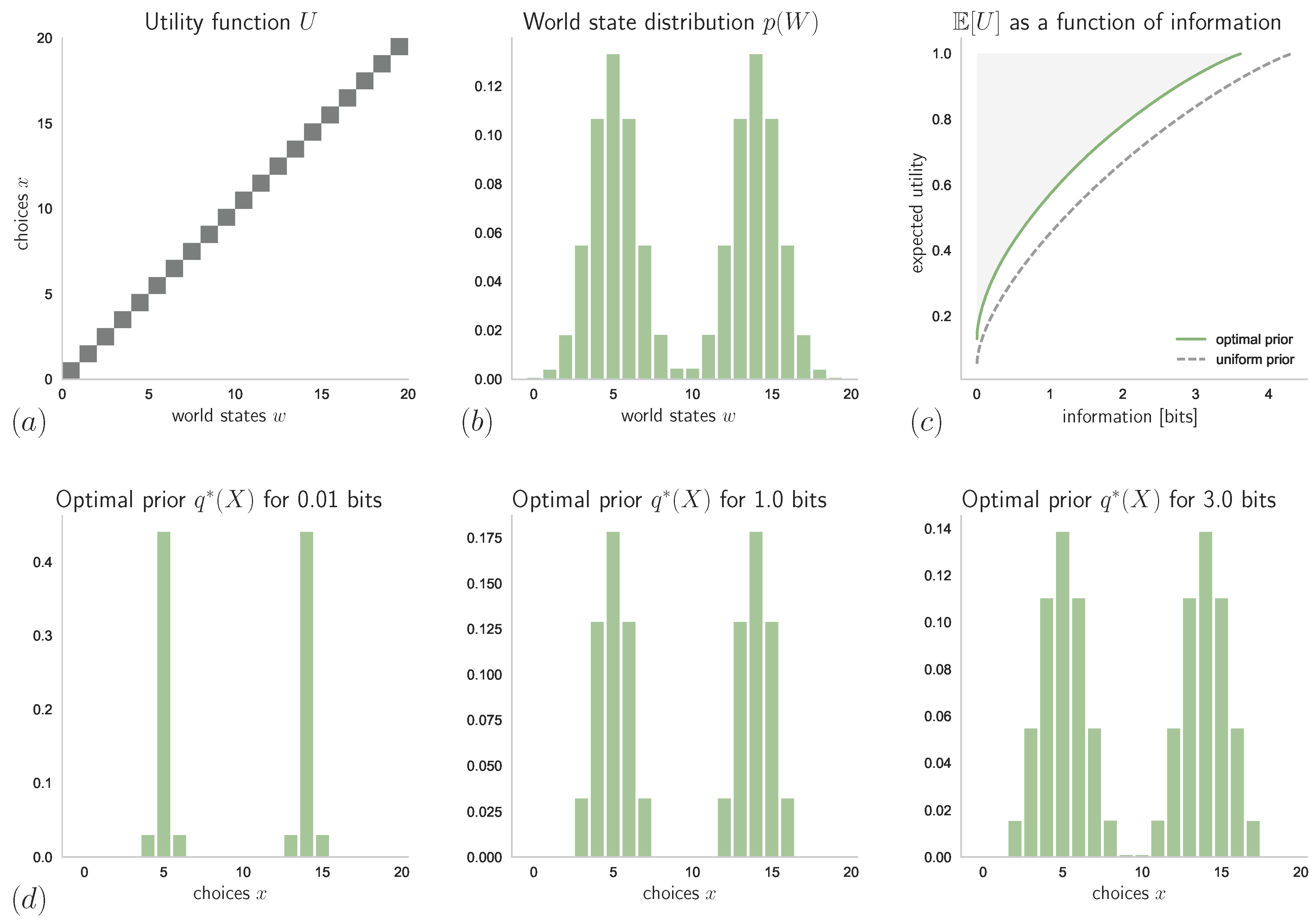
4. Example: Absolute Identification Task with Known and Unknown Stimulus Distribution
4.1. Known Stimulus Distribution
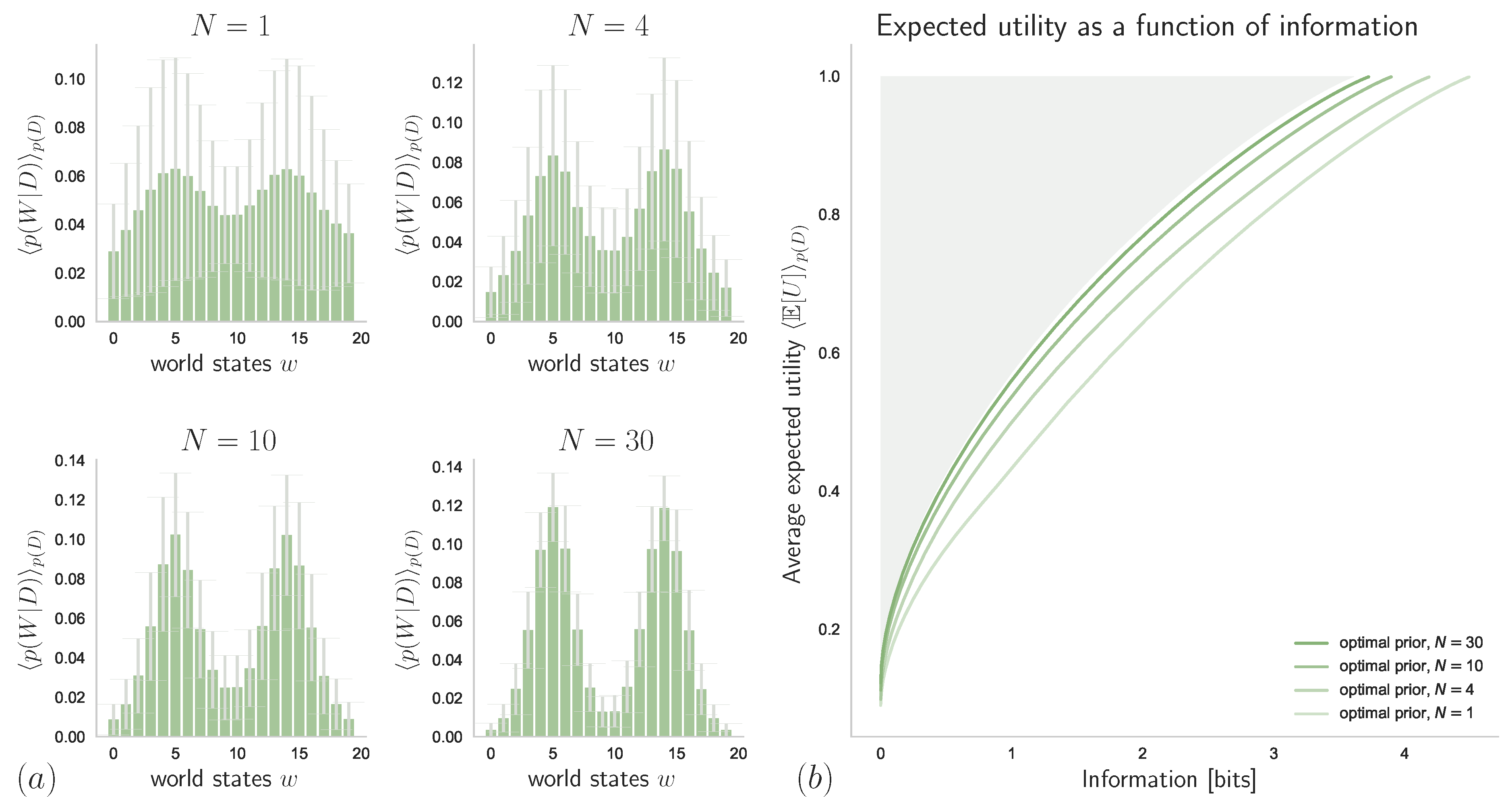
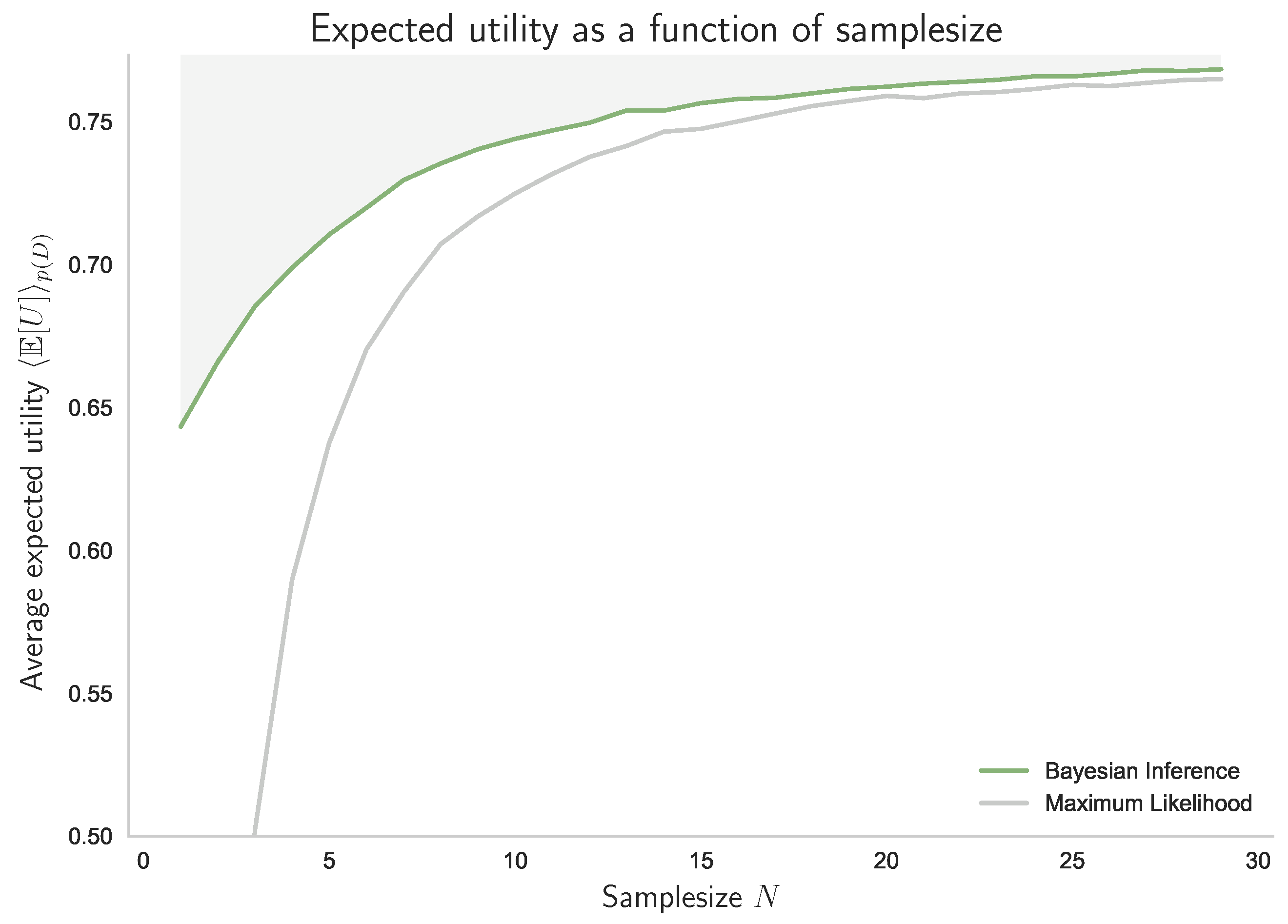
4.2. Unknown Stimulus Distribution
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Proofs of Technical Results from Section 2 and Section 3
- (i)
- , i.e., contains more uncertainty relative to q than p (Definition 4).
- (iii)
- for a q-stochastic matrix A, i.e., and .
- (v)
- for all and , where , and the arrows indicate that is ordered decreasingly.
References
- Von Neumann, J.; Morgenstern, O. Theory of Games and Economic Behavior; Princeton University Press: Princeton, NJ, USA, 1944. [Google Scholar]
- Simon, H.A. A Behavioral Model of Rational Choice. Q. J. Econ. 1955, 69, 99–118. [Google Scholar] [CrossRef]
- Russell, S.J.; Subramanian, D. Provably Bounded-optimal Agents. J. Artif. Intell. Res. 1995, 2, 575–609. [Google Scholar] [CrossRef]
- Ochs, J. Games with Unique, Mixed Strategy Equilibria: An Experimental Study. Games Econ. Behav. 1995, 10, 202–217. [Google Scholar] [CrossRef]
- Lipman, B.L. Information Processing and Bounded Rationality: A Survey. Can. J. Econ. 1995, 28, 42–67. [Google Scholar] [CrossRef]
- Aumann, R.J. Rationality and Bounded Rationality. Games Econ. Behav. 1997, 21, 2–14. [Google Scholar] [CrossRef]
- Gigerenzer, G.; Selten, R. Bounded Rationality: The Adaptive Toolbox; MIT Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Mattsson, L.G.; Weibull, J.W. Probabilistic choice and procedurally bounded rationality. Games Econ. Behav. 2002, 41, 61–78. [Google Scholar] [CrossRef]
- Jones, B.D. Bounded Rationality and Political Science: Lessons from Public Administration and Public Policy. J. Public Adm. Res. Theory 2003, 13, 395–412. [Google Scholar] [CrossRef]
- Sims, C.A. Implications of rational inattention. J. Monet. Econ. 2003, 50, 665–690. [Google Scholar] [CrossRef]
- Wolpert, D.H. Information Theory—The Bridge Connecting Bounded Rational Game Theory and Statistical Physics. In Complex Engineered Systems: Science Meets Technology; Braha, D., Minai, A.A., Bar-Yam, Y., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 262–290. [Google Scholar]
- Howes, A.; Lewis, R.L.; Vera, A. Rational adaptation under task and processing constraints: Implications for testing theories of cognition and action. Psychol. Rev. 2009, 116, 717–751. [Google Scholar] [CrossRef] [PubMed]
- Still, S. Information-theoretic approach to interactive learning. Europhys. Lett. 2009, 85, 28005. [Google Scholar] [CrossRef]
- Tishby, N.; Polani, D. Information Theory of Decisions and Actions. In Perception-Action Cycle: Models, Architectures, and Hardware; Cutsuridis, V., Hussain, A., Taylor, J.G., Eds.; Springer: New York, NY, USA, 2011; pp. 601–636. [Google Scholar]
- Spiegler, R. Bounded Rationality and Industrial Organization; Oxford University Press: Oxford, UK, 2011. [Google Scholar]
- Kappen, H.J.; Gómez, V.; Opper, M. Optimal control as a graphical model inference problem. Mach. Learn. 2012, 87, 159–182. [Google Scholar] [CrossRef]
- Burns, E.; Ruml, W.; Do, M.B. Heuristic Search when Time Matters. J. Artif. Intell. Res. 2013, 47, 697–740. [Google Scholar] [CrossRef]
- Ortega, P.A.; Braun, D.A. Thermodynamics as a theory of decision-making with information-processing costs. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 2013, 469, 20120683. [Google Scholar] [CrossRef]
- Lewis, R.L.; Howes, A.; Singh, S. Computational Rationality: Linking Mechanism and Behavior through Bounded Utility Maximization. Top. Cogn. Sci. 2014, 6, 279–311. [Google Scholar] [CrossRef]
- Acerbi, L.; Vijayakumar, S.; Wolpert, D.M. On the Origins of Suboptimality in Human Probabilistic Inference. PLoS Comput. Biol. 2014, 10, e1003661. [Google Scholar] [CrossRef]
- Gershman, S.J.; Horvitz, E.J.; Tenenbaum, J.B. Computational rationality: A converging paradigm for intelligence in brains, minds, and machines. Science 2015, 349, 273–278. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Renyi, A. On Measures of Entropy and Information. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Volume 1: Contributions to the Theory of Statistics; University of California Press: Berkeley, CA, USA, 1961; pp. 547–561. [Google Scholar]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On Information and Sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Dalton, H. The Measurement of the Inequality of Incomes. Econ. J. 1920, 30, 348–361. [Google Scholar] [CrossRef]
- Marshall, A.W.; Olkin, I.; Arnold, B.C. Inequalities: Theory of Majorization and Its Applications, 2nd ed.; Springer: New York, NY, USA, 2011. [Google Scholar]
- Joe, H. Majorization and divergence. J. Math. Anal. Appl. 1990, 148, 287–305. [Google Scholar] [CrossRef]
- Hardy, G.H.; Littlewood, J.; Pólya, G. Inequalities; Cambridge University Press: Cambridge, UK, 1934. [Google Scholar]
- Arnold, B.C. Majorization and the Lorenz Order: A Brief Introduction; Springer: New York, NY, USA, 1987. [Google Scholar]
- Pečarić, J.E.; Proschan, F.; Tong, Y.L. Convex Functions, Partial Orderings, and Statistical Applications; Academic Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Bhatia, R. Matrix Analysis; Springer: New York, NY, USA, 1997. [Google Scholar]
- Arnold, B.C.; Sarabia, J.M. Majorization and the Lorenz Order with Applications in Applied Mathematics and Economics; Springer International Publishing: Berlin, Germany, 2018. [Google Scholar]
- Lorenz, M.O. Methods of Measuring the Concentration of Wealth. Publ. Am. Stat. Assoc. 1905, 9, 209–219. [Google Scholar] [CrossRef]
- Pigou, A.C. Wealth and Welfare; Macmillan: New York, NY, USA, 1912. [Google Scholar]
- Ruch, E.; Mead, A. The principle of increasing mixing character and some of its consequences. Theor. Chim. Acta 1976, 41, 95–117. [Google Scholar] [CrossRef]
- Rossignoli, R.; Canosa, N. Limit temperature for entanglement in generalized statistics. Phys. Lett. 2004, 323, 22–28. [Google Scholar] [CrossRef]
- Muirhead, R.F. Some Methods applicable to Identities and Inequalities of Symmetric Algebraic Functions of n Letters. Proc. Edinb. Math. Soc. 1902, 21, 144–162. [Google Scholar] [CrossRef]
- Brandão, F.G.S.L.; Horodecki, M.; Oppenheim, J.; Renes, J.M.; Spekkens, R.W. Resource Theory of Quantum States Out of Thermal Equilibrium. Phys. Rev. Lett. 2013, 111, 250404. [Google Scholar] [CrossRef] [PubMed]
- Horodecki, M.; Oppenheim, J. Fundamental limitations for quantum and nanoscale thermodynamics. Nat. Commun. 2013, 4, 2056. [Google Scholar] [CrossRef]
- Gour, G.; Müller, M.P.; Narasimhachar, V.; Spekkens, R.W.; Halpern, N.Y. The resource theory of informational nonequilibrium in thermodynamics. Phys. Rep. 2015, 583, 1–58. [Google Scholar] [CrossRef]
- Schur, I. Über eine Klasse von Mittelbildungen mit Anwendungen auf die Determinanten-Theorie. Sitz. Berl. Math. Ges. 1923, 22, 9–20. [Google Scholar]
- Karamata, J. Sur une inégalité relative aux fonctions convexes. Publ. L’Institut Math. 1932, 1, 145–147. [Google Scholar]
- Hardy, G.; Littlewood, J.; Pólya, G. Some Simple Inequalities Satisfied by Convex Functions. Messenger Math. 1929, 58, 145–152. [Google Scholar]
- Canosa, N.; Rossignoli, R. Generalized Nonadditive Entropies and Quantum Entanglement. Phys. Rev. Lett. 2002, 88, 170401. [Google Scholar] [CrossRef] [PubMed]
- Gorban, A.N.; Gorban, P.A.; Judge, G. Entropy: The Markov Ordering Approach. Entropy 2010, 12, 1145–1193. [Google Scholar] [CrossRef]
- Csiszár, I. A class of measures of informativity of observation channels. Period. Math. Hung. 1972, 2, 191–213. [Google Scholar] [CrossRef]
- Amari, S. α-Divergence Is Unique, Belonging to Both f-Divergence and Bregman Divergence Classes. IEEE Trans. Inf. Theory 2009, 55, 4925–4931. [Google Scholar] [CrossRef]
- Khinchin, A.Y. Mathematical Foundations of Information Theory; Dover Books on Advanced Mathematics, Dover: New York, NY, USA, 1957. [Google Scholar]
- Csiszár, I. Axiomatic Characterizations of Information Measures. Entropy 2008, 10, 261–273. [Google Scholar] [CrossRef]
- Aczél, J.; Forte, B.; Ng, C.T. Why the Shannon and Hartley Entropies Are ‘Natural’. Adv. Appl. Probab. 1974, 6, 131–146. [Google Scholar] [CrossRef]
- Faddeev, D.K. On the concept of entropy of a finite probabilistic scheme. Usp. Mat. Nauk 1956, 11, 227–231. [Google Scholar]
- Tverberg, H. A New Derivation of the Information Function. Math. Scand. 1958, 6, 297–298. [Google Scholar] [CrossRef]
- Kendall, D.G. Functional equations in information theory. Probab. Theory Relat. Fields 1964, 2, 225–229. [Google Scholar] [CrossRef]
- Lee, P.M. On the Axioms of Information Theory. Ann. Math. Stat. 1964, 35, 415–418. [Google Scholar] [CrossRef]
- Aczel, J. On different characterizations of entropies. In Probability and Information Theory; Behara, M., Krickeberg, K., Wolfowitz, J., Eds.; Springer: Berlin/Heidelberg, Germany, 1969; pp. 1–11. [Google Scholar]
- Veinott, A.F. Least d-Majorized Network Flows with Inventory and Statistical Applications. Manag. Sci. 1971, 17, 547–567. [Google Scholar] [CrossRef]
- Ruch, E.; Schranner, R.; Seligman, T.H. The mixing distance. J. Chem. Phys. 1978, 69, 386–392. [Google Scholar] [CrossRef]
- Hobson, A. A new theorem of information theory. J. Stat. Phys. 1969, 1, 383–391. [Google Scholar] [CrossRef]
- Leinster, T. A short characterization of relative entropy. arXiv 2017, arXiv:1712.04903. [Google Scholar]
- Everett, H. Generalized Lagrange Multiplier Method for Solving Problems of Optimum Allocation of Resources. Oper. Res. 1963, 11, 399–417. [Google Scholar] [CrossRef]
- Ortega, P.A.; Braun, D.A. A conversion between utility and information. In Proceedings of the 3rd Conference on Artificial General Intelligence (AGI-2010), Washington, DC, USA, 5–8 March 2010; Atlantis Press, Springer International Publishing: Cham, Switzerland, 2010. [Google Scholar]
- Genewein, T.; Leibfried, F.; Grau-Moya, J.; Braun, D.A. Bounded Rationality, Abstraction, and Hierarchical Decision-Making: An Information-Theoretic Optimality Principle. Front. Robot. AI 2015, 2, 27. [Google Scholar] [CrossRef]
- Gottwald, S.; Braun, D.A. Systems of bounded rational agents with information-theoretic constraints. Neural Comput. 2019, 1–37. [Google Scholar] [CrossRef]
- Hihn, H.; Gottwald, S.; Braun, D.A. Bounded Rational Decision-Making with Adaptive Neural Network Priors. In Artificial Neural Networks in Pattern Recognition; Pancioni, L., Schwenker, F., Trentin, E., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 213–225. [Google Scholar]
- Leibfried, F.; Grau-Moya, J.; Bou-Ammar, H. An Information-Theoretic Optimality Principle for Deep Reinforcement Learning. arXiv 2018, arXiv:1708.01867v5. [Google Scholar]
- Grau-Moya, J.; Leibfried, F.; Vrancx, P. Soft Q-Learning with Mutual-Information Regularization. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 March 2019. [Google Scholar]
- Ortega, P.A.; Stocker, A. Human Decision-Making under Limited Time. In Proceedings of the 30th Conference on Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016. [Google Scholar]
- Schach, S.; Gottwald, S.; Braun, D.A. Quantifying Motor Task Performance by Bounded Rational Decision Theory. Front. Neurosci. 2018, 12, 932. [Google Scholar] [CrossRef]
- Friston, K.J. The free-energy principle: A rough guide to the brain? Trends Cogn. Sci. 2009, 13, 293–301. [Google Scholar] [CrossRef]
- Hinton, G.E.; van Camp, D. Keeping the Neural Networks Simple by Minimizing the Description Length of the Weights. In Proceedings of the Sixth Annual Conference on Computational Learning Theory, Santa Cruz, CA, USA, 26–28 July 1993; ACM: New York, NY, USA, 1993; pp. 5–13. [Google Scholar]
- MacKay, D.J.C. Developments in Probabilistic Modelling with Neural Network—Ensemble Learning. In Neural Networks: Artificial Intelligence and Industrial Applications; Kappen, B., Gielen, S., Eds.; Springer: London, UK, 1995; pp. 191–198. [Google Scholar]
- Blahut, R.E. Computation of channel capacity and rate-distortion functions. IEEE Trans. Inf. Theory 1972, 18, 460–473. [Google Scholar] [CrossRef]
- Arimoto, S. An algorithm for computing the capacity of arbitrary discrete memoryless channels. IEEE Trans. Inf. Theory 1972, 18, 14–20. [Google Scholar] [CrossRef]
- Csiszár, I.; Tusnády, G. Information geometry and alternating minimization procedures. Stat. Decis. Suppl. Issue 1984, 1, 205–237. [Google Scholar]
- Shannon, C.E. Coding theorems for a discrete source with a fidelity criterion. IRE Int. Conv. Rec. 1959, 7, 142–163. [Google Scholar]
- Tsuyoshi, A. Majorization, doubly stochastic matrices, and comparison of eigenvalues. Linear Algebra Its Appl. 1989, 118, 163–248. [Google Scholar]
- Cohen, J.E.; Derriennic, Y.; Zbăganu, G. Majorization, monotonicity of relative entropy, and stochastic matrices. In Doeblin and Modern Probability (Blaubeuren, 1991); Amer. Math. Soc.: Providence, RI, USA, 1993; Volume 149, pp. 251–259. [Google Scholar]
- Latif, N.; Pečarić, D.; Pečarić, J. Majorization, Csiszár divergence and Zipf-Mandelbrot law. J. Inequal. Appl. 2017, 2017, 197. [Google Scholar] [CrossRef] [PubMed]
- Jiao, J.; Courtade, T.A.; No, A.; Venkat, K.; Weissman, T. Information Measures: The Curious Case of the Binary Alphabet. IEEE Trans. Inf. Theory 2014, 60, 7616–7626. [Google Scholar] [CrossRef]
- Amari, S.; Cichocki, A. Information geometry of divergence functions. Bull. Pol. Acad. Sci. 2010, 58, 183–195. [Google Scholar] [CrossRef]
- Amari, S.; Karakida, R.; Oizumi, M. Information geometry connecting Wasserstein distance and Kullback-Leibler divergence via the entropy-relaxed transportation problem. Inf. Geom. 2018, 1, 13–37. [Google Scholar] [CrossRef]
- McKelvey, R.D.; Palfrey, T.R. Quantal Response Equilibria for Normal Form Games. Games Econ. Behav. 1995, 10, 6–38. [Google Scholar] [CrossRef]
- Todorov, E. Efficient computation of optimal actions. Proc. Natl. Acad. Sci. USA 2009, 106, 11478–11483. [Google Scholar] [CrossRef]
- Vul, E.; Goodman, N.; Griffiths, T.L.; Tenenbaum, J.B. One and Done? Optimal Decisions From Very Few Samples. Cogn. Sci. 2014, 38, 599–637. [Google Scholar] [CrossRef]
- Ortega, P.A.; Braun, D.A. A Minimum Relative Entropy Principle for Learning and Acting. J. Artif. Int. Res. 2010, 38, 475–511. [Google Scholar] [CrossRef]
- Candeal, J.C.; De Miguel, J.R.; Induráin, E.; Mehta, G.B. Utility and entropy. Econ. Theory 2001, 17, 233–238. [Google Scholar] [CrossRef]
- Keramati, M.; Dezfouli, A.; Piray, P. Speed/Accuracy Trade-Off between the Habitual and the Goal-Directed Processes. PLoS Comput. Biol. 2011, 7, 1–21. [Google Scholar] [CrossRef]
- Keramati, M.; Smittenaar, P.; Dolan, R.J.; Dayan, P. Adaptive integration of habits into depth-limited planning defines a habitual-goal–directed spectrum. Proc. Natl. Acad. Sci. USA 2016, 113, 12868–12873. [Google Scholar] [CrossRef]
- Ortega, P.A.; Braun, D.A.; Tishby, N. Monte Carlo methods for exact amp; efficient solution of the generalized optimality equations. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–5 June 2014; pp. 4322–4327. [Google Scholar]
- Laming, D.R.J. Information Theory of Choice-Reaction Times; Academic Press: Oxford, UK, 1968. [Google Scholar]
- Ratcliff, R. A theory of memory retrieval. Psychol. Rev. 1978, 85, 59–108. [Google Scholar] [CrossRef]
- Townsend, J.; Ashby, F. The Stochastic Modeling of Elementary Psychological Processes (Part 2); Cambridge University Press: Cambridge, UK, 1983. [Google Scholar]
- Ratcliff, R.; Starns, J.J. Modeling confidence judgments, response times, and multiple choices in decision making: Recognition memory and motion discrimination. Psychol. Rev. 2013, 120, 697–719. [Google Scholar] [CrossRef]
- Shadlen, M.; Hanks, T.; Churchland, A.K.; Kiani, R.; Yang, T. The Speed and Accuracy of a Simple Perceptual Decision: A Mathematical Primer. In Bayesian Brain: Probabilistic Approaches to Neural Coding; MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Frazier, P.I.; Yu, A.J. Sequential Hypothesis Testing Under Stochastic Deadlines. In Proceedings of the 20th International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 3–6 December 2007; Curran Associates Inc.: Red Hook, NY, USA, 2007; pp. 465–472. [Google Scholar]
- Drugowitsch, J.; Moreno-Bote, R.; Churchland, A.K.; Shadlen, M.N.; Pouget, A. The cost of accumulating evidence in perceptual decision making. J. Neurosci. 2012, 32, 3612–3628. [Google Scholar] [CrossRef]
- Simon, H.A. Models of Bounded Rationality; MIT Press: Cambridge, MA, USA, 1982. [Google Scholar]
- Pezzulo, G.; Rigoli, F.; Chersi, F. The Mixed Instrumental Controller: Using Value of Information to Combine Habitual Choice and Mental Simulation. Front. Psychol. 2013, 4, 92. [Google Scholar] [CrossRef]
- Viejo, G.; Khamassi, M.; Brovelli, A.; Girard, B. Modeling choice and reaction time during arbitrary visuomotor learning through the coordination of adaptive working memory and reinforcement learning. Front. Behav. Neurosci. 2015, 9, 225. [Google Scholar] [CrossRef] [PubMed]
- Aczel, J.; Daroczy, Z. On Measures of Information and Their Characterizations; Academic Press: New York, NY, USA, 1975. [Google Scholar]
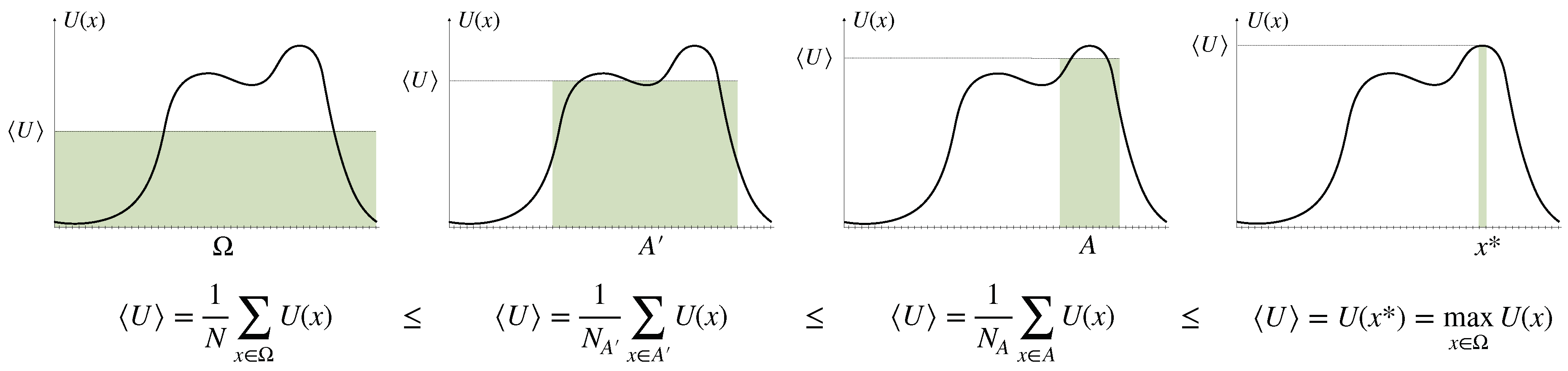

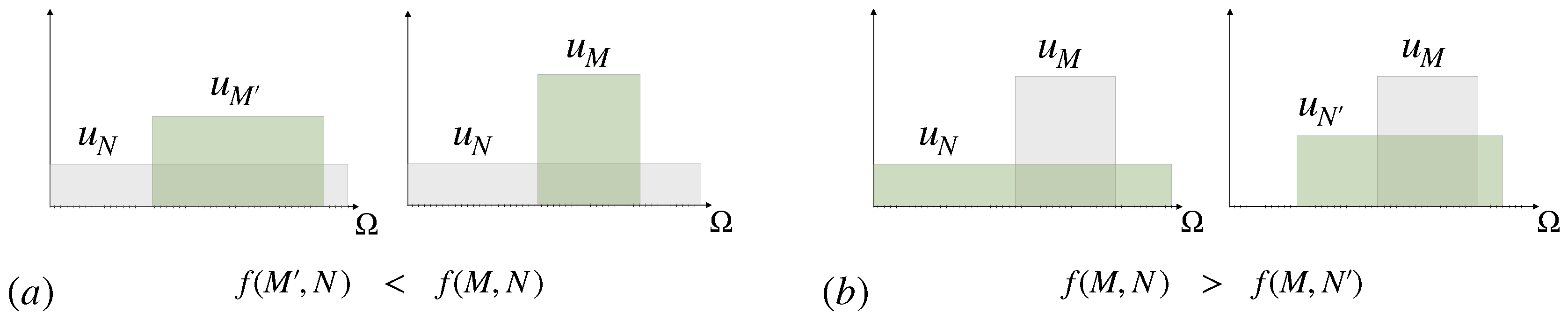
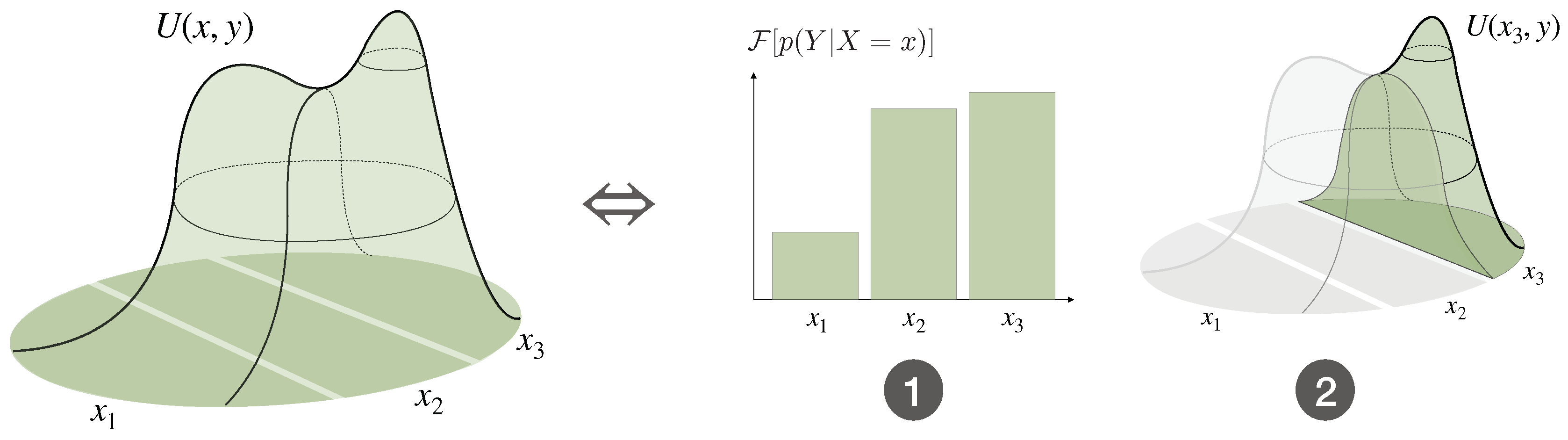
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gottwald, S.; Braun, D.A. Bounded Rational Decision-Making from Elementary Computations That Reduce Uncertainty. Entropy 2019, 21, 375. https://doi.org/10.3390/e21040375
Gottwald S, Braun DA. Bounded Rational Decision-Making from Elementary Computations That Reduce Uncertainty. Entropy. 2019; 21(4):375. https://doi.org/10.3390/e21040375
Chicago/Turabian StyleGottwald, Sebastian, and Daniel A. Braun. 2019. "Bounded Rational Decision-Making from Elementary Computations That Reduce Uncertainty" Entropy 21, no. 4: 375. https://doi.org/10.3390/e21040375
APA StyleGottwald, S., & Braun, D. A. (2019). Bounded Rational Decision-Making from Elementary Computations That Reduce Uncertainty. Entropy, 21(4), 375. https://doi.org/10.3390/e21040375