Phase Transition in Frustrated Magnetic Thin Film—Physics at Phase Boundaries
Abstract
:1. Introduction
2. Physics in Two Dimensions: Frustration Effects
2.1. Frustration
2.2. Non-Collinear Spin Configurations
3. Exactly Solved Frustrated Models
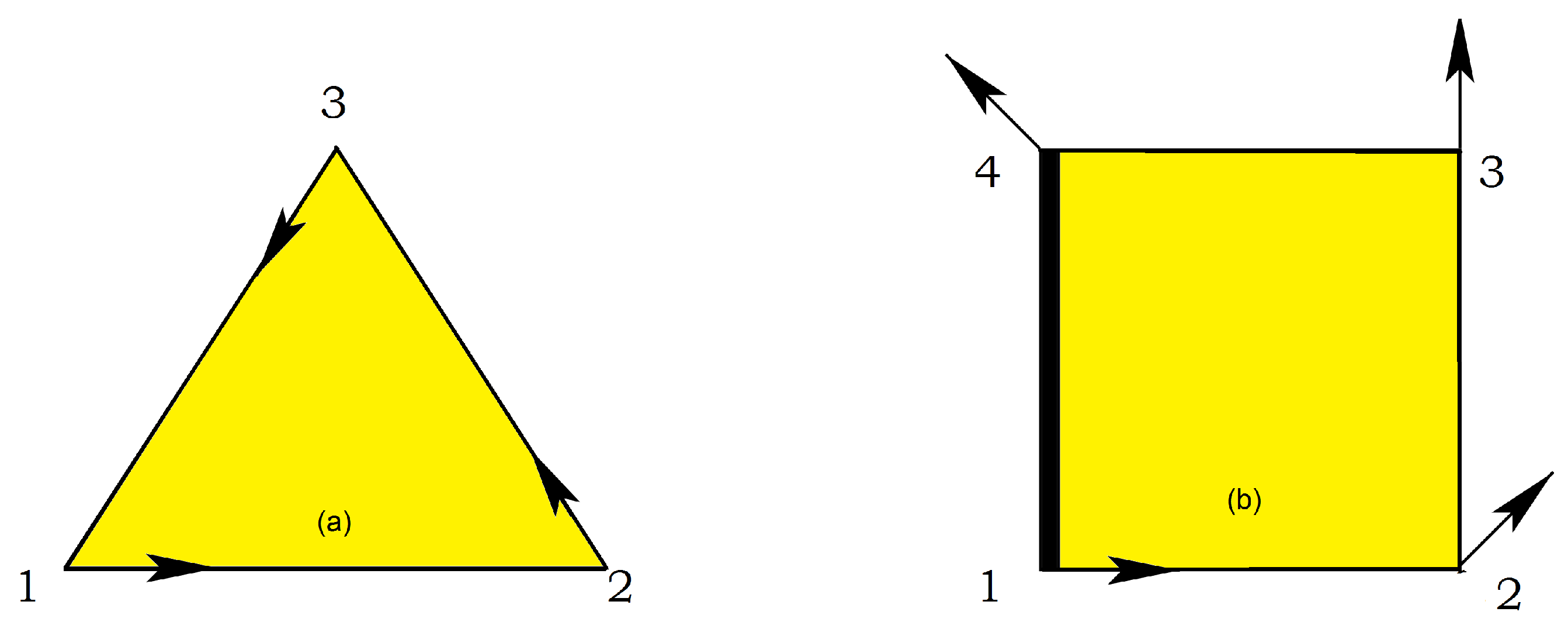
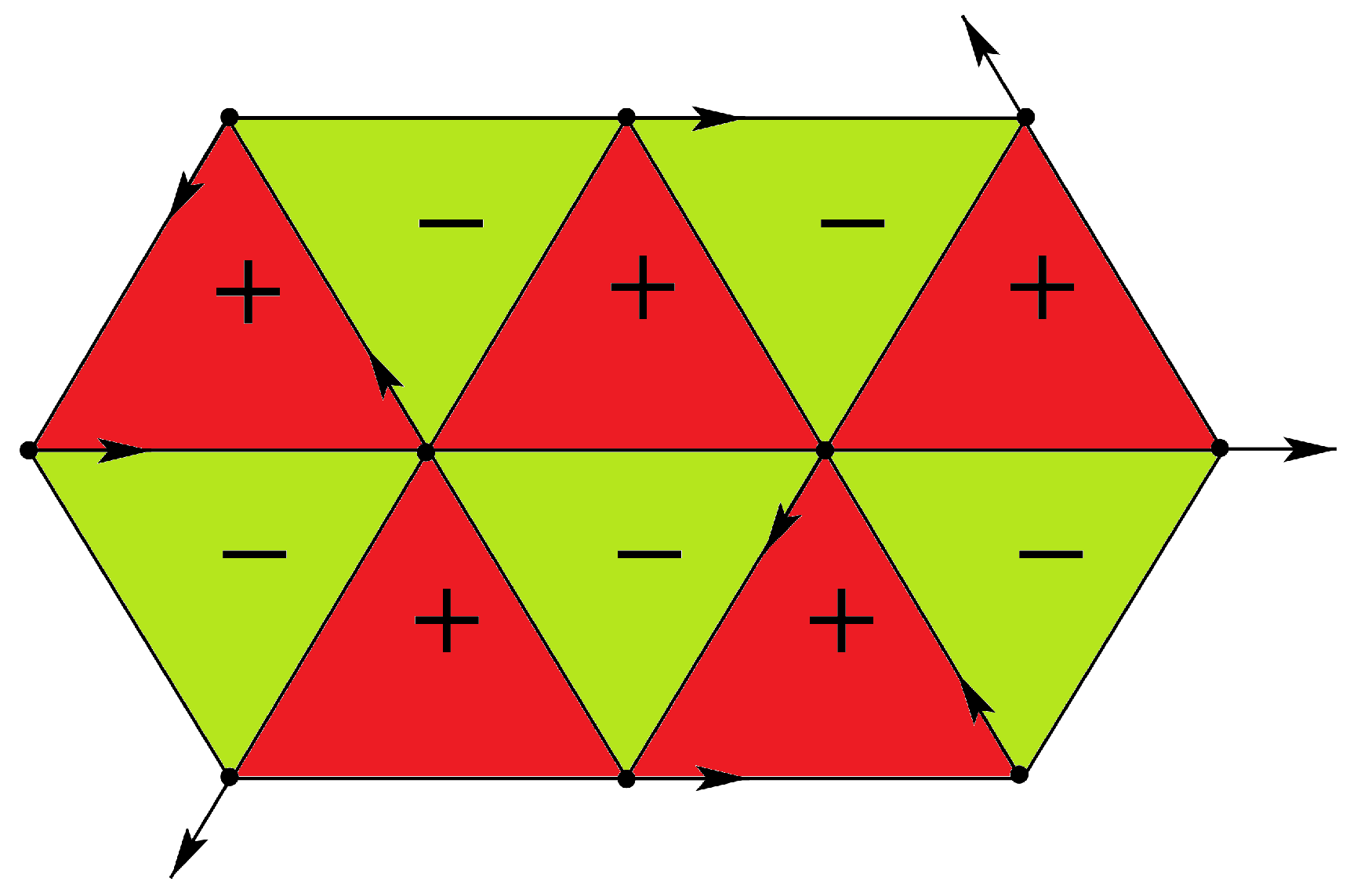
3.1. Example of the Decimation Method
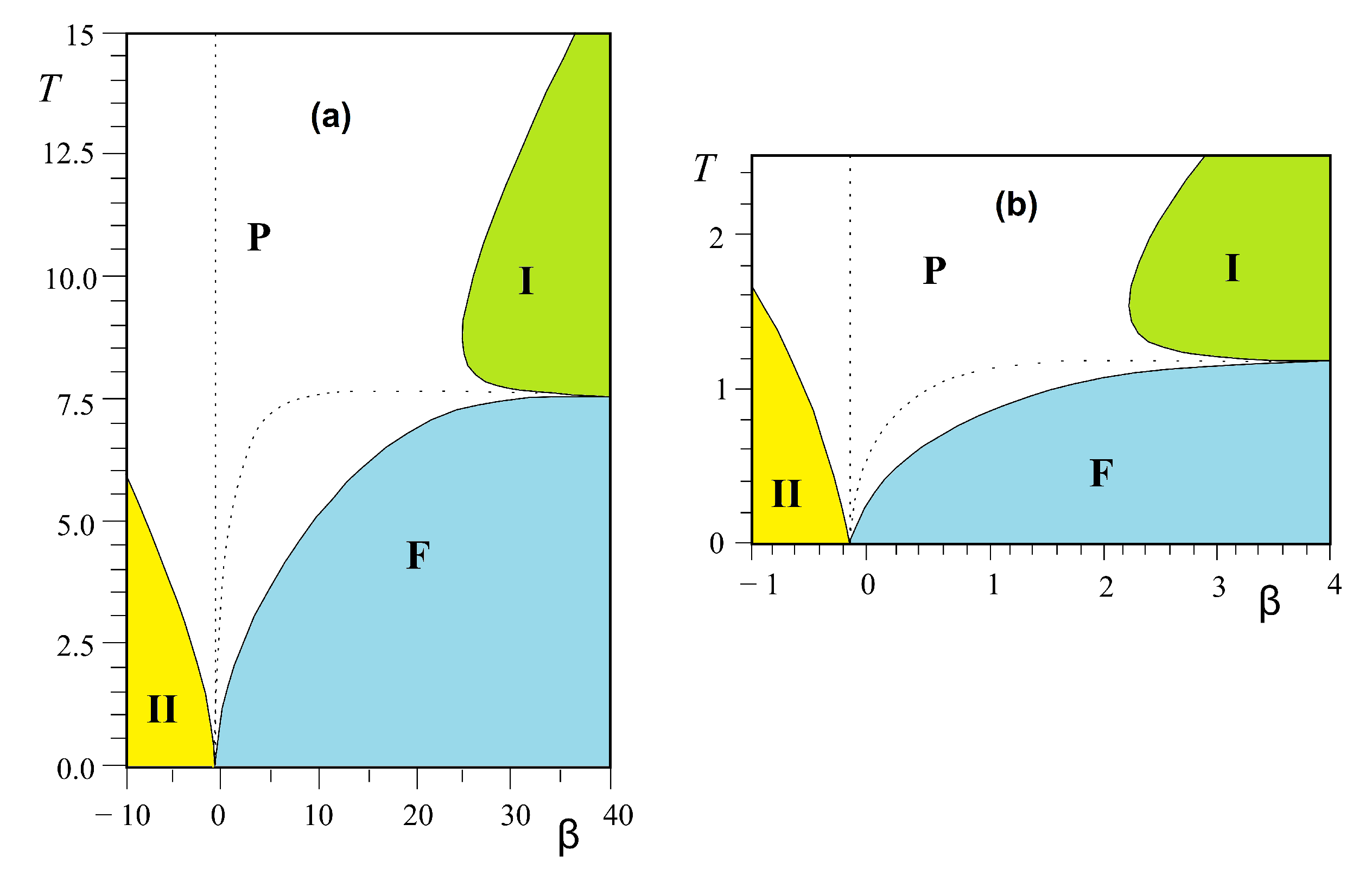
3.2. Disorder Line, Reentrance
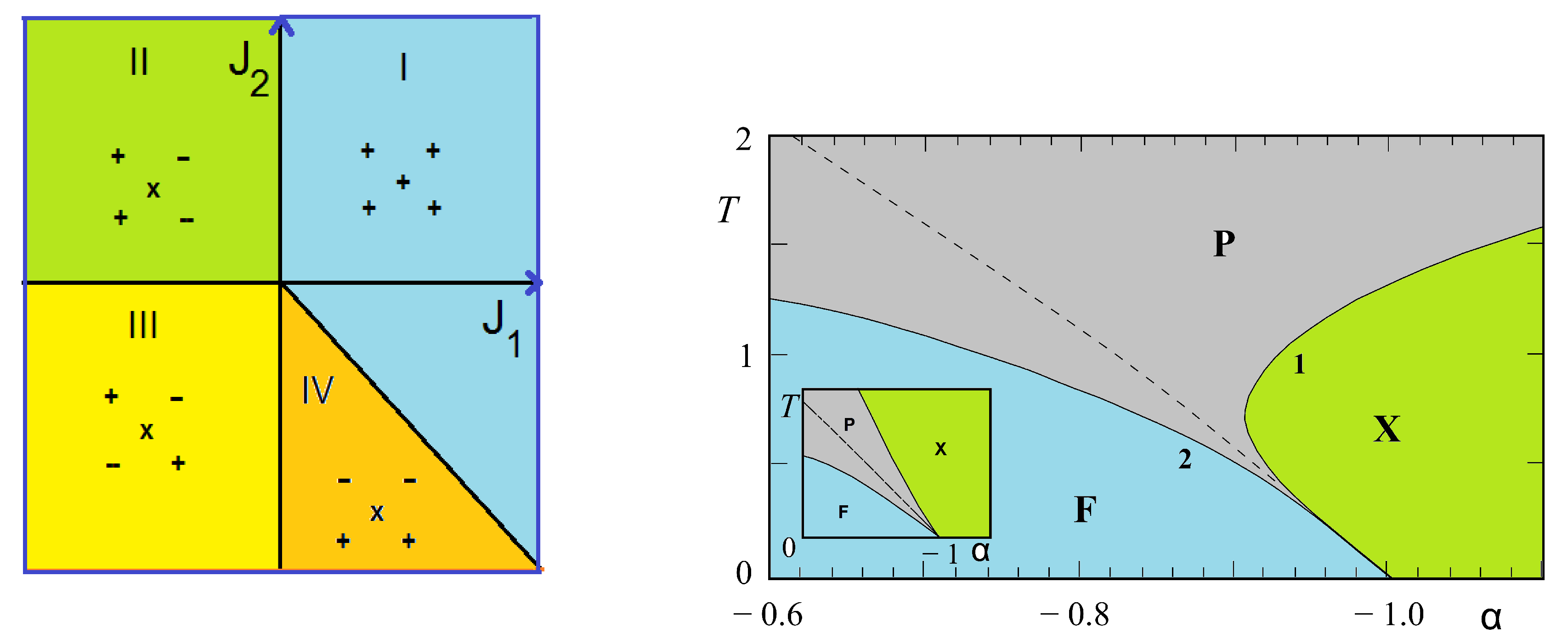
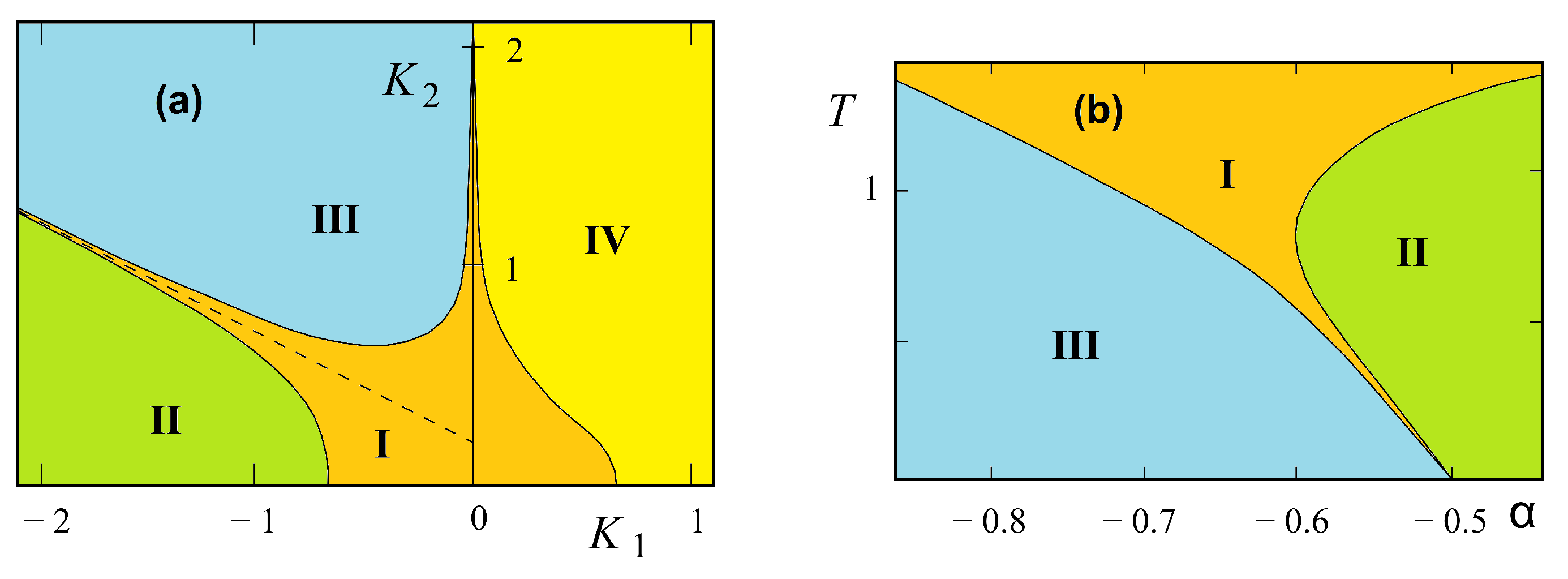
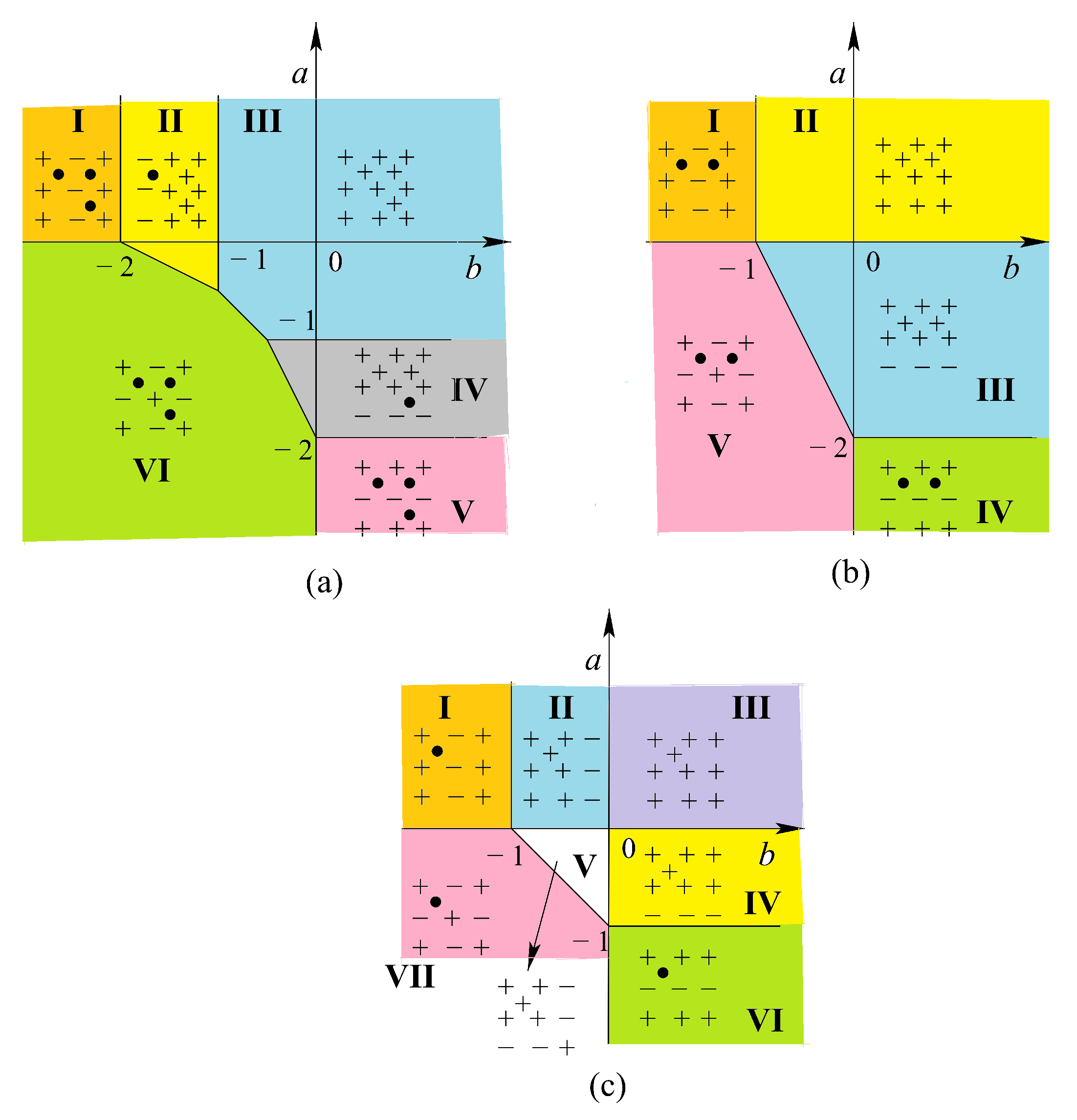
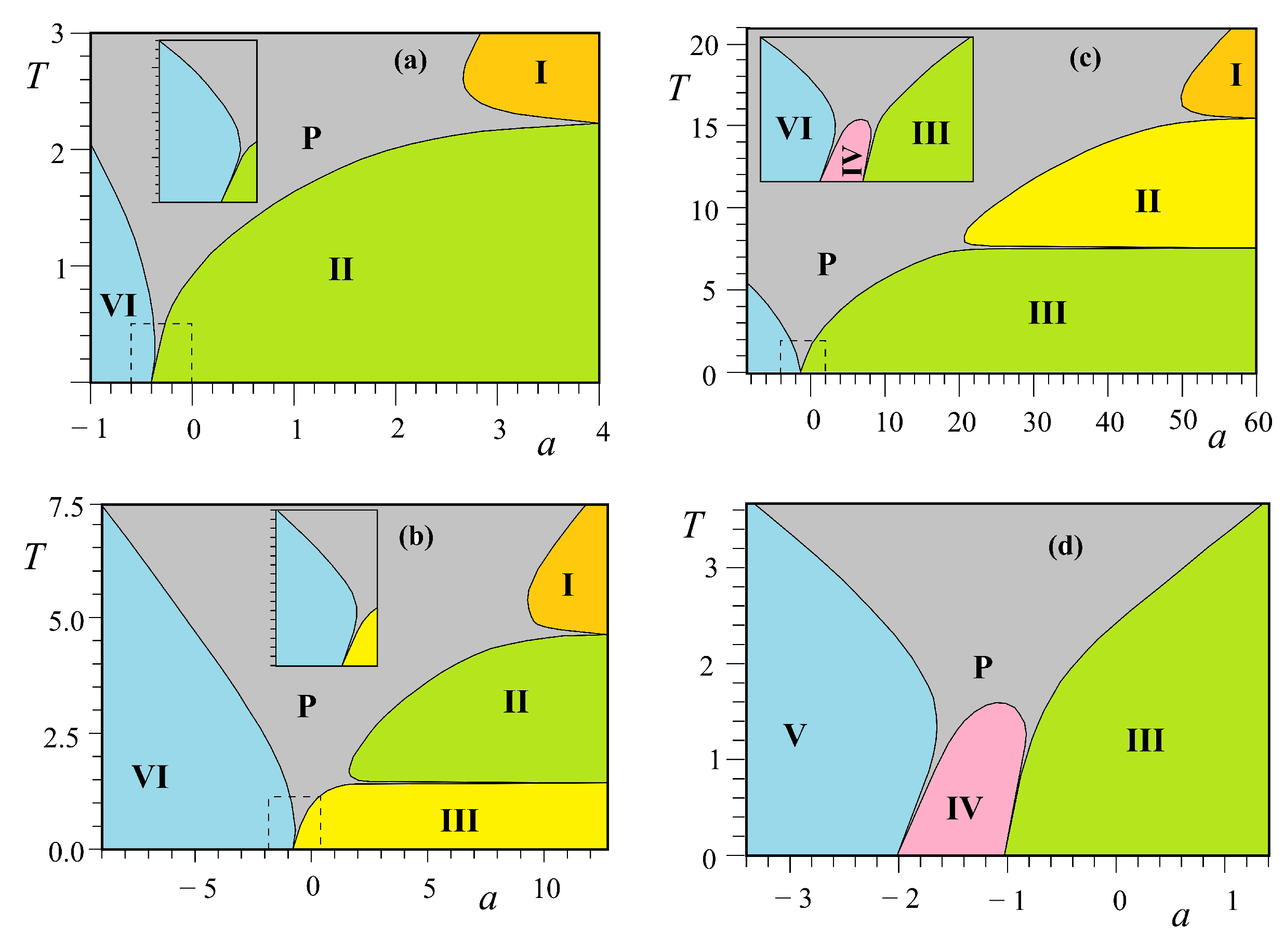
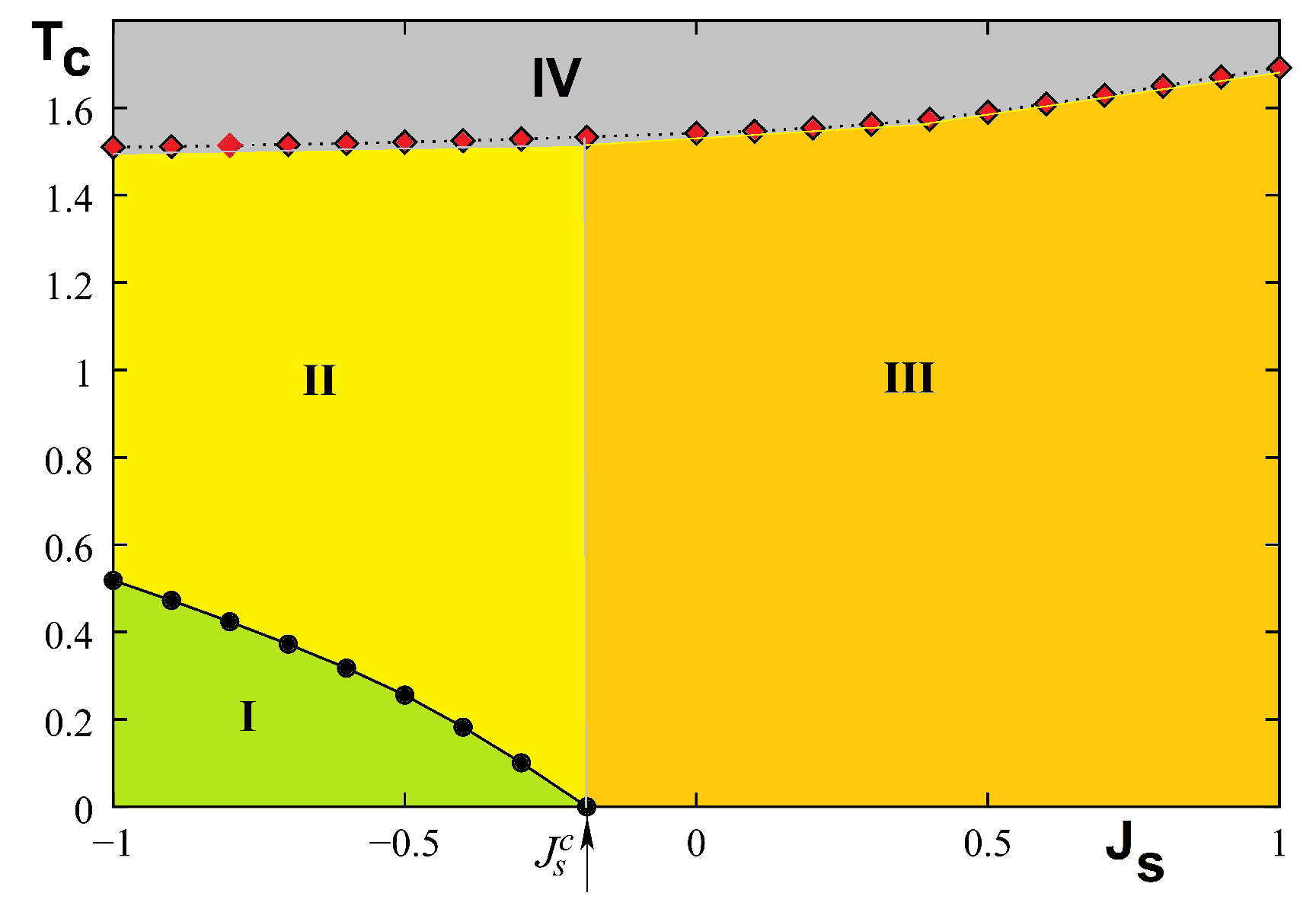
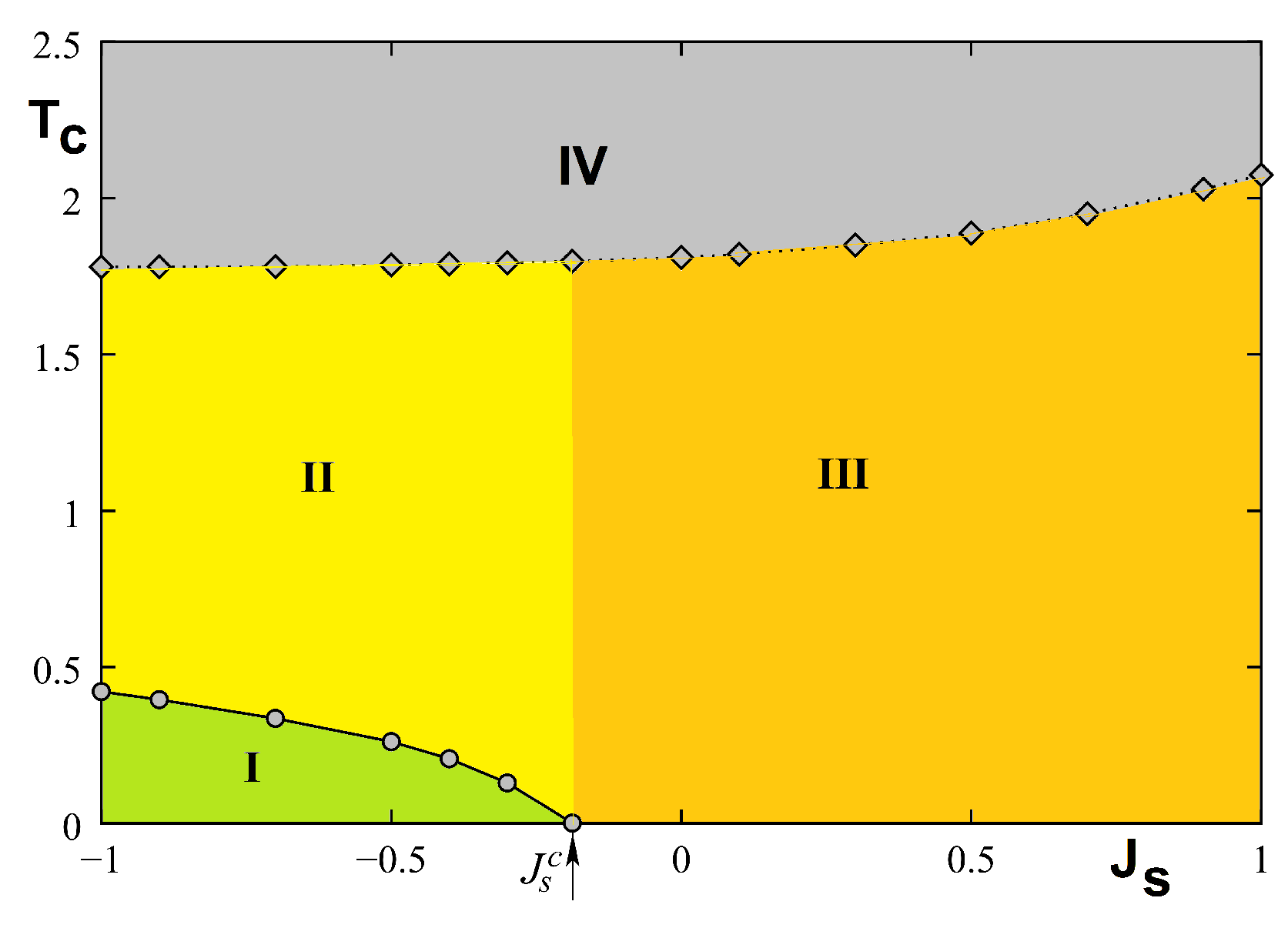
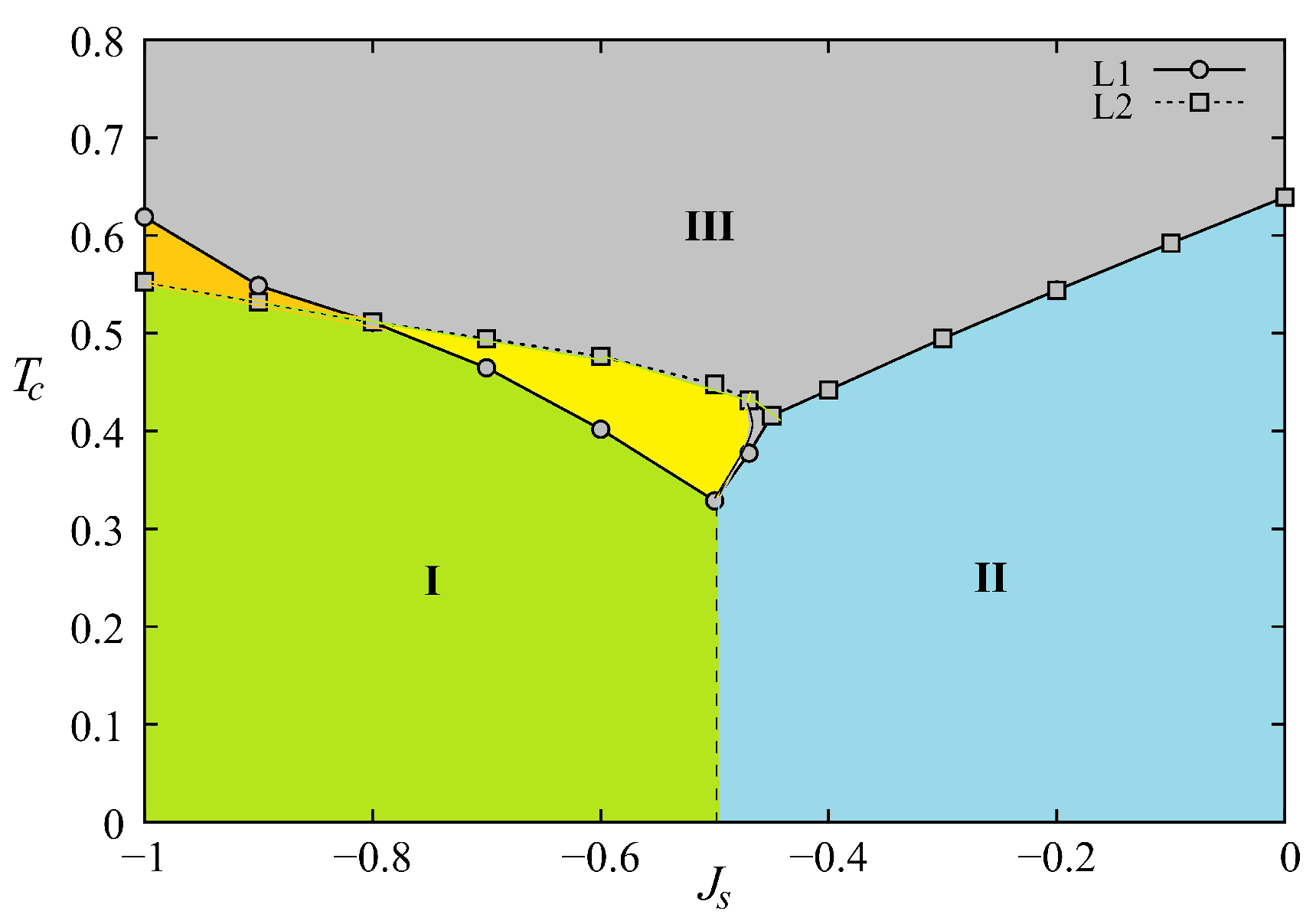
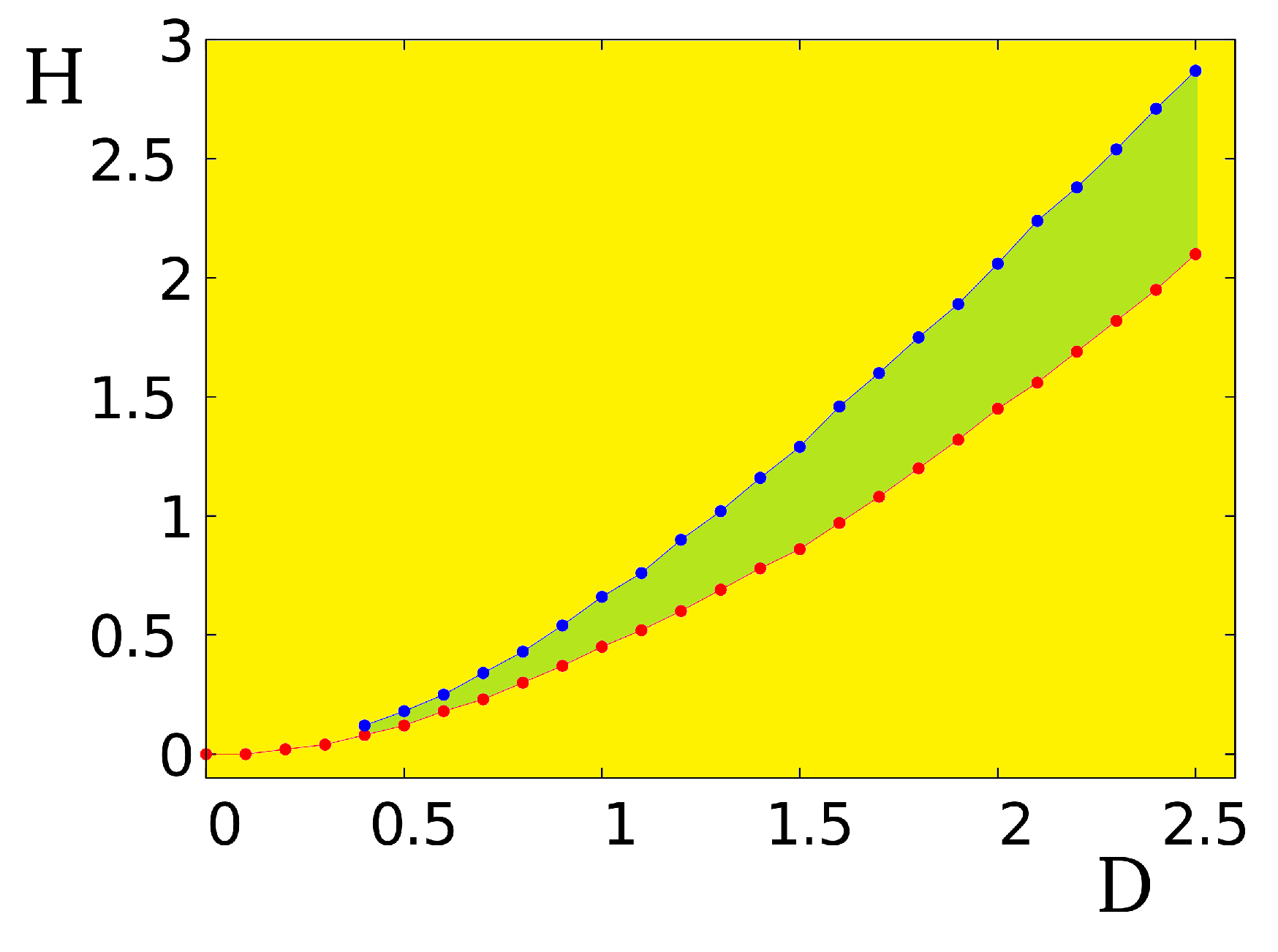
3.3. Phase Diagram
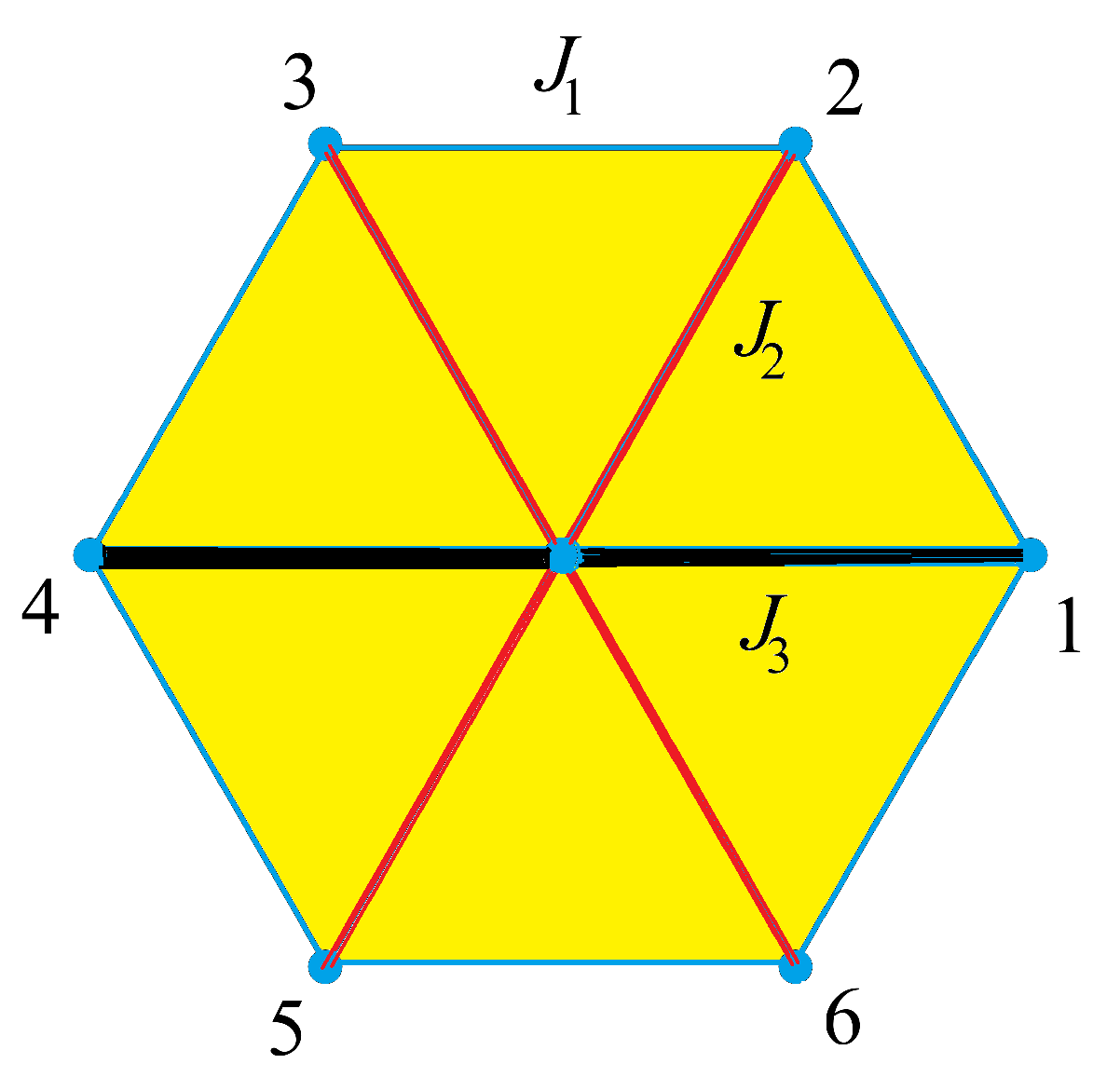
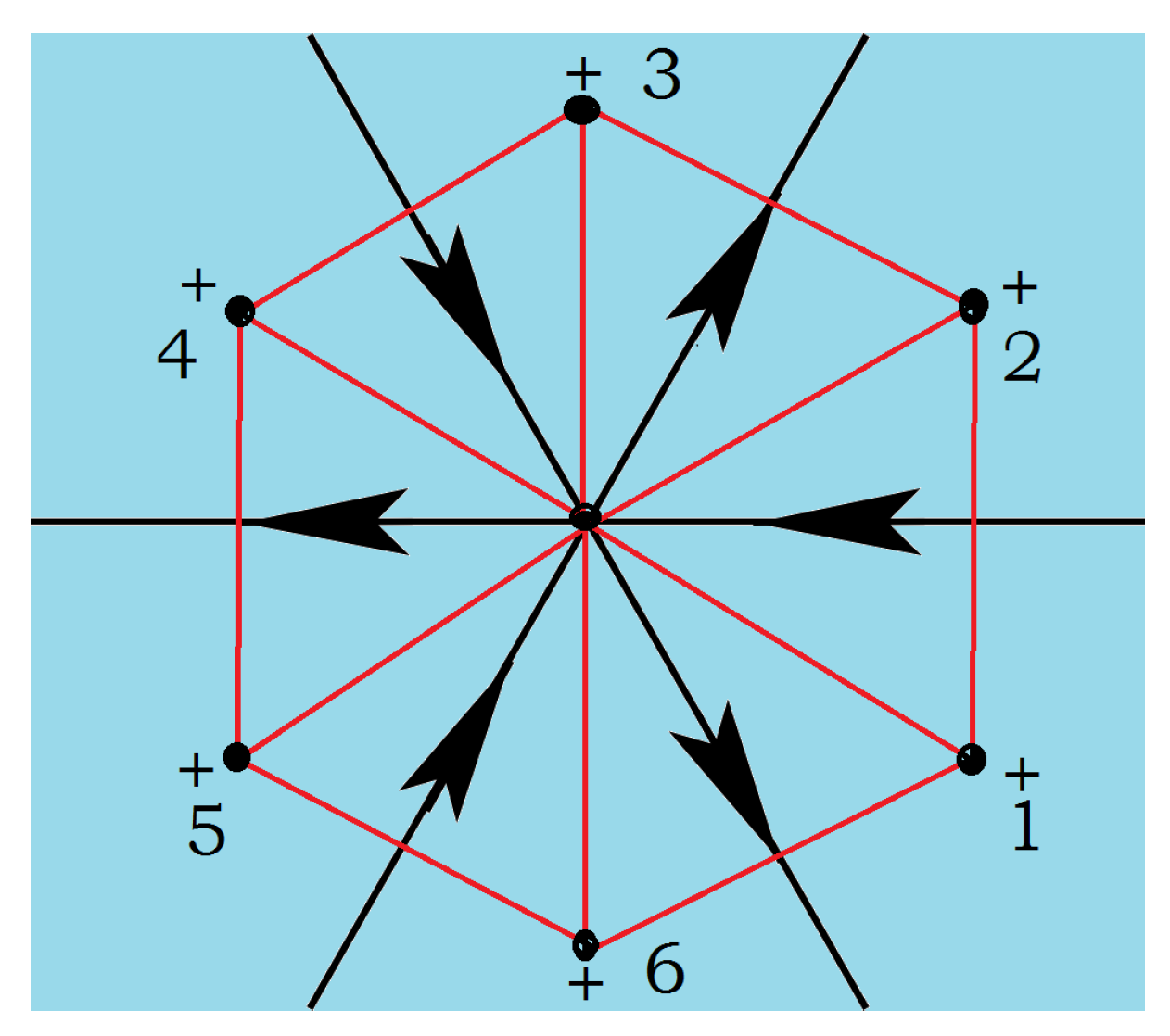
3.3.1. Kagomé Lattice
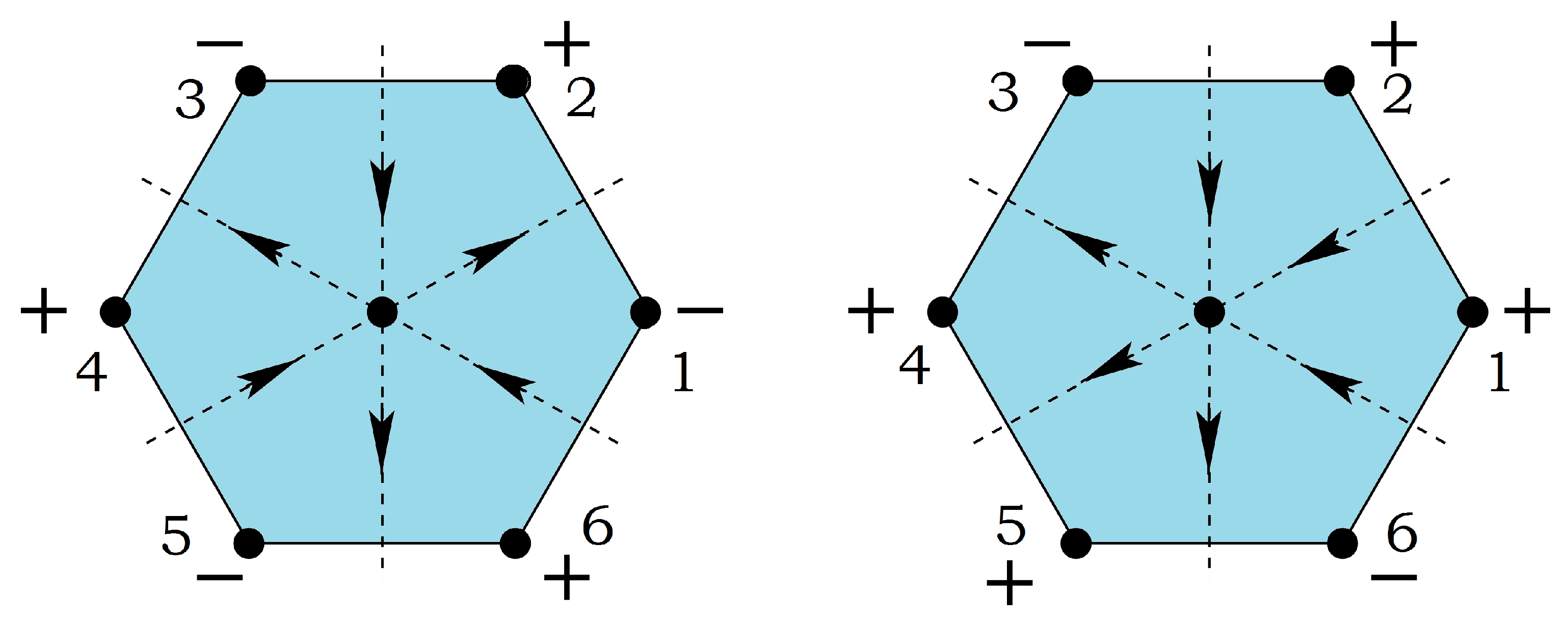
3.3.2. Centered Honeycomb Lattice
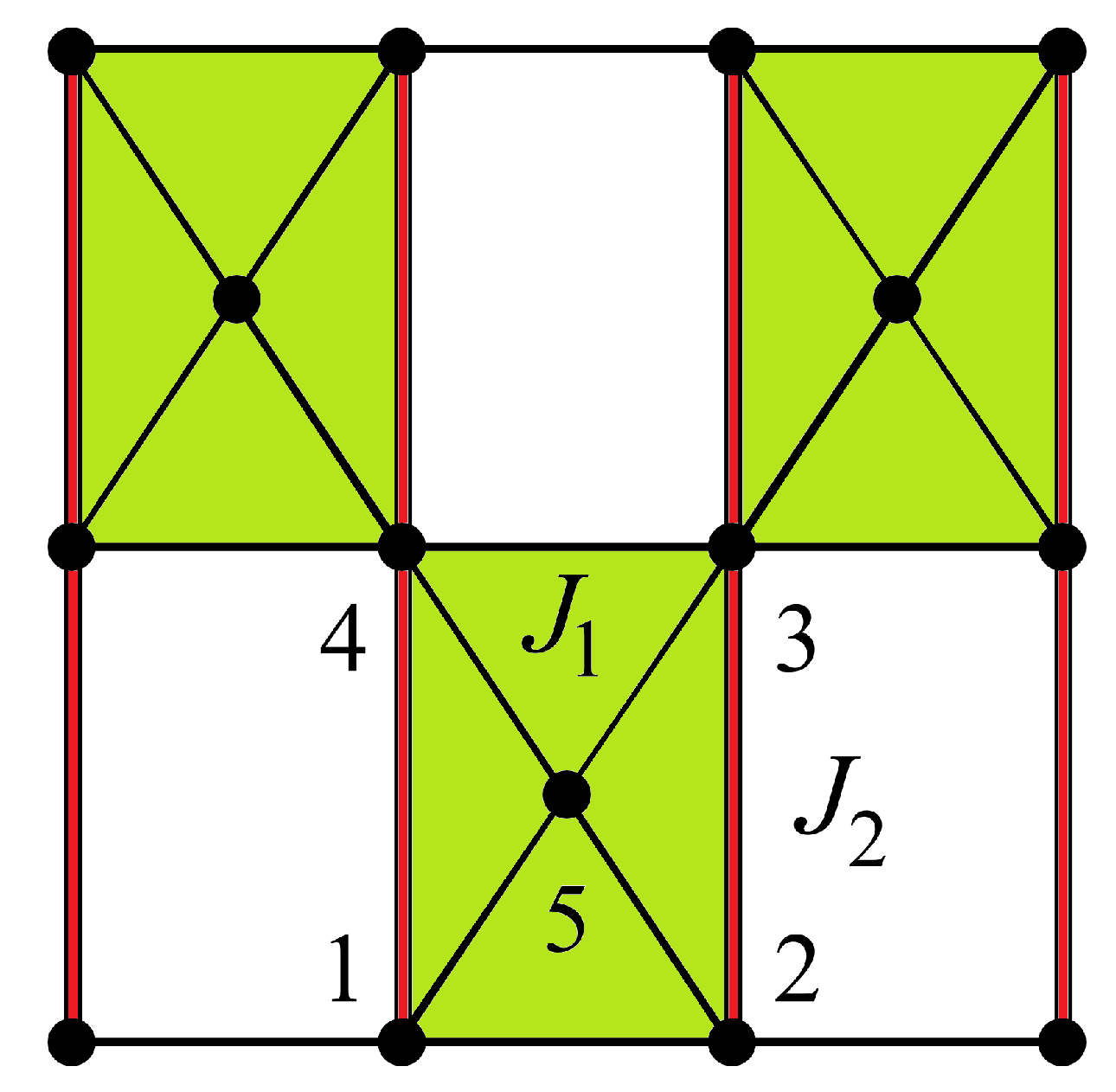
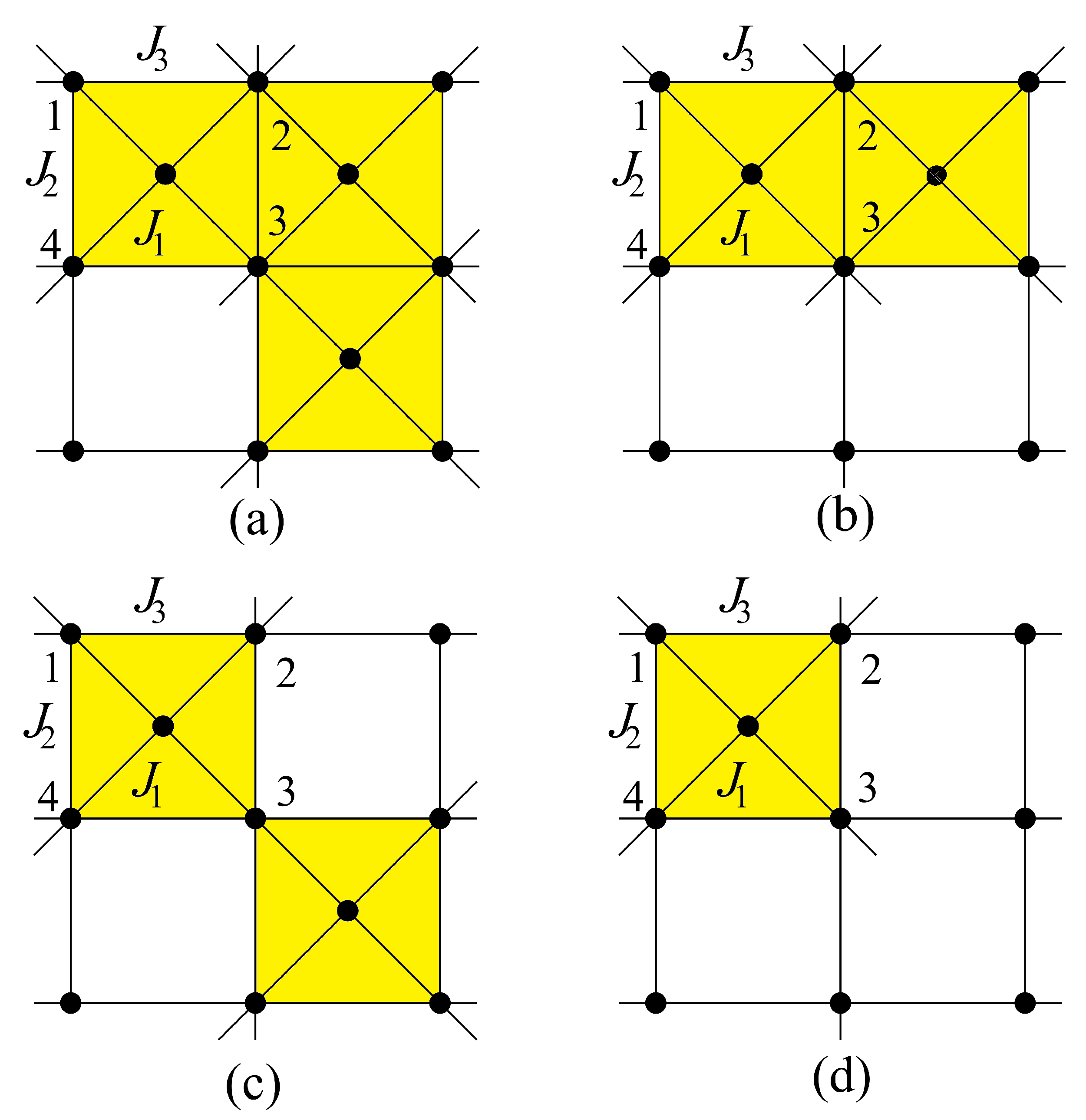
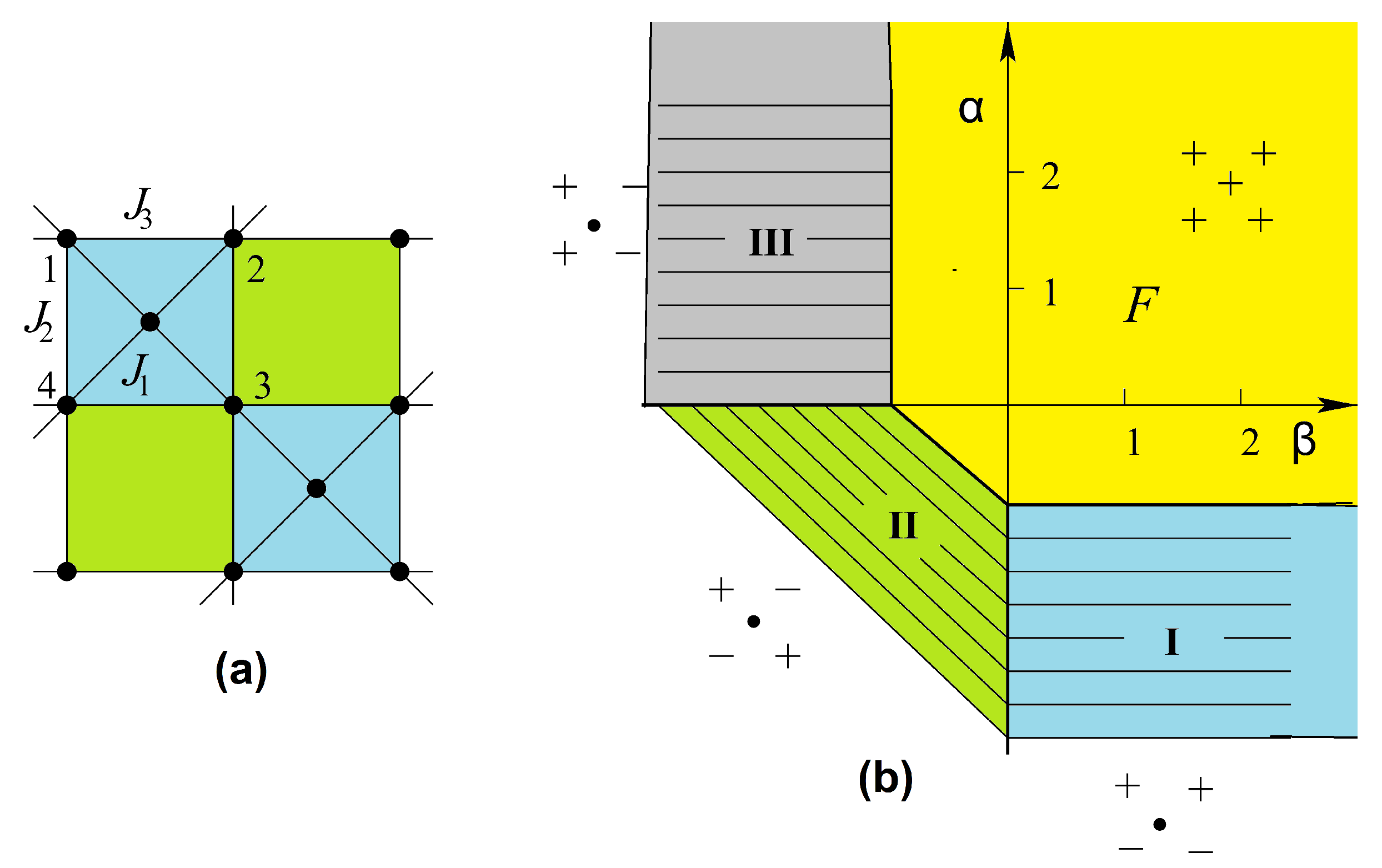
3.3.3. Centered Square Lattices
3.4. Summary and Discussion
- (1)
- the partial disorder at equilibrium: disorder is not equally shared on all particles as usually the case in unfrustrated systems.
- (2)
- the reentrance: this occurs around the phase boundary when T increases → the phase with larger entropy will win at finite T. In other words, this is a kind of selection by entropy.
- (3)
- the disorder line: this line occurs in the paramagnetic phase. It separates the pre-ordering zones between two nearby ordered phases.
4. Physics of Thin Films: Surface Magnetism, Background
4.1. Surface Parameters
4.2. Surface Spin Waves: Simple Examples
- Film of simple cubic latticewhere (in-plane coordination number) and .
- Film of body-centered cubic latticewhere
5. Frustrated Thin Films: Surface Phase Transition
5.1. Frustrated Surfaces
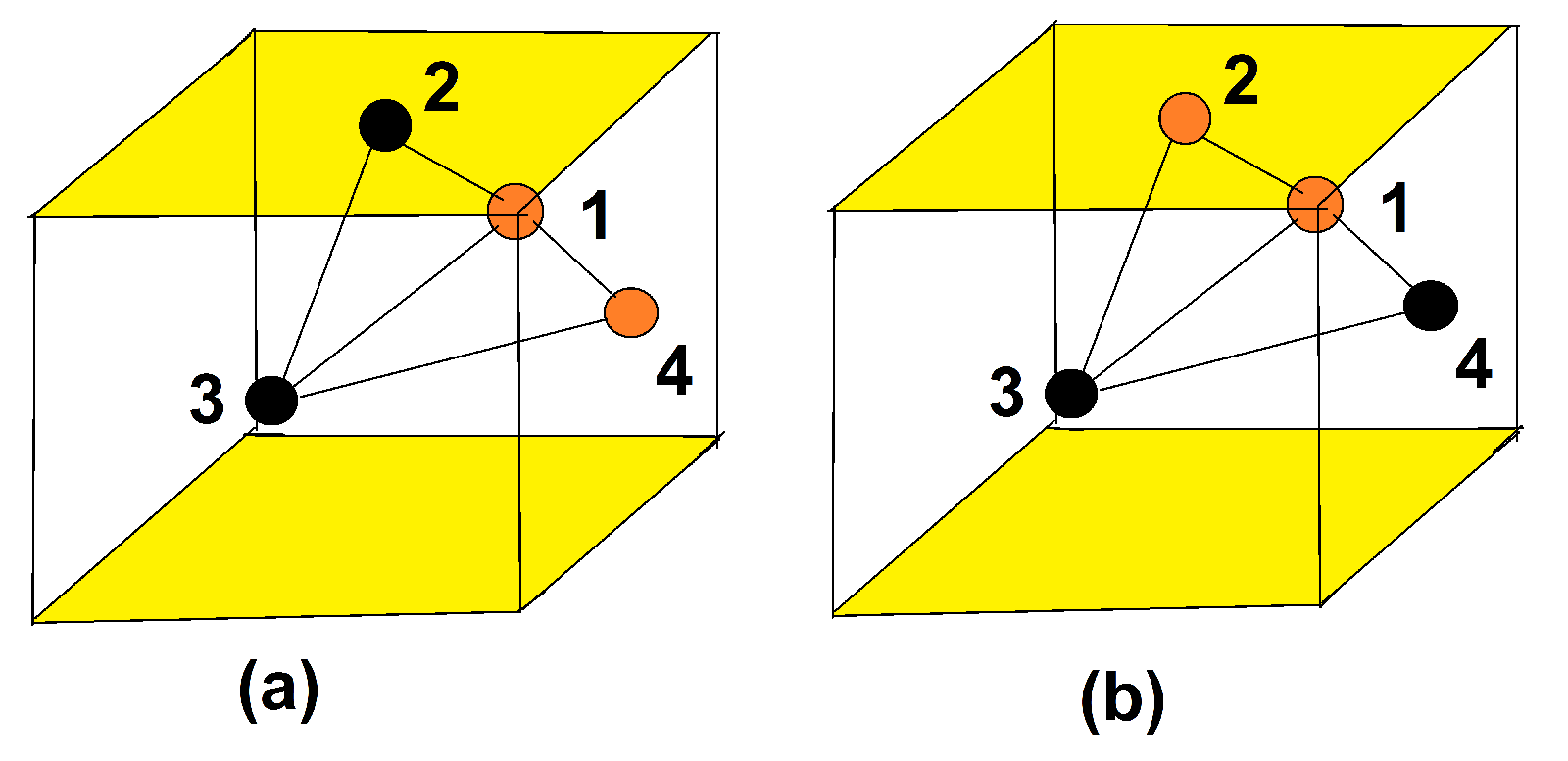
5.2. Model
5.3. Ground State
5.4. Results from the Green’s Function Method
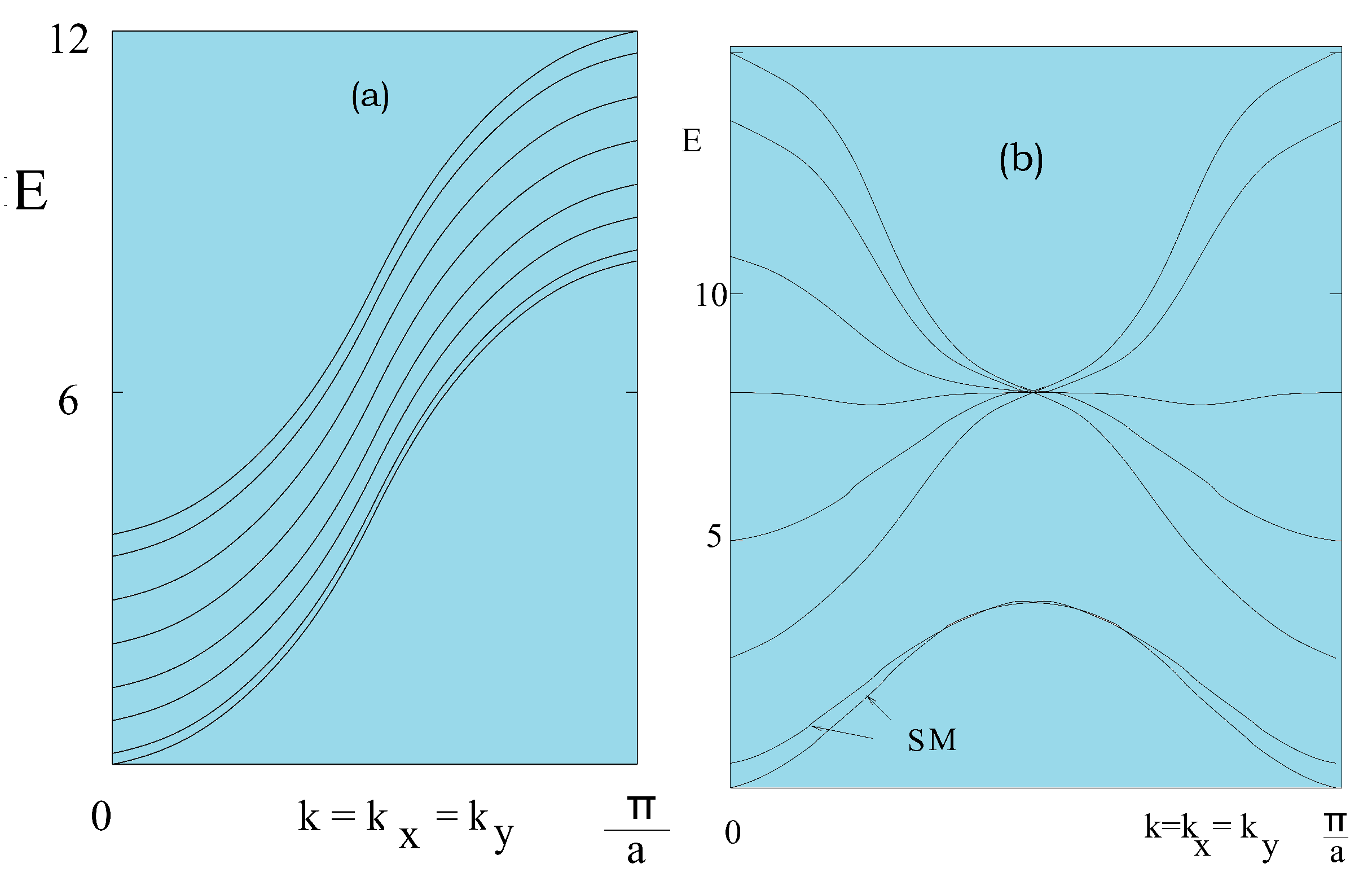
5.4.1. Phase Transition and Phase Diagram of the Quantum Case
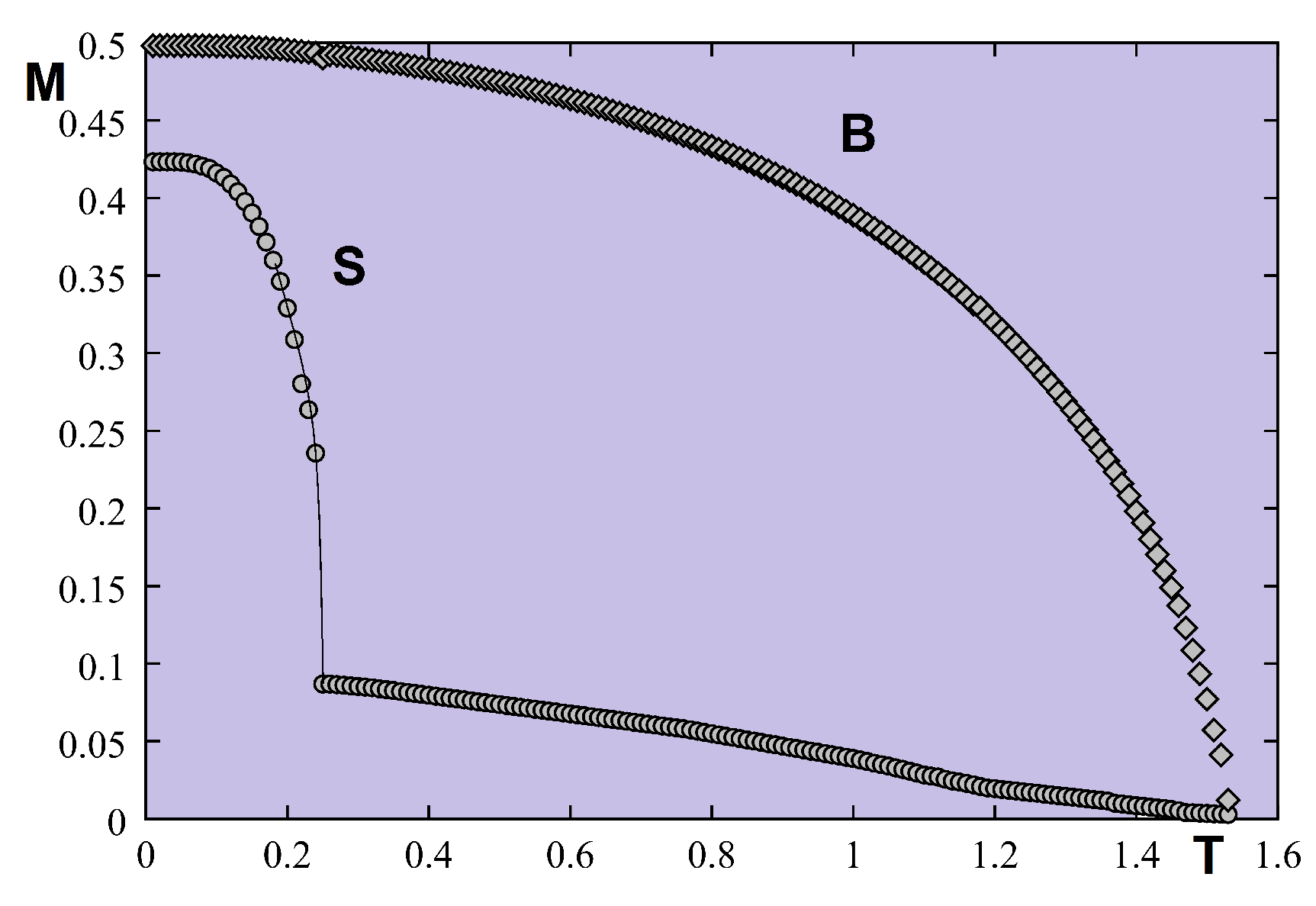
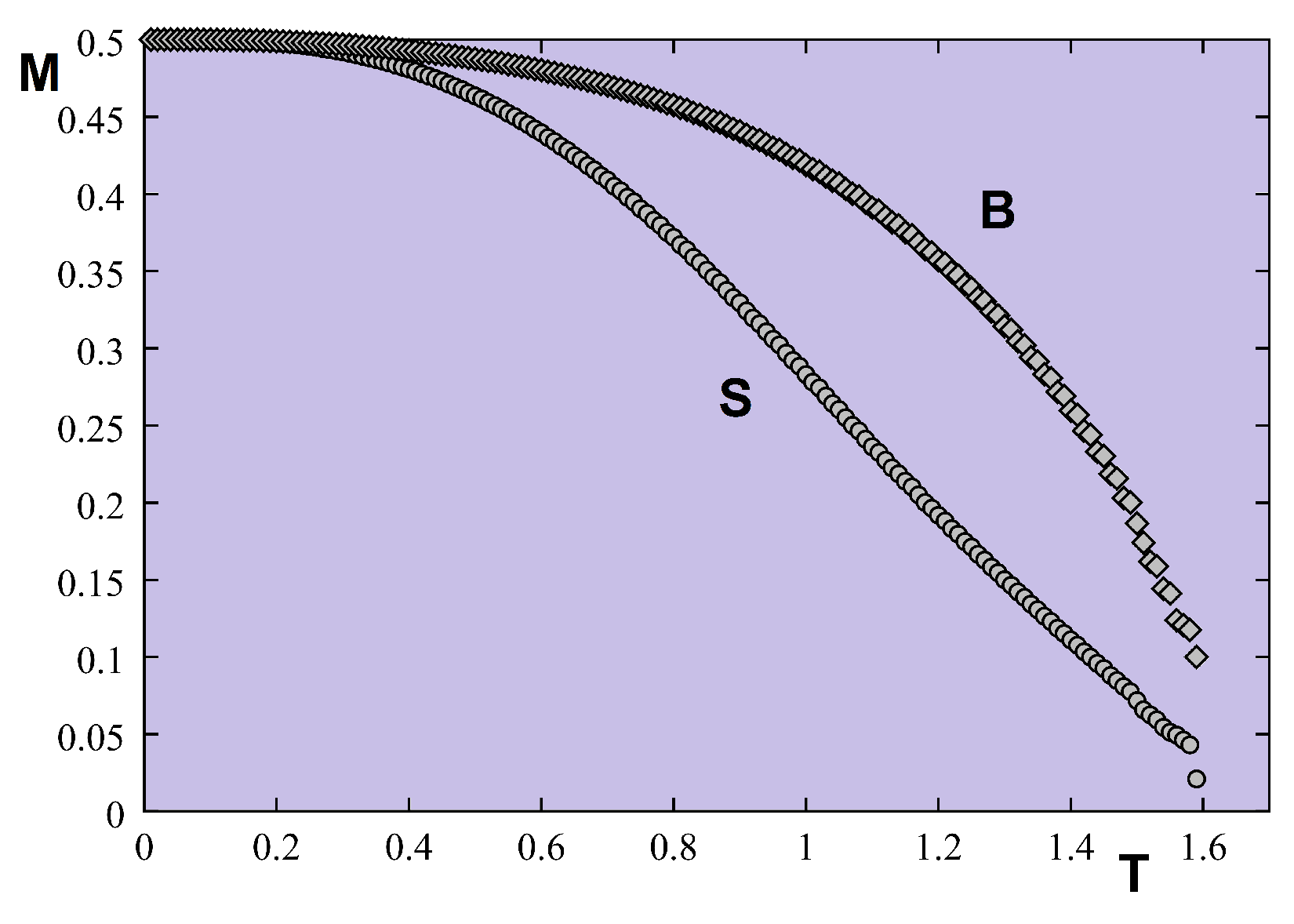
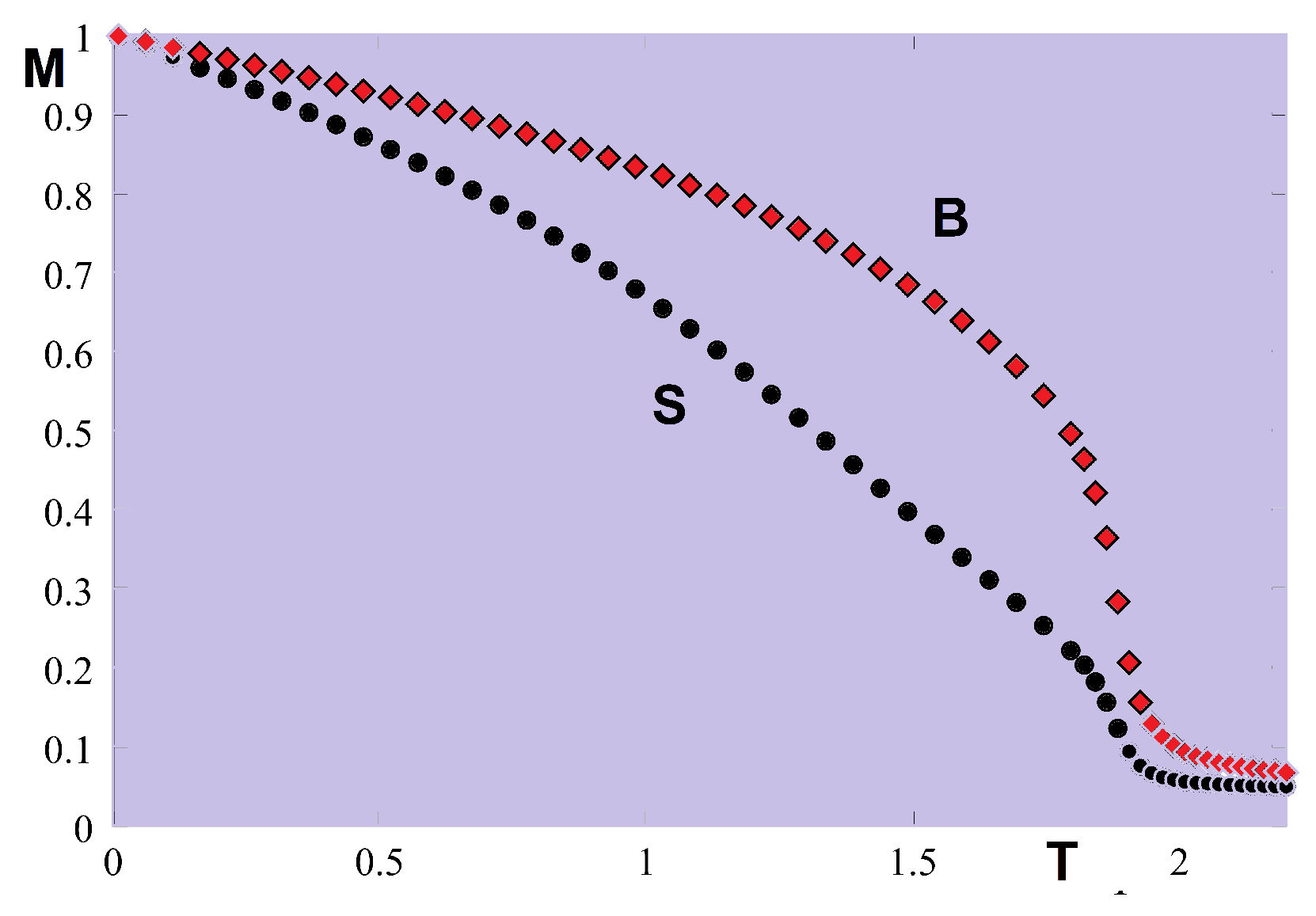
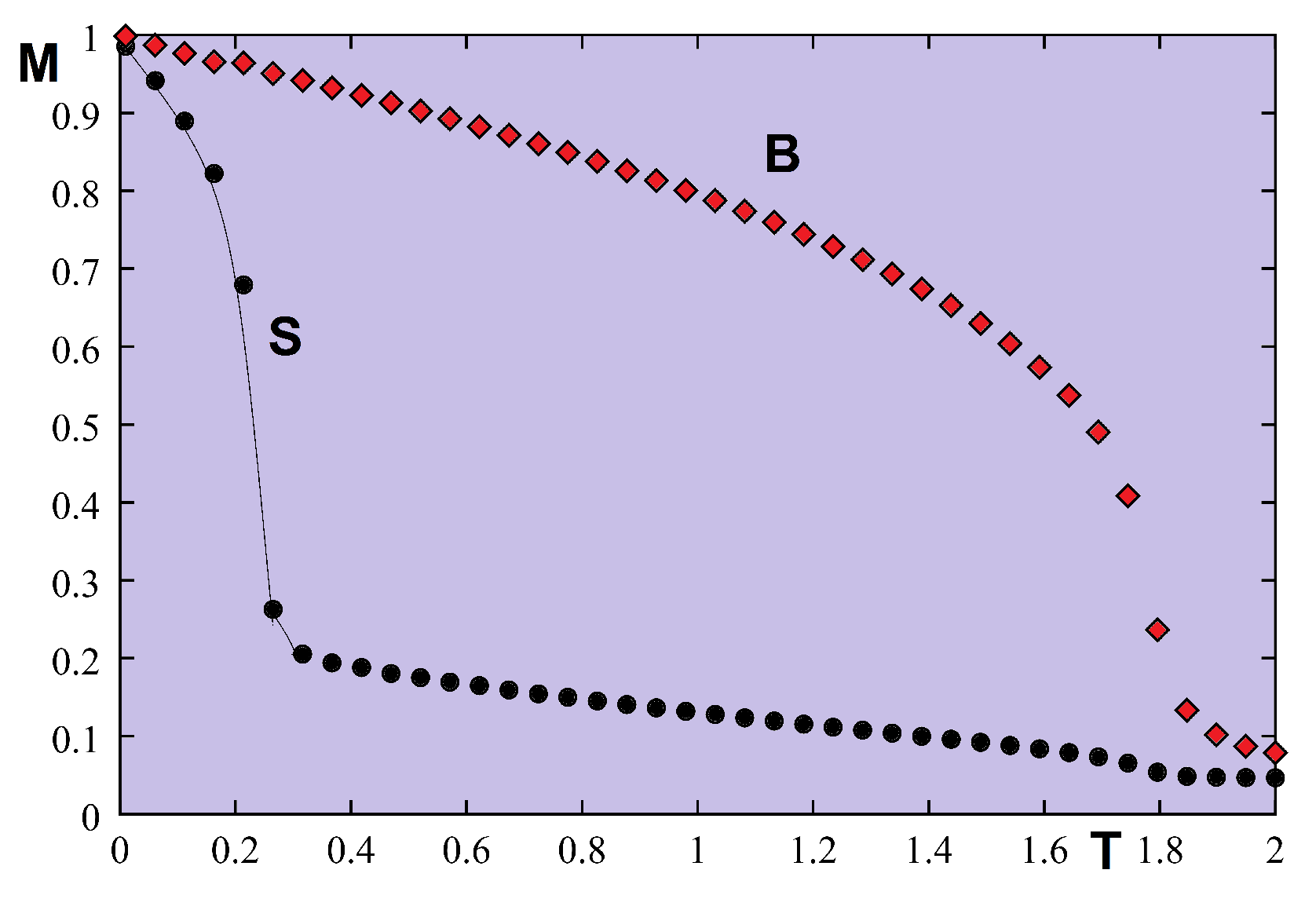
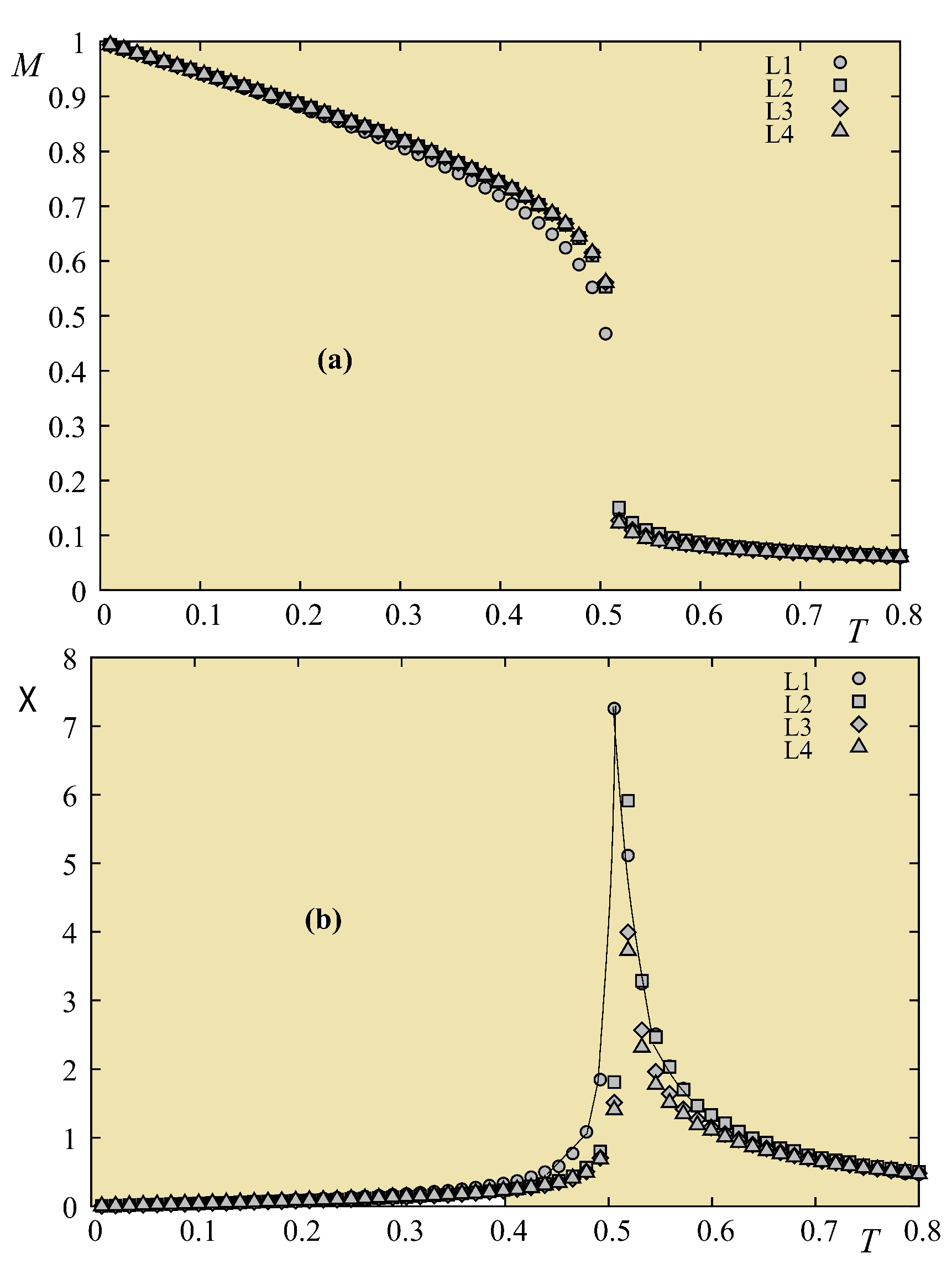
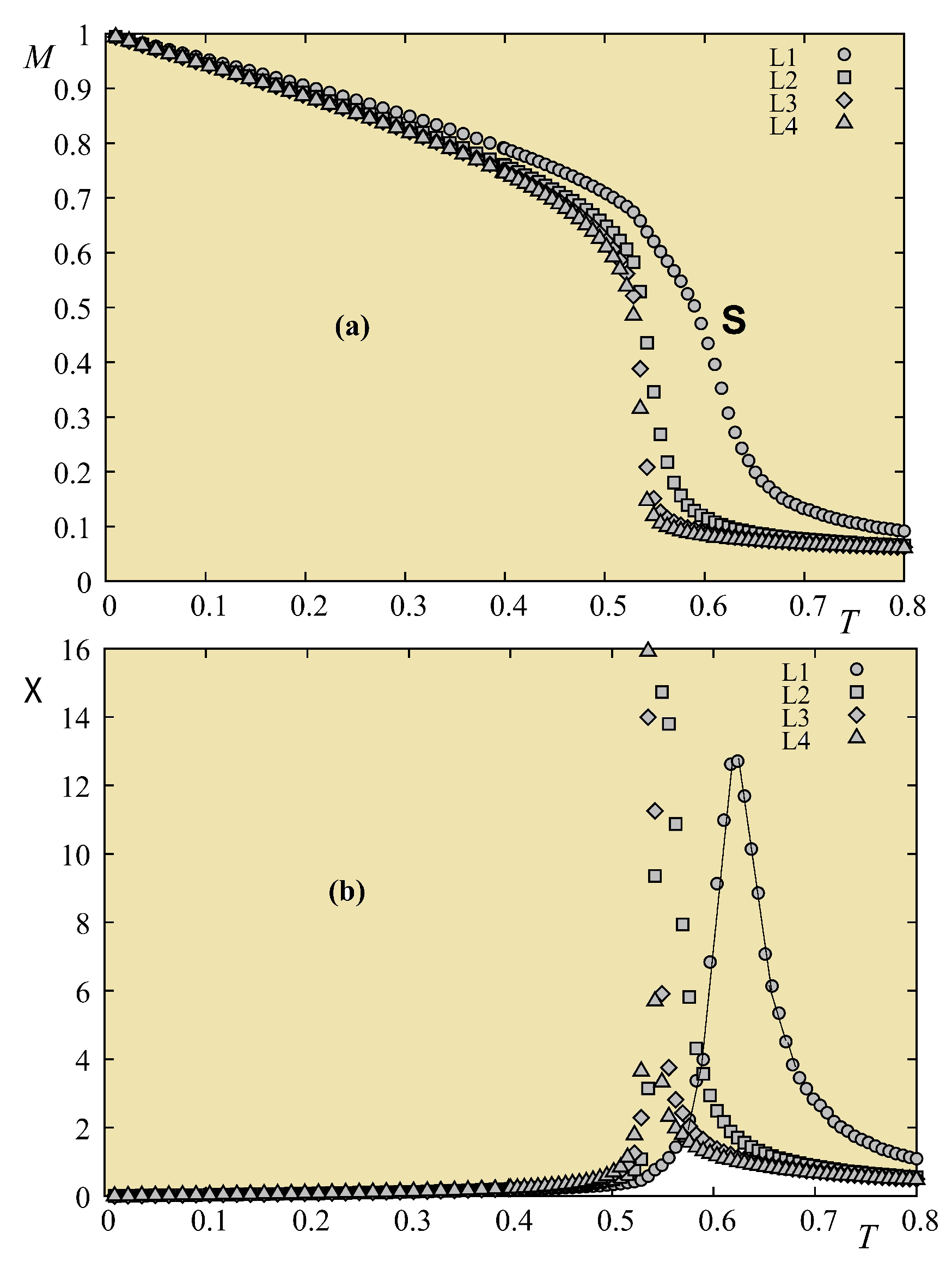
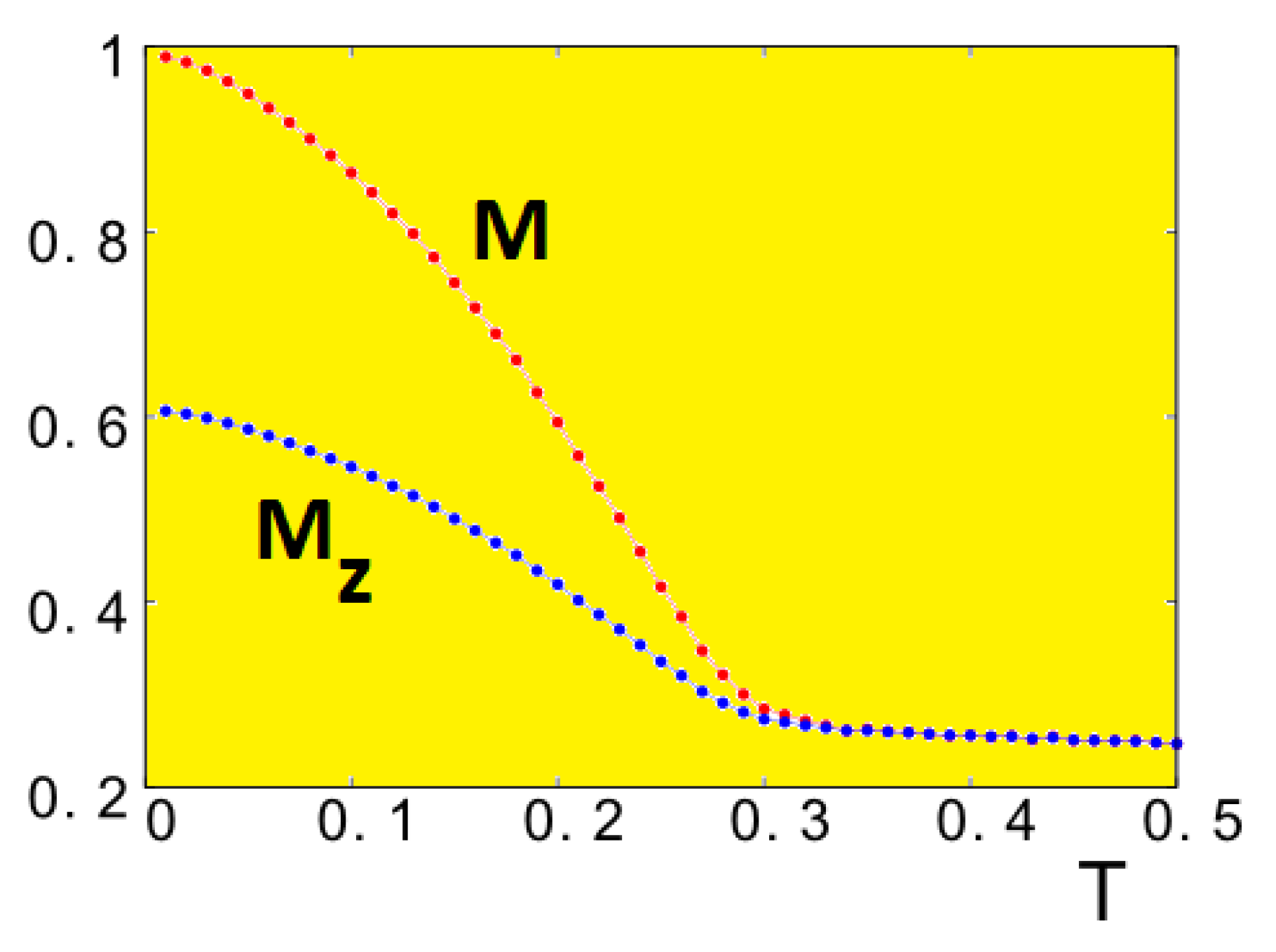
5.4.2. Monte Carlo Results
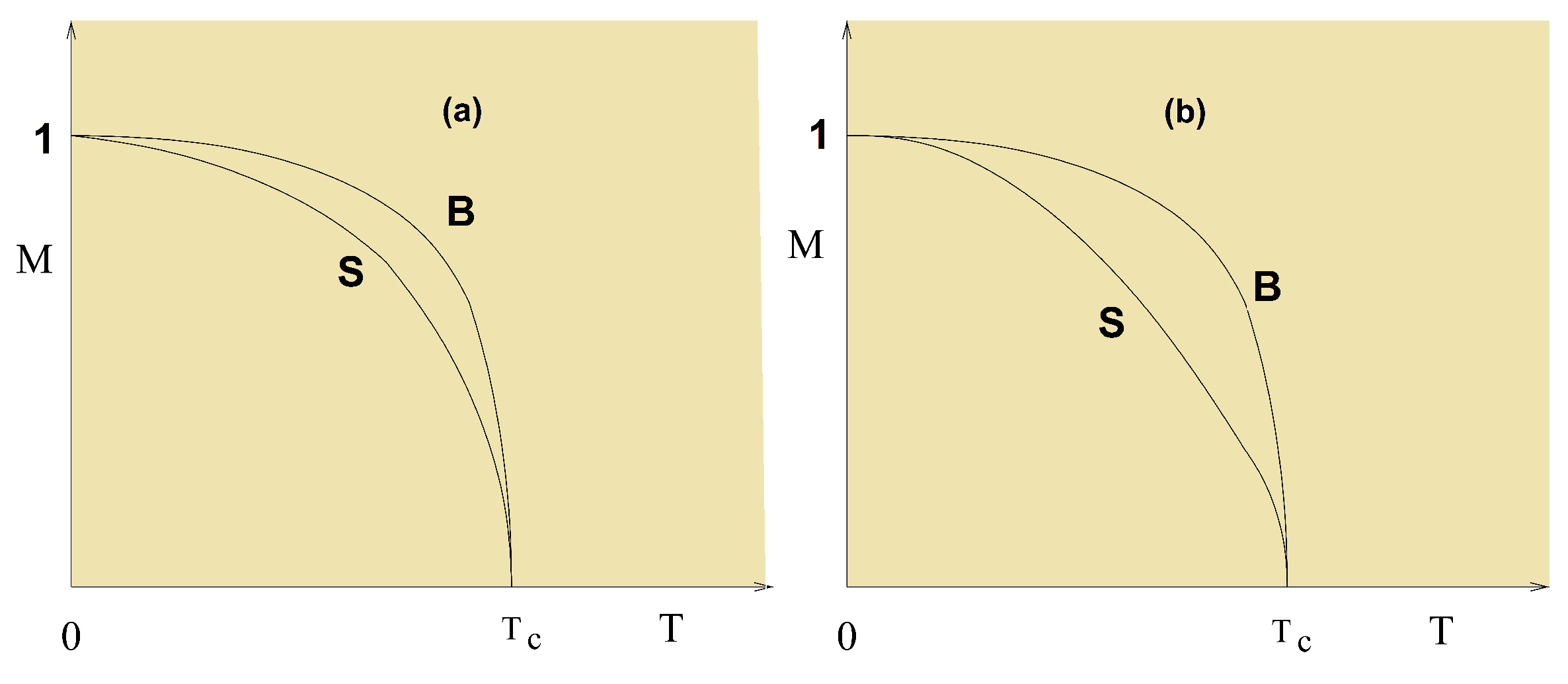
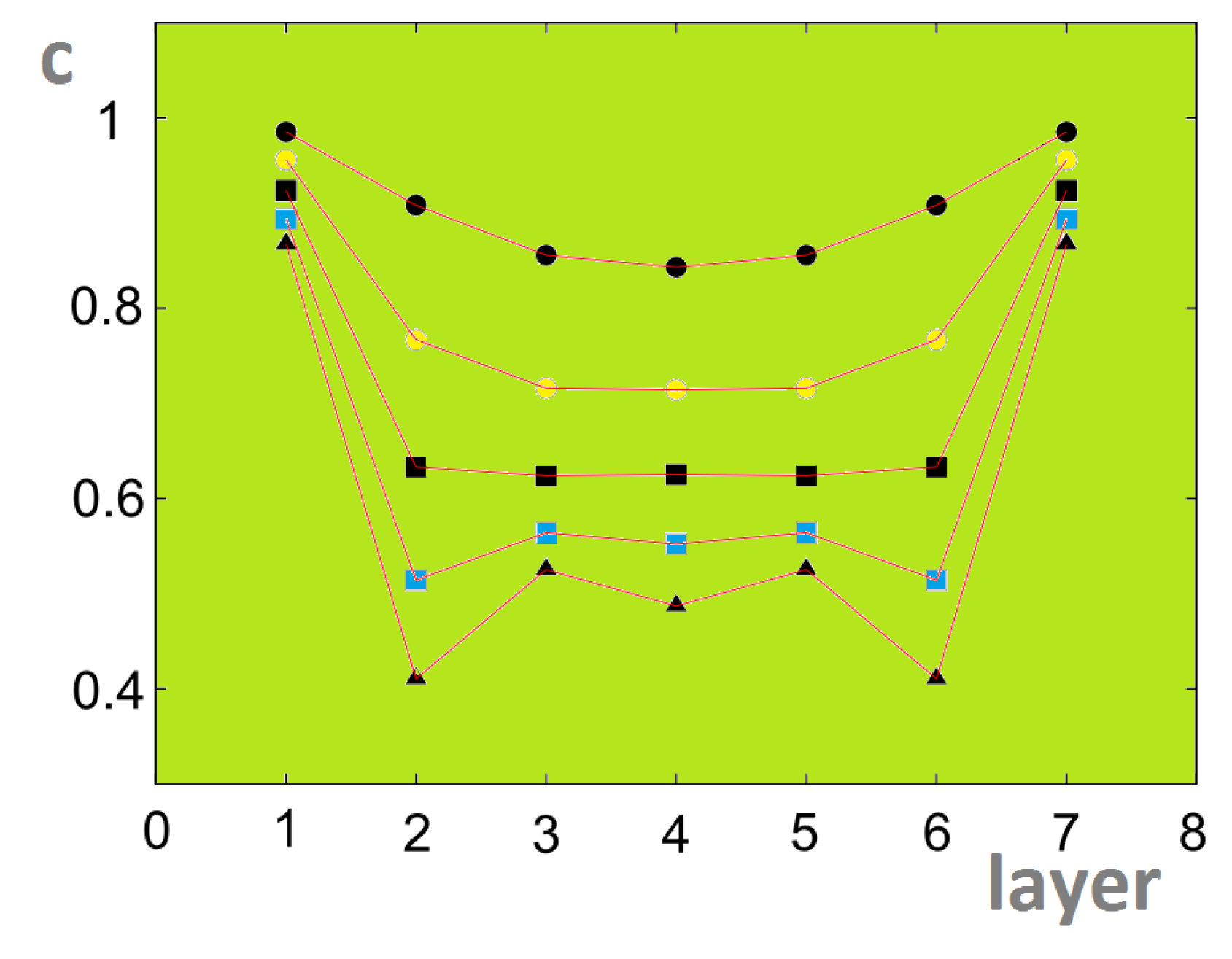
5.5. Frustrated Thin Films
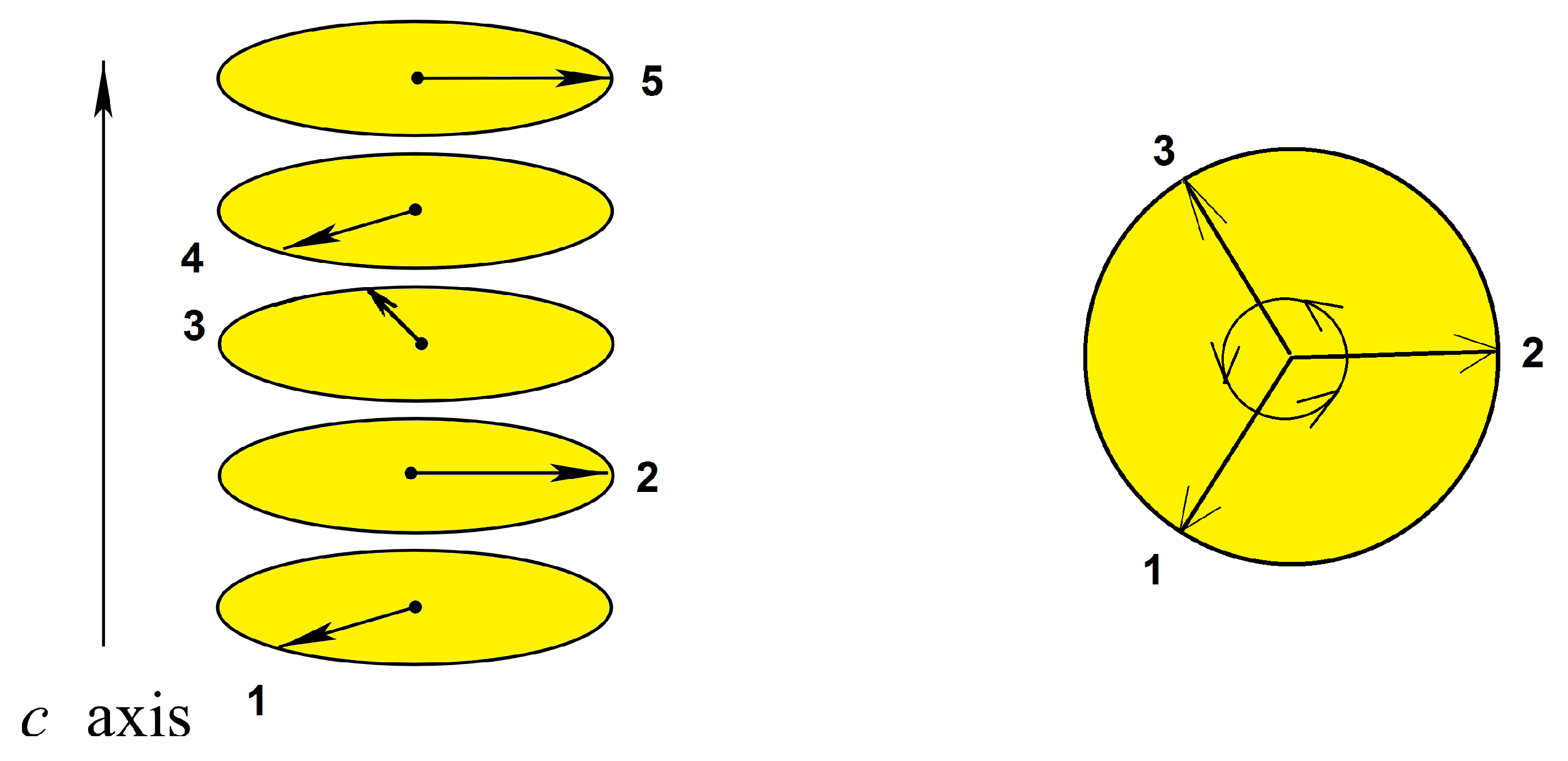
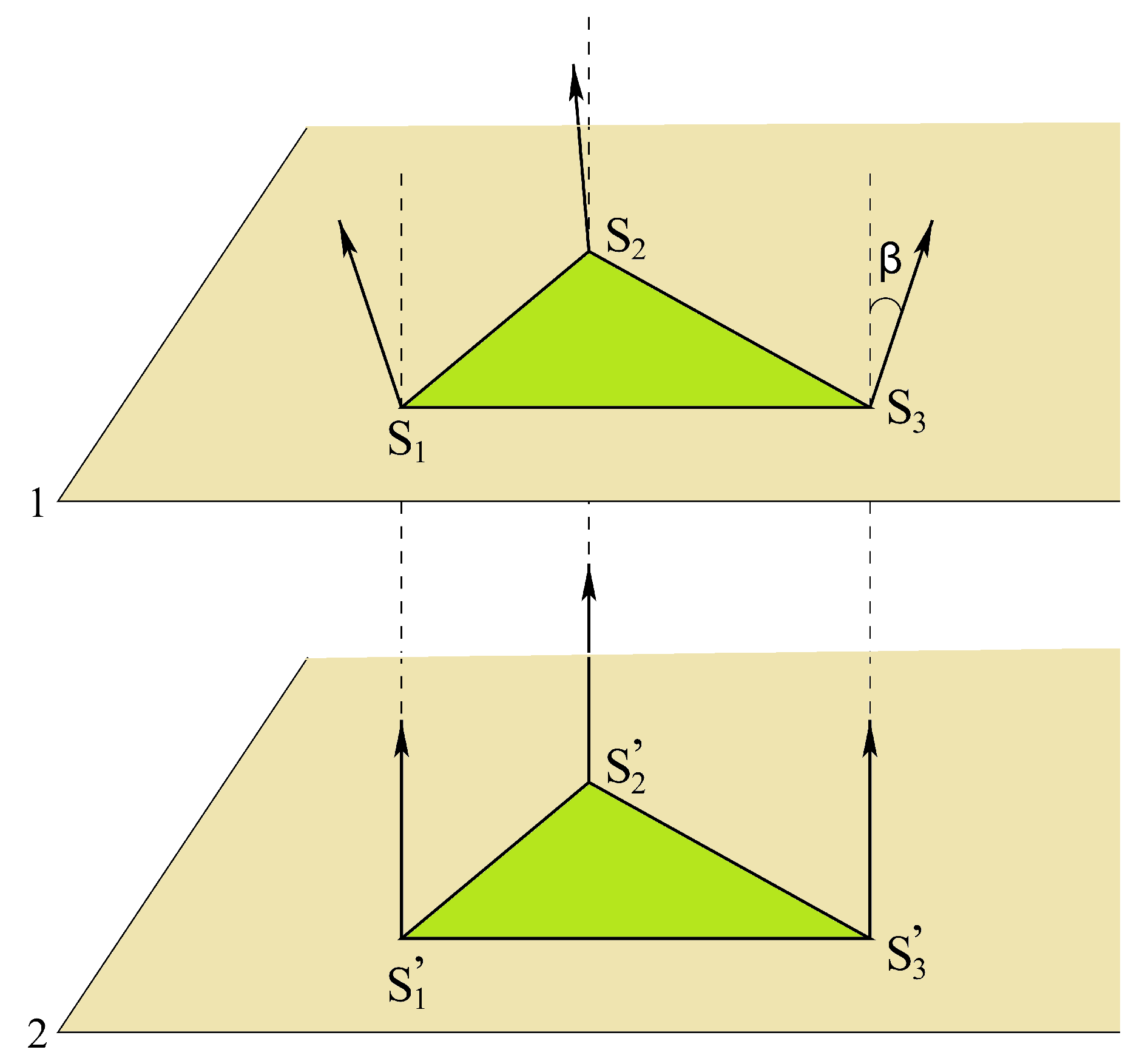
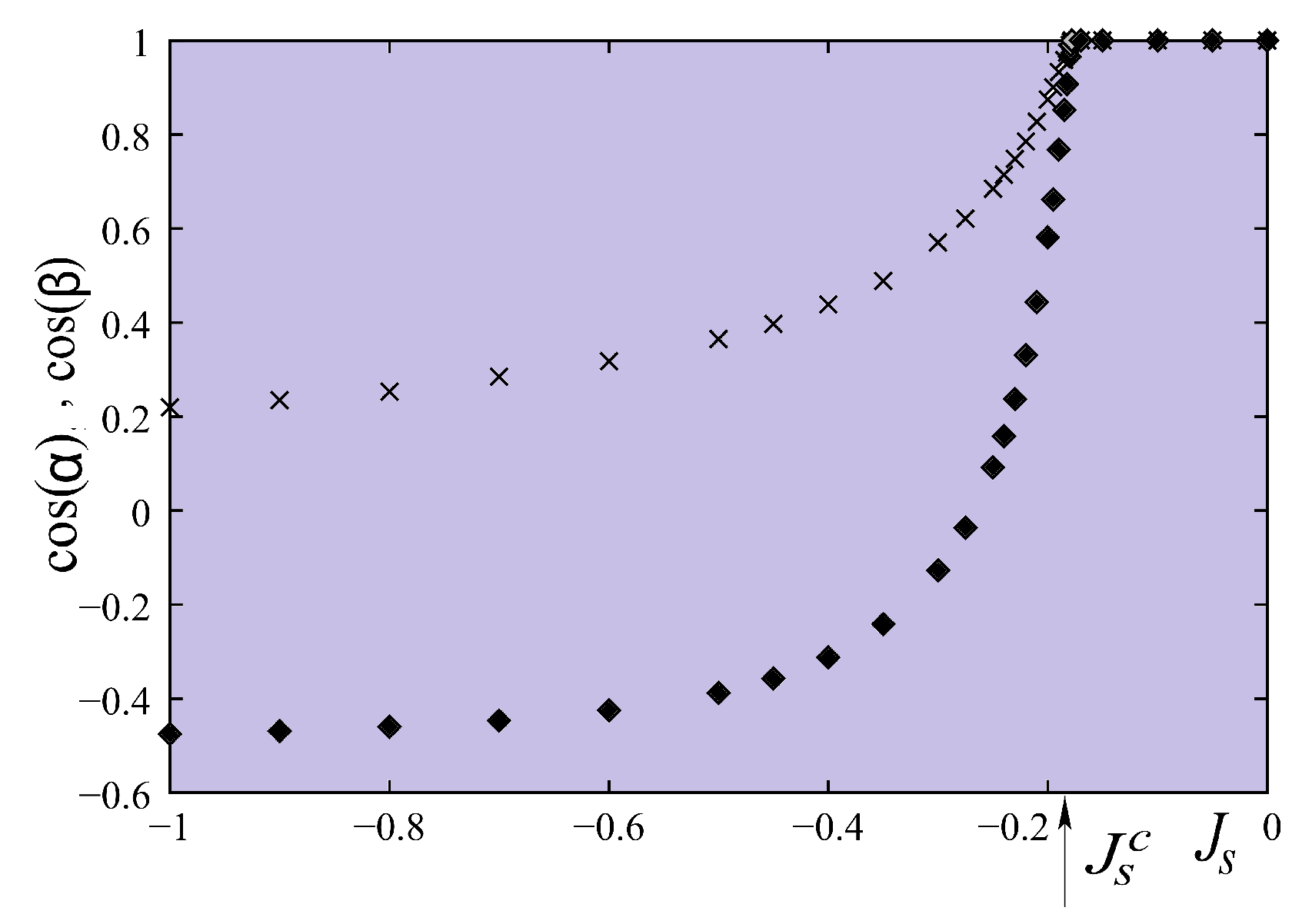
5.6. Helimagnetic Films
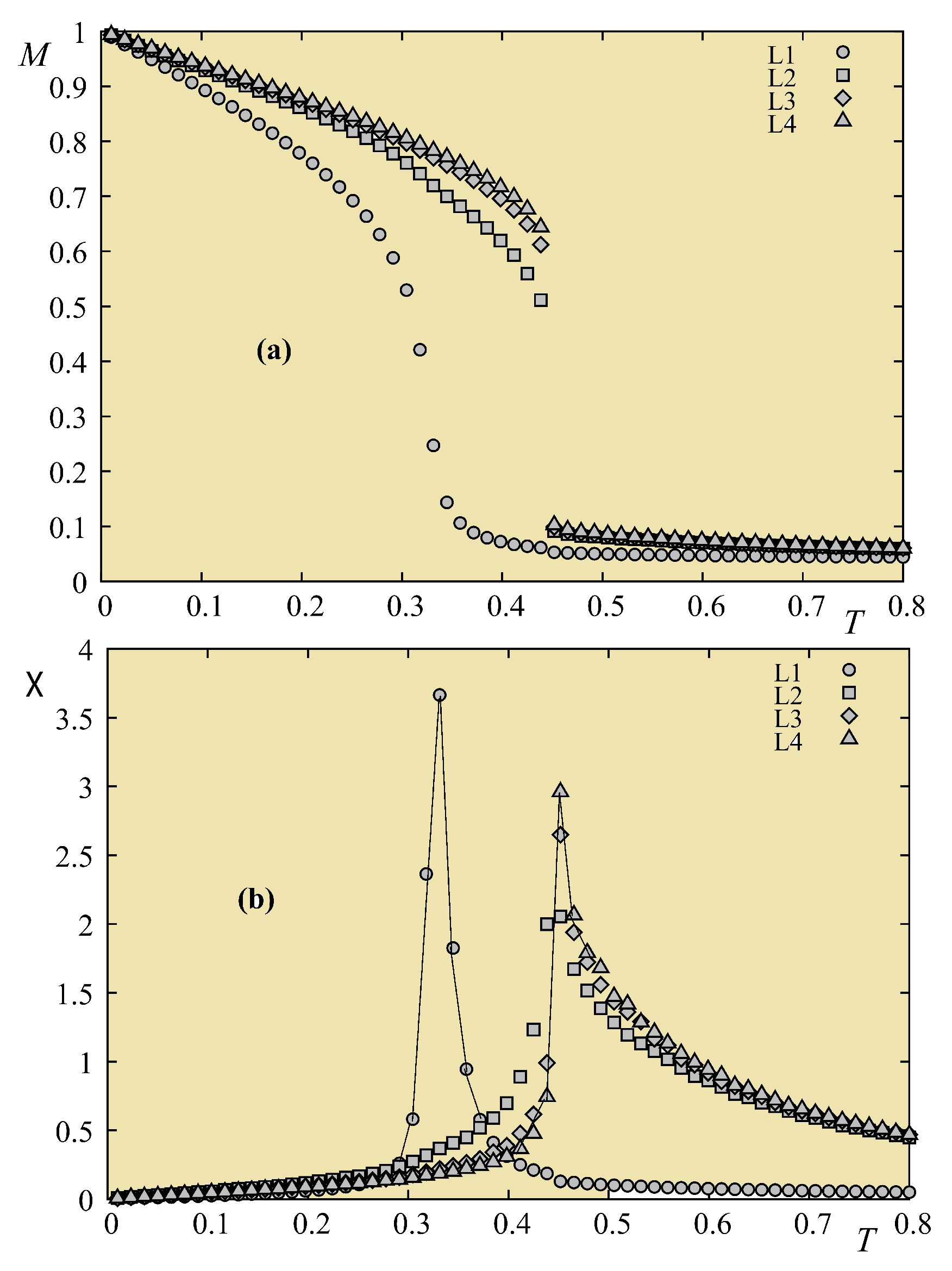
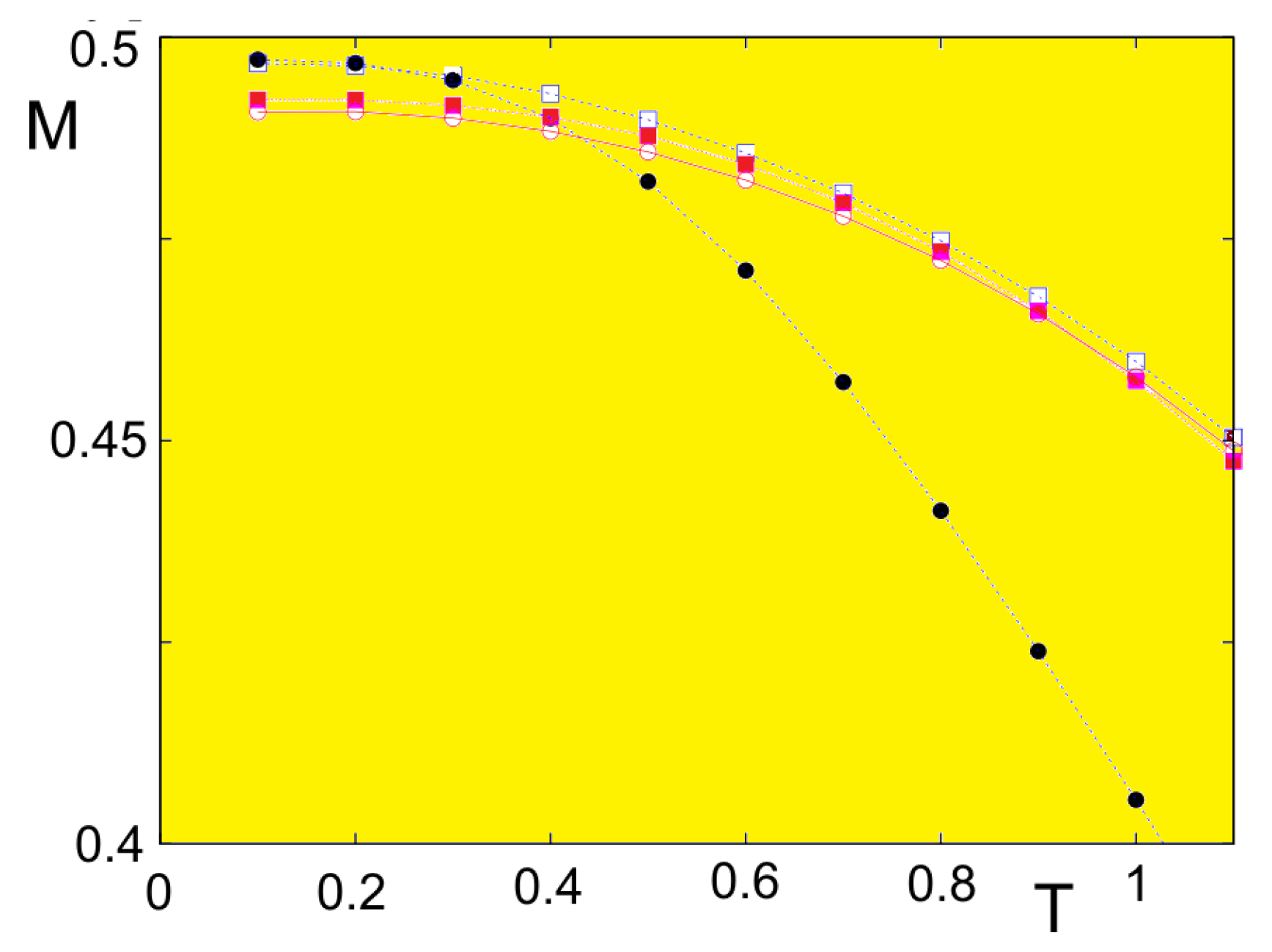
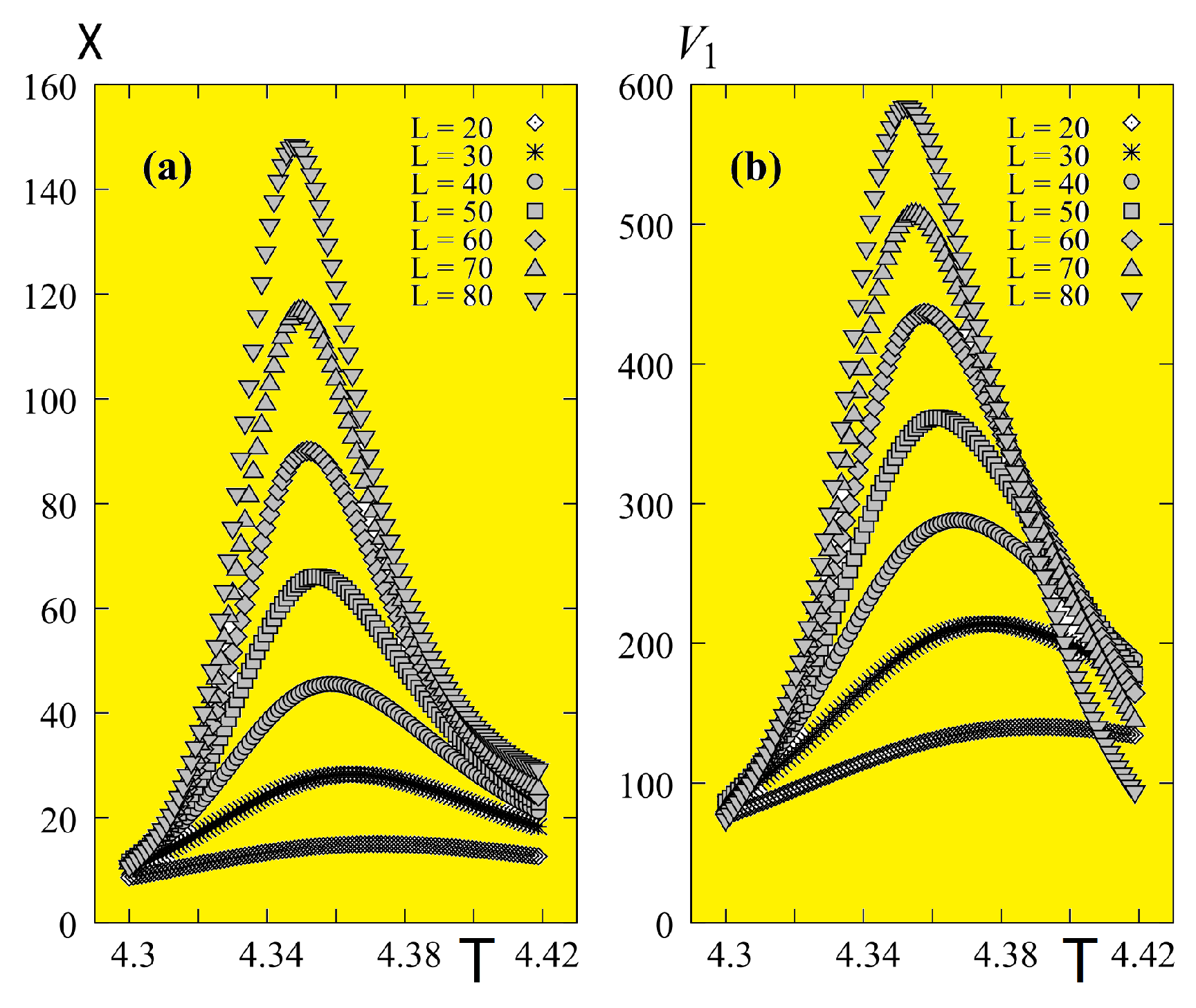
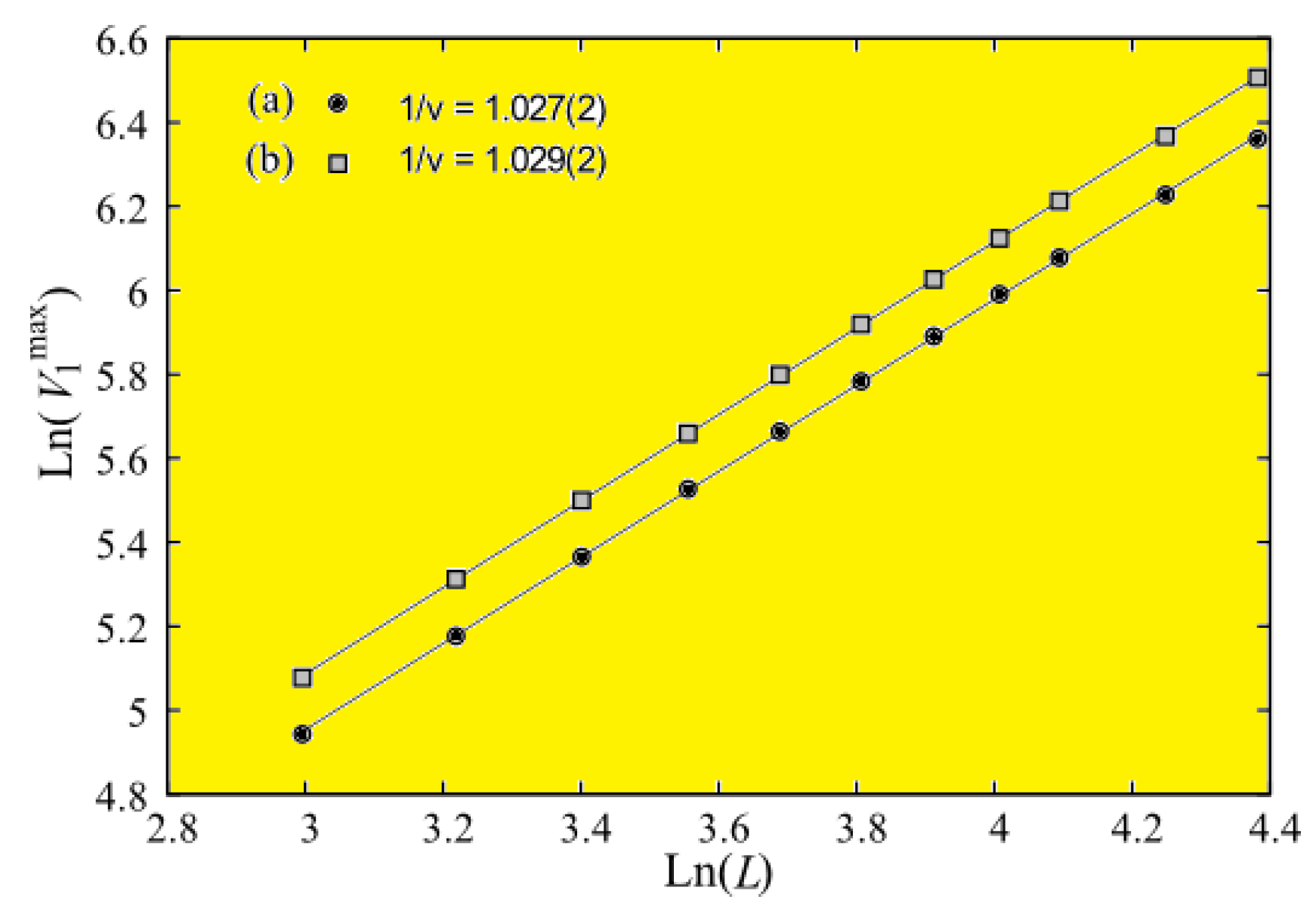
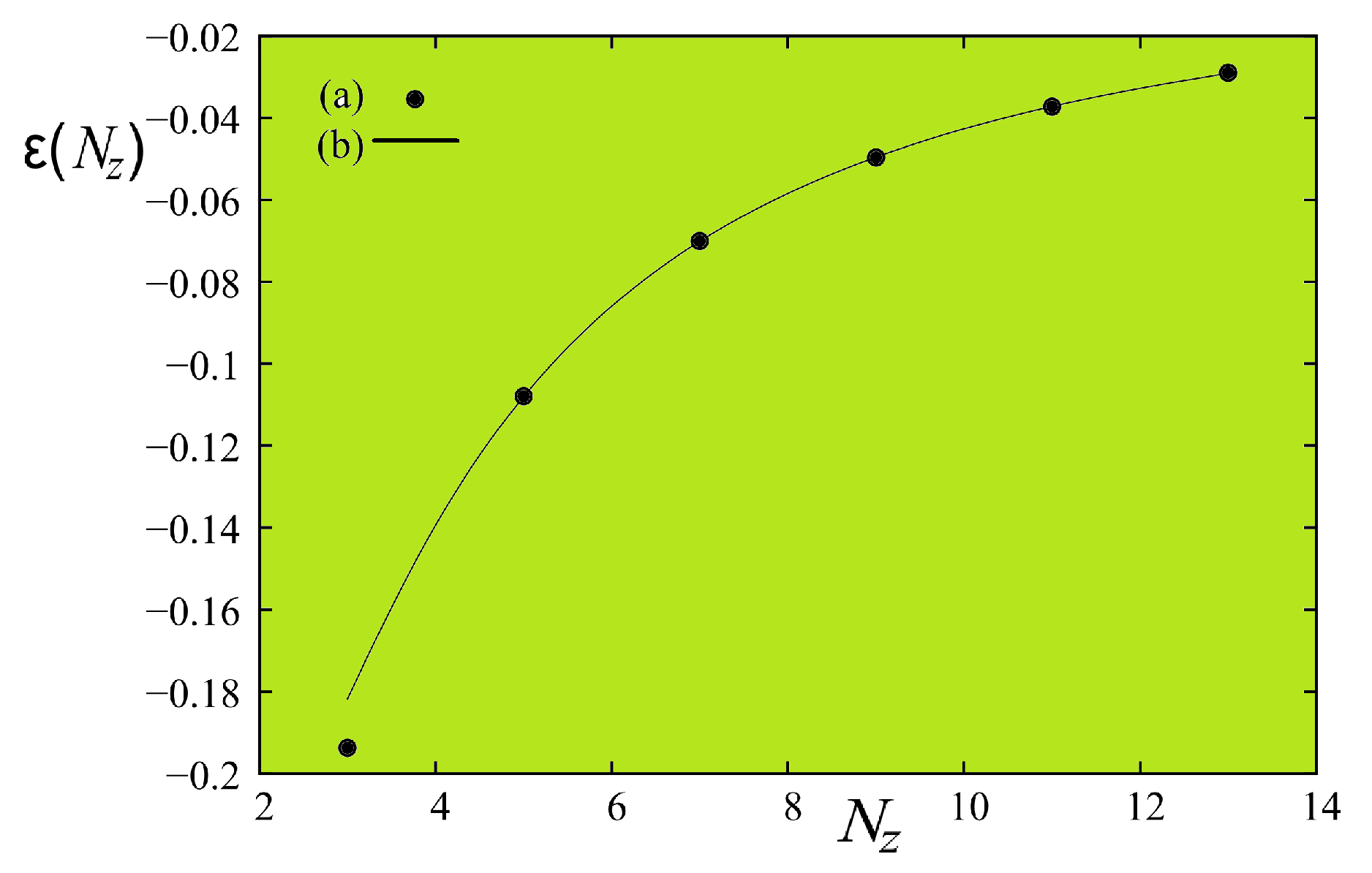
6. Criticality of Thin Films
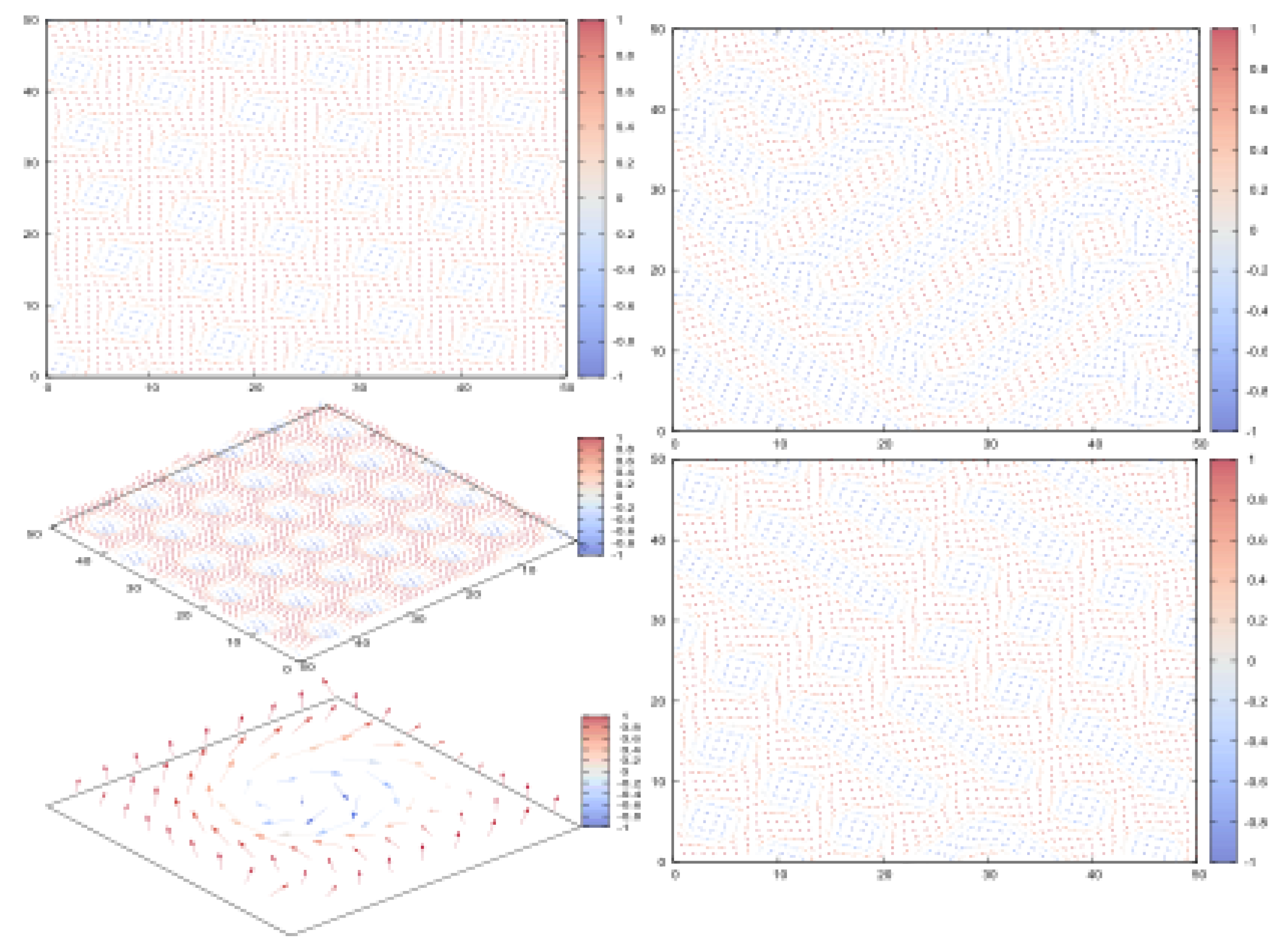
7. Skyrmions in Thin Films and Superlattices
8. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| bcc | body-centered cubic (lattice) |
| DM | Dzyaloshinskii-Moriya |
| fcc | face-centered cubic (lattice) |
| GS | ground state |
| hcp | hexagonal close-packed (lattice) |
| MC | Monte Carlo |
| nn | nearest neighbors |
| nnn | next-nearest neighbors |
| PBC | periodic boundary conditions |
| SW | spin wave |
| 2D | two dimensions |
| 3D | three dimensions |
References
- Diep, H.T. (Ed.) Frustrated Spin Systems, 2nd ed.; World Scientific: Singapore, 2013. [Google Scholar]
- Diep, H.T. Statistical Physics—Fundamentals and Application to Condensed Matter; World Scientific: Singapore, 2015. [Google Scholar]
- Zinn-Justin, J. Quantum Field Theory and Critical Phenomena, 4th ed.; Oxford University Press: London, UK, 2002. [Google Scholar]
- Zangwill, A. Physics at Surfaces; Cambridge University Press: London, UK, 1988. [Google Scholar]
- Bland, J.A.C.; Heinrich, B. (Eds.) Ultrathin Magnetic Structures; Springer: Berlin, Germany, 1994; Volumes I and II. [Google Scholar]
- Diep, H.T. Theory of Magnetism—Application to Surface Physics; World Scientific: Singapore, 2014. [Google Scholar]
- Baibich, M.N.; Broto, J.M.; Fert, A.; Van Dau, F.N.; Petroff, F.; Etienne, P.; Creuzet, G.; Friederich, A.; Chazelas, J. Giant Magnetoresistance of (001)Fe/(001)Cr Magnetic Superlattices. Phys. Rev. Lett. 1988, 61, 2472. [Google Scholar] [CrossRef] [PubMed]
- Grunberg, P.; Schreiber, R.; Pang, Y.; Brodsky, M.B.; Sowers, H. Layered Magnetic Structures: Evidence for Antiferromagnetic Coupling of Fe Layers across Cr Interlayers. Phys. Rev. Lett. 1986, 57, 2442. [Google Scholar] [CrossRef] [PubMed]
- Binash, G.; Grunberg, P.; Saurenbach, F.; Zinn, W. Enhanced magnetoresistance in layered magnetic structures with antiferromagnetic interlayer exchange. Phys. Rev. B 1989, 39, 4828. [Google Scholar] [CrossRef]
- Barthélémy, A.; Fert, A.; Contour, J.-P.; Bowen, M.; Cros, V.; De Teresa, J.M.; Hamzic, A.; Faini, J.C.; George, J.M.; Grollier, J.; et al. Magnetoresistance and spin electronics. J. Magn. Magn. Mater. 2002, 68, 242–245. [Google Scholar] [CrossRef]
- Fert, A.; Cros, V.; Sampaio, J. Skyrmions on the track. Nat. Nanotechnol. 2013, 8, 152. [Google Scholar] [CrossRef] [PubMed]
- Toulouse, G. Theory of the frustration effect in spin glasses. Commun. Phys. 1977, 2, 115. [Google Scholar]
- Villain, J. Spin glass with non-random interactions. J. Phys. C 1977, 10, 1717. [Google Scholar] [CrossRef]
- Zverev, V.I.; Tishin, A.M.; Chernyshov, A.S.; Mudryk, Y.; Gschneidner, K.A., Jr.; Pecharsky, V.K. Magnetic and magnetothermal properties and the magnetic phase diagram of high purity single crystalline terbium along the easy magnetization direction. J. Phys. Condens. Matter 2014, 26, 066001. [Google Scholar] [CrossRef] [PubMed]
- Zverev, V.I.; Tishin, A.M.; Min, Y.; Mudryk, Y.; Gschneidner, K.A., Jr.; Pecharsky, V.K. Magnetic and magnetothermal properties, and the magnetic phase diagram of single-crystal holmium along the easy magnetization direction. J. Phys. Condens. Matter 2015, 27, 146002. [Google Scholar] [CrossRef]
- Stishov, S.M.; Petrova, A.E.; Khasanov, S.; Panova, G.K.; Shikov, A.A.; Lashley, J.C.; Wu, D.; Lograsso, T.A. Magnetic phase transition in the itinerant helimagnet MnSi: Thermodynamic and transport properties. Phys. Rev. B 2007, 76, 052405. [Google Scholar] [CrossRef]
- Gaulin, B.D.; Gardner, J.S. Experimental Studies of Frustrated Pyrochlore Antiferromagnets. In Frustrated Spin Systems, 2nd ed.; Diep, H.T., Ed.; World Scientific: Singapore, 2013; pp. 474–507. [Google Scholar]
- Bramwell, S.T.; Gingras, M.J.P.; Holdsworth, P.C.W. Spin Ice. In Frustrated Spin Systems, 2nd ed.; Diep, H.T., Ed.; World Scientific: Singapore, 2013; pp. 383–474. [Google Scholar]
- Wannier, G.H. Antiferromagnetism, The Triangular Ising Net. Phys. Rev. 1950, 79, 357. [Google Scholar] [CrossRef]
- Wannier, G.H. Erratum. Phys. Rev. B 1973, 7, 5017. [Google Scholar] [CrossRef]
- Yoshimori, A. A New Type of Antiferromagnetic Structure in the Rutile Type Crystal. J. Phys. Soc. Jpn. 1959, 14, 807. [Google Scholar] [CrossRef]
- Villain, J. La structure des substances magnetiques. Phys. Chem. Solids 1959, 11, 303–309. [Google Scholar] [CrossRef]
- Kaplan, T.A. Classical Spin-Configuration Stability in the Presence of Competing Exchange Forces. Phys. Rev. 1959, 116, 888. [Google Scholar] [CrossRef]
- Dzyaloshinskii, I.E. Thermodynamical Theory of “Weak” Ferromagnetism in Antiferromagnetic Substances. Sov. Phys. JETP 1957, 5, 1259. [Google Scholar]
- Moriya, T. Anisotropic superexchange interaction and weak ferromagnetism. Phys. Rev. 1960, 120, 91. [Google Scholar] [CrossRef]
- Berge, B.; Diep, H.T.; Ghazali, A.; Lallemand, P. Phase transitions in two-dimensional uniformly frustrated XY spin systems. Phys. Rev. B 1986, 34, 3177. [Google Scholar] [CrossRef]
- Boubcheur, E.H.; Diep, H.T. Critical behavior of the two-dimensional fully frustrated XY model. Phys. Rev. B 1998, 58, 5163–5165. [Google Scholar] [CrossRef]
- Ngo, V.T.; Diep, H.T. Phase transition in Heisenberg stacked triangular antiferromagnets: End of a controversy. Phys. Rev. 2008, 78, 031119. [Google Scholar] [CrossRef]
- Ngo, V.T.; Diep, H.T. Stacked triangular XY antiferromagnets: End of a controversial issue on the phase transition. J. Appl. Phys. 2008, 103, 07C712. [Google Scholar] [CrossRef]
- Diep, H.T. First-Order Transition in the hexagonal-close-packed lattice with vector spins. Phys. Rev. B 1992, 45, 2863. [Google Scholar] [CrossRef]
- Hoang, D.-T.; Diep, H.T. Hexagonal-close-packed lattice: Ground state and phase transition. Phys. Rev. E 2012, 85, 041107. [Google Scholar] [CrossRef] [PubMed]
- Diep, H.T.; Giacomini, H. Frustration—Exactly Solved Models. In Frustrated Spin Systems; Diep, H.T., Ed.; World Scientific: Singapore, 2013; pp. 1–58. [Google Scholar]
- Baxter, R.J. Exactly solved Models in Statistical Mechanics; Academic Press: New York, NY, USA, 1982. [Google Scholar]
- Diep, H.T.; Debauche, M.; Giacomini, H. Exact solution of an anisotropic centered honeycomb Ising lattice: Reentrance and partial disorder. Phys. Rev. B 1991, 43, 8759(R). [Google Scholar] [CrossRef]
- Stephenson, J. Ising Model Spin Correlations on the Triangular Lattice IV—Anisotropic Ferromagnetic and Antiferromagnetic Lattices. J. Math. Phys. 1970, 11, 420. [Google Scholar] [CrossRef]
- Stephenson, J. Range of order in antiferromagnets with next-nearest neighbor coupling. Can. J. Phys. 1970, 48, 2118–2122. [Google Scholar] [CrossRef]
- Stephenson, J. Ising Model with Antiferromagnetic Next-Nearest-Neighbor Coupling: Spin Correlations and Disorder Points. Phys. Rev. B 1970, 1, 4405. [Google Scholar] [CrossRef]
- Rujan, P. Cellular automata and statistical mechanical models. J. Stat. Phys. 1987, 49, 139. [Google Scholar] [CrossRef]
- Kano, K.; Naya, S. Antiferromagnetism—The Kagomé Ising Net. Prog. Theor. Phys. 1953, 10, 158. [Google Scholar] [CrossRef]
- Azaria, P.; Diep, H.T.; Giacomini, H. Coexistence of order and disorder and reentrance in an exactly solvable model. Phys. Rev. Lett. 1987, 59, 1629. [Google Scholar] [CrossRef]
- Debauche, M.; Diep, H.T.; Azaria, P.; Giacomini, H. Exact phase diagram of a generalized Kagomé Ising lattice: Reentrance and disorder lines. Phys. Rev. B 1991, 44, 2369. [Google Scholar] [CrossRef]
- Gaaff, A.; Hijmans, J. Symmetry relations in the sixteen-vertex model. Physica A 1975, 80, 149–171. [Google Scholar] [CrossRef]
- Suzuki, M.; Fisher, M.E. Zeros of the partition function for the Heisenberg, ferroelectric, and general Ising models. J. Math. Phys. 1971, 12, 235. [Google Scholar] [CrossRef]
- Wu, F.Y. Exact results on a general lattice statistical model. Solid Stat. Commun. 1972, 10, 115–117. [Google Scholar] [CrossRef]
- Sacco, J.E.; Wu, F.Y. Thirty-two vertex model on a triangular lattice. J. Phys. A 1975, 8, 1780–1787. [Google Scholar] [CrossRef]
- Debauche, M.; Diep, H.T. Successive reentrances and phase transitions in exactly solved dilute centered square Ising lattices. Phys. Rev. B 1992, 46, 8214. [Google Scholar] [CrossRef]
- Diep, H.T.; Debauche, M.; Giacomini, H. Reentrance and Disorder Solutions in Exactly Solvable Ising Models. J. Magn. Magn. Mater. 1992, 184, 104–107. [Google Scholar] [CrossRef]
- Blankschtein, D.; Ma, M.; Berker, A. Fully and partially frustrated simple-cubic Ising models: Landau-Ginzburg-Wilson theory. Phys. Rev. B 1984, 30, 1362. [Google Scholar] [CrossRef]
- Diep, H.T.; Lallemand, P.; Nagai, O. Simple cubic fully frustrated Ising crystal by Monte Carlo simulations. J. Phys. C 1985, 18, 1067. [Google Scholar] [CrossRef]
- Blankschtein, D.; Ma, M.; Nihat Berker, A.; Grest, G.S.; Soukoulis, C.M. Orderings of a stacked frustrated triangular system in three dimensions. Phys. Rev. B 1984, 29, 5250. [Google Scholar] [CrossRef]
- Nagai, O.; Horiguchi, T.; Miyashita, S. Properties and Phase Transitions in Frustrated Ising Systems, Chapter 4. In Frustrated Spin Systems, 2nd ed.; Diep, H.T., Ed.; World Scientific: Singapore, 2013. [Google Scholar]
- Azaria, P.; Diep, H.T.; Giacomini, H. First order transition, multicriticality and reentrance in a BCC lattice with Ising spins. Europhys. Lett. 1989, 9, 755. [Google Scholar] [CrossRef]
- Santamaria, C.; Diep, H.T. Evidence of a Partial Disorder in a Frustrated Heisenberg System. J. Appl. Phys. 1997, 81, 5276. [Google Scholar] [CrossRef]
- Quartu, R.; Diep, H.T. Partial Order in Frustrated Quantum Spin Systems. Phys. Rev. B 1997, 55, 2975. [Google Scholar] [CrossRef]
- Boucheur, E.H.; Quartu, R.; Diep, H.T.; Nagai, O. Non collinear XY spin system: First-order transition and evidence of a reentrance. Phys. Rev. B 1998, 58, 400. [Google Scholar] [CrossRef]
- Horiguchi, T. Ising model with frustration on a three-dimensional lattice. Physica A 1987, 146, 613–621. [Google Scholar] [CrossRef]
- Foster, D.P.; Gérard, C.; Puha, I. Critical behaviour of fully frustrated Potts models. J. Phys. A Math. Gen. 2001, 34, 5183. [Google Scholar]
- Foster, D.P.; Gérard, C. Critical behavior of the fully frustrated q-state Potts piled-up-domino model. Phys. Rev. B 2004, 70, 014411. [Google Scholar] [CrossRef]
- Diep, T.-H.; Levy, J.C.S.; Nagai, O. Effect of surface spin-waves and surface anisotropy in magnetic thin films at finite temperatures. Phys. Stat. Solidi (b) 1979, 9, 351. [Google Scholar]
- Diep, H.T. Quantum effects in antiferromagnetic thin films. Phys. Rev. B 1991, 43, 8509. [Google Scholar] [CrossRef]
- Bogolyubov, N.N.; Tyablikov, S.V. Retarded and Advanced Green Functions in Statistical Physics. Soviet Phys. Doklady 1959, 4, 589. [Google Scholar]
- Quartu, R.; Diep, H.T. Phase diagram of body-centered tetragonal Helimagnets. J. Magn. Magn. Mater. 1998, 182, 38. [Google Scholar] [CrossRef]
- Diep, H.T. Quantum Theory of Helimagnetic Thin Films. Phys. Rev. B 2015, 91, 014436. [Google Scholar] [CrossRef]
- Mermin, N.D.; Wagner, H. Absence of Ferromagnetism or Antiferromagnetism in One- or Two-Dimensional Isotropic Heisenberg Models. Phys. Rev. Lett. 1966, 17, 1133. [Google Scholar] [CrossRef]
- Ngo, V.T.; Diep, H.T. Effects of frustrated surface in Heisenberg thin films. Phys. Rev. B 2007, 75, 035412. [Google Scholar] [CrossRef]
- Ngo, V.T.; Diep, H.T. Frustration effects in antiferrormagnetic face-centered cubic Heisenberg films. J. Phys. Condens. Matter 2007, 19, 386202. [Google Scholar]
- Hoang, D.T.; Kasperski, M.; Puszkarski, H.; Diep, H.T. Re-orientation transition in molecular thin films: Potts model with dipolar interaction. J. Phys. Condens. Matter 2013, 25, 056006. [Google Scholar] [CrossRef] [PubMed]
- Santamaria, C.; Diep, H.T. Dipolar interactions in magnetic thin: Perpendicular to in-plane ordering transition. J. Magn. Magn. Mater. 2000, 212, 23–28. [Google Scholar] [CrossRef]
- Santamaria, C.; Quartu, R.; Diep, H.T. Frustration effect in a quantum Heisenberg Spin System. J. Appl. Phys. 1998, 84, 1953. [Google Scholar] [CrossRef]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of State Calculations by Fast Computing Machines. J. Chem. Phys. 1953, 21, 1087. [Google Scholar] [CrossRef]
- Binder, K.; Heermann, D.W. Monte Carlo Simulation in Statistical Physics; Springer: Berlin, Germany, 1992. [Google Scholar]
- Ferrenberg, A.M.; Swendsen, R.H. New Monte Carlo technique for studying phase transitions. Phys. Rev. Lett. 1988, 61, 2635. [Google Scholar] [CrossRef]
- Ferrenberg, A.M.; Swendsen, R.H. New Monte Carlo Technique for Studying Phase Transitions. Phys. Rev. Lett. 1989, 63, 1658. [Google Scholar] [CrossRef]
- Ferrenberg, A.M.; Landau, D.P. Critical behavior of the three-dimensional Ising model: A high-resolution Monte Carlo study. Phys. Rev. B 1991, 44, 5081. [Google Scholar] [CrossRef]
- Harada, I.; Motizuki, K. Effect of Magnon-Magnon Interaction on Spin Wave Dispersion and Magnon Sideband in MnS. J. Phys. Soc. Jpn. 1972, 32, 927. [Google Scholar] [CrossRef]
- Diep, H.T. Magnetic transitions in Helimagnets. Phys. Rev. B 1989, 39, 397. [Google Scholar] [CrossRef]
- Diep, H.T. Low-temperature properties of quantum Heisenberg helimagnets. Phys. Rev. B 1989, 40, 741. [Google Scholar] [CrossRef]
- El Hog, S.; Diep, H.T. Helimagnetic Thin Films: Surface Reconstruction, Surface Spin-Waves, Magnetization. J. Magn. Magn. Mater. 2016, 400, 276–281. [Google Scholar] [CrossRef]
- El Hog, S.; Diep, H.T. Partial Phase Transition and Quantum Effects in Helimagnetic Films under an Applied Field. J. Magn. Magn. Mater. 2017, 429, 102. [Google Scholar] [CrossRef]
- Phu, X.P.; Ngo, V.T.; Diep, H.T. Critical Behavior of Magnetic Thin Films. Surf. Sci. 2009, 603, 109–116. [Google Scholar]
- Capehart, T.W.; Fisher, M.E. Susceptibility scaling functions for ferromagnetic Ising films. Phys. Rev. B 1976, 13, 5021. [Google Scholar] [CrossRef]
- Barber, M.N. Finite-Size Scaling. In Phase Transitions and Critical Phenomena; Domb, C., Lebowitz, J.L., Eds.; Academic Press: New York, NY, USA, 1983; Volume 8, pp. 146–268. [Google Scholar]
- Bunker, A.; Gaulin, B.D.; Kallin, C. Multiple-histogram Monte Carlo study of the Ising antiferromagnet on a stacked triangular lattice. Phys. Rev. B 1993, 48, 15861. [Google Scholar] [CrossRef]
- Phu, X.P.; Ngo, V.T.; Diep, H.T. Cross-Over from First to Second Order Transition in Frustrated Ising Antiferromagnetic Films. Phys. Rev. E 2009, 79, 061106. [Google Scholar]
- Skyrme, T.H.R. A non-linear field theory. Proc. R. Soc. A 1961, 260, 127. [Google Scholar]
- Skyrme, T.H.R. A unified field theory of mesons and baryons. Nucl. Phys. 1962, 31, 556. [Google Scholar] [CrossRef]
- Bogdanov, A.N.; Röler, U.K.; Shestakov, A.A. Skyrmions in liquid crystals. Phys. Rev. E 2003, 67, 016602. [Google Scholar] [CrossRef] [PubMed]
- Leonov, A.O.; Dragumov, I.E.; Röler, U.K.; Bogdanov, A.N. Theory of skyrmion states in liquid crystals. Phys. Rev. E 2014, 90, 042502. [Google Scholar] [CrossRef] [PubMed]
- Ackerman, P.J.; Trivedi, R.P.; Senyuk, B.; Lagemaat, J.V.D.; Smalyukh, I.I. Two-dimensional skyrmions and other solitonic structures in confinement-frustrated chiral nematics. Phys. Rev. E 2014, 90, 012505. [Google Scholar] [CrossRef] [PubMed]
- Ezawa, M. Giant Skyrmions Stabilized by Dipole-Dipole Interactions in Thin Ferromagnetic Films. Phys. Rev. Lett. 2010, 105, 197202. [Google Scholar] [CrossRef]
- Yu, X.Z.; Kanazawa, N.; Onose, Y.; Kimoto, K.; Zhang, W.Z.; Ishiwata, S.; Matsui, Y.; Tokura, Y. Near room-temperature formation of a skyrmion crystal in thin-films of the helimagnet FeGe. Nat. Mater. 2011, 10, 106. [Google Scholar] [CrossRef]
- Yu, X.Z.; Onose, Y.; Kanazawa, N.; Park, J.H.; Han, J.H.; Matsui, Y.; Nagaosa, N.; Tokura, Y. Real-space observation of a two-dimensional skyrmion crystal. Nature 2010, 465, 901. [Google Scholar] [CrossRef]
- Mühlbauer, S.; Binz, B.; Jonietz, F.; Pfleiderer, C.; Rosch, A.; Neubauer, A.; Georgii, R.; Böni, B. Skyrmion Lattice in a Chiral Magnet. Science 2009, 323, 915. [Google Scholar] [CrossRef]
- Bauer, A.; Pfleiderer, C. Magnetic phase diagram of MnSi inferred from magnetization and ac susceptibility. Phys. Rev. B 2012, 85, 214418. [Google Scholar] [CrossRef]
- Leonov, A.O.; Monchesky, T.L.; Romming, N.; Kubetzka, A.; Bogdanov, A.N.; Wiesendanger, R. The properties of isolated chiral skyrmions in thin magnetic films. New J. Phys. 2016, 18, 065003. [Google Scholar] [CrossRef]
- El Hog, S.; Diep, H.T.; Puszkarski, H. Theory of Magnons in Spin Systems with Dzyaloshinskii-Moriya Interaction. J. Phys. Condens. Matter 2017, 29, 305001. [Google Scholar] [CrossRef] [PubMed]
- Phillips, J.C. Stretched exponential relaxation in molecular and electronic glasses. Rep. Prog. Phys. 1996, 96, 1193. [Google Scholar] [CrossRef]
- El Hog, S.; Bailly-Reyre, A.; Diep, H.T. Stability and Phase Transition of Skyrmion Crystals Generated by Dzyaloshinskii-Moriya Interaction. J. Mag. Mag. Mater. 2018, 455, 32–38. [Google Scholar] [CrossRef]
- Rosales, H.D.; Cabra, D.C.; Pujol, P. Three-sublattice Skyrmions crystal in the antiferromagnetic triangular lattice. Phys. Rev. B 2015, 92, 214439. [Google Scholar] [CrossRef]
- Buhrandt, S.; Fritz, L. Skyrmion lattice phase in three-dimensional chiral magnets from Monte Carlo simulations. Phys. Rev. B 2013, 88, 195137. [Google Scholar] [CrossRef]
- Kwon, H.Y.; Kang, S.P.; Wu, Y.Z.; Won, C. Magnetic generated by Dzyaloshinskii-Moriya interaction. J. Appl. Phys. 2013, 113, 133911. [Google Scholar] [CrossRef]
- Kwon, H.Y.; Bu, K.M.; Wu, Y.Z.; Won, C. Effect of anisotropy and dipole interaction on long-range order magnetic structures generated by Dzyaloshinskii-Moriya interaction. J. Magn. Magn. Mater. 2012, 324, 2171. [Google Scholar] [CrossRef]
- Jiang, W.; Zhang, X.; Yu, G.; Zhang, W.; Wang, X.; Jungfleisch, M.B.; Pearson, J.E.; Cheng, X.; Heinonen, O.; Wang, K.L.; et al. Direct observation of the skyrmion Hall effect. Nat. Phys. 2017, 13, 162–169. [Google Scholar] [CrossRef]
- Gilbert, D.A.; Maranville, B.B.; Balk, A.L.; Kirby, P.J.; Fischer, P.; Piercen, J.; Unguris, D.T.; Borchers, J.A.; Liu, K. Realization of ground-state artificial skyrmion lattices at room temperature. Nat. Commun. 2015, 6, 8462. [Google Scholar] [CrossRef]
- Kang, W.; Huang, Y.; Zhang, X.; Zhou, Y.; Zhao, W. Skyrmion-Electronics: An Overview and Outlook. Proc. IEEE 2016, 104, 2040–2061. [Google Scholar] [CrossRef]
- Parkin, S.S.P.; Hayashi, M.; Thomas, L. Magnetic domain-wall racetrack memory. Science 2008, 320, 190–194. [Google Scholar] [CrossRef]
- Zhang, X.; Ezawa, M.; Zhou, Y. Magnetic skyrmion logic gates: Conversion, duplication and merging of skyrmions. Sci. Rep. 2015, 5, 9400. [Google Scholar] [CrossRef]
- Zhou, Y.; Ezawa, M. A reversible conversion between a skyrmion and a domain-wall pair in junction geometry. Nat. Commun. 2014, 5, 4652. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, Y.; Ezawa, M.; Zhao, G.P.; Zhao, W. Magnetic skyrmion transistor: Skyrmion motion in a voltage-gated nanotrack. Sci. Rep. 2015, 5, 11369. [Google Scholar] [CrossRef]
- Kim, J.S.; Jung, S.H.; Jung, M.-H.; You, C.-Y.; Swagten, H.J.M.; Koopmans, B. Voltage controlled propagating spin waves on a perpendicularly magnetized nanowire. arXiv, 2014; arXiv:1401.6910. [Google Scholar]
- Shiota, Y.; Murakami, S.; Bonell, F.; Nozaki, T.; Shinjo, T.; Suzuki, Y. Quantitative evaluation of voltage-induced magnetic anisotropy change by magnetoresistance measurement. Appl. Phys. Express 2011, 4, 43005. [Google Scholar] [CrossRef]
- Huang, Y.; Kang, W.; Zhang, X.; Zhou, Y.; Zhao, W. Magnetic skyrmion-based synaptic devices. Nanotechnology 2017, 28, 08LT02. [Google Scholar] [CrossRef]
- Li, S.; Kang, W.; Huang, Y.; Zhang, X.; Zhou, Y.; Zhao, W. Magnetic skyrmion-based artificial neuron device. Nanotechnology 2017, 28, 31LT01. [Google Scholar] [CrossRef]
- Sharafullin, I.F.; Nugumanov, A.G.; Yuldasheva, A.R.; Zharmukhametov, A.R.; Diep, H.T. Modeling of magnetoelectric and surface properties in superlattices and nanofilms of multiferroics. J. Magn. Magn. Mater. 2019, 475, 453–457. [Google Scholar] [CrossRef]
- Sharafullin, I.F.; Kharrasov, M.K.; Diep, H.T. Magneto-Ferroelectric Interaction in Superlattices: Monte Carlo Study of Phase Transitions. J. Magn. Magn. Mater. 2019, 476, 258–267. [Google Scholar] [CrossRef]
- Sharafullin, I.F.; Kharrasov, M.K.; Diep, H.T. Dzyaloshinskii-Moriya Interaction in Magneto-Ferroelectric Superlattices: Spin Waves and Skyrmions. arXiv, 2018; arXiv:1812.11344. [Google Scholar]
| 1 | ||||||
| 3 | ||||||
| 5 | ||||||
| 7 | ||||||
| 9 | ||||||
| 11 | ||||||
| 13 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Diep, H.T. Phase Transition in Frustrated Magnetic Thin Film—Physics at Phase Boundaries. Entropy 2019, 21, 175. https://doi.org/10.3390/e21020175
Diep HT. Phase Transition in Frustrated Magnetic Thin Film—Physics at Phase Boundaries. Entropy. 2019; 21(2):175. https://doi.org/10.3390/e21020175
Chicago/Turabian StyleDiep, Hung T. 2019. "Phase Transition in Frustrated Magnetic Thin Film—Physics at Phase Boundaries" Entropy 21, no. 2: 175. https://doi.org/10.3390/e21020175
APA StyleDiep, H. T. (2019). Phase Transition in Frustrated Magnetic Thin Film—Physics at Phase Boundaries. Entropy, 21(2), 175. https://doi.org/10.3390/e21020175





