Estimating the Bed-Load Layer Thickness in Open Channels by Tsallis Entropy
Abstract
:1. Introduction
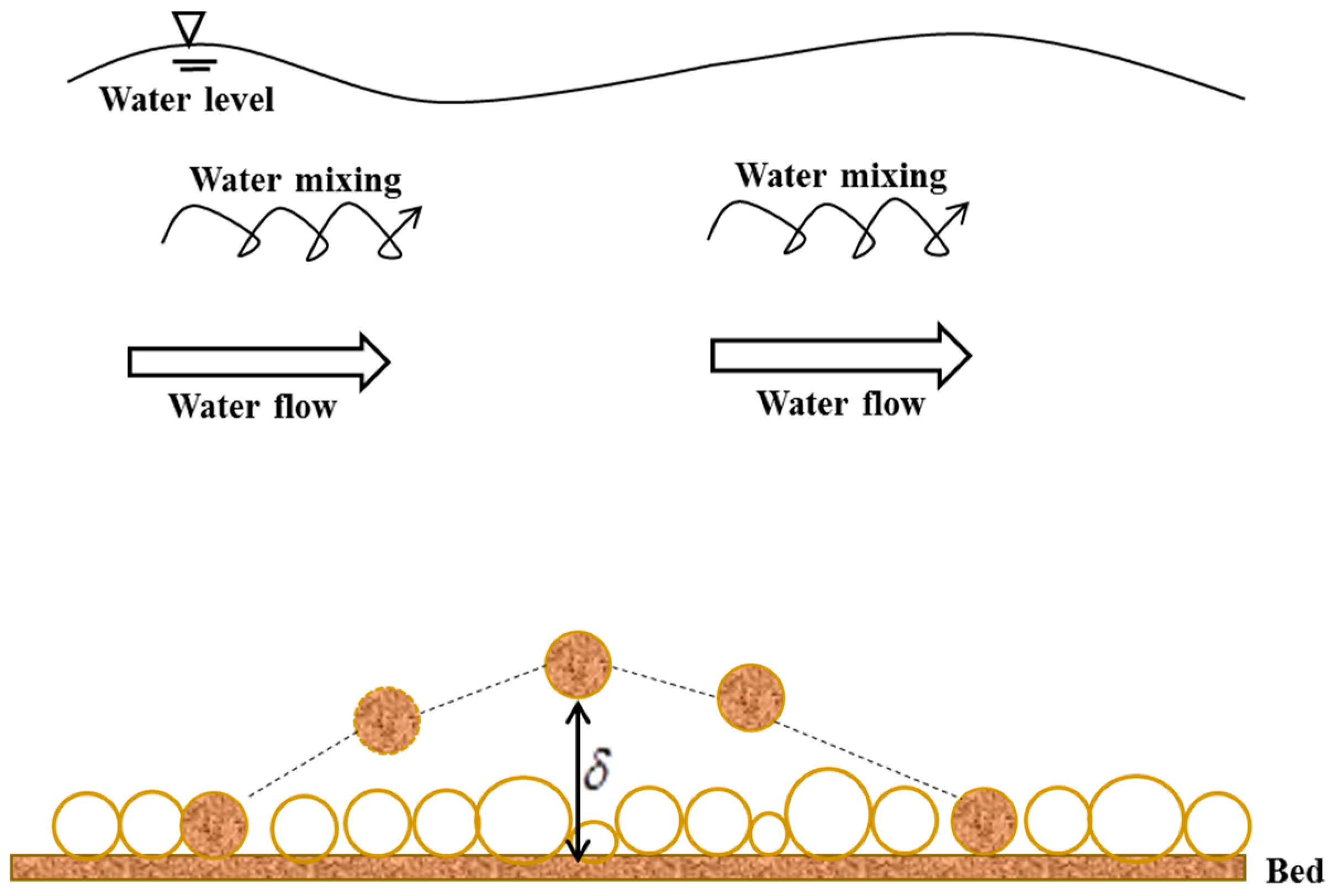
2. Methodology for Determination of the Bed-Load Thickness
2.1. Definition of the Tsallis Entropy
2.2. Constraint Equations
2.3. Maximization of Entropy
2.4. Estimation of Lagrange Multipliers
2.5. Hypothesis on Cumulative Distribution Function
2.6. Estimation of an Expression for Bed-Load Layer Thickness
3. Comparison with Laboratory Data Sets and Discussion
3.1. Selection of Laboratory Data Sets
3.2. Some Developed Deterministic Models
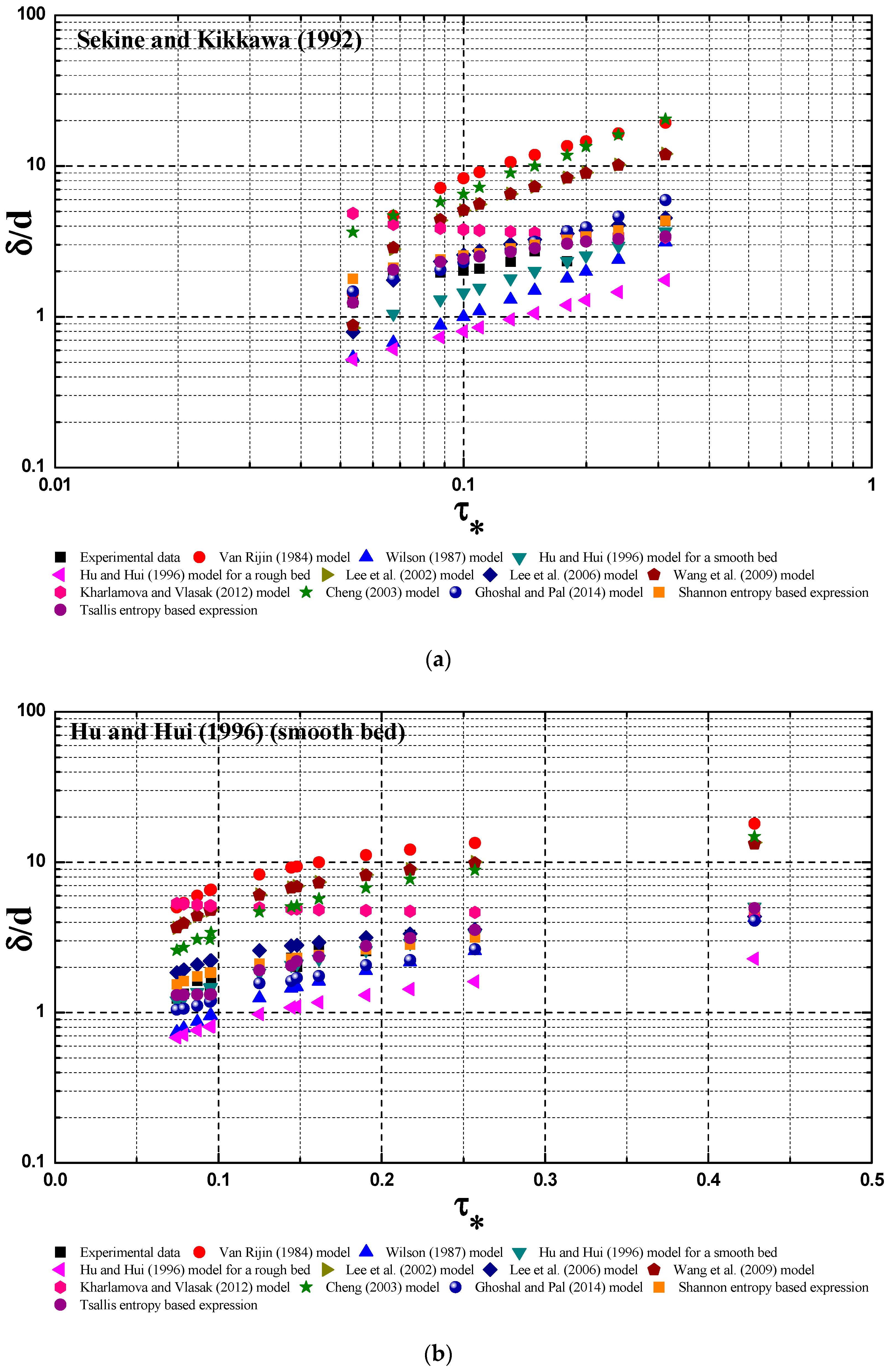
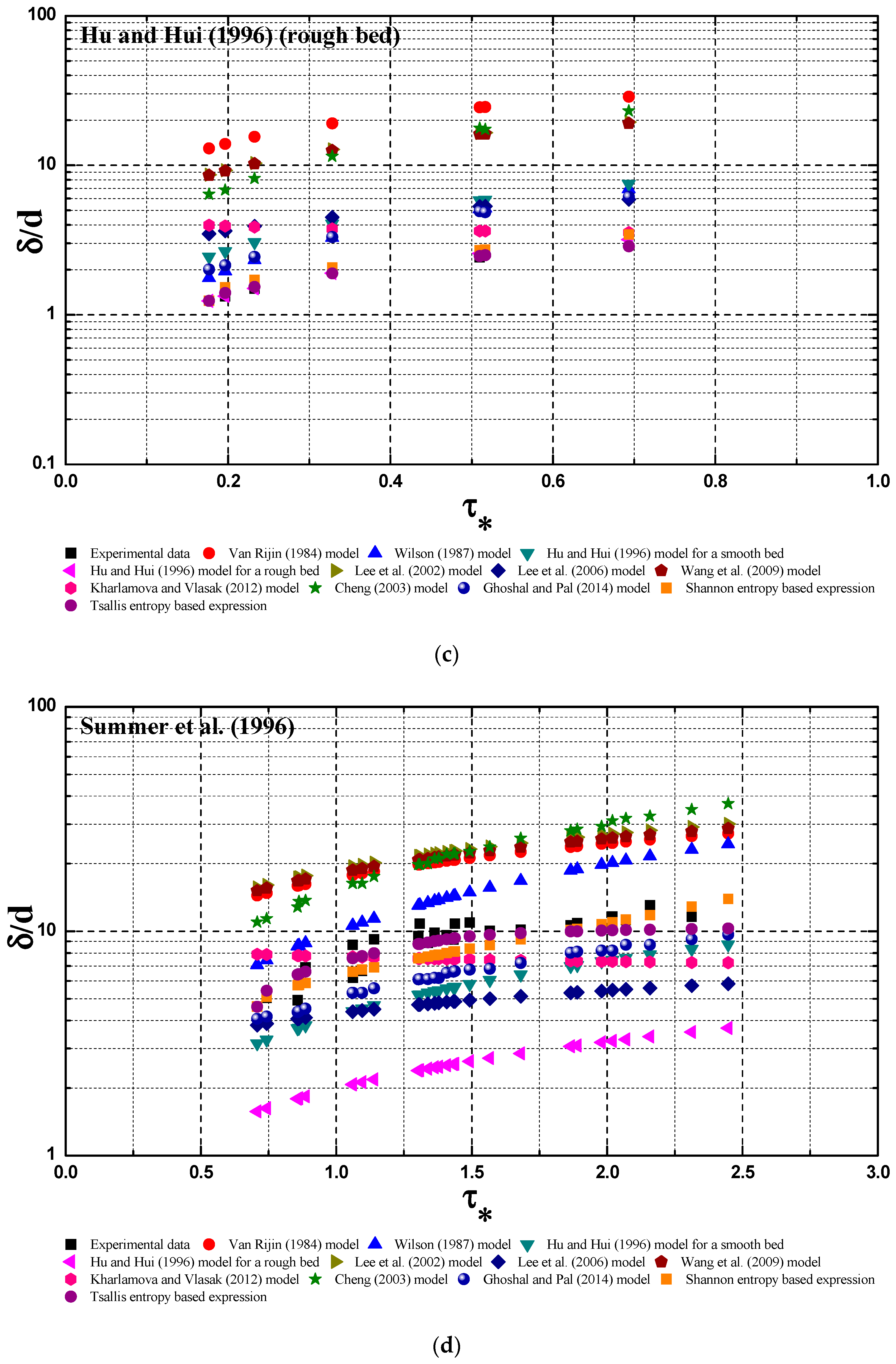
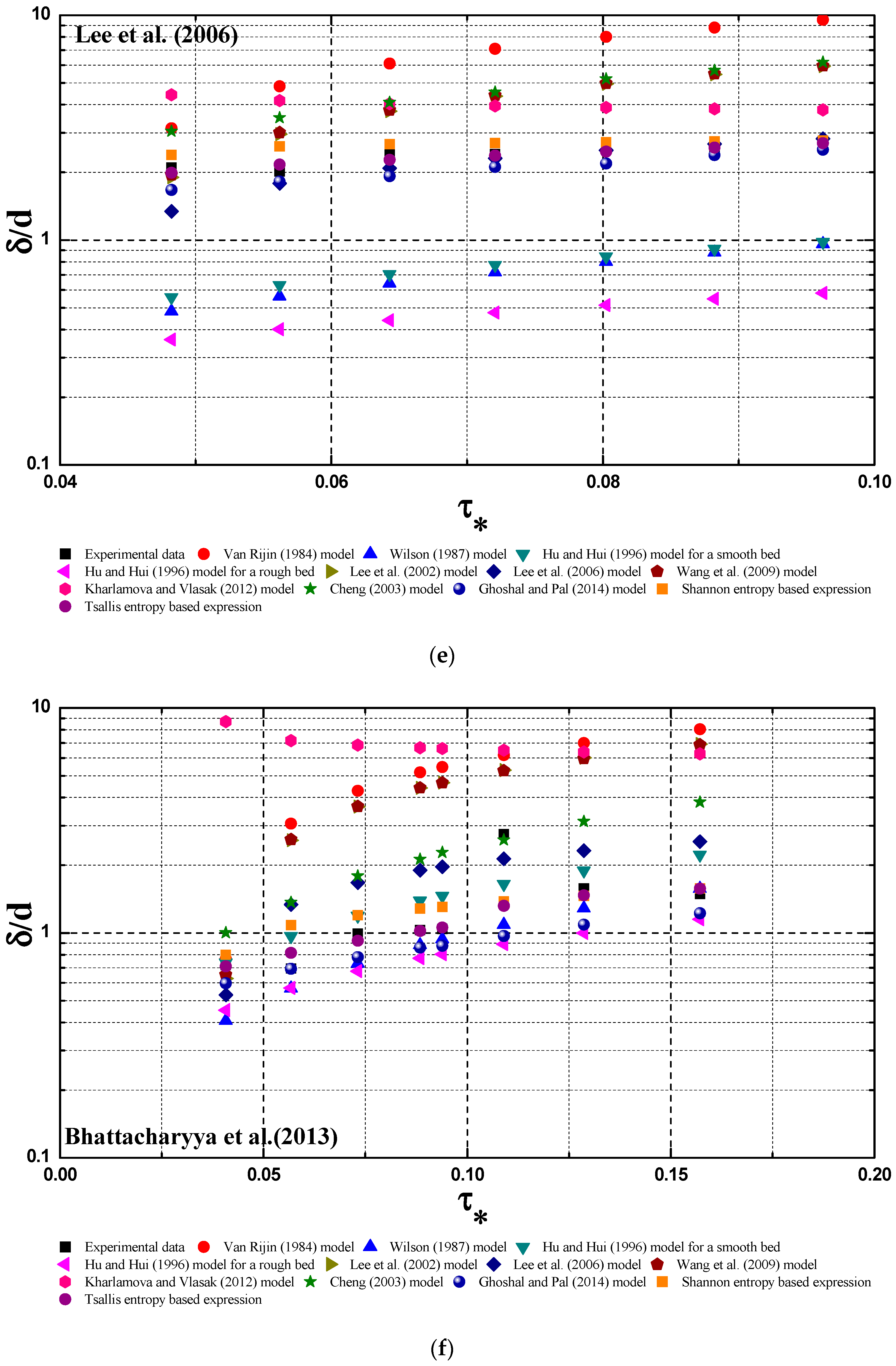
3.3. Comparsion Results
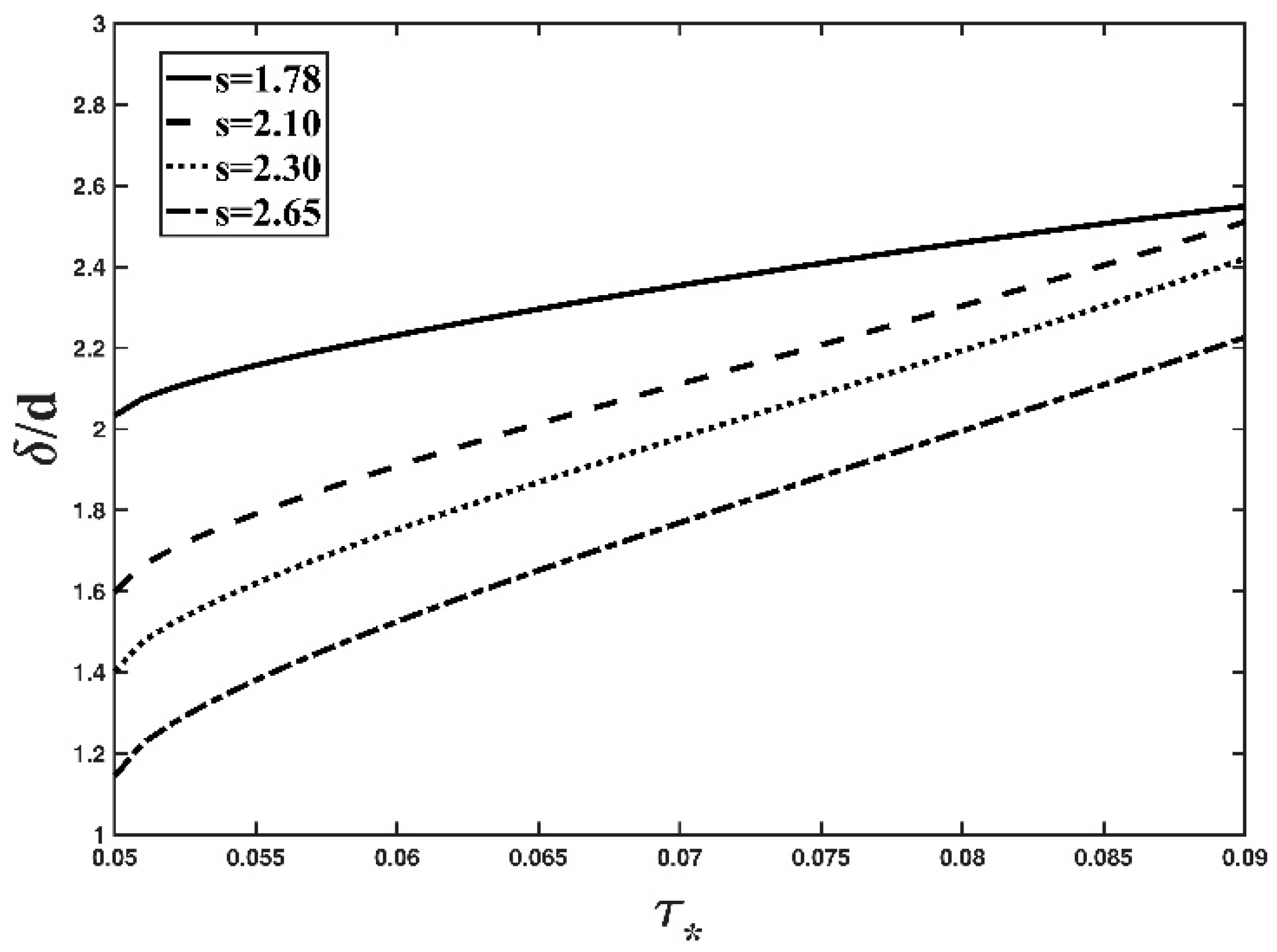
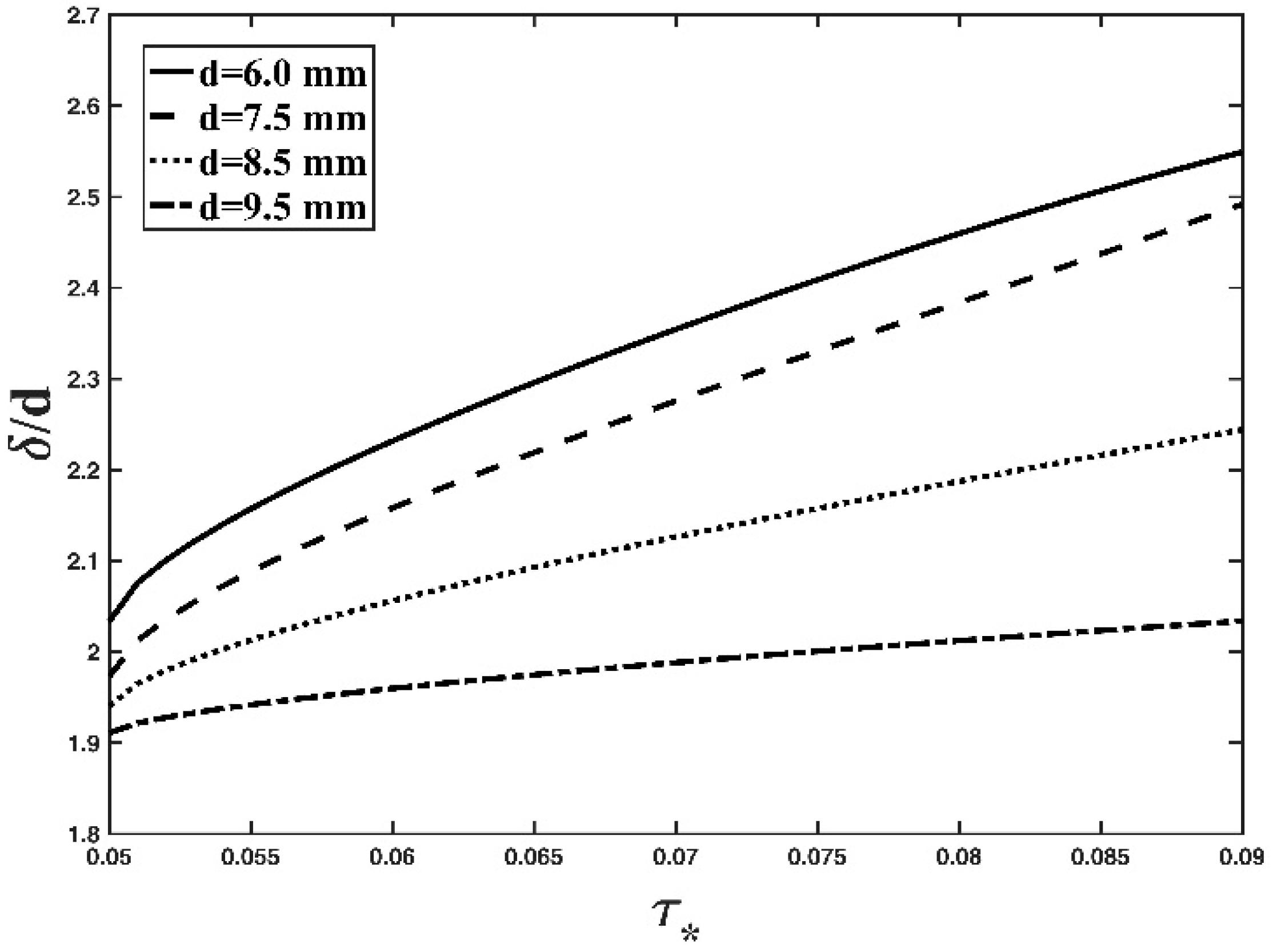
3.4. Physical Interpretation
4. Conclusions
- (1)
- A mathematical expression that could predict the bed-load thickness in open channel was derived by adopting the Tsallis entropy theory, coupled with the maximum entropy principle.
- (2)
- The derived expression by the Tsallis entropy could agree with the collected six laboratory data sets fairly well.
- (3)
- The derived expression by the Tsallis entropy was compared with other deterministic models for six collected laboratory data sets. The expression shows better prediction accuracy for experimental data than other deterministic models.
- (4)
- The derived Tsallis entropy-based expression has a comparable prediction ability for experimental data to the Shannon entropy based expression, considering the uncertainty associated with the experimental data.
- (5)
- Based on the Tsallis entropy based expression in this study, either an increase in mass density of the particle or in particle diameter leads to a reduction in the thickness of the bed-load layer in an open channel, in accordance with previous studies and our understanding of the dynamic mechanisms of the bed-load transport in the channel.
Author Contributions
Funding
Conflicts of Interest
References
- Cheng, N.S. A diffusive model for evaluating thickness of bedload layer. Adv. Water Resour. 2003, 26, 875–882. [Google Scholar] [CrossRef]
- Ghoshal, K.; Pal, D. An analytical model for bedload layer thickness. Acta Mech. 2014, 225, 701–714. [Google Scholar] [CrossRef]
- Kumbhakar, M.; Kundu, S.; Ghoshal, K. An explicit analytical expression for bed-load layer thickness based on maximum entropy principle. Phys. Lett. A 2018, 382, 2297–2304. [Google Scholar] [CrossRef]
- Chien, N.; Wan, Z. Sediment Transport Mechanics; Science Press: Beijing, China, 1983. [Google Scholar]
- Graf, W.H. Hydraulics of Sediment Transport; Water Resources Publication: Highlands Ranch, CO, USA, 1984. [Google Scholar]
- Einstein, H.A. The Bed-Load Function for Sediment Transportation in Open Channel Flow; United States Department of Agriculture: Washington, DC, USA, 1950.
- Van Rijn, L.C. Sediment transport, part I: Bed load transport. J. Hydraul. Eng. 1984, 110, 1431–1456. [Google Scholar] [CrossRef]
- Wilson, K.C. Analysis of bed-load motion at high shear stress. J. Hydraul. Eng. 1987, 113, 97–103. [Google Scholar] [CrossRef]
- Bialik, R.J.; Nikora, V.I.; Rowinski, P.M. 3D Lagrangian modelling of saltating particles diffusion in turbulent water flow. Acta Geophys. 2012, 60, 1639–1660. [Google Scholar] [CrossRef]
- Lukerchenko, N.; Piatsevich, S.; Chara, Z.; Vlasak, P. 3D numerical model of the spherical particle saltation in a channel with a rough fixed bed. J. Hydrol. Hydromech. 2009, 57, 100–112. [Google Scholar] [CrossRef]
- Moreno, P.A.; Bombardelli, F.A. 3D numerical simulation of particle–particle collisions in saltation mode near stream beds. Acta Geophys. 2012, 60, 1661–1688. [Google Scholar] [CrossRef]
- Singh, V.P.; Sivakumar, B.; Cui, H.J. Tsallis entropy theory for modelling in water engineering: A review. Entropy 2017, 19, 641. [Google Scholar] [CrossRef]
- Chiu, C.L.; Said, C.A.A. Maximum and mean velocities and entropy in open-channel flow. J. Hydraul. Eng. 1995, 121, 26–35. [Google Scholar] [CrossRef]
- Cui, H.; Singh, V.P. One dimensional velocity distribution in open channels using Tsallis entropy. J. Hydrol. Eng. 2014, 19, 290–298. [Google Scholar] [CrossRef]
- Luo, H.; Singh, V.P. Entropy theory for two-dimensional velocity distribution. J. Hydrol. Eng. 2011, 16, 303–315. [Google Scholar] [CrossRef]
- Kumbhakar, M.; Ghoshal, K. One-dimensional velocity distribution in open channels using Renyi entropy. Stoch. Environ. Res. Risk Assess. 2017, 31, 949–959. [Google Scholar] [CrossRef]
- Luo, H.; Singh, V.; Schmidt, A. Comparative study of 1D entropy-based and conventional deterministic velocity distribution equations for open channel flows. J. Hydrol. 2018, 563, 679–693. [Google Scholar] [CrossRef]
- Chiu, C.L.; Jin, W.; Chen, Y.C. Mathematical models of distribution of sediment concentration. J. Hydraul. Eng. 2000, 1, 16–23. [Google Scholar] [CrossRef]
- Cui, H.; Singh, V.P. Suspended sediment concentration in open channels using Tsallis entropy. J. Hydrol. Eng. 2013, 19, 966–977. [Google Scholar] [CrossRef]
- Kumbhakar, M.; Ghoshal, K.; Singh, V.P. Derivation of Rouse equation for sediment concentration using Shannon entropy. Physics A 2017, 465, 494–499. [Google Scholar] [CrossRef]
- Sterling, M.; Knight, D. An attempt at using the entropy approach to predict the transverse distribution of boundary shear stress in open channel flow. Stoch. Environ. Res. Risk Assess. 2002, 16, 127–142. [Google Scholar] [CrossRef]
- Bonakdari, H.; Sheikh, Z.; Tooshmalani, M. Comparison between Shannon and Tsallis entropies for prediction of shear stress distribution in open channels. Stoch. Environ. Res. Risk Assess. 2015, 29, 1–11. [Google Scholar] [CrossRef]
- Zhu, Z. A Simple Explicit Expression for the Flocculation Dynamics Modeling of Cohesive Sediment Based on Entropy Considerations. Entropy 2018, 20, 845. [Google Scholar] [CrossRef]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Singh, V.P. Tsallis entropy theory for derivation of infiltration equations. Trans. ASABE 2010, 53, 447–463. [Google Scholar] [CrossRef]
- Jaynes, E.T. Information theory and statistical mechanics I. Phys. Rev. 1957, 106, 620–630. [Google Scholar] [CrossRef]
- Jaynes, E.T. Information theory and statistical mechanics II. Phys. Rev. 1957, 108, 171–190. [Google Scholar] [CrossRef]
- Jaynes, E.T. On the rationale of maximum entropy methods. Proc. IEEE 1982, 70, 939–952. [Google Scholar] [CrossRef]
- Hu, C.; Hui, Y. Bed-load transport I: Mechanical characteristics. J. Hydraul. Eng. 1996, 122, 245–254. [Google Scholar] [CrossRef]
- Hu, C.; Hui, Y. Bed-load transport II: Stochastic characteristics. J. Hydraul. Eng. 1996, 122, 255–261. [Google Scholar] [CrossRef]
- Sekine, M.; Kikkawa, H. Mechanics of saltating grains. J. Hydraul. Eng. 1992, 118, 536–558. [Google Scholar] [CrossRef]
- Sumer, B.M.; Kozakiewicz, A.; Fredsøe, J.; Deigaard, R. Velocity and concentration profiles in sheet-flow layer of movable bed. J. Hydraul. Eng. 1996, 122, 549–558. [Google Scholar] [CrossRef]
- Lee, H.Y.; Lin, Y.T.; You, J.; Wang, H. On three-dimensional continuous saltating process of sediment particles near the channel bed. J. Hydraul. Res. 2006, 44, 374–389. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Ojha, S.P.; Mazumder, B.S. Evaluation of the saltation process of bed materials by video imaging under altered bed roughness. Earth Surf. Proces. Landf. 2013, 38, 1339–1353. [Google Scholar] [CrossRef]
- Lee, H.Y.; You, J.Y.; Lin, Y.T. Continuous saltating process of multiple sediment particles. J. Hydraul. Eng. 2002, 128, 443–450. [Google Scholar] [CrossRef]
- Wang, H.W.; Lee, H.Y.; Lee, P.N. Three-dimensional saltating processes of multiple sediment particles. Int. J. Sediment Res. 2009, 24, 16–32. [Google Scholar] [CrossRef]
- Kharlamova, I.; Vlasak, P. Numerical model of saltation in open channel with rough bed. In Proceedings of the Colloquium Fluid Dynamics, Prague, Czech Republic, 24–26 October 2012; pp. 1–7. [Google Scholar]
- Soulsby, R.L.; Whitehouse, R.J.S. Threshold of sediment motion in coastal environments. In Proceedings of the 13th Australasian Coastal and Ocean Engineering Conference and the 6th Australasian Port and Harbour Conference, Cristchurch, New Zealand, 7–11 September 1997; pp. 145–150. [Google Scholar]
| Data Series | The Diameter of the Particle d (mm) | Specific Gravity s | Dimensionless Diameter of the Particle d* | Dimensionless Shear Stress τ* Range |
|---|---|---|---|---|
| Sekine and Kikkawa [31] | 5 | 2.50 | 122.52 | 0.05–0.31 |
| Hu and Hui [29] (smooth bed) | 3 | 2.64 | 75.73 | 0.07–0.43 |
| Hu and Hui [30] (rough bed) | 4 | 2.64 | 100.98 | 0.10–0.70 |
| Sumer et al. [32] | 2.6 | 1.14 | 28.90 | 0.70–2.50 |
| Lee et al. [33] | 6 | 1.78 | 118.23 | 0.04–0.10 |
| Bhattacharyya et al. [34] | 2 | 2.65 | 50.57 | 0.04–0.16 |
| Data Source | Parameter Estimation | Fitting Result | |||
|---|---|---|---|---|---|
| Sekine and Kikkawa [31] | −1.30 | 0.50 | 0.35 | 3 | 12.11 |
| Hu and Hui [29] (for a smooth bed) | 1.06 | −0.26 | 1 | 3 | 7.31 |
| Hu and Hui [30] (for a rough bed) | −2.67 | 1.07 | 0.65 | 3 | 5.26 |
| Sumer et al. [32] | −0.18 | 0.06 | 0.5 | 3 | 8.94 |
| Lee et al. [33] | −17.90 | 6.48 | 0.65 | 3 | 5.33 |
| Bhattacharyya et al. [34] | −4.82 | 3.15 | 0.85 | 3 | 1.47 |
| Experimental Data | Fitting Result: R Value | |||||
|---|---|---|---|---|---|---|
| Sekine and Kikkawa [32] | Hu and Hui [29] (Smooth Bed) | Hu and Hui [30] (Rough Bed) | Sumer et al. [32] | Lee et al. [33] | Bhattacharyya et al. [34] | |
| Van Rijin [7] model | 294.17 | 305.29 | 881.50 | 131.04 | 174.93 | 302.16 |
| Wilson [8] model | 45.11 | 33.79 | 74.35 | 56.29 | 70.48 | 24.50 |
| Hu and Hui [29] model for a smooth bed | 25.32 | 7.33 | 112.73 | 38.39 | 68.32 | 30.73 |
| Hu and Hui [30] model for a rough bed | 60.29 | 50.40 | 2.88 *** | 71.88 | 80.49 | 32.73 |
| Lee et al. [35] model | 147.78 | 198.67 | 557.56 | 152.62 | 72.19 | 246.15 |
| Lee et al. [33] model | 22.51 | 27.51 | 133.69 | 45.24 | 12.15 | 62.84 |
| Wang et al. [36] model | 147.42 | 197.46 | 548.35 | 142.91 | 73.02 | 244.97 |
| Kharlamova and Vlasak [37] model | 75.57 | 153.26 | 108.05 | 29.60 | 68.64 | 559.16 |
| Cheng [1] model | 266.08 | 131.53 | 503.15 | 138.30 | 88.09 | 87.75 |
| Ghoshal and Pal [2] model | 21.09 | 23.19 | 74.45 | 28.32 | 13.77 | 23.01 |
| The Shannon entropy-based model | 14.06 | 11.00 | 6.75 | 9.34 | 10.54 | 21.05 |
| The Tsallis entropy-based model | 12.11 *** | 7.31 *** | 5.26 | 8.94 *** | 5.33 *** | 7.59 *** |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Z.; Yu, J. Estimating the Bed-Load Layer Thickness in Open Channels by Tsallis Entropy. Entropy 2019, 21, 123. https://doi.org/10.3390/e21020123
Zhu Z, Yu J. Estimating the Bed-Load Layer Thickness in Open Channels by Tsallis Entropy. Entropy. 2019; 21(2):123. https://doi.org/10.3390/e21020123
Chicago/Turabian StyleZhu, Zhongfan, and Jingshan Yu. 2019. "Estimating the Bed-Load Layer Thickness in Open Channels by Tsallis Entropy" Entropy 21, no. 2: 123. https://doi.org/10.3390/e21020123
APA StyleZhu, Z., & Yu, J. (2019). Estimating the Bed-Load Layer Thickness in Open Channels by Tsallis Entropy. Entropy, 21(2), 123. https://doi.org/10.3390/e21020123






