Linguistic Laws in Speech: The Case of Catalan and Spanish
Abstract
:1. Introduction
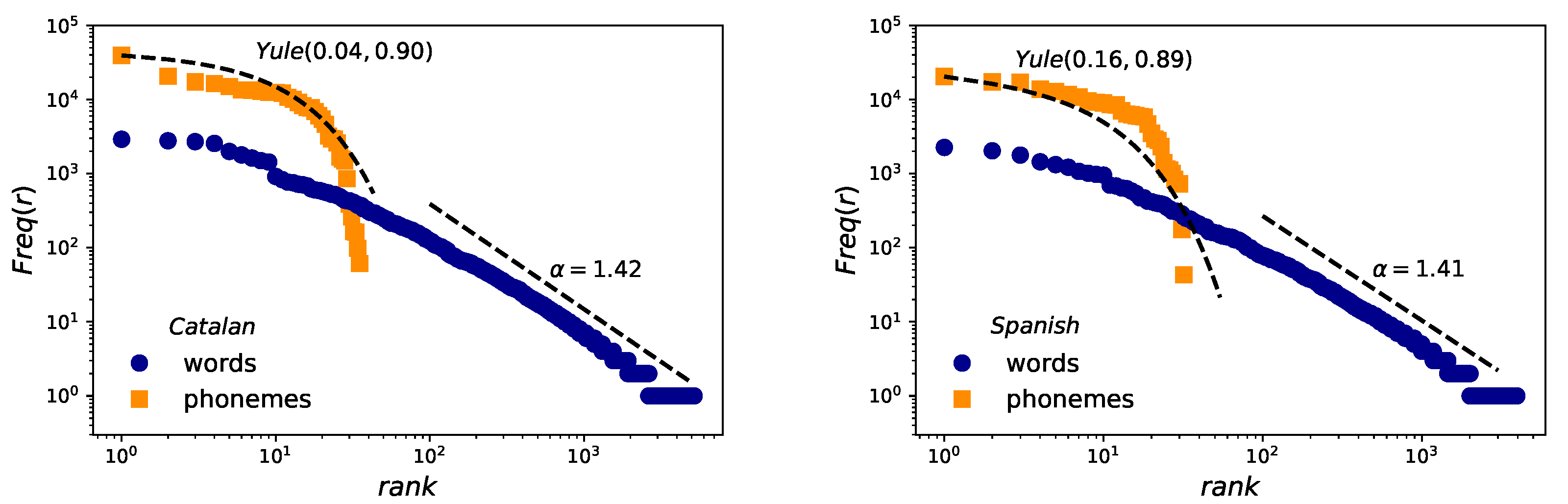
- Zipf’s law. After some notable precursors (as Pareto [5], Estoup [6] or Condon [7] among others), George Kingsley Zipf formulated and explained in [8,9] one of the most popular quantitative linguistic observations known in his honor as Zipf’s Law. He observed that the number of occurrences of words with a given rank can be expressed as , when ordering the words of written corpus in decreasing order by their frequency. This is a solid linguistic law proven in many written corpus [10] and in speech [11], even though its variations have been discussed in many contexts [12,13,14].
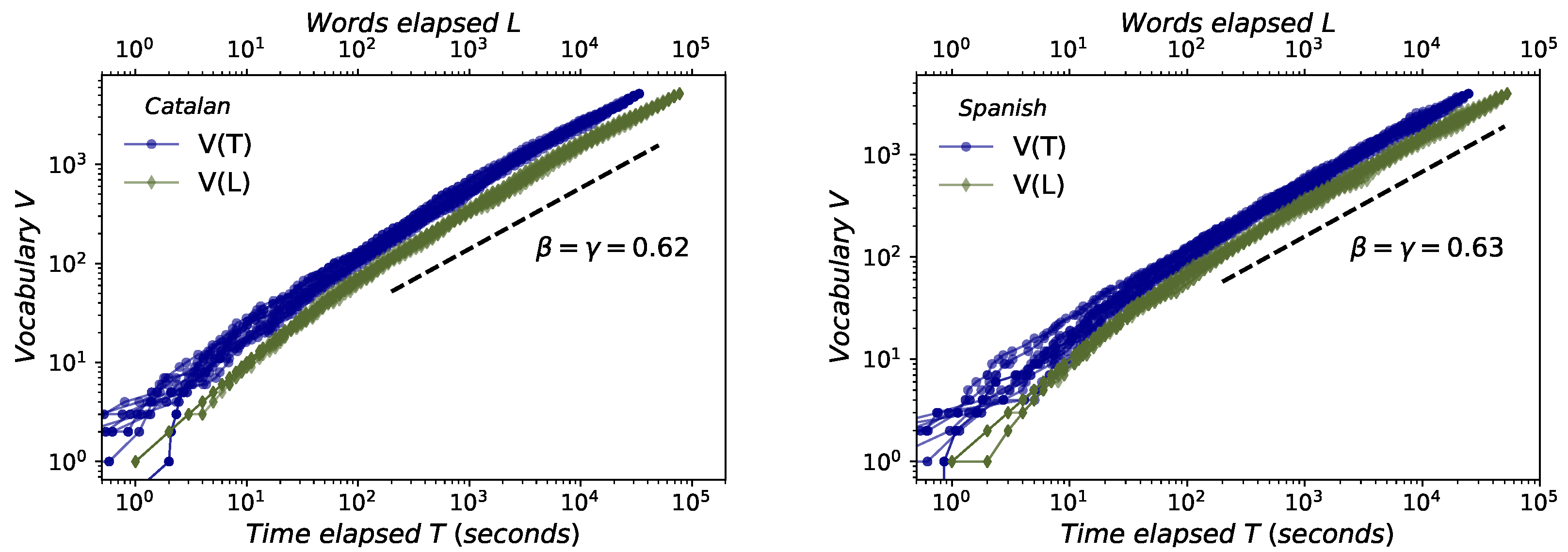
- Herdan’s law. Although with little-known precedents [15], Herdan’s law [16] (also known as Heap’s law, because it was also formulated later by Heaps in [17]) describes that the average growth of new different words V in a text of size L follows [16]. Thus, Herdan’s law shows the evolution of the number V of different words in a text (types) as its size increases, measured in the total number of words (L). L obviously is obtained by the summation of the number of occurrences of each word (tokens), for each different words types that appear in the text.
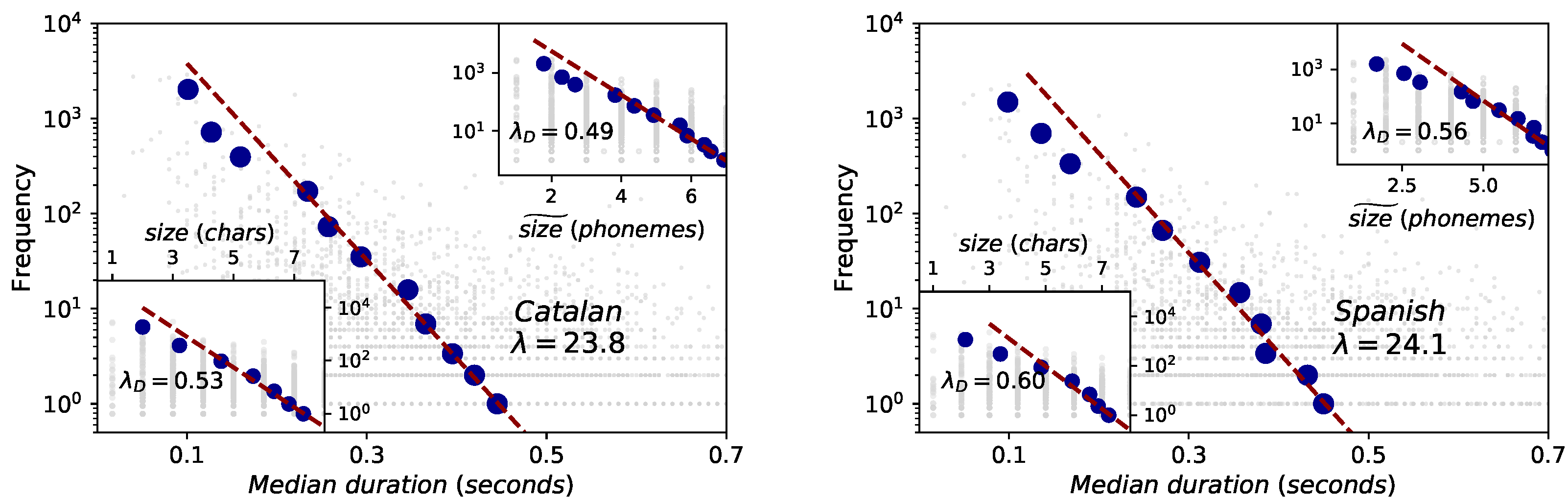
- Brevity law. Also known as Zipf’s law of abbreviation, its original qualitative statement claims that the more a word is used, the shorter it tends to be [8,9,18]. In texts or transcriptions, usually the way of measuring the word size is using the number of characters that compose the word. In this way, brevity law has been empirically proven in texts from almost a thousand languages of eighty different linguistic families [19], but also holds acoustically when measuring the time duration of words [29,30].The leap from the classical qualitative conception of brevity law to a quantitative proposal has recently been made [4,31]. In information-theoretic terms [32], if a certain symbol i has a probability of appearing in a given symbolic code with a -ary alphabet, then its minimum (optimal) expected description length . Deviating from optimality can be effectively modelled by adding a pre-factor, such that the description length of symbol i is , where . So, the closer is to one, the closer it is the system to optimal compression. Reordering terms, one finds an exponentially decaying dependence between the frequency of a unit and its size (see [4] for further details on the mathematical formulation).
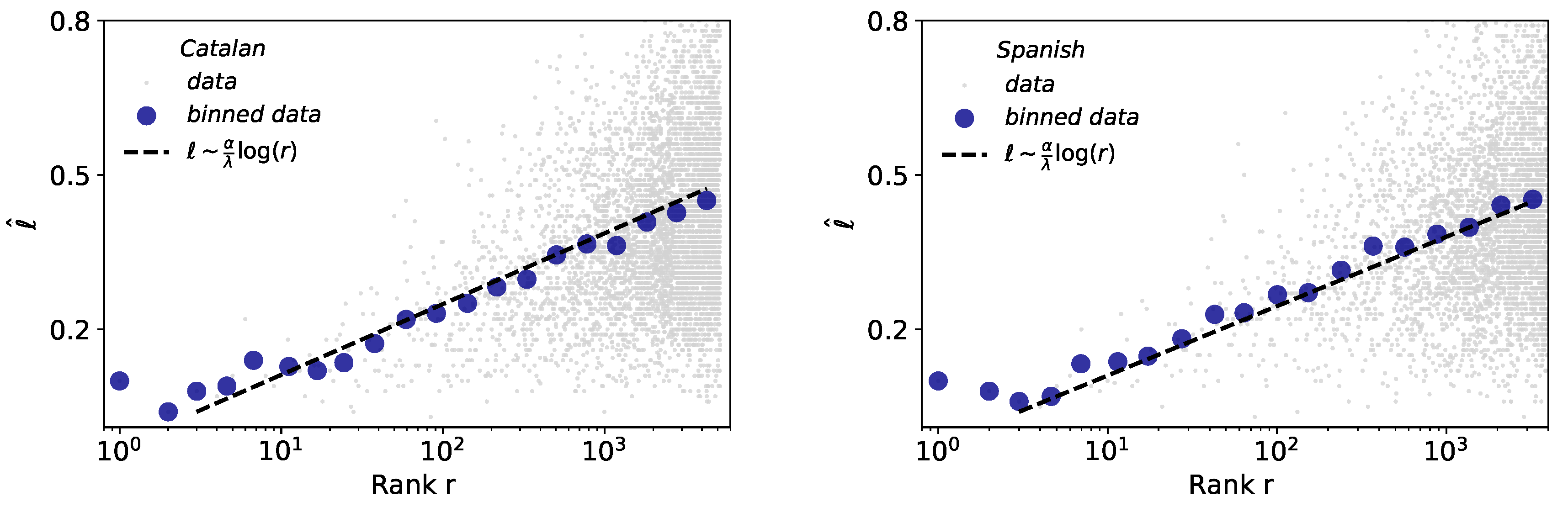
- Size-rank law. Zipf’s law and brevity law involve frequencies. Taking advantage of the new mathematical formulation of the latter, these can now be combined [4] in such a way the “size” of a unit i is mathematically related to its rank via (Zipf) and (brevity law) exponents. Experimentally, is therefore an observable parameter which indeed combines Zipf and Brevity exponents in a size-rank plot, and this law predicts that the larger linguistic units tend to have a higher rank following a specific logarithmic relation [4].
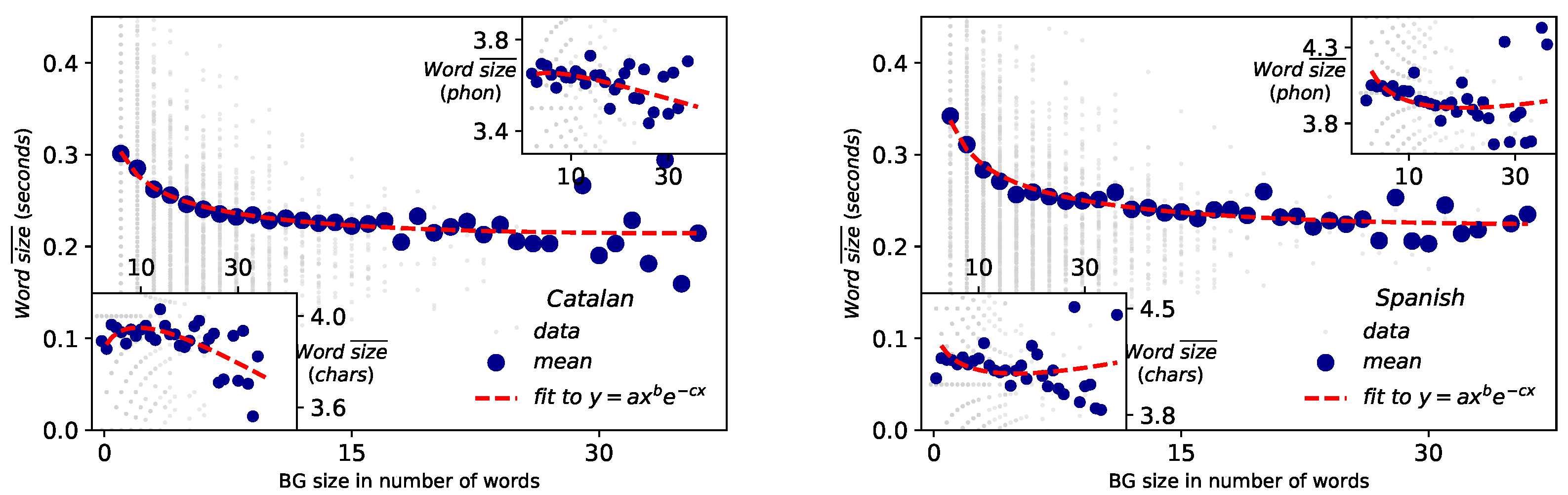
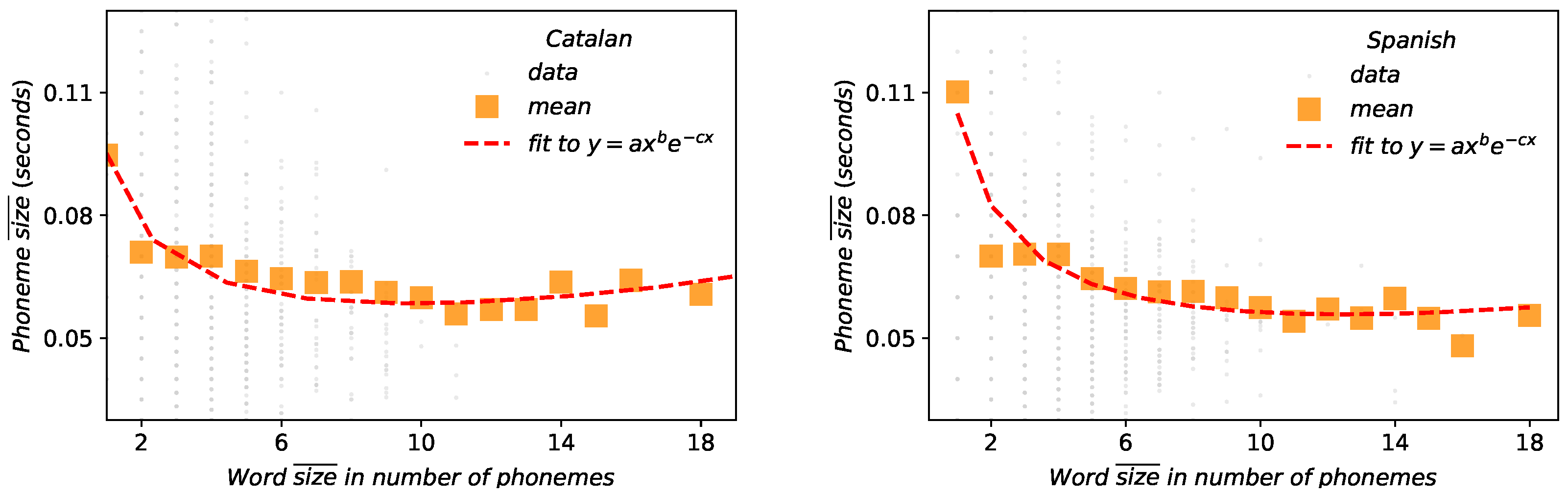
- Menzerath-Altmann law. Again after some forerunners [20], Paul Menzerath established that there is a negative correlation between the length of a linguistic construct and the length of its constituents [21,22]. Subsequently, a mathematical formulation law was heuristically proposed by Gabriel Altmann [23,24]: if n stands for the size of the linguistic construct and y is the constituent size, then , being a, b and c free parameters of the model, whose interpretation remains controversial [33]. Definitely, Menzerath–Altmann’s law could be simplified and generalized qualitatively as “the longer a language construct the shorter its components (constituents).” [23,34]. This law has been revised in different linguistic levels under multiple and polyhedral perspectives [1,33,34], but above all in written texts. Recently some researchers are turning back to the phonetic origins of the law [35] and new mathematical models explaining the actual formulation have been proposed [4].
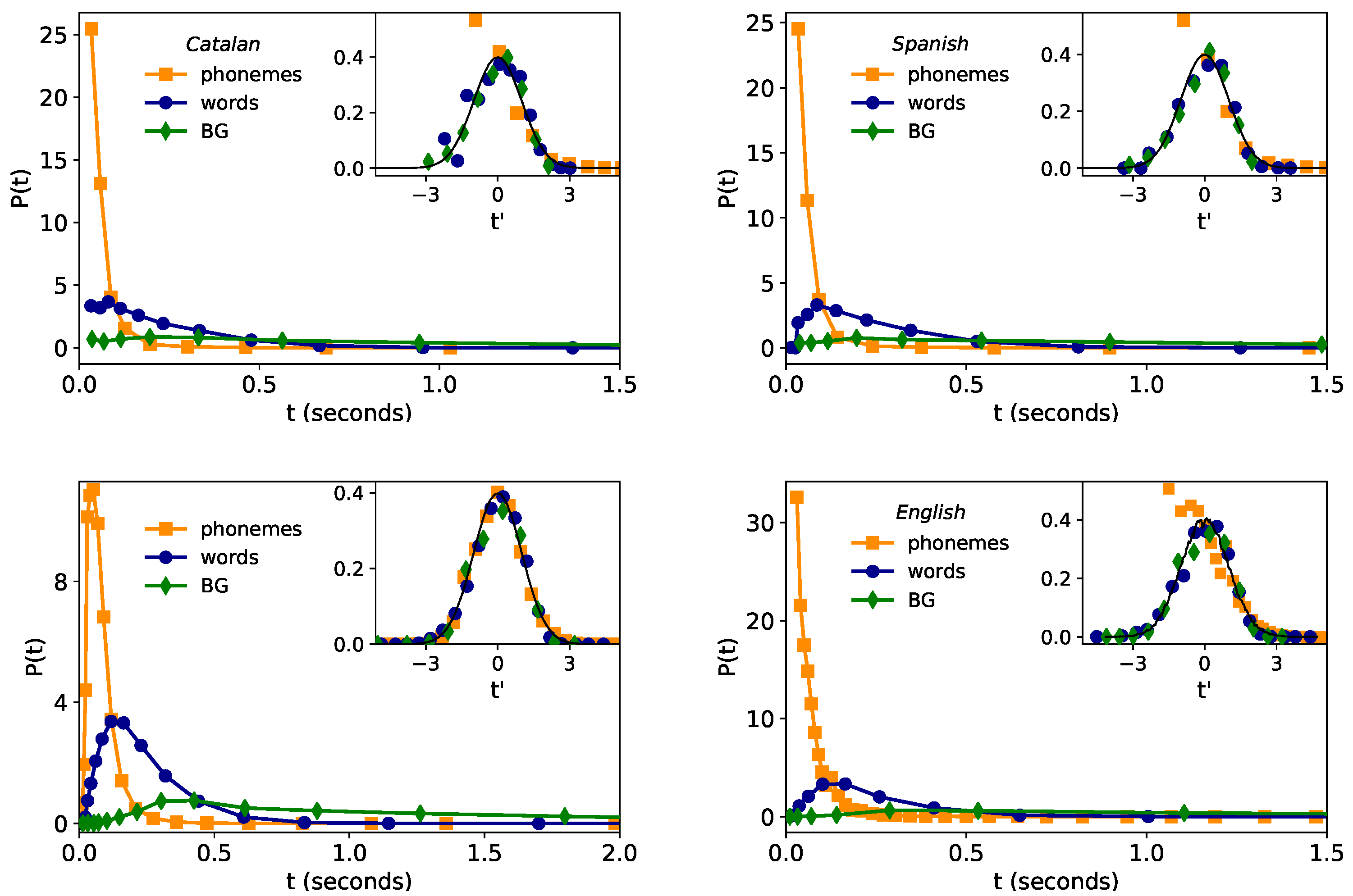
- Lognormality law. Previous studies have found consistently lognormal distributions for spoken phonemes in several languages [25,26,27,28,36] and in word and breath groups (BGs) duration for English [4,37]. In [4] it was confirmed that the time duration of phonemes, words and breath groups in speech are well described by lognormal distribution for the English language. Moreover, in [4] a general stochastic model was presented to explain and justify such lognormality at all linguistic levels only assuming that the lowest (phonemic) level follows a lognormal distribution, hence claiming the universal validity of the lognormal shape and its proposal as a ‘lognormality law’.
2. Results
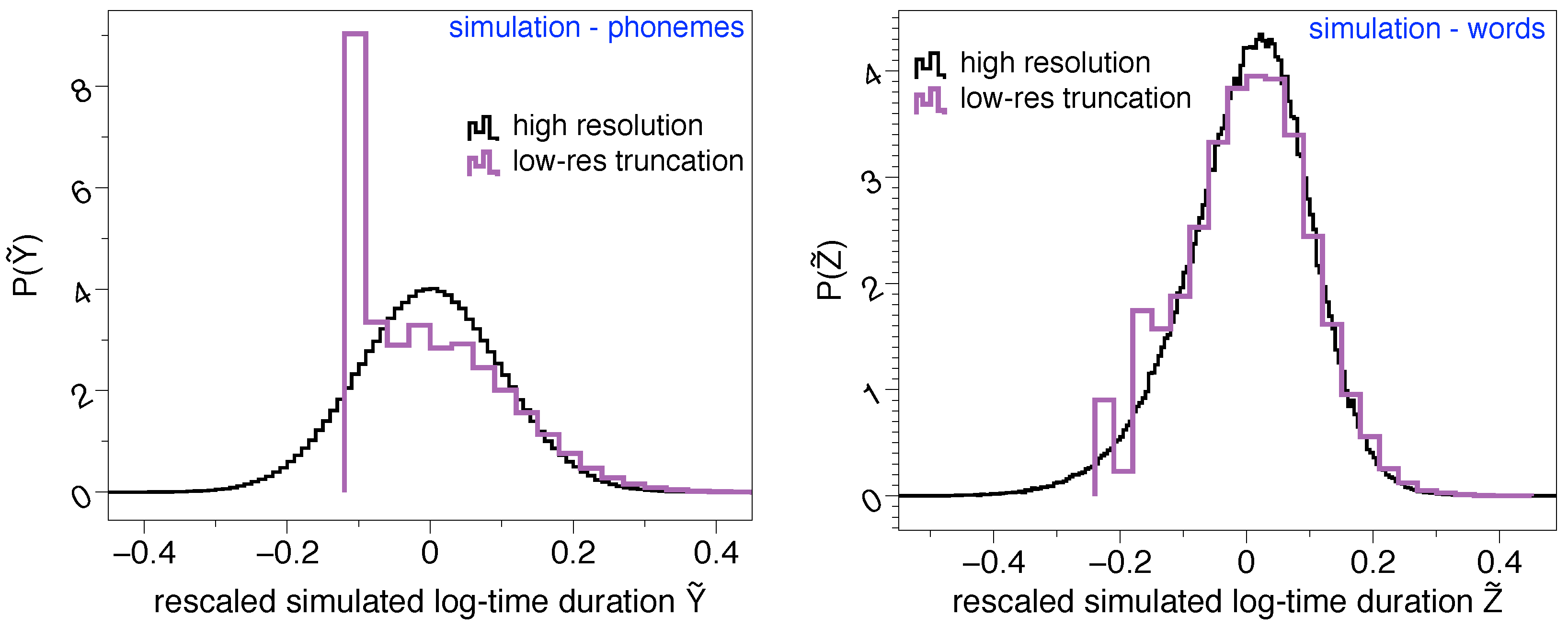
2.1. Lognormality Law and Low-Resolution Effects
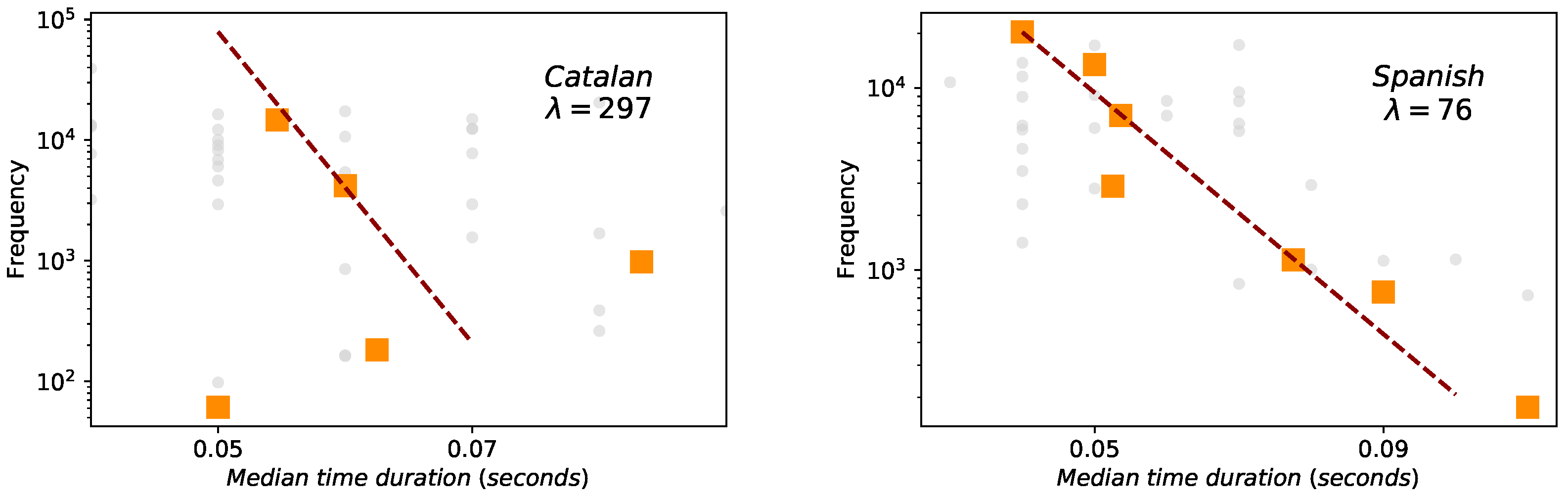
2.2. Zipf’s Law for Words and Yule Distribution for Phonemes
2.3. Herdan–Heaps’s Law
2.4. Brevity Law
2.5. Size-Rank Law
2.6. Menzerath–Altmann’s Law (MAL)
3. Discussion
The other major theoretical factor working against an interest in frequency of use in language is the distinction, traditionally traced back to Ferdinand de Sausurre (1916), between the knowledge that speakers have of the signs and structures of their language and the way language is used by actual speakers communicating with one another. American structuralists, including those of the generativist tradition, accept this distinction and assert furthermore that the only worthwhile object of study is the underlying knowledge of language (Chomsky 1965 and subsequent works). In this view, any focus on the frequency of use of the patterns or items of language is considered irrelevant.
4. Materials and Methods
Data and Reproducibility
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| BG | Breath group |
| LND | Lognormal distribution |
| MAL | Menzerath–Altmann’s Law |
References
- Köhler, R.; Altmann, G.; Piotrowski, R.G. Quantitative Linguistik/Quantitative Linguistics: Ein Internationales Handbuch/an International Handbook; Walter de Gruyter: Berlin, Germany, 2008; Volume 27. [Google Scholar]
- Grzybek, P. History of quantitative linguistics. Glottometrics 2012, 23, 70–80. [Google Scholar]
- Best, K.H.; Rottmann, O. Quantitative Linguistics, an Invitation; RAM-Verlag: Ludenscheid, Germany, 2017. [Google Scholar]
- Torre, I.G.; Luque, B.; Lacasa, L.; Kello, C.T.; Hernández-Fernández, A. On the physical origin of linguistic laws and lognormality in speech. R. Soc. Open Sci. 2019, 6. [Google Scholar] [CrossRef] [PubMed]
- Pareto, V. Cours d’économie Politique; Librairie Droz; Imprime en Suisse: Geneva, Swizerland, 1964; Volume 1. (In French) [Google Scholar]
- Estoup, J.B. Gammes Sténographiques. Recueil de Textes Choisis pour L’acquisition Méthodique de la Vitesse, Précédé d’une Introduction par J.-B. Estoup; Sténographique: Paris, France, 1912. (In French) [Google Scholar]
- Condon, E.U. Statistics of vocabulary. Science 1928, 67, 300. [Google Scholar] [CrossRef] [PubMed]
- Zipf, G.K. The Psychobiology of Language, an Introduction to Dynamic Philology; Houghton–Mifflin: Boston, MA, USA, 1935. [Google Scholar]
- Zipf, G.K. Human Behavior and the Principle of Least Effort; Addison–Wesley: Cambridge, MA, USA, 1949. [Google Scholar]
- Altmann, E.G.; Gerlach, M. Statistical laws in linguistics. In Creativity and Universality in Language; Springer: Cham, Germany, 2016; pp. 7–26. [Google Scholar]
- Bian, C.; Lin, R.; Zhang, X.; Ma, Q.D.Y.; Ivanov, P.C. Scaling laws and model of words organization in spoken and written language. EPL (Europhysics Letters) 2016, 113, 18002. [Google Scholar] [CrossRef]
- Ferrer-i Cancho, R. The variation of Zipf’s law in human language. Eur. Phys. J. B 2005, 44, 249–257. [Google Scholar] [CrossRef]
- Baixeries, J.; Elvevag, B.; Ferrer-i Cancho, R. The evolution of the exponent of Zipf’s law in language ontogeny. PLoS ONE 2013, 8. [Google Scholar] [CrossRef]
- Neophytou, K.; van Egmond, M.; Avrutin, S. Zipf’s Law in Aphasia Across Languages: A Comparison of English, Hungarian and Greek. J. Quant. Linguist. 2017, 24, 178–196. [Google Scholar] [CrossRef]
- Kuraszkiewicz, W.; Łukaszewicz, J. Ilość różnych wyrazów w zależności od długości tekstu. Pamiętnik Literacki: Czasopismo Kwartalne Poświęcone Historii i Krytyce Literatury Polskiej 1951, 42, 168–182. (In Polish) [Google Scholar]
- Herdan, G. Type-Token Mathematics: A Textbook of Mathematical Linguistics; De Gruyter Mouton: Berlin, Germany, 1960. [Google Scholar]
- Heaps, H.S. Information Retrieval, Computational and Theoretical Aspects; Academic Press: Cambridge, MA, USA, 1978. [Google Scholar]
- Zipf, G.K. Selected Studies of the Principle of Relative Frequency in Language; De Gruyter Mouton: Berlin, Germany, 1932. [Google Scholar]
- Bentz, C.; i Cancho, R.F. Zipf’s Law of Abbreviation as a Language Universal; Universitätsbibliothek Tübingen: Tübingen, The Netherlands, 2016. [Google Scholar]
- Grégoire, A. Variation de la dure de la syllabe française suivant sa place dans les groupements phonetiques. La Parole 1899, 1, 161–176. (In French) [Google Scholar]
- Menzerath, P.; Oleza, J. Spanische Lautdauer: Eine Experimentelle Untersuchung; De Gruyter Mouton: Berlin, Germany, 1928. (In German) [Google Scholar]
- Menzerath, P. Die Architektonik des Deutschen Wortschatzes; Dümmler: Berlin, Germany, 1954; Volume 3. (In German) [Google Scholar]
- Altmann, G. Prolegomena to Menzerath’s law. Glottometrika 1980, 2, 1–10. [Google Scholar]
- Altmann, G.; Schwibbe, M. Das Menzertahsche Gesetz in Informationsverbarbeitenden Systemen; Georg Olms: Hildesheim, Germany, 1989. (In German) [Google Scholar]
- Herdan, G. The relation between the dictionary distribution and the occurrence distribution of word length and its importance for the study of Quantitative Linguistics. Biometrika 1958, 45, 222–228. [Google Scholar] [CrossRef]
- Rosen, K.M. Analysis of speech segment duration with the lognormal distribution: A basis for unification and comparison. J. Phon. 2005, 33, 411–426. [Google Scholar] [CrossRef]
- Gopinath, D.P.; Veena, S.; Nair, A.S. Modeling of Vowel Duration in Malayalam Speech using Probability Distribution. In Proceedings of the Speech Prosody, Campinas, Brazil, 6–9 May 2008; pp. 6–9. [Google Scholar]
- Shaw, J.A.; Kawahara, S. Effects of surprisal and entropy on vowel duration in Japanese. Language Speech 2017, 62, 80–114. [Google Scholar] [CrossRef] [PubMed]
- Gahl, S. Time and thyme are not homophones: The effect of lemma frequency on word durations in spontaneous speech. Language 2008, 84, 474–496. [Google Scholar] [CrossRef]
- Tomaschek, F.; Wieling, M.; Arnold, D.; Baayen, R.H. Word frequency, Vowel Length and Vowel Quality in Speech Production: An EMA Study of the Importance of Experience. Available online: https://ids-pub.bsz-bw.de/frontdoor/index/index/docId/5957 (accessed on 23 November 2019).
- Ferrer-i-Cancho, R.; Bentz, C.; Seguin, C. Optimal coding and the origins of Zipfian laws. arXiv 2019, arXiv:1906.01545. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory (Wiley Series in Telecommunications and Signal Processing); Wiley-Interscience: New York, NY, USA, 2006. [Google Scholar]
- Cramer, I. The Parameters of the Altmann-Menzerath Law. J. Quant. Linguist. 2005, 12, 41–52. [Google Scholar] [CrossRef]
- Grzybek Peter, N.; Stadlober, E.; Kelih Emmerich, N. The Relationship of Word Length and Sentence Length: The Inter-Textual Perspective. In Advances In Data Analysis; Springer: Berlin/Heidelberg, Germany, 2007; pp. 611–618. [Google Scholar]
- Mačutek, J.; Chromý, J.; Koščová, M. Menzerath-Altmann Law and Prothetic /v/ in Spoken Czech. J. Quant. Linguist. 2019, 26, 66–80. [Google Scholar] [CrossRef]
- Sayli, O. Duration Analysis and Modeling for Turkish Text-to-Speech Synthesis. Master’s Thesis, Bogaziei University, Istanbul, Turkey, 2002. [Google Scholar]
- Greenberg, S.; Carvey, H.; Hitchcock, L.; Chang, S. Temporal properties of spontaneous speech-a syllable-centric perspective. J. Phon. 2003, 31, 465–485. [Google Scholar] [CrossRef]
- Luque, J.; Luque, B.; Lacasa, L. Scaling and universality in the human voice. J. R. Soc. Interface 2015, 12, 20141344. [Google Scholar] [CrossRef]
- Torre, I.G.; Luque, B.; Lacasa, L.; Luque, J.; Hernández-Fernández, A. Emergence of linguistic laws in human voice. Sci. Rep. 2017, 7, 43862. [Google Scholar] [CrossRef]
- Garrido, J.M.; Escudero, D.; Aguilar, L.; Cardeñoso, V.; Rodero, E.; de-la Mota, C.; González, C.; Rustullet, S.; Larrea, O.; Laplaza, Y.; et al. Glissando: A corpus for multidisciplinary prosodic studies in Spanish and Catalan. Lang. Resour. Eval. 2013, 47, 945–971. [Google Scholar] [CrossRef]
- Fernández Planas, A. Así se Habla: Nociones Fundamentales de Fonética General y Española.; Apuntes de Catalán, Gallego y Euskara; Horsori Editorial: Barcelona, Spain, 2005. (In Spanish) [Google Scholar]
- Pitt, M.A.; Dilley, L.; Johnson, K.; Kiesling, S.; Raymond, W.; Hume, E.; Fosler-Lussier, E. Buckeye Corpus of Conversational Speech, 2nd release; Columbus, OH: Department of Psychology, Ohio State University, 2007. Available online: http://sldr.org/voir_depot.php?id=776&lang=en&sip=0 (accessed on 23 November 2019).
- Pitt, M.A.; Johnson, K.; Hume, E.; Kiesling, S.; Raymond, W. The Buckeye corpus of conversational speech: Labeling conventions and a test of transcriber reliability. Speech Commun. 2005, 45, 89–95. [Google Scholar] [CrossRef]
- Eliason, S.R. Maximum Likelihood Estimation: Logic and Practice; Sage Publications: Tucson, AZ, USA, 1993; Volume 96. [Google Scholar]
- Clauset, A.; Shalizi, C.R.; Newman, M.E. Power-law distributions in empirical data. SIAM Rev. 2009, 51, 661–703. [Google Scholar] [CrossRef]
- Gillespie, C.S. Fitting Heavy Tailed Distributions: The poweRlaw Package. J. Stat. Softw. 2015, 64, 1–16. [Google Scholar] [CrossRef]
- Lü, L.; Zhang, Z.K.; Zhou, T. Zipf’s law leads to Heaps’ law: Analyzing their relation in finite-size systems. PLoS ONE 2010, 5, e14139. [Google Scholar] [CrossRef] [PubMed]
- Font-Clos, F.; Boleda, G.; Corral, A. A scaling law beyond Zipf’s law and its relation to Heaps’ law. New J. Phys. 2013, 15, 093033. [Google Scholar] [CrossRef]
- Ferrer-i Cancho, R. Compression and the origins of Zipf’s law for word frequencies. Complexity 2016, 21, 409–411. [Google Scholar] [CrossRef]
- Bybee, J. Frequency of Use and the Organization of Language; Oxford University Press: Oxford, UK, 2007. [Google Scholar]
- Quatieri, T.F. Discrete-Time Speech Signal Processing: Principles and Practice; Prentice Hall PTR: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Borleffs, E.; Maassen, B.A.M.; Lyytinen, H.; Zwarts, F. Measuring orthographic transparency and morphological-syllabic complexity in alphabetic orthographies: A narrative review. Read. Writ. 2017, 30, 1617–1638. [Google Scholar] [CrossRef]
- Rojo, G. Sobre la configuración estadística de los corpus textuales. Lingüística 2017, 33, 121–134. (In Spanish) [Google Scholar] [CrossRef]
- Tolchinsky, L.; Martí, A.; Llaurado, A. The growth of the written lexicon in Catalan From childhood to adolescence. Writ. Lang. Lit. 2010, 13, 206–235. [Google Scholar] [CrossRef]
- Baken, R.; Orlikoff, R. Clinical Measurement of Speech and Voice (Speech Science); Cengage Learning: Boston, MA, USA, 2000. [Google Scholar]
- Casas, B.; Hernández-Fernández, A.; Català, N.; i Cancho, R.F.; Baixeries, J. Polysemy and brevity versus frequency in language. Comput. Speech Lang. 2019, 58, 1–50. [Google Scholar] [CrossRef]
- Tsao, Y.C.; Weismer, G. Interspeaker variation in habitual speaking rate: Evidence for a neuromuscular component. J. Speech Lang. Hear. Res. 1997, 40, 858–866. [Google Scholar] [CrossRef] [PubMed]
- Garrido, J.M. SegProso: A Praat-Based Tool for the Automatic Detection and Annotation of Prosodic Boundaries in Speech Corpora. In Proceedings of the TRASP 2013, Barcelona, Spain, 30 August 2013; pp. 74–77. [Google Scholar]
| Mathematical Formulation | Details | References | |
|---|---|---|---|
| Zipf’s law | f: frequency r: rank : parameter | [5,6,7,8,9] | |
| Herdan-Heaps’ law | L: text size/time elapsed V: vocabulary : parameter | [15,16,17] | |
| Brevity law | f: frequency ℓ: size : parameter | [4,8,9,18,19] | |
| Size-rank law | ℓ: size r: rank : parameter | [4,9,18] | |
| Menzerath-Altmann’s law | n: size of the whole y: size of the parts : parameters | [4,20,21,22,23,24] | |
| Lognormality law | t: time duration : parameters | [4,25,26,27,28] |
| Number of Elements | Median Duration (secs.) | |||||||
|---|---|---|---|---|---|---|---|---|
| Phonemes | Words | BG | Phon | Word | BG | |||
| Tokens | Types | Tokens | Types | Tokens | ||||
| Catalan | 35 | |||||||
| Spanish | 32 | |||||||
| English | 64 | |||||||
| Words | Zipf | Herdan-Heaps | Brevity | Size-Rank | Menzerath-Altmann | Lognormality | |||
|---|---|---|---|---|---|---|---|---|---|
| Catalan | - | - | |||||||
| Spanish | - | - | |||||||
| English | |||||||||
| Phonemes | Yule | Brevity | Menzerath-Altmann | Lognormality | ||||
|---|---|---|---|---|---|---|---|---|
| Catalan | 297 | - | - | |||||
| Spanish | 76 | - | - | |||||
| English | 127 | |||||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hernández-Fernández, A.; G. Torre, I.; Garrido, J.-M.; Lacasa, L. Linguistic Laws in Speech: The Case of Catalan and Spanish. Entropy 2019, 21, 1153. https://doi.org/10.3390/e21121153
Hernández-Fernández A, G. Torre I, Garrido J-M, Lacasa L. Linguistic Laws in Speech: The Case of Catalan and Spanish. Entropy. 2019; 21(12):1153. https://doi.org/10.3390/e21121153
Chicago/Turabian StyleHernández-Fernández, Antoni, Iván G. Torre, Juan-María Garrido, and Lucas Lacasa. 2019. "Linguistic Laws in Speech: The Case of Catalan and Spanish" Entropy 21, no. 12: 1153. https://doi.org/10.3390/e21121153
APA StyleHernández-Fernández, A., G. Torre, I., Garrido, J.-M., & Lacasa, L. (2019). Linguistic Laws in Speech: The Case of Catalan and Spanish. Entropy, 21(12), 1153. https://doi.org/10.3390/e21121153





