Predicting the Evolution of Physics Research from a Complex Network Perspective
Abstract
1. Introduction
2. Materials and Methods
2.1. GEP Method
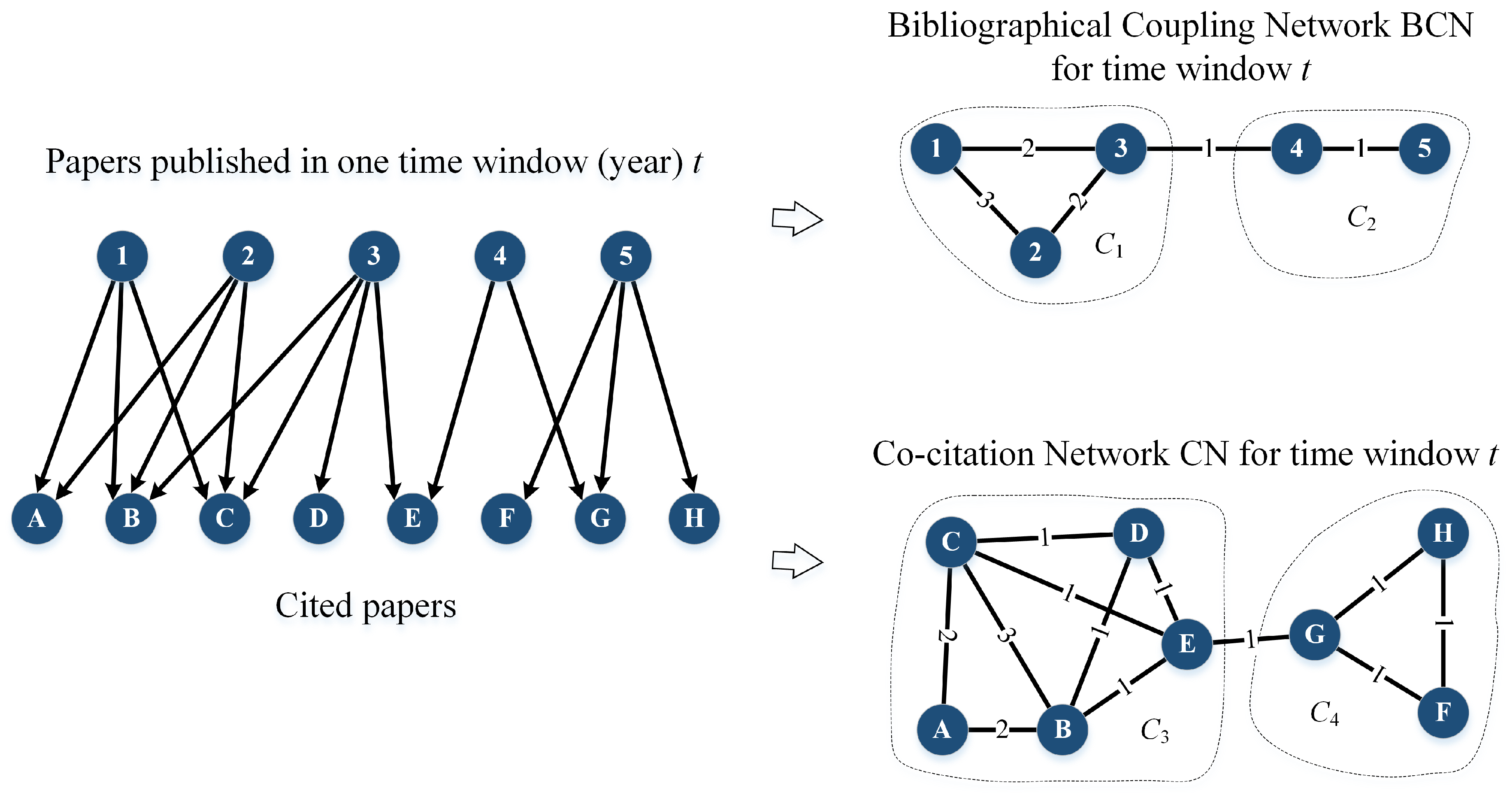
2.2. Bibliographic Coupling Network and Co-Citation Network
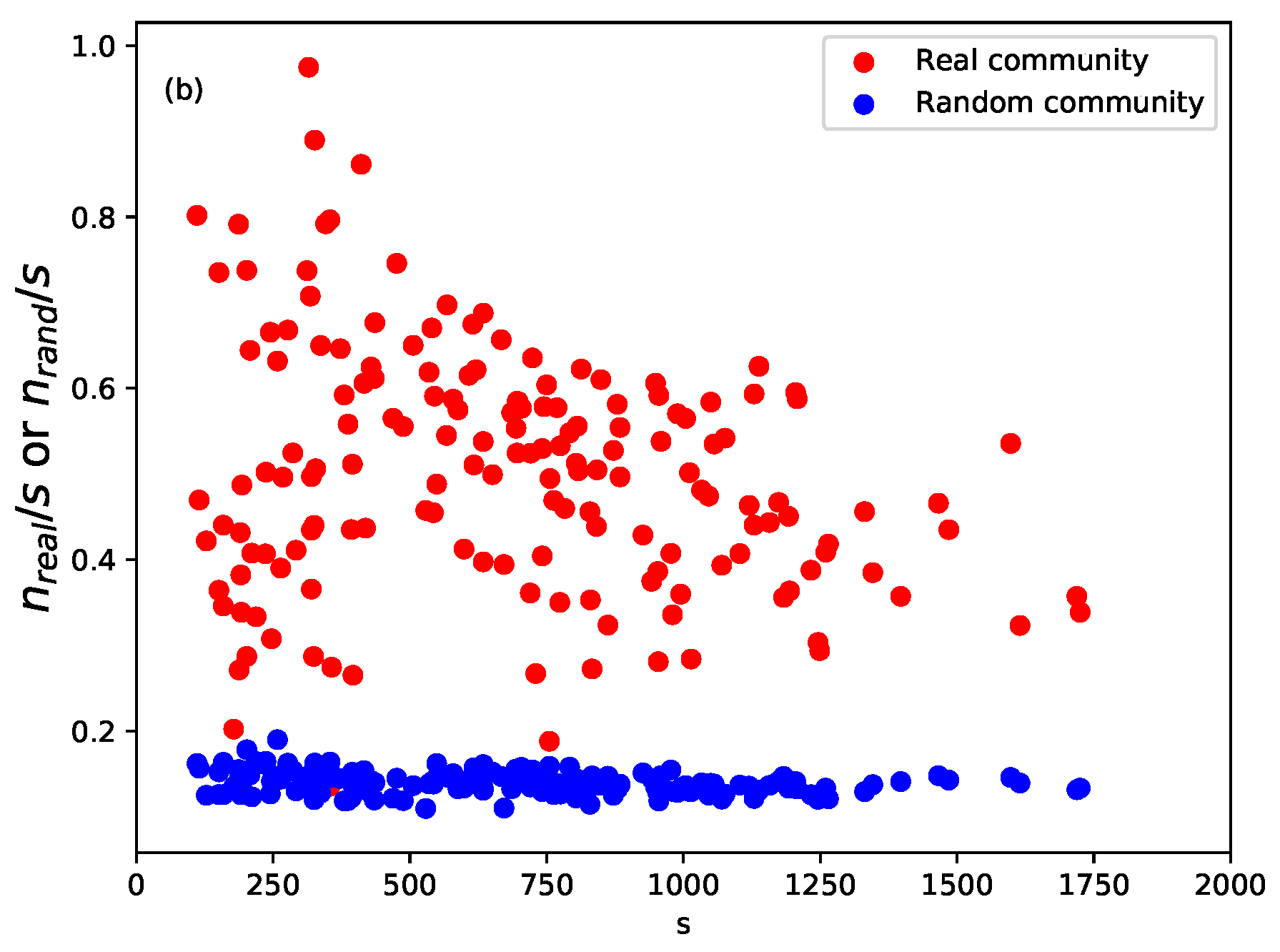
2.3. Community Detection and Validation
2.4. Intimacy Indices
2.5. GED Method
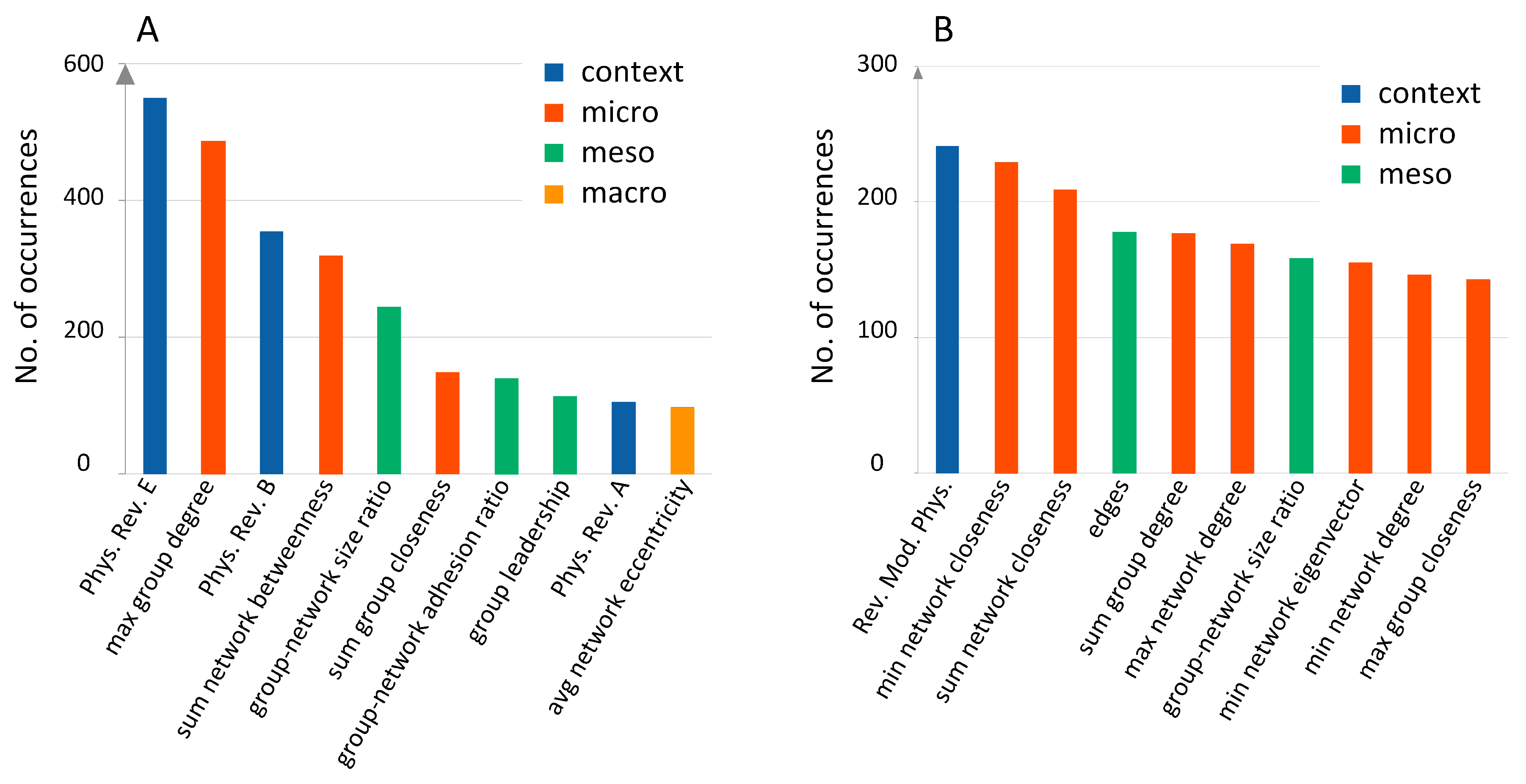
2.6. Feature Ranking
3. Results
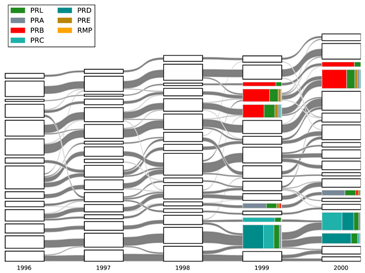
3.1. Physics Research Evolution for 1981–2010
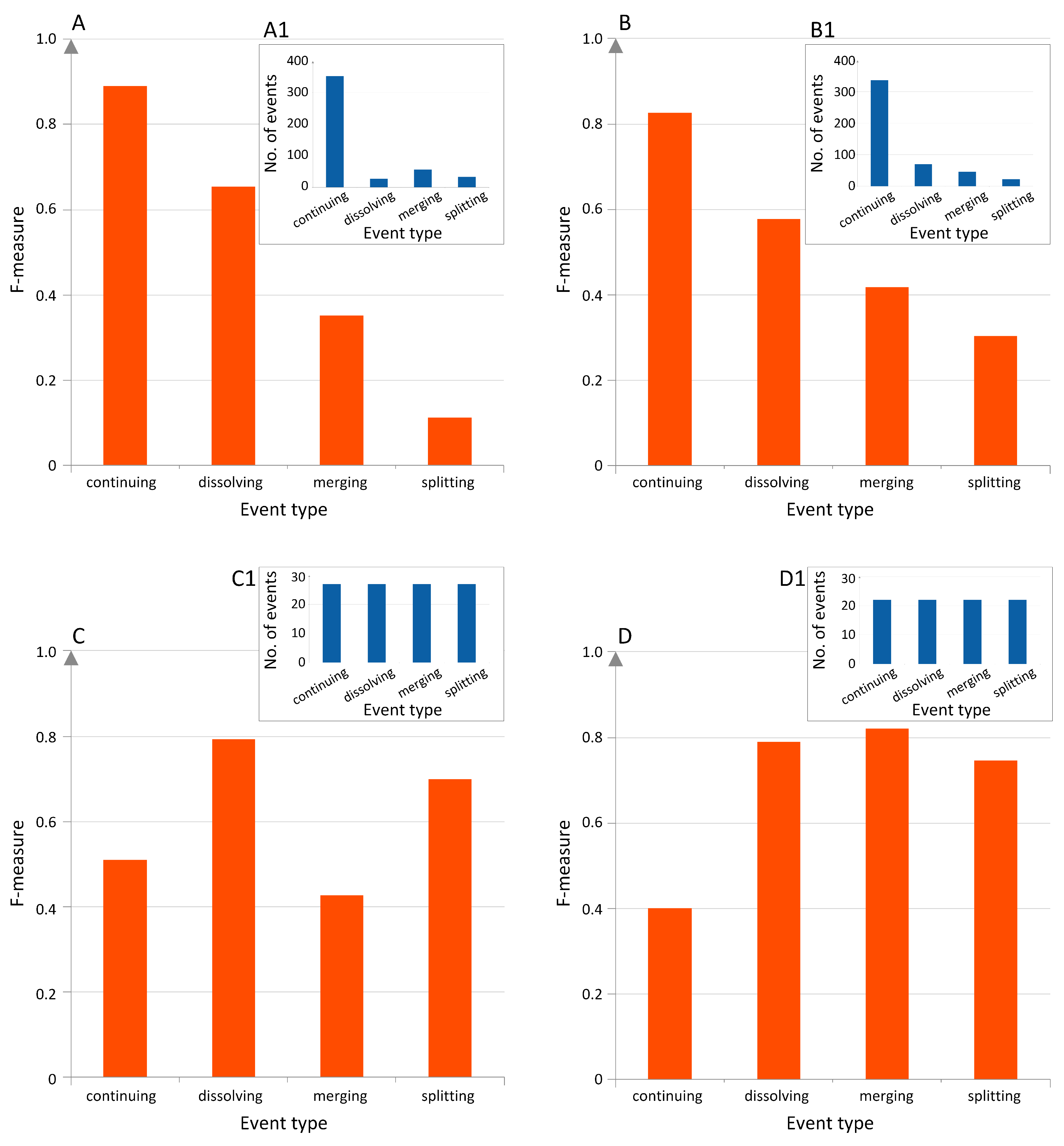
3.2. Event Labeling
- Continuing: A research field is said to be continuing when the problems identified and solutions obtained from one year to another are of an incremental nature. It is likely to correspond to the repeated hypothesis testing picture of the progress of science proposed by Karl Popper [33]. Therefore, in the CN, this would appear as a group of papers that are repeatedly cited together year-by-year. In the BCN, this shows up as groups of articles from successive years sharing more or less the same reference list.
- Dissolving: A research field is thought to disappear in the following year if the problems are solved or abandoned, and no new significant work is done after this. For the CN, we will find a group of papers that are cited up to a given year, but receiving very few new citations afterwards. In the BCN, no new relevant papers are published in the field; hence, the reference chain terminates.
- Splitting: A research field splits in the following year, when the community of scientists who used to work on the same problems starts to form two or more sub-communities, which are more and more distant from one another. In terms of the CN, we will find a group of papers that are almost always cited together up till a given year, breaking up into smaller and disjoint groups of papers that are cited together in the next year. In the BCN, we will find the transition between new papers citing a group of older papers to new papers citing only a part of this reference group.
- Merging: Multiple research fields are considered to have merged in the following year when the previously disjoint communities of scientists found a mutual interest in each other’s field so that they solve the problems in their own domain using methods from another domain. In the CN, we find previously distinct groups of papers that are cited together by papers published after a given year. In the BCN, newly published papers will form a group commonly citing several previously disjoint groups of older papers.
3.3. Future Events’ Prediction
3.4. Predictive Feature Ranking
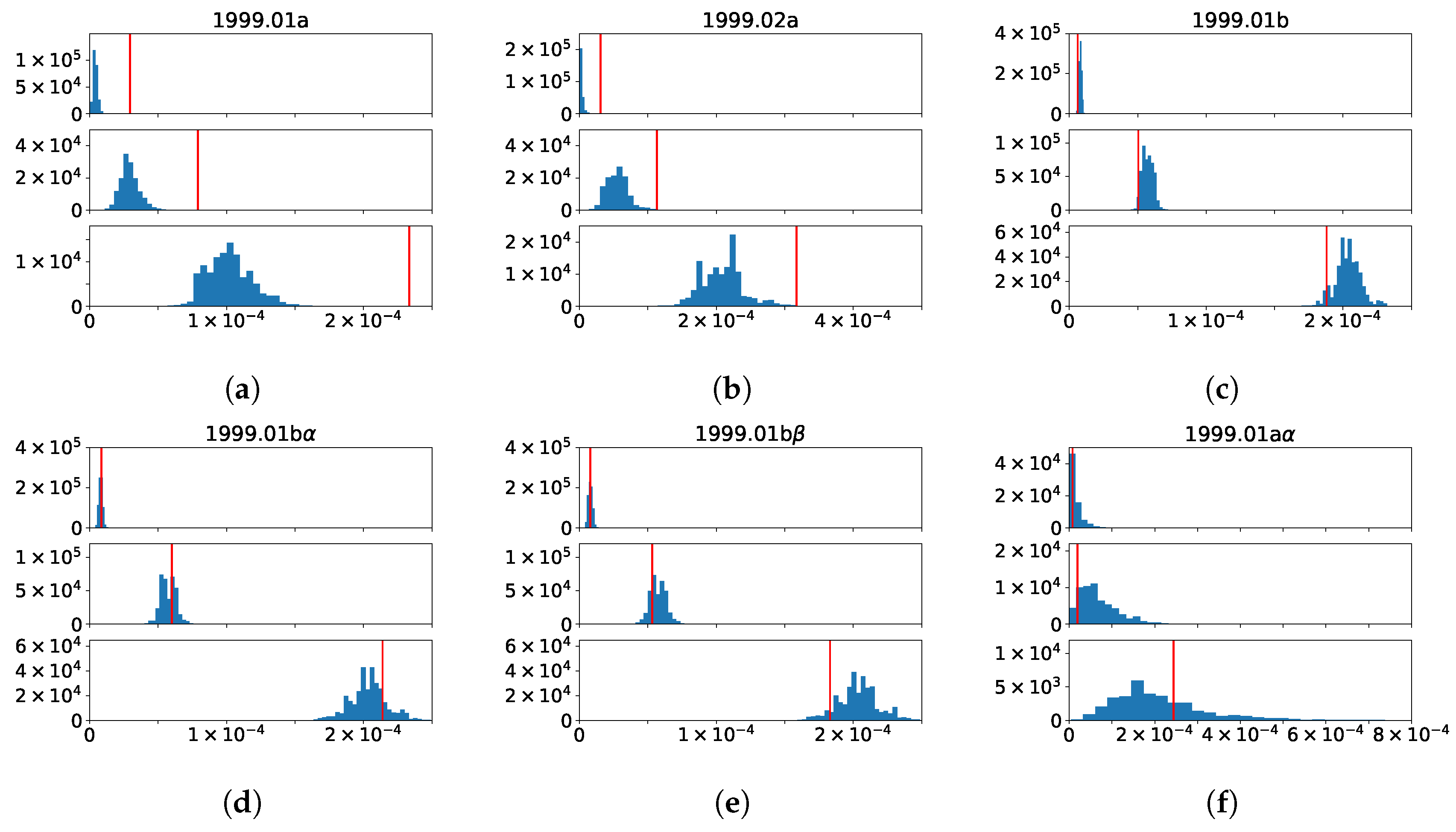
3.5. Changes to the Betweenness Distributions Associated with Merging and Splitting Events in BCN
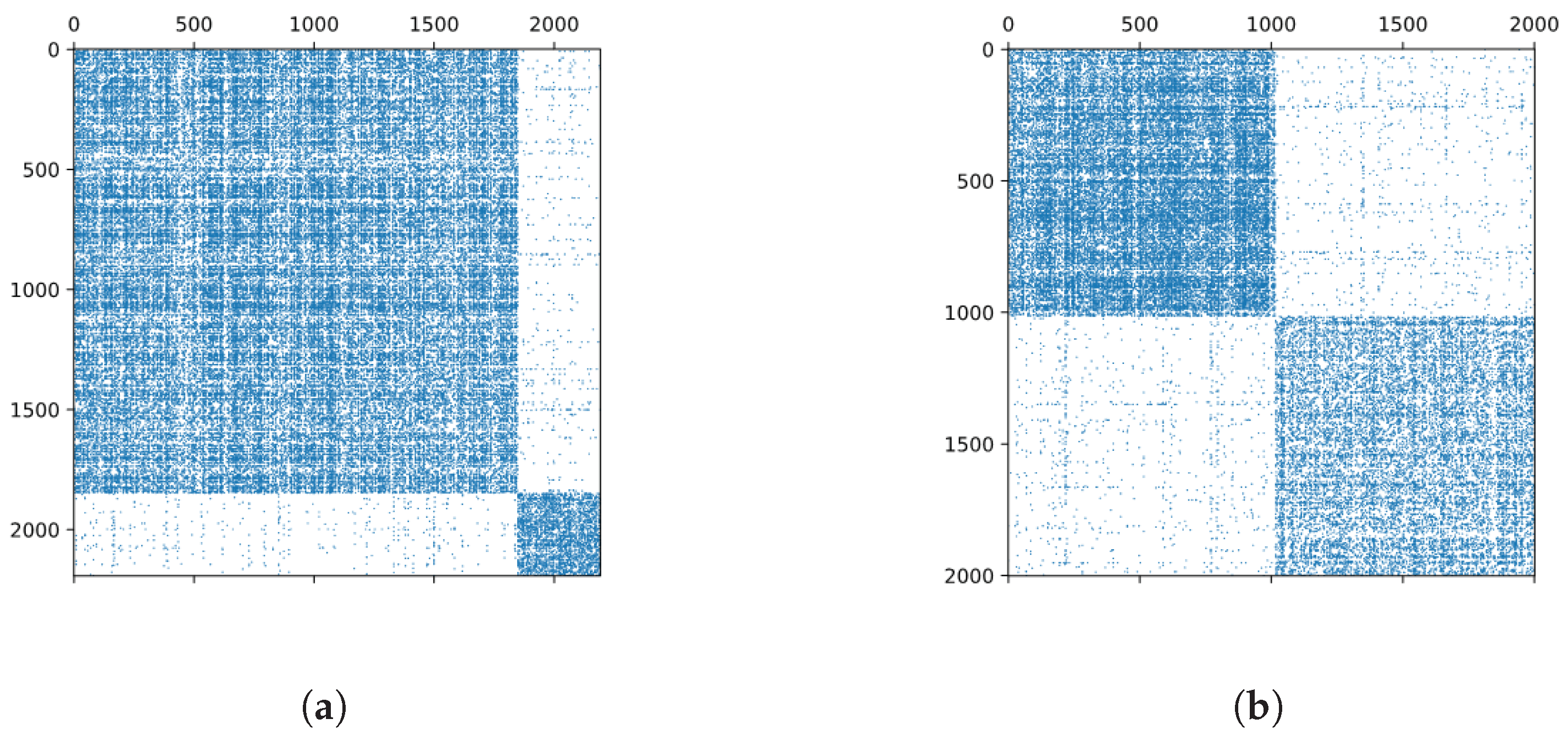
3.5.1. 1999.01 + 1999.02 → 2000.03
3.5.2. 1999.01 → 2000.02 + 2000.03
3.5.3. 1999.11 + 1999.12 → 2000.15
3.5.4. 1999.04 → 2000.06 and 1999.13 → 2000.16
4. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| PR | Physical Review |
| PRA | Physical Review A |
| PRB | Physical Review B |
| PRC | Physical Review C |
| PRD | Physical Review D |
| PRE | Physical Review E |
| PRL | Physical Review Letters |
| RMP | Reviews of Modern Physics |
| BCN | Bibliographic coupling network |
| CN | Co-citation network |
| GEP | Group evolution prediction |
| GED | Group evolution discover |
| SI | Supplementary Information |
References
- Chen, P.; Redner, S. Community structure of the physical review citation network. J. Inf. 2010, 4, 278–290. [Google Scholar] [CrossRef]
- Rosvall, M.; Bergstrom, C.T. Mapping Change in Large Networks. PLoS ONE 2010, 5, e8694. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Nanetti, A.; Cheong, S.A. Knowledge evolution in physics research: An analysis of bibliographic coupling networks. PLoS ONE 2017, 12, e0184821. [Google Scholar] [CrossRef] [PubMed]
- Helbing, D.; Brockmann, D.; Chadefaux, T.; Donnay, K.; Blanke, U.; Woolley-Meza, O.; Moussaid, M.; Johansson, A.; Krause, J.; Schutte, S.; et al. Saving Human Lives: What Complexity Science and Information Systems can Contribute. J. Stat. Phys. 2015, 158, 735–781. [Google Scholar] [CrossRef] [PubMed]
- Zeng, A.; Shen, Z.; Zhou, J.; Wu, J.; Fan, Y.; Wang, Y.; Stanley, H.E. The science of science: From the perspective of complex systems. Phys. Rep. 2017, 714–715, 1–73. [Google Scholar] [CrossRef]
- Fortunato, S.; Bergstrom, C.T.; Börner, K.; Evans, J.A.; Helbing, D.; Milojević, S.; Petersen, A.M.; Radicchi, F.; Sinatra, R.; Uzzi, B.; et al. Science of science. Science 2018, 359, 185. [Google Scholar] [CrossRef]
- Hicks, D.; Wouters, P.; Waltman, L.; de Rijcke, S.; Rafols, I. Bibliometrics: The Leiden Manifesto for research metrics. Nature 2015, 520, 429–431. [Google Scholar] [CrossRef]
- Radicchi, F.; Fortunato, S.; Castellano, C. Universality of citation distributions: Toward an objective measure of scientific impact. Proc. Natl. Acad. Sci. USA 2008, 105, 17268–17272. [Google Scholar] [CrossRef]
- Wang, D.; Song, C.; Barabási, A.L. Quantifying Long-Term Scientific Impact. Science 2013, 342, 127–132. [Google Scholar] [CrossRef]
- Ke, Q.; Ferrara, E.; Radicchi, F.; Flammini, A. Defining and identifying Sleeping Beauties in science. Proc. Natl. Acad. Sci. USA 2015, 112, 7426–7431. [Google Scholar] [CrossRef]
- Small, H. Visualizing science by citation mapping. J. Am. Soc. Inf. Sci. 1999, 50, 799–813. [Google Scholar] [CrossRef]
- Boyack, K.W.; Klavans, R.; Börner, K. Mapping the backbone of science. Scientometrics 2005, 64, 351–374. [Google Scholar] [CrossRef]
- Bollen, J.; Van de Sompel, H.; Hagberg, A.; Bettencourt, L.; Chute, R.; Rodriguez, M.A.; Balakireva, L. Clickstream Data Yields High-Resolution Maps of Science. PLoS ONE 2009, 4, e4803. [Google Scholar] [CrossRef]
- Perc, M. Self-organization of progress across the century of physics. Sci. Rep. 2013, 3, 1720. [Google Scholar] [CrossRef]
- Kuhn, T.; Perc, M.; Helbing, D. Inheritance Patterns in Citation Networks Reveal Scientific Memes. Phys. Rev. X 2014, 4, 041036. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, H.; Lu, J.; Zhang, G. Detecting and predicting the topic change of Knowledge-based Systems: A topic-based bibliometric analysis from 1991 to 2016. Knowl.-Based Syst. 2017, 133, 255–268. [Google Scholar] [CrossRef]
- Van Eck, N.J.; Waltman, L. Software survey: VOSviewer, a computer program for bibliometric mapping. Scientometrics 2010, 84, 523–538. [Google Scholar] [CrossRef]
- Palla, G.; Barabási, A.L.; Vicsek, T. Quantifying social group evolution. Nature 2007, 446, 664–667. [Google Scholar] [CrossRef]
- Carrasquilla, J.; Melko, R.G. Machine learning phases of matter. Nat. Phys. 2017, 13, 431–434. [Google Scholar] [CrossRef]
- Ahneman, D.T.; Estrada, J.G.; Lin, S.; Dreher, S.D.; Doyle, A.G. Predicting reaction performance in C–N cross-coupling using machine learning. Science 2018, 360, 186–190. [Google Scholar] [CrossRef]
- Saganowski, S.; Bródka, P.; Koziarski, M.; Kazienko, P. Analysis of group evolution prediction in complex networks. PLoS ONE 2019, 14, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Saganowski, S.; Gliwa, B.; Bródka, P.; Zygmunt, A.; Kazienko, P.; Koźlak, J. Predicting Community Evolution in Social Networks. Entropy 2015, 17, 3053–3096. [Google Scholar] [CrossRef]
- İlhan, N.; Öğüdücü, G. Feature identification for predicting community evolution in dynamic social networks. Eng. Appl. Artif. Intell. 2016, 55, 202–218. [Google Scholar] [CrossRef]
- Pavlopoulou, M.E.G.; Tzortzis, G.; Vogiatzis, D.; Paliouras, G. Predicting the evolution of communities in social networks using structural and temporal features. In Proceedings of the 2017 12th International Workshop on Semantic and Social Media Adaptation and Personalization (SMAP), Bratislava, Slovakia, 9–10 July 2017; pp. 40–45. [Google Scholar] [CrossRef]
- Bródka, P.; Saganowski, S.; Kazienko, P. GED: The method for group evolution discovery in social networks. Soc. Netw. Anal. Min. 2013, 3, 1–14. [Google Scholar] [CrossRef]
- Tajeuna, E.G.; Bouguessa, M.; Wang, S. Tracking the evolution of community structures in time-evolving social networks. In Proceedings of the 2015 IEEE International Conference on Data Science and Advanced Analytics (DSAA), Paris, France, 19–21 October 2015; pp. 1–10. [Google Scholar] [CrossRef]
- Alhajj, R.; Rokne, J. (Eds.) Encyclopedia of Social Network Analysis and Mining; Springer: New York, NY, USA, 2014. [Google Scholar] [CrossRef]
- Brodka, P.; Musial, K.; Kazienko, P. A Performance of Centrality Calculation in Social Networks. In Proceedings of the 2009 International Conference on Computational Aspects of Social Networks, Fontainebleau, France, 24–27 June 2009; pp. 24–31. [Google Scholar] [CrossRef]
- Blondel, V.D.; Guillaume, J.L.; Lambiotte, R.; Lefebvre, E. Fast unfolding of communities in large networks. J. Stat. Mech. Theory Exp. 2008, 2008, P10008. [Google Scholar] [CrossRef]
- APS Data Sets for Research. Available online: https://journals.aps.org/datasets (accessed on 26 December 2019).
- Javed, M.A.; Younis, M.S.; Latif, S.; Qadir, J.; Baig, A. Community detection in networks: A multidisciplinary review. J. Netw. Comput. Appl. 2018, 108, 87–111. [Google Scholar] [CrossRef]
- Yang, J.; Honavar, V. Feature Subset Selection Using a Genetic Algorithm. In Feature Extraction, Construction and Selection: A Data Mining Perspective; Liu, H., Motoda, H., Eds.; The Springer International Series in Engineering and Computer Science; Springer: Boston, MA, USA, 1998; pp. 117–136. [Google Scholar] [CrossRef]
- Popper, K.R. All Life Is Problem Solving; Routledge: London, UK, 2010. [Google Scholar]
- Kotthoff, L.; Thornton, C.; Hoos, H.H.; Hutter, F.; Leyton-Brown, K. Auto-WEKA 2.0: Automatic model selection and hyperparameter optimization in WEKA. J. Mach. Learn. Res. 2017, 18, 1–5. [Google Scholar]
- Platt, J. Fast Training of Support Vector Machines Using Sequential Minimal Optimization. In Advances in Kernel Methods—Support Vector Learning; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Atkeson, C.G.; Moore, A.W.; Schaal, S. Locally Weighted Learning. Artif. Intell. Rev. 1997, 11, 11–73. [Google Scholar] [CrossRef]
- Frank, E.; Witten, I.H. Generating Accurate Rule Sets Without Global Optimization. In Proceedings of the Fifteenth International Conference on Machine Learning, Madison, WI, USA, 24–27 July 1998; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1998; pp. 144–151. [Google Scholar]
- Leydesdorff, L.; Opthof, T. Scopus’s source normalized impact per paper (SNIP) versus a journal impact factor based on fractional counting of citations. J. Am. Soc. Inf. Sci. Technol. 2010, 61, 2365–2369. [Google Scholar] [CrossRef]


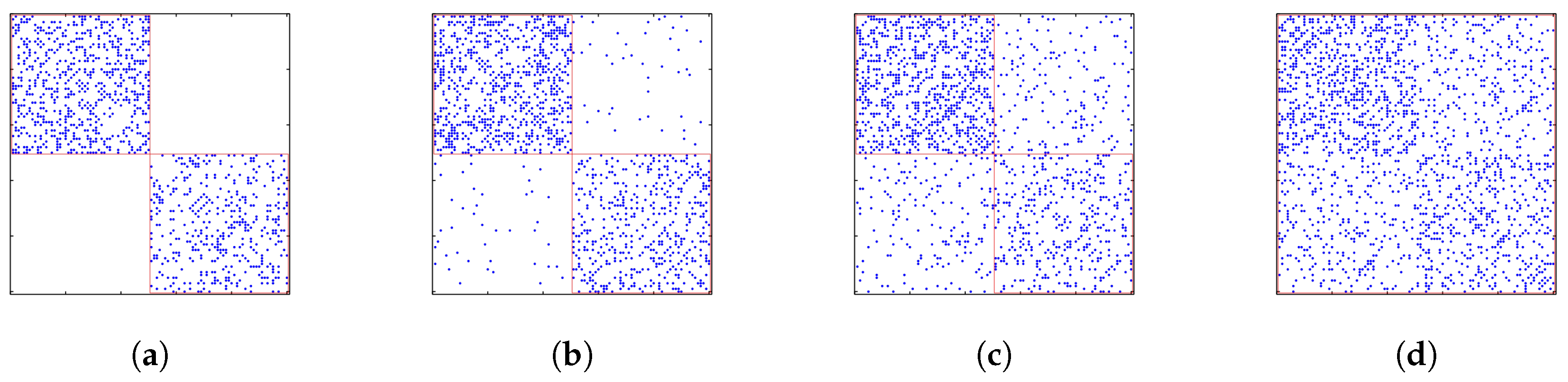

| TC in 1999 | Event | TC in 2000 |
|---|---|---|
| 1999.01 | split | 2000.02, 2000.03 |
| 1999.01, 1999.02 | merge | 2000.03 |
| 1999.04 | continue | 2000.06 |
| 1999.11, 1999.12 | merge | 2000.15 |
| 1999.13 | continue | 2000.16 |
| Percentile | |||
|---|---|---|---|
| 25 | 50 | 75 | |
| 1999.01 | 8.06 × 10−6 | 5.73 × 10−5 | 2.05 × 10−4 |
| 5.90 × 10−5 | 1.58 × 10−4 | 4.67 × 10−4 | |
| 7.77 × 10−6 | 1.95 × 10−5 | 2.44 × 10−4 | |
| 5.29 × 10−6 | 4.96 × 10−5 | 2.48 × 10−4 | |
| 6.22 × 10−6 | 5.04 × 10−5 | 1.88 × 10−4 | |
| 8.59 × 10−6 | 6.00 × 10−5 | 2.14 × 10−4 | |
| 7.97 × 10−6 | 5.32 × 10−5 | 1.83 × 10−4 | |
| 2.47 × 10−6 | 5.54 × 10−5 | 2.13 × 10−4 | |
| 3.08 × 10−5 | 1.13 × 10−4 | 3.17 × 10−4 | |
| 2.14 × 10−7 | 1.44 × 10−5 | 1.60 × 10−4 | |
| 1999.11 | 1.73 × 10−5 | 9.04 × 10−5 | 2.81 × 10−4 |
| 6.38 × 10−5 | 1.98 × 10−4 | 4.61 × 10−4 | |
| 9.91 × 10−6 | 6.17 × 10−5 | 2.17 × 10−4 | |
| 1999.12 | 6.56 × 10−6 | 4.54 × 10−5 | 1.62 × 10−4 |
| 2.74 × 10−5 | 9.08 × 10−5 | 2.33 × 10−4 | |
| 2.52 × 10−6 | 2.69 × 10−5 | 1.20 × 10−4 | |
| 1999.04 | 1999.13 | |||||||
|---|---|---|---|---|---|---|---|---|
| Size | Percentile | Size | Percentile | |||||
| 25 | 50 | 75 | 25 | 50 | 75 | |||
| 1999.00 | 12 | 9.0 × 10−5 | 1.1 × 10−3 | 2.3 × 10−3 | 1 | - | - | 1.8 × 10−3 |
| 1999.01 | 56 | 1.6 × 10−4 | 4.2 × 10−4 | 1.0 × 10−3 | 6 | 2.0 × 10−4 | 4.9 × 10−4 | 6.5 × 10−4 |
| 1999.02 | 6 | 3.0 × 10−4 | 5.1 × 10−4 | 7.4 × 10−4 | 2 | 6.0 × 10−4 | - | 2.6 × 10−4 |
| 1999.03 | 25 | 1.6 × 10−5 | 4.3 × 10−4 | 8.1 × 10−4 | 0 | - | - | - |
| 1999.04 | - | - | - | - | 8 | 1.5 × 10−4 | 4.8 × 10−4 | 8.0 × 10−4 |
| 1999.05 | 179 | 4.9 × 10−5 | 1.7 × 10−4 | 4.5 × 10−4 | 4 | 2.2 × 10−4 | 4.3 × 10−4 | 6.5 × 10−4 |
| 1999.06 | 110 | 8.7 × 10−5 | 2.0 × 10−4 | 6.2 × 10−4 | 40 | 5.9 × 10−5 | 1.6 × 10−4 | 4.5 × 10−4 |
| 1999.07 | 29 | 1.7 × 10−4 | 5.6 × 10−4 | 1.2 × 10−3 | 44 | 1.4 × 10−4 | 3.1 × 10−4 | 5.5 × 10−4 |
| 1999.08 | 63 | 1.1 × 10−4 | 3.2 × 10−4 | 8.6 × 10−4 | 17 | 2.2 × 10−4 | 5.2 × 10−4 | 8.5 × 10−4 |
| 1999.09 | 49 | 7.8 × 10−5 | 2.6 × 10−4 | 8.0 × 10−4 | 99 | 8.0 × 10−5 | 2.5 × 10−4 | 4.8 × 10−4 |
| 1999.10 | 53 | 1.2 × 10−4 | 3.8 × 10−4 | 8.2 × 10−4 | 254 | 3.6 × 10−5 | 8.8 × 10−5 | 2.7 × 10−4 |
| 1999.11 | 89 | 1.0 × 10−4 | 3.2 × 10−4 | 9.2 × 10−4 | 71 | 1.4 × 10−4 | 3.4 × 10−4 | 5.7 × 10−4 |
| 1999.12 | 53 | 8.7 × 10−5 | 2.9 × 10−4 | 9.3 × 10−4 | 39 | 1.3 × 10−4 | 2.7 × 10−4 | 4.6 × 10−4 |
| 1999.13 | 9 | 1.3 × 10−4 | 4.2 × 10−4 | 1.1 × 10−3 | - | - | - | - |
| 1999.14 | 62 | 1.4 × 10−4 | 4.8 × 10−4 | 1.0 × 10−3 | 210 | 4.2 × 10−5 | 1.0 × 10−4 | 2.7 × 10−4 |
| 1999.15 | 17 | 1.8 × 10−4 | 3.6 × 10−4 | 9.7 × 10−4 | 176 | 5.1 × 10−5 | 1.3 × 10−4 | 3.1 × 10−4 |
| b | 88 | 2.1 × 10−6 | 2.2 × 10−5 | 5.8 × 10−5 | 27 | 9.1 × 10−11 | 4.3 × 10−6 | 1.8 × 10−5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, W.; Saganowski, S.; Kazienko, P.; Cheong, S.A. Predicting the Evolution of Physics Research from a Complex Network Perspective. Entropy 2019, 21, 1152. https://doi.org/10.3390/e21121152
Liu W, Saganowski S, Kazienko P, Cheong SA. Predicting the Evolution of Physics Research from a Complex Network Perspective. Entropy. 2019; 21(12):1152. https://doi.org/10.3390/e21121152
Chicago/Turabian StyleLiu, Wenyuan, Stanisław Saganowski, Przemysław Kazienko, and Siew Ann Cheong. 2019. "Predicting the Evolution of Physics Research from a Complex Network Perspective" Entropy 21, no. 12: 1152. https://doi.org/10.3390/e21121152
APA StyleLiu, W., Saganowski, S., Kazienko, P., & Cheong, S. A. (2019). Predicting the Evolution of Physics Research from a Complex Network Perspective. Entropy, 21(12), 1152. https://doi.org/10.3390/e21121152






