4.1. Synthetic Dataset 1 (Metachanges along Time)
We defined six levels of time intervals between change points referring to the work in [
13,
25]. The interval lengths were 100,000, 50,000, 10,000, 5000, 1000, and 500. The change points were set using a Bernoulli distribution oscillating between
and
. For each combination of two intervals, we generated the streams based on the scheme above. Each stream contained 100 change points. In what follows,
and
indicate the first and second interval lengths, respectively.
We confirmed the effectiveness of MCD by comparing it with a volatility detector (VD) [
13]. We used the SEED algorithm [
13] and the sequential MDL-change statistics algorithm (SMDL) [
8] for change detection. SEED was based on ADWIN2 [
21] and its parameters were set to
, and
, which are the same as those in [
13]. The window size
w of SMDL was set to
, and the threshold parameter
was set to
. For the Bernoulli distribution, the change score
of SMDL at time
t was calculated as
where
,
, and
. If
,
t is regarded as a change point. We determined that
t was a change point if the change score
was the maximum. The parameter of MCD-T was set to
. Below, we discuss the dependency of MCD-T on
r in
Figure 5. For VD, buffer size
and reservoir size
, which were the same as in [
13]. We also discuss the dependency of VD on
B and
R below in
Figure 6. In running SEED [
13], we used the Java source code provided by the authors (
https://www.cs.auckland.ac.nz/research/groups/kmg/DavidHuang.html). We started to use change points when its number reached
for MCD-T and VD because the buffer and the reservoir of VD are not full until
intervals arrive.
We investigated the trade-off between detection delay and accuracy in terms of benefit and false alarm rate, defined as in [
8,
26]. For MCD-T, we first fixed the threshold parameter
and converted MCAT
in Equation (
11) to binary alarms
. That is,
, where
denotes the binary function that takes 1 if and only if
t is true. We evaluated MCD-T by varying
. We let
be a maximum tolerant delay of metachange detection. When the metachange really started from
, we defined the
benefit of an alarm at time
t as
The number of
false alarms was calculated as
We visualized the performance by plotting the recall rate of the total benefit,
b, against the false alarm rate,
, with
varying. Likewise, for VD,
was calculated using the
relative volatility between the variances of the buffer and the reservoir by varying the threshold parameter
. We evaluated all four combinations of change detectors SEED and SMDL and metachange detectors MCD-T and VD by calculating the average and standard deviation of the area under the curve (AUC) of the benefit vs. FAR curves. The AUC scores were calculated over 50 sequences. The delay parameter was set to
.
Table 1 shows the average AUC scores.
Table 1 shows that MCD-T with SEED or MCD-T with SMDL outperforms VD with SEED or VD with SMDL. This indicates the effectiveness of MCD-T.
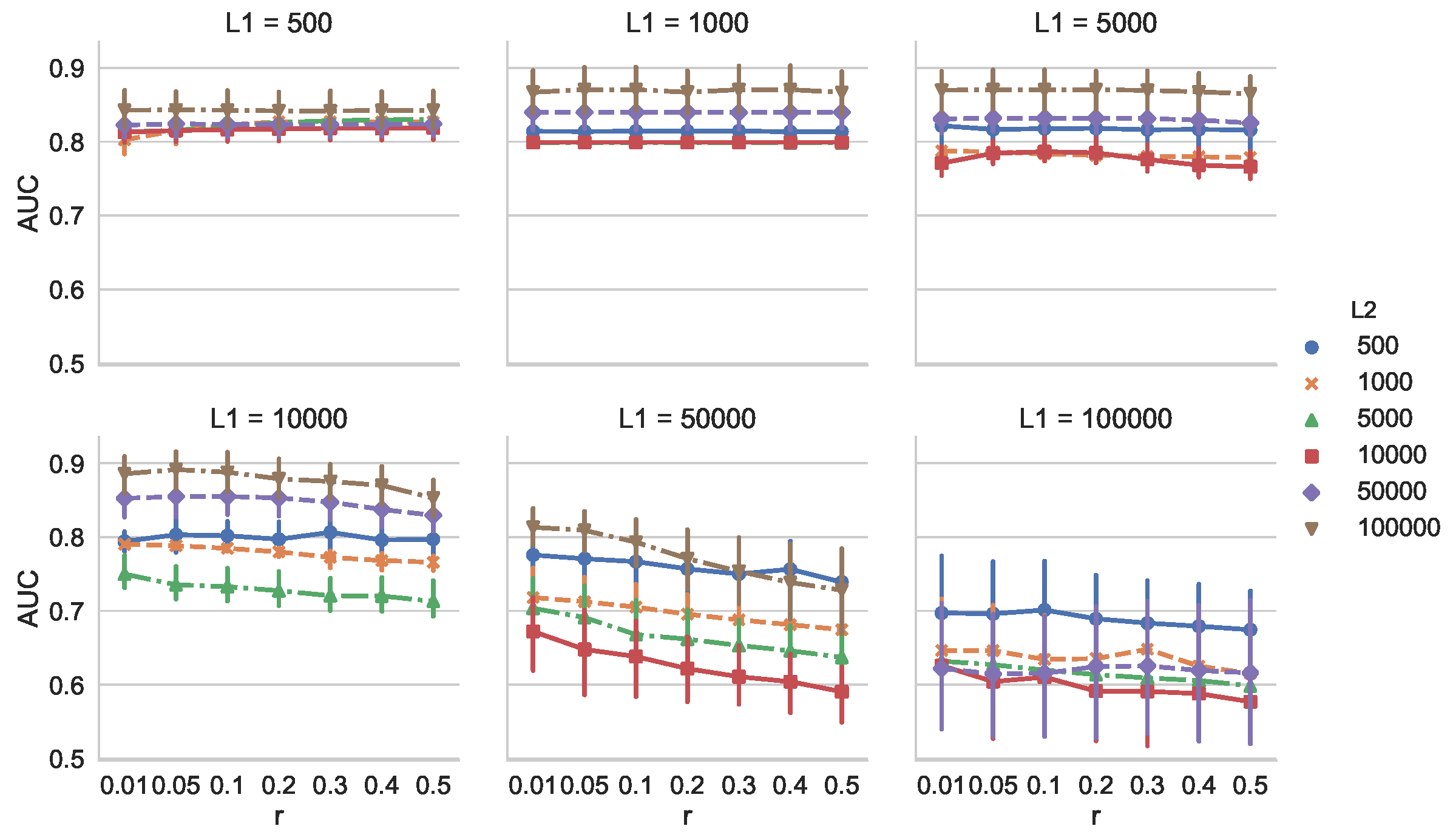
Because MCD-T depends on discounting parameter
r and the change detection algorithm used, we investigated these effects. First, we examined the dependency of AUC on
r for all combinations of
and
. We calculated AUC for 30 times with
and
. We used SEED [
13] as the change detection algorithm, and its parameters were set to the same values as above. The dataset used was also the same as in the previous experiment.
Figure 5 shows that, when
is relatively small (e.g.,
), AUC is not heavily dependent on
r. When
is larger, however, we observe that the larger
r is, the smaller AUC is. This is because, with an increase of
, the number of false alarms of SEED also increases. In such situations, MCD-T is more prone to the false alarms when
r is larger.
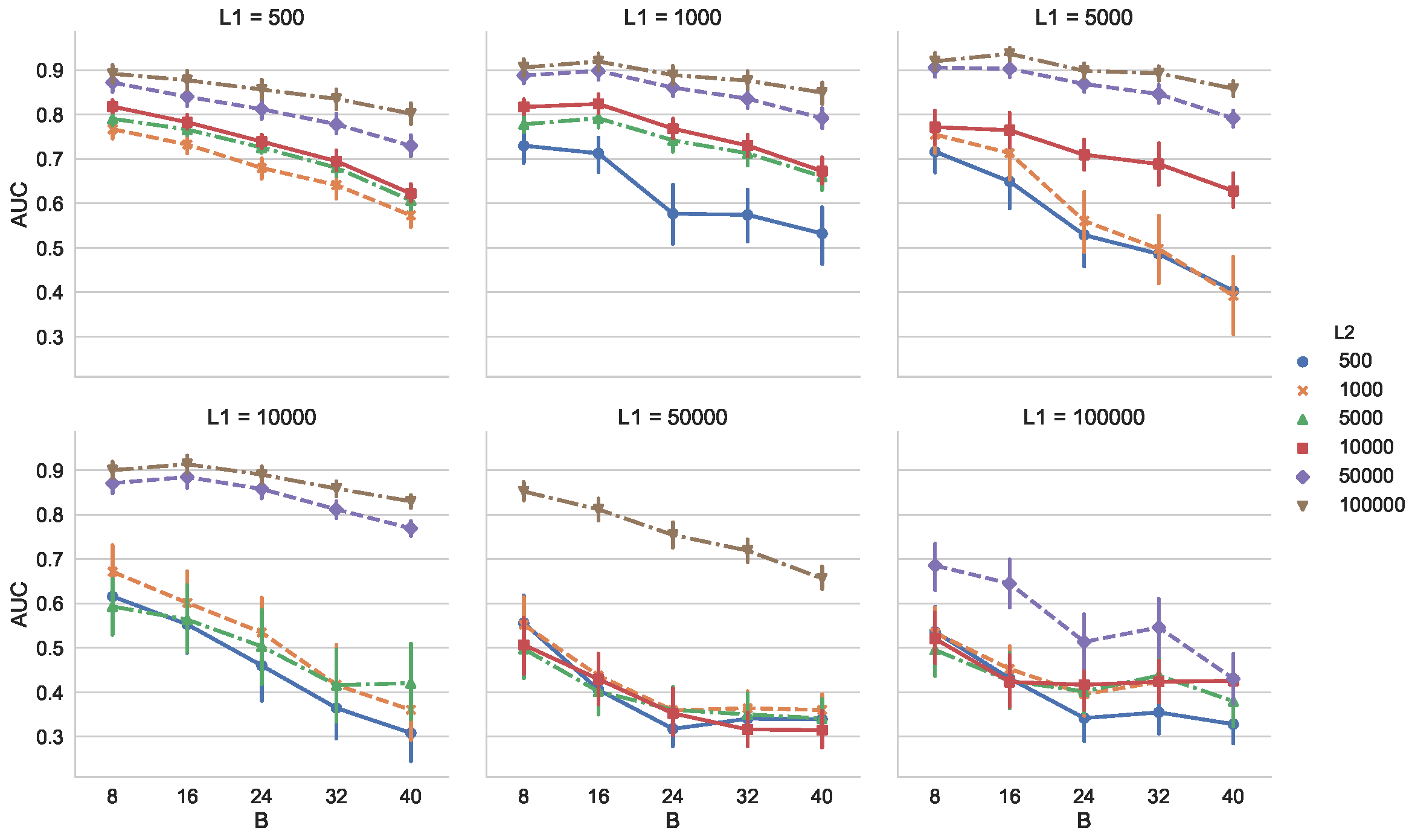
Figure 6 shows the dependency of AUC of VD on the buffer size
B and the reservoir size
R (
) for comparison. We calculated AUC for 50 times. We observe from
Figure 6 that AUC decreases as
B increases. In addition, we also see that MCD-T outperforms VD for various combinations of
r and
by comparing
Figure 5 with
Figure 6.
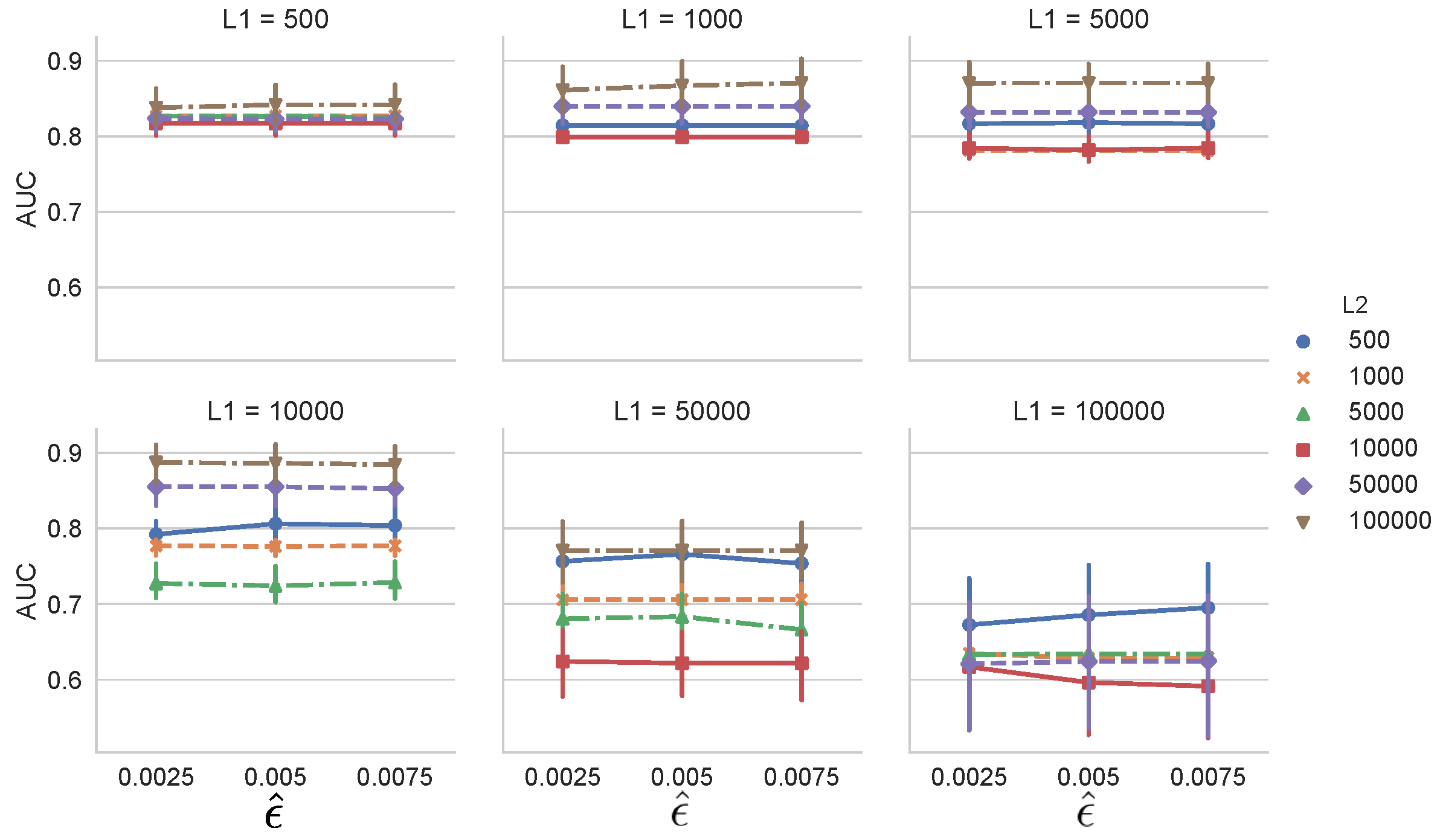
Next, we investigated the effect of the change detection algorithm used. We used SEED by changing the parameter
, and
. Other conditions and the dataset were the same as in the previous experiment. Here,
is a hyperparameter that controls the threshold parameter [
13].
Figure 7 shows that AUC does not heavily depend on
for all combinations of
and
. In general, the threshold parameter of the change detection algorithm controls the performance of MCD-T. Hence, it should be carefully set.
4.2. Synthetic Dataset 2 (Metachanges along State)
We generated a data stream with length
, where
. The generated data stream contained a metachange along state. In the former part, each datum was drawn from
After we repeated the procedure 10 times, we obtained a subsequence with length
. In the latter part, each datum was drawn from
A metachange along state occurred at
. For change detection, we employed four algorithms for comparison: (1) SMDL [
8], a semi-instant method with the MDL change statistics; (2) ChangeFinder (CF) [
1,
2,
4], a state-of-the-art method of abrupt change detection; (3) Bayesian online change point detection (BOCPD) [
3], a retrospective online change point detection with a Bayesian scheme; and (4) ADWIN2 [
21], adaptive windowing methods. As we assumed a situation where change and metachange mechanisms do not vary significantly, we decided to choose the best combinations of parameters of each change detection algorithm by grid search, as in [
8,
27]. We generated 10 sequences with the scheme above and calculated the F-scores for each combination of the following parameters:
SMDL: Window size (), (), (). Threshold parameter .
CF: Discounting rate . Threshold parameter (regression orders , smoothing parameters ).
BOCPD: Parameter related to change intervals . Threshold parameter .
ADWIN2: Confidence parameter .
F-score is defined as the harmonic mean of
precision and
recall, which are calculated using the number of
true positives (TP),
false positives (FP), and
false negatives (FN) as follows [
9]:
TP is the number of true change points that are
-neighbors of estimated change points. Thus,
FP and
FN are calculated as
and
, where
ℓ and
m are calculated as
and
, where
ℓ and
m denotes the total number of estimated and true change points, respectively. Finally, we calculated
and
for each method. In this experiment, we set
to 100.
After optimizing the parameters of each change detection algorithm, we generated 30 data streams with the scheme above and detected change points and the metachange. In the metachange detection, we compared MCD-S with SMDL. We chose SMDL for comparison because it calculates a change score at each time based on changes of parameters with MDL. Hence, a change rate of scores between change points is regarded as the degree of metachange along state. Hereafter, we refer to SMDL for metachange detection as SMDL metachange (SMDL-MC) and the window parameter as
. We calculated MCAS in Equation (
16) for MCD-S and the change rate
for SMDL-MC.
is the
change score at time
t for a univariate normal distribution [
8]:
where
,
, and
are the maximum likelihood estimators of standard deviations calculated for
,
and
, respectively.
is the normalizer of the normalized maximum likelihood code length [
20]
where
is the gamma function. In this paper,
and
. The window parameters
h of MCD-S and
of SMDL-MC were set to
(
),
(
), and
(
). In calculating the F-scores, the maximum tolerant delay was set to
.
Table 2 shows the average AUC values of MCD-S and SMDL-MC for the detection of metachanges along state at
. The first and second rows in the header represent change detection and metachange detection algorithms, respectively. The best parameters for each combination of change detection and metachange detection algorithms are
(
),
(
), and
(
).
Table 2 shows that MCD-S outperforms SMDL-MC overall because MCD-S deals with metachanges along state directly in terms of MCAS, whereas SMDL-MC only quantifies the difference in code lengths between situations where there is a change and where there is no change.
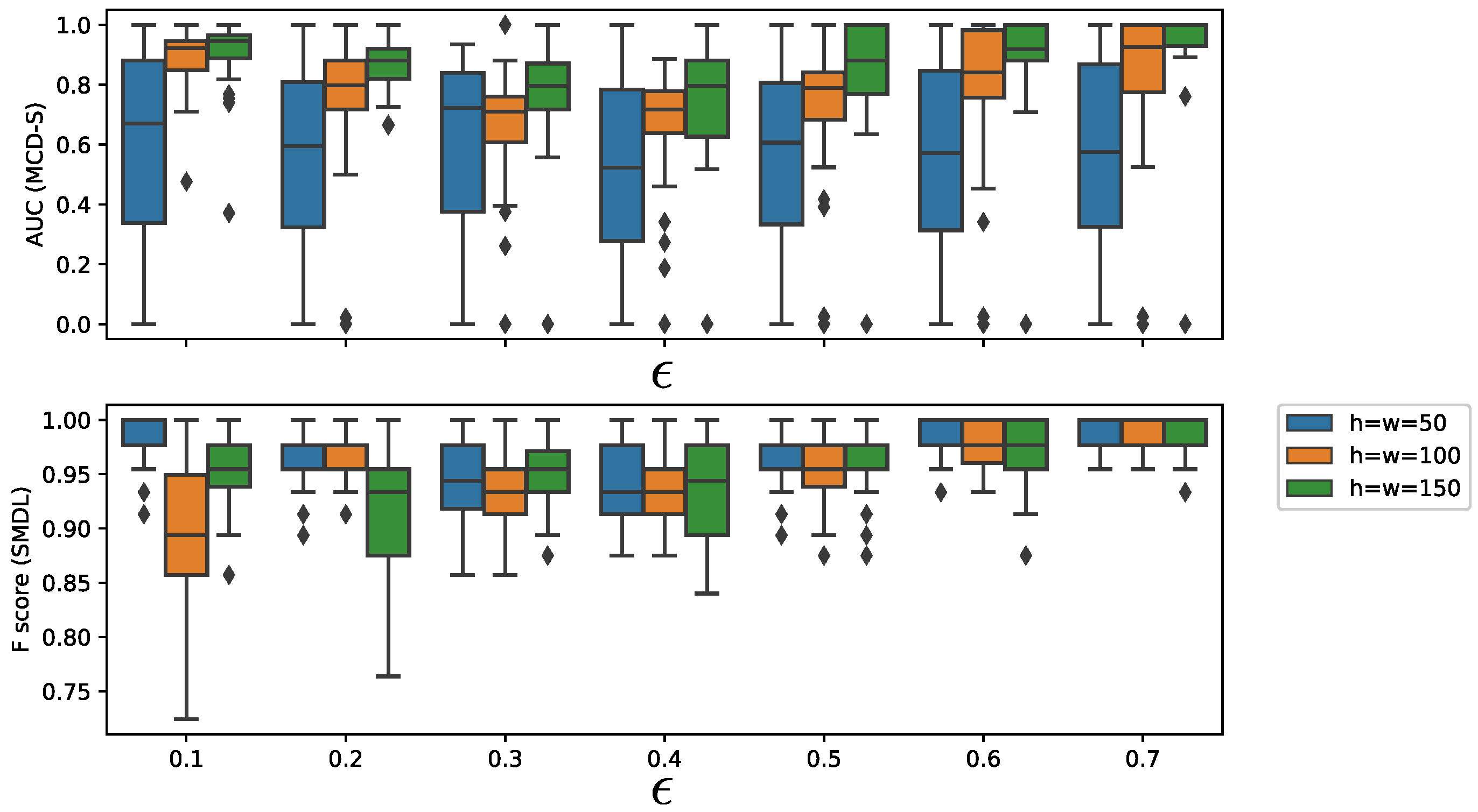
We further investigated the effects of window size
h and threshold parameters of the change detection algorithms. We chose SMDL [
8] for change detection.
Figure 8 shows the dependency of AUC on
h and threshold parameter
of SMDL. The interval length was set to
, threshold parameter was set to
, and
, where
w is the window parameter of SMDL.
Figure 8 (top and bottom) shows the dependency of AUC of MCD-S on the threshold parameter
of SMDL and the dependency of F-score of SMDL on
, respectively. We observe in
Figure 8 (top) that AUC of MCD-S decreases between
and
, but, when
exceeds
, AUC begins to increase for
. This reflects the fact that there are many local maximum points of the change scores of SMDL, leading to false alarms of change points around
–
. It is noticeable that F-scores of SMDL decrease for
, and for
, but AUCs of MCD-S do not do so much. This is because SMDL detects many false positive change points, but it detects the metachange point accurately.
As for the dependency of AUC on window size h, we observe that AUC generally increases as h increases for the same .
4.3. Synthetic Dataset 3 (Metachanges Along Time and State)
We generated a data stream that contained metachanges along both time and state. The stream consisted of two subsequences. The former part repeated changes of mean. Each instance was drawn from Equation (
20) with
. We repeated the procedure for 50 times and obtained a subsequence with length
. The latter part comprised the following four parts, each with length
:
In total, we obtained a data stream with length . A metachange along both time and state occurred at . We chose lengths and among 400, 450, and 500.
We detected the metachange in the following three ways: we first detected change points with the same algorithms as in
Section 4.2, and then detected the metachanges with MCD-T, MCD-S, and MCD. The parameters of the change detection algorithms were tuned as in
Section 4.2. The ranges of parameters were the same as those in
Section 4.2. except that, for SMDL, the threshold parameter
for all combinations of
and
. The parameter of MCD-T was selected among
and MCD-S was among
. The window size of SMDL were selected among
, and the maximum tolerant delay was
. We chose the weight parameter
in Equation (
17) among
. For VD, the buffer and reservoir sizes (
B and
R) were selected among
. All the parameters were selected with grid search for the AUCs of metachange detection to be maximum.
Table 3 shows the average AUC values.
Table 3a–c show average AUC values with MCD-T, MCD-S, and MCD.
Table 3a shows that MCD combined with SMDL as the change detection algorithm outperforms MCD-S and MCD-T.
Table 4 shows the best parameters for each combination of intervals. We observe that the more intensive a metachange along time is, the bigger
r is and the less
becomes. These results reflect the fact that it is necessary to adapt to recent data, and MCAT increases in such a situation, leading to the decrease of
.
4.4. Real Dataset: Human Action Recognition Data
We applied MCD to the detection of metachanges in human action recognition data called HASC-PAC2016 dataset [
28] (HASC-PAC2016 dataset is publicly available at
http://hub.hasc.jp/). The data were collected from the Human Activity Sensing Consortium (HASC,
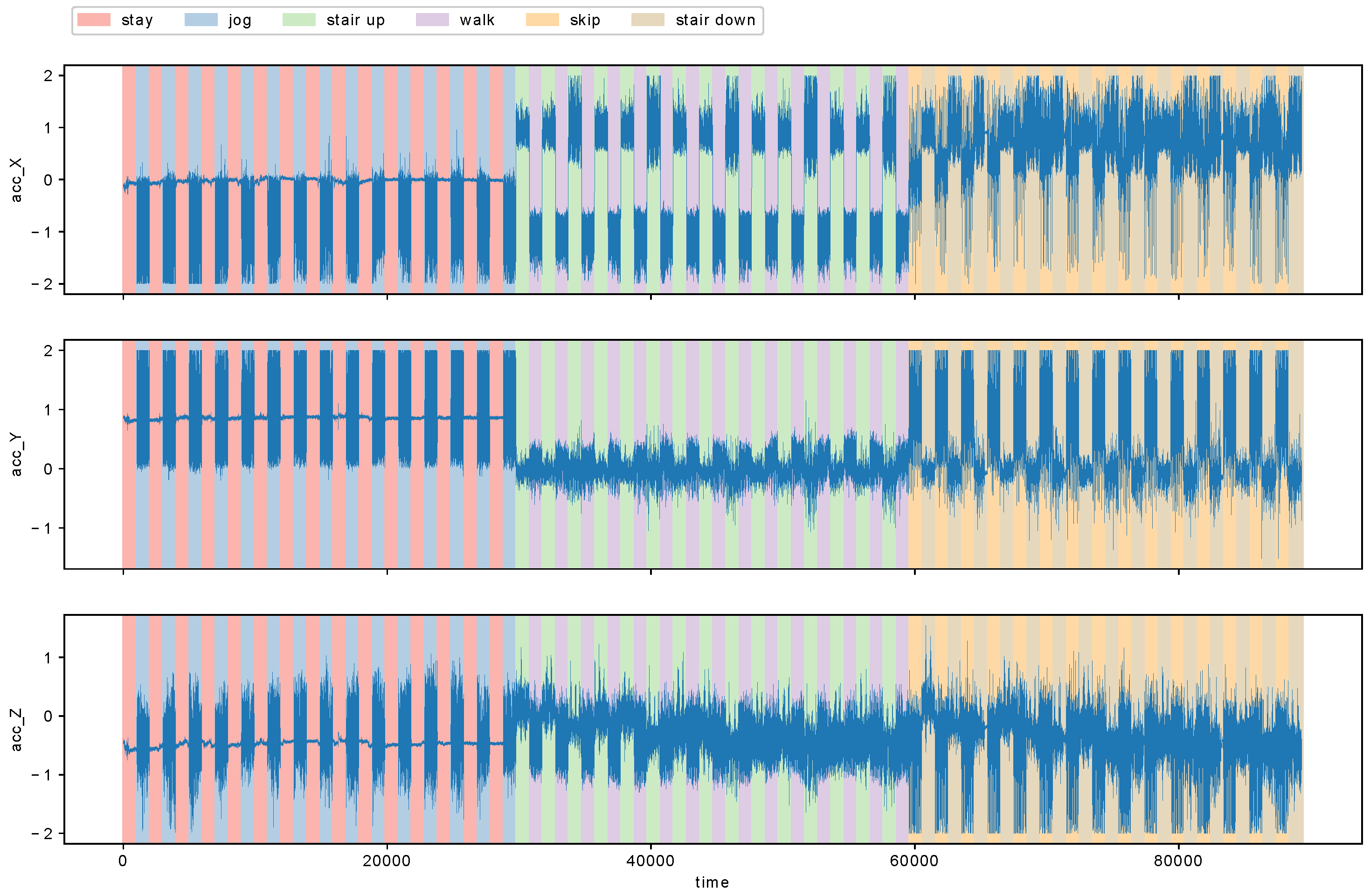
http://hasc.jp/). HASC-PAC2016 dataset contains sequences of acceleration data for three axes, and each sequence is segmented into one of six action labels: “stay”, “walk”, “jog”, “skip”, “stair up”, (go upstairs) and “stair down” (go downstairs). For this experiment, we aimed to evaluate the effectiveness of our proposed algorithm MCD by using a data stream with ground truth of “changes of action changes” and “changes of intervals of actions”. The former corresponds to metachanges along state, and the latter to metachanges along time. We combined each action into a data stream as follows: first, we repeated “stay” and “walk” alternately for 15 times; then “jog” and “skip” for 15 times; and, finally, “stair up” and “stair down” for 15 times. We repeated each pair of actions for 15 times because “stair up” and “stair down” have only 15 files, which are the fewest in all the six actions. We obtained a data stream of length 89,324.
Table 5 shows the files used for a participant named Person06023. We read the files sequentially in alphabetical order for each action.
Figure 9 shows the data stream we obtained. Here, acc_X, acc_Y, and acc_Z represent accelerations for
x-,
y-, and
z-axes, respectively.
First, we detected change points with SMDL [
8]. It was a challenge to determine the hyperparameters of SMDL—window size
w and threshold parameter
—in an online change detection. We tuned
w and
with the remaining dataset for Person06023, which alternated “stay” and “walk” four times, and “jog” and “skip” likewise. Although this dataset lacked “stair up” and “stair down”, we thought that it was enough to estimate the best configuration of
w and
. We calculated F-score as described in
Section 4.2 for the change points between different action labels. We selected
and
among
and
.
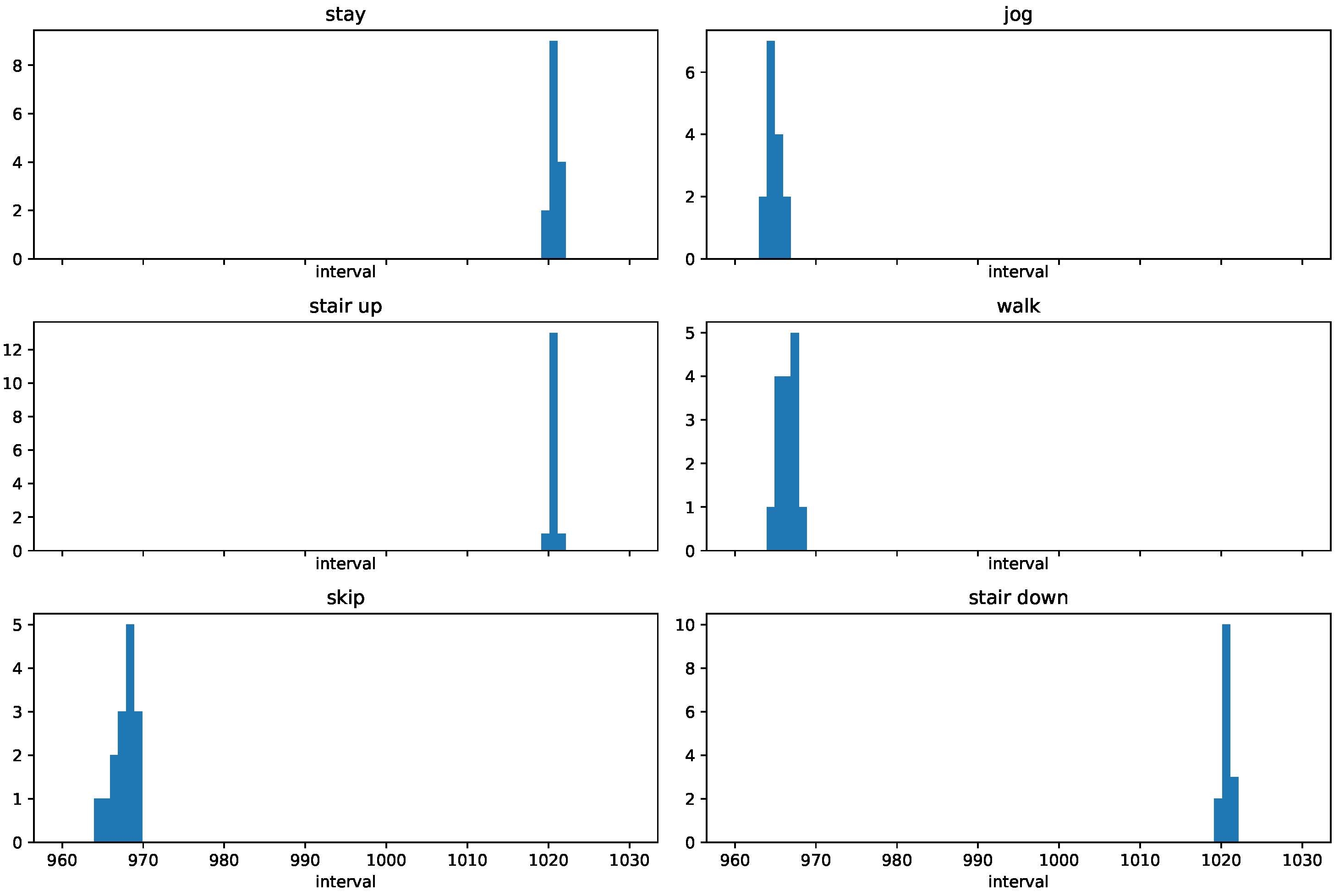
Figure 10 shows histograms of intervals for each action label. We observe in
Figure 10 that most of the intervals are around 960–970 for “jog”, “walk”, and “skip”, whereas, for “stay”, “stair up”, and “stair down”, the intervals are around 1020. We can see that
was enough to detect changes.
We applied SMDL to the stream and obtained the estimated change scores
at each time point. We calculated
with the multivariate normal distribution. Specifically,
is calculated as
where
,
, and
.
,
, and
.
Note that
in Equation (
21) is the normalizer of the NML code length [
29,
30]:
where
m is the dimension of the data stream,
is the gamma function, and
is calculated as
We set and .
Next, we defined the ground truths for metachanges along state at two time points where the changes of action label changes occurred:
29,752 from “jog” to “stair up”, and
59,588 from “walk” to “skip”. Moreover, we also defined the ground truths for metachanges along time at time points where the changes of intervals occurred. We see in
Figure 10 that the distributions are significantly different between four types of “changes of action changes”: from “stay” to “jog”, from “jog” to “stair up”, from “stair up” to “walk”, and from “skip” to “stair down”.
We detected metachanges along time with MCD-T and volatility detector (VD) [
13], and compared them.
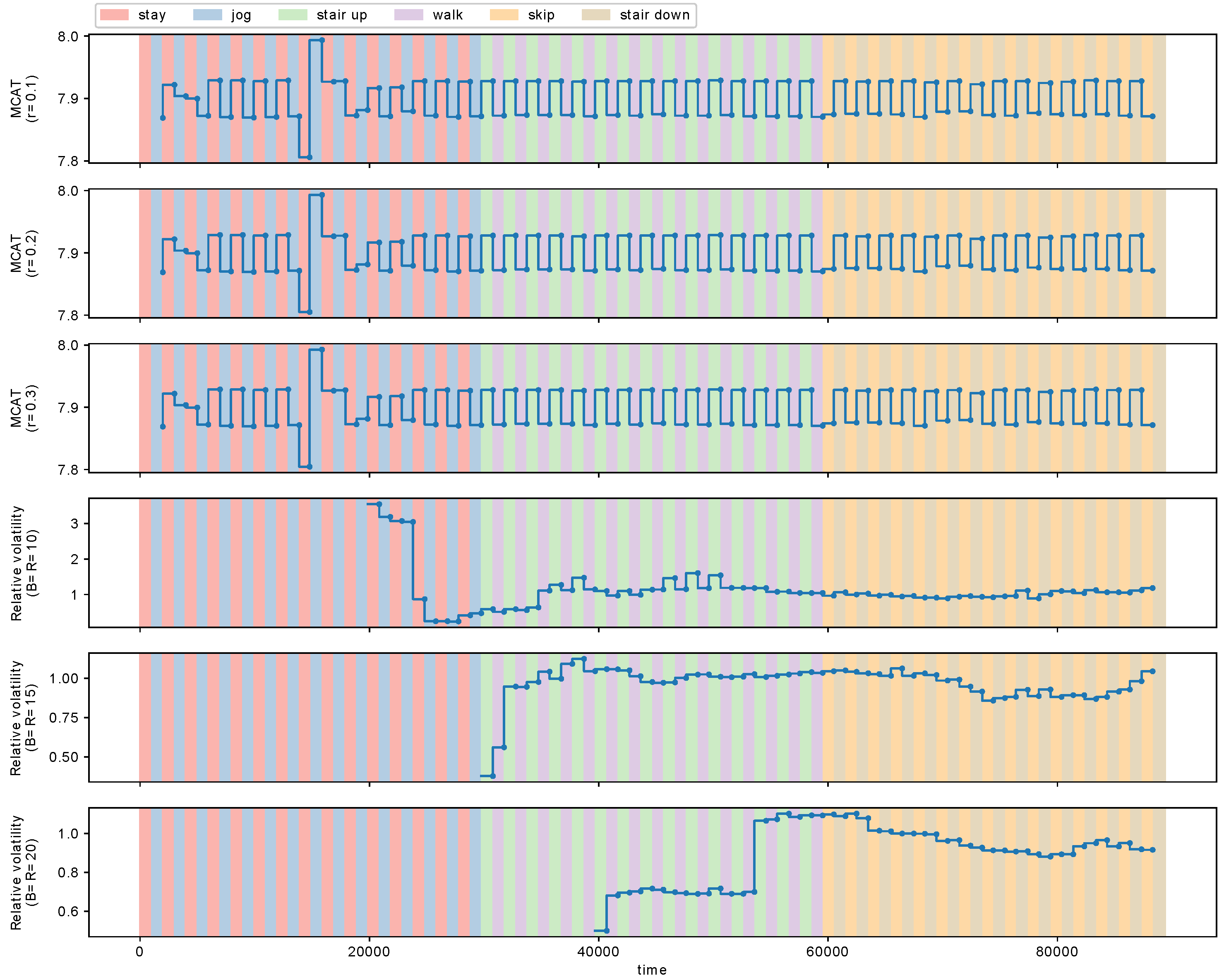
Figure 11 shows the estimated MCAT with MCD-T and the relative volatility with VD. The parameter of MCD-T was set to
, whereas one of VD was
.
Figure 11 shows the results.
We observe in
Figure 11 that MCAT detects the metachanges along time between the four action pairs, respectively, for
and
. However, the relative volatility fails to detect some of these metachanges along time.
We detected metachanges along state with MCD-S and the change rate of the MDL change statistics [
8].
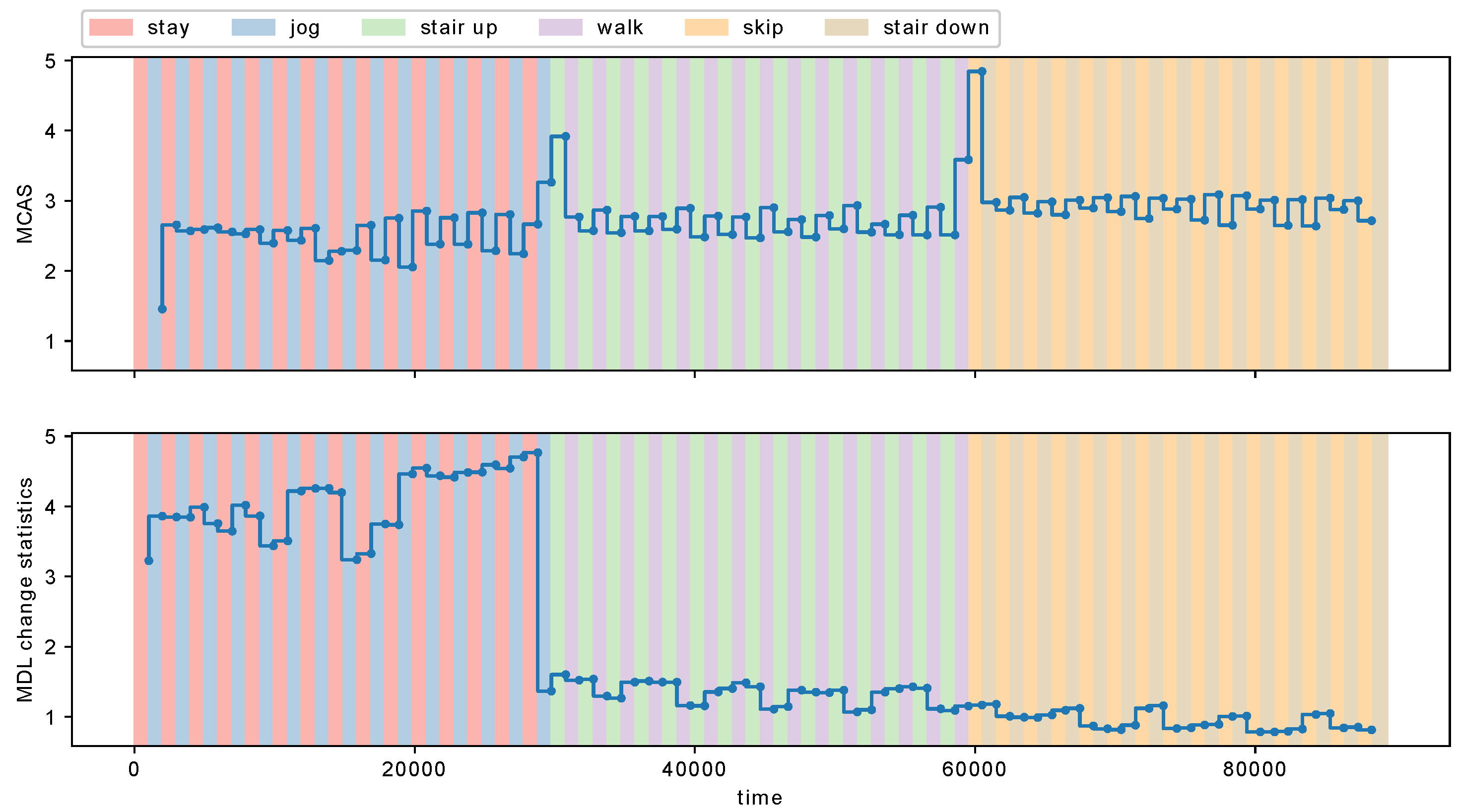
Figure 12 shows the estimated MCAS with MCD-S and the MDL change statistics. We observe in
Figure 12 that both MCD-S and the MDL change statistics detect a time point around
29,752 from “jog” to “stair up”. However, the MDL change statistics do not change significantly at a time point around
59,588, where a metachange along state happened from “walk” to “skip”. It indicates that the change rate of the MDL change statistics failed to detect the metachange along state around
59,588, whereas MCD-S detected it successfully.
In summary, the proposed algorithm MCD detected metachanges along both time and state more accurately than other methods.
4.5. Real Dataset: Production Condition Data
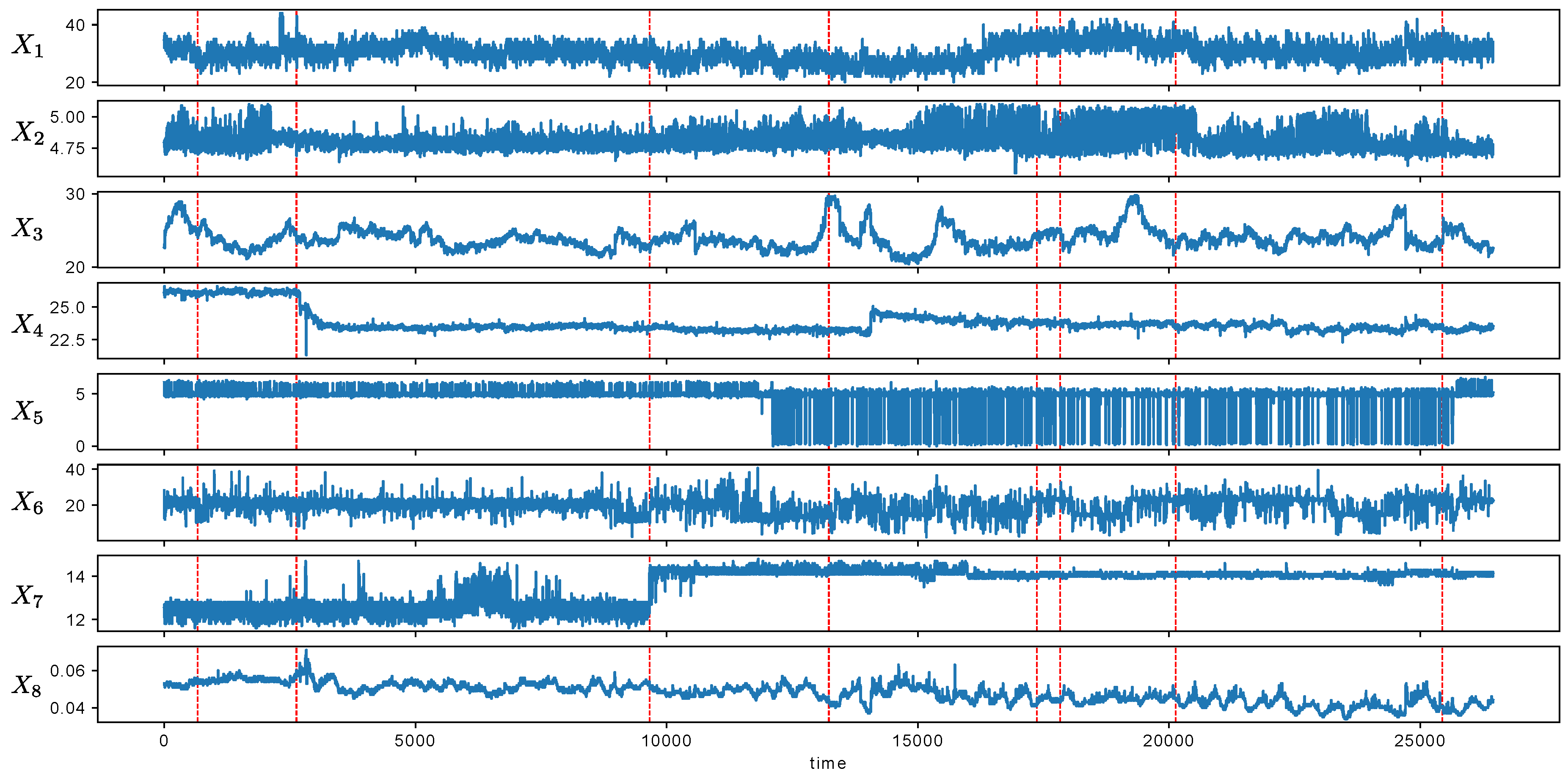
We applied MCD to the detection of metachanges in the production condition data. The data were collected from a factory of a manufacturing company. Each datum comprised eight attributes, and the length of the stream was 26,450. The factory reported that important events occurred 10 times during the study period, at
668, 2634, 2635, 9663, 13,230, 13,231, 17,372, 17,832, 20,131, and 25,441.
Figure 13 shows the attributes from the stream. The dashed line indicates the time points where important events occurred. We investigated whether the detected metachanges were signs of important events, and we finally concluded that it might be true. The details are as follows.
Figure 13 shows that the scales of attributes were different. Hence, we normalized each attribute
X to
, where
and
are the sample mean and standard deviation, respectively, which were calculated with the first 250 time points. First, we applied SMDL [
8] to the stream and obtained the estimated change scores
at each time. We calculated
with the multivariate normal distribution in Equation (
21). The window sizes
w of SMDL and
h of MCD were set to
by field knowledge that it roughly represents a unit of production. Moreover,
and
in Equation (
22) were set to 60 and
, respectively. Next, we detected change points
as time points where the change scores
were locally maximum within an interval where
. We set
when the total change points detected was less than 0.5% of the total length. It is a business demand by a factory, and so there were not many alarms. The number of detected change points was 97 (0.37%). Finally, we determined the discounting parameter
r and the weight parameter
of MCD in Equation (
17) with the first 5000 time points. We selected
and
so that the AUC score at
and
would be the maximum. The AUC score was calculated using Equations (
18) and (
19).
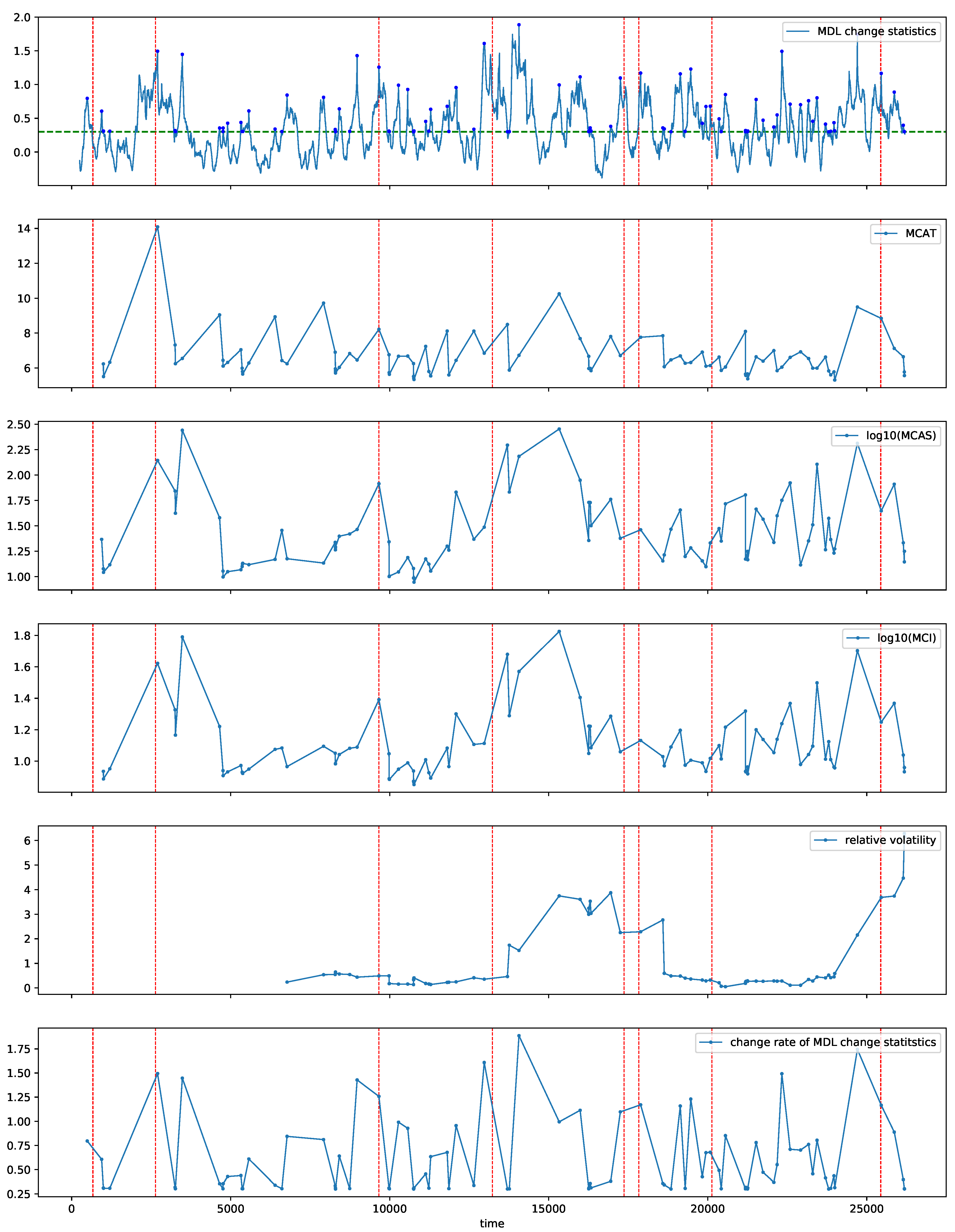
Figure 14 shows the MDL change statistics
calculated with SMDL [
8] (
Figure 14, top), the estimated MCAT
(
Figure 14, second), logarithm of the estimated MCAS
(
Figure 14, third), and logarithm of the estimated MCI
(
Figure 14, fourth). We also estimated the relative volatility with VD [
13,
25] (
Figure 14, fifth) and the change rate of the MDL change statistics
(
Figure 14, bottom) for comparison in detecting metachanges along both time and state. For VD, the buffer size
B and the reservoir size
R were both set to 10. In
Figure 14 (top), the red points indicate the detected change points.
We summarize what can be seen for metachange statistics in
Figure 14 as follows:
: The trend of MCI increases roughly after
, which can be interpreted as a combination of MCAT and MCAS in
Figure 14. The relative volatility and the change rate of the MDL change statistics do not show such a significant sign.
13,230, 13,231, 17,372, 17,832: For time points between 10,000 and 15,000, the trend of MCI increases. It is also due to the combination of MCAT and MCAS, but is more influenced by MCAS. It might also be a sign of important events at 17,372 and 17,832 as well as 13,230 and 13,231. The relative volatility increases after 13,231, which might be a sign of the important event at 17,372. However, the change rate of the MDL change statistics does not show such a significant sign.
25,440: For time points between 20,000 and 25,000, the trend of MCI increases with large fluctuations. It is also more influenced by MCAS. It might also be a sign of important events at 25,440. The relative volatility increases for the time points, but the change rate of the MDL change statistics does not show such a significant sign.
In summary, we can observe a sign of metachange for each important event. We therefore infer that there might have been some symptoms that should be analyzed using field knowledge.