Depolarizing Channel Mismatch and Estimation Protocols for Quantum Turbo Codes
Abstract
1. Introduction
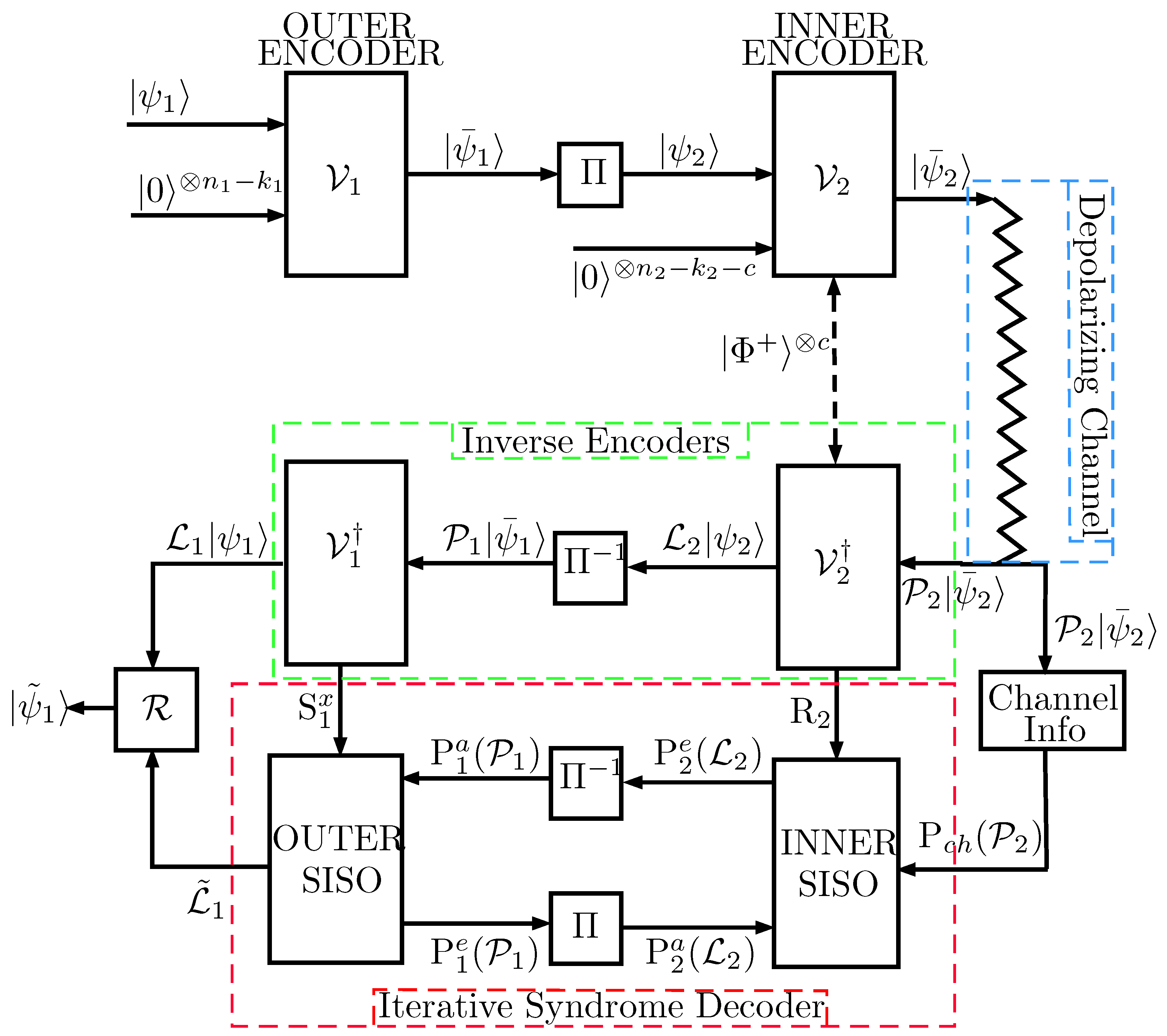
2. Preliminaries: The Quantum Depolarizing Channel and Quantum Turbo Codes
2.1. Quantum Depolarizing Channel
2.2. Quantum Turbo Codes
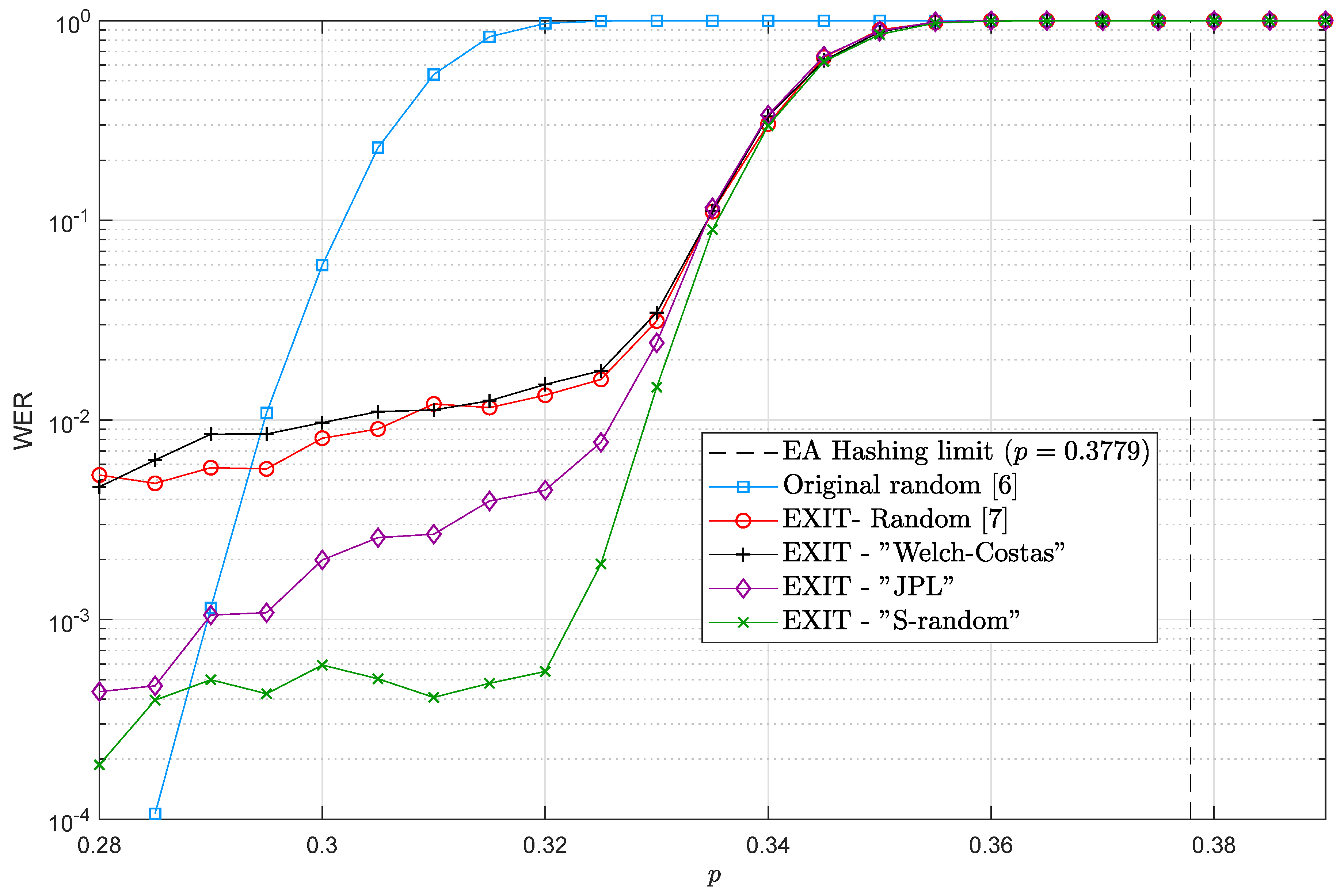
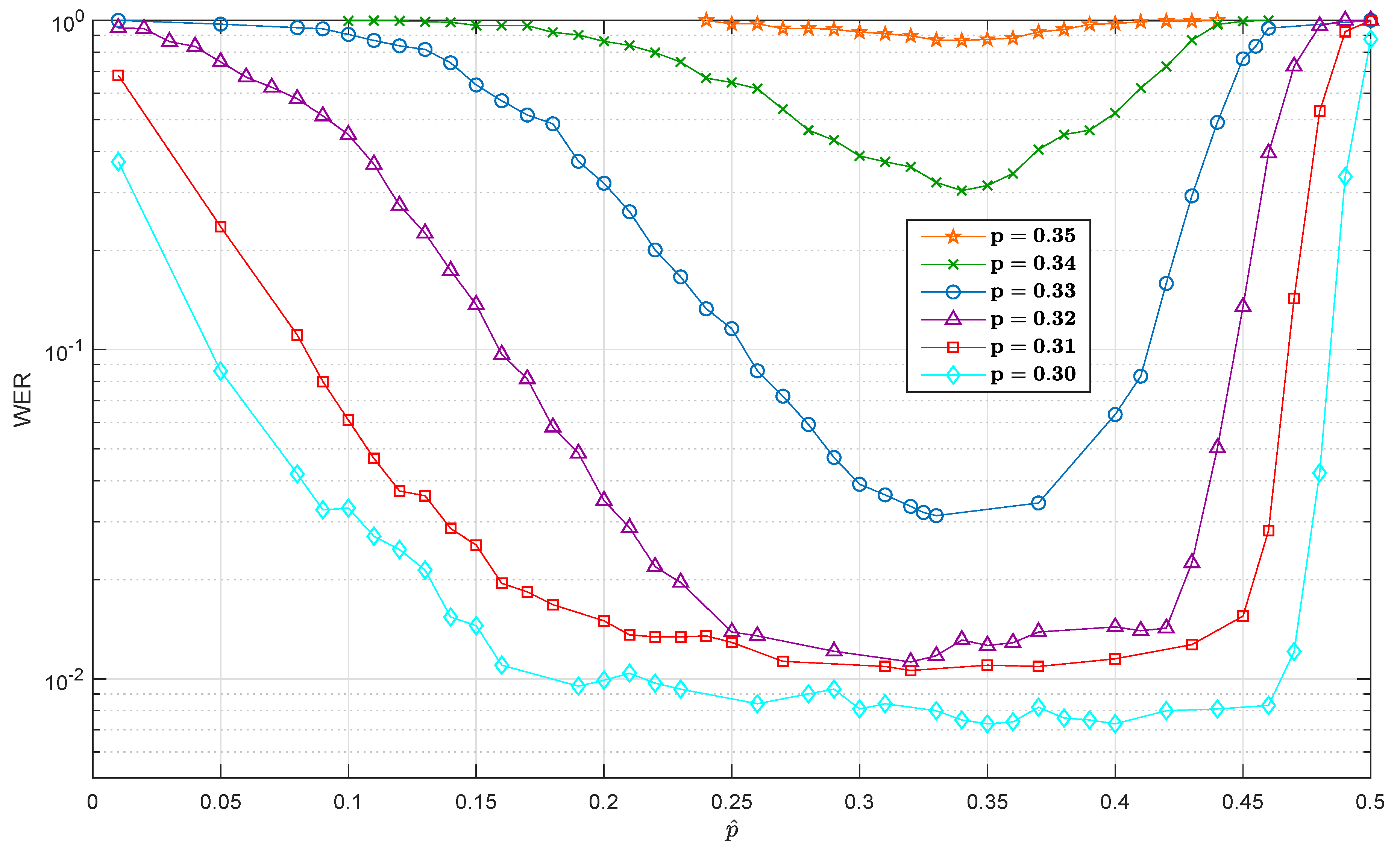
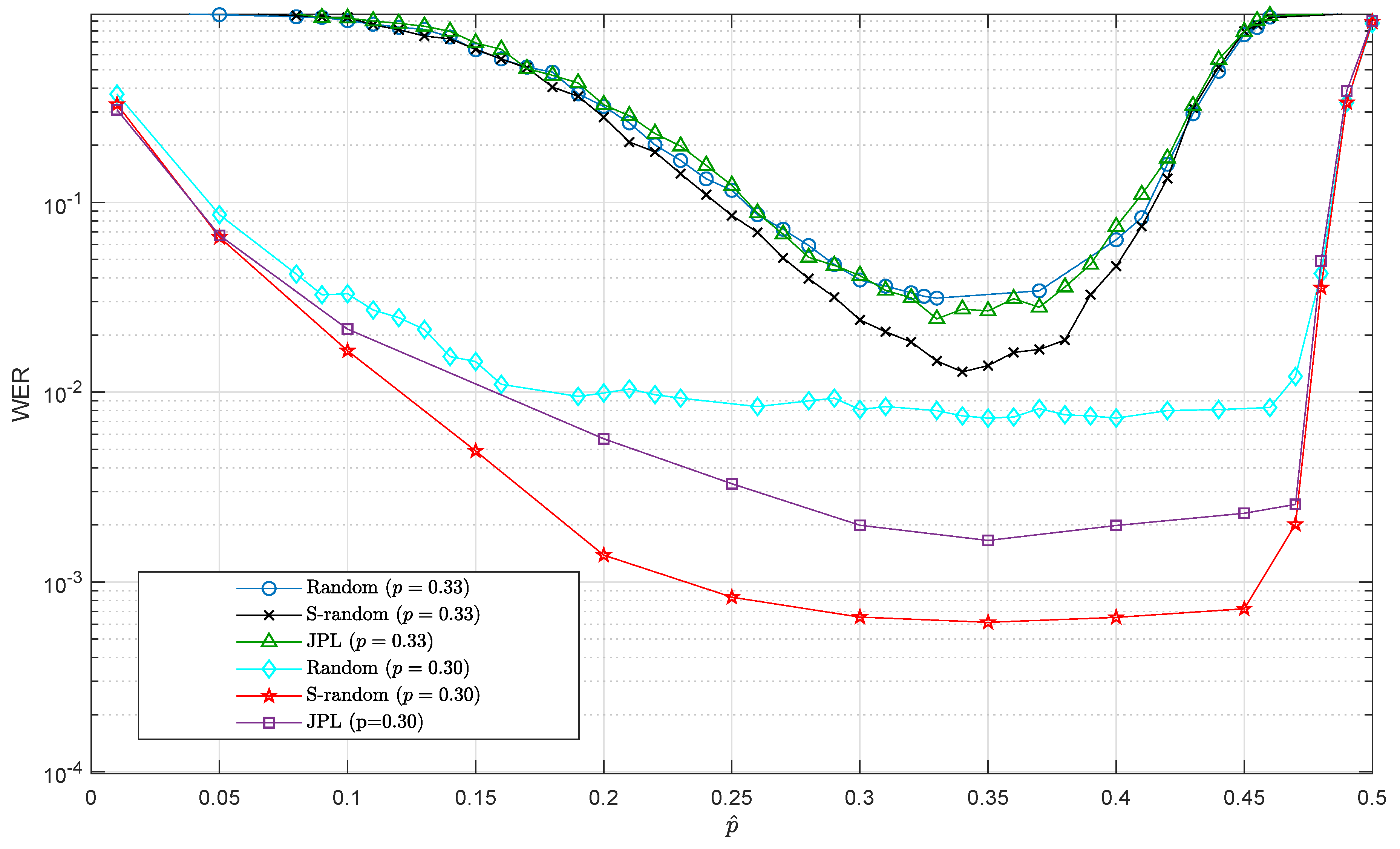
3. Quantum Turbo Decoder Performance with Depolarizing Probability Mismatch
Interleaver Impact
- S-random interleaver with parameter and
- JPL interleaver.
4. Estimating the Depolarizing Probability
4.1. Off-Line Estimation Framework
4.1.1. Quantum Channel Estimation
- Number of channel invocations: For our encoding-decoding system in Figure 1, sequential channel invocations are not considered. The reason is that once a quantum state goes through the operation of the depolarization channel, it cannot be sent again through the channel. Therefore, the number of channel invocations will be set to .
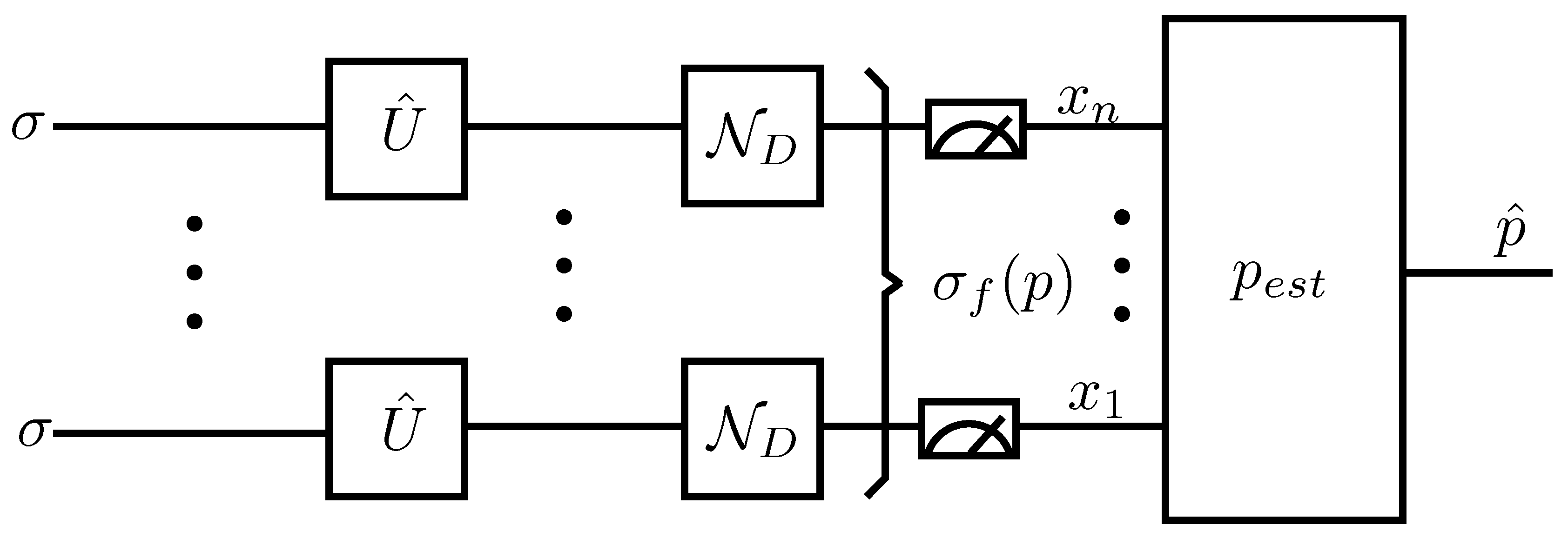
- Unitary transformation: The goal of the unitary transformation, , applied to the n input quantum probes, , is to introduce correlations among the quantum probes. In the particular case where the transformation is diagonal, it results in independent instances of the quantum probes, i.e., in an independent channel use protocol. Figure 6 shows such an estimation protocol.Furthermore, if n is set to one, the above scheme reduces to the simplest estimation protocol, called single-qubit, single-channel (SQSC). If we denote by the Fisher information of this SQSC estimation protocol, then for any n greater than one, it can be shown [22] that the corresponding overall Fisher information is given by . Therefore, for n channel invocations, the quantum Cramér–Rao bound is:so that the variance bound decreases linearly with n. In this section, we will use the estimation protocol shown in Figure 6.
- Input probe : Two different state probes are considered (We consider noiseless probes that are only affected by the depolarizing channel. Research about constructing robust quantum probe states to face such adverse noise has been addressed in [25,26].).
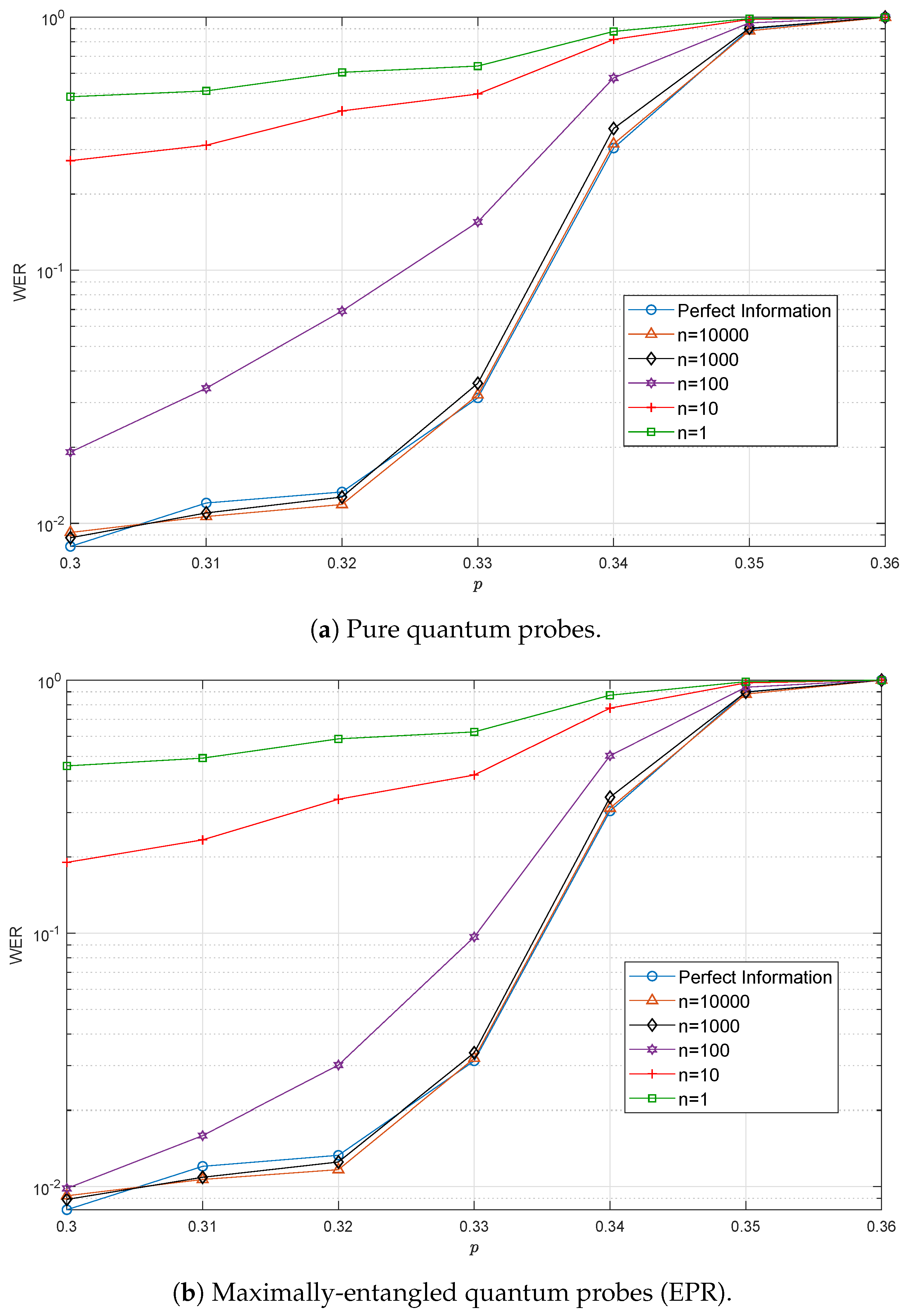
- Unentangled pure states: The Fisher information for unentangled pure states as probes has been calculated in [27] to be:
- Maximally entangled pure states: When entanglement is available, maximally entangled pure states or EPR pairs can be used as probes for the depolarizing channel. It can be shown that if just one of the qubits of is transformed by the depolarizing channel (i.e., the EPR pair goes through an extended channel ), then the corresponding Fisher information (Note that the expressions in [24,27] are given for the depolarizing channel defined as (1). Here, we use the relationship to adapt such expressions for the depolarizing channel defined as (2).) is [24]:Note that this type of protocol requires that one of the entangled qubits is not affected by noise. This is not an issue in our scenario, since the codes we consider are entanglement assisted (there is pre-shared entanglement between the coder and the decoder), and thus, this protocol is suitable for the estimation of the depolarizing probability. It can be shown that the Fisher information value in (9), higher than in (8) due to entanglement, is the largest value that can be achieved by SQSC estimation protocols for the depolarizing channel [22].
4.1.2. Computation of the Average Word Error Rate
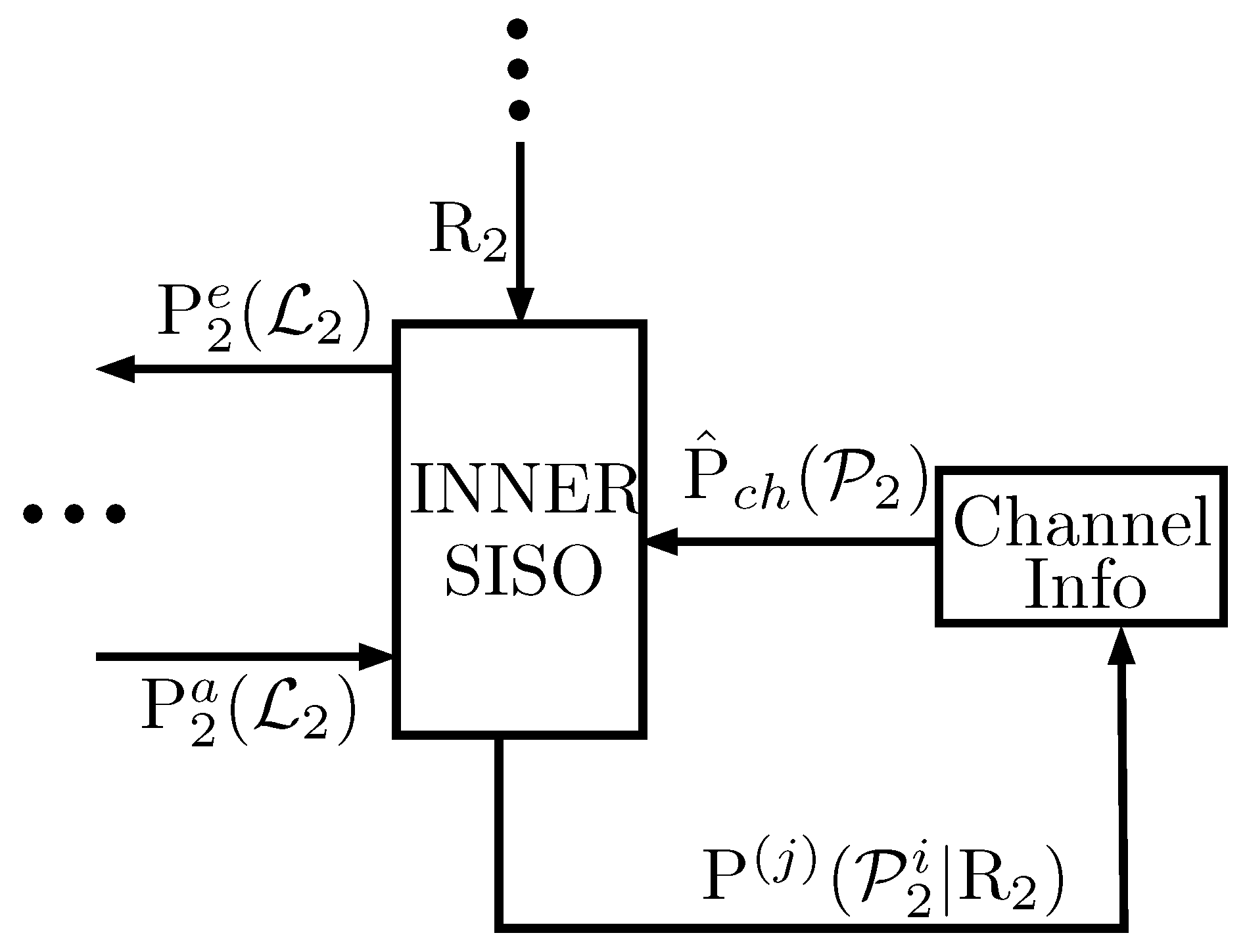
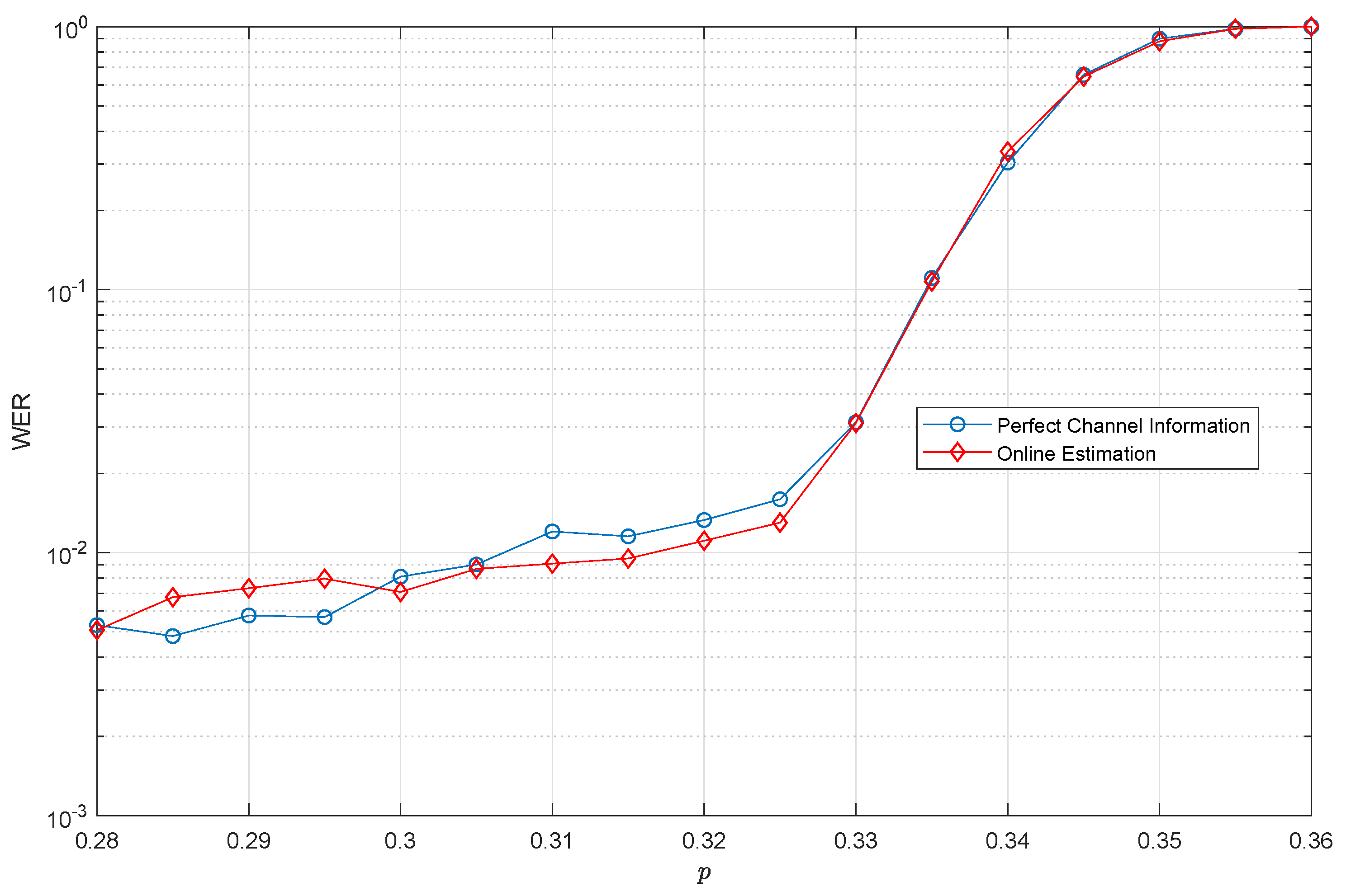
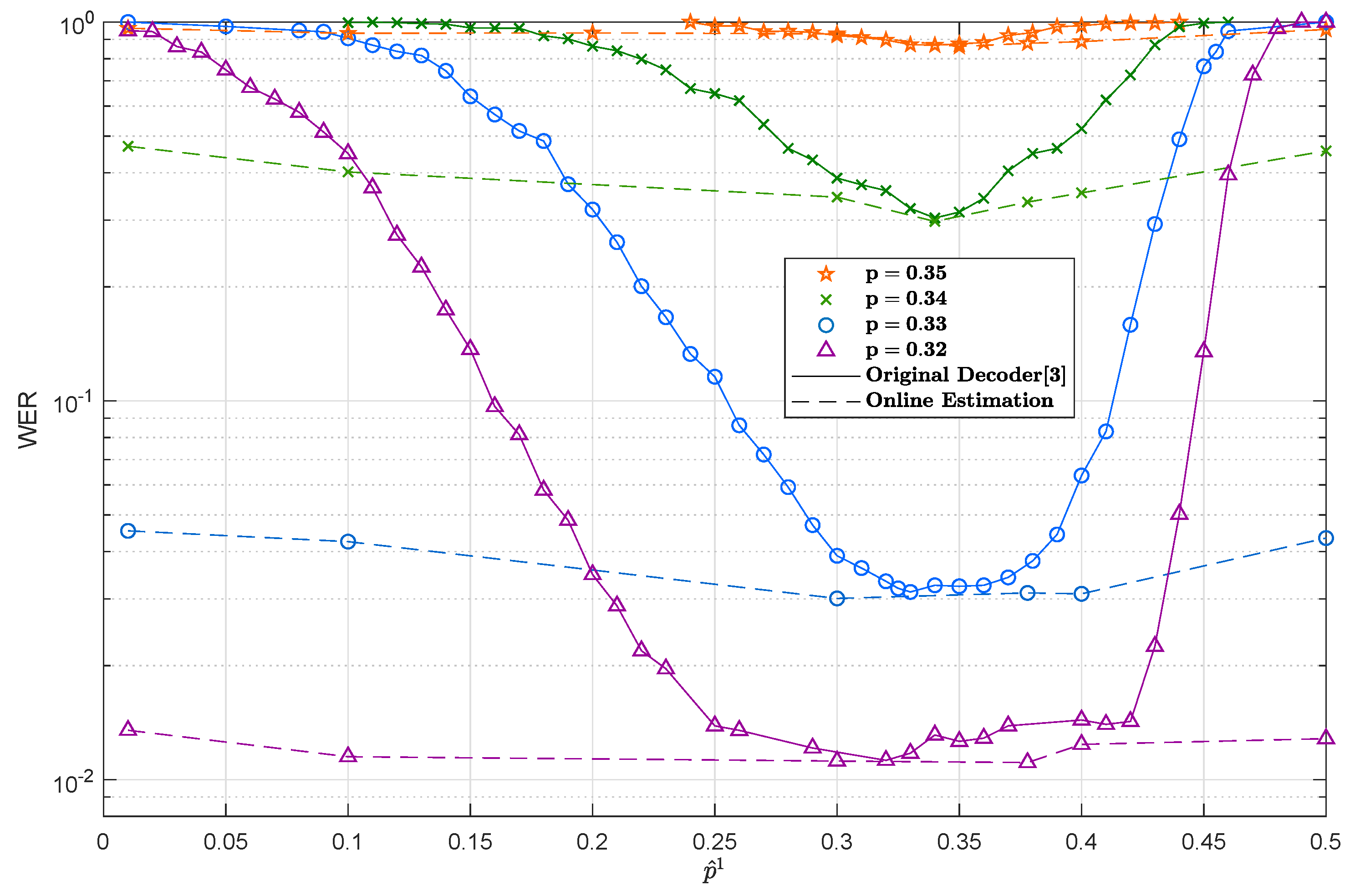
4.2. On-Line Estimation Framework
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| QECC | Quantum error correction code |
| QCC | Quantum convolutional code |
| QTC | Quantum turbo code |
| QLDPC | Quantum low density parity check |
| QIRCC | Quantum irregular convolutional code |
| QURC | Quantum unity rate code |
| EXIT | Extrinsic information transfer |
| EPR | Einstein–Podolsky–Rosen |
| SISO | Soft-input soft-output |
| JPL | Jet Propulsion Laboratory |
| WER | Word error rate |
| SQSC | Single-qubit single-channel |
| SLD | Symmetric logarithmic derivative |
References
- Poulin, D.; Tillich, J.; Ollivier, H. Quantum Serial Turbo Codes. IEEE Trans. Inf. Theory 2009, 55, 2776–2798. [Google Scholar] [CrossRef]
- Babar, Z.; Chandra, D.; Nguyen, H.V.; Botsinis, P.; Alanis, D.; Ng, S.X.; Hanzo, L. Duality of Quantum and Classical Error Correction Codes: Design Principles amp; Examples. IEEE Commun. Surv. Tutor. 2018, 21, 970–1010. [Google Scholar] [CrossRef]
- Berrou, C.; Glavieux, A.; Thitimajshima, P. Near Shannon limit error-correcting coding and decoding: Turbo-codes. 1. In Proceedings of the IEEE International Conference on Communications, Geneva, Switzerland, 23–26 May 1993; Volume 2, pp. 1064–1070. [Google Scholar]
- Wilde, M.M.; Hsieh, M.; Babar, Z. Entanglement-Assisted Quantum Turbo Codes. IEEE Trans. Inf. Theory 2014, 60, 1203–1222. [Google Scholar] [CrossRef]
- Houshmand, M.; Wilde, M.M. Recursive Quantum Convolutional Encoders are Catastrophic: A Simple Proof. IEEE Trans. Inf. Theory 2013, 59, 6724–6731. [Google Scholar] [CrossRef][Green Version]
- Babar, Z.; Ng, S.X.; Hanzo, L. EXIT-Chart-Aided Near-Capacity Quantum Turbo Code Design. IEEE Trans. Veh. Technol. 2015, 64, 866–875. [Google Scholar] [CrossRef]
- Babar, Z.; Botsinis, P.; Alanis, D.; Ng, S.X.; Hanzo, L. The Road From Classical to Quantum Codes: A Hashing Bound Approaching Design Procedure. IEEE Access 2015, 3, 146–176. [Google Scholar] [CrossRef]
- Nguyen, H.V.; Babar, Z.; Alanis, D.; Botsinis, P.; Chandra, D.; Ng, S.X.; Hanzo, L. EXIT-Chart Aided Quantum Code Design Improves the Normalised Throughput of Realistic Quantum Devices. IEEE Access 2016, 4, 10194–10209. [Google Scholar] [CrossRef]
- Babar, Z.; Nguyen, H.V.; Botsinis, P.; Alanis, D.; Chandra, D.; Ng, S.X.; Hanzo, L. Serially Concatenated Unity-Rate Codes Improve Quantum Codes Without Coding-Rate Reduction. IEEE Commun. Lett. 2016, 20, 1916–1919. [Google Scholar] [CrossRef]
- Etxezarreta Martinez, J.; Crespo, P.M.; Garcia-Frías, J. On the Performance of Interleavers for Quantum Turbo Codes. Entropy 2019, 21, 633. [Google Scholar] [CrossRef]
- Chandra, D.; Babar, Z.; Ng, S.X.; Hanzo, L. Near-Hashing-Bound Multiple-Rate Quantum Turbo Short-Block Codes. IEEE Access 2019, 7, 52712–52730. [Google Scholar] [CrossRef]
- Xie, Y.; Li, J.; Malaney, R.; Yuan, J. Channel identification and its impact on quantum LDPC code performance. In Proceedings of the Australian Communications Theory Workshop (AusCTW), Wellington, New Zealand, 30 January–2 February 2012; pp. 140–144. [Google Scholar]
- Xie, Y.; Li, J.; Malaney, R.; Yuan, J. Improved quantum LDPC decoding strategies for the misidentified quantum depolarization channel. In Proceedings of the 2016 24th European Signal Processing Conference (EUSIPCO), Budapest, Hungary, 29 August–2 September 2016; pp. 493–497. [Google Scholar]
- Reed, M.; Asenstorfer, J. A Novel Variance Estimator for Turbo-Code Decoding. Ph.D. Thesis, Office of Continuing Education, Monash University, Melbourne, Australia, 1997; pp. 173–178. [Google Scholar]
- Summers, T.A.; Wilson, S.G. SNR mismatch and online estimation in turbo decoding. IEEE Trans. Commun. 1998, 46, 421–423. [Google Scholar] [CrossRef]
- Worm, A.; Hoeher, P.; Wehn, N. Turbo-decoding without SNR estimation. IEEE Commun. Lett. 2000, 4, 193–195. [Google Scholar] [CrossRef]
- Khalighi, M.A. Effect of mismatched SNR on the performance of log-MAP turbo detector. IEEE Trans. Veh. Technol. 2003, 52, 1386–1397. [Google Scholar] [CrossRef]
- Ho, M.; Pietrobon, S. A variance mismatch study for serial concatenated turbo codes. In Proceedings of the 2nd International Symposium on Turbo Codes and Related Topics, Brest, France, 4–7 September 2000; pp. 483–485. [Google Scholar]
- Hsian, P.C.; Chin, P. Evaluation of variance mismatch for serial turbo codes with Talwar penalty function under interference of impulsive noise. J. Eng. Sci. Technol. 2010, 5, 350–360. [Google Scholar]
- Jeruchim, M. Techniques for Estimating the Bit Error Rate in the Simulation of Digital Communication Systems. IEEE J. Sel. Areas Commun. 1984, 2, 153–170. [Google Scholar] [CrossRef]
- Mohseni, M.; Rezakhani, A.T.; Lidar, D.A. Quantum-process tomography: Resource analysis of different strategies. Phys. Rev. A 2008, 77, 032322. [Google Scholar] [CrossRef]
- Collins, D.; Stephens, J. Depolarizing-channel parameter estimation using noisy initial states. Phys. Rev. A 2015, 92, 032324. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, O.E.; Gill, R.D. Fisher information in quantum statistics. J. Phys. A Math. Gen. 2000, 33, 4481–4490. [Google Scholar] [CrossRef]
- Hotta, M.; Karasawa, T.; Ozawa, M. Ancilla-assisted enhancement of channel estimation for low-noise parameters. Phys. Rev. A 2005, 72, 052334. [Google Scholar] [CrossRef]
- Oszmaniec, M.; Augusiak, R.; Gogolin, C.; Kołodyński, J.; Acín, A.; Lewenstein, M. Random Bosonic States for Robust Quantum Metrology. Phys. Rev. X 2016, 6, 041044. [Google Scholar] [CrossRef]
- Yingkai, O.; Nathan, S.; Damian, M. Robust quantum metrology with explicit symmetric states. arXiv 2019, arXiv:quant-ph/1908.02378. [Google Scholar]
- Fujiwara, A. Quantum channel identification problem. Phys. Rev. A 2001, 63, 042304. [Google Scholar] [CrossRef]

| Config. | Encoder | R | E | m | Seed Transformation |
|---|---|---|---|---|---|
| EXIT- optimized | Outer | 0 | 3 | ||
| Inner | 3 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Etxezarreta Martinez, J.; Crespo, P.M.; Garcia-Frías, J. Depolarizing Channel Mismatch and Estimation Protocols for Quantum Turbo Codes. Entropy 2019, 21, 1133. https://doi.org/10.3390/e21121133
Etxezarreta Martinez J, Crespo PM, Garcia-Frías J. Depolarizing Channel Mismatch and Estimation Protocols for Quantum Turbo Codes. Entropy. 2019; 21(12):1133. https://doi.org/10.3390/e21121133
Chicago/Turabian StyleEtxezarreta Martinez, Josu, Pedro M. Crespo, and Javier Garcia-Frías. 2019. "Depolarizing Channel Mismatch and Estimation Protocols for Quantum Turbo Codes" Entropy 21, no. 12: 1133. https://doi.org/10.3390/e21121133
APA StyleEtxezarreta Martinez, J., Crespo, P. M., & Garcia-Frías, J. (2019). Depolarizing Channel Mismatch and Estimation Protocols for Quantum Turbo Codes. Entropy, 21(12), 1133. https://doi.org/10.3390/e21121133






