Complex Chaotic Attractor via Fractal Transformation
Abstract
1. Introduction
2. The Complex Chaotic Systems Based on Rotation Transformation
2.1. Rotation Multiwing Chaotic System
2.2. Rotation Multiscroll Chaotic System
2.3. Rotation Compound Chaotic System
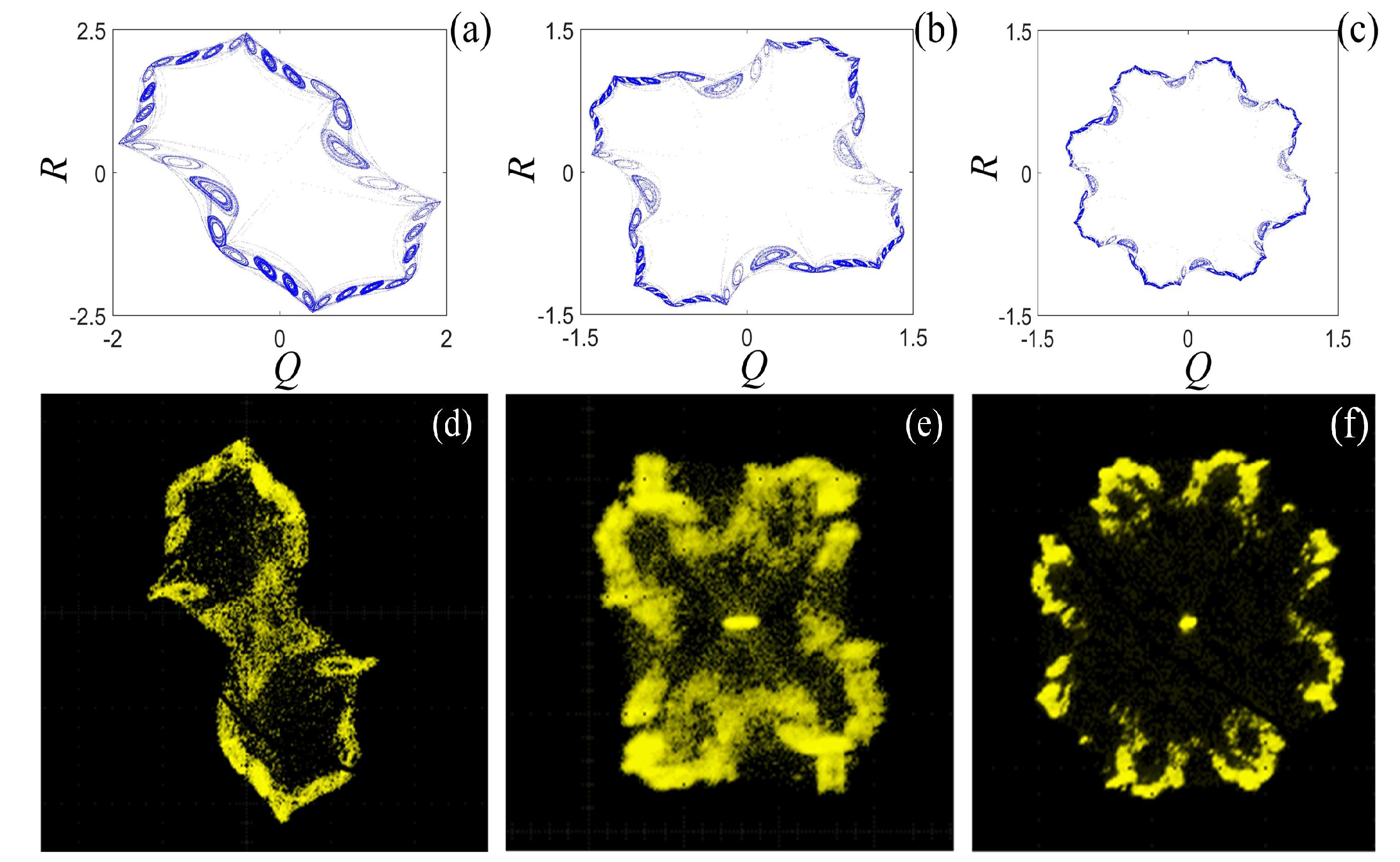
3. Chaotic Attractors with Fractal Transformation
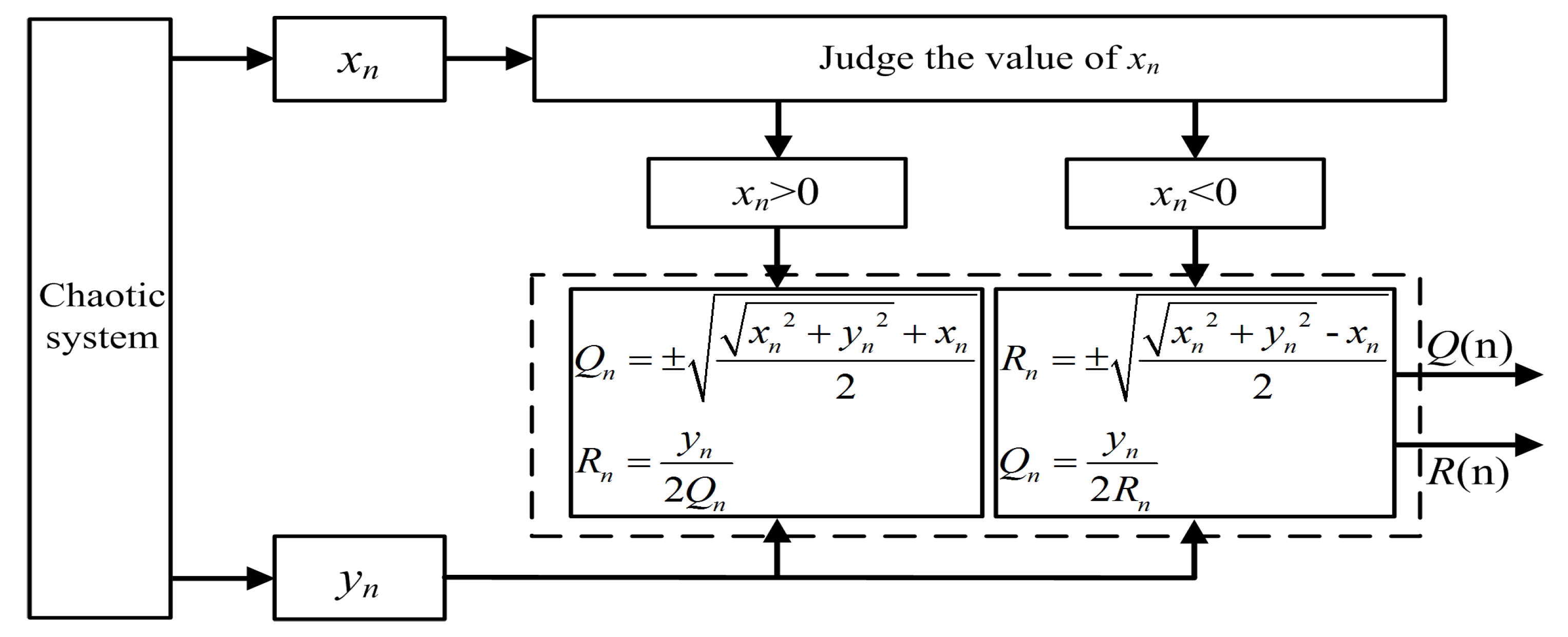
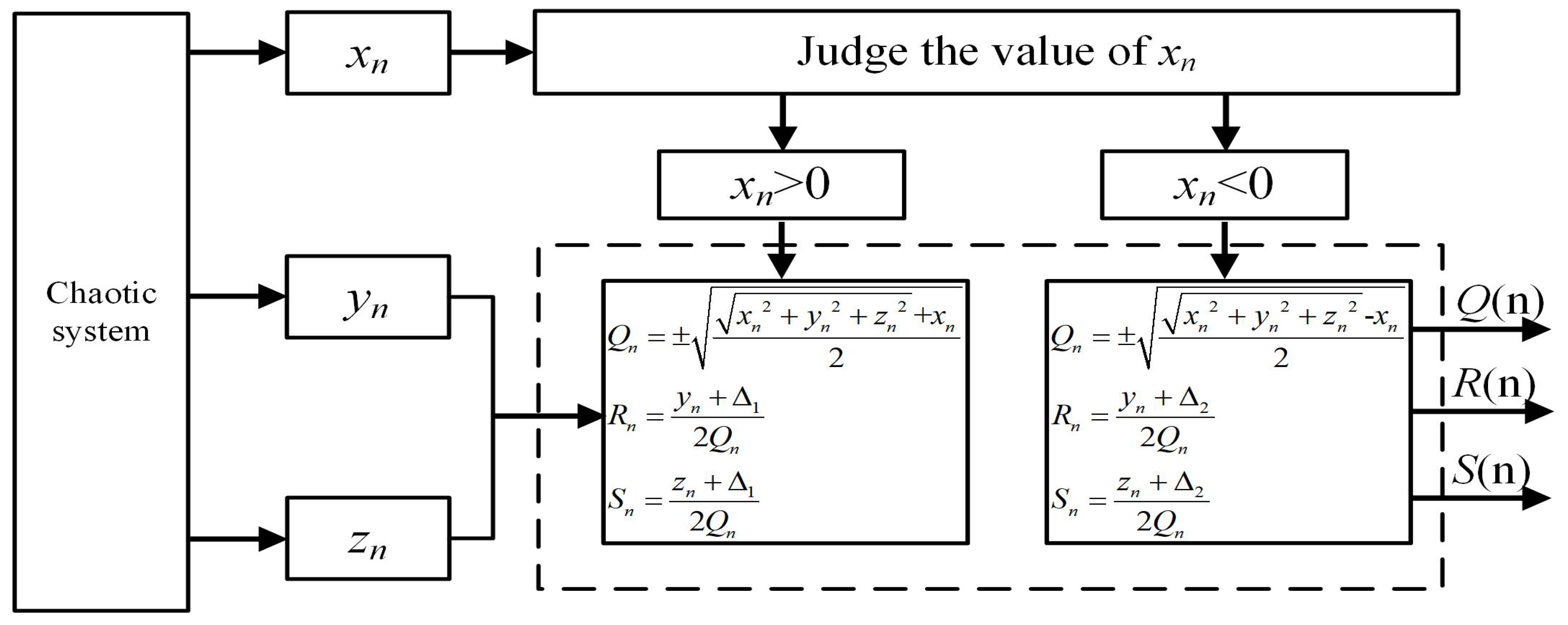
3.1. The Fractal Algorithm
3.1.1. The Binary Fractal Algorithm
3.1.2. The Ternary Fractal Algorithm
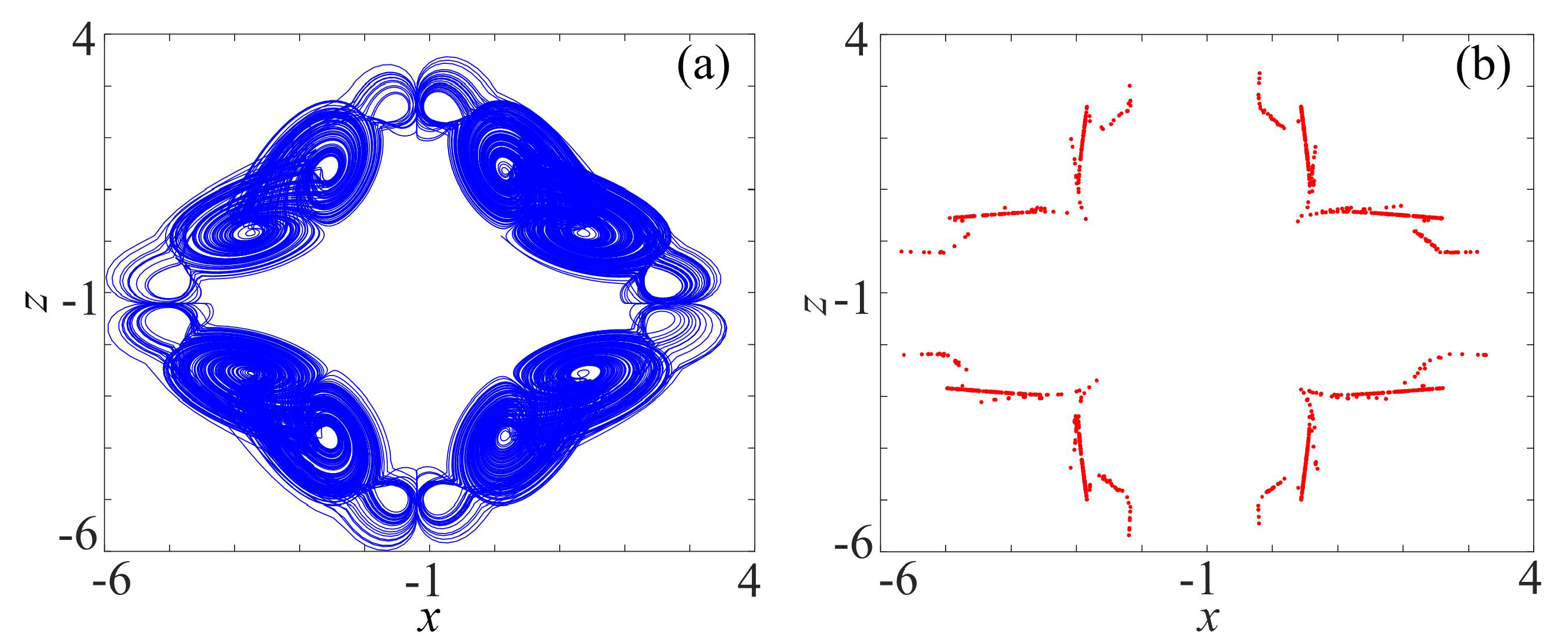
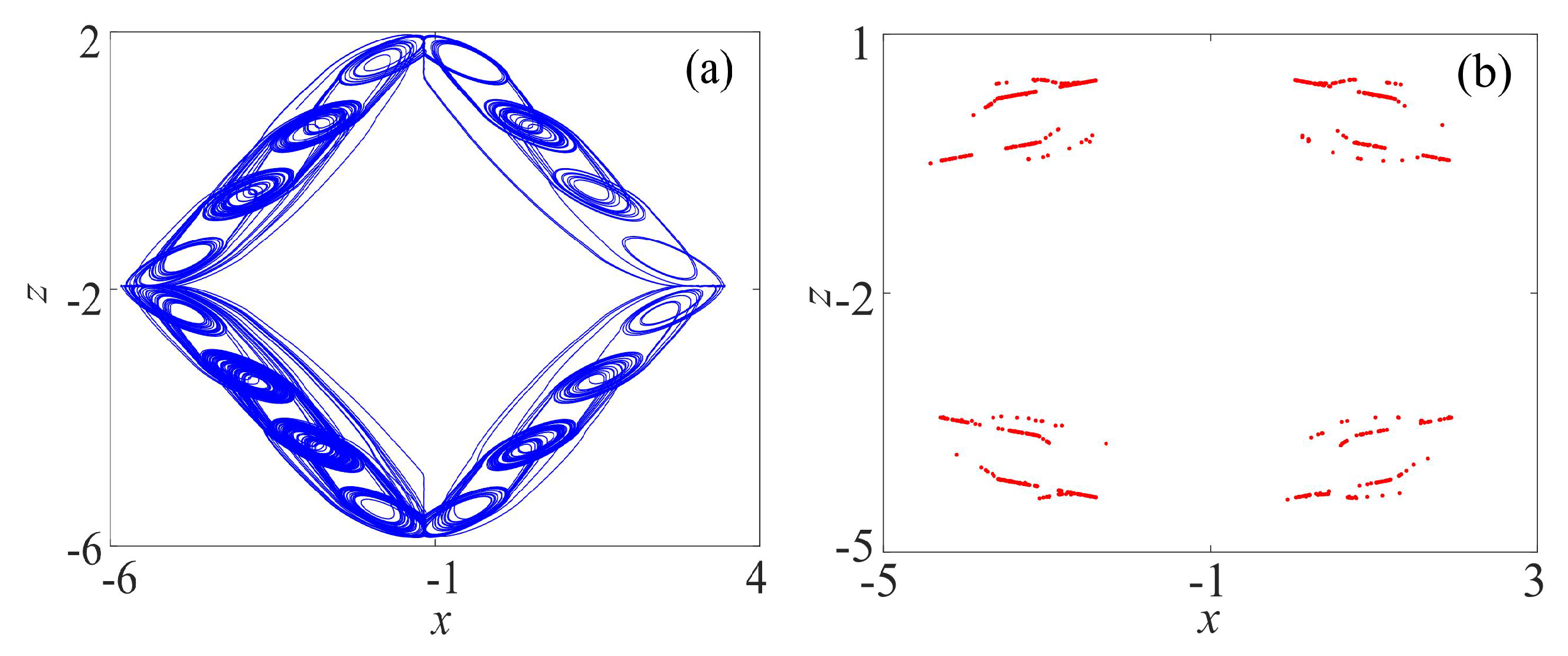
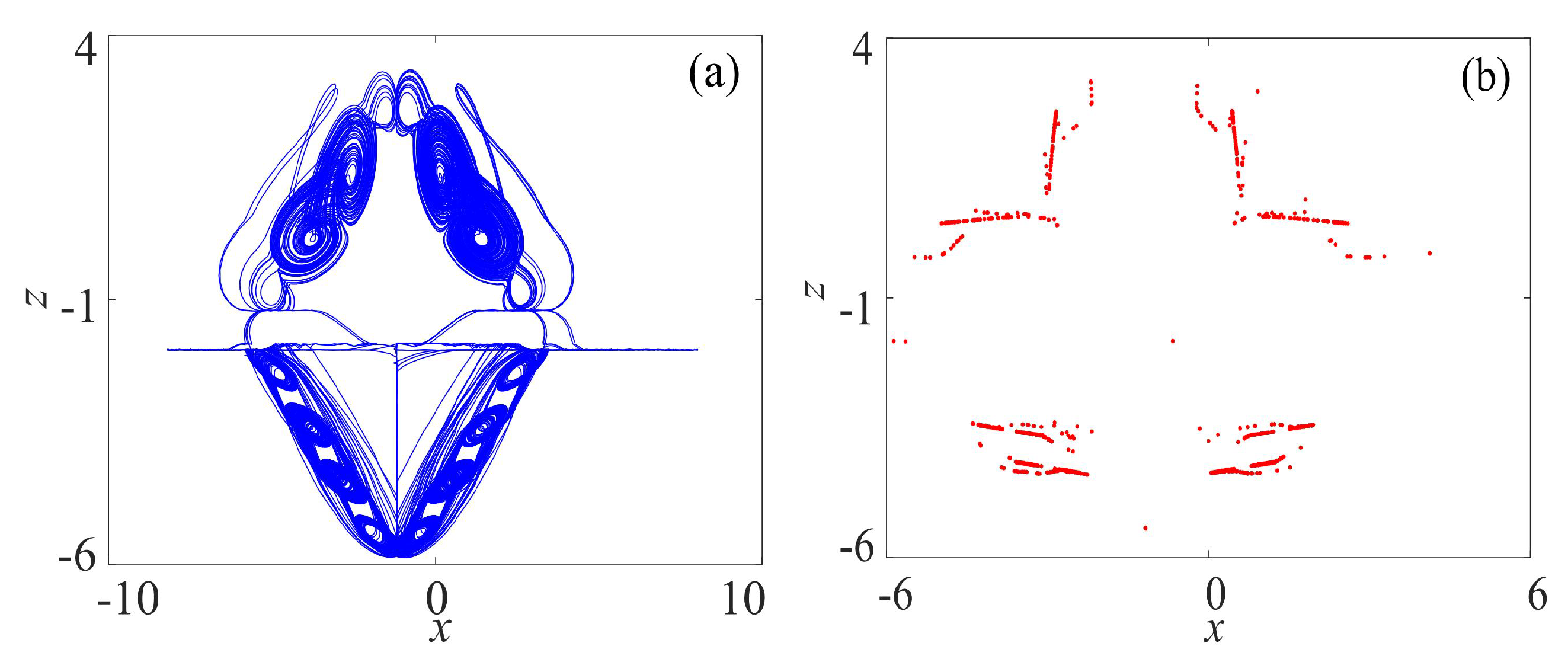
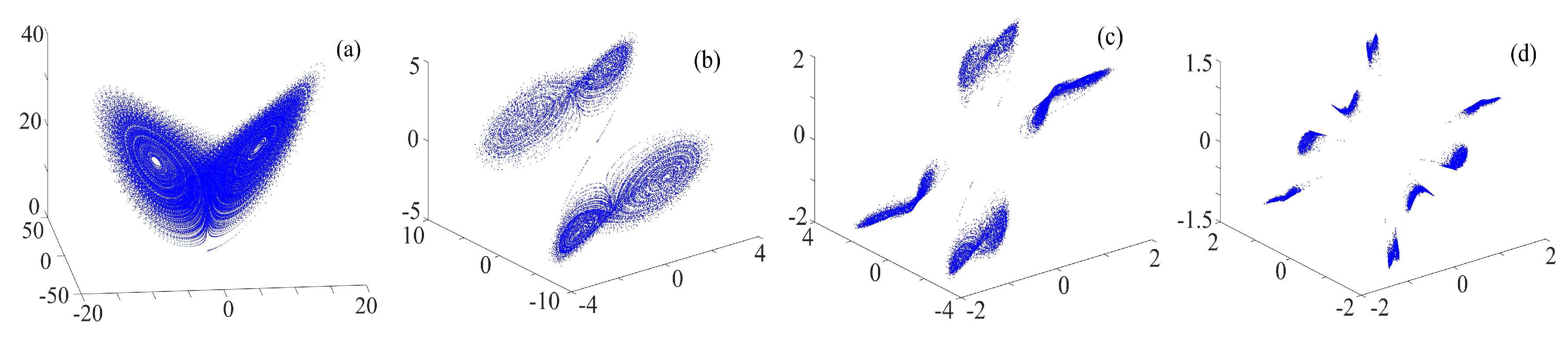
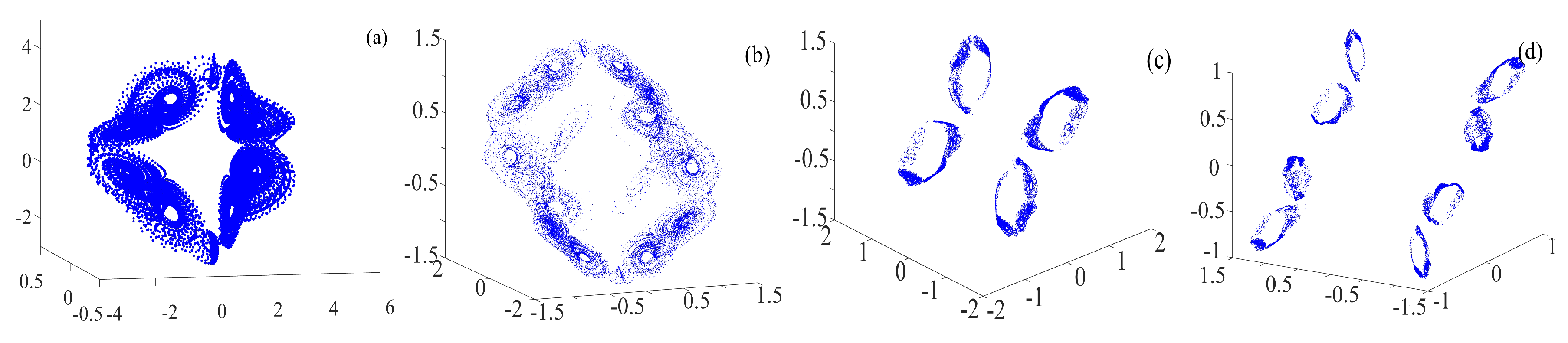
3.2. Complex Chaotic Attractors with the Binary Fractal Transformation
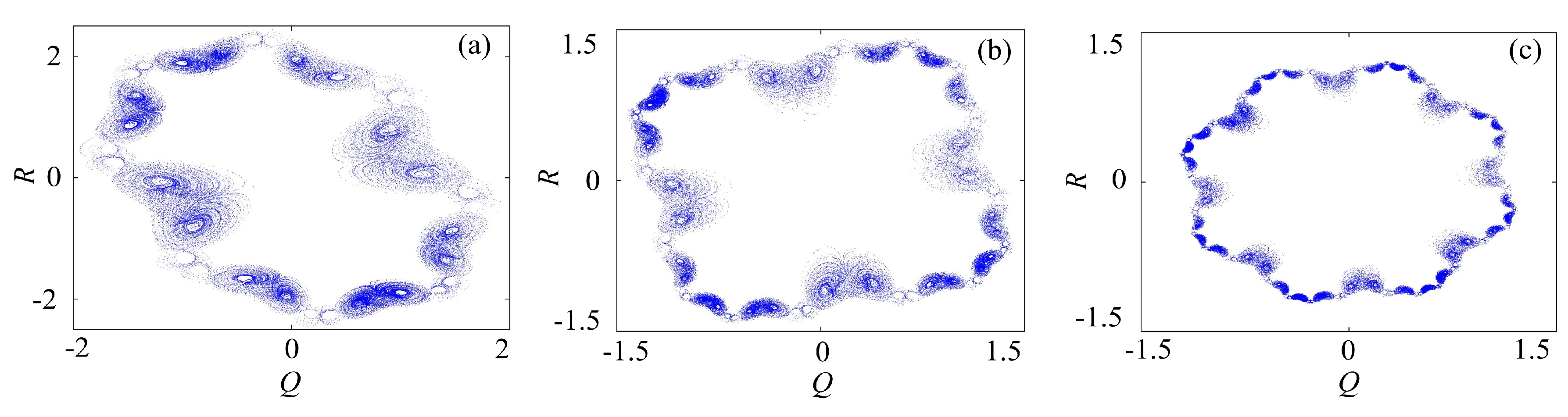
3.2.1. Rotation Multiwing with the Binary Fractal Transformation
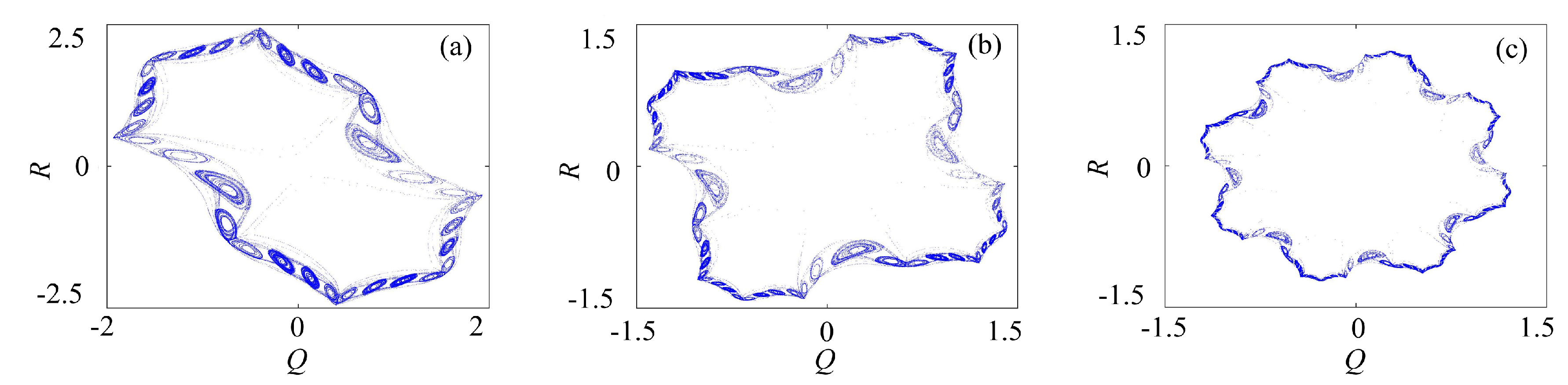
3.2.2. Rotation Multiscroll with the Binary Fractal Transformation
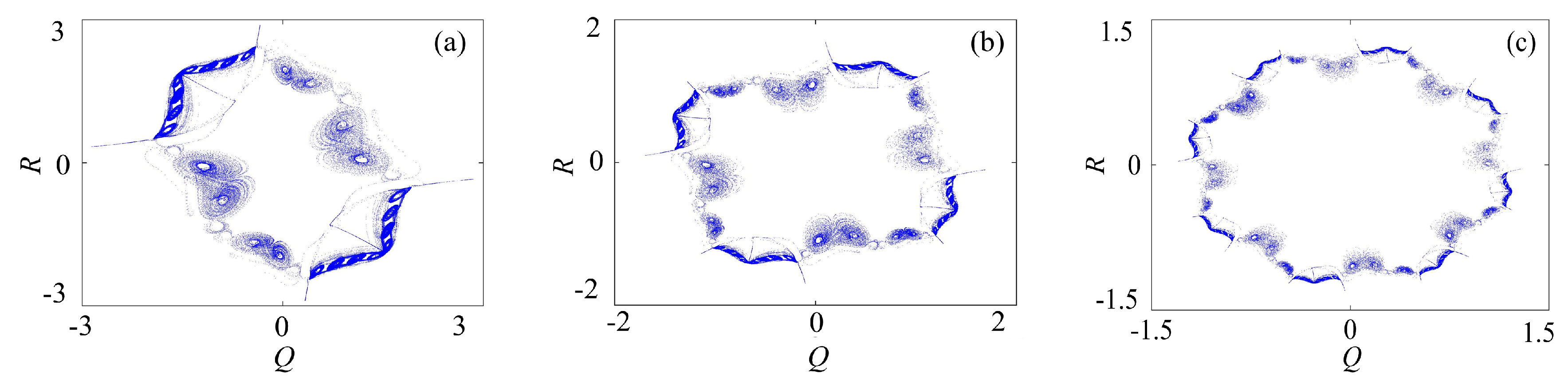
3.2.3. Rotation Compound Chaotic System with the Binary Fractal Transformation
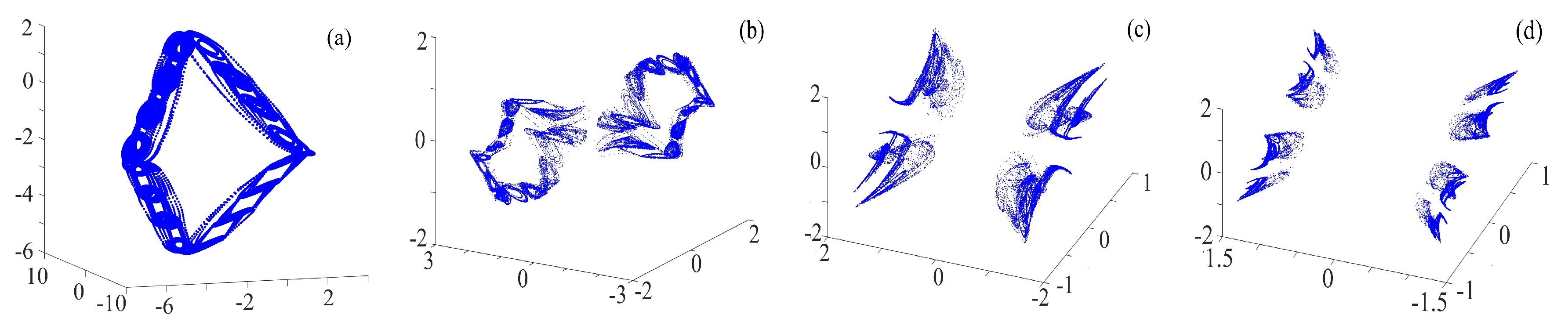
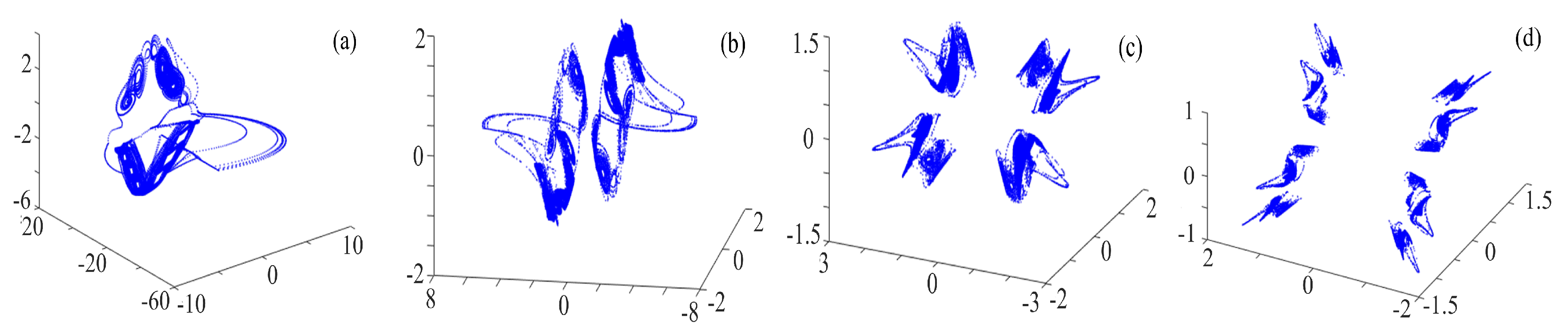
3.3. Chaotic Attractors with the Ternary Fractal Transformation
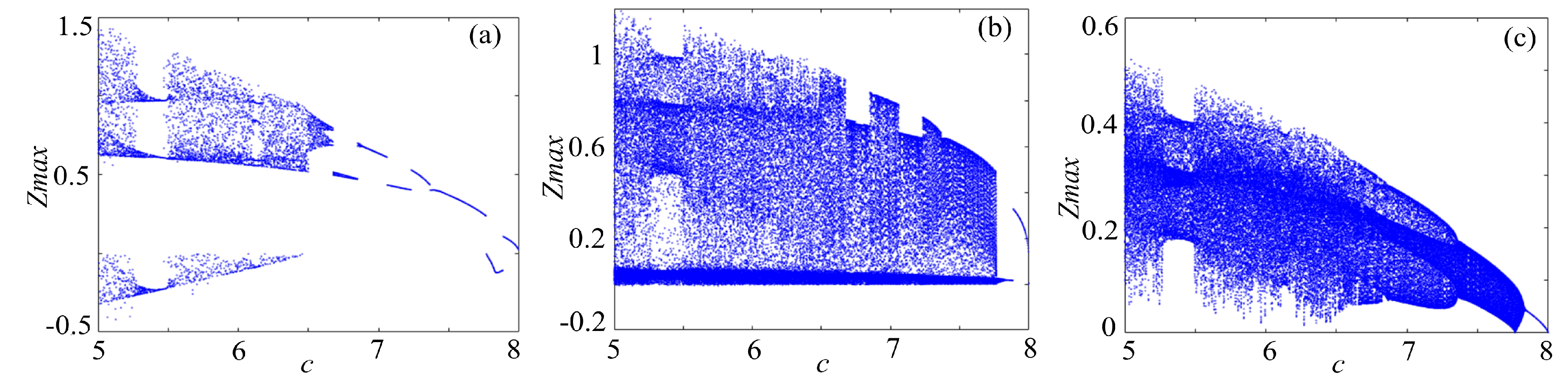
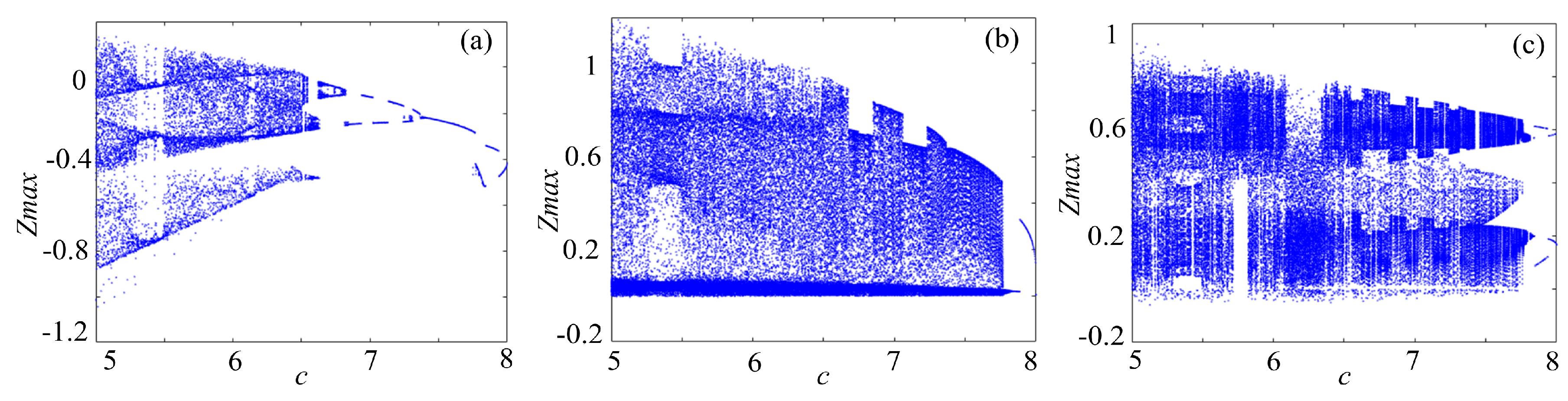
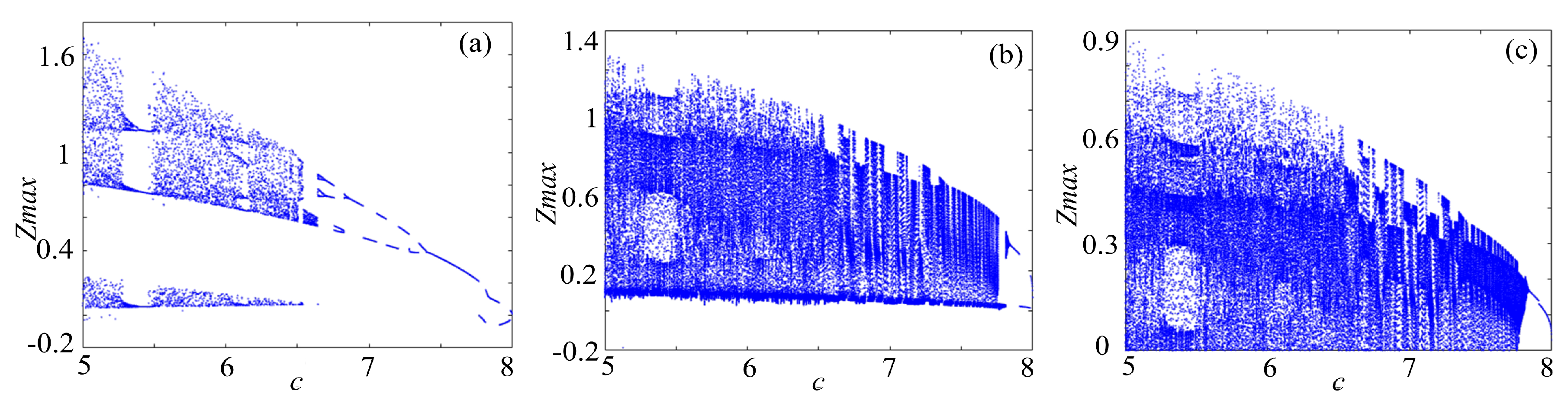
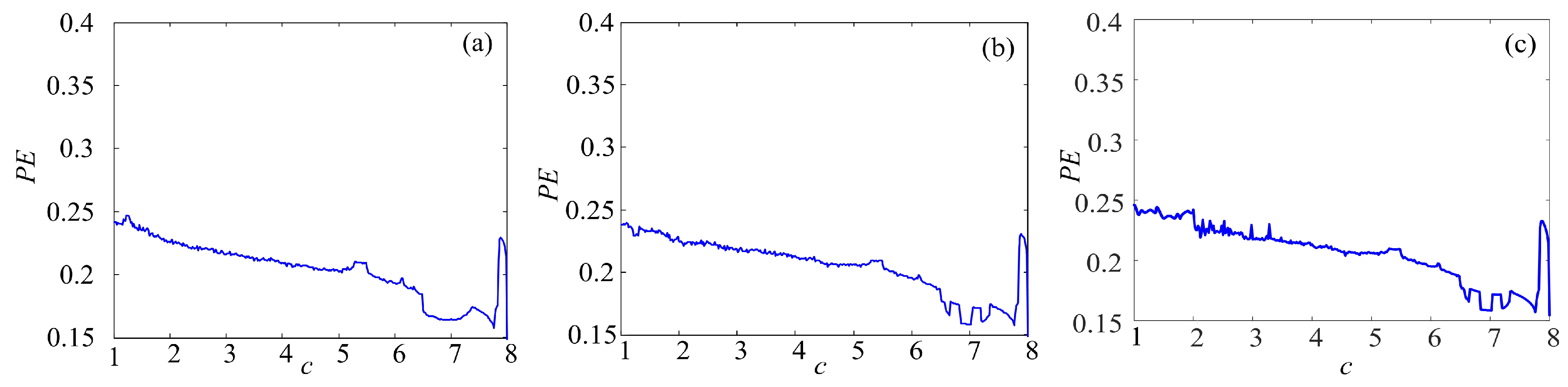
4. Dynamics Analysis of the Complex Chaotic Systems
4.1. Bifurcation Diagram
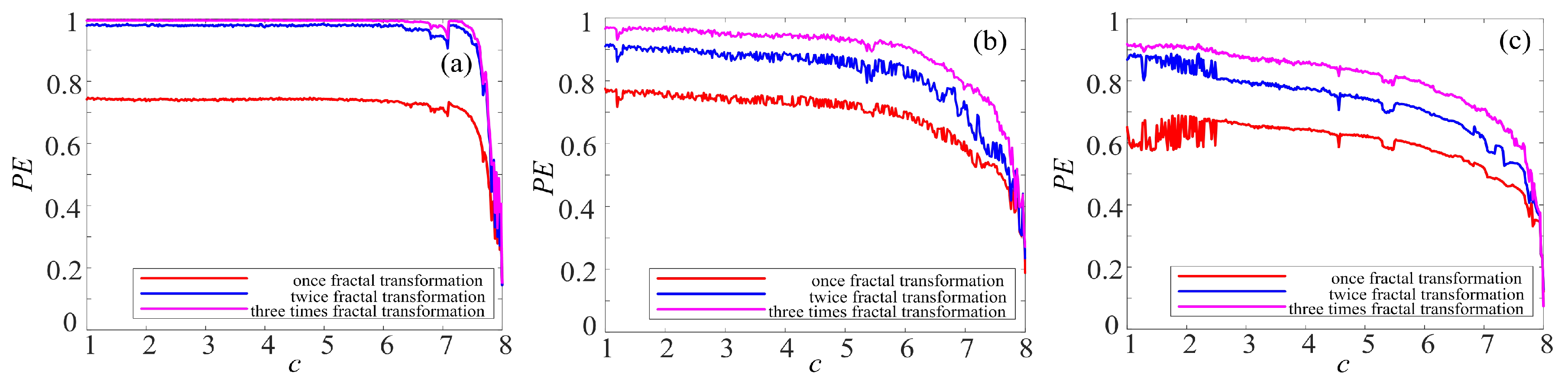
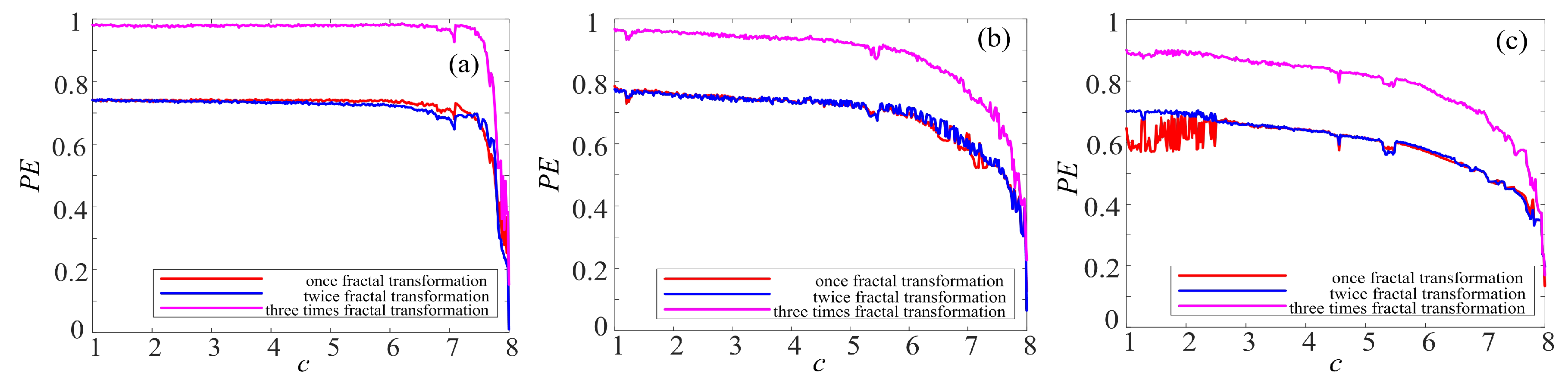
4.2. Complexity Analysis
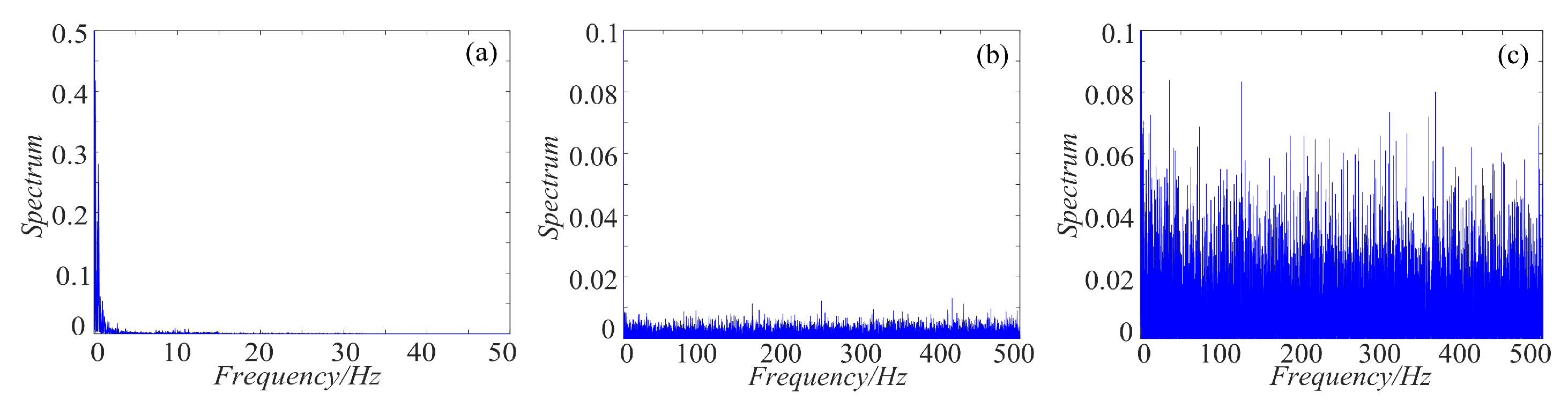
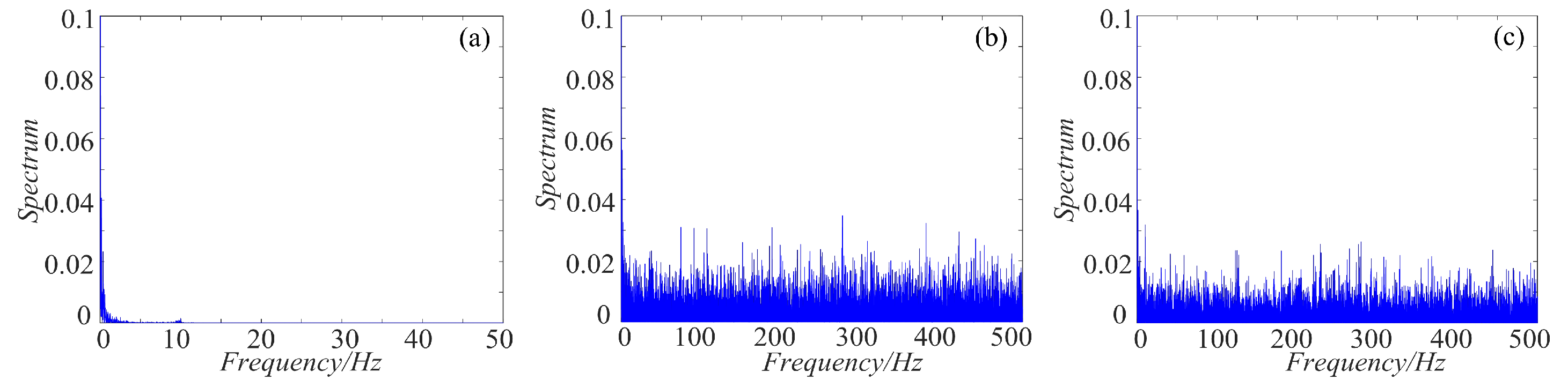
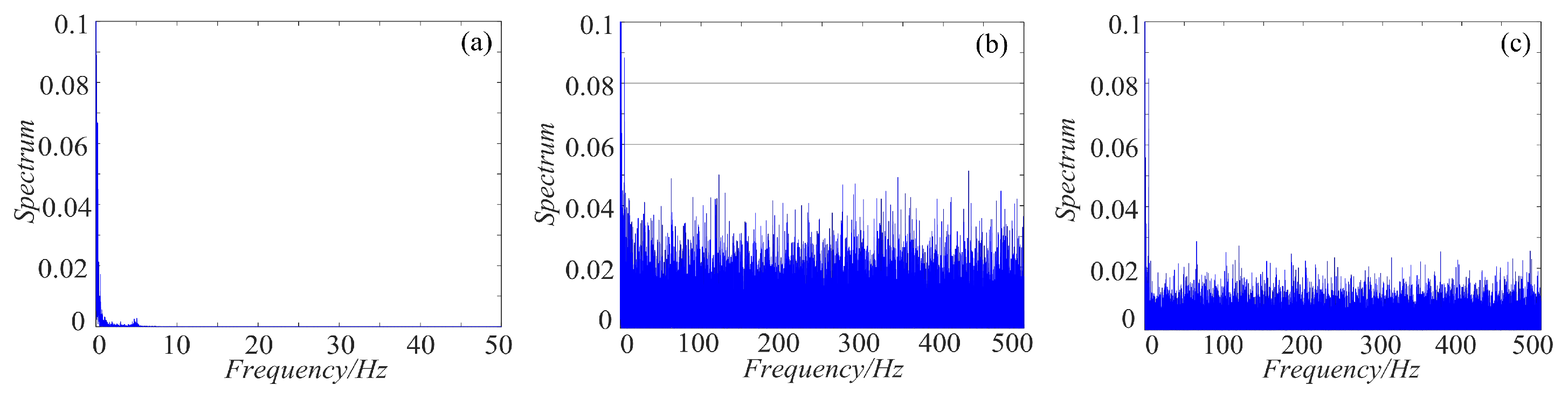
4.3. Spectrum Distribution Characteristics
5. DSP Implementation
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Li, C.B.; Sprott, J.C. Multistability in the Lorenz system: A broken butterfly. Int. J. Bifurcat. Chaos 2014, 24, 1450131. [Google Scholar] [CrossRef]
- Blake, M. Universal charge diffusion and the butterfly effect in holographic theories. Phys. Rev. Lett. 2016, 117, 1465–1466. [Google Scholar] [CrossRef] [PubMed]
- Xie, Y.Q.; Yu, J.Y.; Guo, S.Y.; Ding, Q.; Wang, E. Image encryption scheme with compressed sensing based on new three-dimensional chaotic system. Entropy 2019, 21, 819. [Google Scholar] [CrossRef]
- Zuo, T.; Sun, K.H.; Ai, X.X.; Wang, H. High-order grid multiscroll chaotic attractors generated by the second-generation current conveyor circuit. IEEE Trans. Circuits Syst. 2014, 61, 818–822. [Google Scholar] [CrossRef]
- Yadav, V.K.; Das, S.; Bhadauria, B.S.; Singh, A.K.; Srivastava, M. Stability analysis, chaos control of a fractional order chaotic chemical reactor system and its function projective synchronization with parametric uncertainties. Acta Phys. Sin. 2017, 53, 594–605. [Google Scholar] [CrossRef]
- Ai, W.; Sun, K.H.; Fu, Y.L. Design of multiwing-multiscroll grid compound chaotic system and its circuit implementation. Int. J. Mod. Phys. C 2018, 29, 1850049. [Google Scholar] [CrossRef]
- Yu, S.M.; Tang, W.K.S.; Lü, J.H.; Chen, G. Design and implementation of multiwing butterfly chaotic attractors via Lorenz-type systems. Int. J. Bifurcat. Chaos 2010, 20, 1002538. [Google Scholar] [CrossRef]
- Zhang, L.M.; Sun, K.H. Solution and dynamics of a fractional-order 5-D hyperchaotic system with four wings. Eur. Phys. J. Plus 2017, 132, 31. [Google Scholar] [CrossRef]
- Zhang, C.X.; Yu, S.M. A novel methodology for constructing a multi-wing chaotic and hyperchaotic system with a unified step function switching control. Chin. Phys. B 2016, 25, 83–94. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, C.; Zhou, L.L. Generating hyperchaotic multi-wing attractor in a 4D memristive circuit. Nonlinear Dyn. 2016, 85, 1–11. [Google Scholar] [CrossRef]
- Yuan, F.; Wang, G.Y.; Wang, X.W. Extreme multistability in a memristor-based multi-scroll hyper-chaotic system. Chaos 2016, 26, 073107. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.Q.; Liu, C.X. Generation of multi-scroll chaotic attractors via the saw-tooth function. Int. J. Mod. Phys. B 2008, 22, 2399–2405. [Google Scholar] [CrossRef]
- Bao, B.C.; Zhou, G.H.; Xu, J.P.; Liu, Z. Multiscroll chaotic attractors from a modified colpitts oscillator model. Int. J. Bifurcat. Chaos 2010, 20, 2203–2211. [Google Scholar] [CrossRef]
- Yu, S.M.; Tang, W.K.S.; Chen, G. Generation of nm-scroll attractors under a Chua-circuit framework. Int. J. Bifurcat. Chaos 2007, 17, 3951–3964. [Google Scholar] [CrossRef]
- Kengne, J.; Njikam, S.M.; Signing, V.R. A plethora of coexisting strange attractors in a simple Jerk system with hyperbolic tangent nonlinearity. Chaos Soliton Fract. 2018, 106, 201–213. [Google Scholar] [CrossRef]
- Chen, Z.; Wen, G.L.; Zhou, H.; Chen, J. Generation of grid multi-scroll chaotic attractors via hyperbolic tangent function series. Optik 2016, 130, 594–600. [Google Scholar] [CrossRef]
- Shen, C.W.; Yu, S.M.; Lü, J.H. Design and circuit implementation of discrete-time chaotic systems with modulus of triangular wave functions. Int. J. Bifurcat. Chaos 2014, 24, 1450048. [Google Scholar] [CrossRef]
- Liu, C.X.; Yi, J.; Xi, X.C.; An, L.M.; Qian, Y.; Fu, Y.Q. Research on the multi-scroll chaos generation based on Jerk model. Procedia Eng. 2012, 29, 957–961. [Google Scholar]
- Chen, L.; Pan, W.; Wu, R.; Tenreiro Machado, J.A.; Lopes, A.M. Design and implementation of grid multi-scroll fractional-order chaotic attractors. Chaos 2016, 26, 084303. [Google Scholar] [CrossRef]
- Wang, C.H.; Liu, X.M.; Xia, H. Multi-piecewise quadratic nonlinearity memristor and its 2n-scroll and 2n+1-scroll chaotic attractors system. Chaos 2017, 27, 33114. [Google Scholar] [CrossRef]
- Escalante-González, R.J.; Campos-Cantón, E. Generation of chaotic attractors without equilibria via piecewise linear systems. Int. J. Mod Phys. C 2016, 28, 1750008. [Google Scholar] [CrossRef]
- Muñoz-Pacheco, J.M.; Zambrano-Serrano, E.; Félix-Beltrán, O.; Gómez-Pavón, L.C.; Luis-Ramos, A. Synchronization of PWL function-based 2D and 3D multi-scroll chaotic systems. Nonlinear Dyn. 2012, 70, 1633. [Google Scholar] [CrossRef]
- Ontañón-García, L.J.; Campos-Cantón, E. Preservation of a two-wing Lorenz-like attractor with stable equilibria. J. Frankl. Inst. 2013, 350, 2867–2880. [Google Scholar] [CrossRef]
- Ontañón-García, L.J.; Jiménez-López, E.; Campos-Cantón, E. A family of hyperchaotic multi-scroll attractors in Rn. Appl. Math. Comput. 2014, 233, 522–533. [Google Scholar]
- Ma, J.; Wu, X.Y.; Chu, R.T.; Zhang, L. Selection of multi-scroll attractors in Jerk circuits and their verification using Pspice. Nonlinear Dyn. 2014, 76, 1951. [Google Scholar] [CrossRef]
- Hong, Q.H.; Xie, Q.G.; Xiao, P. A novel approach for generating multi-direction multi-double-scroll attractors. Nonlinear Dyn. 2017, 87, 1015. [Google Scholar] [CrossRef]
- Mandelbrot, B.; Wheeler, J. The Fractal Geometry of Nature; W. H. Freeman: New York, NY, USA, 1983; Volume 147, p. 468. [Google Scholar]
- Guo, Y.L.; Qi, G.Y.; Hamam, Y. A multi-wing spherical chaotic system using fractal process. Nonlinear Dyn. 2016, 85, 1–11. [Google Scholar] [CrossRef]
- Bouallegue, K.; Chaari, A.; Toumi, A. Multi-scroll and multi-wing chaotic attractor generated with Julia process fractal. Chaos Soliton Fract. 2011, 44, 79–85. [Google Scholar] [CrossRef]
- Bouallegue, K. Chaotic attractors with separated scrolls. Chaos 2015, 25, 073108. [Google Scholar] [CrossRef]
- Bouallegue, K. Gallery of chaotic attractors generated by fractal network. Int. J. Bifurcat. Chaos 2015, 25, 1530002. [Google Scholar] [CrossRef]
- He, S.B.; Sun, K.H.; Wang, H.H. Complexity analysis and DSP implementation of the fractional-order Lorenz hyperchaotic system. Entropy 2015, 17, 8299–8311. [Google Scholar] [CrossRef]
- Gao, H.Q.; Wang, Y.J.; Kang, S.Q.; Le, Z.; Wang, J.Q.; Wei, J.J. Realization of digital chaotic signal generation circuits. Appl. Mech. Mater. 2014, 716, 1352–1355. [Google Scholar] [CrossRef]
- Sun, K.H.; Sprott, J.C. Dynamics of a simplified Lorenz system. Int. J. Bifurcat. Chaos 2009, 19, 1357–1366. [Google Scholar] [CrossRef]
- Ai, X.X.; Sun, K.H.; He, S.B.; Wang, H.H. Design of grid multiscroll chaotic attractors via transformations. Int. J. Bifurcat. Chaos 2015, 25, 1530027. [Google Scholar] [CrossRef]
- Wolf, A.; Swift, J.; Swinney, H.; Vastano, J.A. Determining Lyapounov exponents from a time series. Physica D 1985, 16, 285–317. [Google Scholar] [CrossRef]
- Matsumoto, T. A chaotic attractor from Chua’s circuit. IEEE Trans. Circuits Syst. 1984, 31, 1055–1058. [Google Scholar] [CrossRef]
- Ai, X.X.; Sun, K.H.; He, S.B. Compound attractors between different chaotic systems. Acta Phys. Sin. 2014, 63, 40503. [Google Scholar]
- Zhang, C.X.; Yu, S.M.; Chen, G.R. Design and implementation of compound chaotic attractors. Int. J. Bifurcat. Chaos 2012, 22, 367–369. [Google Scholar] [CrossRef]
- Lin, Y.; Wang, C.H.; He, H.Z.; Zhou, L.L. A novel four-wing non-equilibrium chaotic system and its circuit implementation. Pramana 2016, 86, 801–807. [Google Scholar] [CrossRef]
- Sun, K.H.; He, S.B.; He, Y.; Yin, L.Z. Complexity analysis of chaotic pseudo-random sequences based on spectral entropy algorithm. Acta Phys. Sin. 2013, 62, 709–712. [Google Scholar]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef] [PubMed]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, S.; Sun, K.; He, S.; Ai, W. Complex Chaotic Attractor via Fractal Transformation. Entropy 2019, 21, 1115. https://doi.org/10.3390/e21111115
Dai S, Sun K, He S, Ai W. Complex Chaotic Attractor via Fractal Transformation. Entropy. 2019; 21(11):1115. https://doi.org/10.3390/e21111115
Chicago/Turabian StyleDai, Shengqiu, Kehui Sun, Shaobo He, and Wei Ai. 2019. "Complex Chaotic Attractor via Fractal Transformation" Entropy 21, no. 11: 1115. https://doi.org/10.3390/e21111115
APA StyleDai, S., Sun, K., He, S., & Ai, W. (2019). Complex Chaotic Attractor via Fractal Transformation. Entropy, 21(11), 1115. https://doi.org/10.3390/e21111115





