Dynamical Sampling with Langevin Normalization Flows
Abstract
1. Introduction
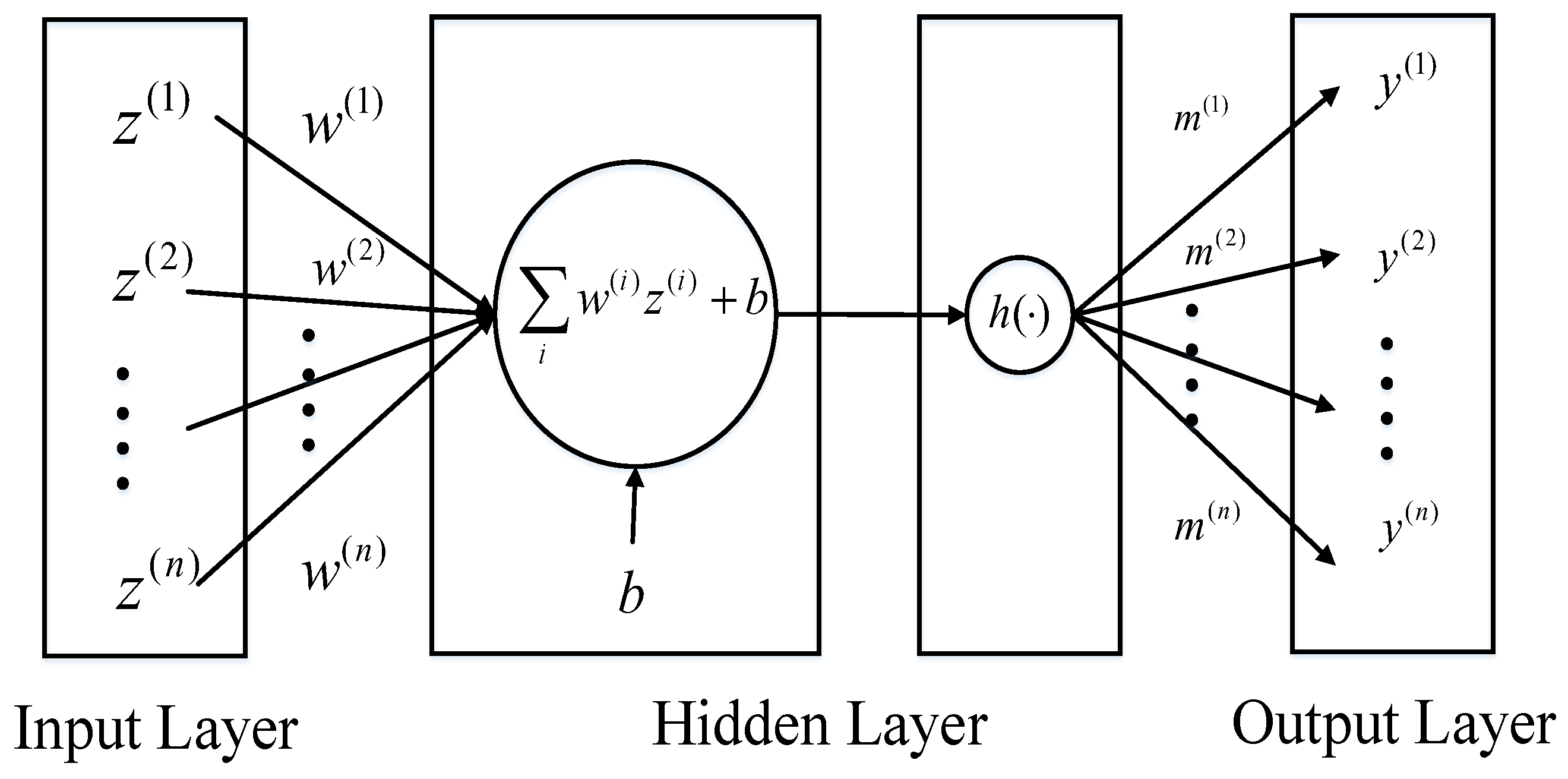
2. Preliminary
2.1. Normalization Flows
2.2. Langevin Diffusions
3. Langevin Normalization Flows
3.1. Main Idea
3.2. Difference between Normalization Flows and Langevin Normalization Flows
4. Dynamical Sampling Using Langevin Normalization Flows
4.1. Main Idea
4.2. Loss Function of the Training Procedure
4.3. Unnormalized Probability Distributions
| Algorithm 1 Training NFLMC |
| Input: target distribution , step size , learning rate , scale parameter , Langevin step length , number of iterations , sample number N, the initial distribution , the transformation distribution , the energy function U, the gradient of energy function and the second order gradient . Output: the parameters of the sampler. Initializing the parameters of the neural network. for to do Sample N samples from the proposal distribution . for to do Obtaining through Equation (9). for to do Obtaining through Equation (10). Calculating the loss through Equation (24). Obtaining by using Equation (18). Calculating through Equation (25). Updating in the transformation functions. |
5. Applicability of NFLMC
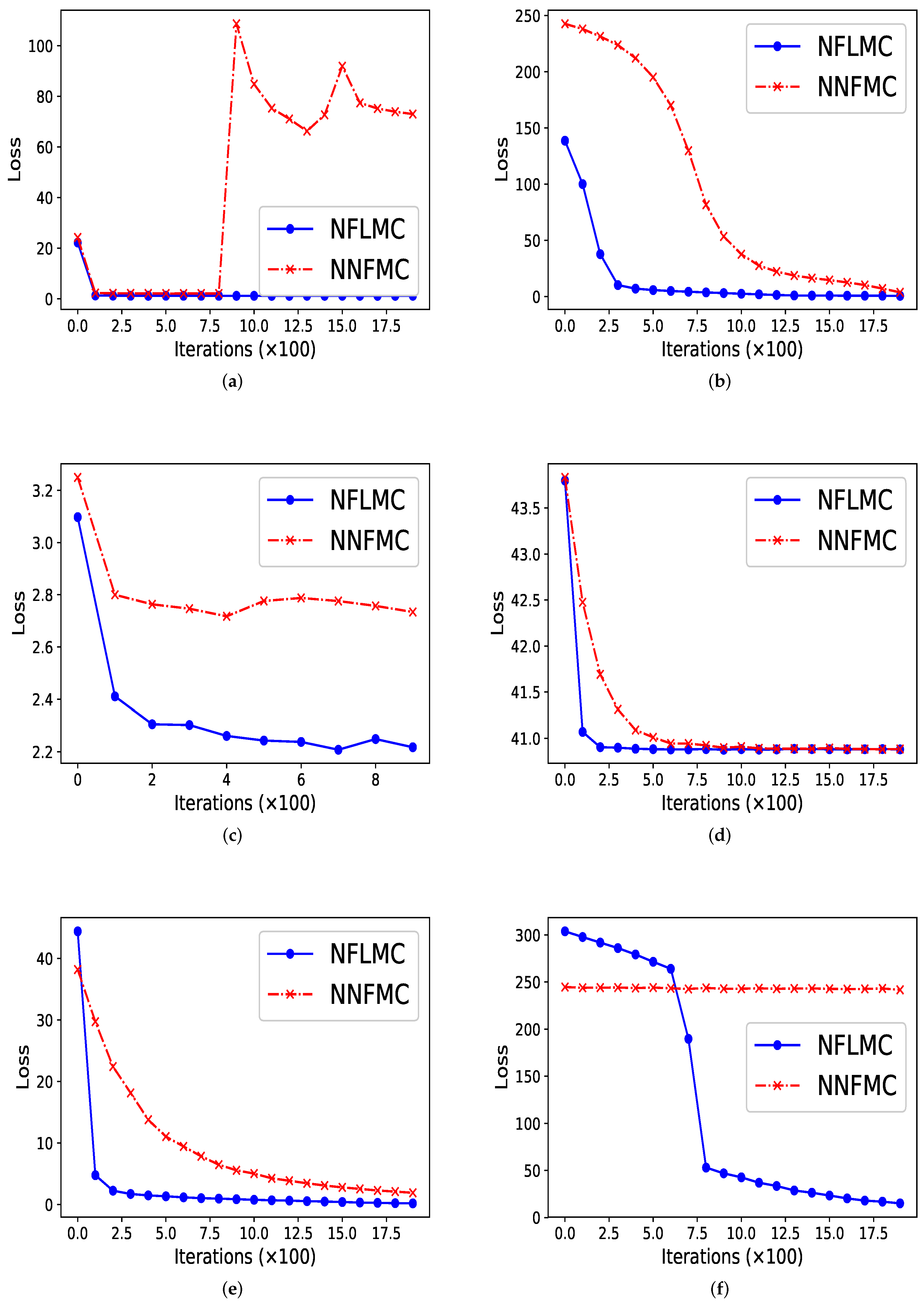
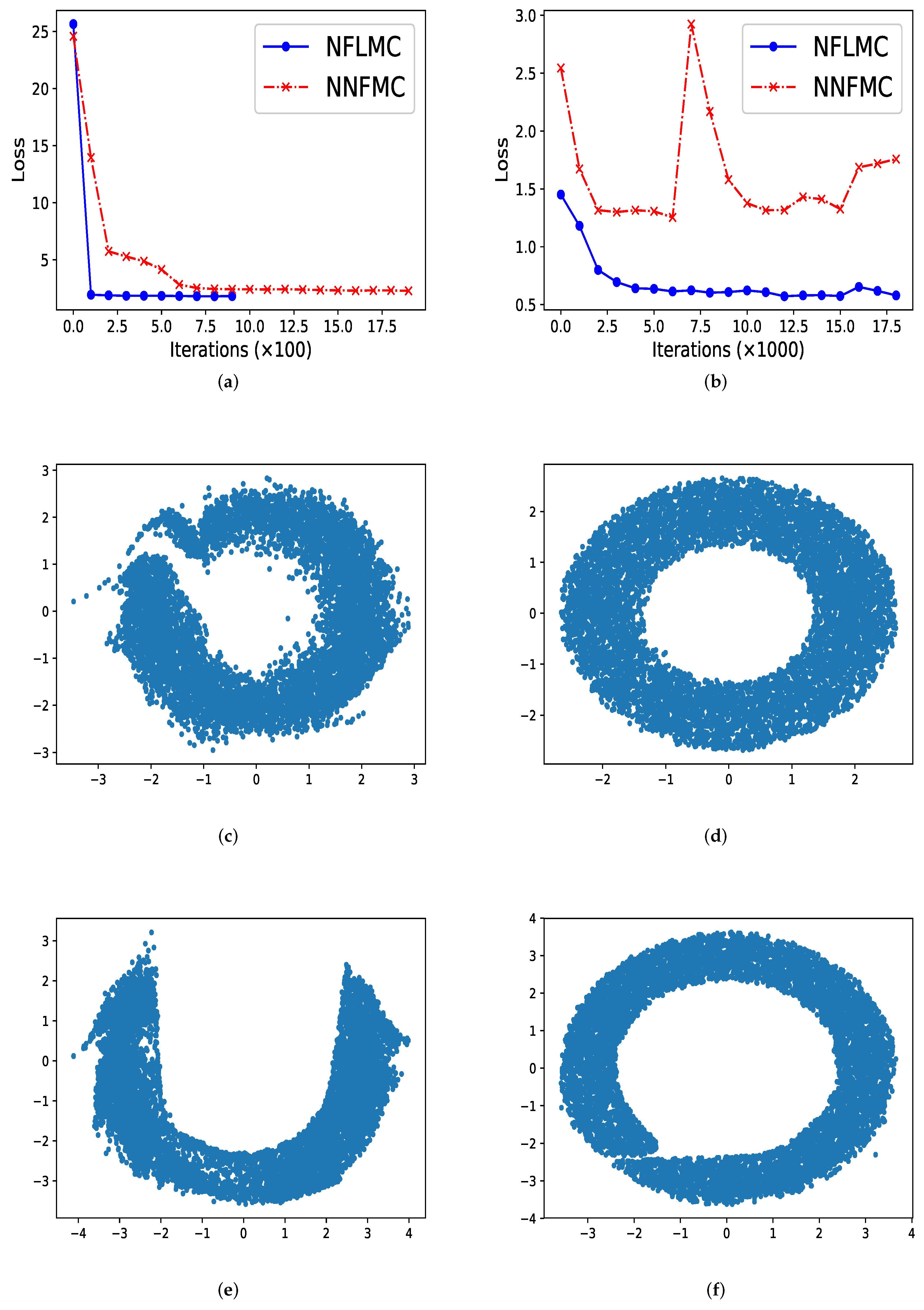
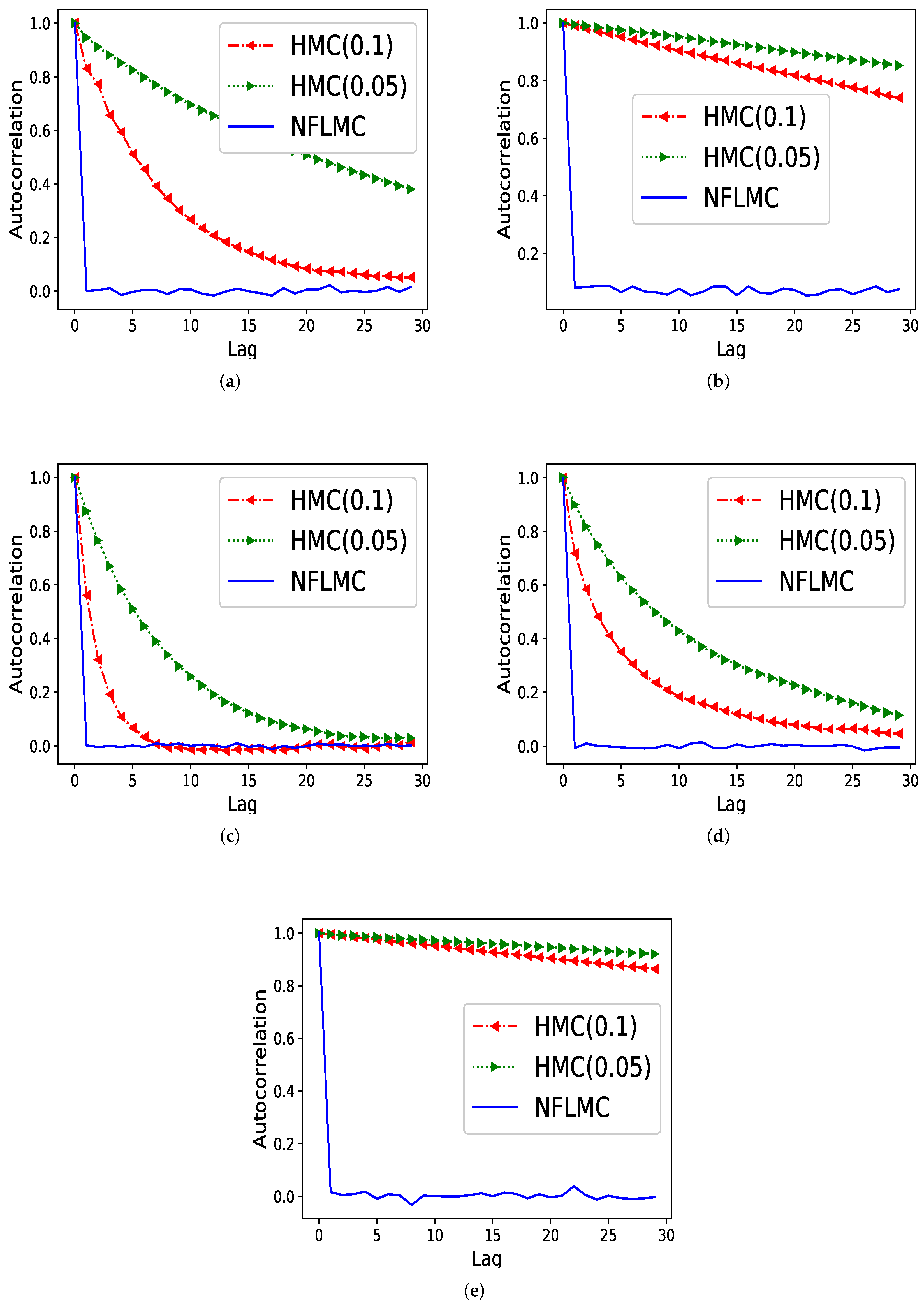
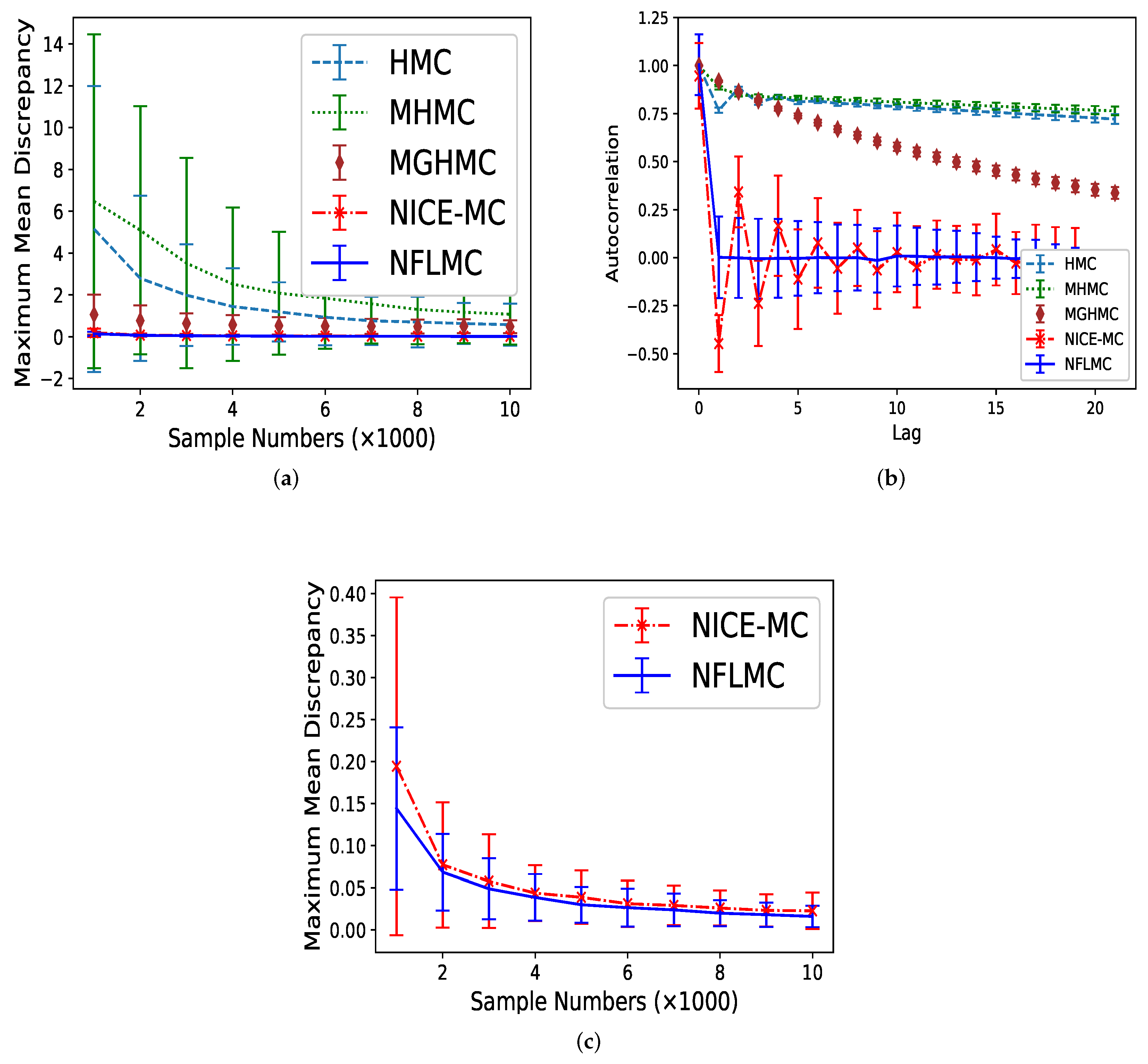
5.1. Varieties of Unimodal Distributions
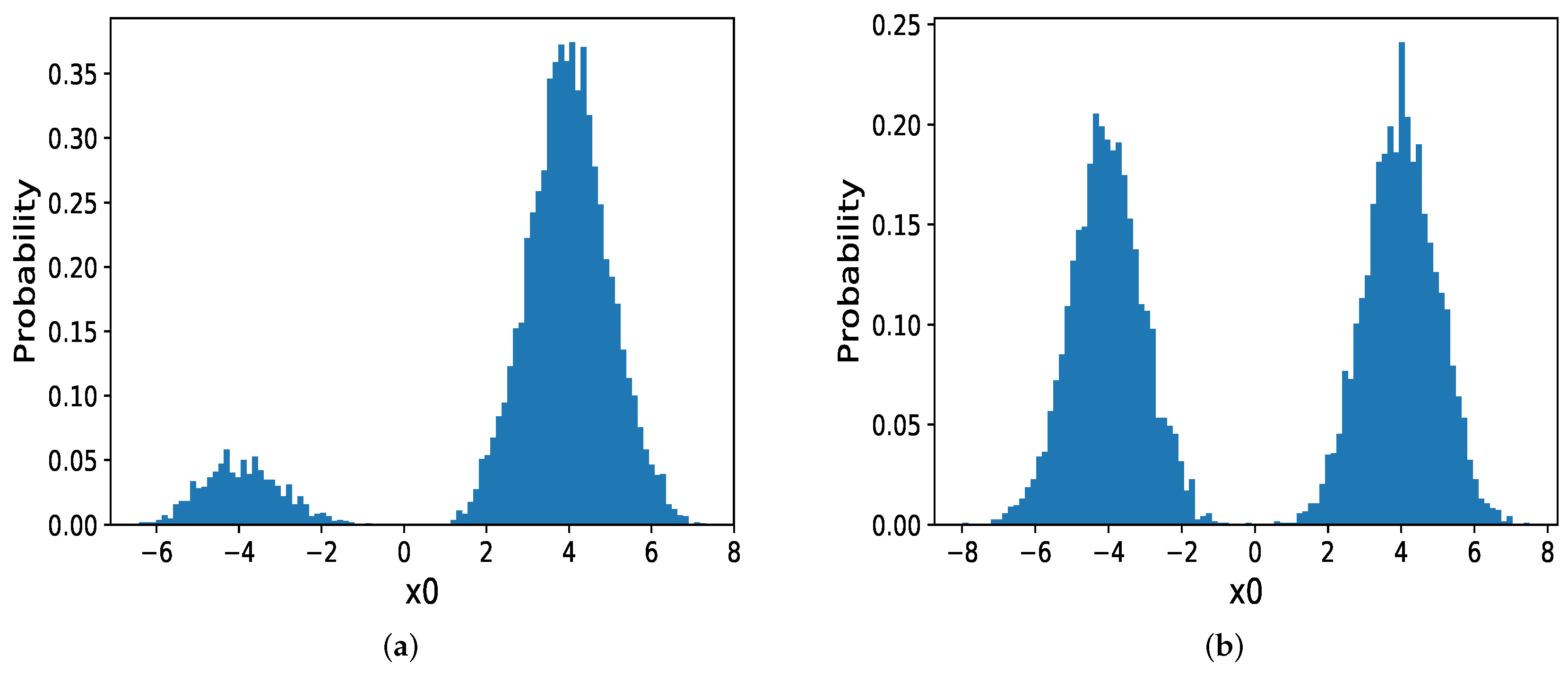
5.2. Mixtures of Gaussian Distributions
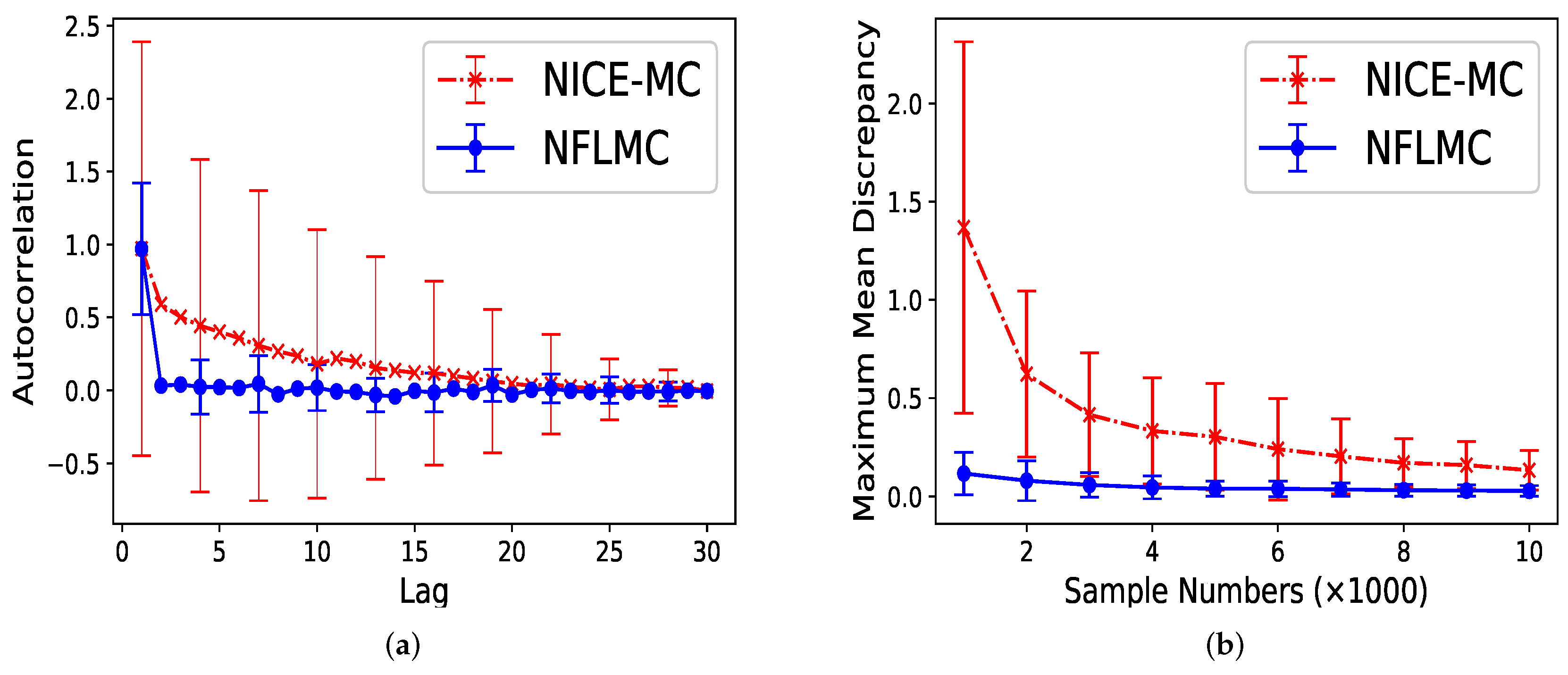
5.3. Bayesian Logistic Regression
6. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gunji, Y.P.; Murakami, H.; Tomaru, T.; Basios, V. Inverse Bayesian inference in swarming behaviour of soldier crabs. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2018, 376, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Imani, M.; Ghoreishi, S.F.; Allaire, D.; Braga-Neto, U.M. MFBO-SSM: Multi-fidelity Bayesian optimization for fast inference in state-space models. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27–28 January 2019; pp. 7858–7865. [Google Scholar]
- Livingstone, S.; Girolami, M. Information-geometric Markov chain Monte Carlo methods using diffusions. Entropy 2014, 16, 3074–3102. [Google Scholar] [CrossRef]
- Robert, C.P.; Casella, G. Monte Carlo Statistical Methods; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Altieri, N.; Duvenaud, D. Variational Inference with Gradient Flows. Available online: http://approximateinference.org/accepted/AltieriDuvenaud2015.pdf (accessed on 10 November 2015).
- Blei, D.; Kucukelbir, A.; McAuliffe, J. Variational inference: a review for statisticians. J. Am. Stat. Assoc. 2017, 112, 859–887. [Google Scholar] [CrossRef]
- Hock, K.; Earle, K. Markov chain Monte Carlo used in parameter inference of magnetic resonance spectra. Entropy 2016, 18, 57. [Google Scholar] [CrossRef]
- Seo, J.; Kim, Y. Approximated information analysis in Bayesian inference. Entropy 2015, 17, 1441–1451. [Google Scholar] [CrossRef]
- Imani, M.; Ghoreishi, S.F.; Braga-Neto, U.M. Bayesian control of large MDPs with unknown dynamics in data-poor environments. In Proceedings of the Advances in Neural Information Processing Systems (NIPS 2018), Montreal, QC, Canada, 3–8 December 2018; pp. 8146–8156. [Google Scholar]
- Sun, S. A review of deterministic approximate inference techniques for Bayesian machine learning. Neural Comput. Appl. 2013, 23, 2039–2050. [Google Scholar] [CrossRef]
- Neal, R.M. Slice sampling. Ann. Stat. 2003, 31, 705–741. [Google Scholar] [CrossRef]
- Li, Q.; Newton, K. Diffusion equation-assisted Markov chain Monte Carlo methods for the inverse radiative transfer equation. Entropy 2019, 21, 291. [Google Scholar] [CrossRef]
- Skeel, R.; Fang, Y. Comparing Markov chain samplers for molecular simulation. Entropy 2017, 19, 561. [Google Scholar] [CrossRef]
- Brooks, S.; Gelman, A.; Jones, G.; Meng, X. Handbook of Markov chain Monte Carlo; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Hokman, M.D.; Gelman, A. The no-u-turn sampler: Adaptively setting path lengths in Hamiltonian Monte Carlo. J. Mach. Learn. Res. 2014, 15, 1593–1623. [Google Scholar]
- Wang, Z.; Mohamed, S.; Freitas, N. Adaptive Hamiltonian and Riemann manifold Monte Carlo. In Proceedings of the International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013; pp. 1462–1470. [Google Scholar]
- Duane, S.; Kennedy, A.D.; Pendleton, B.J.; Roweth, D. Hybrid Monte Carlo. Phys. Lett. B 1987, 195, 216–222. [Google Scholar] [CrossRef]
- Celeux, G.; Hurn, M.; Robort, C.P. Computational and inferential difficulties with mixture posterior distributions. J. Am. Stat. Assoc. 2000, 95, 957–970. [Google Scholar] [CrossRef]
- Neal, R.M. Annealed importance sampling. Stat. Comput. 2001, 11, 125–139. [Google Scholar] [CrossRef]
- Rudoy, D.; Wolfe, P.J. Monte Carlo methods for multi-modal distributions. In Proceedings of the Fortieth Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 6–9 November 2006; pp. 2019–2023. [Google Scholar]
- Sminchisescu, C.; Welling, M. Generalized darting Monte Carlo. In Proceedings of the Artificial Intelligence and Statistics, San Juan, Puerto Rico, 21–24 March 2007; pp. 516–523. [Google Scholar]
- Craiu, R.V. Learn from thy neighbor: parallel-chain and regional adaptive MCMC. J. Am. Stat. Assoc. 2009, 104, 1454–1466. [Google Scholar] [CrossRef][Green Version]
- Girolami, M.; Calderhead, B. Riemann manifold Langevin and Hamiltonian Monte Carlo methods. J. R. Stat. Soc. 2011, 73, 123–214. [Google Scholar] [CrossRef]
- Tripuraneni, N.; Rowland, M.; Ghahramani, Z.; Turner, R. Magnetic Hamiltonian Monte Carlo. In Proceedings of the International Conference on Machine Learning, Sydney, NSW, Australia, 6–11 August 2017; pp. 3453–3461. [Google Scholar]
- Ahn, S.; Chen, Y.; Welling, M. Distributed and adaptive darting Monte Carlo through regenerations. In Proceedings of the Artificial Intelligence and Statistics, Scottsdale, AZ, USA, 29–30 April 2013; pp. 108–116. [Google Scholar]
- Lan, S.; Streets, J.; Shahbaba, B. Wormhole Hamiltonian Monte Carlo. In Proceedings of the AAAI Conference on Artificial Intelligence, Quebec City, QC, Canada, 27–31 July 2014; pp. 1953–1959. [Google Scholar]
- Rezende, D.; Mohamed, S. Variational inference with normalizing flows. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 1530–1538. [Google Scholar]
- Hastings, W.K. Monte Carlo sampling methods using Markov chains and their applications. Biometrika 1970, 57, 97–109. [Google Scholar] [CrossRef]
- Song, J.; Zhao, S.; Ermon, S. A-nice-mc: Adversarial training for MCMC. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 5140–5150. [Google Scholar]
- Zhang, Y.; Wang, X.; Chen, C.; Henao, R.; Fan, K.; Carin, L. Towards unifying Hamiltonian Monte Carlo and slice sampling. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 1741–1749. [Google Scholar]
- Dinh, L.; Sohl-Dickstein, J.; Bengio, S. Density estimation using real NVP. arXiv 2016, arXiv:1605.08803. [Google Scholar]
- Paige, B.; Wood, F. Inference networks for sequential Monte Carlo in graphical models. In Proceedings of the International Conference on Machine Learning, New York City, NY, USA, 19–24 June 2016; pp. 3040–3049. [Google Scholar]
- Papamakarios, G.; Murray, I. Fast ε-free inference of simulation models with Bayesian conditional density estimation. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 1028–1036. [Google Scholar]
- Ballé, J.; Laparra, V.; Simoncelli, E.P. Density modeling of images using a generalized normalization transformation. arXiv 2015, arXiv:1511.06281. [Google Scholar]
- Kingma, D.P.; Salimans, T.; Jozefowicz, R.; Chen, X.; Sutskever, I.; Welling, M. Improved variational inference with inverse autoregressive flow. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 4743–4751. [Google Scholar]
- Dinh, L.; Krueger, D.; Bengio, Y. NICE: Non-linear independent components estimation. arXiv 2014, arXiv:1410.8516. [Google Scholar]
- Oord, A.V.D.; Dieleman, S.; Zen, H.; Simonyan, K.; Vinyals, O.; Graves, A.; Kalchbrenner, N.; Senior, A.; Kavukcuoglu, K. Wavenet: A generative model for raw audio. arXiv 2016, arXiv:1609.03499. [Google Scholar]
- Durrett, R. Stochastic Calculus: A Practical Introduction; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Øksendal, B. Stochastic differential equations. In Stochastic Differential Equations; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Roberts, G.O.; Stramer, O. Langevin diffusions and Metropolis-Hastings algorithms. Methodol. Comput. Appl. Probab. 2002, 4, 337–357. [Google Scholar] [CrossRef]
- Kloeden, P.E.; Platen, E. Numerical Solution of Stochastic Differential Equations; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Martino, L.; Read, J. On the flexibility of the design of multiple try Metropolis schemes. Comput. Stat. 2013, 28, 2797–2823. [Google Scholar] [CrossRef]
- Roberts, G.O.; Stramer, O. A kernel two-sample test. J. Mach. Learn. Res. 2012, 13, 723–773. [Google Scholar]
- Sohl-Dickstein, J.; Mudigonda, M.; DeWeese, M.R. Hamiltonian Monte Carlo without detailed balance. In Proceedings of the International Conference on Machine Learning, Beijing, China, 21–26 June 2014; pp. 719–726. [Google Scholar]
- Livingstone, S.; Betancourt, M.; Byrne, S.; Girolami, M. On the geometric ergodicity of Hamiltonian Monte Carlo. arXiv 2016, arXiv:1601.08057. [Google Scholar] [CrossRef]
- Freedman, D.A. Statistical Models: Theory and Practice; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- MacKay, D.J.C. The evidence framework applied to classification networks. Neural Comput. 1992, 4, 720–736. [Google Scholar] [CrossRef]
- Dua, D.M.; Graff, C. UCI Machine Learning Repository. 2017. Available online: https://archive.ics.uci.edu/ml/index.php (accessed on 10 November 2017).
- Hanley, J.A.; McNeil, B.J. A method of comparing the areas under receiver operating characteristic curves derived from the same cases. Radiology 1983, 148, 839–843. [Google Scholar] [CrossRef] [PubMed]
| Data | LR | VBLR | HMC | NFLMC |
|---|---|---|---|---|
| Ha | 69.3 ± 0.2 | 69.3 ± 0.1 | 69.3 ± 0.2 | 69.4 ± 0.1 |
| Pi | 76.6 ± 0.2 | 76.2 ± 0.1 | 76.6 ± 0.1 | 76.6± 0.1 |
| Ma | 82.5 ± 0.3 | 83.1 ± 0.1 | 83.1 ± 0.1 | 83.1 ± 0.2 |
| Bl | 76.0 ± 0.2 | 76.0 ± 0.2 | 76.0 ± 0.3 | 76.0 ± 0.1 |
| Im | 77.7 ± 0.3 | 77.75 ± 0.4 | 83.2 ± 0.2 | 83.3 ± 0.2 |
| In | 75.8 ± 0.3 | 73.2 ± 0.2 | 73.2 ± 0.2 | 74.1 ± 0.2 |
| He | 75.9 ± 0.2 | 75.9 ± 0.2 | 75.9 ± 0.2 | 75.9 ± 0.1 |
| Ge | 71.5 ± 0.1 | 71.5 ± 0.1 | 72.5 ± 0.2 | 73.0 ± 0.1 |
| Au | 86.9 ± 0.2 | 87.6 ± 0.2 | 87.6 ± 0.2 | 87.7 ± 0.1 |
| Data | LR | VBLR | HMC | NFLMC |
|---|---|---|---|---|
| Ha | 62.7 ± 0.1 | 63.2 ± 0.1 | 63.0 ± 0.2 | 63.2 ± 0.1 |
| Pi | 79.2 ± 0.2 | 79.3 ± 0.1 | 79.3 ± 0.1 | 79.5 ± 0.1 |
| Ma | 89.9 ± 0.1 | 89.8 ± 0.1 | 89.89 ± 0.1 | 89.9 ± 0.2 |
| Bl | 73.5 ± 0.3 | 73.4 ± 0.3 | 74.4 ± 0.3 | 73.5 ± 0.2 |
| Im | 76.7 ± 0.3 | 78.5 ± 0.5 | 89.2 ± 0.2 | 89.3 ± 0.3 |
| In | 73.2 ± 0.3 | 73.2 ± 0.2 | 72.4 ± 0.2 | 72.8 ± 0.4 |
| He | 80.1 ± 0.2 | 81.3 ± 0.2 | 82.2 ± 0.3 | 84.8 ± 0.2 |
| Ge | 74.7 ± 0.2 | 75.5 ± 0.2 | 76.7 ± 0.3 | 76.9 ± 0.1 |
| Au | 92.5 ± 0.2 | 93.9 ± 0.2 | 93.9 ± 0.3 | 94.0 ± 0.2 |
| Data | HMC | NFLMC | Data | HMC | NFLMC |
|---|---|---|---|---|---|
| Ha | 107.69 | 2503.75 | In | 408.87 | 3590.34 |
| Pi | 73.08 | 3534.50 | He | 1093.10 | 3200.00 |
| Ma | 670.72 | 2570.69 | Ge | 7.19 | 2842.92 |
| Bl | 808.84 | 2824.87 | Au | 220.60 | 2538.25 |
| Im | 1879.78 | 1917.54 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, M.; Sun, S.; Liu, Y. Dynamical Sampling with Langevin Normalization Flows. Entropy 2019, 21, 1096. https://doi.org/10.3390/e21111096
Gu M, Sun S, Liu Y. Dynamical Sampling with Langevin Normalization Flows. Entropy. 2019; 21(11):1096. https://doi.org/10.3390/e21111096
Chicago/Turabian StyleGu, Minghao, Shiliang Sun, and Yan Liu. 2019. "Dynamical Sampling with Langevin Normalization Flows" Entropy 21, no. 11: 1096. https://doi.org/10.3390/e21111096
APA StyleGu, M., Sun, S., & Liu, Y. (2019). Dynamical Sampling with Langevin Normalization Flows. Entropy, 21(11), 1096. https://doi.org/10.3390/e21111096





