Quantification of Information Exchange in Idealized and Climate System Applications
Abstract
1. Introduction
2. Methods
2.1. Transfer Entropy
2.1.1. Estimation of TE-Binning
2.1.2. Estimation of TE-Kernel
2.1.3. Estimation of TE-K-Nearest Neighbor
2.1.4. Estimation of TE-Linear
2.1.5. Assumptions in the Practical Estimation of TE
2.2. Liang and Kleeman Information Flow
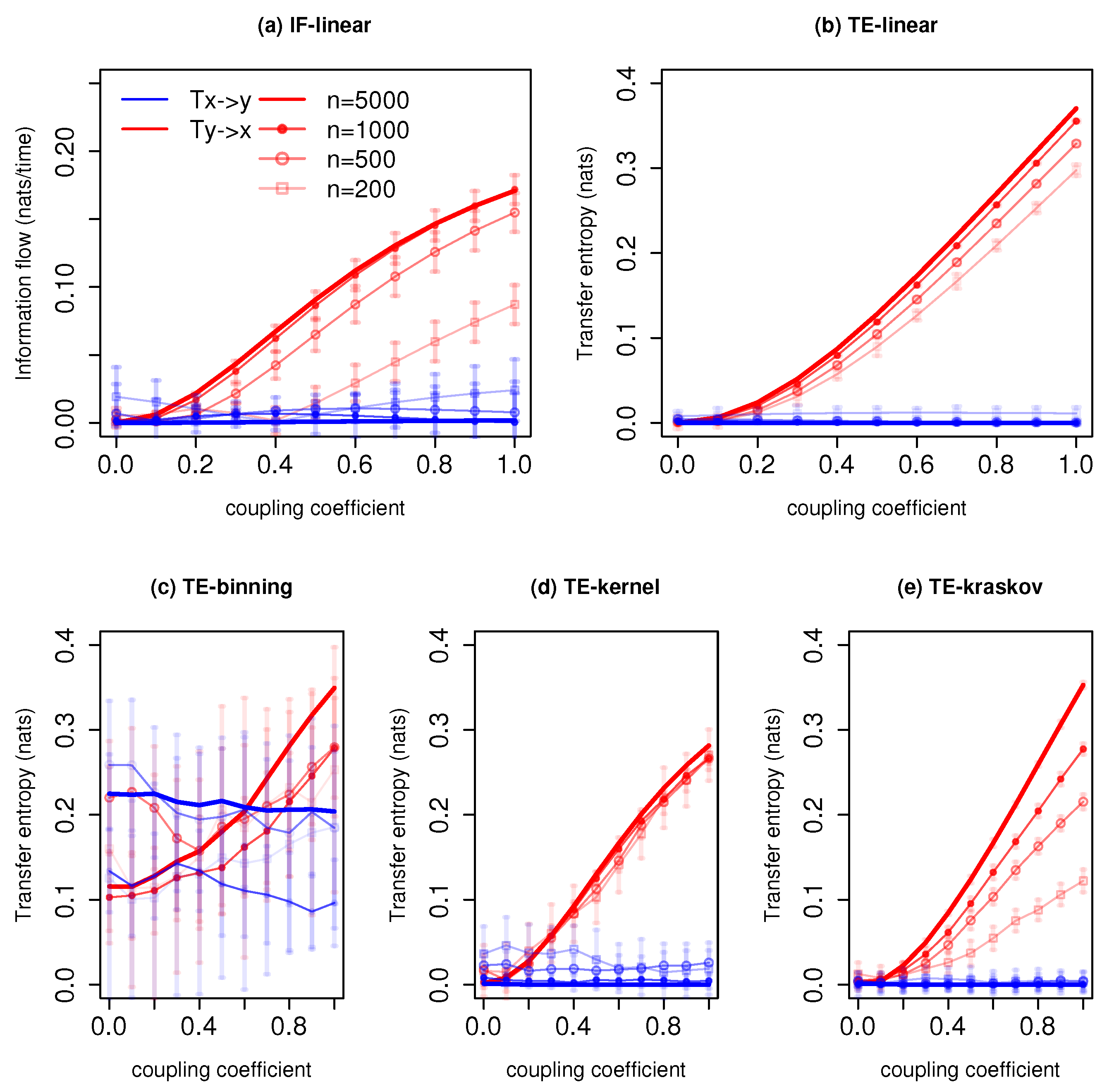
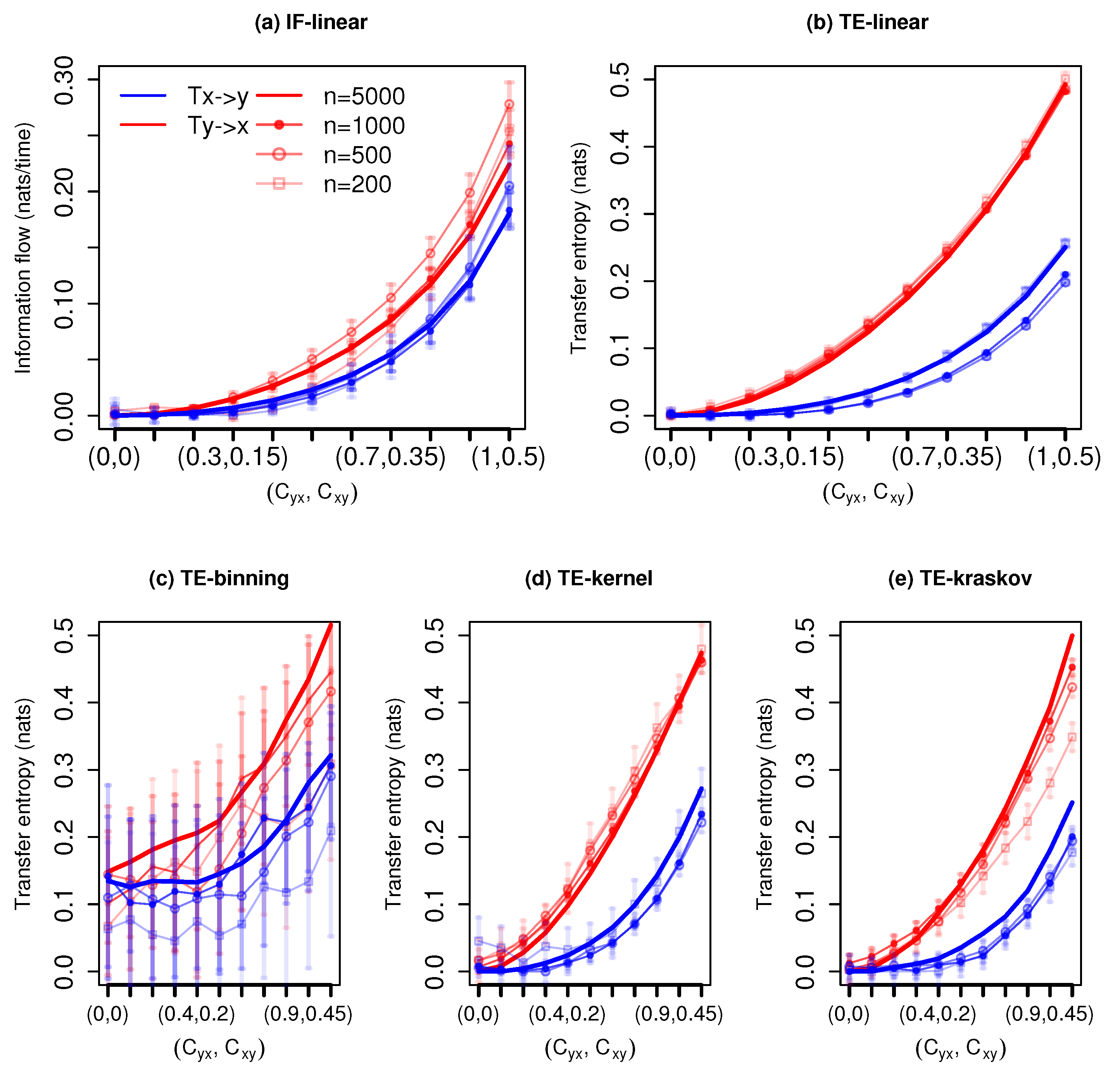
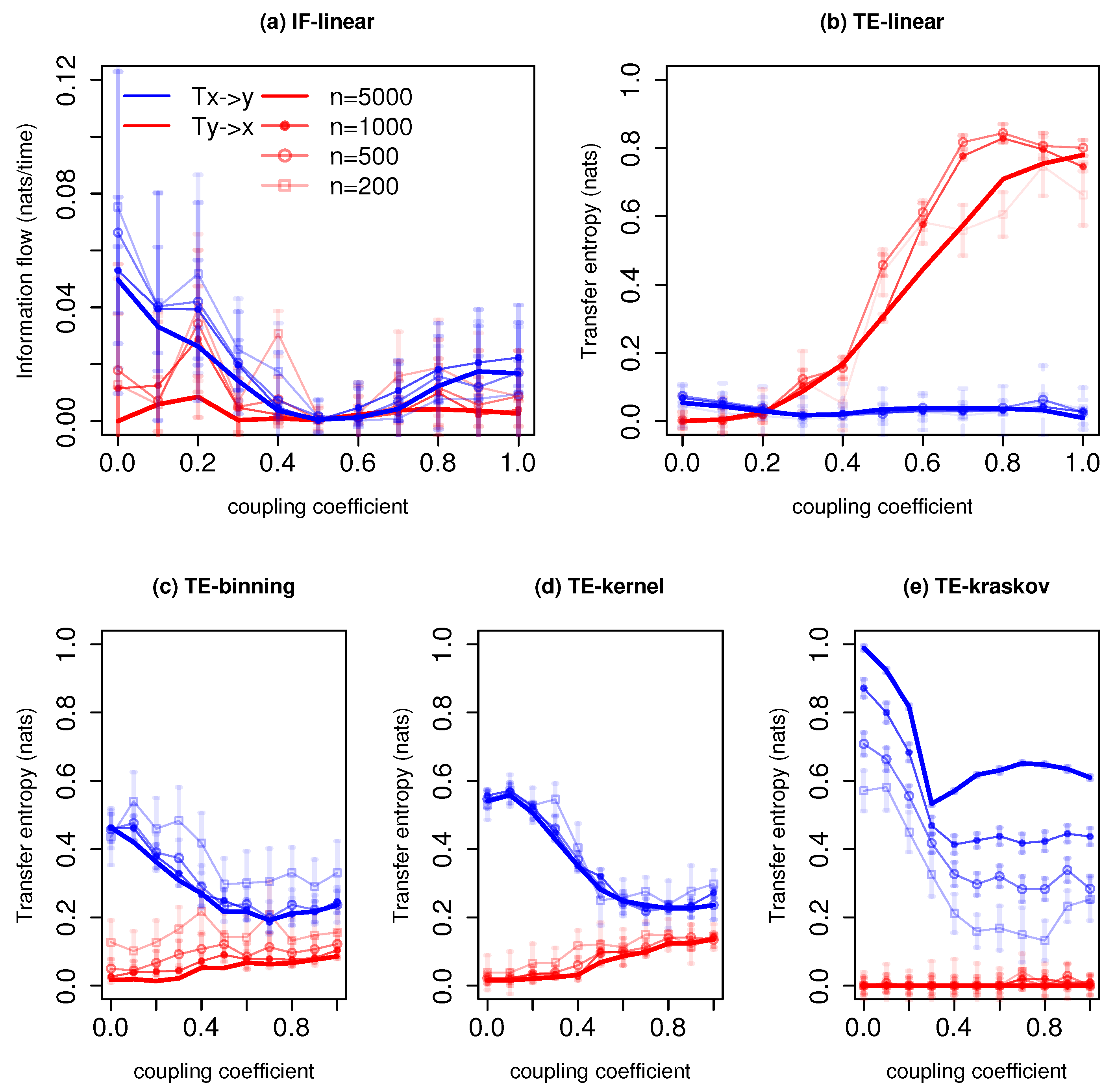
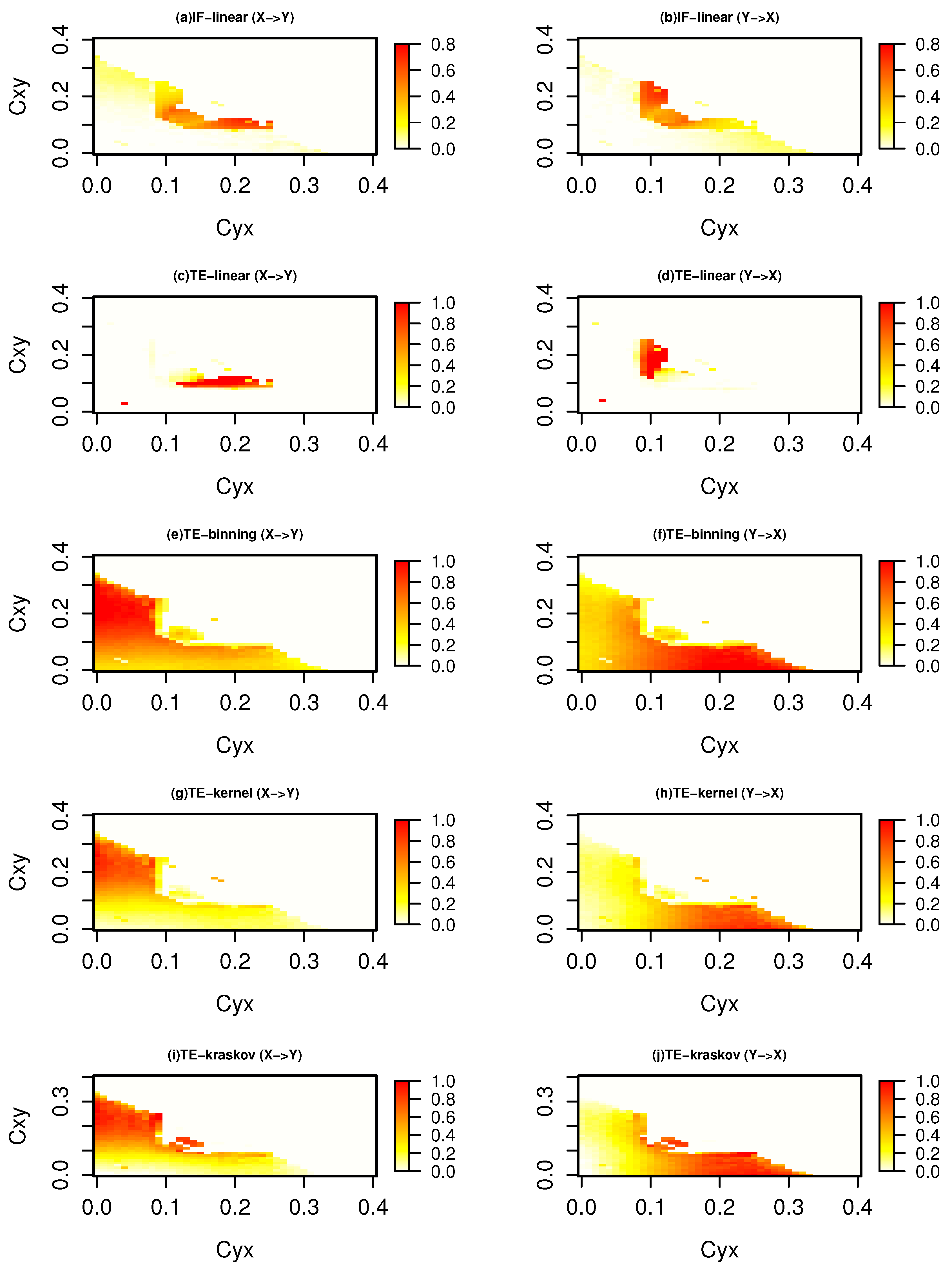
3. Results
3.1. Applications to Idealized Systems
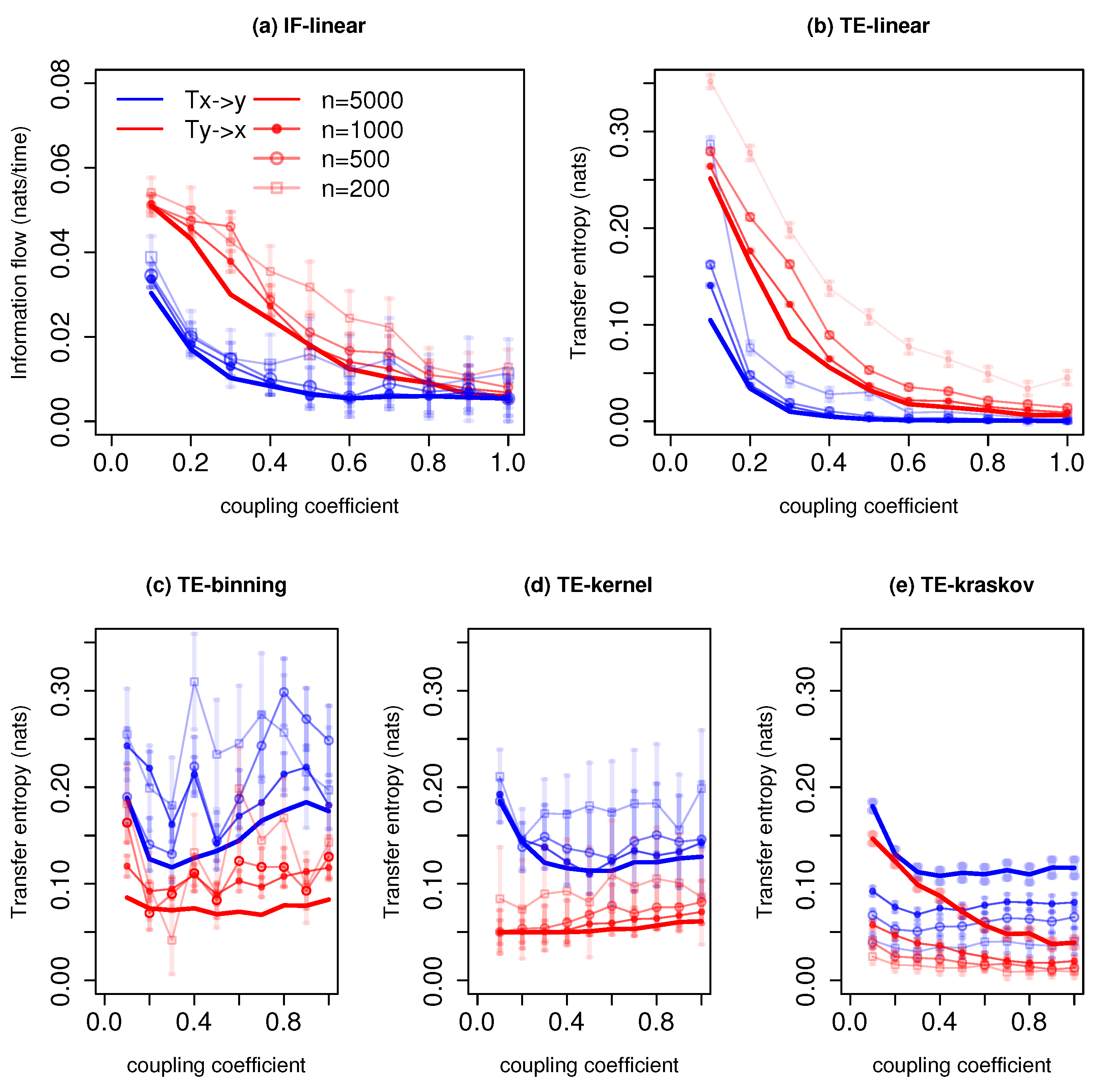
3.1.1. Unidirectional Linearly-Coupled Autoregressive System
3.1.2. Bidirectional Coupled Linear Autoregressive System
3.1.3. Nonlinear Unidirectional Coupled Anticipatory System
3.1.4. Bidirectional Coupled Non-Linear System
3.1.5. Two-Scale Lorenz-96 Model
3.2. Application to Climate Phenomena
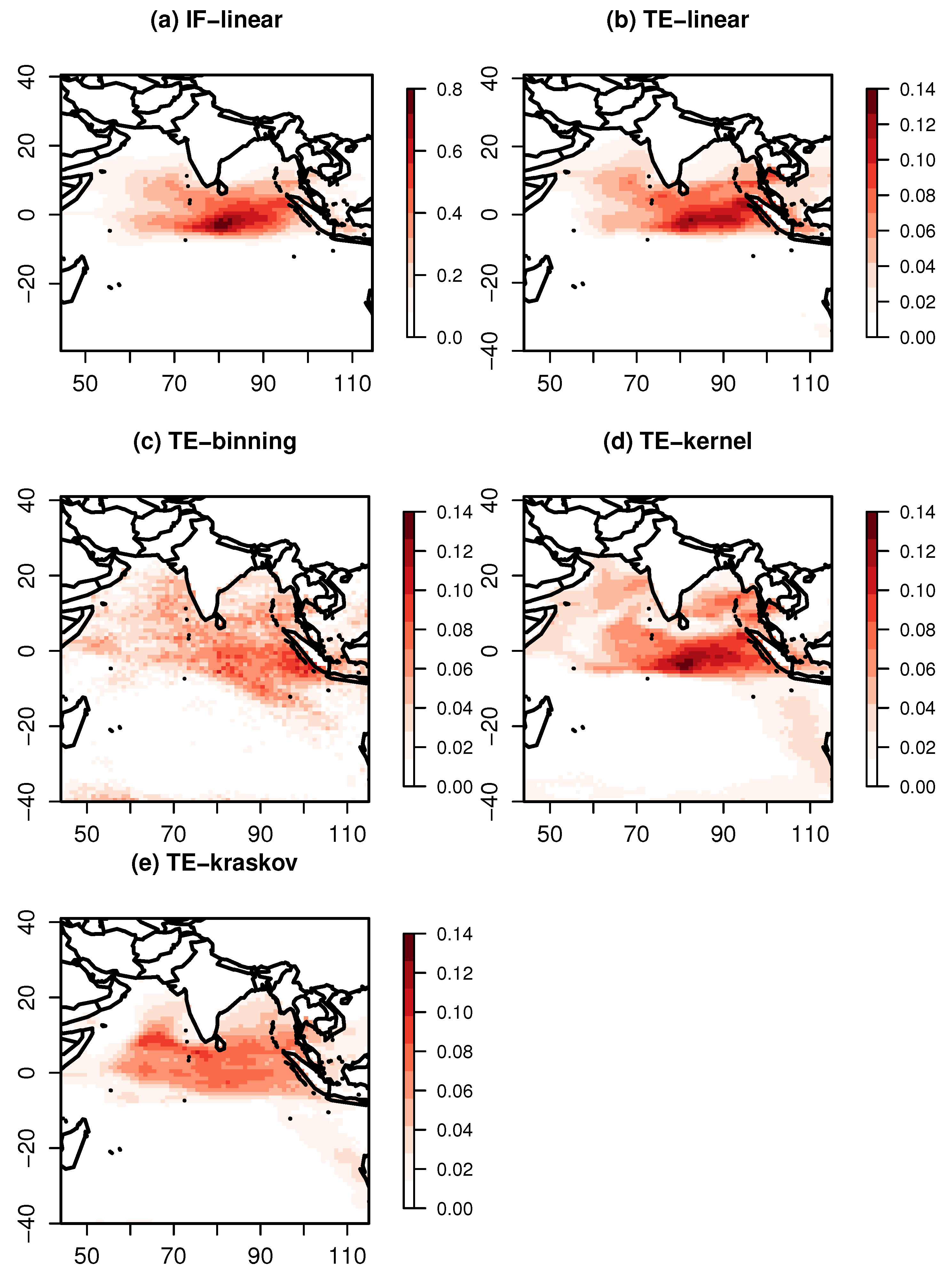
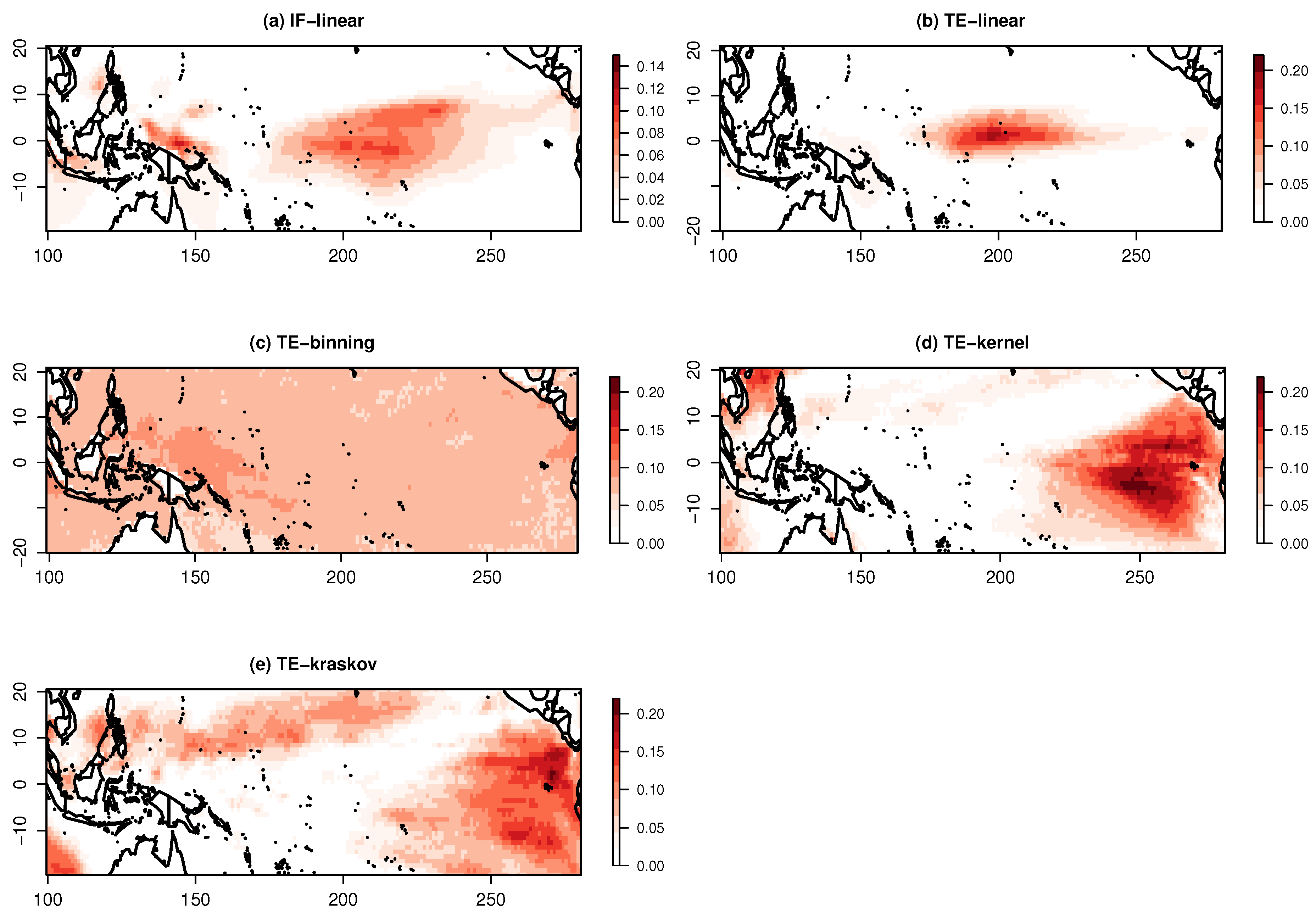
3.2.1. Information Exchange between Indian and Pacific Ocean
3.2.2. Information Exchange between Nao and European Near-Surface Temperatures
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| TE | Transfer Entropy |
| IF | Information Flow |
| MI | Mutual Information |
| CMI | Conditional Mutual Information |
| AI | Active Information storage |
| C | Coupling Coefficient |
| NAO | North Atlantic Oscillation |
| ENSO | El-Niño Southern Oscillation |
| SST | Sea Surface Temperature |
| IOD | Indian Ocean dipole |
References
- Shannon, C.E. A Mathematical Theory of Communication. Bell Labs Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Liang, X.S. Uncertainty generation in deterministic fluid flows. Dyn. Atmos. Oceans 2011, 52, 51–79. [Google Scholar] [CrossRef]
- Tödter, J.; Ahrens, B. A second-order exact ensemble square root filter for nonlinear data assimilation. Mon.Weather Rev. 2015, 143, 1347–1367. [Google Scholar] [CrossRef]
- Kirchgessner, P.; Tödter, J.; Ahrens, B.; Nerger, L. The smoother extension of the nonlinear ensemble transform filter. Dyn. Meteorol. Oceanogr. 2017, 69, 1327766. [Google Scholar] [CrossRef]
- Schelte, B.; Winterhalder, M.; Eichler, M.; Peifer, M.; Hellwig, B.; Guschlbauer, B.; Leucking, C.; Dahlhaus, R.; Timmer, J. Testing for directed influences among neural signals using partial directed coherence. J. Neurosci. Methods 2006, 152, 210–219. [Google Scholar] [CrossRef]
- Vicente, R.; Wibral, M.; Lindner, M.; Pipa, G. Transfer entropy a model free measure of effective connectivity for the neurosciences. J. Comput. Neurosci. 2011, 30, 45–67. [Google Scholar] [CrossRef]
- Stips, A.; Macias, D.; Coughlan, C.; Garcia-Gorriz, E.; Liang, X.S. On the causal structure between CO2 and global temperature. Nat. Sci. Rep. 2016, 6, 21691. [Google Scholar] [CrossRef]
- Bhaskar, A.; Ramesh, D.S.; Vichare, G.; Koganti, T.; Gurubaran, S. Quantitative assessment of drivers of recent global temperature variability: an information theoretic approach. Clim. Dyn. 2017, 49, 3877–3886. [Google Scholar] [CrossRef]
- Knuth, K.H.; Gotera, A.; Curry, C.T.; Huyser, K.A.; Wheeler, K.R.; Rossow, W.B. Revealing relationships among relevant climate variables with information theory. arXiv 2013, arXiv:1311.4632. [Google Scholar]
- Ruddell, B.L.; Kumar, P. Ecohydrologic process networks: 1. Identification. Water Resour. Res. 2009, 45, 03419. [Google Scholar] [CrossRef]
- Bennett, A.; Nijssen, B.; Gengxin, O.; Clark, M.; Nearing, G. Quantifying process connectivity with transfer entropy in hydrological models. Water Resour. Res. 2019, 55, 4613–4629. [Google Scholar] [CrossRef]
- Gerken, T.; Ruddell, B.L.; Yu, R.; Stoy, P.C.; Drewry, D.T. Robust observations of land-to-atmosphere feedbacks using the information flows of FLUXNET. npj Clim. Atmos. Sci. 2019, 2, 1–37. [Google Scholar] [CrossRef]
- Yu, R.; Ruddell, B.L.; Kang, M.; Kim, J.; Childers, D. Anticipating global terrestrial ecosystem state change using FLUXNET. Glob. Chang. Biol. 2019, 25, 2352–2367. [Google Scholar] [CrossRef] [PubMed]
- Tissot, G.; Duran, L.; Cordier, L.; Jimenez, L.; Noack, B.R. Granger causality in wall-bounded turbulence. J. Phys. 2014, 506, 012006. [Google Scholar] [CrossRef]
- Boccaletti, S.; Kurths, J.; Osipov, G.; Valladares, D.; Zhou, C. The synchronization of chaotic systems. Phys. Rep. 2002, 366, 1–101. [Google Scholar] [CrossRef]
- Ahrens, B.; Walser, A. Information based skill scores for probabilistic forecasts. Mon. Weather Rev. 2008, 136, 352–363. [Google Scholar] [CrossRef]
- Klein, S.A.; Soden, B.J.; Lau, N.C. Remote sea surface temperature variations during ENSO: Evidence for a tropical atmospheric bridge. J. Clim. 1999, 12, 917–932. [Google Scholar] [CrossRef]
- Lanzante, J.R. Lag relationships involving tropical sea surface temperatures. J. Clim. 1996, 9, 2568–2578. [Google Scholar] [CrossRef]
- Runge, J.; Petoukhov, V.; Kurth, J. Quantifying the strength and delay of climatic interactions: The ambiguities of cross correlation and a novel measure based on graphical models. J. Clim. 2014, 27, 720–739. [Google Scholar] [CrossRef]
- Granger, C.W.J. Investigating causal relations by econometric models and cross-spectral methods. Econometrica 1969, 37, 424–438. [Google Scholar] [CrossRef]
- Schreiber, T. Measuring information transfer. Phys. Rev. 2000, 85, 461–464. [Google Scholar] [CrossRef] [PubMed]
- Runge, J. Quantifying information transfer and mediation along causal pathways in complex systems. Phys. Rev. E 2015, 92, 062829. [Google Scholar] [CrossRef] [PubMed]
- Campuzano, S.A.; Santis, A.D.; Pavon–Carrasco, F.J.; Osete, M.L.; Qamili, E. Transfer Entropy between South Atlantic Anomaly and Global Sea Level for the last 300 years. Nat. Hazards Earth Syst. Sci. Discuss. 2016. [Google Scholar] [CrossRef]
- Liang, X.S.; Kleeman, R. Information transfer between dynamical system components. Phys. Rev. Lett. 2005, 95, 244101. [Google Scholar] [CrossRef] [PubMed]
- Liang, X.S. Information flow and causality as rigorous notions ab initio. Phys. Rev. E 2016, 94, 052201. [Google Scholar] [CrossRef] [PubMed]
- Liang, X.S. Unraveling the cause–effect relation between time series. Phys. Rev. E 2014, 90, 052150. [Google Scholar] [CrossRef]
- Vaid, B.H.; Liang, X.S. The changing relationship between the convection over the western Tibetan Plateau and the sea surface temperature in the northern Bay of Bengal. Tellus A Dyn. Meteorol. Oceanogr. 2018, 70, 1440869. [Google Scholar] [CrossRef]
- Bai, C.; Zhang, R.; Bao, S.; Liang, X.S.; Guo, W. Forecasting the tropical cyclone genesis over the northwest Pacific through identifying the causal factors in the cyclone–climate Interactions. J. Atmos. Ocean. Technol. 2017, 35, 247–259. [Google Scholar] [CrossRef]
- Lorenz, E.N. Predictability-a problem partly solved. In Proceedings of the ECMWF Seminar Predictability; ECMWF: Reading, UK, 1996; Volume I, pp. 1–19. [Google Scholar]
- Runge, J. Causal network reconstruction from time series: From theoretical assumptions to practical estimation. Chaos 2018, 28, 075310. [Google Scholar] [CrossRef]
- Wibral, M.; Pampu, N.; Priesemann, V.; Siebenhuehner, F.; Seiwert, H.; Lindner, M.; Lizier J, T.; Vicente, R. Measuring Information-Transfer Delays. PLoS ONE 2013, 8. [Google Scholar] [CrossRef]
- Wollstadt, P.; Sellers, K.K.; Rudelt, L.; Priesemann, V.; Hutt, A.; Frohlich, F.; Wibral, M. Breakdown of local information processing may underlie isoflurane anesthesia effects. PLoS Comput. Biol. 2017, 13, e1005511. [Google Scholar] [CrossRef] [PubMed]
- Scott, D.W. On optimal and data-based histograms. Biometrika 1979, 66, 605–610. [Google Scholar] [CrossRef]
- Freedman, D.; Diaconis, P. On the histogram as a density estimator: L2 theory Probab. Theory Relat. Fields 1981, 57, 453–476. [Google Scholar] [CrossRef]
- Kang, M.; Ruddell, B.L.; Cho, C.; Chun, C.; Kim, J. Identifying CO2 advection on a hill slope using information flow. Agric. For. Meteorol. 2017, 232, 265–278. [Google Scholar] [CrossRef]
- Ruddell, B.L.; Kumar, P. Ecohydrologic process networks: 2. Analysis and characterization. Water Resour. Res. 2009, 45, 03420. [Google Scholar] [CrossRef]
- Gencaga, D.; Knuth, K.H.; Rossow, W.B. A Recipe for the estimation of information flow in a dynamical system. Entropy 2015, 17, 438–470. [Google Scholar] [CrossRef]
- Kantz, H.; Schreiber, T. Nonlinear Time Series Analysis; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Goodwell, A.; Kumar, P. Temporal Information Partitioning Networks (TIPNets): A process network approach to infer ecohydrologic shifts. Water Resour. Res. 2017, 53, 5899–5919. [Google Scholar] [CrossRef]
- Lizier, J.T. JIDT: an information–theoretic toolkit for studying the dynamics of complex systems. Front. Robot. AI 2014, 1, 11. [Google Scholar] [CrossRef]
- Kraskov, A.; Stögbauer, H.; Grassberger, P. Estimating mutual information. Phys. Rev. E 2004, 69, 066138. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley: New York, NY, USA, 1991. [Google Scholar]
- Liang, X.S.; Kleeman, R. A rigorous formalism of information transfer between dynamical system components. I. Discrete mapping. Phys. D 2007, 231, 1–9. [Google Scholar] [CrossRef]
- Liang, X.S. Information flow within stochastic dynamical systems. Phys. Rev. E 2008, 78, 031113. [Google Scholar] [CrossRef] [PubMed]
- Rosenblum, M.G.; Pikovsky, A.S.; Kurths, J. From phase to lag synchronization in coupled chaotic oscillators. Phys. Rev. Lett. 1997, 78, 4193. [Google Scholar] [CrossRef]
- Voss, H.U. Anticipating chaotic synchronization. Phys. Rev. E 2000, 61, 5115. [Google Scholar] [CrossRef] [PubMed]
- Scolozzi, R.; Geneletti, D. The anthroposphere as an anticipatory system: Open questions on steering the climate. Sci. Total. Environ. 2017, 579, 957–965. [Google Scholar] [CrossRef]
- Hahs, D.W.; Pethel, S.D. Distinguishing anticipation from causality: Anticipatory bias in the estimation of information flow. Phys. Rev Lett. 2011, 107, 128701. [Google Scholar] [CrossRef]
- Zhu, J.; Bellanger, J.J.; Shu, H.; Jeannès, R. Contribution to Transfer Entropy Estimation via the k -Nearest-Neighbors Approach. Entropy 2015, 17, 4173–4201. [Google Scholar] [CrossRef]
- Wiesenfeldt, M.; Parlitz, U.; Lauterborn, W. Mixed state analysis of multivariate time series. Int. J. Bifurc. Chaos 2001, 11, 2217–2226. [Google Scholar] [CrossRef]
- Lungarella, M.; Ishiguro, K.; Kuniyoshi, Y.; Otsu, N. Methods for quantifying the causal structure of bivariate time series. Int. J. Bifurcat. Chaos. 2007, 17, 903–921. [Google Scholar] [CrossRef]
- Herrera, S.; Fernàndez, J.; Rodrìguez, M.A.; Gutièrrez, J.M. Spatio-temporal error growth in the multi-scale Lorenz’96 model. Nonlin. Process. Geophys. 2010, 17, 329–337. [Google Scholar] [CrossRef]
- Lau, N.C.; Nath, M.J. The role of the atmospheric bridge in linking tropical Pacific ENSO events to extratropical SST anomalies. J. Clim. 1996, 9, 2036–2057. [Google Scholar] [CrossRef]
- Ashok, K.; Guan, Z.; Yamagata, T. A Look at the relationship between the ENSO and the Indian Ocean Dipole. J. Meteor. Soc. Jpn. 2003, 81, 41–56. [Google Scholar] [CrossRef]
- Ummenhofer, C.C.; England, M.; McIntosh, P.; Meyers, G.; Pook, M.; Risbey, J.; Sen Gupta, A.; Taschetto, A.S. What causes southeast Australias worst droughts? Geophys. Res. Lett. 2009, 36, L04706. [Google Scholar] [CrossRef]
- Cai, W.; Cowan, T. Dynamics of late autumn rainfall reduction over southeastern Australia. Geophys. Res. Lett. 2008, 35, L09708. [Google Scholar] [CrossRef]
- Hong, C.C.; Li, T.; Luo, J.J. Asymmetry of the Indian Ocean dipole. Part 2: Model diagnosis. J. Clim. 2008, 21, 4849–4858. [Google Scholar] [CrossRef]
- Yamagata, T.; Behera, S.K.; Luo, J.J.; Masson, S.; Jury, M.R.; Rao, S.A. Coupled ocean-atmosphere variability in the tropical Indian Ocean. Earths Climate: The Ocean–Atmosphere Interaction. Am. Geophys. Union 2004, 147, 189–211. [Google Scholar] [CrossRef]
- Luo, J.J.; Zhang, R.; Behera, S.K.; Masumoto, Y.; Jin, F.F.; Lukas, R.; Yamagata, T. Interaction between El Niño and extreme Indian Ocean dipole. J. Clim. 2010, 23, 726–742. [Google Scholar] [CrossRef]
- Meyers, G.; McIntosh, P.; Pigot, L.; Pook, M. The years of El Niño, La Niña, and interactions with the tropical Indian Ocean. J. Clim. 2007, 20, 2872–2880. [Google Scholar] [CrossRef]
- Fischer, A.S.; Terray, P.; Guilyardi, E.; Gualdi, S.; Delecluse, P. Two independent triggers for the Indian Ocean dipole zonal mode in a coupled GCM. J. Clim. 2005, 18, 3428–3449. [Google Scholar] [CrossRef]
- Saji, N.H.; Goswami, B.N.; Vinayachandran, P.N.; Yamagata, T. A dipole mode in the tropical Indian Ocean. Nature 1999, 401, 360–363. [Google Scholar] [CrossRef]
- Ashok, K.; Guan, Z.; Yamagata, T. Impact of the Indian Ocean dipole on the relationship between the Indian monsoon rainfall and ENSO. Geophys. Res. Lett. 2001, 28, 4499–4502. [Google Scholar] [CrossRef]
- Annamalai, H.; Xie, S.P.; McCreary, J.P.; Murtugudde, R. Impact of Indian Ocean sea surface temperature on developing El Niño. J. Clim. 2005, 18, 302–319. [Google Scholar] [CrossRef]
- Wollstadt, P.; Martınez Zarzuela, M.; Vicente, R.; Dıaz-Pernas, F.J.; Wibral, M. Efficient Transfer Entropy Analysis of Non-Stationary Neural Time Series. PLoS ONE 2014, 9, 7–e102833. [Google Scholar] [CrossRef] [PubMed]
- Hirahara, S.; Ishii, M.; Fukuda, Y. Centennial-scale sea surface temperature analysis and its uncertainty. J. Clim. 2014, 27, 57–75. [Google Scholar] [CrossRef]
- Ueda, H.; Matsumoto, J. A possible triggering process of east–west asymmetric anomalies over the Indian Ocean in relation to 1997/98 El Niño. J. Meteor. Soc. Jpn. 2001, 8, 803–818. [Google Scholar] [CrossRef]
- Behera, S.K.; Yamagata, T. Influence of the Indian Ocean dipole on the Southern Oscillation. J. Meteor. Soc. Jpn. 2003, 81, 169–177. [Google Scholar] [CrossRef]
- Barnston, A.G.; Livezey, R.E. Classification, seasonality and persistence of low-frequency atmospheric circulation patterns. Mon. Weather Rev. 1987, 115, 1083–1126. [Google Scholar] [CrossRef]
- Papadimas, C.D.; Bartzokas, A.; Lolis, C.J.; Hatzianastassiou, N. Sea-level pressure-air temperature teleconnections during northern hemisphere winter. Theor. Appl. Climatol. 2012, 108, 173–189. [Google Scholar] [CrossRef]
- Trigo, R.M.; Osborn, T.J.; Corte Real, J. The North Atlantic Oscillation influence on Europe: Climate impacts and associated physical mechanisms. Clim. Res. 2002, 20, 9–17. [Google Scholar] [CrossRef]
- Gàmiz-Fortis, S.R.; Esteban-Parra, M.J.; Pozo-Vàzquez, D.; Castro-Dìez, Y. Variability of the monthly European temperature and its association with the Atlantic sea-surface temperature from interannual to multidecadal scales. Int. J. Climatol. 2011, 31, 2115–2140. [Google Scholar] [CrossRef]
- Harris, I.C.; Jones, P.D. CRU TS4.01: Climatic Research Unit (CRU) Time-Series (TS) version 4.01 of high-resolution gridded data of month–by–month variation in climate (Jan. 1901–Dec. 2016). Cent. Environ. Data Anal. 2017. [Google Scholar] [CrossRef]
- Christensen, J.H.; Carter, T.R.; Giorgi, F. PRUDENCE employs new methods to assess European climate change. EOS 2002, 83, 147. [Google Scholar] [CrossRef]
- Runge, J.; Heitzig, J.; Petoukhov, V.; Kurths, J. Escaping the curse of dimensionality in estimating multivariate transfer entropy. Phys. Rev. Lett. 2012, 108, 258701. [Google Scholar] [CrossRef] [PubMed]
- Wanner, H.; Broennimann, S.; Casty, C.; Gyalistras, D.; Luterbacher, J.; Schmutz, C.; Stephenson, D.B.; Xoplaki, E. North Atlantic Oscillation–concepts and studies. Surv. Geophys. 2001, 22, 321–382. [Google Scholar] [CrossRef]
| Method | N4 to IOD (lag=3) | IOD to N4 (lag=0) | IOD to N4 (lag=7) | Units | |
|---|---|---|---|---|---|
| IF-linear | 1.0 * | 1.2 * | 1.1 * | nats/month | |
| TE-linear | 0.7 * | 1.3 * | 1.4 * | nats | |
| TE-binning | 0.5 * | 0.9 * | 0.7 | nats | |
| TE-kernel | 0.3 * | 1.5 * | 1.6 * | nats | |
| TE-kraskov | 0.1 * | 1.1 * | 0.9 * | nats |
| Method | NAO to TS | TS to NAO | Units | Region |
|---|---|---|---|---|
| IF-linear | 0.02 | 0.09 * | nats/month | British Isles |
| TE-linear | 0.318 * | 0.314 * | nats | British Isles |
| TE-kernel | 0.4 * | 0.38 * | nats | British Isles |
| TE-kraskov | 0.3 * | 0.2 * | nats | British Isles |
| IF-linear | 0.08 * | 0.05 | nats/month | Scandinavia |
| TE-linear | 0.14 * | 0.14 * | nats | Scandinavia |
| TE-kernel | 0.24 * | 0.2 * | nats | Scandinavia |
| TE-kraskov | 0.16 * | 0.17 * | nats | Scandinavia |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pothapakula, P.K.; Primo, C.; Ahrens, B. Quantification of Information Exchange in Idealized and Climate System Applications. Entropy 2019, 21, 1094. https://doi.org/10.3390/e21111094
Pothapakula PK, Primo C, Ahrens B. Quantification of Information Exchange in Idealized and Climate System Applications. Entropy. 2019; 21(11):1094. https://doi.org/10.3390/e21111094
Chicago/Turabian StylePothapakula, Praveen Kumar, Cristina Primo, and Bodo Ahrens. 2019. "Quantification of Information Exchange in Idealized and Climate System Applications" Entropy 21, no. 11: 1094. https://doi.org/10.3390/e21111094
APA StylePothapakula, P. K., Primo, C., & Ahrens, B. (2019). Quantification of Information Exchange in Idealized and Climate System Applications. Entropy, 21(11), 1094. https://doi.org/10.3390/e21111094





