Polynomial and Wavelet-Type Transfer Function Models to Improve Fisheries’ Landing Forecasting with Exogenous Variables
Abstract
1. Introduction
2. Materials and Methods
2.1. Environmental Setting and Data
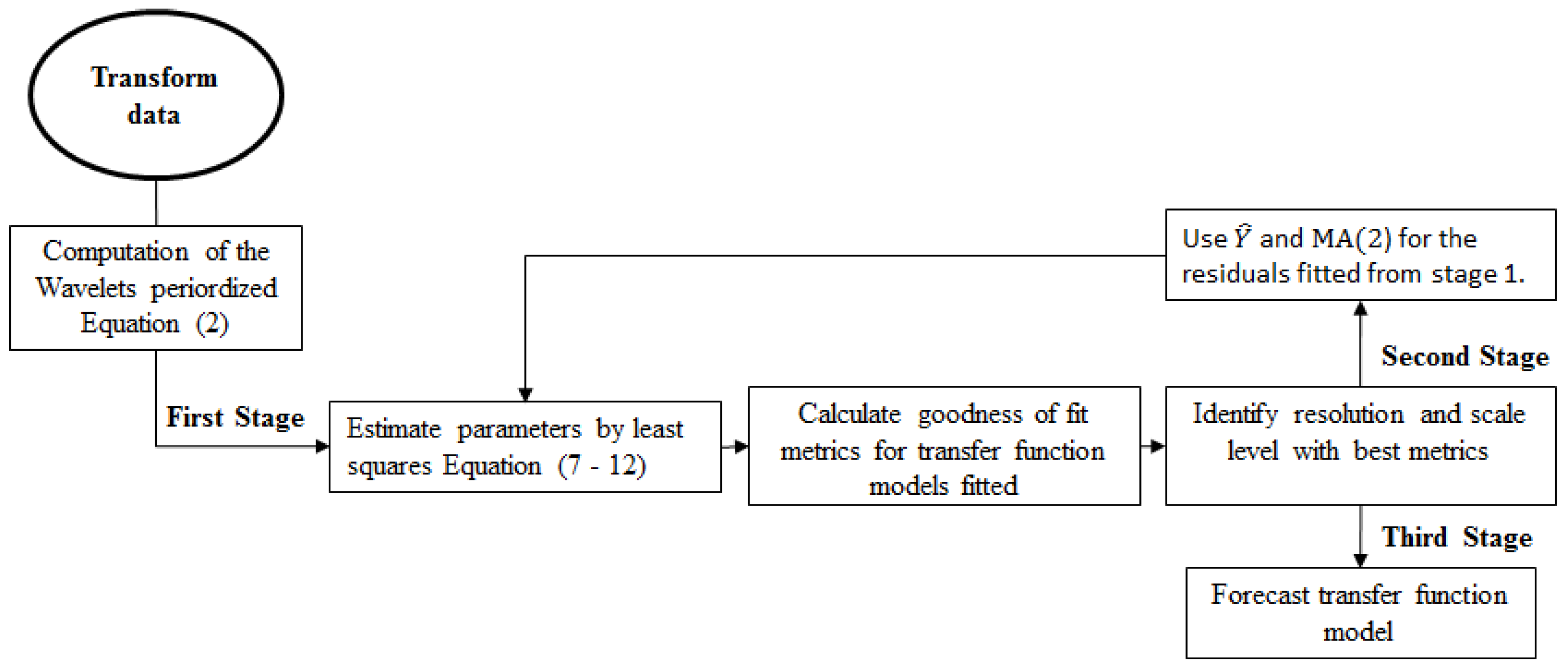
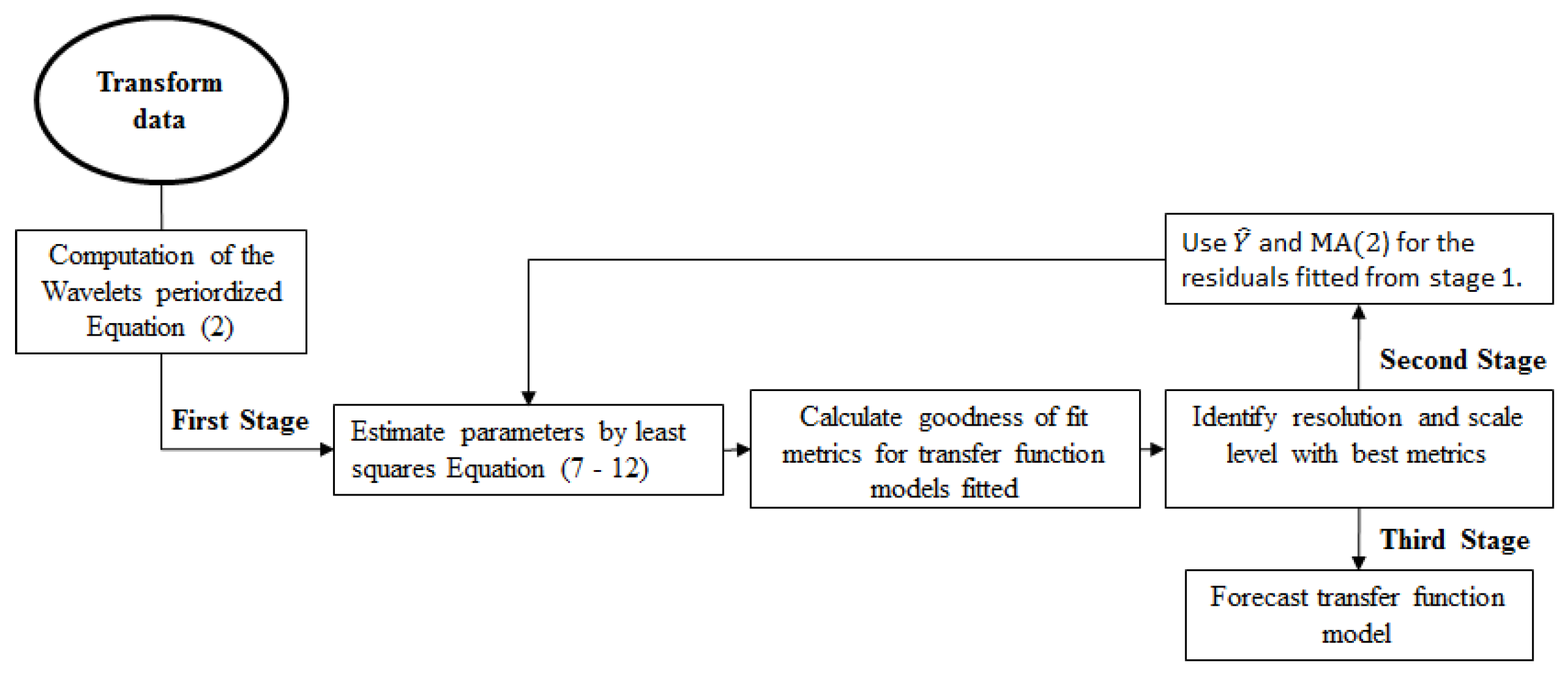
2.2. Wavelet Transfer Function Model
Estimators of Time Varying Coefficients
2.3. Polynomial Transfer Function Model
Model Validation Methods
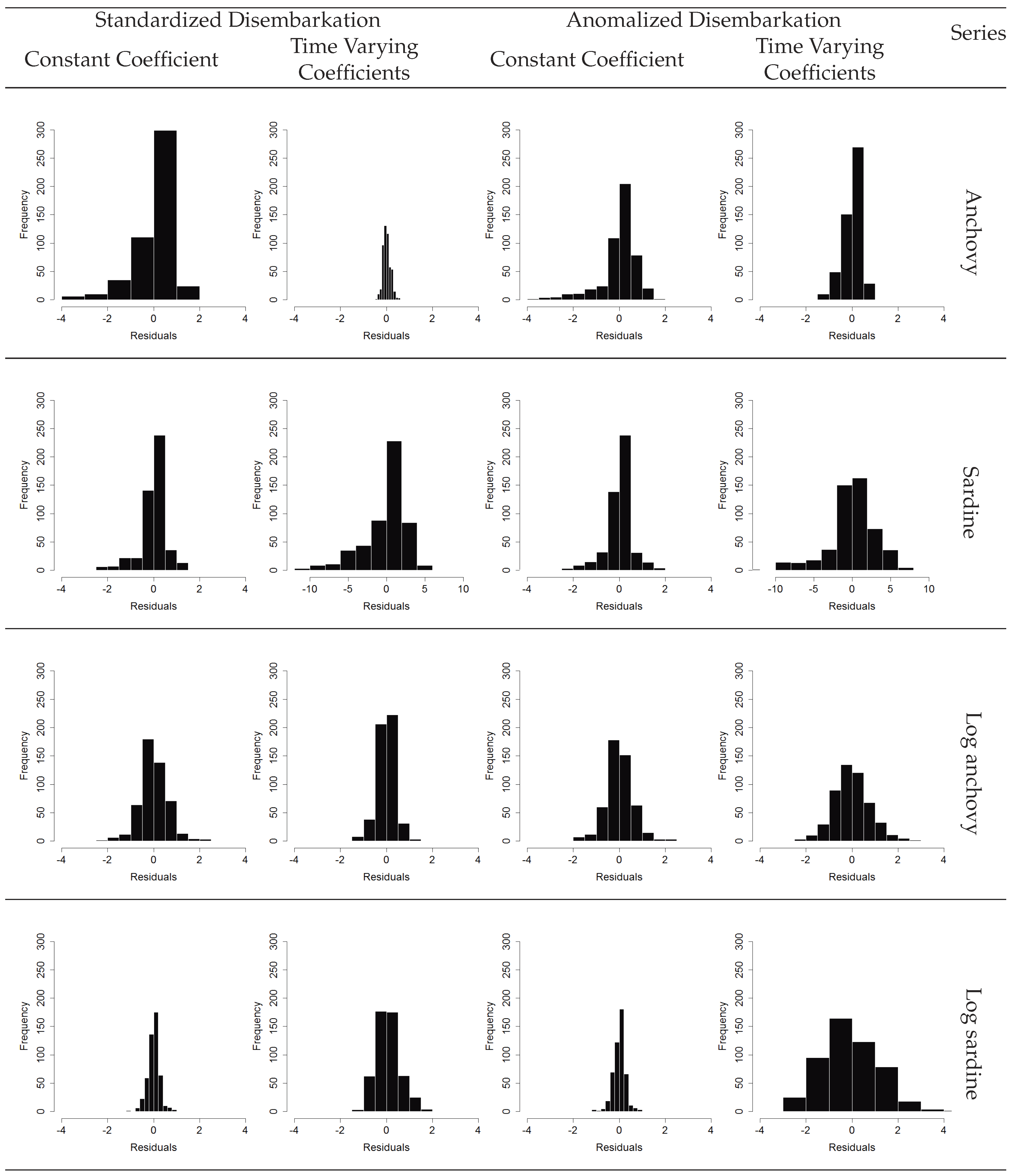
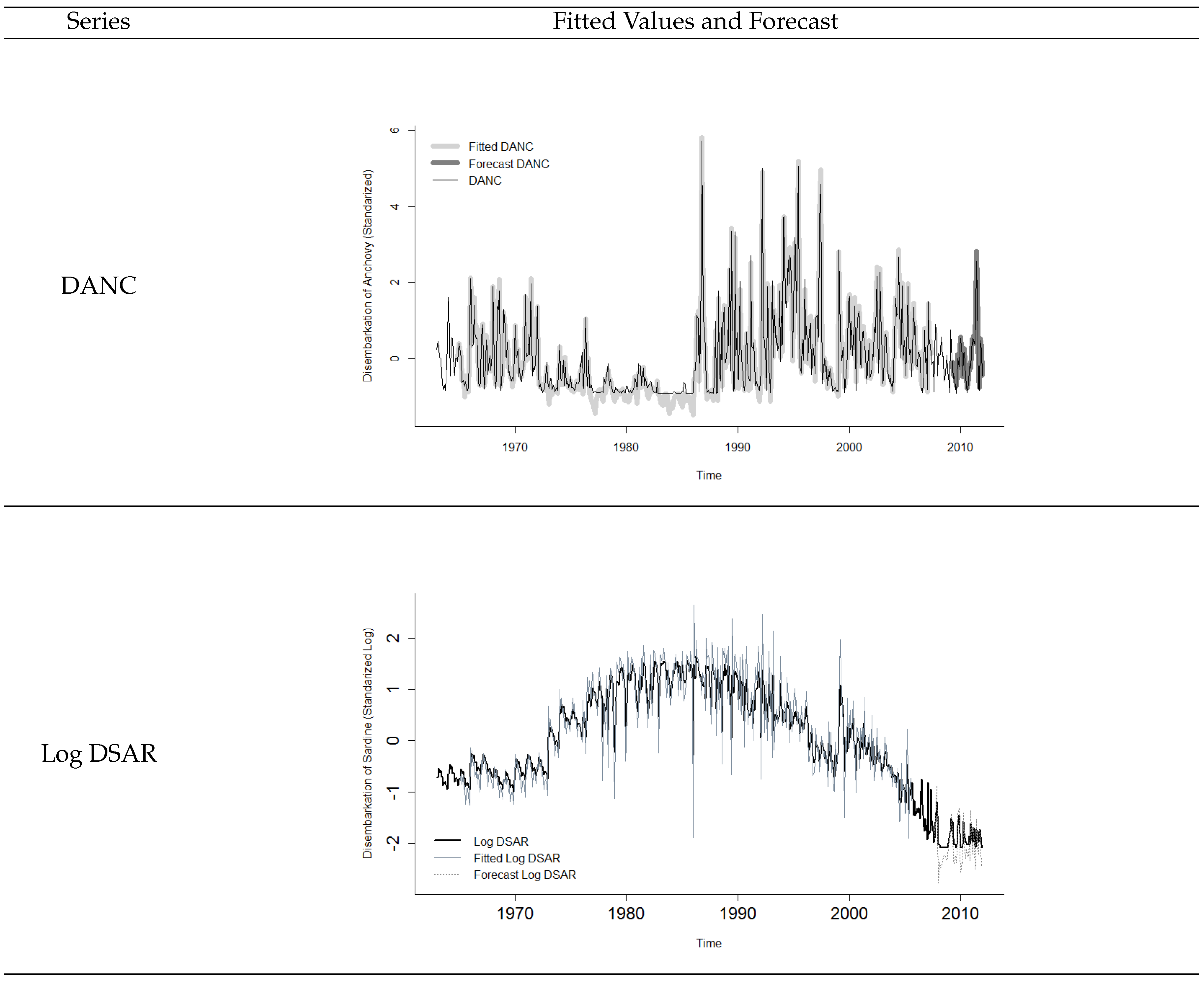
3. Results and Discussion
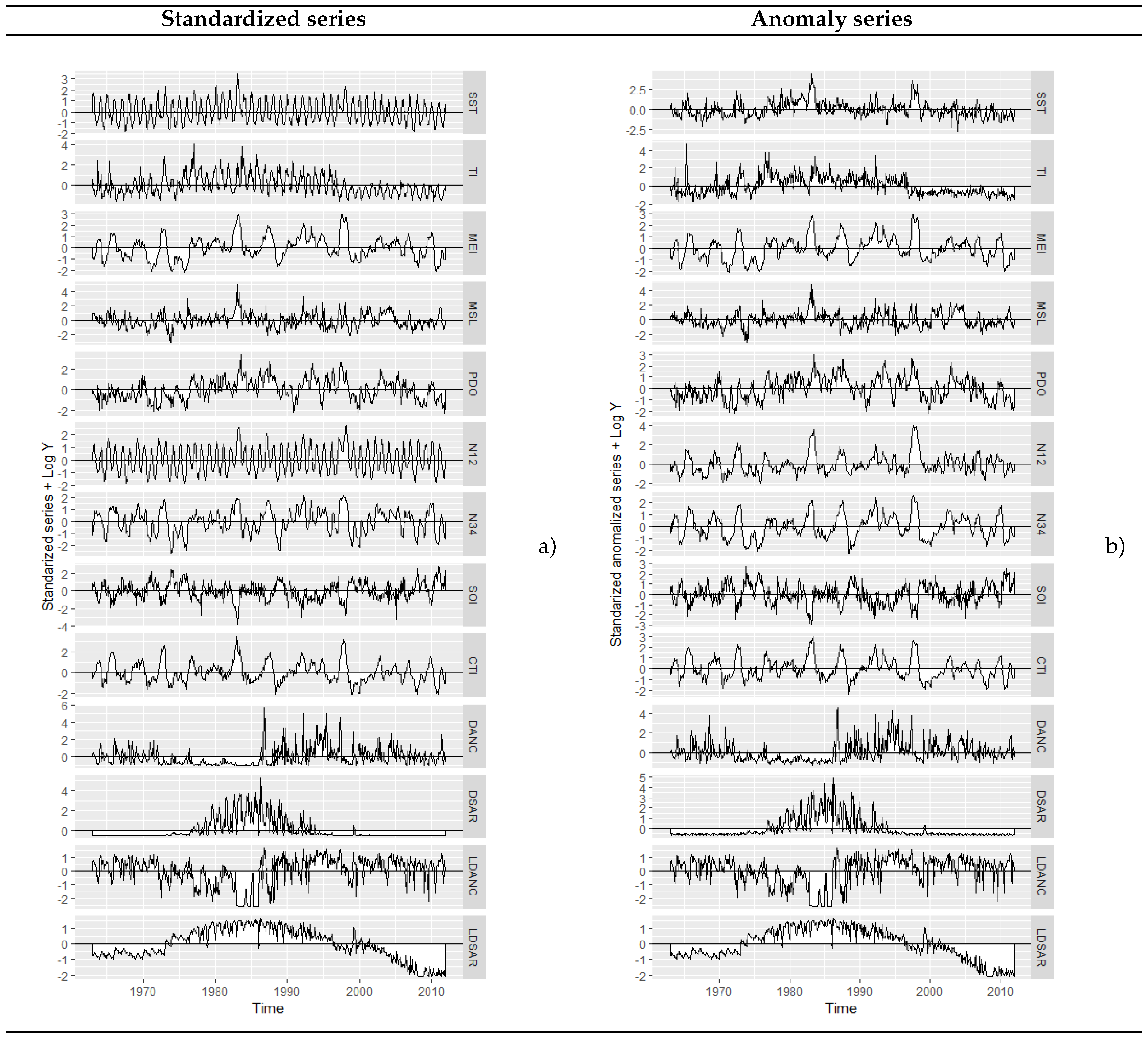
3.1. Data Analysis
3.1.1. Variable Anomaly
3.1.2. Variable Standardization
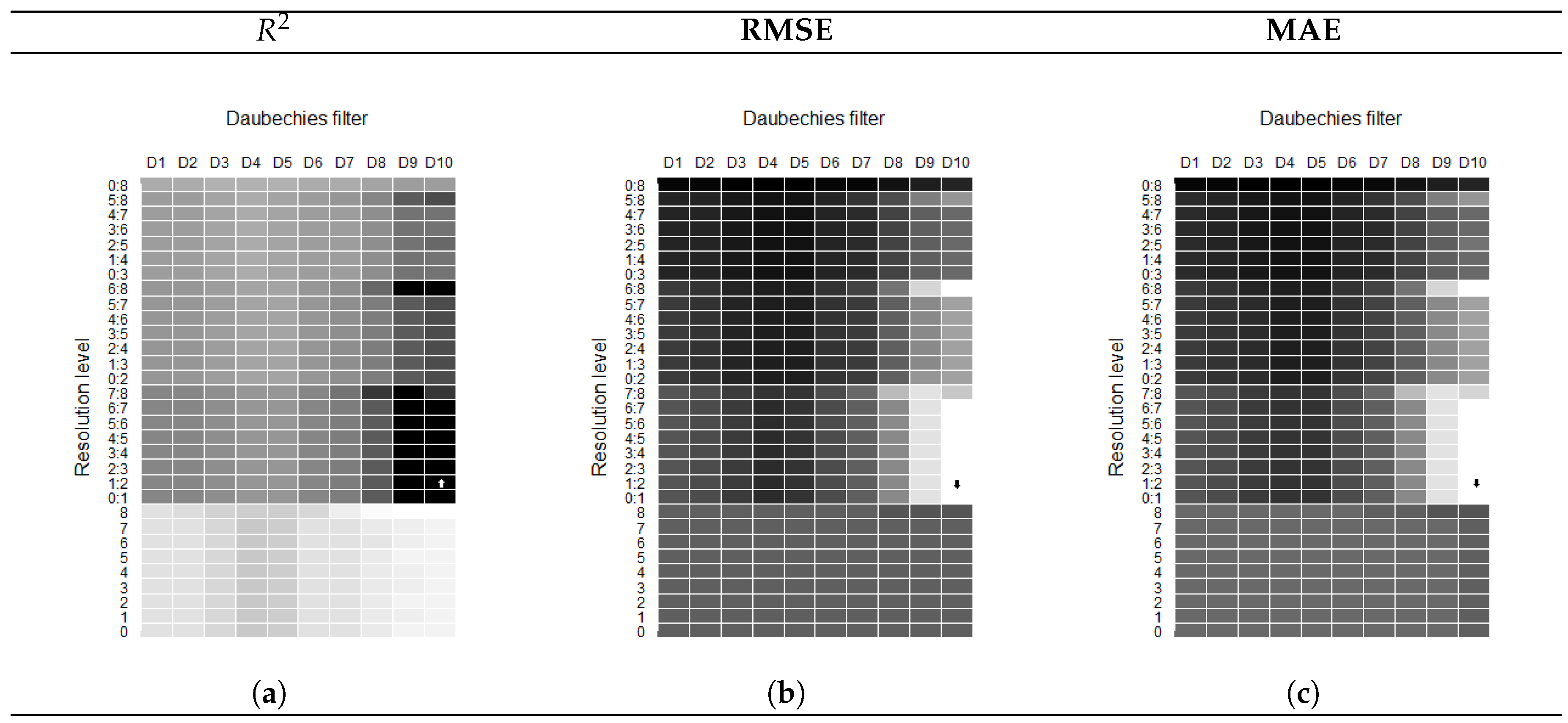
3.2. Validation Results and Time Series Predictability
Wavelet Transfer Function Models
3.3. Constant Coefficient Transfer Function Models
3.4. Comparison between Transfer Function Modeling Approaches
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lum Kong, A. Impacts of Global Climate Changes on Caribbean Fisheries Resources: Research needs. In Caribbean Food Systems: Developing a Research Agenda; Global Environmental Changeand Food Systems (GECAFS): StAugustine, Trinidad, Spain, 2002. [Google Scholar]
- Plaza, F.; Salas, R.; Yáñez, E. Identifying ecosystem patterns from time series of anchovy (Engraulis ringens) and sardine (Sardinops sagax) landings in northern Chile. J. Stat. Comput. Simul. 2018, 88, 1863–1881. [Google Scholar] [CrossRef]
- Zhou, S.; Smith, A.D.; Punt, A.E.; Richardson, A.J.; Gibbs, M.; Fulton, E.A.; Pascoe, S.; Bulman, C.; Bayliss, P.; Sainsbury, K. Ecosystem-based fisheries management requires a change to the selective fishing philosophy. Proc. Natl. Acad. Sci. USA 2010, 107, 9485–9489. [Google Scholar] [CrossRef] [PubMed]
- Silva, C.; Yáñez, E.; Barbieri, M.A.; Bernal, C.; Aranis, A. Forecasts of swordfish (Xiphias gladius) and common sardine (Strangomera bentincki) off Chile under the A2 IPCC climate change scenario. Prog. Oceanogr. 2015, 134, 343–355. [Google Scholar] [CrossRef]
- Garcia, S.M. The Ecosystem Approach to Fisheries: Issues, Terminology, Principles, Institutional Foundations, Implementation and Outlook (No. 443); Food & Agriculture Org.: Rome, Italy, 2003. [Google Scholar]
- Hiddink, J.; Ter Hofstede, R. Climate induced increases in species richness of marine fishes. Glob. Chang. Biol. 2008, 14, 453–460. [Google Scholar] [CrossRef]
- Gutiérrez-Estrada, J.C.; Silva, C.; Yáñez, E.; Rodríguez, N.; Pulido-Calvo, I. Monthly catch forecasting of anchovy Engraulis ringens in the north area of Chile: Non-linear univariate approach. Fish. Res. 2007, 86, 188–200. [Google Scholar] [CrossRef]
- Gutiérrez-Estrada, J.C.; Yáñez, E.; Pulido-Calvo, I.; Silva, C.; Plaza, F.; Bórquez, C. Pacific sardine (Sardinops sagax, Jenyns 1842) landings prediction. A neural network ecosystemic approach. Fish. Res. 2009, 100, 116–125. [Google Scholar] [CrossRef]
- Yáñez, E.; Plaza, F.; Gutiérrez-Estrada, J.C.; Rodríguez, N.; Barbieri, M.; Pulido-Calvo, I.; Bórquez, C. Anchovy (Engraulis ringens) and sardine (Sardinops sagax) abundance forecast off northern Chile: A multivariate ecosystemic neural network approach. Prog. Oceanogr. 2010, 87, 242–250. [Google Scholar] [CrossRef]
- Silva, C.; Barbieri, M.A.; Yáñez, E.; Gutiérrez-Estrada, J.C.; DelValls, T.Á. Using indicators and models for an ecosystem approach to fisheries and aquaculture management: The anchovy fishery and Pacific oyster culture in Chile: Case studies. Lat. Am. J. Aquat. Res. 2012, 40, 955–969. [Google Scholar] [CrossRef]
- Shabri, A.; Samsudin, R. Fishery landing forecasting using wavelet-based autoregressive integrated moving average models. Math. Prob. Eng. 2015, 2015. [Google Scholar] [CrossRef]
- Rodriguez, N.; Palma, W.; Yañez, E.; Rubio, J.M. Wavelet additive forecasting model to support the fisheries industry. Adv. Sci. Lett. 2013, 19, 3679–3682. [Google Scholar] [CrossRef]
- SERNAPESCA. Anuarios Estadísticos de Pesca. Servicio Nacional de Pesca, Ministerio de Economía, Fomento y Recons-trucción; Chile 1978–2012. Available online: http://ww2.sernapesca.cl/index.php?option=com_remository&Itemid=54&func=select&id=2 (accessed on 5 November 2019).
- Yáñez, E.; Barbieri, M.; Silva, C.; Nieto, K.; Espındola, F. Climate variability and pelagic fisheries in northern Chile. Prog. Oceanogr. 2001, 49, 581–596. [Google Scholar] [CrossRef]
- Yáñez, E.; Hormazábal, S.; Silva, C.; Montecinos, A.; Barbieri, M.A.; Valdenegro, A.; Órdenes, A.; Gómez, F. Coupling between the environment and the pelagic resources exploited off northern Chile: Ecosystem indicators and a conceptual model. Lat. Am. J. Aquat. Res. 2008, 36. [Google Scholar] [CrossRef]
- de Guenni, L.B.; García, M.; Muñoz, Á.G.; Santos, J.L.; Cedeño, A.; Perugachi, C.; Castillo, J. Predicting monthly precipitation along coastal Ecuador: ENSO and transfer function models. Theor. Appl. Climatol. 2017, 129, 1059–1073. [Google Scholar] [CrossRef]
- Moura, M.S.d.A.; Morettin, P.A.; Toloi, C.; Chiann, C. Transfer function models with time-varying coefficients. J. Probab. Stat. 2012. [Google Scholar] [CrossRef]
- Cohen, A.; Daubechies, I.; Vial, P. Wavelets on the interval and fast wavelet transforms. Appl. Comput. Harmon. Anal. 1993, 1, 54–81. [Google Scholar] [CrossRef]
- Vidakovic, B. Statistical Modeling by Wavelets; John Wiley & Sons: New York, NY, USA, 2009; Volume 503. [Google Scholar]
- Webster, R.; Lark, R. GP Nason: Wavelet Methods in Statistics with r. Math. Geosci. 2011, 43, 261–263. [Google Scholar] [CrossRef]
- Zou, Y.; Yu, L.; He, K. Wavelet entropy based analysis and forecasting of crude oil price dynamics. Entropy 2015, 17, 7167–7184. [Google Scholar] [CrossRef]
- Misiti, M.; Misiti, Y.; Oppenheim, G.; Poggi, J.M. Wavelet Toolbox; The MathWorks Inc.: Natick, MA, USA, 1996; Volume 15, p. 21. [Google Scholar]
- Box, G.E.; Jenkins, G.M.; Reinsel, G.C.; Ljung, G.M. Time Series Analysis: Forecasting and Control; John Wiley & Sons: New York, NY, USA, 2015. [Google Scholar]
- Shumway, R.H.; Stoffer, D.S. Time Series Analysis and Its Applications: With R Examples; Springer: New York, NY, USA, 2017. [Google Scholar]
- Diodato, N.; De Guenni, L.; Garcia, M.; Bellocchi, G. Decadal Oscillation in the Predictability of Palmer Drought Severity Index in California. Climate 2019, 7, 6. [Google Scholar] [CrossRef]
- Veloz, A.; Salas, R.; Allende-Cid, H.; Allende, H.; Moraga, C. Identification of lags in nonlinear autoregressive time series using a flexible fuzzy model. Neural Process. Lett. 2016, 43, 641–666. [Google Scholar] [CrossRef]
- Sansó, B.; Guenni, L. Venezuelan rainfall data analysed by using a Bayesian space–time model. J. R. Stat. Soc. Ser. C (Appl. Stat.) 1999, 48, 345–362. [Google Scholar] [CrossRef]
| Type | Variable | |
|---|---|---|
| SST | Sea surface temperature from Antofagasta Coastal Oceanographic Station | |
| Local Climatic | TI | Turbulence index from Antofagasta Coastal Oceanographic Station |
| MSL | Mean sea level from Antofagasta Coastal Oceanographic Station | |
| Global Climatic | MEI | El Niño multivariate Southern Oscillation index |
| PDO | Pacific Decadal Oscillation index | |
| N12 | Pacific sea surface temperature index (Niño Zone 1 + 2) | |
| N34 | Pacific sea surface temperature index (Niño Zone 3 + 4) | |
| SOI | Southern Oscillation index | |
| CTI | Cold tongue index | |
| Local Fisheries | DANC | Disembarkation anchovy (Engraulis ringens) in northern Chile |
| DSAR | Disembarkation sardine (Sardinops sagax) in northern Chile | |
| X | Standardized | Anomalized | Standardized | Anomalized | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Anchovy | Log Anchovy | Anchovy | Log Anchovy | Sardine | Log Sardine | Sardine | Log Sardine | |||||||||
| Lag | CCF | Lag | CCF | Lag | CCF | Lag | CCF | Lag | CCF | Lag | CCF | Lag | CCF | Lag | CCF | |
| SST | - | - | - | - | 15 | 7 | - | - | 20 | 0.22 | 15 | 0.13 | 15 | 0.12 | ||
| TI | 2 | - | - | 2 | 10 | 18 | 18 | 0.23 | 2 | 18 | ||||||
| MEI | - | - | - | - | - | - | 5 | 10 | - | - | - | - | - | - | ||
| MSL | - | - | 7 | 3 | 7 | - | - | - | - | 3 | - | - | ||||
| PDO | - | - | - | - | - | - | - | - | - | - | 2 | - | - | - | - | |
| N12 | 22 | 5 | - | - | 5 | - | - | 24 | - | - | - | - | ||||
| N34 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - |
| SOI | - | - | - | - | - | - | - | - | 23 | - | - | - | - | - | - | |
| CTI | - | - | - | - | - | - | - | - | 12 | 22 | 0.11 | - | - | - | - | |
| DSAR | - | - | 5 | - | - | 5 | 1 | 1 | 1 | 1 | ||||||
| DANC | 1 | 1 | 1 | 1 | 10 | 7 | - | - | 7 | |||||||
| T | Y | X | L | Type Coefficient | Fitted | Forecast | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | R | Pearson | Spearman | Kendall | RMSE | MAE | R | |||||
| Anchovy | |||||||||||||
| N | DANC | DANC | 1 | Constant | 0.851 | 0.559 | 0.821 | 0.964 | 0.882 | 0.727 | 0.603 | 0.464 | 0.796 |
| TI | 2 | ||||||||||||
| N12 | 22 | Wavelet | 0.165 | 0.128 | 0.978 | 0.990 | 0.971 | 0.865 | 0.138 | 0.106 | 0.969 | ||
| A | DANC | DANC | 1 | Constant | 0.831 | 0.568 | 0.826 | 0.966 | 0.919 | 0.771 | 0.660 | 0.571 | 0.750 |
| SST | 15 | ||||||||||||
| TI | 2 | Wavelet | 0.416 | 0.309 | 0.904 | 0.956 | 0.943 | 0.796 | 0.265 | 0.207 | 0.824 | ||
| MSL | 3 | ||||||||||||
| Log N | DANC | DANC | 1 | Constant | 0.603 | 0.451 | 0.862 | 0.953 | 0.950 | 0.813 | 0.770 | 0.575 | 0.748 |
| MSL | 7 | ||||||||||||
| N12 | 5 | Wavelet | 0.391 | 0.286 | 0.883 | 0.932 | 0.929 | 0.775 | 0.717 | 0.806 | 0.564 | ||
| LDSAR | 5 | ||||||||||||
| Log A | DANC | DANC | 1 | Constant | 0.604 | 0.447 | 0.860 | 0.950 | 0.948 | 0.808 | 0.792 | 0.548 | 0.751 |
| SST | 7 | ||||||||||||
| TI | 10 | ||||||||||||
| MEI | 5 | Wavelet | 0.818 | 0.620 | 0.652 | 0.714 | 0.637 | 0.458 | 0.599 | 0.493 | 0.681 | ||
| MSL | 7 | ||||||||||||
| N12 | 5 | ||||||||||||
| LDSAR | 5 | ||||||||||||
| Sardine | |||||||||||||
| N | DSAR | DSAR | 1 | Constant | 0.610 | 0.380 | 0.858 | 0.943 | 0.640 | 0.472 | 0.167 | 0.135 | 0.500 |
| TI | 18 | ||||||||||||
| MEI | 10 | ||||||||||||
| SOI | 23 | Wavelet | 1.033 | 0.734 | 0.672 | 0.715 | 0.538 | 0.374 | 1.308 | 1.072 | 0.500 | ||
| CTI | 12 | ||||||||||||
| DANC | 10 | ||||||||||||
| A | DSAR | DSAR | 1 | Constant | 0.614 | 0.381 | 0.859 | 0.947 | 0.744 | 0.584 | 0.139 | 0.109 | 0.619 |
| SST | 13 | ||||||||||||
| TI | 12 | ||||||||||||
| SOI | 23 | Wavelet | 1.377 | 0.998 | 0.590 | 0.557 | 0.290 | 0.192 | 0.887 | 0.749 | 0.499 | ||
| CTI | 18 | ||||||||||||
| Log N | DSAR | DSAR | 1 | Constant | 0.274 | 0.199 | 0.918 | 0.962 | 0.966 | 0.840 | 0.303 | 0.258 | 0.688 |
| SST | 20 | ||||||||||||
| TI | 18 | ||||||||||||
| PDO | 2 | Wavelet | 1.013 | 1.261 | 0.613 | 0.614 | 0.607 | 0.432 | 0.357 | 0.285 | 0.547 | ||
| N12 | 24 | ||||||||||||
| CTI | 22 | ||||||||||||
| LDANC | 7 | ||||||||||||
| Log A | DSAR | DSAR | 1 | Constant | 0.276 | 0.200 | 0.916 | 0.961 | 0.966 | 0.840 | 0.277 | 0.239 | 0.706 |
| SST | 15 | ||||||||||||
| TI | 18 | Wavelet | 0.417 | 0.542 | 0.562 | 0.755 | 0.762 | 0.565 | 1.291 | 1.249 | 0.502 | ||
| LDANC | 7 | ||||||||||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vivas, E.; Allende-Cid, H.; Salas, R.; Bravo, L. Polynomial and Wavelet-Type Transfer Function Models to Improve Fisheries’ Landing Forecasting with Exogenous Variables. Entropy 2019, 21, 1082. https://doi.org/10.3390/e21111082
Vivas E, Allende-Cid H, Salas R, Bravo L. Polynomial and Wavelet-Type Transfer Function Models to Improve Fisheries’ Landing Forecasting with Exogenous Variables. Entropy. 2019; 21(11):1082. https://doi.org/10.3390/e21111082
Chicago/Turabian StyleVivas, Eliana, Héctor Allende-Cid, Rodrigo Salas, and Lelys Bravo. 2019. "Polynomial and Wavelet-Type Transfer Function Models to Improve Fisheries’ Landing Forecasting with Exogenous Variables" Entropy 21, no. 11: 1082. https://doi.org/10.3390/e21111082
APA StyleVivas, E., Allende-Cid, H., Salas, R., & Bravo, L. (2019). Polynomial and Wavelet-Type Transfer Function Models to Improve Fisheries’ Landing Forecasting with Exogenous Variables. Entropy, 21(11), 1082. https://doi.org/10.3390/e21111082






