The Connection between Bayesian Inference and Information Theory for Model Selection, Information Gain and Experimental Design
Abstract
1. Introduction
2. Bayesian Inference and Information Theory
2.1. Bayesian Inference
2.2. Information Theory
2.3. From Bayesian Inference to Information Theory
3. Bayesian Model Selection
3.1. Model Evidence via Posterior Density Estimates
3.2. Model Evidence via Dirac at the Maximum a Posteriori Estimate
3.3. Model Evidence via the Chib Estimate
3.4. Model Evidence via the Akaike Information Criterion
3.5. Model Evidence via Multivariate Gaussian Posterior Estimates
3.6. Model Evidence via the Kashyap Information Criterion Correction
3.7. Model Evidence via the Schwarz Information Criterion Correction
3.8. Model Evidence via the Gelfand and Dey Estimate
4. Bayesian View on the Information Gain
4.1. Information Entropy during Bayesian Inference
4.2. Bayesian Experimental Design and Information Gain
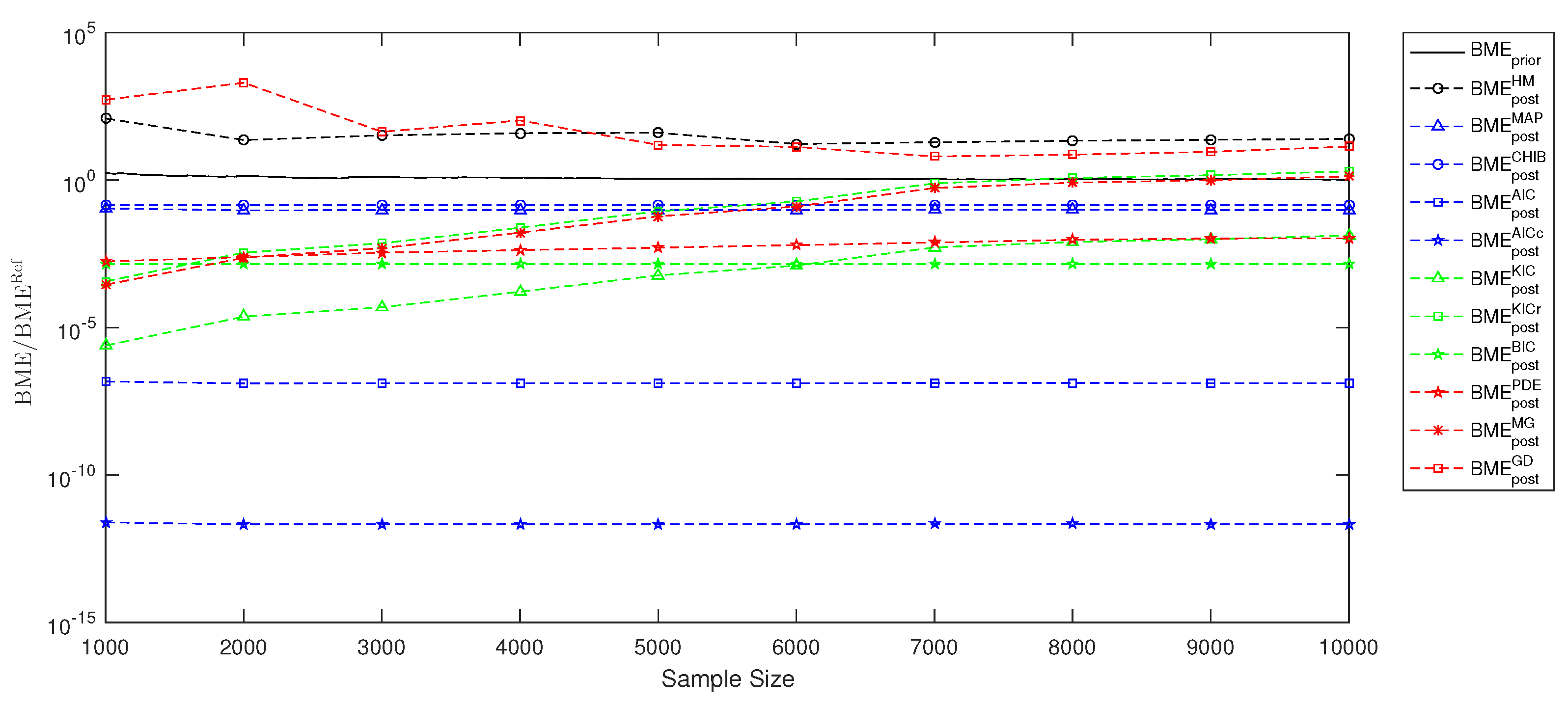
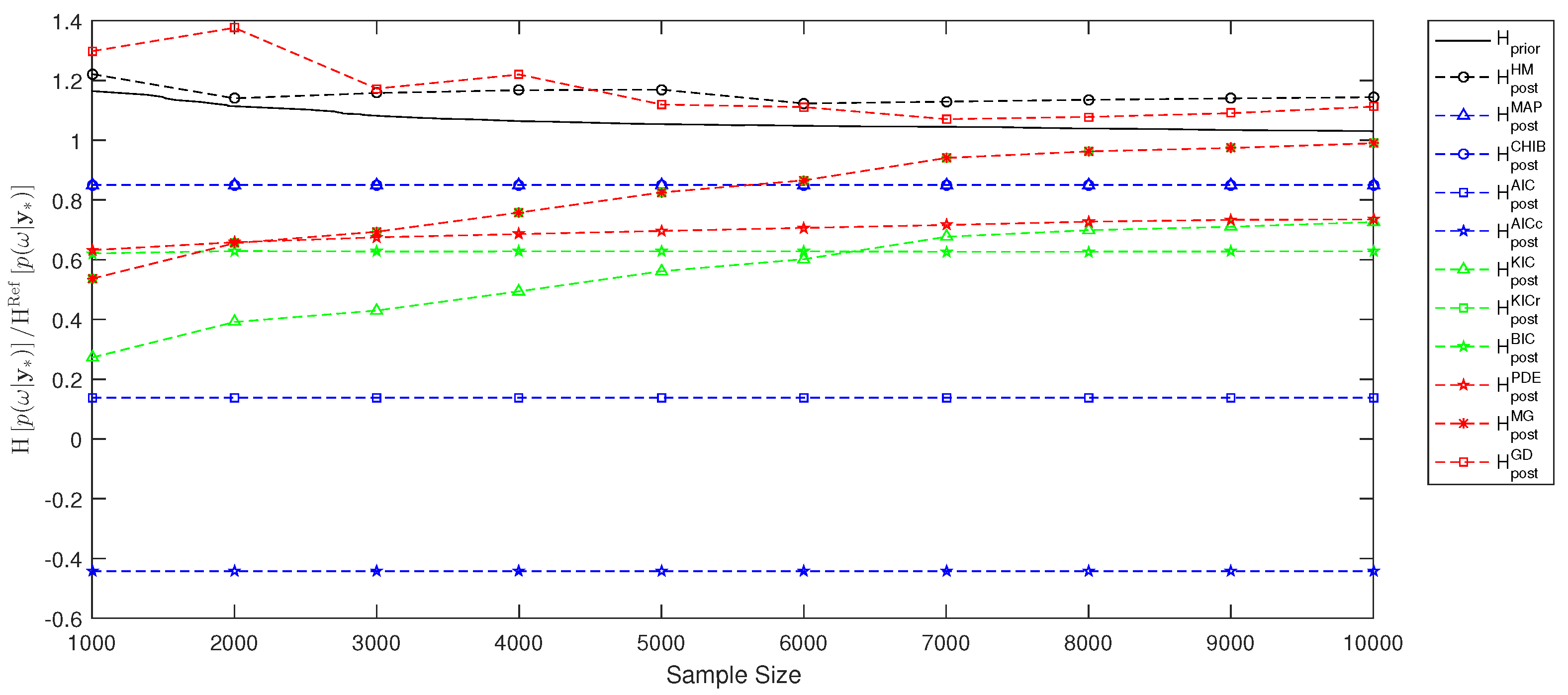
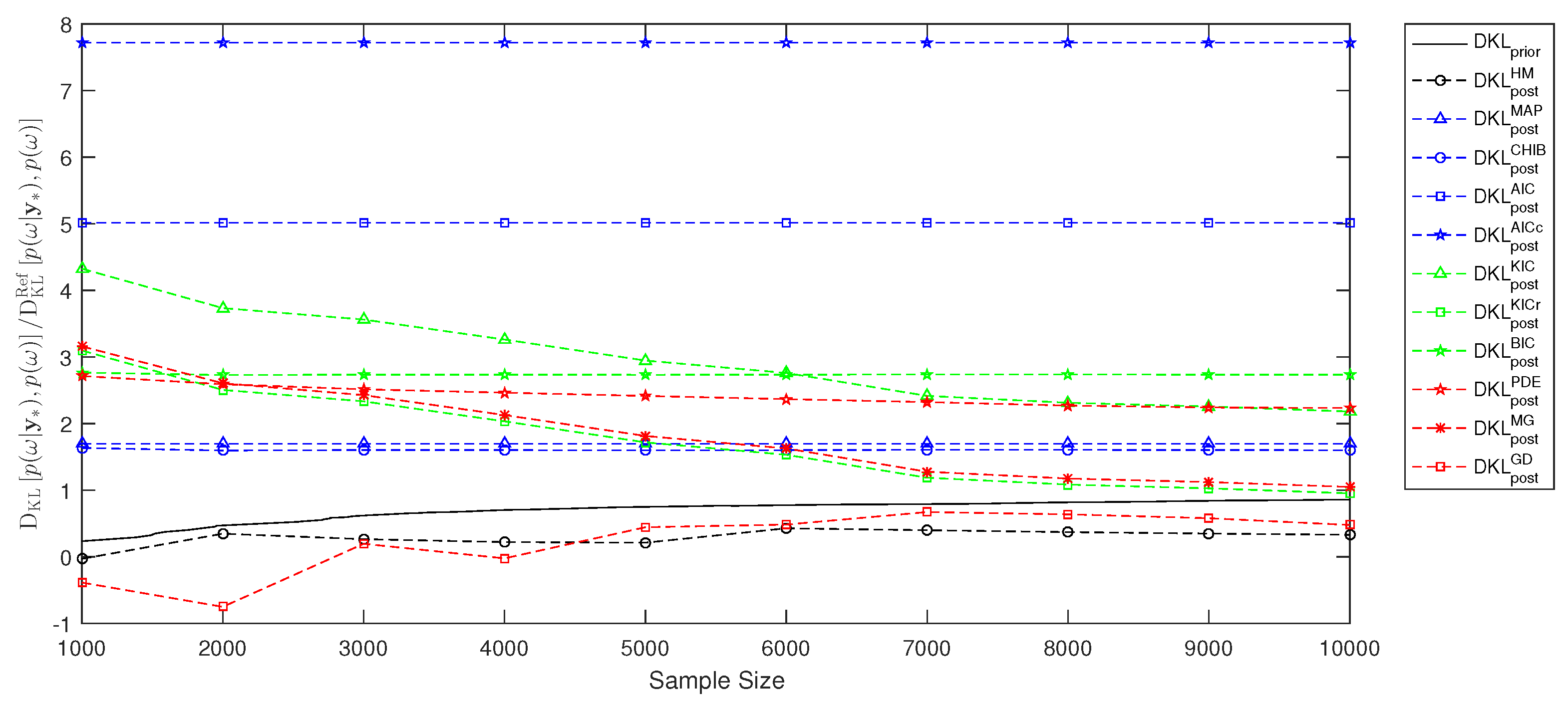
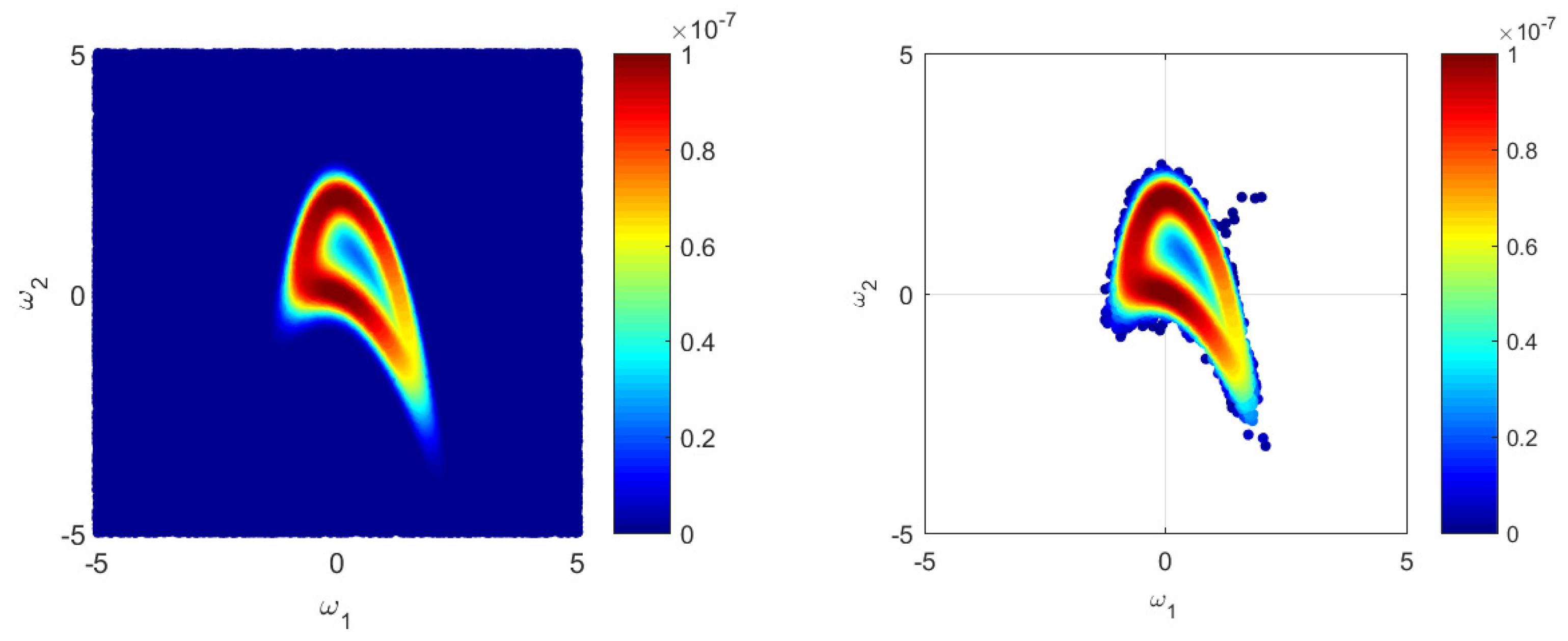
5. Model Evidence, Information Entropy and Experiment Utility for a Test Case
5.1. Scenario Set Up
5.2. Bayesian Model Selection
5.3. Information Entropy and Bayesian Experimental Design
6. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kolmogorov, A.N.; Bharucha-Reid, A.T. Foundations of the Theory of Probability: Second English Edition; Courier Dover Publications: New York, NY, USA, 2018. [Google Scholar]
- Lia, O.; Omre, H.; Tjelmeland, H.; Holden, L.; Egeland, T. Uncertainties in reservoir production forecasts. AAPG Bull. 1997, 81, 775–802. [Google Scholar]
- Smith, A.F.; Gelfand, A.E. Bayesian statistics without tears: A sampling–resampling perspective. Am. Stat. 1992, 46, 84–88. [Google Scholar]
- Gilks, W.; Richardson, S.; Spiegelhalter, D. Markov Chain Monte Carlo in Practice; Chapmann & Hall: London, UK, 1996. [Google Scholar]
- Höge, M.; Guthke, A.; Nowak, W. The hydrologist’s guide to Bayesian model selection, averaging and combination. J. Hydrol. 2019, 572, 96–107. [Google Scholar] [CrossRef]
- Schöniger, A.; Wöhling, T.; Samaniego, L.; Nowak, W. Model selection on solid ground: Rigorous comparison of nine ways to evaluate Bayesian model evidence. Water Resour. Res. 2014, 50, 9484–9513. [Google Scholar] [CrossRef]
- Draper, D. Assessment and propagation of model uncertainty. J. R. Stat. Society. Ser. B (Methodol.) 1995, 57, 45–97. [Google Scholar] [CrossRef]
- Raftery, A.E. Bayesian model selection in social research. Sociol. Methodol. 1995, 25, 111–163. [Google Scholar] [CrossRef]
- Oladyshkin, S.; Nowak, W. Data-driven uncertainty quantification using the arbitrary polynomial chaos expansion. Reliab. Eng. Syst. Saf. 2012, 106, 179–190. [Google Scholar] [CrossRef]
- Liu, P.; Elshall, A.S.; Ye, M.; Beerli, P.; Zeng, X.; Lu, D.; Tao, Y. Evaluating marginal likelihood with thermodynamic integration method and comparison with several other numerical methods. Water Resour. Res. 2016, 52, 734–758. [Google Scholar] [CrossRef]
- Xiao, S.; Reuschen, S.; Köse, G.; Oladyshkin, S.; Nowak, W. Estimation of small failure probabilities based on thermodynamic integration and parallel tempering. Mech. Syst. Signal Process. 2019, 133, 106248. [Google Scholar] [CrossRef]
- Skilling, J. Nested sampling for general Bayesian computation. Bayesian Anal. 2006, 1, 833–859. [Google Scholar] [CrossRef]
- Elsheikh, A.; Oladyshkin, S.; Nowak, W.; Christie, M. Estimating the Probability of CO2 Leakage Using Rare Event Simulation. In Proceedings of the ECMOR XIV-14th European Conference on the Mathematics of Oil Recovery, Catania, Italy, 8–11 September 2014. [Google Scholar]
- Volpi, E.; Schoups, G.; Firmani, G.; Vrugt, J.A. Sworn testimony of the model evidence: Gaussian mixture importance (GAME) sampling. Water Resour. Res. 2017, 53, 6133–6158. [Google Scholar] [CrossRef]
- Sundar, V.; Shields, M.D. Reliability analysis using adaptive kriging surrogates with multimodel inference. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2019, 5, 04019004. [Google Scholar] [CrossRef]
- Mohammadi, F.; Kopmann, R.; Guthke, A.; Oladyshkin, S.; Nowak, W. Bayesian selection of hydro-morphodynamic models under computational time constraints. Adv. Water Resour. 2018, 117, 53–64. [Google Scholar] [CrossRef]
- Gamerman, D.; Lopes, H.F. Markov Chain Monte Carlo: Stochastic Simulation for Bayesian Inference; Chapmann & Hall: London, UK, 2006. [Google Scholar]
- Jensen, J.L.W.V. Sur les fonctions convexes et les inégalités entre les valeurs moyennes. Acta Math. 1906, 30, 175–193. [Google Scholar] [CrossRef]
- Newton, M.A.; Raftery, A.E. Approximate Bayesian inference with the weighted likelihood bootstrap. J. R. Stat. Soc. Ser. B (Methodol.) 1994, 56, 3–26. [Google Scholar] [CrossRef]
- Lenk, P. Simulation pseudo-bias correction to the harmonic mean estimator of integrated likelihoods. J. Comput. Graph. Stat. 2009, 18, 941–960. [Google Scholar] [CrossRef]
- Gelfand, A.E.; Dey, D.K. Bayesian model choice: Asymptotics and exact calculations. J. R. Stat. Soc. Ser. B (Methodol.) 1994, 56, 501–514. [Google Scholar] [CrossRef]
- Chib, S. Marginal likelihood from the Gibbs output. J. Am. Stat. Assoc. 1995, 90, 1313–1321. [Google Scholar] [CrossRef]
- Chib, S.; Jeliazkov, I. Marginal likelihood from the Metropolis–Hastings output. J. Am. Stat. Assoc. 2001, 96, 270–281. [Google Scholar] [CrossRef]
- Liu, C.; Liu, Q. Marginal likelihood calculation for the Gelfand–Dey and Chib methods. Econ. Lett. 2012, 115, 200–203. [Google Scholar] [CrossRef]
- Wiener, N. Cybernetics; John Wiley & Sons. Inc.: New York, NY, USA, 1948. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Good, I. Some terminology and notation in information theory. Proc. IEE-Part C Monogr. 1956, 103, 200–204. [Google Scholar] [CrossRef]
- Shannon, C.E.; Weaver, W. The mathematical theory of communication. Ill. Press. Urbana I 1949, 11, 117. [Google Scholar]
- Murari, A.; Peluso, E.; Cianfrani, F.; Gaudio, P.; Lungaroni, M. On the use of entropy to improve model selection criteria. Entropy 2019, 21, 394. [Google Scholar] [CrossRef]
- Gresele, L.; Marsili, M. On maximum entropy and inference. Entropy 2017, 19, 642. [Google Scholar] [CrossRef]
- Cavanaugh, J.E. A large-sample model selection criterion based on Kullback’s symmetric divergence. Stat. Probab. Lett. 1999, 42, 333–343. [Google Scholar] [CrossRef]
- Vecer, J. Dynamic Scoring: Probabilistic Model Selection Based on Utility Maximization. Entropy 2019, 21, 36. [Google Scholar] [CrossRef]
- Cliff, O.; Prokopenko, M.; Fitch, R. Minimising the Kullback–Leibler divergence for model selection in distributed nonlinear systems. Entropy 2018, 20, 51. [Google Scholar] [CrossRef]
- Chaloner, K.; Verdinelli, I. Bayesian experimental design: A review. Stat. Sci. 1995, 10, 273–304. [Google Scholar] [CrossRef]
- Lindley, D.V. On a measure of the information provided by an experiment. Ann. Math. Stat. 1956, 27, 986–1005. [Google Scholar] [CrossRef]
- Fischer, R. Bayesian experimental design—studies for fusion diagnostics. AIP Conf. Proc. 2004, 735, 76–83. [Google Scholar]
- Nowak, W.; Guthke, A. Entropy-based experimental design for optimal model discrimination in the geosciences. Entropy 2016, 18, 409. [Google Scholar] [CrossRef]
- Richard, M.D.; Lippmann, R.P. Neural network classifiers estimate Bayesiana posterio probabilities. Neural Comput. 1991, 3, 461–483. [Google Scholar] [CrossRef]
- Rubinstein, R.Y.; Kroese, D.P. The Cross-Entropy Method: A Unified Approach to Combinatorial Optimization, Monte-Carlo Simulation and Machine Learning; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Granziol, D.; Ru, B.; Zohren, S.; Dong, X.; Osborne, M.; Roberts, S. MEMe: An accurate maximum entropy method for efficient approximations in large-scale machine learning. Entropy 2019, 21, 551. [Google Scholar] [CrossRef]
- Zellner, A. Optimal information processing and Bayes’s theorem. Am. Stat. 1988, 42, 278–280. [Google Scholar]
- Mohammad-Djafari, A. Entropy, information theory, information geometry and Bayesian inference in data, signal and image processing and inverse problems. Entropy 2015, 17, 3989–4027. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. In Selected Papers of Hirotugu Akaike; Springer: Berlin/Heidelberg, Germany, 1974; pp. 215–222. [Google Scholar]
- Sugiura, N. Further analysts of the data by Akaike’s information criterion and the finite corrections: Further analysts of the data by Akaike’s. Commun. Stat. Theory Methods 1978, 7, 13–26. [Google Scholar] [CrossRef]
- Kashyap, R.L. Optimal choice of AR and MA parts in autoregressive moving average models. IEEE Trans. Pattern Anal. Mach. Intell. 1982, PAMI-4, 99–104. [Google Scholar] [CrossRef]
- Kass, R.E.; Raftery, A.E. Bayes Factors. J. Am. Stat. Assoc. 1995, 90, 773–795. [Google Scholar] [CrossRef]
- Hammersley, J.M. Monte Carlo Methods for solving multivariable problems. Ann. N. Y. Acad. Sci. 1960, 86, 844–874. [Google Scholar] [CrossRef]
- Camacho, R.A.; Martin, J.L.; McAnally, W.; Díaz-Ramirez, J.; Rodriguez, H.; Sucsy, P.; Zhang, S. A comparison of Bayesian methods for uncertainty analysis in hydraulic and hydrodynamic modeling. JAWRA J. Am. Water Resour. Assoc. 2015, 51, 1372–1393. [Google Scholar] [CrossRef]
- Kullback, S. Information Theory and Statistics; Courier Corporation: North Chelmsford, MA, USA, 1997. [Google Scholar]
- Soofi, E.S. Information theory and Bayesian statistics. Bayesian Analysis in Statistics and Econometrics: Essays in Honor of Arnold Zellnge; Wiley: New York, NY, USA, 1996; pp. 179–189. [Google Scholar]
- Stone, J.V. Information Theory: A Tutorial Introduction; Sebtel Press: London, UK, 2015. [Google Scholar]
- Botev, Z.I.; Grotowski, J.F.; Kroese, D.P. Kernel density estimation via diffusion. Ann. Stat. 2010, 38, 2916–2957. [Google Scholar] [CrossRef]
- Silverman, B.W. Density Estimation for Statistics and Data Analysis; Routledge: Abingdon-on-Thames, UK, 2018. [Google Scholar]
- Sheather, S.J.; Jones, M.C. A reliable data-based bandwidth selection method for kernel density estimation. J. R. Stat. Soc. Ser. B (Methodol.) 1991, 53, 683–690. [Google Scholar] [CrossRef]
- Goldman, S. Information Theory; Prentice-Hall: Englewood Cliffs, NJ, USA, 1953. [Google Scholar]
- McEliece, R.; Mac Eliece, R.J. The Theory of Information and Coding; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Neuman, S.P. Maximum likelihood Bayesian averaging of uncertain model predictions. Stoch. Environ. Res. Risk Assess. 2003, 17, 291–305. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Leube, P.; Geiges, A.; Nowak, W. Bayesian assessment of the expected data impact on prediction confidence in optimal sampling design. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Hastings, W.K. Monte Carlo sampling methods using Markov chains and their applications. Biometrika 1970, 57, 97–109. [Google Scholar] [CrossRef]
| Estimate and Equation Number | Non-Normalized Cross Entropy | Cross Entropy | Information Entropy |
|---|---|---|---|
| PDE estimate (19) | No assumptions | No assumptions | Kernel density estimation |
| MAP estimate (20) | No assumptions | No assumptions | MAP point estimates |
| Chib estimate (21) | MAP point value | MAP point value | MAP point estimates |
| AIC estimate (24) | No assumptions | No assumptions | AIC estimates |
| AICc estimate (26) | No assumptions | No assumptions | AICc estimates |
| MG estimate (28) | No assumptions | No assumptions | MG estimates |
| KIC estimate (30) | MAP point estimates | MAP point estimates | KIC estimates |
| KICr estimate (32) | MAP point estimates | MAP point estimates | MG estimates |
| BIC estimate (34) | MAP point estimates | Asymptotical limit for growing data size | |
| GD estimates * (35) | No assumptions | No assumptions | MG estimates |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oladyshkin, S.; Nowak, W. The Connection between Bayesian Inference and Information Theory for Model Selection, Information Gain and Experimental Design. Entropy 2019, 21, 1081. https://doi.org/10.3390/e21111081
Oladyshkin S, Nowak W. The Connection between Bayesian Inference and Information Theory for Model Selection, Information Gain and Experimental Design. Entropy. 2019; 21(11):1081. https://doi.org/10.3390/e21111081
Chicago/Turabian StyleOladyshkin, Sergey, and Wolfgang Nowak. 2019. "The Connection between Bayesian Inference and Information Theory for Model Selection, Information Gain and Experimental Design" Entropy 21, no. 11: 1081. https://doi.org/10.3390/e21111081
APA StyleOladyshkin, S., & Nowak, W. (2019). The Connection between Bayesian Inference and Information Theory for Model Selection, Information Gain and Experimental Design. Entropy, 21(11), 1081. https://doi.org/10.3390/e21111081




