Quantum Dynamics in a Fluctuating Environment
Abstract
1. Introduction
2. Theoretical Framework
3. Application and Discussion
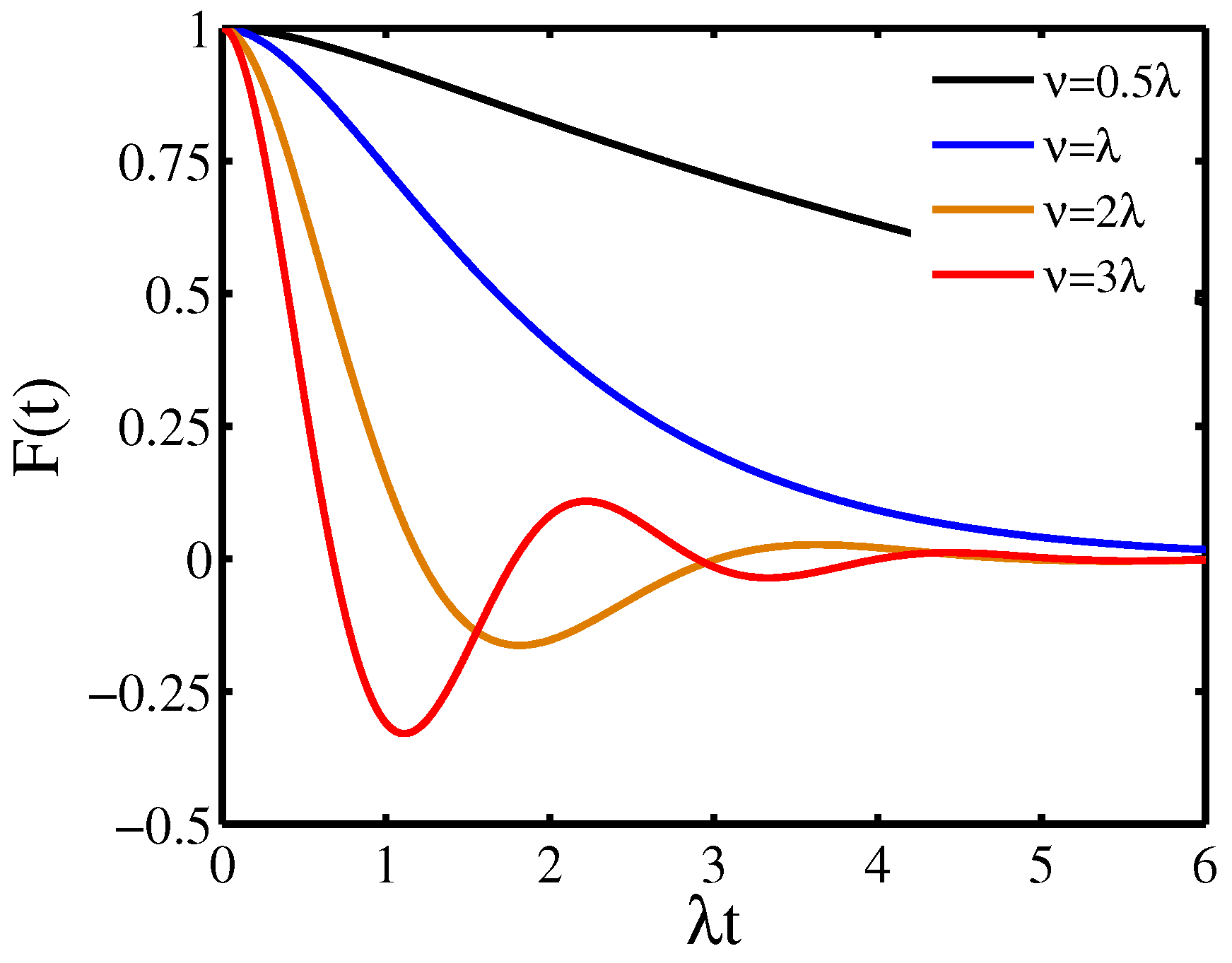
3.1. Quantum Dynamics Induced by the RTN Process
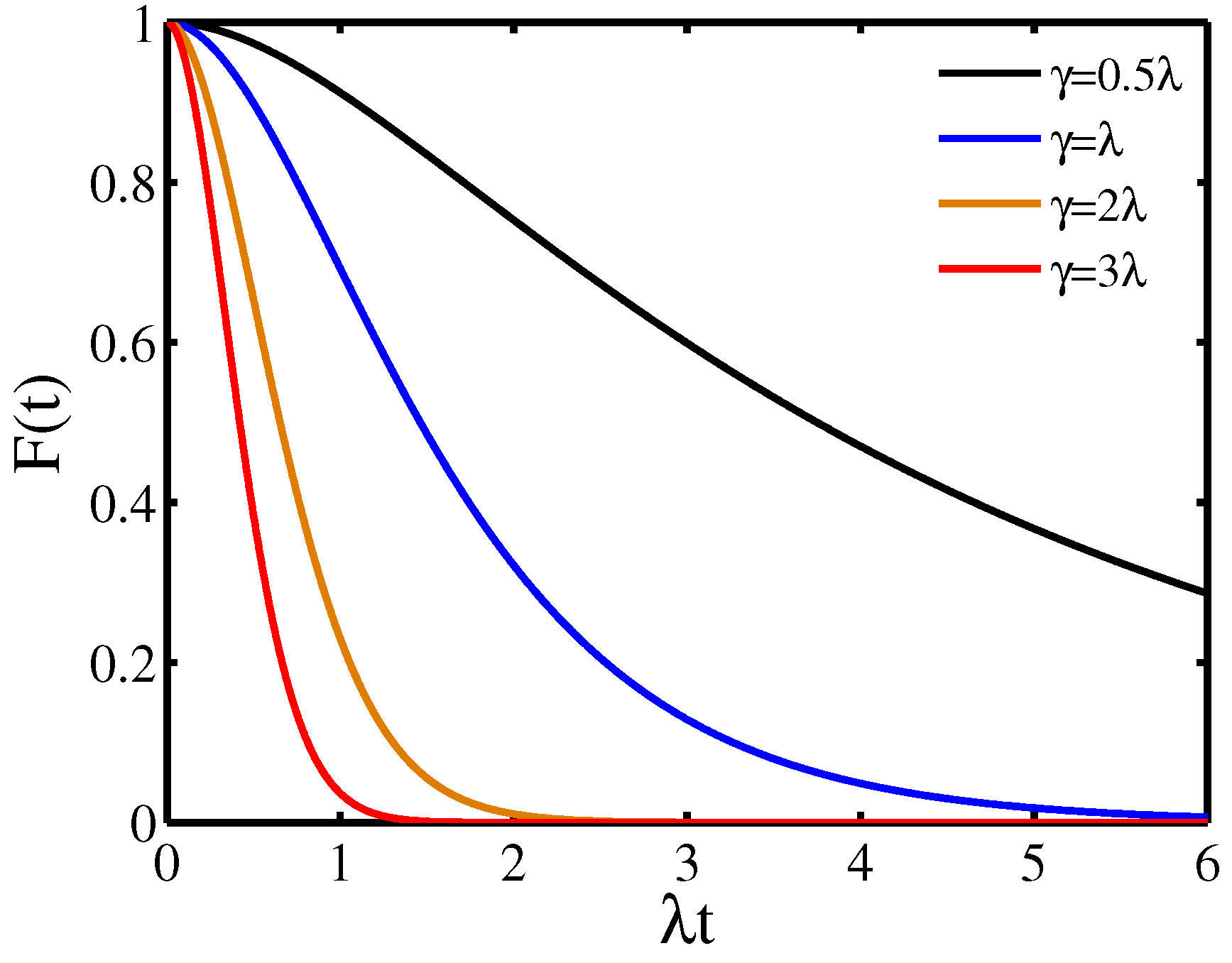
3.2. Quantum Dynamics Induced by the OUN Process
4. Conclusions
Funding
Conflicts of Interest
References
- Breuer, H.P.; Petruccione, F. The Theory of Open Quantum Systems; Oxford University Press: New York, NY, USA, 2002. [Google Scholar]
- Zurek, W.H. Decoherence, einselection, and the quantum origins of the classical. Rev. Mod. Phys. 2003, 75, 715. [Google Scholar] [CrossRef]
- Sauer, S.; Gneiting, C.; Buchleitner, A. Optimal Coherent Control to Counteract Dissipation. Phys. Rev. Lett. 2013, 111, 030405. [Google Scholar] [CrossRef]
- Di Stefano, P.G.; Paladino, E.; Pope, T.J.; Falci, G. Coherent manipulation of noise-protected superconducting artificial atoms in the Lambda scheme. Phys. Rev. A 2016, 93, 051801. [Google Scholar] [CrossRef]
- Suter, D.; Álvarez, G.A. Colloquium: Protecting quantum information against environmental noise. Rev. Mod. Phys. 2016, 88, 041001. [Google Scholar] [CrossRef]
- Kang, L.; Zhang, Y.; Xu, X.; Tang, X. Quantum measurement of a double quantum dot coupled to two kinds of environment. Phys. Rev. B 2017, 96, 235417. [Google Scholar] [CrossRef]
- Gorini, V.; Kossakowski, A.; Sudarshan, E.C.G. Completely positive dynamical semigroups of N-level systems. J. Math. Phys. 1976, 17, 821. [Google Scholar] [CrossRef]
- Lindblad, G. On the generators of quantum dynamical semigroups. Commun. Math. Phys. 1976, 48, 119. [Google Scholar] [CrossRef]
- Breuer, H.; Laine, E.; Piilo, J. Measure for the Degree of Non-Markovian Behavior of Quantum Processes in Open Systems. Phys. Rev. Lett. 2009, 103, 210401. [Google Scholar] [CrossRef] [PubMed]
- Rivas, A.; Huelga, S.F.; Plenio, M.B. Entanglement and Non-Markovianity of Quantum Evolutions. Phys. Rev. Lett. 2010, 105, 050403. [Google Scholar] [CrossRef]
- Tu, M.W.Y.; Zhang, W.M. Non-Markovian decoherence theory for a double-dot charge qubit. Phys. Rev. B 2008, 78, 235311. [Google Scholar] [CrossRef]
- Zhang, W.M.; Lo, P.Y.; Xiong, H.N.; Tu, M.W.Y.; Nori, F. General Non-Markovian Dynamics of Open Quantum Systems. Phys. Rev. Lett. 2012, 109, 170402. [Google Scholar] [CrossRef] [PubMed]
- Chruściński, D.; Maniscalco, S. Degree of Non-Markovianity of Quantum Evolution. Phys. Rev. Lett. 2014, 112, 120404. [Google Scholar] [CrossRef]
- Rivas, A.; Huelga, S.F.; Plenio, M.B. Quantum Non-Markovianity: Characterization, quantification and detection. Rep. Prog. Phys. 2014, 77, 094001. [Google Scholar] [CrossRef] [PubMed]
- Breuer, H.; Laine, E.; Piilo, J.; Vacchini, B. Colloquium : Non-Markovian dynamics in open quantum systems. Rev. Mod. Phys. 2016, 88, 021002. [Google Scholar] [CrossRef]
- de Vega, I.; Alonso, D. Dynamics of Non-Markovian open quantum systems. Rev. Mod. Phys. 2017, 89, 015001. [Google Scholar] [CrossRef]
- Alipour, S.; Rezakhani, A.T.; Babu, A.P.; Mølmer, K.; Möttönen, M.; Ala-Nissila, T. Correlation Picture Approach to Open-Quantum-System Dynamics. arXiv, 2019; arXiv:1903.03861. [Google Scholar]
- Anderson, P.W. A Mathematical Model for the Narrowing of Spectral Lines by Exchange or Motion. J. Phys. Soc. Jpn. 1954, 9, 316. [Google Scholar] [CrossRef]
- Kubo, R. Note on the Stochastic Theory of Resonance Absorption. J. Phys. Soc. Jpn. 1954, 9, 935. [Google Scholar] [CrossRef]
- Shibata, F.; Arimitsu, T. Expansion Formulas in Nonequilibrium Statistical Mechanics. J. Phys. Soc. Jpn. 1980, 49, 891. [Google Scholar] [CrossRef]
- Martens, C.C. Communication: Decoherence in a nonequilibrium environment: An analytically solvable model. J. Chem. Phys. 2010, 133, 241101. [Google Scholar] [CrossRef]
- Martens, C.C. Theory and simulation of the loss of coherence in thermal and nonequilibrium environments. J. Phys. B 2012, 45, 154008. [Google Scholar] [CrossRef]
- Martens, C.C. Quantum dephasing of a two-state system by a nonequilibrium harmonic oscillator. J. Chem. Phys. 2013, 139, 024109. [Google Scholar] [CrossRef] [PubMed]
- Ban, M.; Kitajima, S.; Shibata, F. Relaxation process of quantum system: Stochastic Liouville equation and initial correlation. Phys. Rev. A 2010, 82, 022111. [Google Scholar] [CrossRef]
- Chenu, A.; Beau, M.; Cao, J.; del Campo, A. Quantum Simulation of Generic Many-Body Open System Dynamics Using Classical Noise. Phys. Rev. Lett. 2017, 118, 140403. [Google Scholar] [CrossRef]
- Hsieh, C.Y.; Cao, J. A unified stochastic formulation of dissipative quantum dynamics. I. Generalized hierarchical equations. J. Chem. Phys. 2018, 148, 014103. [Google Scholar] [CrossRef]
- Hsieh, C.Y.; Cao, J. A unified stochastic formulation of dissipative quantum dynamics. II. Beyond linear response of spin baths. J. Chem. Phys. 2018, 148, 014104. [Google Scholar] [CrossRef]
- Magazzù, L.; Valenti, D.; Carollo, A.; Spagnolo, B. Multi-State Quantum Dissipative Dynamics in Sub-Ohmic Environment: The Strong Coupling Regime. Entropy 2015, 17, 2341. [Google Scholar] [CrossRef]
- Magazzù, L.; Carollo, A.; Spagnolo, B.; Valenti, D. Quantum dissipative dynamics of a bistable system in the sub-Ohmic to super-Ohmic regime. J. Stat. Mech. 2016, 2016, 054016. [Google Scholar] [CrossRef]
- Lombardo, F.C.; Villar, P.I. Nonunitary geometric phases: A qubit coupled to an environment with random noise. Phys. Rev. A 2013, 87, 032338. [Google Scholar] [CrossRef]
- Lombardo, F.C.; Villar, P.I. Corrections to the Berry phase in a solid-state qubit due to low-frequency noise. Phys. Rev. A 2014, 89, 012110. [Google Scholar] [CrossRef]
- Lombardo, F.C.; Villar, P.I. Correction to the geometric phase by structured environments: The onset of non-Markovian effects. Phys. Rev. A 2015, 91, 042111. [Google Scholar] [CrossRef]
- Cai, X.; Zheng, Y. Decoherence induced by non-Markovian noise in a nonequilibrium environment. Phys. Rev. A 2016, 94, 042110. [Google Scholar] [CrossRef]
- Cai, X.; Zheng, Y. Quantum dynamical speedup in a nonequilibrium environment. Phys. Rev. A 2017, 95, 052104. [Google Scholar] [CrossRef]
- Fuliński, A. Exact nonmarkovianity measure based on time autocorrelation functions. Europhys. Lett. 2017, 118, 60002. [Google Scholar] [CrossRef]
- Cai, X.; Zheng, Y. Non-Markovian decoherence dynamics in nonequilibrium environments. J. Chem. Phys. 2018, 149, 094107. [Google Scholar] [CrossRef]
- Cai, X.; Meng, R.; Zhang, Y.; Wang, L. Geometry of quantum evolution in a nonequilibrium environment. Europhys. Lett. 2019, 125, 30007. [Google Scholar] [CrossRef]
- Yan, Y.A.; Shao, J. Equivalence of stochastic formulations and master equations for open systems. Phys. Rev. A 2018, 97, 042126. [Google Scholar] [CrossRef]
- De Chiara, G.; Palma, G.M. Berry Phase for a Spin 1/2 Particle in a Classical Fluctuating Field. Phys. Rev. Lett. 2003, 91, 090404. [Google Scholar] [CrossRef]
- Rabenstein, K.; Sverdlov, V.A.; Averin, D.V. Qubit Decoherence by Gaussian Low-Frequency Noise. Jetp Lett. 2004, 79, 646. [Google Scholar] [CrossRef][Green Version]
- Kuvshinov, V.I.; Kuzmin, A.V. Decoherence induced by squeezing control errors in optical and ion trap holonomic quantum computations. Phys. Rev. A 2006, 73, 052305. [Google Scholar] [CrossRef]
- Huang, C.H.; Goan, H.S. Robust quantum gates for stochastic time-varying noise. Phys. Rev. A 2017, 95, 062325. [Google Scholar] [CrossRef]
- Bergli, J.; Galperin, Y.M.; Altshuler, B.L. Decoherence of a qubit by non-Gaussian noise at an arbitrary working point. Phys. Rev. B 2006, 74, 024509. [Google Scholar] [CrossRef]
- Burkard, G. Non-Markovian qubit dynamics in the presence of 1/f noise. Phys. Rev. B 2009, 79, 125317. [Google Scholar] [CrossRef]
- Paladino, E.; Faoro, L.; Falci, G.; Fazio, R. Decoherence and 1/f Noise in Josephson Qubits. Phys. Rev. Lett. 2002, 88, 228304. [Google Scholar] [CrossRef] [PubMed]
- Paladino, E.; Faoro, L.; DÁrrigoa, A.; Falci, G. Decoherence and 1/f Noise in Josephson Qubits. Physica E 2003, 18, 29. [Google Scholar] [CrossRef]
- Paladino, E.; Faoro, L.; Falci, G. Decoherence Due to Discrete Noise in Josephson Qubits. Adv. Sol. State Phys. 2003, 43, 747. [Google Scholar]
- Falci, G.; D’Arrigo, A.; Mastellone, A.; Paladino, E. Initial Decoherence in Solid State Qubits. Phys. Rev. Lett. 2005, 94, 167002. [Google Scholar] [CrossRef]
- Schriefl, J.; Makhlin, Y.; Shnirman, A.; Schön, G. Decoherence from ensembles of two-level fluctuators. New J. Phys. 2006, 8, 1. [Google Scholar] [CrossRef]
- Galperin, Y.M.; Altshuler, B.L.; Bergli, J.; Shantsev, D.V. Non-Gaussian Low-Frequency Noise as a Source of Qubit Decoherence. Phys. Rev. Lett. 2006, 96, 097009. [Google Scholar] [CrossRef]
- Paladino, E.; Galperin, Y.M.; Falci, G.; Altshuler, B.L. 1/f noise: Implications for solid-state quantum information. Rev. Mod. Phys. 2014, 86, 361. [Google Scholar] [CrossRef]
- Barkai, E.; Jung, Y.; Silbey, R. Time-Dependent Fluctuations in Single Molecule Spectroscopy: A Generalized Wiener-Khintchine Approach. Phys. Rev. Lett. 2001, 87, 207403. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y.; Brown, F.L.H. Single-Molecule Photon Counting Statistics via Generalized Optical Bloch Equations. Phys. Rev. Lett. 2003, 90, 238305. [Google Scholar] [CrossRef] [PubMed]
- Brokmann, X.; Hermier, J.P.; Messin, G.; Desbiolles, P.; Bouchaud, J.P.; Dahan, M. Statistical Aging and Nonergodicity in the Fluorescence of Single Nanocrystals. Phys. Rev. Lett. 2003, 90, 120601. [Google Scholar] [CrossRef] [PubMed]
- Bourret, R.C. Brownian motion of harmonic oscillator with stochastic frequency. Physica 1973, 65, 303. [Google Scholar] [CrossRef]
- Wódkiewicz, K.; Shore, B.W.; Eberly, J.H. Noise in strong laser-atom interactions: Frequency fluctuations and nonexponential correlations. Phys. Rev. A 1984, 30, 2390. [Google Scholar] [CrossRef]
- Abel, B.; Marquardt, F. Decoherence by quantum telegraph noise: A numerical evaluation. Phys. Rev. B 2008, 78, 201302. [Google Scholar] [CrossRef]
- Neuenhahn, C.; Kubala, B.; Abel, B.; Marquardt, F. Recent progress in open quantum systems: Non-Gaussian noise and decoherence in fermionic systems. Phys. Status Solidi B 2009, 246, 1018. [Google Scholar] [CrossRef]
- Ayachi, A.; Chouikha, W.B.; Jaziri, S.; Bennaceur, R. Telegraph noise effects on two charge qubits in double quantum dots. Phys. Rev. A 2014, 89, 012330. [Google Scholar] [CrossRef]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, X. Quantum Dynamics in a Fluctuating Environment. Entropy 2019, 21, 1040. https://doi.org/10.3390/e21111040
Cai X. Quantum Dynamics in a Fluctuating Environment. Entropy. 2019; 21(11):1040. https://doi.org/10.3390/e21111040
Chicago/Turabian StyleCai, Xiangji. 2019. "Quantum Dynamics in a Fluctuating Environment" Entropy 21, no. 11: 1040. https://doi.org/10.3390/e21111040
APA StyleCai, X. (2019). Quantum Dynamics in a Fluctuating Environment. Entropy, 21(11), 1040. https://doi.org/10.3390/e21111040




