On the Impossibility of First-Order Phase Transitions in Systems Modeled by the Full Euler Equations
Abstract
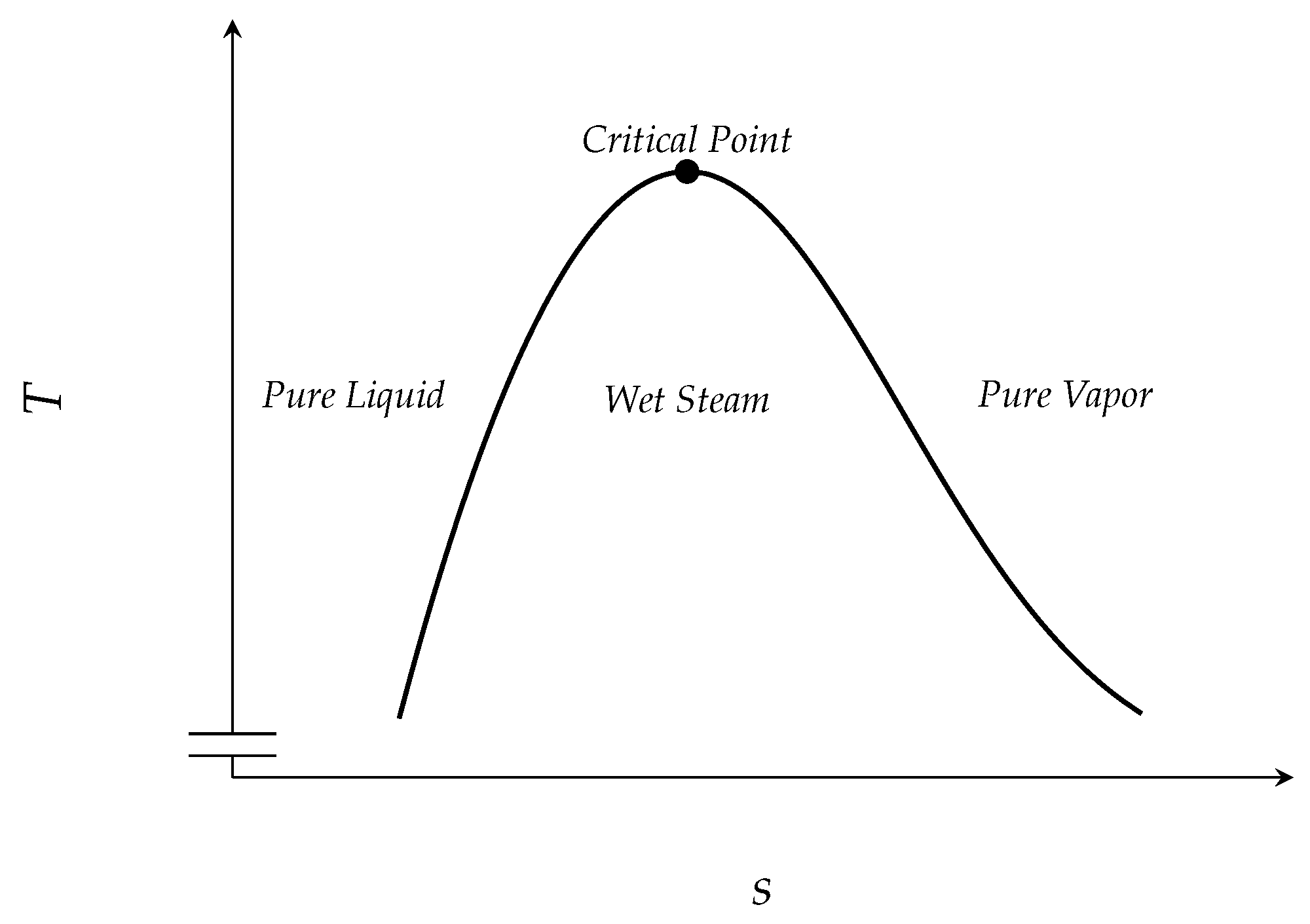
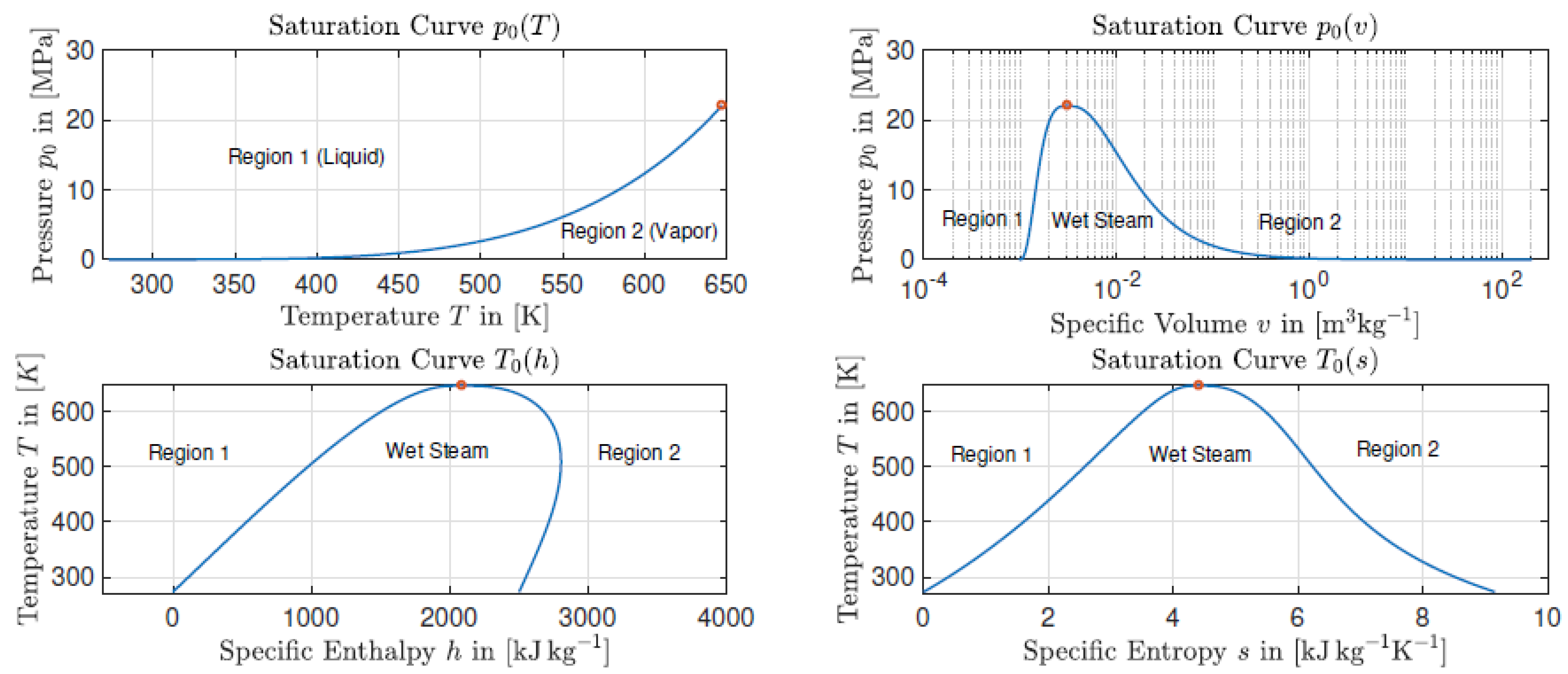
1. Introduction
2. Balance Laws and Entropy Inequality
3. Contradiction Argument
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Fan, H.; Slemrod, M. Dynamic flows with liquid/vapor phase transitions. In Handbook of Mathematical Fluiddynamics; Friedlander, S., Serre, D., Eds.; Elsevier: Amsterdam, The Netherlands, 2002; Volume 1, pp. 373–420. [Google Scholar] [CrossRef]
- Zein, A. Numerical Methods for Multiphase Mixture Conservation Laws with Phase Transition. Ph.D. Thesis, Otto-von-Guericke-Universität Magdeburg, Magdeburg, Germany, 2010. [Google Scholar]
- Abeyaratne, R.; Knowles, J.K. Kinetic relations and the propagation of phase boundaries in solids. Arch. Ration. Mech. Anal. 1991, 114, 119–154. [Google Scholar] [CrossRef]
- Hantke, M.; Thein, F. A general existence result for isothermal two-phase flows with phase transition. arXiv 2017, arXiv:1703.09431. [Google Scholar]
- Hantke, M.; Dreyer, W.; Warnecke, G. Exact solutions to the Riemann problem for compressible isothermal Euler equations for two phase flows with and without phase transition. Q. Appl. Math. 2013, 71, 509–540. [Google Scholar] [CrossRef]
- Hantke, M.; Thein, F. Why condensation by compression in pure water vapor cannot occur in an approach based on Euler equations. Quart. Appl. Math. 2015, 73, 575–591. [Google Scholar] [CrossRef]
- Chen, G.Q. Euler Equations and Related Hyperbolic Conservation Laws. In Handbook of Differential Equations Evolutionary Equations; Dafermos, C., Feireisl, E., Eds.; Elsevier: Amsterdam, The Netherlands, 2005; Volume 2, pp. 1–104. [Google Scholar] [CrossRef]
- Thein, F. Results for Two Phase Flows with Phase Transition. Ph.D. Thesis, Otto-von-Guericke-Universität Magdeburg, Magdeburg, Germany, 2018. [Google Scholar]
- Dafermos, C.M. Hyperbolic Conservation Laws in Continuum Physics; Springer: Berlin, Germany, 2000; Volume 325, p. 826. [Google Scholar] [CrossRef]
- LeFloch, P. Hyperbolic Systems of Conservation Laws: The Theory of Classical and Nonclassical Shock Waves; Lectures in Mathematics, Birkhäuser Verlag: Basel, Switzerland, 2002. [Google Scholar]
- Bartelmann, M.; Feuerbacher, B.; Krüger, T.; Lüst, D.; Rebhan, A.; Wipf, A. Theoretische Physik; Springer Spektrum: Berlin/Heidelberg, Germany, 2015. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifschitz, E.M. Lehrbuch der theoretischen Physik, Bd. V Statistische Physik, 8th ed.; Akad.-Verl.: Berlin, Germany, 1987; pp. XVII, 517 S. [Google Scholar]
- Wagner, W.; Kruse, A. Properties of Water and Steam: The Industrial Standard IAPWS-IF97 for the Thermodynamic Properties and Supplementary Equations for Other Properties: Tables Based on These Equations; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Hantke, M.; Thein, F. Singular and selfsimilar solutions for Euler equations with phase transitions. Bull. Braz. Math. Soc. (N.S.) 2016, 47, 779–786. [Google Scholar] [CrossRef]
- Müller, I. Thermodynamics; Interaction of Mechanics and Mathematics Series; Pitman: Berkely, CA, USA, 1985. [Google Scholar]
- Dreyer, W.; Duderstadt, F.; Hantke, M.; Warnecke, G. Bubbles in liquids with phase transition. Part 1. On phase change of a single vapor bubble in liquid water. Contin. Mech. Thermodyn. 2012, 24, 461–483. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hantke, M.; Thein, F. On the Impossibility of First-Order Phase Transitions in Systems Modeled by the Full Euler Equations. Entropy 2019, 21, 1039. https://doi.org/10.3390/e21111039
Hantke M, Thein F. On the Impossibility of First-Order Phase Transitions in Systems Modeled by the Full Euler Equations. Entropy. 2019; 21(11):1039. https://doi.org/10.3390/e21111039
Chicago/Turabian StyleHantke, Maren, and Ferdinand Thein. 2019. "On the Impossibility of First-Order Phase Transitions in Systems Modeled by the Full Euler Equations" Entropy 21, no. 11: 1039. https://doi.org/10.3390/e21111039
APA StyleHantke, M., & Thein, F. (2019). On the Impossibility of First-Order Phase Transitions in Systems Modeled by the Full Euler Equations. Entropy, 21(11), 1039. https://doi.org/10.3390/e21111039




