Fuzzy Coordination Control Strategy and Thermohydraulic Dynamics Modeling of a Natural Gas Heating System for In Situ Soil Thermal Remediation
Abstract
:1. Introduction
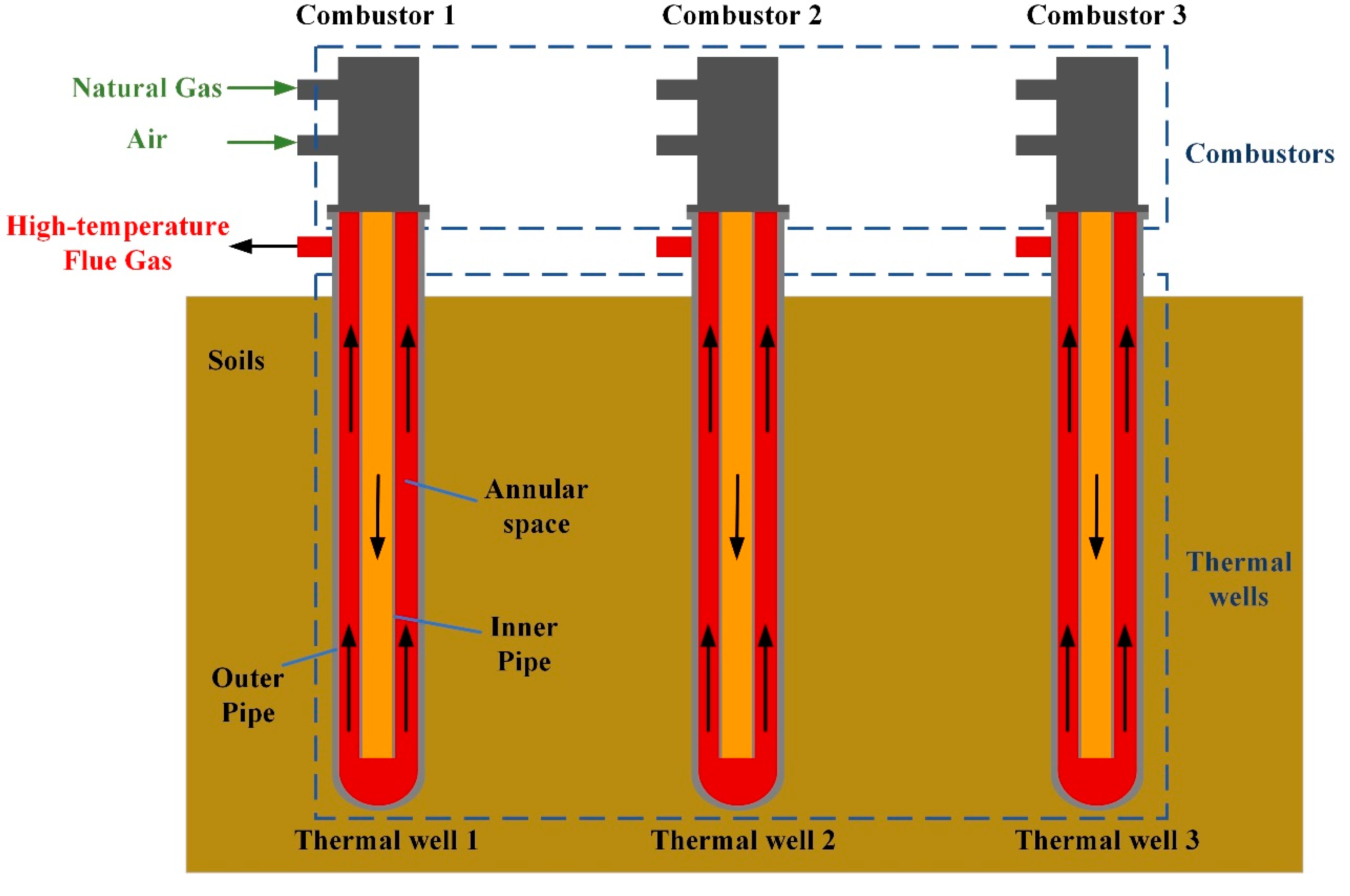
2. System Description and Dynamical Modeling
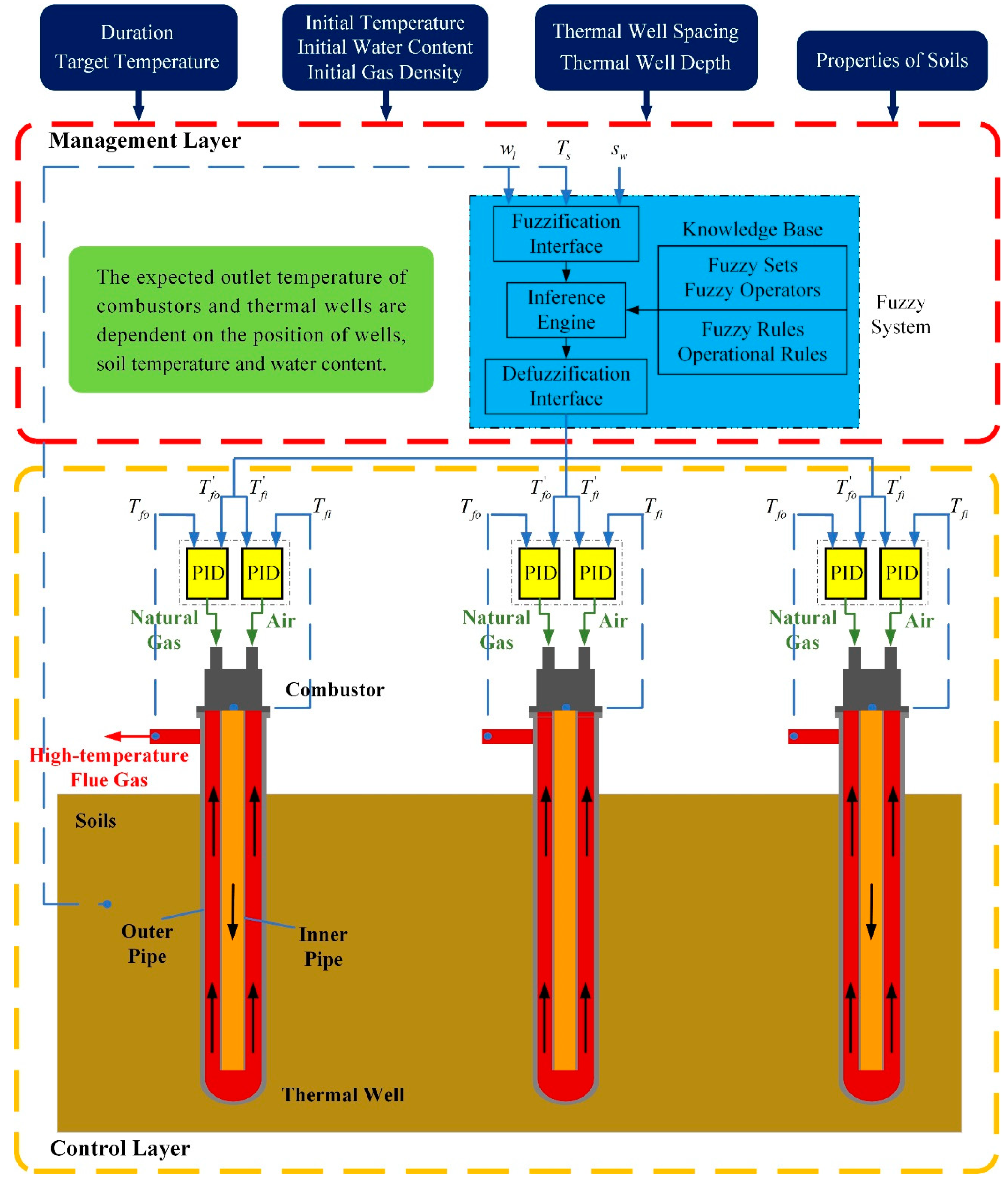
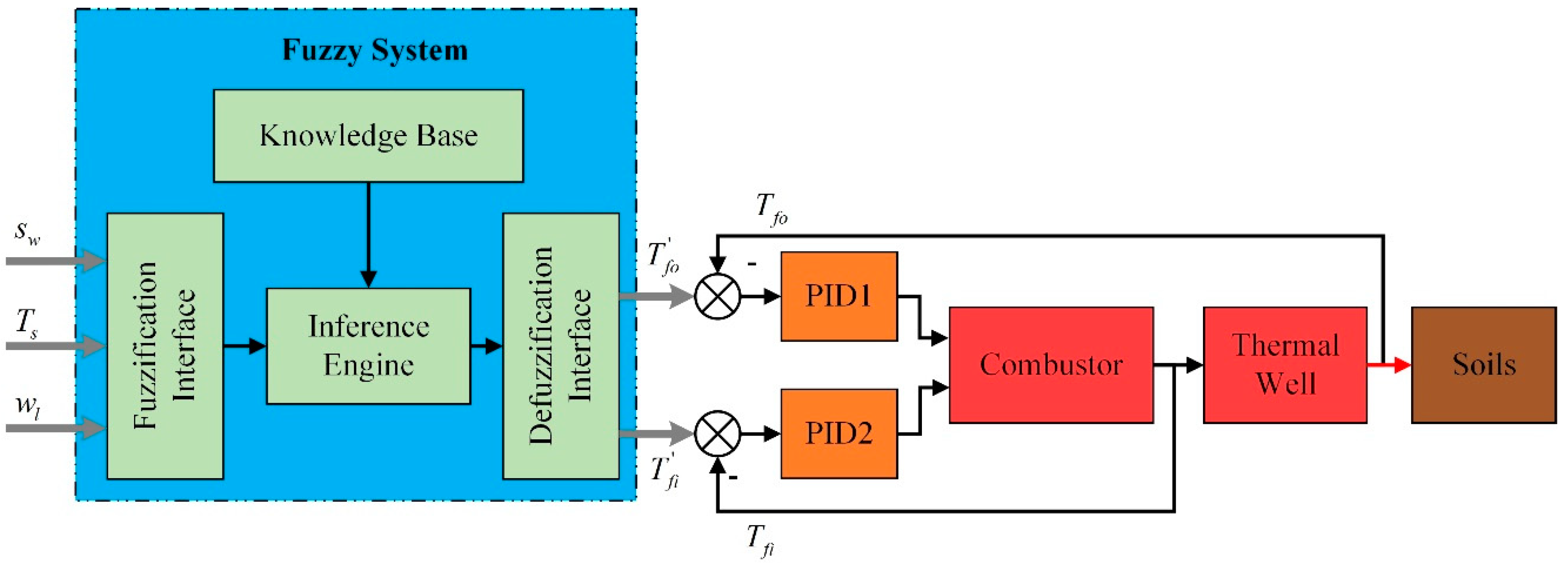
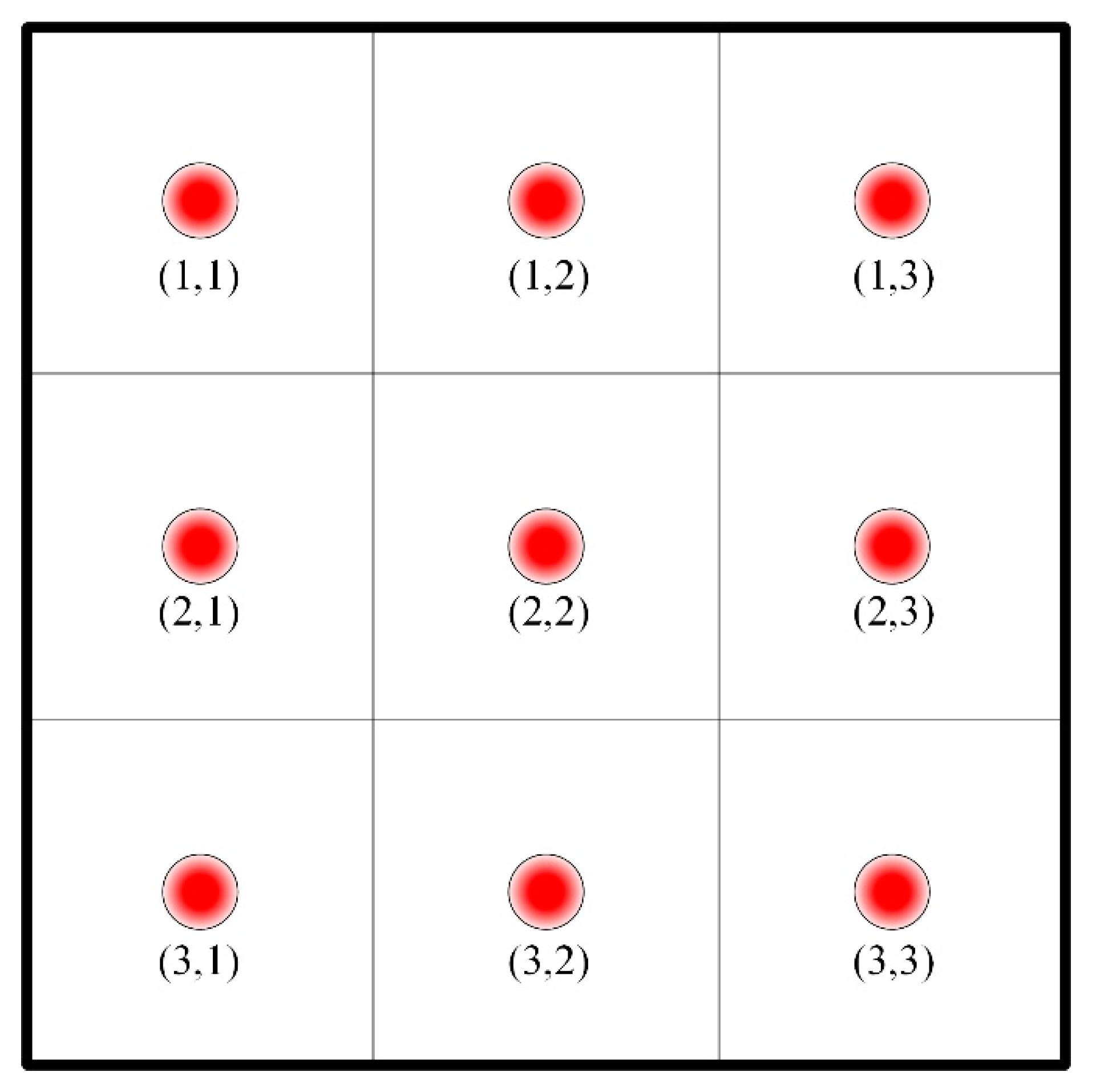
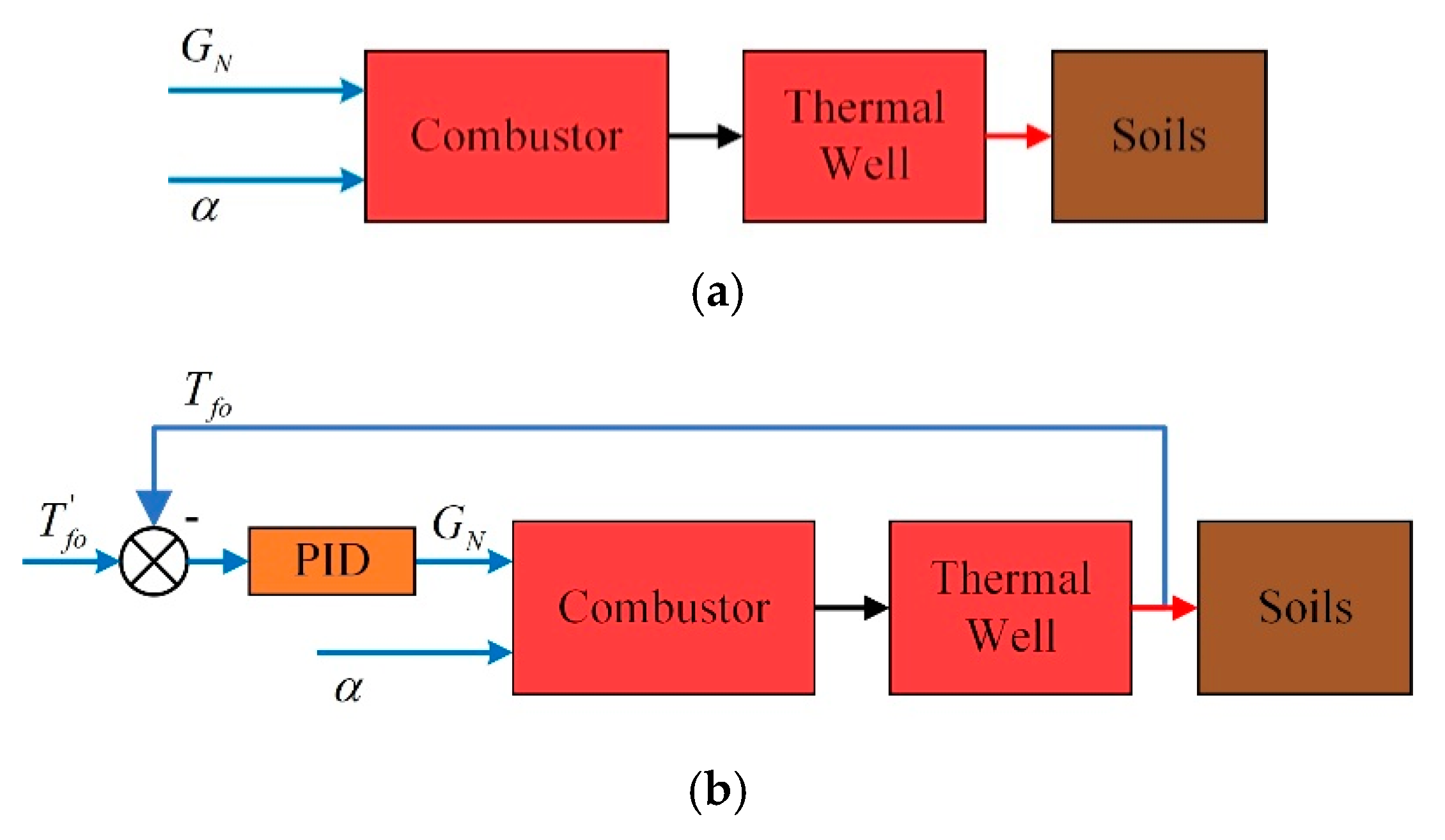
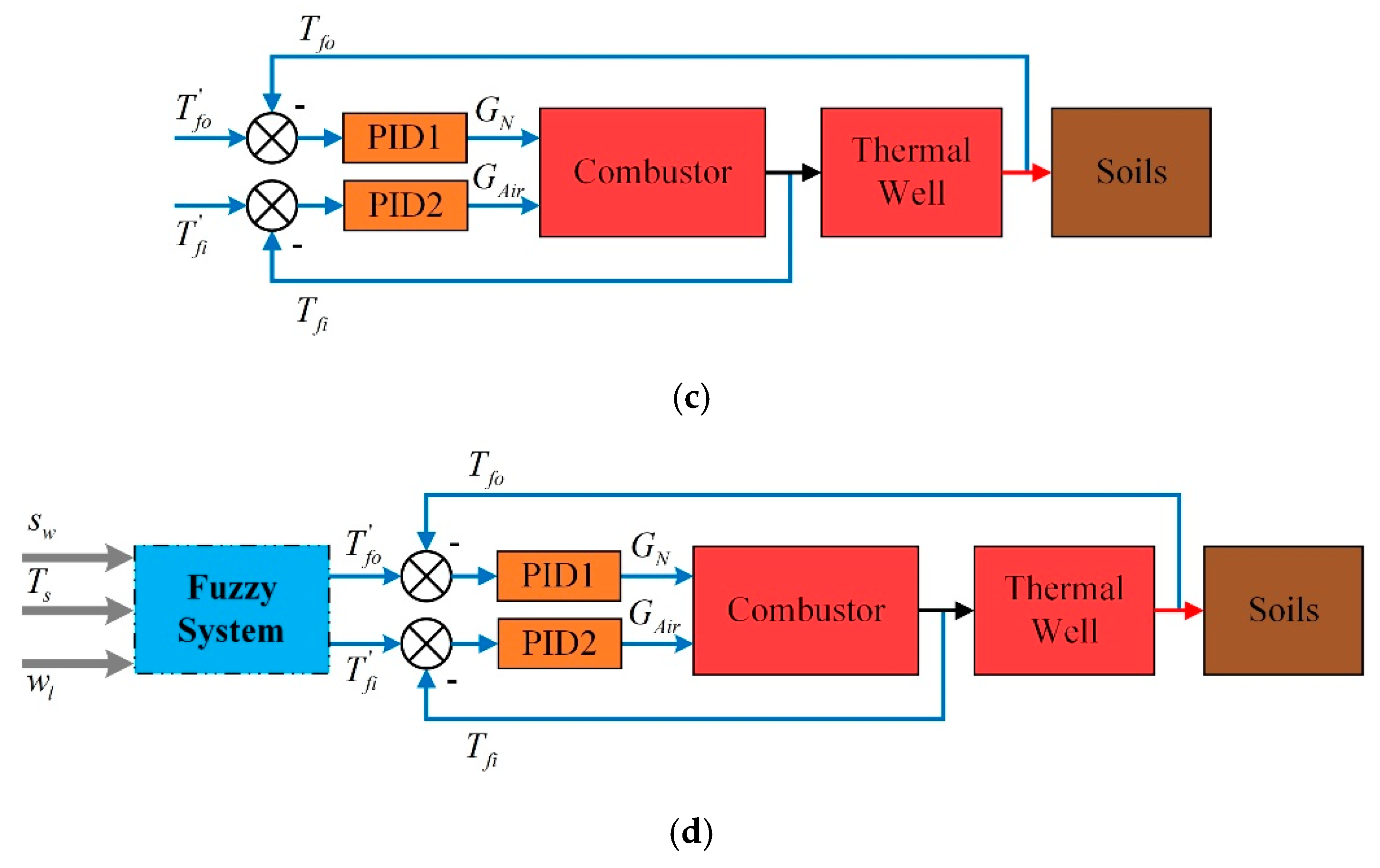
2.1. The Whole Frame of Control Strategy
2.2. Thermohydraulic Dynamics Modeling
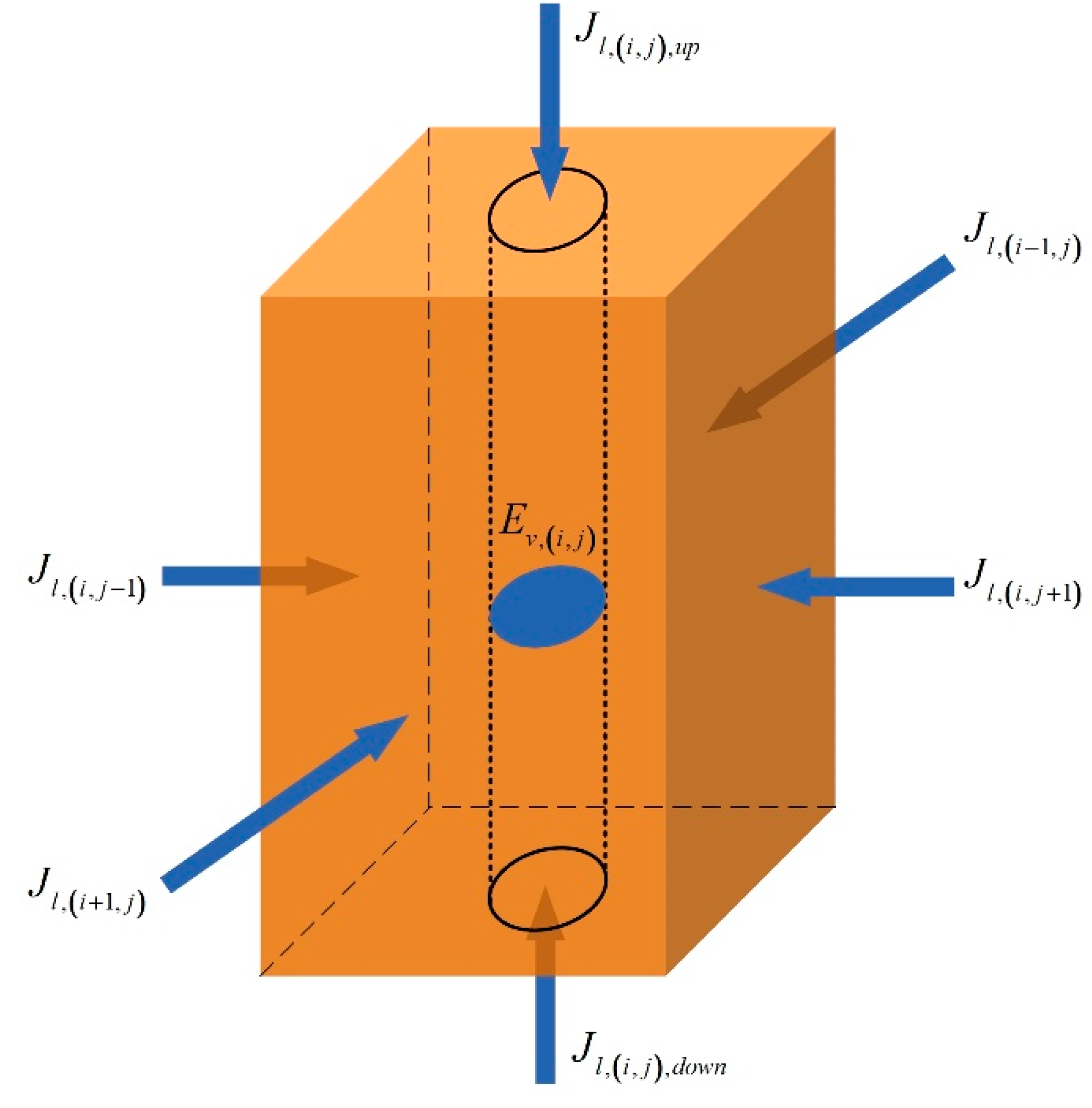
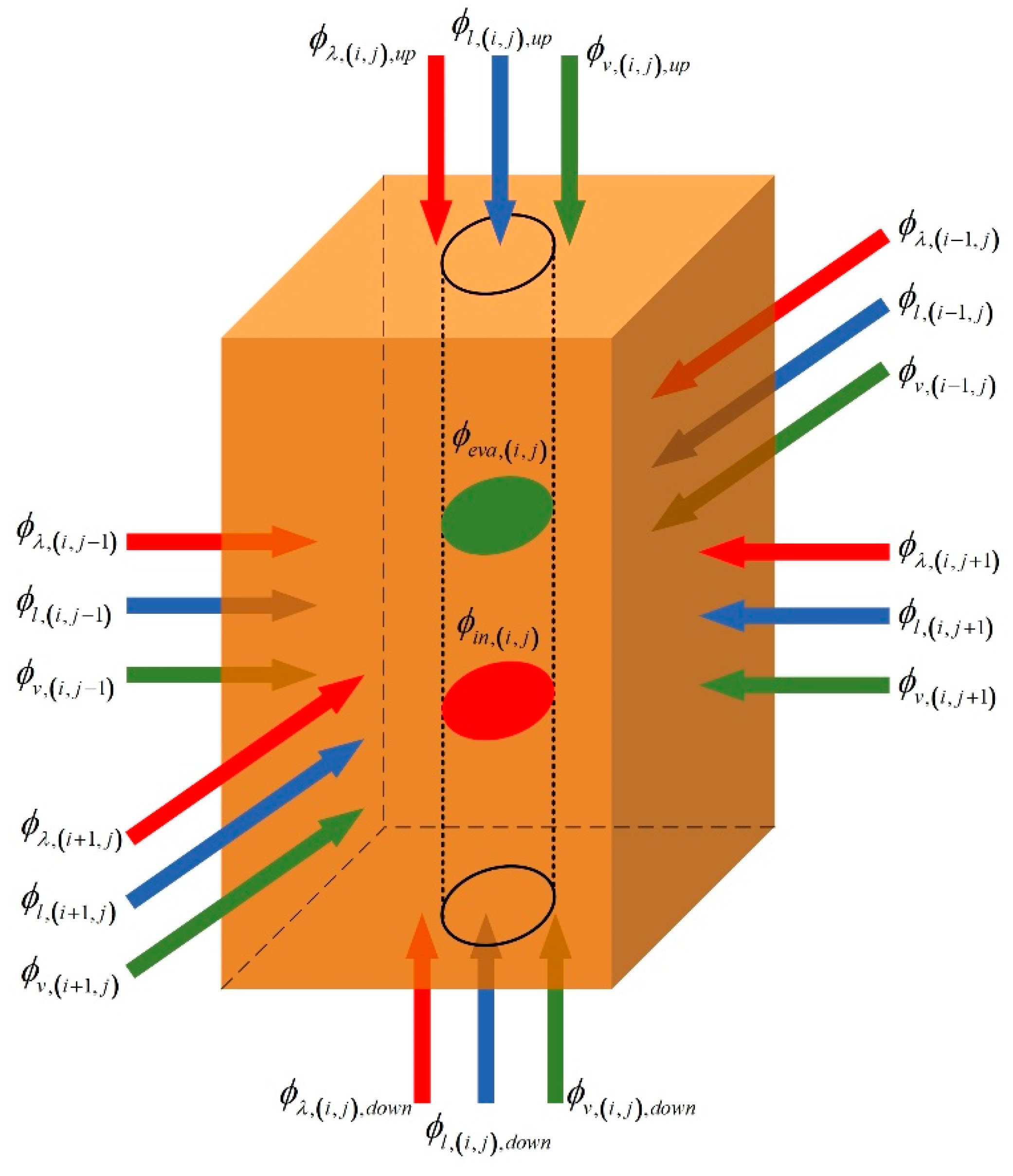
2.2.1. Model of Heating Field
- (1)
- Soil is homogeneous and its type does not change along thermal wells, while soil is considered, in a real situation, a non-homogeneous and non-isotropic porous material. The effect of this assumption on heat conduction can be negligible because thermal conductivities of different dry soils are much less variable. By contrast, fluid flow permeabilities of different layers may vary much [12], so the permeabilities of soils at different locations are actually a little variable.
- (2)
- Convection of fluid in porous media satisfies Darcy’s law.
- (3)
- The gas phase in soils includes noncondensable gases (such as air) and water vapor. The influence of dry air on heat and moisture migration is neglected.
- (4)
- There is no chemical interaction, and the gas is assumed to be ideal gas.
- (5)
- It is assumed that the solid, liquid, and gas phases are continuous in unsaturated soil, separately.
- (6)
- It is assumed that the migration of liquid and gas do not affect each other.
- (7)
- The compressive work and viscous dissipation effects of liquid are negligible.
- (8)
- The effects of contaminants are ignored.
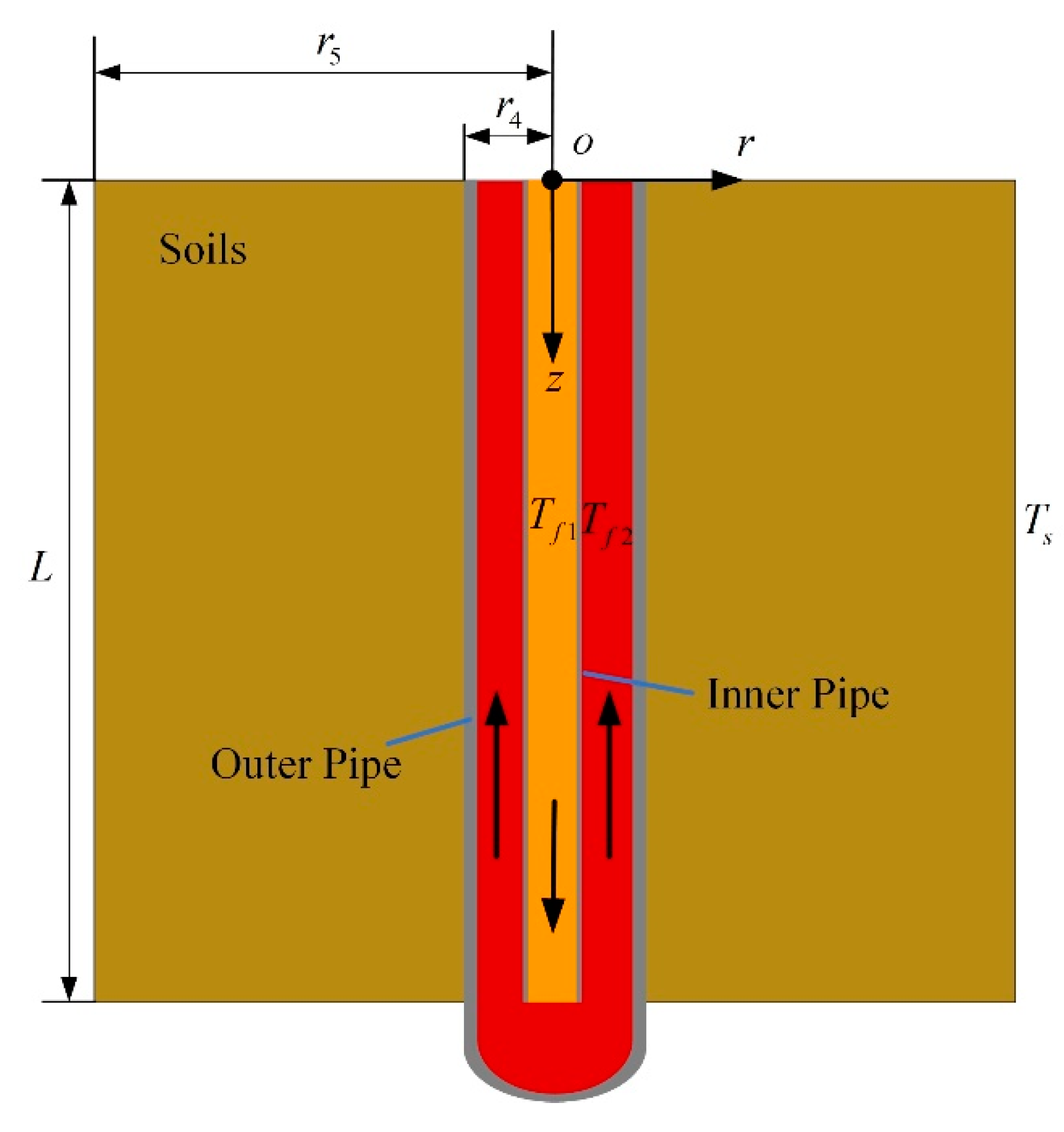
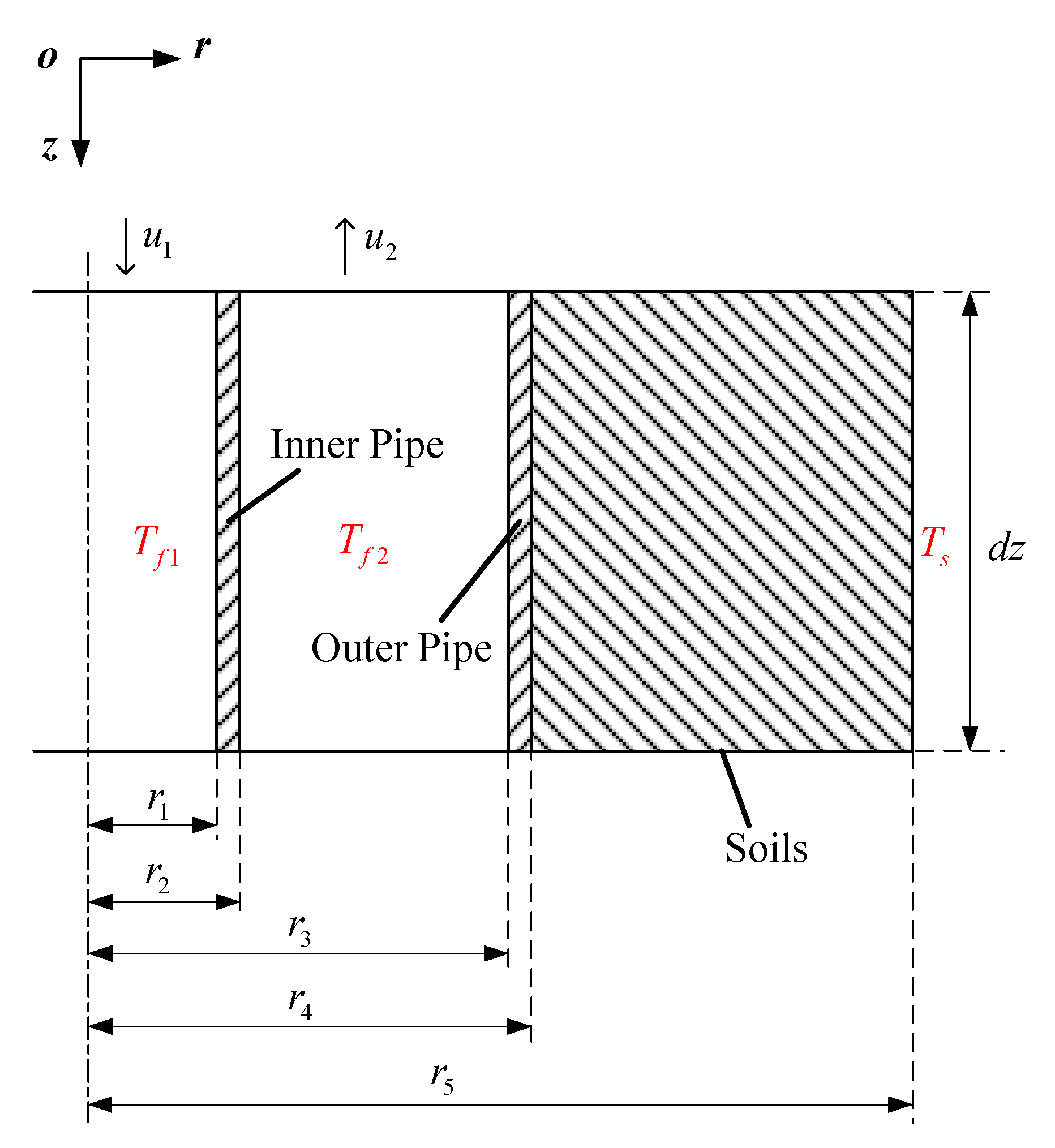
2.2.2. Model of Thermal Well
- (1)
- Soil is homogeneous.
- (2)
- The temperature and speed of the same section of fluid in thermal well are the same.
- (3)
- In the model of thermal wells, the thermophysical parameters of soil are invariable, and moisture transfer is ignored.
- (4)
- The energy loss at the junction of the inner pipe and the bottom of the outer pipe is not considered.
- (5)
- The thermophysical parameters of flue gas do not change with temperature in thermal wells.
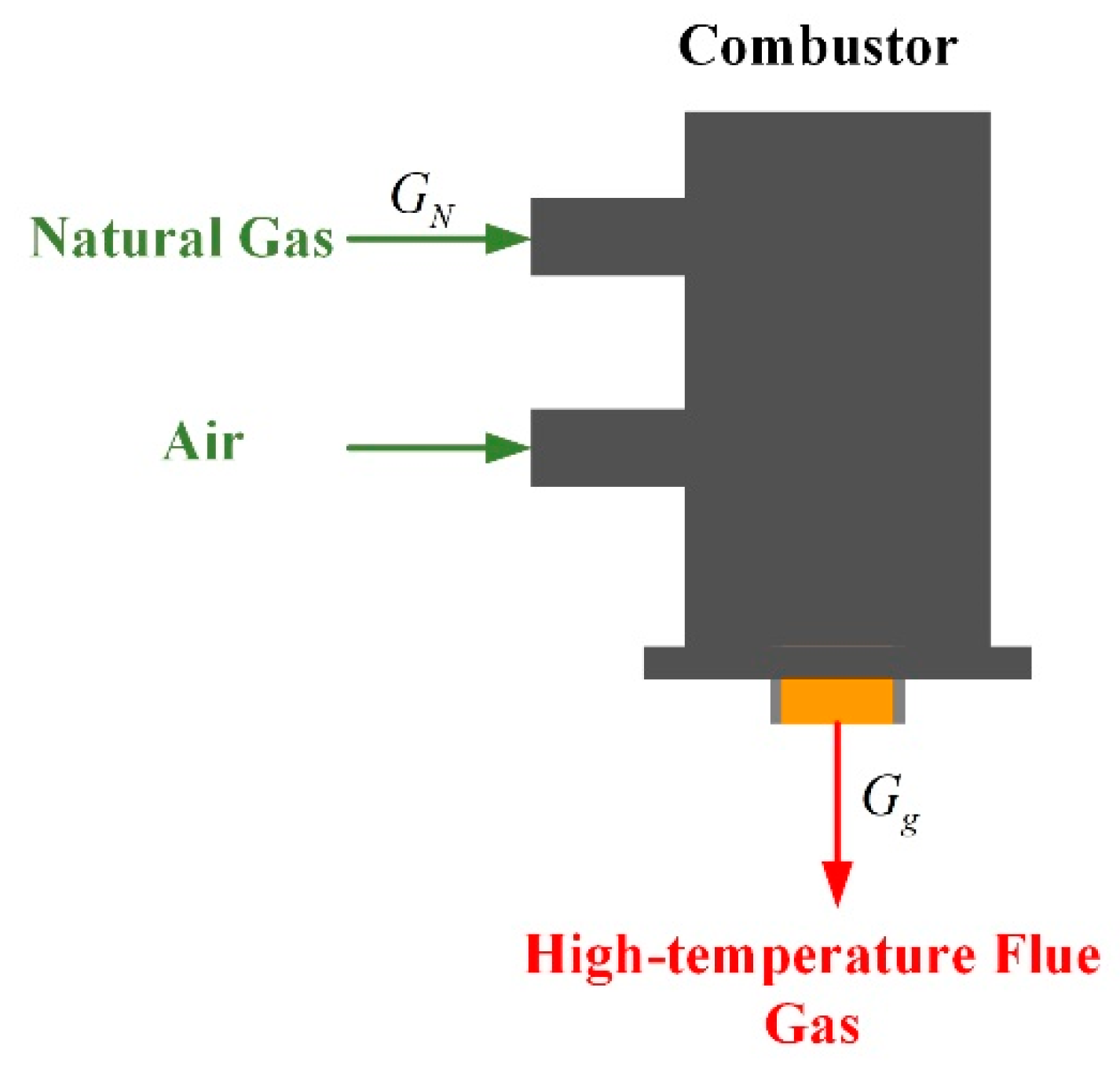
2.2.3. Model of Combustor
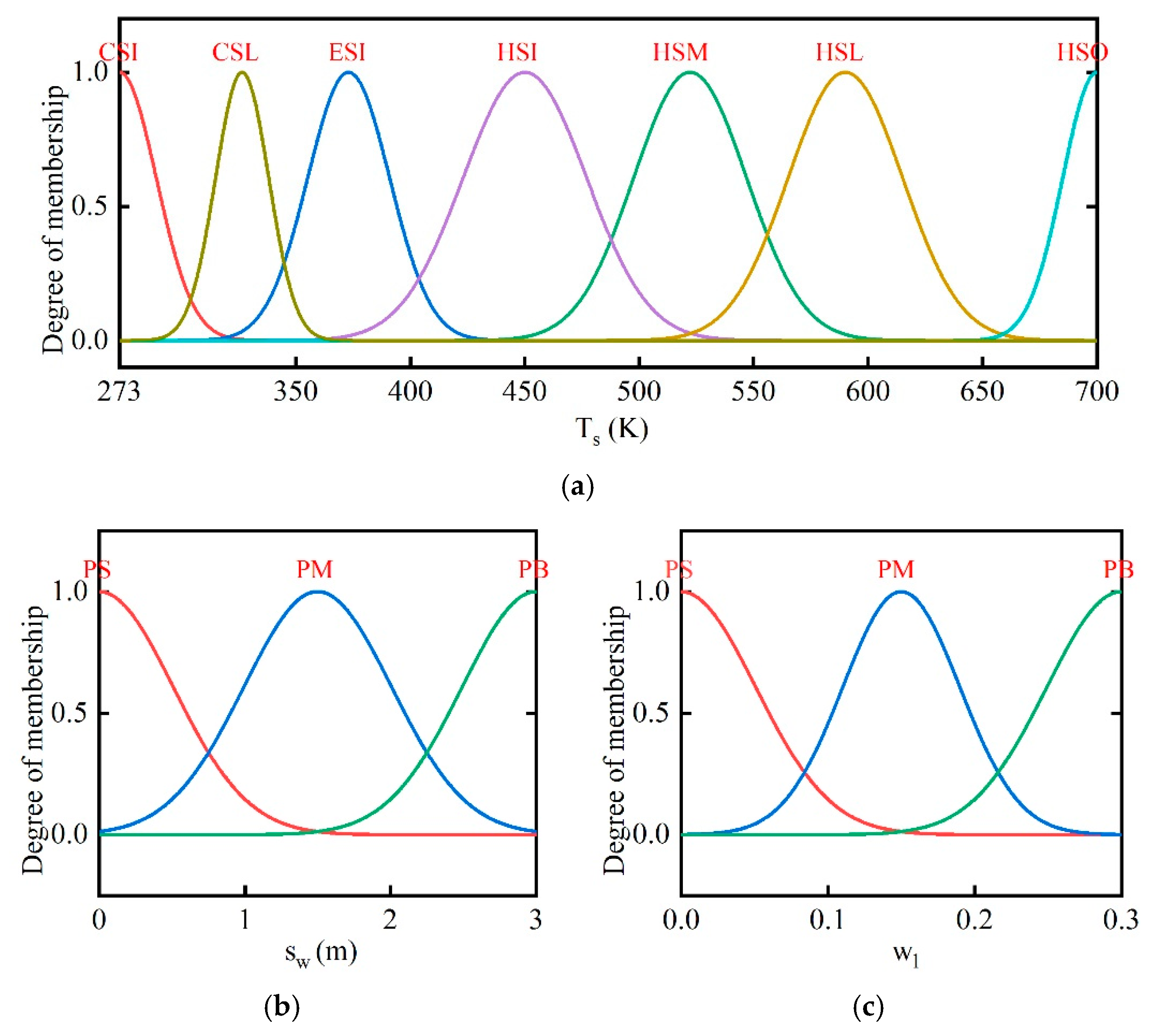
2.3. Fuzzy Coordination Control Strategy
- (1)
- If the position of wells is closer to the boundary, the set values of combustors’ and wells’ outlet temperature should be higher.
- (2)
- As the soil temperature increases and the water content decreases gradually, the desired outlet temperatures of combustors and thermal wells are set to be larger. The temperatures are set to be lower in the early stage and can reduce energy consumption.
3. Results and Discussion
- Case 1: natural gas flow and excess air ratio are constant;
- Case 2: the desired outlet temperature of thermal wells and excess air ratio are constant;
- Case 3: the desired outlet temperature of combustors and thermal wells are constant;
- Case 4: fuzzy coordination control strategy.
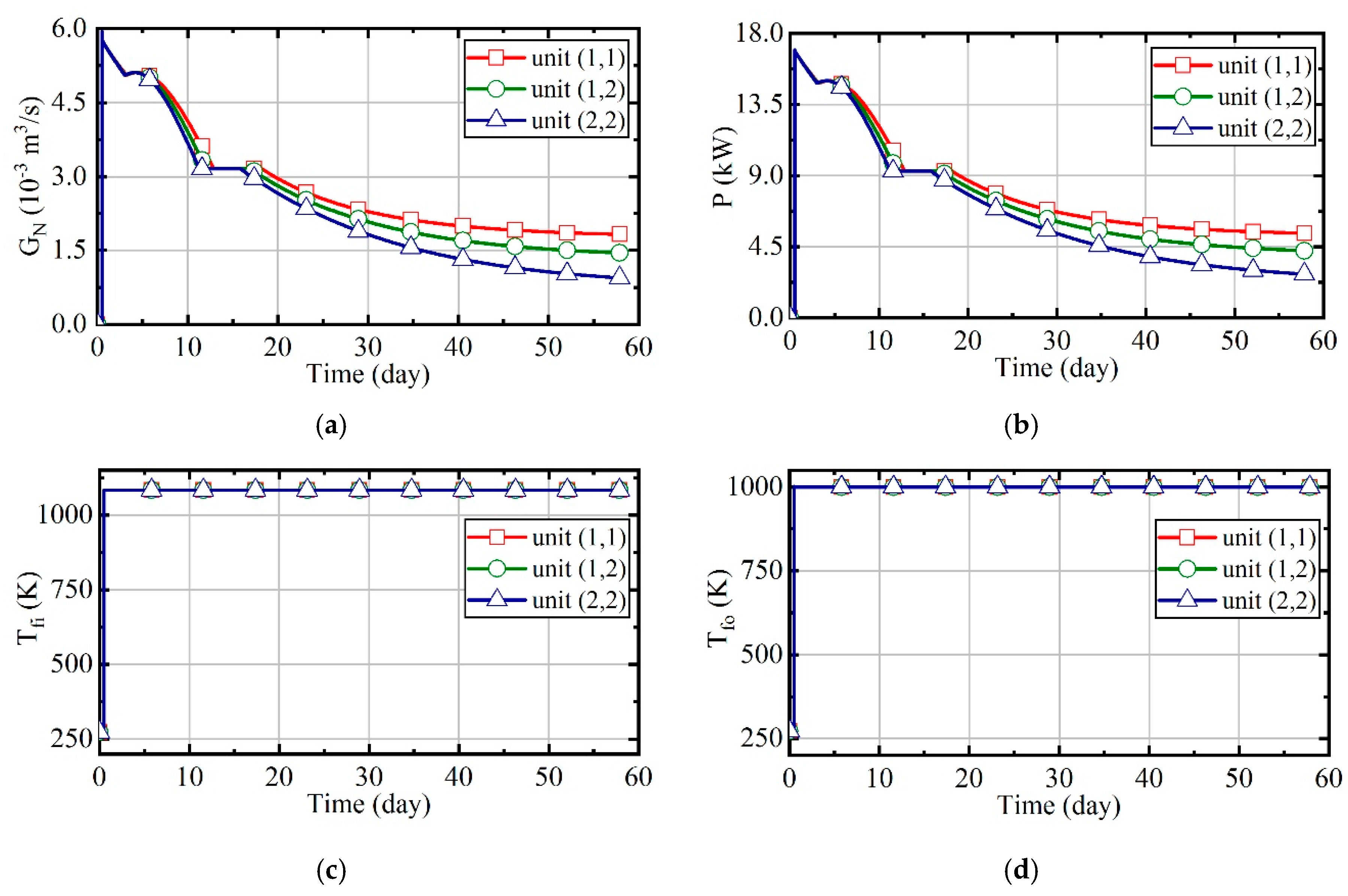
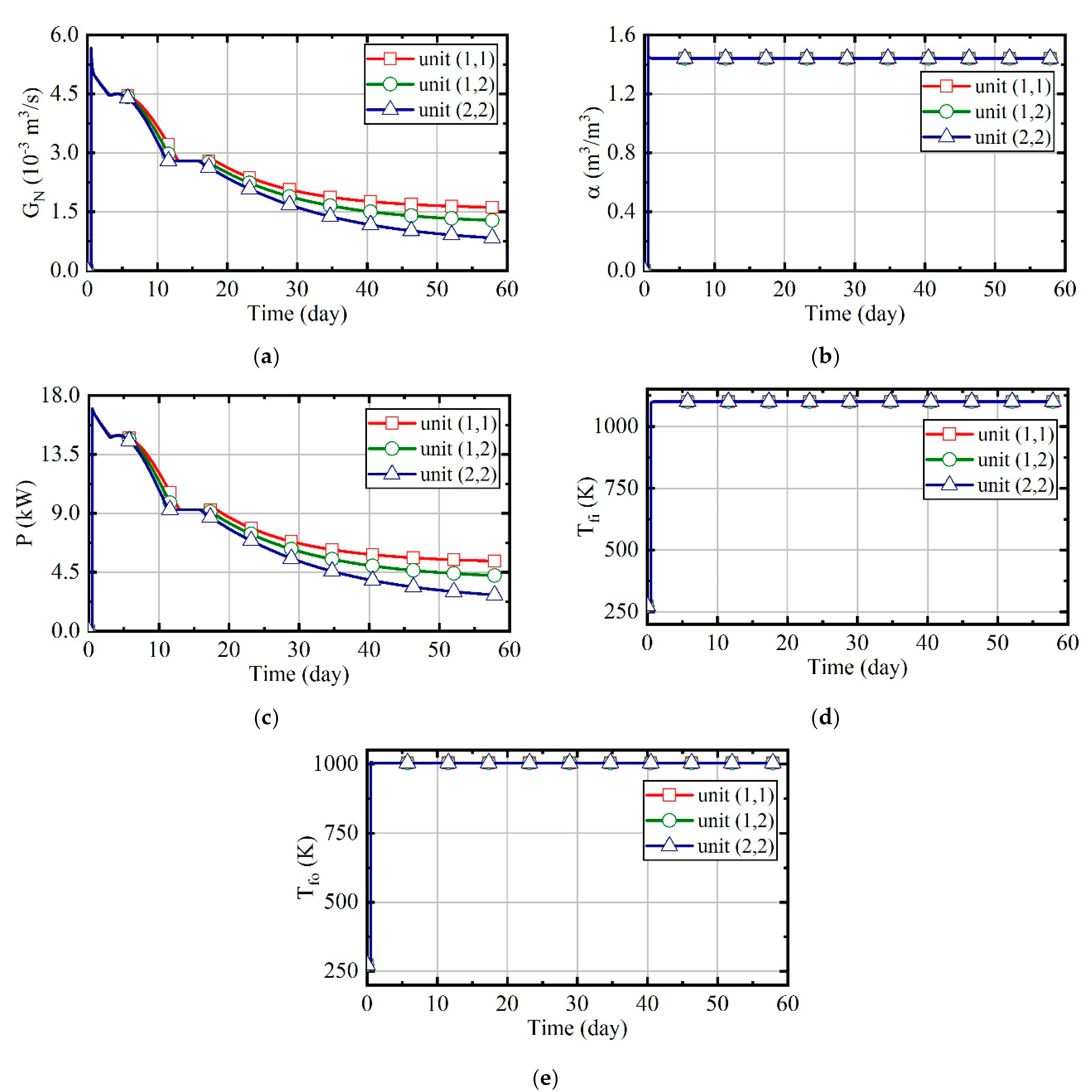
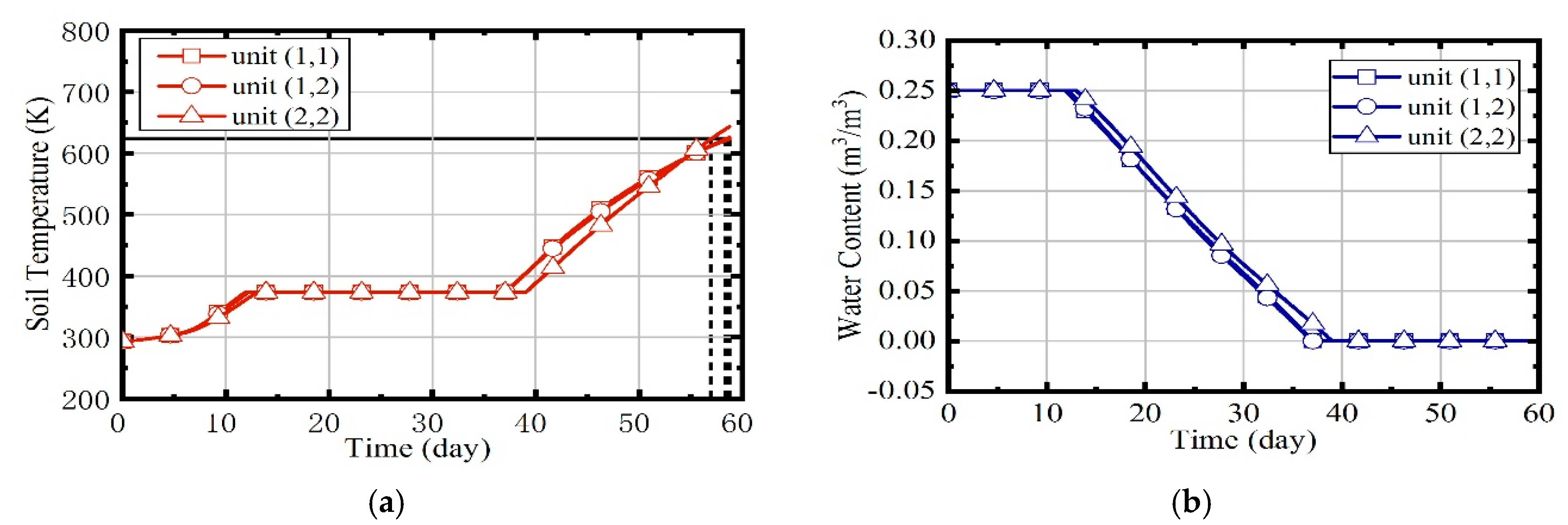
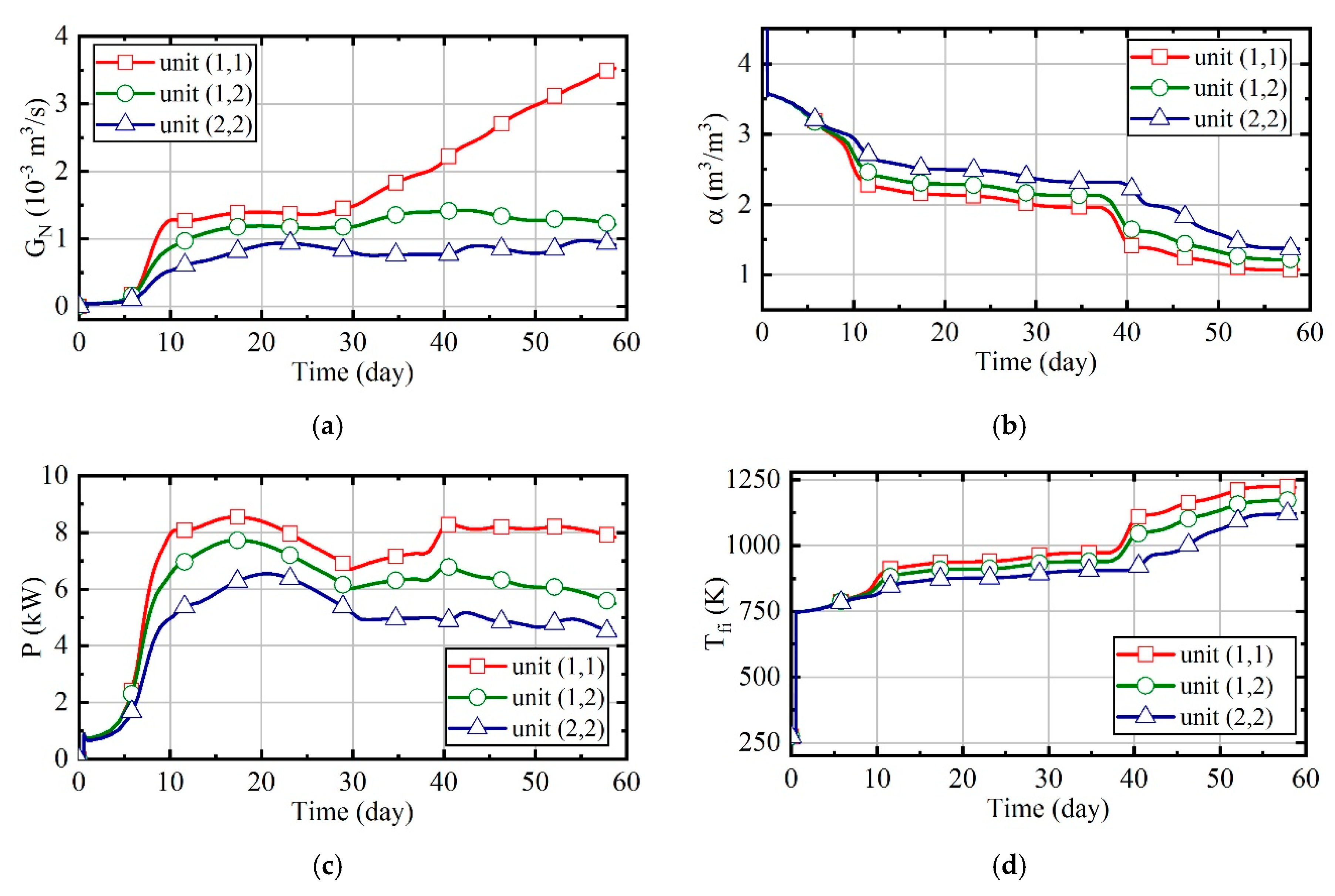
3.1. Case 1: Constant Natural Gas Flow and Excess Air Ratio
3.2. Case 2: Constant Excess Air Ratio and Desired Outlet Temperature of Thermal Wells
3.3. Case 3: Constant Desired Outlet Temperature of Combustors and Thermal Wells
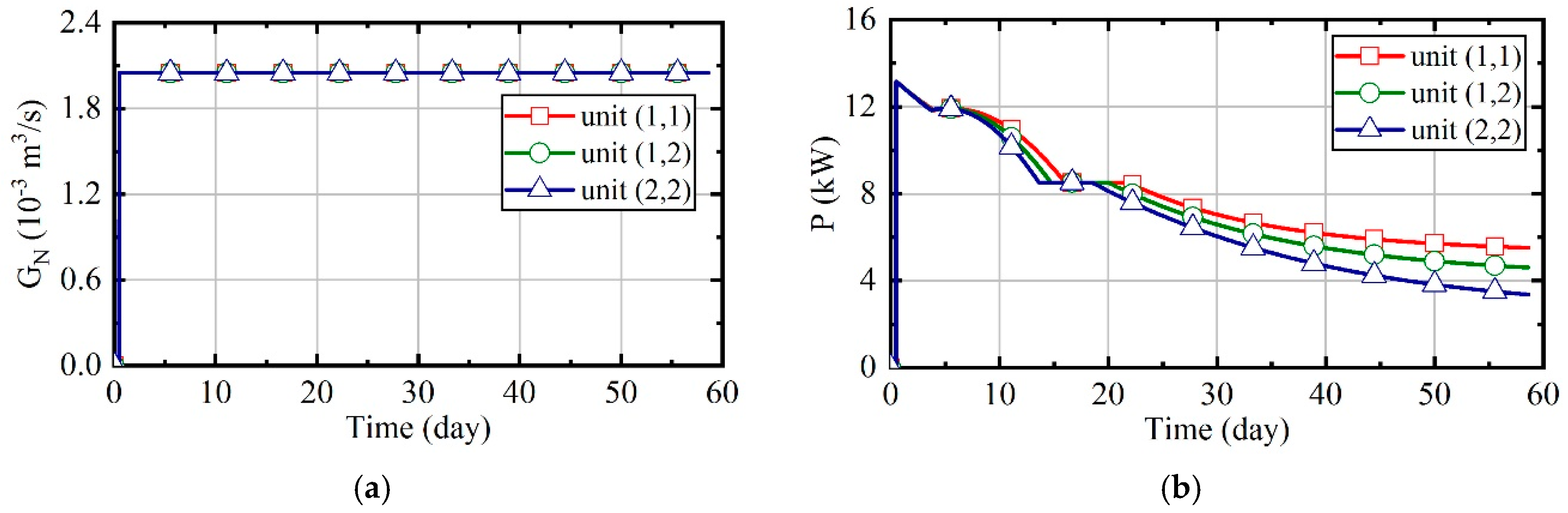
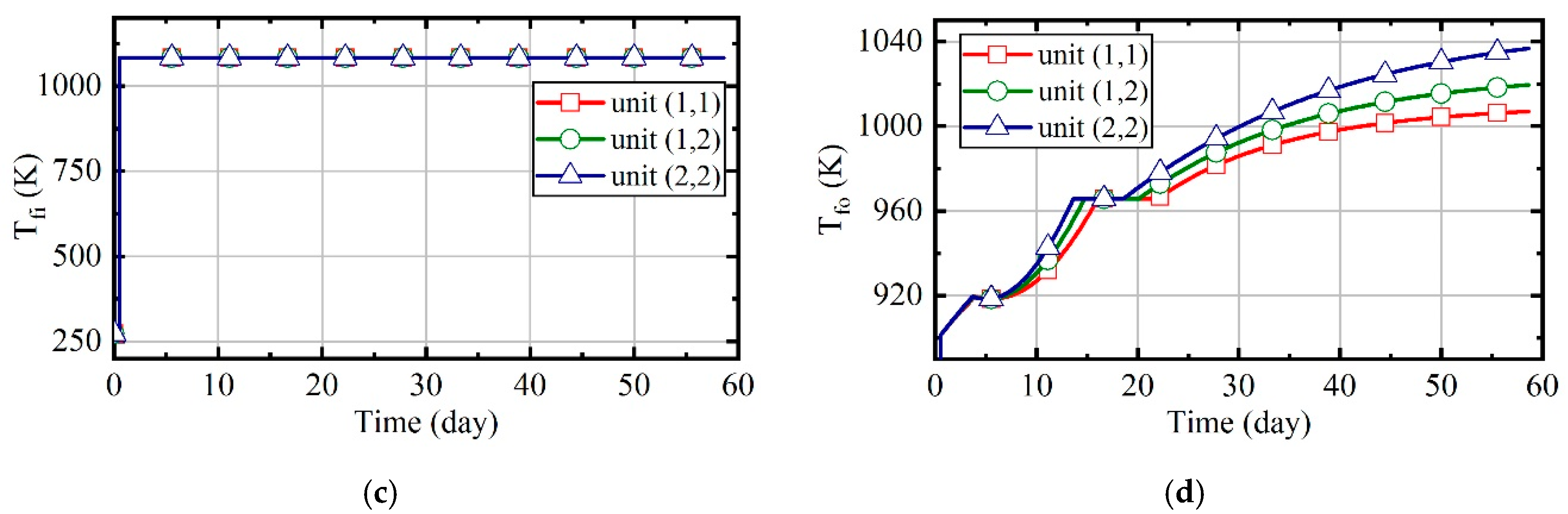
3.4. Case 4: Fuzzy Coordination Control Strategy
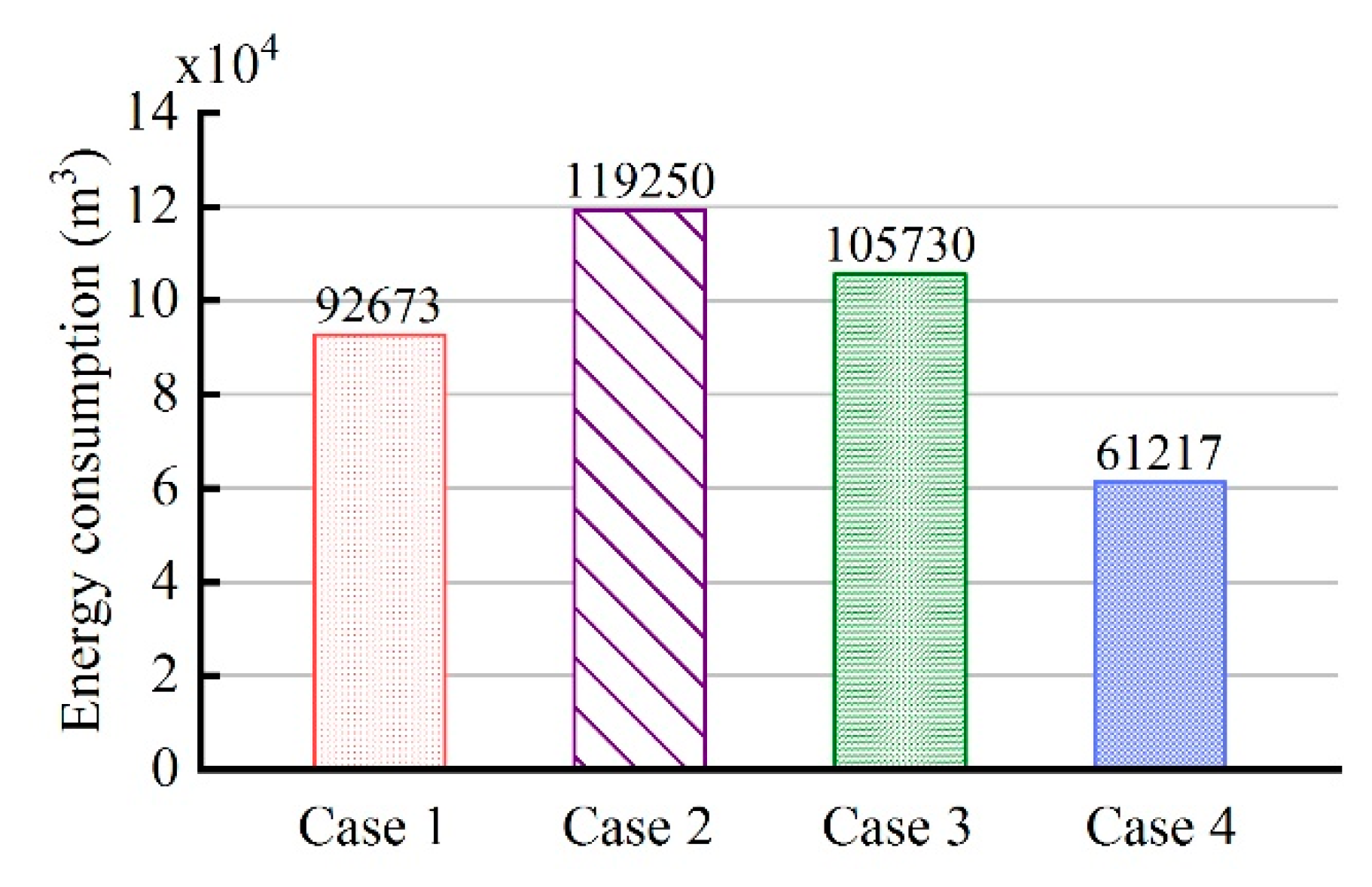
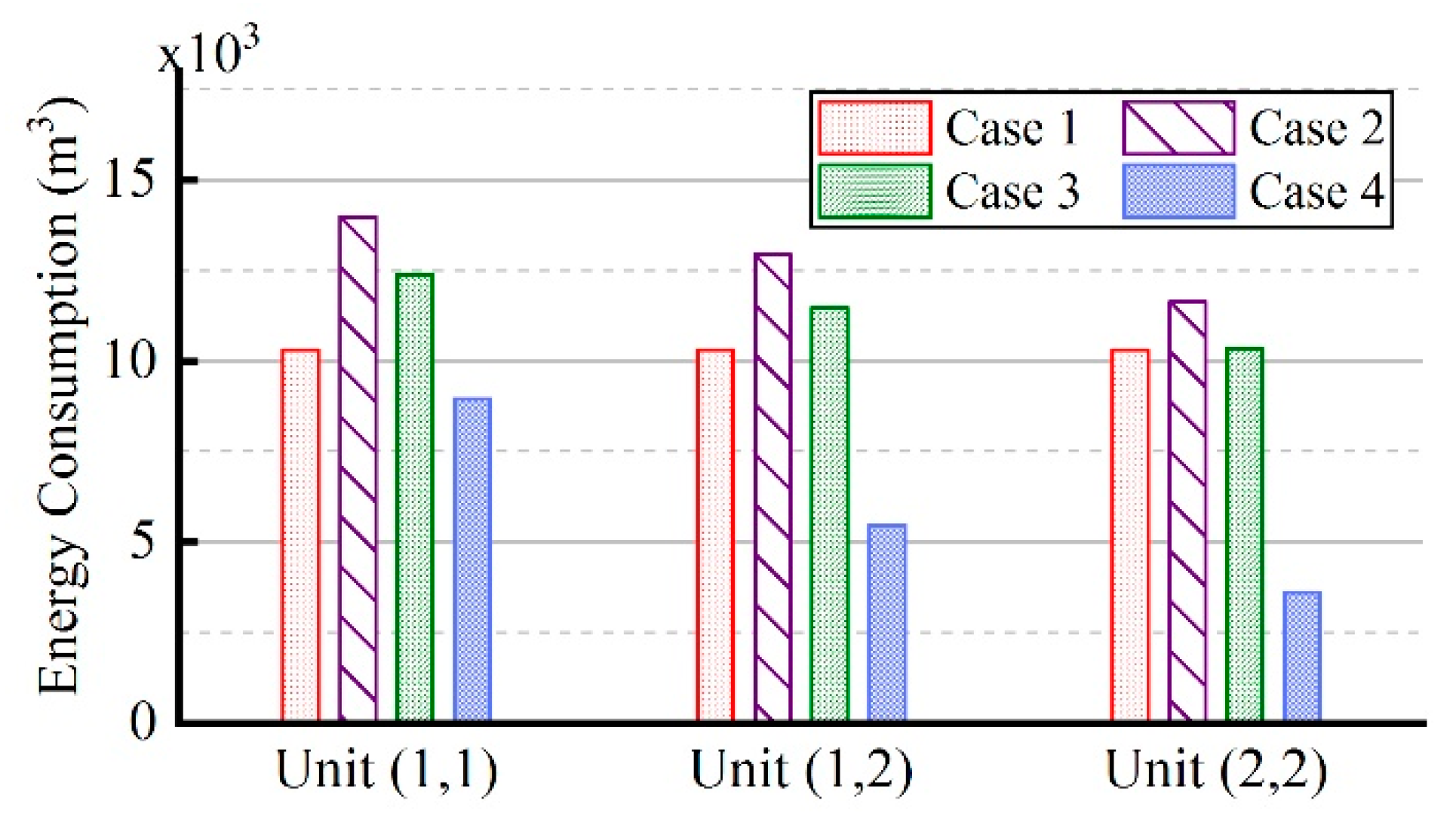
3.5. Comparison of Energy Consumption in Four Cases
4. Conclusions
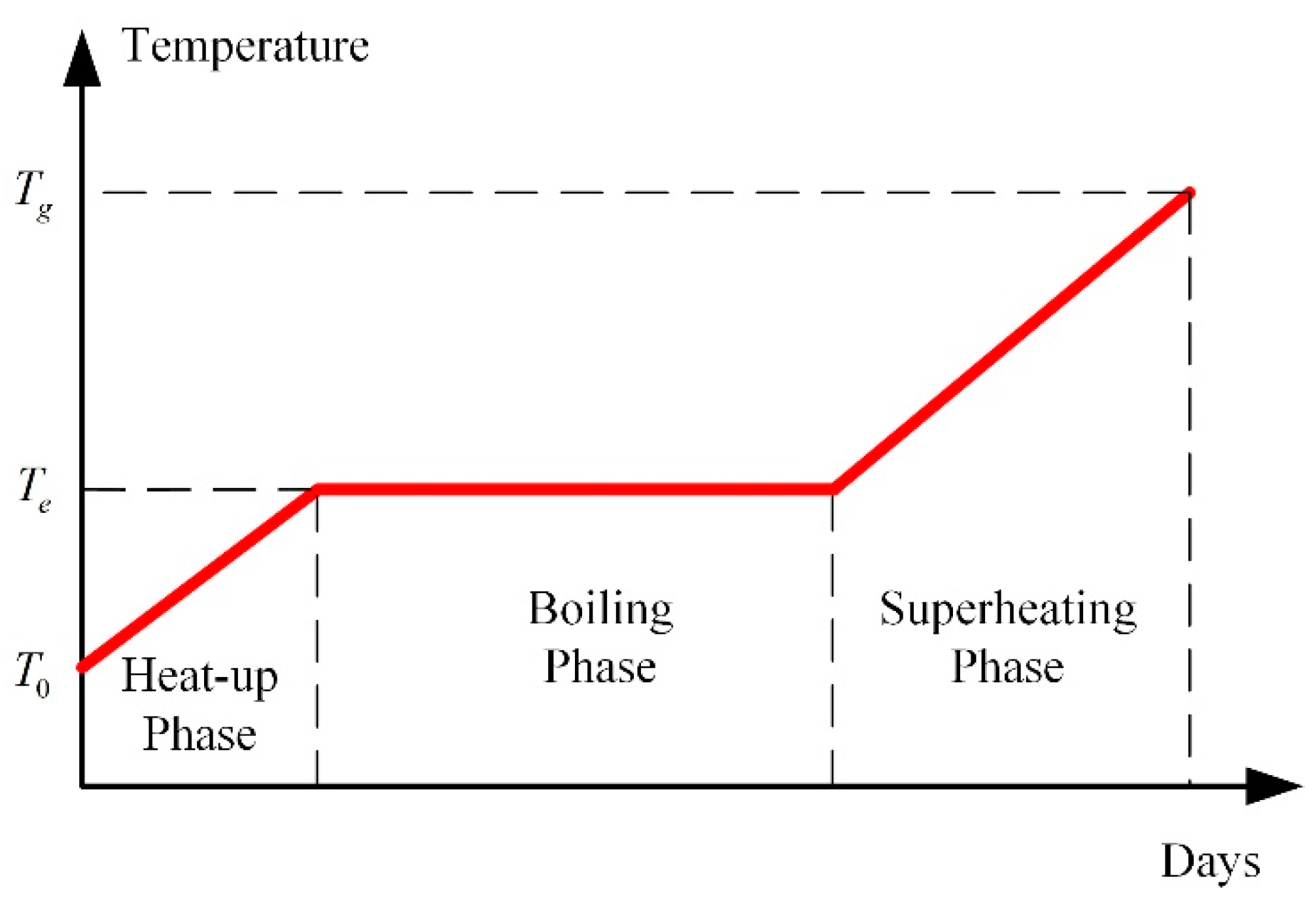
- (1)
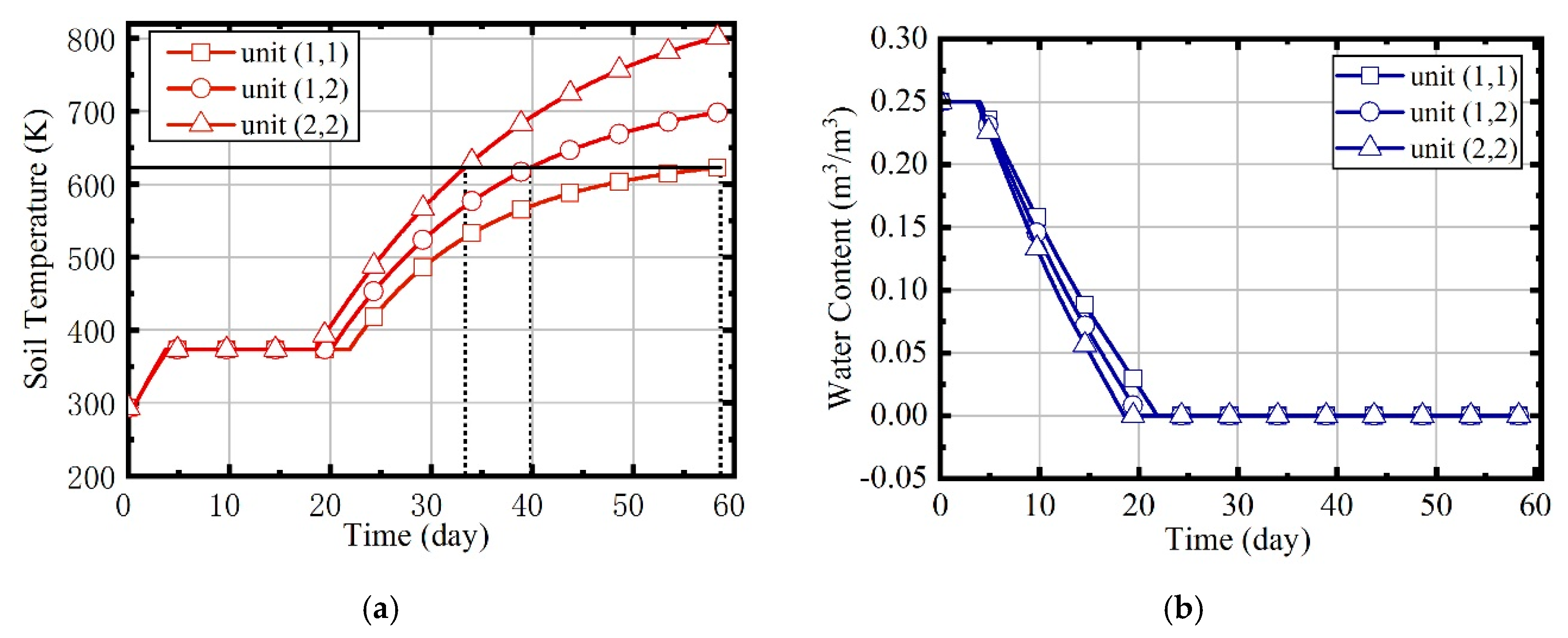
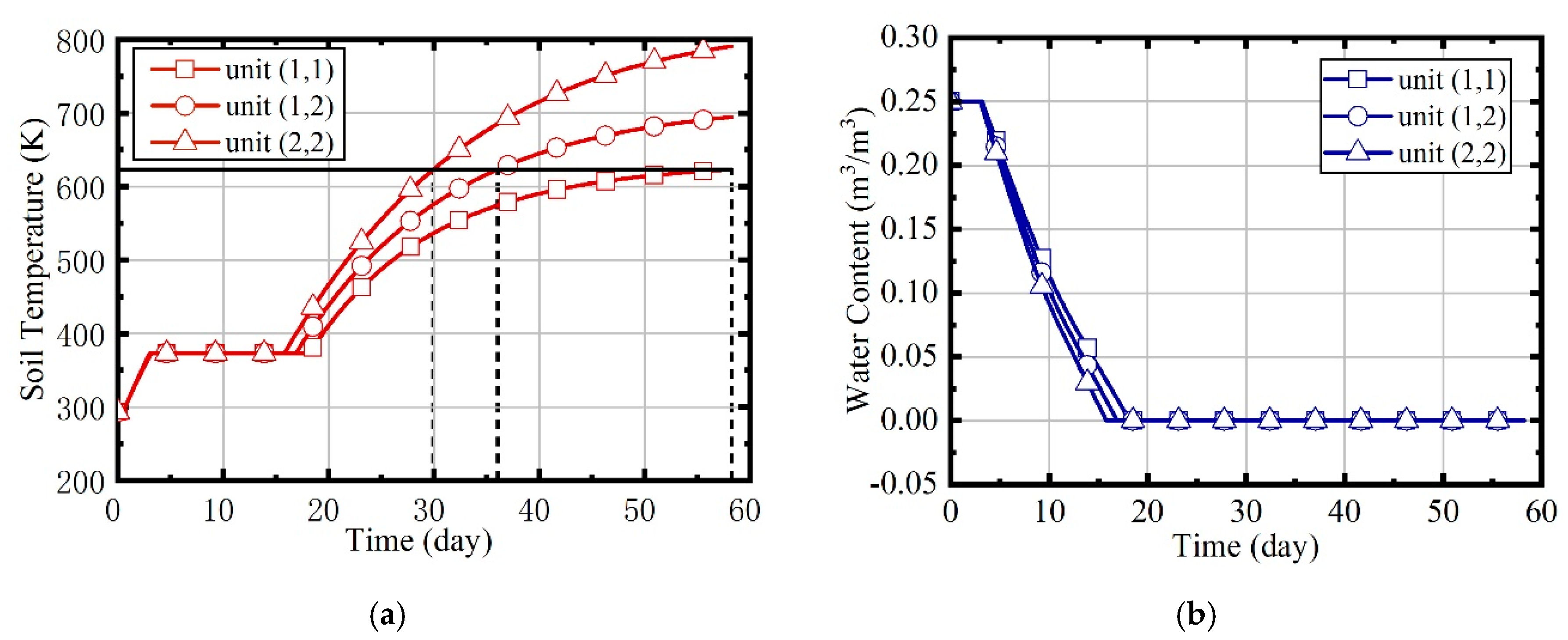
- When the site is heated by indiscriminate energy, the soil at the boundary is warmed more slowly due to the larger heat dissipation;
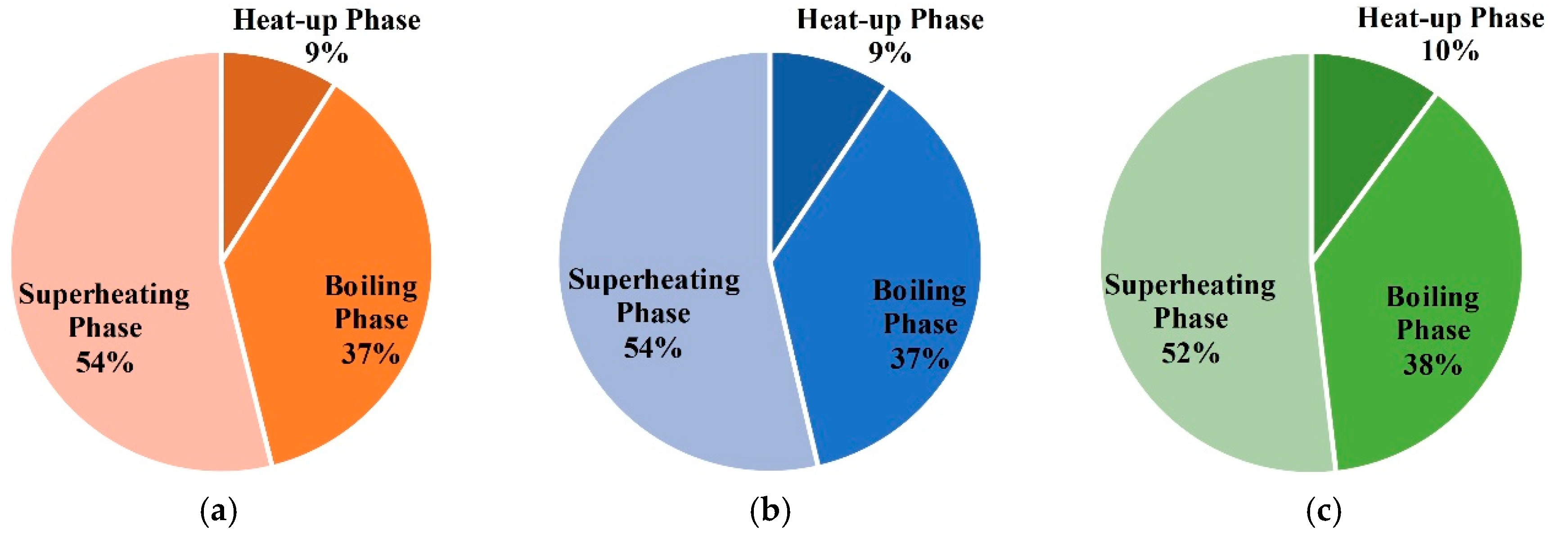
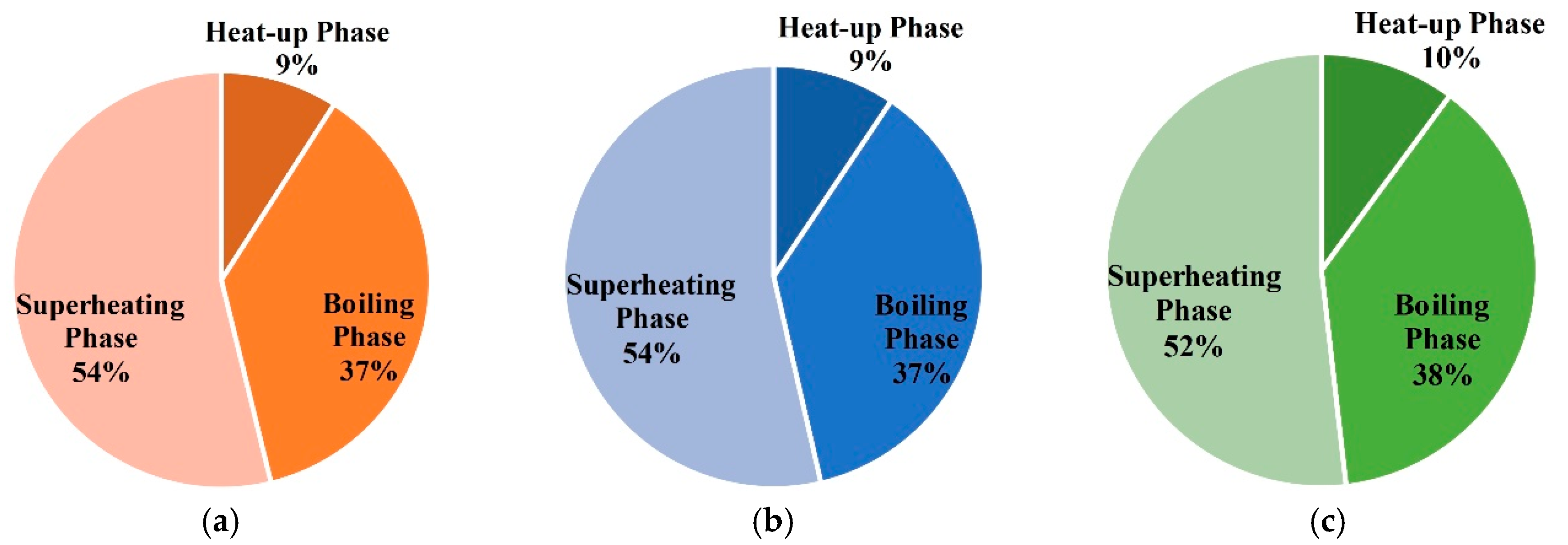
- (2)
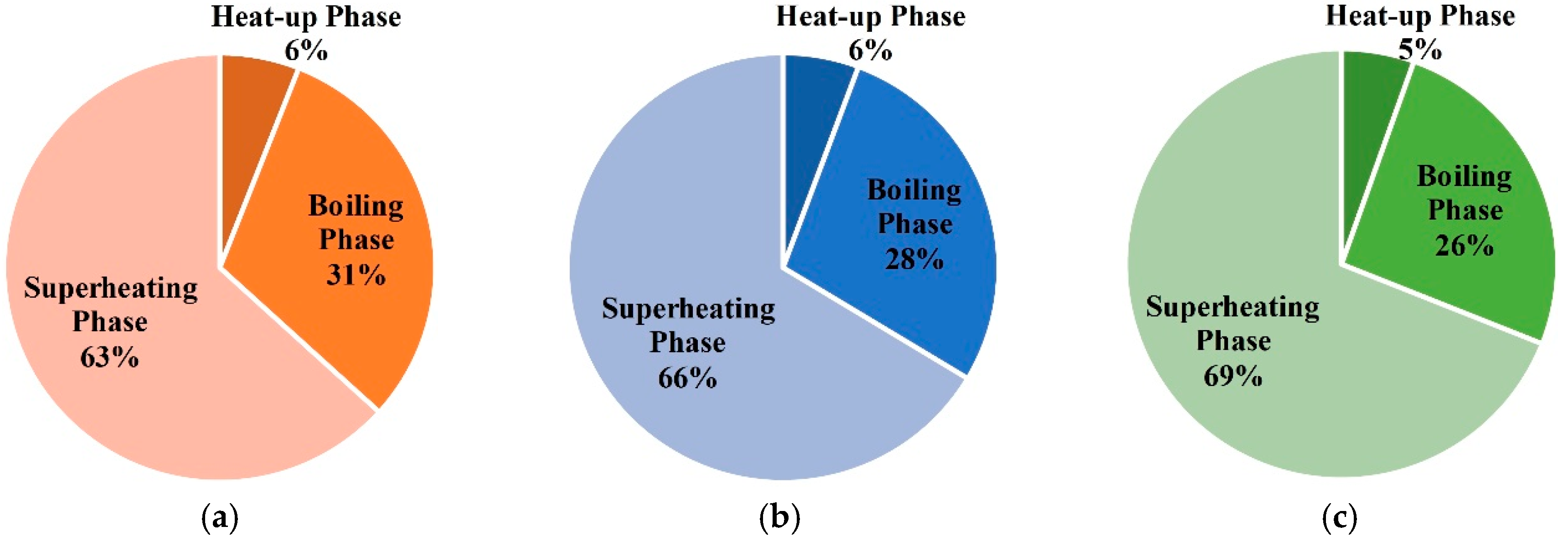
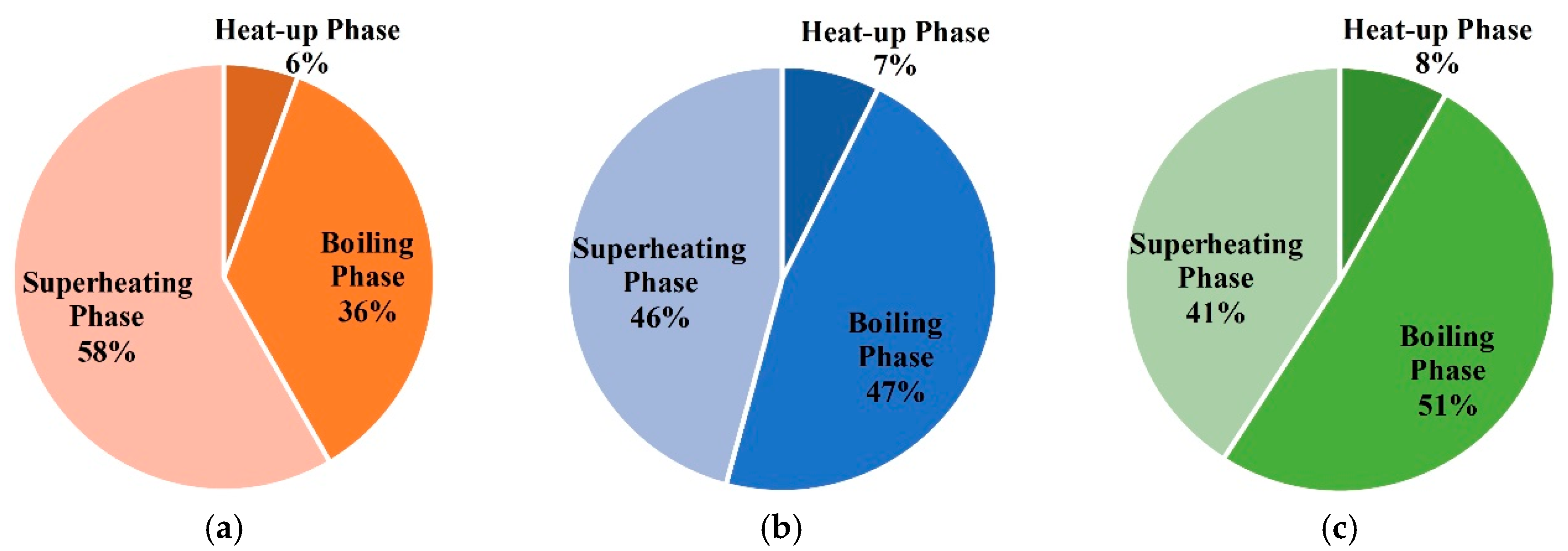
- In the three phases of soil warming, the proportions of energy consumption in the boiling phase and superheating phase are the largest, and that of the heat-up phase is the smallest;
- (3)
- Compared to the traditional control strategy I, that is, constant natural gas flow and excess air ratio, the fuzzy coordination control strategy can reduce energy consumption by 33.9%.
- (4)
- Compared to the traditional control strategy II, that is, constant excess air ratio and desired outlet temperature of wells, the fuzzy coordination control strategy can reduce energy consumption by 48.7%.
- (5)
- After the regulation of the fuzzy coordination control strategy, the soil heating rate is almost the same at different locations, and compared to soils in different locations, the energy consumption of soils located centrally was mostly reduced.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Symbol | |||
| T | Kelvin temperature (K) | Excess air ratio | |
| t | Celsius temperature (℃) | G | Flow |
| w | content of material | Latent heat of water | |
| i | Longitudinal arrangement number of the thermal well | V | Volume (m3) |
| j | Horizontal arrangement number of the thermal well | Thermal conductivity | |
| Density (kg/m3) | u | Flow rate of flue gases (m/s) | |
| h | Convective heat transfer coefficient | R | Thermal resistance |
| Time (s) | Subscript | ||
| E | The mass of liquid evaporated in unit time (kg/s) | s | Soil particle |
| J | The mass of migration (kg/s) | l | Liquid |
| Soil water potential (J/kg) | v | Vapor | |
| A | Area (m2) | f1 | Flue gas in inner pipe |
| D | diffusivity (m/s) | f2 | Flue gas in annular space |
| Porosity of soils (m3/m3) | g | Flue gas | |
| p | Pressure (Pa) | fi | Inlet of thermal wells |
| L | Thermal well depth (m) | fo | Outlet of thermal wells |
| S | Thermal well spacing (m) | N | Natural gas |
| M | Mass (kg) | T | Total |
| c | Specific heat capacity | (i, j) | The number of unit |
| Heat flux (J/s) | up | Surface of soils | |
| P | Heating power of thermal wells (kW) | down | Below the heating zone |
| H | Enthalpy (J/kg) | sd | Side of the unit block |
| r | Radius (m) | lw | Humidity gradient |
| z | Depth (m) | lT | Temperature gradient |
| Q | Heat (J) | a | Atmosphere |
References
- Jaoude, L.A.; Garau, G.; Nassif, N.; Darwish, T.; Castaldi, P. Metal(loid)s immobilization in soils of Lebanon using municipal solid waste compost: Microbial and biochemical impact. Appl. Soil Ecol. 2019, 143, 134–143. [Google Scholar] [CrossRef]
- Xu, J.; Wang, F.; Sun, C.; Zhang, X.; Zhang, Y. Gas thermal remediation of an organic contaminated site: Field trial. Environ. Sci. Pollut. Res. 2019, 26, 6038–6047. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Dong, B.B.; Bai, Y.Y.; Zhang, M.; Xie, Y.F.; Shi, Y.; Du, X.M. Remediation status and practices for contaminated sites in china: Survey-based analysis. Environ. Sci. Pollut. Res. 2018, 25, 33216–33224. [Google Scholar] [CrossRef] [PubMed]
- Van Liedekerke, M.; Prokop, G.; Rabl-Berger, S.; Kibblewhite, M.; Louwagie, G. Progress in the management of contaminated sites in Europe. Ref. Rep. Jt. Res. Centre Eur. Comm. 2014, 1, 4–6. [Google Scholar]
- Sun, Y.; Guan, F.; Yang, W. Removal of Chromium from a Contaminated Soil Using Oxalic Acid, Citric Acid, and Hydrochloric Acid: Dynamics, Mechanisms, and Concomitant Removal of Non-Targeted Metals. Int. J. Environ. Res. Public Health 2019, 16, 2771. [Google Scholar] [CrossRef] [PubMed]
- Pape, A.; Switzer, C.; McCosh, N.; Knapp, C.W. Impacts of thermal and smouldering remediation on plant growth and soil ecology. Geoderma 2015, 243, 1–9. [Google Scholar] [CrossRef]
- Carboneras, M.B.; Rodrigo, M.A.; Canizares, P.; Villaseñor, J.; Fernandez-Morales, F.J. Electro-irradiated technologies for clopyralid removal from soil washing effluents. Sep. Purif. Tech. 2019, 227, 115728. [Google Scholar] [CrossRef]
- Zhao, X.; Qin, L.; Gatheru, W.M.; Cheng, P.; Yang, B.; Wang, J.; Ling, W. Removal of Bound PAH Residues in Contaminated Soils by Fenton Oxidation. Catalysts 2019, 9, 619. [Google Scholar] [CrossRef]
- Bonnard, M.; Devin, S.; Leyval, C.; Morel, J.L.; Vasseur, P. The influence of thermal desorption on genotoxicity of multipolluted soil. Ecotoxicol. Environ. Saf. 2010, 73, 955–960. [Google Scholar] [CrossRef]
- O’Brien, P.L.; DeSutter, T.M.; Casey, F.X.; Khan, E.; Wick, A.F. Thermal remediation alters soil properties—A review. J. Environ. Manag. 2018, 206, 826–835. [Google Scholar] [CrossRef]
- O’Brien, P.L.; DeSutter, T.M.; Casey, F.X.; Derby, N.E.; Wick, A.F. Implications of using thermal desorption to remediate contaminated agricultural soil: physical characteristics and hydraulic processes. J. Environ. Qual. 2016, 45, 1430–1436. [Google Scholar] [CrossRef] [PubMed]
- Stegemeier, G.L.; Vinegar, H.J. Thermal conduction heating for in-situ thermal desorption of soils. Hazard. Radioact. Waste Treat. Tech. Handb. 2001, 1–37. [Google Scholar]
- Aresta, M.; Dibenedetto, A.; Fragale, C.; Giannoccaro, P.; Pastore, C.; Zammiello, D.; Ferragina, C. Thermal desorption of polychlorobiphenyls from contaminated soils and their hydrodechlorination using Pd-and Rh-supported catalysts. Chemosphere 2008, 70, 1052–1058. [Google Scholar] [CrossRef] [PubMed]
- Biache, C.; Mansuy-Huault, L.; Faure, P.; Munier-Lamy, C.; Leyval, C. Effects of thermal desorption on the composition of two coking plant soils: impact on solvent extractable organic compounds and metal bioavailability. Environ. Pollut. 2008, 156, 671–677. [Google Scholar] [CrossRef]
- Sakaguchi, I.; Inoue, Y.; Nakamura, S.; Kojima, Y.; Sasai, R.; Sawada, K.; Katayama, A. Assessment of soil remediation technologies by comparing health risk reduction and potential impacts using unified index, disability-adjusted life years. Clean Tech. Environ. Policy 2015, 17, 1663–1670. [Google Scholar] [CrossRef]
- LaChance, J.; Heron, G.; Baker, R.; Bierschenk, J.M.; Jones, A. Verification of an improved approach for implementing in-situ thermal desorption for the remediation of chlorinated solvents. In Proceedings of the Fifth International Conference on Remediation of Chlorinated and Recalcitrant Compounds, Monterey, CA, USA, 22–25 May 2006. [Google Scholar]
- Kunkel, A.M.; Seibert, J.J.; Elliott, L.J.; Kelley, R.; Katz, L.E.; Pope, G.A. Remediation of elemental mercury using in situ thermal desorption (ISTD). Environ. Sci. Tech. 2006, 40, 2384–2389. [Google Scholar] [CrossRef]
- Chien, Y.C. Field study of in situ remediation of petroleum hydrocarbon contaminated soil on site using microwave energy. J. Hazard. Mater. 2012, 199, 457–461. [Google Scholar] [CrossRef]
- Heron, G.; Lachance, J.; Baker, R. Removal of PCE DNAPL from tight clays using in situ thermal desorption. Groundw. Monit. Remediat. 2013, 33, 31–43. [Google Scholar] [CrossRef]
- Baker, R.S.; Kuhlman, M. A description of the mechanisms of in-situ thermal destruction (ISTD) reactions. In Proceedings of the 2nd International Conference on Oxidation and Reduction Technologies for Soil and Groundwater, Toronto, ON, Canada, 17–21 November 2002. [Google Scholar]
- Vinegar, H.J. Thermal desorption cleans up PCB sites. Power Eng. 1998, 102, 43–46. [Google Scholar]
- Baker, R.S.; Vinegar, H.J.; Stegemeier, G.L. Use of Thermal Conduction to Enhance Soil Vapor Extraction. Contaminated Soils 1999, 4, 39–58. [Google Scholar]
- Cébron, A.; Cortet, J.; Criquet, S.; Biaz, A.; Calvert, V.; Caupert, C.; Pernin, C.; Leyval, C. Biological functioning of PAH-polluted and thermal desorption-treated soils assessed by fauna and microbial bioindicators. Res. Microbiol. 2011, 162, 896–907. [Google Scholar] [CrossRef] [PubMed]
- Vidonish, J.E.; Zygourakis, K.; Masiello, C.A.; Sabadell, G.; Alvarez, P.J. Thermal treatment of hydrocarbon-impacted soils: A review of technology innovation for sustainable remediation. Engineering 2016, 2, 426–437. [Google Scholar] [CrossRef]
- Heron, G.; Parker, K.; Fournier, S.; Wood, P.; Angyal, G.; Levesque, J.; Villecca, R. World’s Largest In Situ Thermal Desorption Project: Challenges and Solutions. Groundw. Monit. Remediat. 2015, 35, 89–100. [Google Scholar] [CrossRef]
- Park, C.M.; Katz, L.E.; Liljestrand, H.M. Mercury speciation during in situ thermal desorption in soil. J. Hazard. Mater. 2015, 300, 624–632. [Google Scholar] [CrossRef]
- Falciglia, P.P.; Giustra, M.G.; Vagliasindi, F.G.A. Low-temperature thermal desorption of diesel polluted soil: Influence of temperature and soil texture on contaminant removal kinetics. J. Hazard. Mater. 2011, 185, 392–400. [Google Scholar] [CrossRef]
- Falciglia, P.P.; Mancuso, G.; Scandura, P.; Vagliasindi, F.G. Effective decontamination of low dielectric hydrocarbon-polluted soils using microwave heating: Experimental investigation and modelling for in situ treatment. Sep. Purif. Technol. 2015, 156, 480–488. [Google Scholar] [CrossRef]
- Falciglia, P.P.; Urso, G.; Vagliasindi, F.G. Microwave heating remediation of soils contaminated with diesel fuel. J. Soils Sediment. 2013, 13, 1396–1407. [Google Scholar] [CrossRef]
- Baker, R.S.; LaChance, J.; Heron, G. In-pile thermal desorption of PAHs, PCBs and dioxins/furans in soil and sediment. Land Contam. Reclam. 2006, 14, 620–624. [Google Scholar] [CrossRef]
- Li, J.; Ang, X.F.; Lee, K.H.; Romanato, F.; Wong, C.C. In-situ monitoring of the thermal desorption of alkanethiols with surface plasmon resonance spectroscopy (SPRS). J. Nanosci. Nanotech. 2010, 10, 4624–4628. [Google Scholar] [CrossRef]
- Bulmău, C.; Mărculescu, C.; Lu, S.; Qi, Z. Analysis of thermal processing applied to contaminated soil for organic pollutants removal. J. Geochem. Explor. 2014, 147, 298–305. [Google Scholar] [CrossRef]
- Laumann, S.; Micić, V.; Fellner, J.; Clement, D.; Hofmann, T. Material flow analysis: An effectiveness assessment tool for in situ thermal remediation. Vadose Zone J. 2013, 12, 1–9. [Google Scholar] [CrossRef]
- De Vries, D.A. The theory of heat and moisture transfer in porous media revisited. Int. J. Heat Mass Transfer 1987, 30, 1343–1350. [Google Scholar] [CrossRef]
- Gardner, W.R.; Hillel, D.; Benyamini, Y. Post-irrigation movement of soil water: 1. Redistribution. Water Resour. Res. 1970, 6, 851–861. [Google Scholar] [CrossRef]
- Santander, R.E.; Bubnovich, V. Assessment of mass and heat transfer mechanisms in unsaturated soil. Int. Commun. Heat Mass Transf. 2002, 29, 531–545. [Google Scholar] [CrossRef]
- Parker, J.C.; Lenhard, R.J.; Kuppusamy, T. A parametric model for constitutive properties governing multiphase flow in porous media. Water Resour. Res. 1987, 23, 618–624. [Google Scholar] [CrossRef]
- Vinegar, H.J.; DeRouffignac, E.P.; Rosen, R.L.; Stegemeier, G.L.; Bonn, M.M.; Conley, D.M.; Arrington, D.H. Situ Thermal Desorption (ISTD) of PCBs; HazWaste World/Superfund XVIII: Washington, DC, USA, 1997. [Google Scholar]
- Li, Y.Z.; Lee, K.M.; Wang, J. Analysis and control of equivalent physical simulator for nanosatellite space radiator. IEEE/ASME Transact. Mechatron. 2009, 15, 79–87. [Google Scholar]
- Fei, J.; Wang, H.; Cao, D. Adaptive Backstepping Fractional Fuzzy Sliding Mode Control of Active Power Filter. Appl. Sci. 2019, 9, 3383. [Google Scholar] [CrossRef]

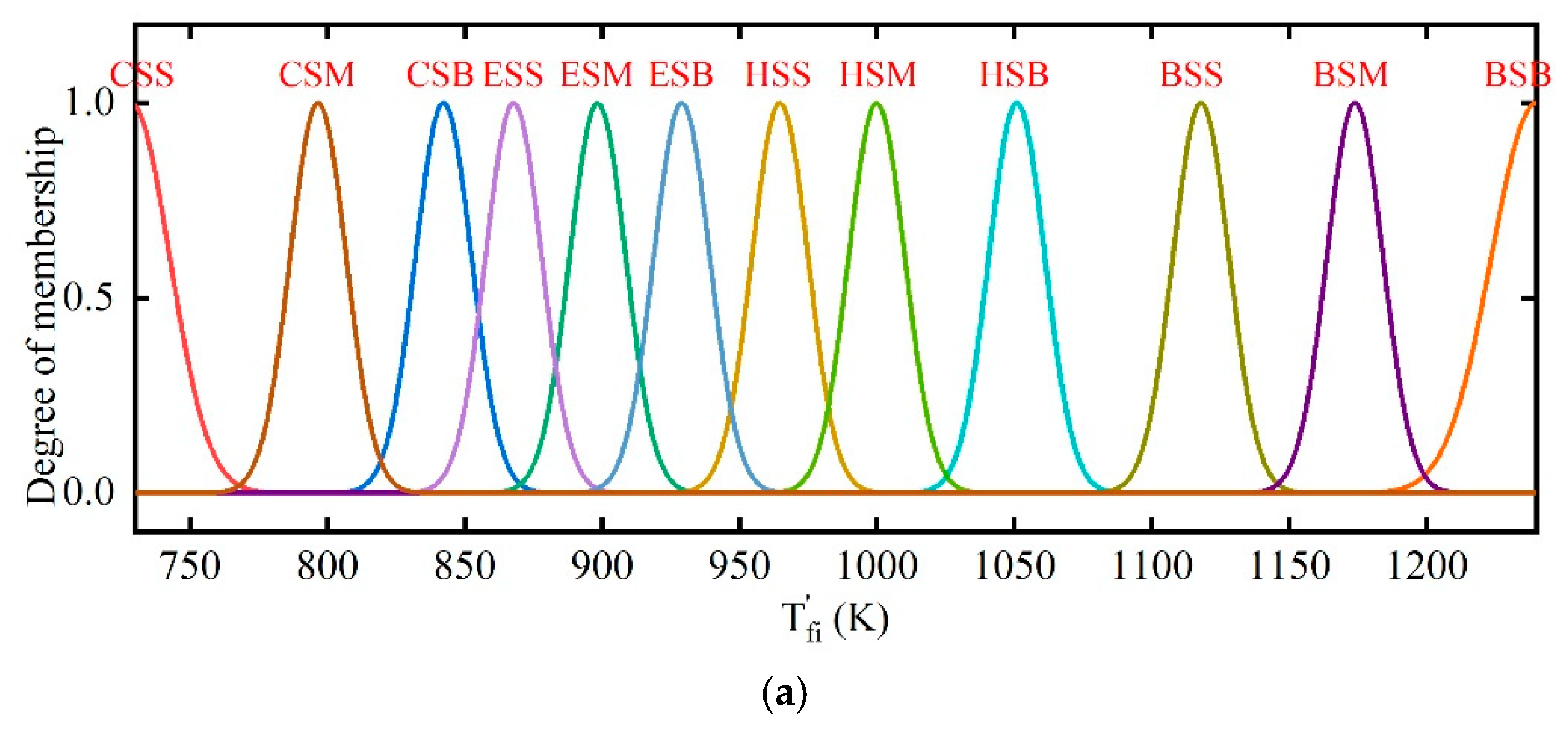
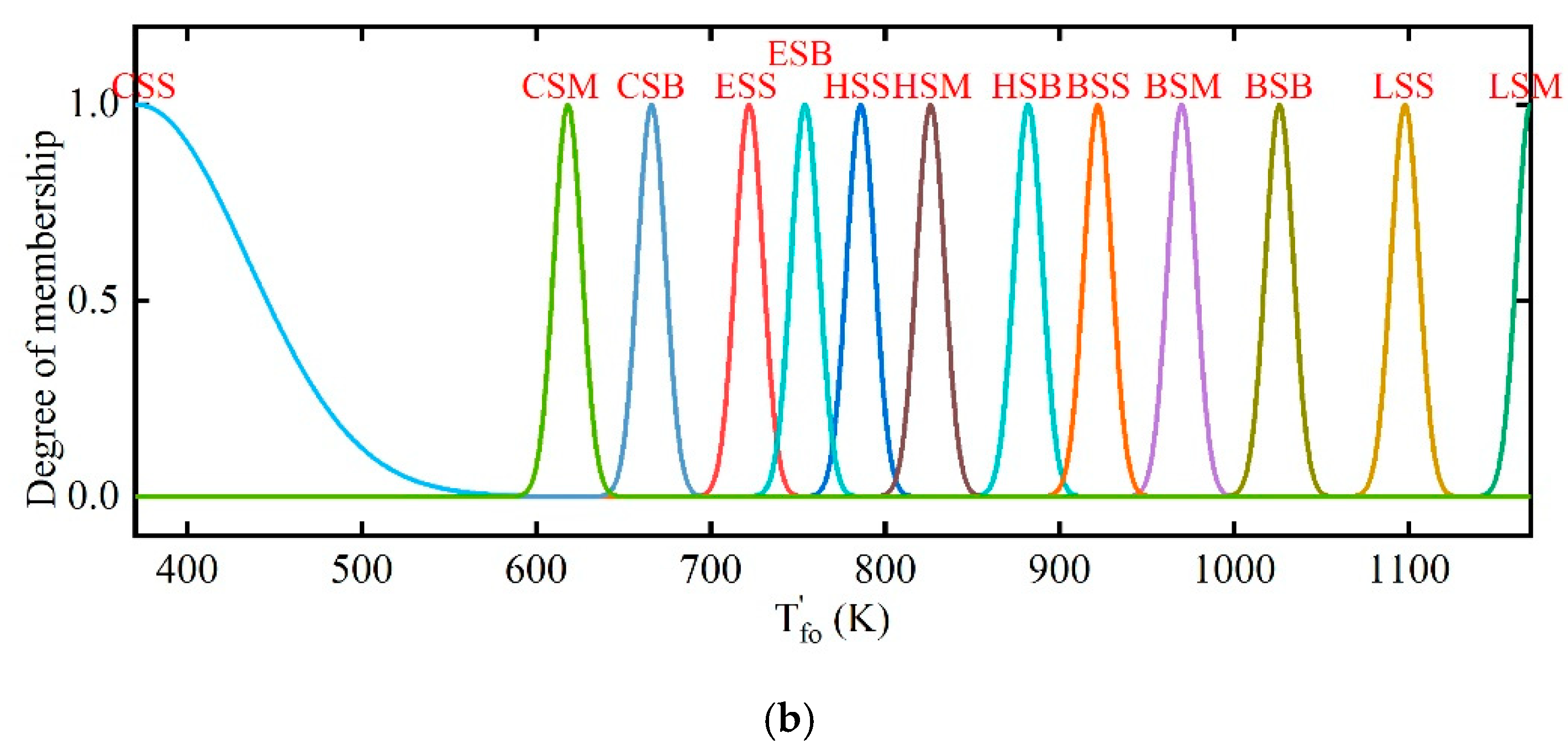


| CSI | PS | - | CSS | CSS | ESI | PB | PB | CSB | CSB |
| CSI | PM | - | CSS | CSS | HSI | PS | - | BSS | BSB |
| CSI | PB | - | CSS | CSS | HSI | PM | - | HSB | BSS |
| CSL | PS | - | CSM | ESS | HSI | PB | - | HSS | HSM |
| CSL | PM | - | CSM | CSB | HSM | PS | - | BSM | LSS |
| CSL | PB | - | CSM | CSM | HSM | PM | - | BSS | BSM |
| ESI | PS | PS | HSS | HSB | HSM | PB | - | HSB | HSB |
| ESI | PS | PM | ESB | HSS | HSL | PS | - | BSB | LSM |
| ESI | PS | PB | ESM | ESB | HSL | PM | - | BSM | BSB |
| ESI | PM | PS | ESB | HSM | HSL | PB | - | BSS | BSM |
| ESI | PM | PM | ESM | ESB | HSO | PS | - | CSB | ESS |
| ESI | PM | PB | ESS | ESS | HSO | PM | - | CSB | ESS |
| ESI | PB | PS | ESM | ESB | HSO | PB | - | CSB | ESS |
| ESI | PB | PM | ESS | ESS |
| Solid Density | Porosity | Saturated Hydraulic Conductivity | Specific Surface Area | Specific Heat of Dry Soils |
|---|---|---|---|---|
| 2650 kg/m3 | 0.37 | 1700 J/(kg·K) |
| Parameters | Values | Parameters | Values |
|---|---|---|---|
| Initial soil temperature | 20 °C | Moisture content | 25% |
| Initial vapor density | 0.748 kg/m3 | Target temperature | 350 °C |
| Well spacing S | 1.5 m | Viscosity of gas phase in soils | 1.81 × 10−5 Pa·s |
| Well depth L | 5 m | Latent heat of water | 2.25 × 106 J/kg |
| Radius of inner pipe | 0.1 m | Radius of outer pipe | 0.15 m |
| Thickness of inner pipe | 0.004 m | Thickness of outer pipe | 0.0045 m |
| Pressure of vacuum wells | 7000 Pa | Specific heat of liquid water | 4.2 × 103 J/(kg·K) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhai, Z.-Z.; Yang, L.-M.; Li, Y.-Z.; Jiang, H.-F.; Ye, Y.; Li, T.-T.; Li, E.-H.; Li, T. Fuzzy Coordination Control Strategy and Thermohydraulic Dynamics Modeling of a Natural Gas Heating System for In Situ Soil Thermal Remediation. Entropy 2019, 21, 971. https://doi.org/10.3390/e21100971
Zhai Z-Z, Yang L-M, Li Y-Z, Jiang H-F, Ye Y, Li T-T, Li E-H, Li T. Fuzzy Coordination Control Strategy and Thermohydraulic Dynamics Modeling of a Natural Gas Heating System for In Situ Soil Thermal Remediation. Entropy. 2019; 21(10):971. https://doi.org/10.3390/e21100971
Chicago/Turabian StyleZhai, Zhuang-Zhuang, Li-Man Yang, Yun-Ze Li, Hai-Feng Jiang, Yuan Ye, Tian-Tian Li, En-Hui Li, and Tong Li. 2019. "Fuzzy Coordination Control Strategy and Thermohydraulic Dynamics Modeling of a Natural Gas Heating System for In Situ Soil Thermal Remediation" Entropy 21, no. 10: 971. https://doi.org/10.3390/e21100971
APA StyleZhai, Z.-Z., Yang, L.-M., Li, Y.-Z., Jiang, H.-F., Ye, Y., Li, T.-T., Li, E.-H., & Li, T. (2019). Fuzzy Coordination Control Strategy and Thermohydraulic Dynamics Modeling of a Natural Gas Heating System for In Situ Soil Thermal Remediation. Entropy, 21(10), 971. https://doi.org/10.3390/e21100971





