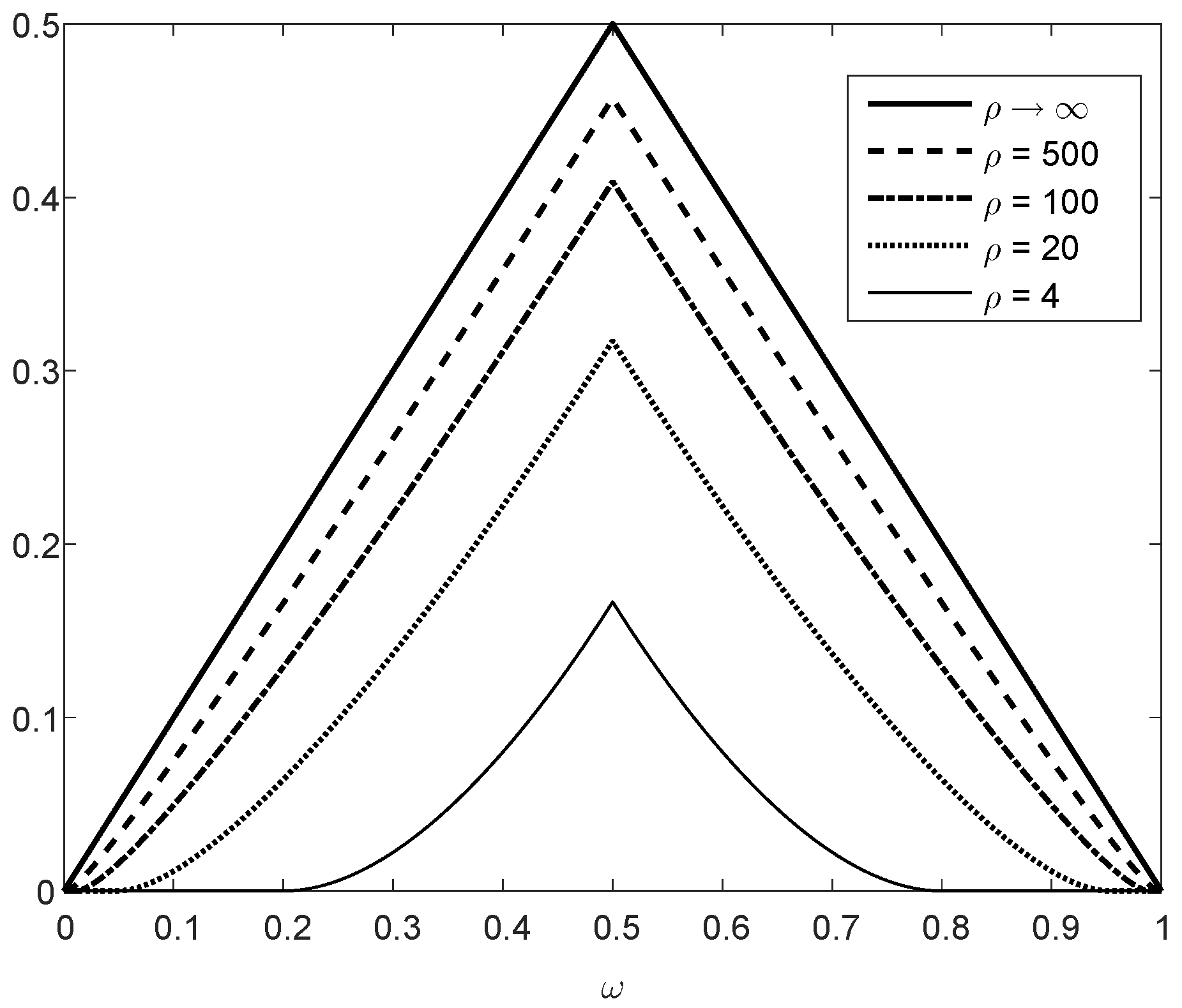
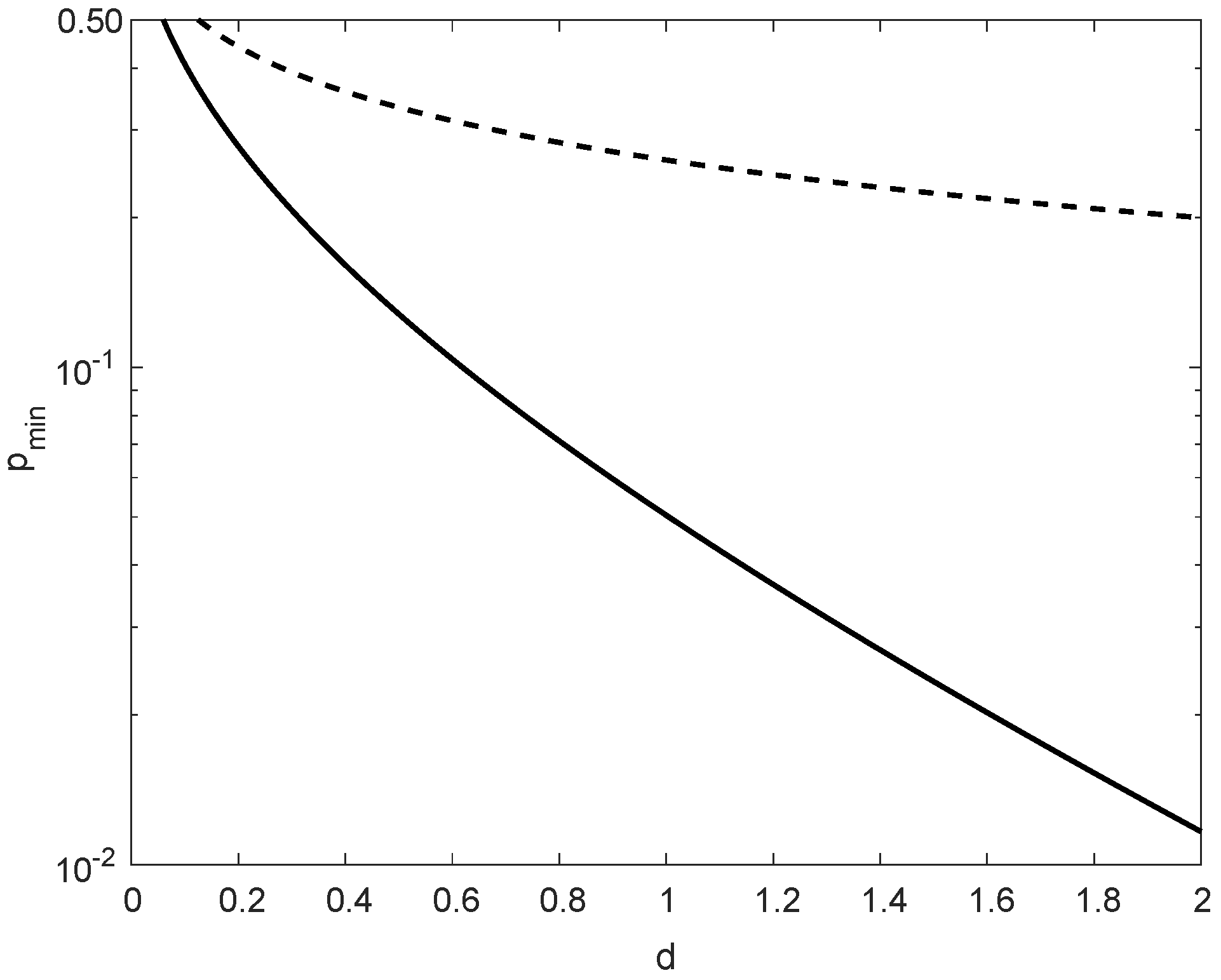
Appendix A. Proof of Theorem 1
We start by proving Item (a). By our assumptions on
and
,
From (
20), (
21), (
A1), (A2) and (A4), it follows that
which imply that, for all
,
Since by assumption
and
are supported on
, and
and
are supported on
(see (A5) and (A6)), it follows that the left side inequality in (
A7) is strict if the infimum in the left side is equal to 0, and the right side inequality in (
A7) is strict if the supremum in the right side is equal to ∞. Hence, due to (
18), (19) and (
23),
Since by assumption
is convex, it follows that its right derivative
exists, and it is monotonically non-decreasing and finite on
(see, e.g., ([
58], Theorem 1.2) or ([
59], Theorem 24.1)). A straightforward generalization of ([
60], Theorem 1.1) (see ([
60], Remark 1)) gives
where
In comparison to ([
60], Theorem 1.1), the requirement that
f is differentiable on
is relaxed here, and the derivative of
f is replaced by its right-side derivative. Note that if
f is differentiable, then
with
as defined in (
A10) is Bregman’s divergence [
61]. The following equality, expressed in terms of Lebesgue-Stieltjes integrals, holds by ([
16], Theorem 1):
From (
18), (19), (
22), (
A8) and (
A11), if
, then
and similarly, if
, then
By combining (
A9), (A12) and (A13), it follows that
and an evaluation of the sum in the right side of (A14) gives (see (
20), (21) and (A3))
Combining (A14)–(A18) gives (
24); (25) is due to the data-processing inequality for
f-divergences (applied to the
-divergence), and the non-negativity of
in (
22).
The
-divergence is an
f-divergence with
for
. The condition in (
22) allows to set here
, implying that (
24) holds in this case with equality.
We next prove Item (b). Let
f be twice differentiable on
(see (
23)), and let
with
. Dividing both sides of (
22) by
, and letting
, yields
. Since this holds for all
, it follows that
. We next show that
in (
26) fulfills the condition in (
22), and therefore it is the largest possible value of
to satisfy (
22). By the mean value theorem of Lagrange, for all
with
, there exists an intermediate value
such that
; hence,
, so the condition in (
22) is indeed fulfilled with
as given in (
26).
We next prove Item (c). Let
be the dual convex function which is given by
for all
with
. Since
,
,
and
are supported on
(see (A5) and (A6)), we have
Consequently, it follows that
where (A23) holds due to (A19) and (A20); (A24) follows from (
24) with
f,
and
replaced by
,
and
, respectively, which then implies that
and
in (
18) and (19) are, respectively, replaced by
and
in (A21) and (A22); finally, (A25) holds due to (A21) and (A22). Since by assumption
f is twice differentiable on
, so is
, and
Hence,
where (A27) follows from (
24) with
f,
and
replaced by
,
and
, respectively; (A28) holds due to (A26), and (A29) holds by substituting
. This proves (
27) and (
30), where (28) is due to the data-processing inequality for
f-divergences, and the non-negativity of
.
Similarly to the condition for equality in (
24), equality in (
27) is satisfied if
for all
, or equivalently
for all
. This
f-divergence is Neyman’s
-divergence where
for all
P and
Q with
(due to (
30), and since
for all
).
The proof of Item (d) follows that same lines as the proof of Items (a)–(c) by replacing the condition in (
22) with a complementary condition of the form
We finally prove Item (e) by showing that the lower and upper bounds in (
24), (
27), (
32) and (
33) are locally tight. More precisely, let
be a sequence of probability mass functions defined on
and pointwise converging to
which is supported on
, let
and
be the probability mass functions defined on
via (
20) and (21) with inputs
and
, respectively, and let
and
be defined, respectively, by (
18) and (19) with
being replaced by
. By the assumptions in (
35) and (36),
Consequently, if
f has a continuous second derivative at unity, then (
24), (
26), (
31), (
32), (A31) and (A32) imply that
and similarly, from (
27), (
30), (
33), (
34), (A31) and (A32),
which, respectively, prove (
37) and (38).
Appendix B. Proof of Theorem 2
We start by proving Item (a). By the assumption that
and
are supported on
for all
, it follows from (
39) that the probability mass functions
and
are supported on
. Consequently, from (
41), also
is supported on
for all
. Due to the product forms of
and
in (
39) and (
41), respectively, we get from (
47) that
and likewise, from (48),
for all
. In view of (
24), (
26), (A35) and (A36), replacing
in (
24) and (
26) with
we obtain that, for all
,
Due to the setting in (
39)–(44), for all
and
,
with
and
is the probability mass function at the channel output at time instant
i. In particular, setting
in (A38) gives
Due to the tensorization property of the
divergence, and since
,
,
and
are product probability measures (see (
39), (
41), (A38) and (A40)), it follows that
and
Substituting (A41) and (A42) into the right side of (A37) gives that, for all
,
Due to (
41) and (A39), since
and (see ([
45], Lemma 5))
for every pair of probability measures
, it follows that
Substituting (A47) and (A48) into the right side of (A43) gives (
45). For proving the looser bound (46) from (
45), and also for later proving the result in Item (c), we rely on the following lemma.
Lemma A1. Let and be non-negative with for all . Then,
- (a)
- (b)
If for at least one index i, then
Proof. Let
be defined as
We have
, and the first two derivatives of
g are given by
and
Since by assumption
for all
i, it follows from (A53) that
for all
, which asserts the convexity of
g on
. Hence, for all
,
where the right-side equality in (A54) is due to (A51) and (A52). This gives (A49).
We next prove Item (b) of Lemma A1. By the Taylor series expansion of the polynomial function
g, we get
for all
. Since by assumption
for all
i, and there exists an index
such that
, it follows that the coefficient of
in the right side of (A55) is positive. This yields (A50). □
We obtain here (46) from (
45) and Item (a) of Lemma A1. To that end, for
, let
with
for every
. Since by (
39), (
40), (43) and (44),
it follows from the data-processing inequality for
f-divergences, and their non-negativity, that
which yields (46) from (
45), (A49), (A56) and (A59).
We next prove Item (b) of Theorem 2. Similarly to the proof of (A37), we get from (
32) (rather than (
24)) that
Combining (A41), (A42), (A47), (A48) and (A60) gives (
49).
We finally prove Item (c) of Theorem 2. In view of (
47) and (48), and by the assumption that
for all
, we get
Since, by assumption
f has a continuous second derivative at unity, (
26), (
31), (A61) and (A62) imply that
From (A56), (A59), and Item (b) of Lemma A1, it follows that
The result in (
50) finally follows from (
45), (
49) and (A63)–(A65). This indeed shows that the lower bounds in the right sides of (
45) and (46), and the upper bound in the right side of (
49) yield a tight result as we let
, leading to the limit in the right side of (
50).
Appendix D. Proof of Theorem 5
The function
in (
55) satisfies
, and for all
which yields the convexity of
on
. This justifies the definition of the
f-divergence
for probability mass functions
P and
Q, which are defined on a finite or countably infinite set
, with
Q supported on
. In the general alphabet setting, sums and probability mass functions are, respectively, replaced by Lebesgue integrals and Radon-Nikodym derivatives. Differentiation of both sides of (A82) with respect to
gives
where
The function
is convex since
and
. Hence,
is an
f-divergence, and it follows from (A83)–(A85) that
which gives (
56), so
is monotonically increasing in
. Double differentiation of both sides of (A82) with respect to
gives
where
The function
is concave, and
. By referring to the
f-divergence
, it follows from (A91)–(A93) that
which gives (57), so
is concave in
for
. Differentiation of both sides of (A93) with respect to
gives that
which implies that
This gives (58), and it completes the proof of Item (a).
We next prove Item (b). From Item (a), the result in (
59) holds for
. We provide in the following a proof of (
59) for all
. In view of (A98), it can be verified that for
,
which, from (A82), implies that
with
The function
is convex for
, with
. By referring to the
f-divergence
, its non-negativity and (A103) imply that for all
Furthermore, we get the following explicit formula for
n-th partial derivative of
with respect to
for
:
where (A107) holds due to (A103); (A108) follows from (A104), and (A110) is satisfied by the definition of the Rényi divergence [
40] which is given by
with
by continuous extension of
at
. For
, the right side of (A110) is simplified to the right side of (58); this holds due to the identity
To prove Item (c), from (
55), for all
which implies by a Taylor series expansion of
that
where
in the right side of (A116) is an intermediate value between 1 and
t. Hence, for
,
where (A117) follows from (A116) since
and
is monotonically decreasing and positive (see (A115));
in the right side of (A117) denotes the indicator function which is equal to 1 if the relation
holds, and it is otherwise equal to zero; (A118) holds since
for all
, and
; finally, (A119) follows by substituting (A114) and (A115) into the right side of (A118), which gives the equality
with
as defined in (
63). Since the first term in the right side of (A119) does not affect an
f-divergence (as it is equal to
for
and some constant
c), and for an arbitrary positive constant
and
for
, we get
, inequality (
61) follows from (A117) and (A119). To that end, note that
defined in (
63) is monotonically increasing in
, and therefore
for all
. Due to the inequality (see, e.g., ([
64], Theorem 5), followed by refined versions in ([
62], Theorem 20) and ([
65], Theorem 9))
the looser lower bound on
in the right side of (62), expressed as a function of the relative entropy
, follows from (
61). Hence, if
P and
Q are not identical, then (
64) follows from (
61) since
and
.
We next prove Item (d). The Taylor series expansion of
implies that, for all
,
where
in the right side of (A122) is an intermediate value between 1 and
t. Consequently, since
and
, it follows from (A122) that, for all
,
Based on (A123)–(A125), it follows that
where (A127) holds due to (A111) (with
). Substituting (A114) and (A115) into the right side of (A127) gives (
65).
We next prove Item (e). Let
P and
Q be probability mass functions such that
, and let
be arbitrarily small. Since the Rényi divergence
is monotonically non-decreasing in
(see ([
66], Theorem 3)), it follows that
, and therefore also
In view of (
61), there exists
such that for all
and, from (
65), there exists
such that for all
Letting
gives the result in (
66) for all
.
Item (f) of Theorem 5 is a direct consequence of ([
45], Lemma 4), which relies on ([
67], Theorem 3). Let
for
(hence,
is the
divergence). If a sequence
converges to a probability measure
Q in the sense that the condition in (
67) is satisfied, and
for all sufficiently large
n, then ([
45], Lemma 4) yields
which gives (
68) from (A114) and (A131).
We next prove Item (g). Inequality (
69) is trivial. Inequality (70) is obtained as follows:
where (A133) follows from (
56), and (A134) holds since the function
given by
is monotonically decreasing in
u (note that by increasing the value of the non-negative variable
u, the probability mass function
gets closer to
Q). This gives (70).
For proving inequality (71), we obtain two upper bounds on
with
. For the derivation of the first bound, we rely on (A83). From (A84) and (A85),
where
is given by
with the convention that
(by a continuous extension of
at
). Since
, and
which implies that
is convex on
, we get
where (A141) holds due to (A83) (recall the convexity of
with
); (A142) holds due to (A138) and since
for
implies that
; finally, (A143) follows from the non-negativity of the
f-divergence
. Consequently, integration over the interval
(
) on the left side of (A141) and the right side of (A143) gives
Note that the same reasoning of (A132)–(A136) also implies that
which gives a second upper bound on the left side of (A145). Taking the minimal value among the two upper bounds in the right sides of (A144) and (A145) gives (71) (see Remark A4).
We finally prove Item (h). From (
55) and (A81), the function
is convex for
with
,
, and it is also differentiable at 1. It is left to prove that the function
, defined as
for
, is convex. From (
55), the function
is given explicitly by
and its second derivative is given by
with
Since
, and
it follows that
for all
; hence, from (A147),
for
, which yields the convexity of the function
on
for all
. This shows that, for every
, the function
satisfies all the required conditions in Theorems 3 and 4. We proceed to calculate the function
in (
51), which corresponds to
, i.e., (see (
72)),
with
where the definition of
is obtained by continuous extension of the function
at
(recall that the function
is given in (
55)). Differentiation shows that
where, for
,
and
From (A156), it follows that
if
,
, and
if
. Since
is therefore monotonically decreasing on
and it is monotonically increasing on
, (A155) implies that
Since
(see (A154)), and
is monotonically increasing on
, it follows that
for all
and
for all
. This implies that
for all
(see (A153)); hence, from (A152), the function
is monotonically increasing on
, and it is continuous over this interval (see (A151)). It therefore follows from (A150) that
for every
and
(independently of
), which proves (73).
Remark A4. None of the upper bounds in the right sides of (A144) and (A145) supersedes the other. For example, if P and Q correspond to and , respectively, and , then the right sides of (A144) and (A145) are, respectively, equal to and . If on the other hand , then the right sides of (A144) and (A145) are, respectively, equal to and .
Appendix E. Proof of Theorem 6
By assumption,
where the probability mass functions
P and
Q are defined on the set
. The majorization relation
is equivalent to the existence of a doubly-stochastic transformation
such that (see Proposition 4)
(See, e.g., ([
32], Theorem 2.1.10) or ([
30], Theorem 2.B.2) or ([
31], pp. 195–204)). Define
The probability mass functions given by
satisfy, respectively, (
20) and (21). The first one is obvious from (A159)–(A161); equality (21) holds due to the fact that
is a doubly stochastic transformation, which implies that for all
Since (by assumption)
and
are supported on
, relations (
20) and (21) hold in the setting of (A159)–(A161), and
is (by assumption) convex and twice differentiable, it is possible to apply the bounds in Theorem 1 (b) and (d). To that end, from (
18), (19), (A160) and (A161),
which, from (
24), (25), (
32), (A160), (A161) and (A164), give that
The difference of the
divergences in the left side of (A166) and the right side of (A167) satisfies
and the substitution of (A169) into the bounds in (A166) and (A167) give the result in (
74) and (
75).
Let
for
, which yields from (
26) and (
31) that
. Since
, it follows from (A169) that the upper and lower bounds in the left side of (
74) and the right side of (75), respectively, coincide for the
-divergence; this therefore yields the tightness of these bounds in this special case.
We next prove (
76). The following lower bound on the second-order Rényi entropy (a.k.a. the collision entropy) holds (see ([
34], (25)–(27))):
where
. This gives
By Cauchy-Schwartz inequality
which, together with (A171), give
In view of the Schur-concavity of the Rényi entropy (see ([
30], Theorem 13.F.3.a.)), the assumption
implies that
and an exponentiation of both sides of (A173) (see the left-side equality in (A170)) gives
Combining (A172) and (A173) gives (
76).
Appendix F. Proof of Theorem 7
We prove Item (a), showing that the set (with ) is non-empty, convex and compact. Note that is a singleton, so the claim is trivial for .
Let
. The non-emptiness of
is trivial since
. To prove the convexity of
, let
, and let
and
be the (positive) maximal and minimal probability masses of
and
, respectively. Then,
and
yield
For every
,
Combining (A175)–(A177) implies that
so
for all
. This proves the convexity of
.
The set of probability mass functions
is clearly bounded; for showing its compactness, it is left to show that
is closed. Let
, and let
be a sequence of probability mass functions in
which pointwise converges to
P over the finite set
. It is required to show that
. As a limit of probability mass functions,
, and since by assumption
for all
, it follows that
which yields
for all
m. Since
for every
m, it follows that also for the limiting probability mass function
P we have
, and
. This proves that
, and therefore
is a closed set.
An alternative proof for Item (a) relies on the observation that, for
,
which yields the convexity and compactness of the set
for all
.
The result in Item (b) holds in view of Item (a), and due to the convexity and continuity of
in
(where
). This implication is justified by the statement that a convex and continuous function over a non-empty convex and compact set attains its supremum over this set (see, e.g., ([
68], Theorem 7.42) or ([
59], Theorem 10.1 and Corollary 32.3.2)).
We next prove Item (c). If
, then
where the lower bound on
is attained when
Q is the probability mass function with
masses equal to
and a single smaller mass equal to
, and the upper bound is attained when
Q is the equiprobable distribution. For an arbitrary
, let
where
can get any value in the interval
defined in (
79). By ([
34], Lemma 1),
and
where
is given in (
80). The Schur-convexity of
(see ([
38], Lemma 1)) and the identity
give that
for all
with
; equalities hold in (A180) if
. The maximization of
and
over all probability mass functions
can be therefore simplified to the maximization of
and
, respectively, over the parameter
which lies in the interval
in (
79). This proves (
82) and (83).
We next prove Item (e), and then prove Item (d). In view of Item (c), the maximum of
over all the probability mass functions
is attained by
with
(see (
79)–(
81)). From (
80),
can be expressed as the
n-length probability vector
The influence of the
-th entry of the probability vector in (A181) on
tends to zero as we let
. This holds since the entries of the vector in (A181) are written in decreasing order, which implies that for all
(with
)
from (A182) and the convexity of
f on
(so,
f attains its finite maximum on every closed sub-interval of
), it follows that
In view of (A181) and (A183), by letting
, the maximization of
over
can be replaced by a maximization of
where
with the free parameter
, and with
(the value of
is determined so that the total mass of
is 1). Hence, we get
The
f-divergence in the right side of (A185) satisfies
where (A188) holds by the definition of the function
in (
84). It therefore follows that
where (A189) holds by combining (
82) and (A185)–(A188); (A190) holds by the continuity of the function
on
, which follows from (
84) and the continuity of the convex function
f on
for
(recall that a convex function is continuous on every closed sub-interval of its domain of region, and by assumption
f is convex on
). This proves (
87), by the definition of
in (
84).
Equality (88) follows from (
87) by replacing
with
, with
as given in (
29); this replacement is justified by the equality
.
Once Item (e) is proved, we return to prove Item (d). To that end, it is first shown that
for all
and integers
, with the functions
and
, respectively, defined in (
77) and (78). Since
for all
, (
77) and (78) give that
so the monotonicity property in (A192) follows from (A191) by replacing
f with
. To prove (A191), let
be a probability mass function which attains the maximum at the right side of (
77), and let
be the probability mass function supported on
, and defined as follows:
Since by assumption
, (A194) implies that
. It therefore follows that
where (A195) and (A201) hold due to (
77); (A196) holds since
; finally, (A198) holds due to (A194), which implies that the two sums in the right side of (A197) are identical, and they equal to the sum in the right side of (A198). This gives (A191), and likewise also (A192) (see (A193)).
where (A202) holds since, due to (A191), the sequence
is monotonically increasing, which implies that the first term of this sequence is less than or equal to its limit. Equality (A203) holds since the limit in its right side exists (in view of the above proof of (
87)), so its limit coincides with the limit of every subsequence; (A204) holds due to (A189) and (A190). A replacement of
f with
gives, from (A193), that
Combining (A202)–(A205) gives the right-side inequalities in (
85) and (86). The left-side inequality in (
85) follows by combining (
77), (A184) and (A186)–(A188), which gives
Likewise, in view of (A193), the left-side inequality in (86) follows from the left-side inequality in (
85) by replacing
f with
.
We next prove Item (f), providing an upper bound on the convergence rate of the limit in (
87); an analogous result can be obtained for the convergence rate to the limit in (88) by replacing
f with
in (
29). To prove (
89), in view of Items (d) and (e), we get that for every integer
where (A209) holds due to monotonicity property in (A191), and also due to the existence of the limit of
; (A210) holds due to (
85); (A211) holds since the function
(as it is defined in (
84)) satisfies
(recall that by assumption
); (A212) holds since
, so the maximization of
over the interval
is the maximum over the maximal values over the sub-intervals
for
; finally, (A213) holds since the maximum of a sum of functions is less than or equal to the sum of the maxima of these functions. If the function
is differentiable on
, and its derivative is upper bounded by
, then by the mean value theorem of Lagrange, for every
,
Combining (A209)–(A214) gives (
89).
We next prove Item (g). By definition, it readily follows that
if
. By the definition in (
77), for a fixed integer
, it follows that the function
is monotonically increasing on
. The limit in the left side of (
90) therefore exists. Since
is convex in
Q, its maximum over the convex set of probability mass functions
is obtained at one of the vertices of the simplex
. Hence, a maximum of
over this set is attained at
with
for some
, and
for
. In the latter case,
Note that
(since the union of
, for all
, includes all the probability mass functions in
which are
supported on
, so
is not an element of this union); hence, it follows that
On the other hand, for every
,
where (A217) holds due to the left-side inequality of (
85), and (A218) is due to (
84). Combining (A217) and (A218), and the continuity of
f at zero (by the continuous extension of the convex function
f at zero), yields (by letting
)
Combining (A216) and (A219) gives (
90) for every integer
. In order to get an upper bound on the convergence rate in (
90), suppose that
,
f is differentiable on
, and
. For every
, we get
where (A220) holds since the sets
are monotonically increasing in
; (A221) follows from (A216)–(A218); (A222) holds by the assumption that
for all
, by the mean value theorem of Lagrange, and since
for all
and
. This proves (
91).
We next prove Item (h). Setting
yields
for every probability mass function
Q which is supported on
. Since
and
, and since by assumption
, it follows that
Combining the assumption in (
92) with (A224) implies that
Hence, (
26), (
31) and (A225) yield
The lower bound on
in the left side of (
94) follows from a combination of (75), the left-side inequality in (A226), and
. Similarly, the upper bound on
in the right side of (95) follows from a combination of (
74), the right-side inequality in (A226), and the equality
. The looser upper bound on
in the right side of (96), expressed as a function of
M and
, follows by combining (
74), (
76), and the right-side inequality in (A226).
The tightness of the lower bound in the left side of (
94) and the upper bound in the right side of (95) for the
divergence is clear from the fact that
if
for all
; in this case,
.
To prove Item (i), suppose that the second derivative of
f is upper bounded on
with
for all
, and there is a need to assert that
for an arbitrary
. Condition (
97) follows from (96) by solving the inequality
, with the variable
, for given
and
(note that
does not depend on
).
Appendix G. Proof of Theorem 8
The proof of Theorem 8 relies on Theorem 6. For
, let
be the non-negative and convex function given by (see, e.g., ([
8], (2.1)) or ([
16], (17)))
and let
be the convex function given by
Let
P and
Q be probability mass functions which are supported on a finite set; without loss of generality, let their support be given by
. Then, for
,
where
designates the order-
Tsallis entropy of a probability mass
P defined on the set
. Equality (A229) also holds for
by continuous extension.
In view of (
26) and (
31), since
for all
, it follows that
and
The combination of (
74) and (
75) under the assumption that
P and
Q are supported on
and
, together with (A229), (A231) and (A232) gives (
100)–(102). Furthermore, the left and right-side inequalities in (
100) hold with equality if
in (A231) and
in (A232) coincide, which implies that the upper and lower bounds in (
74) and (
75) are tight in that case. Comparing
in (A231) and
in (A232) shows that they coincide if
.
To prove Item (b) of Theorem 8, let
and
be probability mass functions supported on
where
,
, and
and
. This yields
. The result in (
103) is proved by showing that, for all
,
which shows that the infimum and supremum in (
103) can be even restricted to the binary alphabet setting. For every
,
where (A235) follows from a Taylor series expansion around
, and the passage in the limit where
shows that (A235) also holds at
(due to the continuous extension of the order-
Tsallis entropy at
). This implies that (A235) holds for all
. We now calculate the lower and upper bounds on
in (
101) and (102), respectively.
Similarly, for
,
and, for
,
The combination of (A235)–(A237) yields (A233); similarly, the combination of (A235), (A238) and (A239) yields (A234).
Appendix N. Proof of Theorem 12
The proof of Theorem 12 relies on Theorem 1, and the proof of Theorem 11.
Let
and, without any loss of generality, let
. For every
, define a deterministic transformation from
to
such that every
is mapped to
, and every
is mapped to
. This corresponds to a conditional probability mass function, for every
, where
if
and
, or if
and
; otherwise,
. Let
with
. Then, for every
, a conditional probability mass function
implies that
satisfies (see (A283))
Under the deterministic transformation
as above, the equiprobable distribution
(independently of
) is mapped to a Bernoulli distribution over the two-elements set
where
Given
, applying Theorem 1 with the transformation
as above gives that
where, from (
18) and (19),
Since, from (212), (213), (A311) and (A312),
it follows from the definition of
in (
26) that for every
where the last inequality holds by the assumption in (
211). Combining (A310) and (A315)–(A317) yields
for every
. Hence,
where (A319) holds by taking expectations with respect to
Y on both sides of (A318).
Referring to the first term in the right side of (A319) gives
where (A320) follows from (A307)–(A309), and (A321) holds due to (A288)–(A290).
Referring to the second term in the right side of (A319) gives
where (A322) follows from (A306)–(A309); (A323) follows from (A16)–(A18); (A325) is due to (A282). Furthermore, we get (since
)
and
Combining (A322)–(A330) gives
which provides tight upper and lower bounds on
if
is small. Note that the lower bound on the left side of (A331) is non-negative since, by the data-processing inequality for the
divergence, the right side of (A331) should be non-negative (see (A306)–(A309)). Finally, combining (A319)–(A332) yields (
214), which proves Item (a).
For proving Item (b), the upper bound on the left side of (A326) is tightened. If the list decoder selects the
L most probable elements from
given the value of
, then
for every
. Hence, the bound in (A326) is replaced by the tighter bound
Combining (A322)–(A325), (A328)–(A330) and (A333) gives the following improved lower bound in the left side of (A331):
It is next shown that the operation
in the left side of (A334) is redundant. From (A282) and (A283),
which then implies that
where (A338) is due the Cauchy-Schwarz inequality applied to the right side of (A337), and (A339) holds since
for all
. From (A335)–(A341),
, which implies that the operation
in the left side of (A334) is indeed redundant. Similarly to the proof of (
214) (see (A319)–(A321)), (A334) yields (
215) while ignoring the operation
in the left side of (A334).
Appendix O. Proof of Theorem 13
For every
, let the
M elements of
be sorted in decreasing order according to the conditional probabilities
. Let
be the
ℓ-th most probable element in
given
, i.e.,
The conditional list decoding error probability, given
, satisfies
and the (average) list decoding error probability satisfies
. Let
denote the equiprobable distribution on
, and let
be given by
with
, where
for
. The function
is convex, and
for
; the
f-divergence
is named as the
divergence (see, e.g., [
54]), i.e.,
for all probability measures
P and
Q. For every
,
where (A346) holds due to the data-processing inequality for
f-divergences, and because of (A344); (A347) holds due to (A345). Furthermore, in view of (A342) and (A344), it follows that
for all
; by the definition of
, it follows that
Substituting (A348) into the right side of (A347) gives that, for all
,
Taking expectations with respect to
Y in (A349) and (A350), and applying Jensen’s inequality to the convex function
, for
, gives
On the other hand, the left side of (A351) is equal to
where (A355) is due to (A345), and since
for all
; (A356) and (A357) hold, respectively, by the simple identities
, and
for
and
; finally, (A358) holds since
for all
. Substituting (A355)–(A358) and rearranging terms gives that
which is the lower bound on the list decoding error probability in (
222).
We next proceed to prove the sufficient conditions for equality in (
222). First, if for all
, the list decoder selects the
most probable elements in
given that
, then equality holds in (A359). In this case, for all
,
where
denotes the
ℓ-th most probable element in
, given
, with ties in probabilities which are resolved arbitrarily (see (A342)). Let
. If, for every
,
is fixed for all
and
is fixed for all
, then equality holds in (A346) (and therefore equalities also hold in (A349) and (A351)). For all
, let the common values of the conditional probabilities
over each of these two sets, respectively, be equal to
and
. Then,
which gives the condition in (
223). Furthermore, if for all
,
, then the operation
in the right side of (A351) is redundant, which causes (A352) to hold with equality as an expectation of a linear function; furthermore, also (A354) holds with equality in this case (since an expectation of a non-negative and bounded function is non-negative and finite). By (
223) and (A344), it follows that
for all
, and therefore the satisfiability of (
224) implies that equalities hold in (A352) and (A354). Overall, under the above condition, it therefore follows that (
222) holds with equality. To verify it explicitly, under conditions (
223) and (
224) which have been derived as above, the right side of (
222) satisfies
where (A361) holds since, under (
224), it follows that
for all
; (A362) holds by straightforward algebra, where
is canceled out; (A363) holds by the condition in (
223); finally, (A364) holds by (A282), (A283) and (A342). This indeed explicitly verifies that the conditions in Theorem 13 yield an equality in (
222).