Entropic Matroids and Their Representation
Abstract
1. Introduction
1.1. Definitions
- For any , (normalization);
- For any , (monotonicity);
- For any , (submodularity).
- Restriction: Given , we define the matroid .
- Contraction: Given an independent set , we define the matroid .
1.2. Entropic Matroids
1.3. Results
2. Further Related Literature
3. Minors of Entropic Matroids
- (i)
- For any , is entropic.
- (ii)
- For any with , is entropic.
- (iii)
- For any independent set A, is entropic.
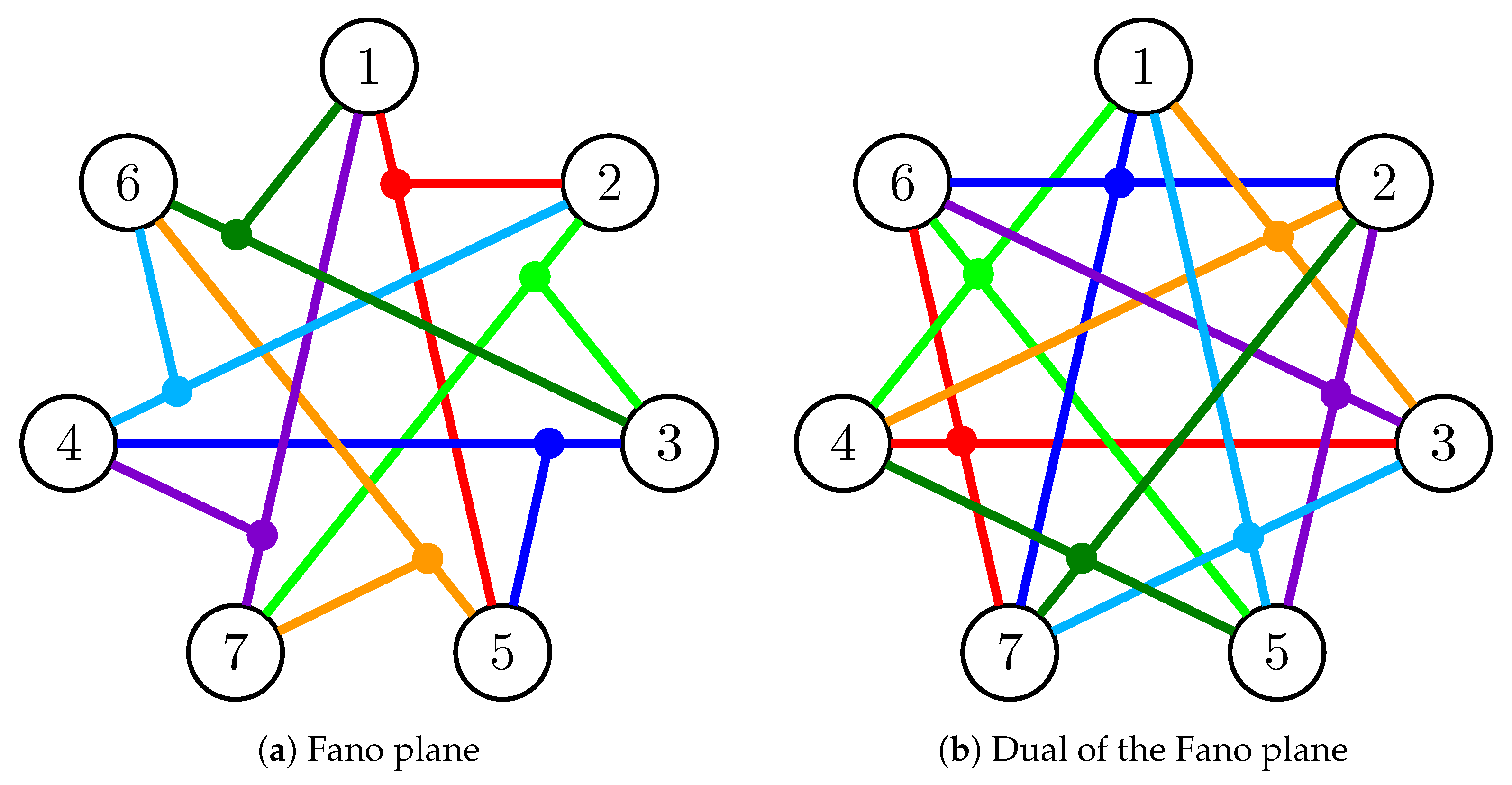
4. Secret-Sharing and Almost Affine Matroids
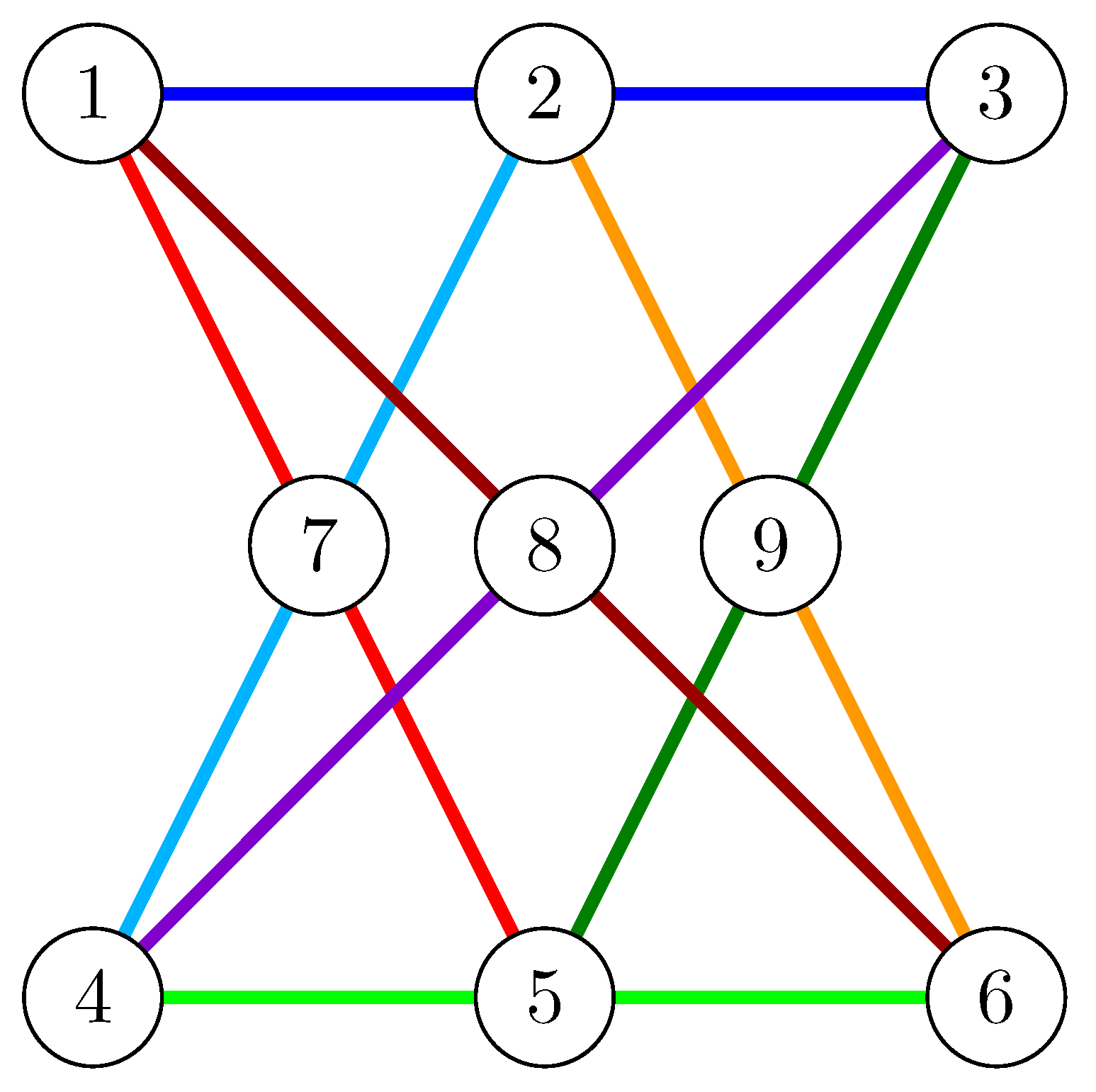
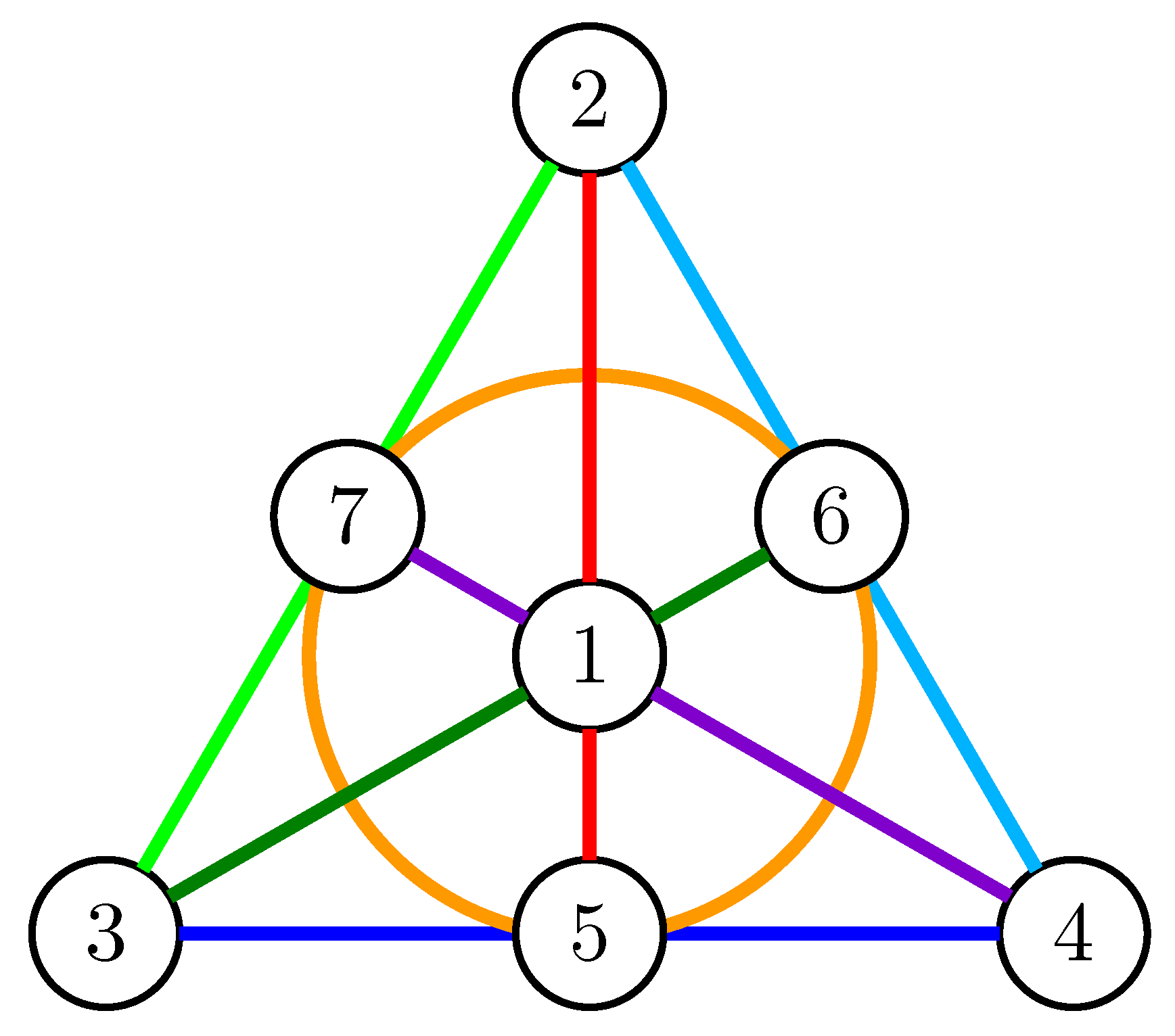
5. The Case
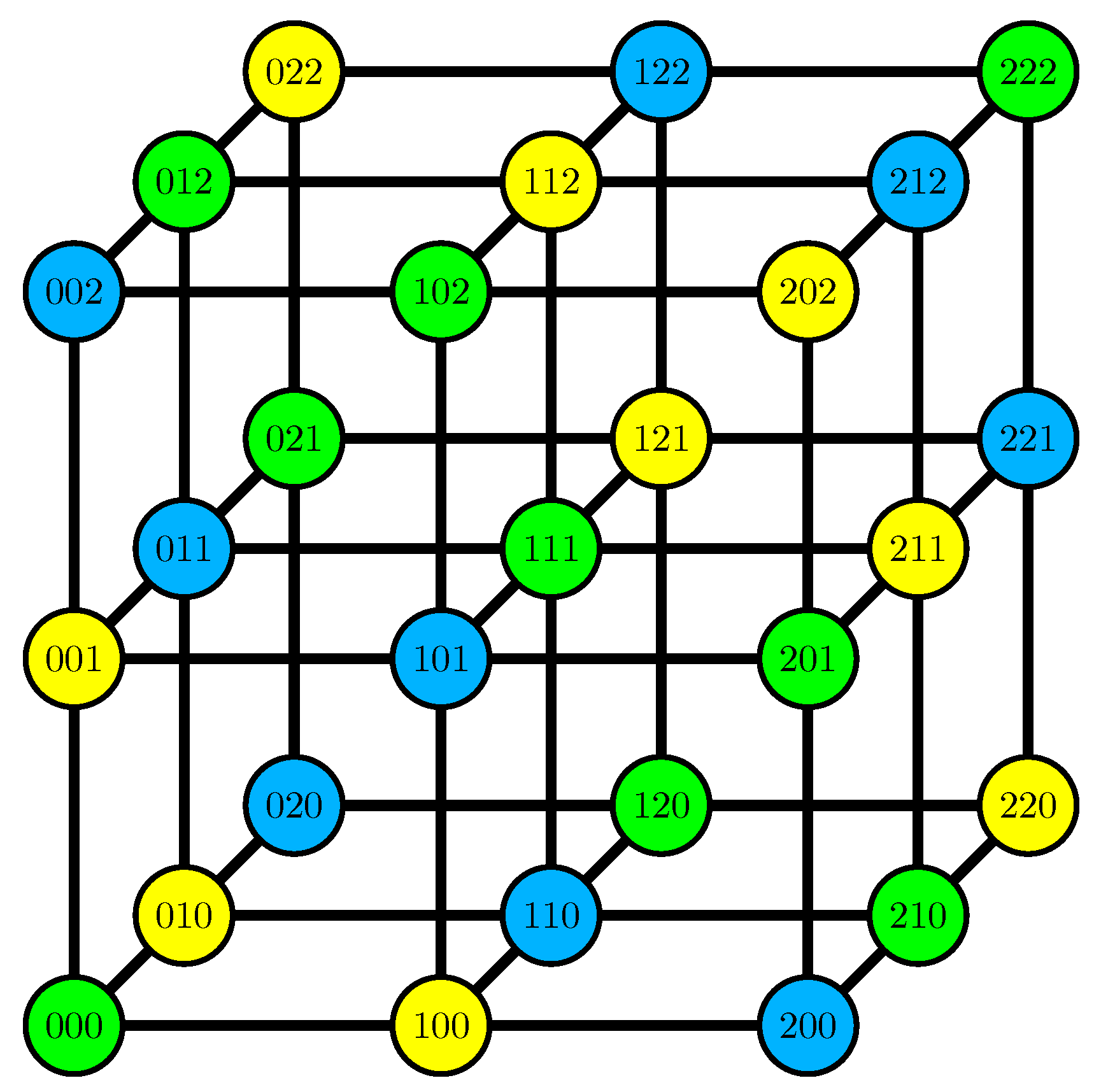
6. The Case
7. Comments for General Primes
8. Application: Entropic Matroids in Coding
Author Contributions
Funding
Conflicts of Interest
References
- Oxley, J.G. Matroid Theory; Oxford University Press: Oxford, UK, 2006; Volume 3. [Google Scholar]
- Woodall, D.R. Matroid Theory: Types of Matroids Lecture Notes. Available online: https://www.maths.nottingham.ac.uk/personal/drw/PG/matroid.ch3.pdf (accessed on 23 September 2019).
- Fujishije, S. Polymatroidal dependence structure of a set of random variables. Inf. Control 1978, 39, 55–72. [Google Scholar] [CrossRef]
- Lovász, L. Submodular functions and convexity. In Mathematical Programming-The State of the Art; Bachem, A., Grötschel, M., Korte, B., Eds.; Springer: Berlin, Germany, 1982; pp. 234–257. [Google Scholar]
- Edmonds, J. Submodular Functions, Matroids and Certain Polyhedra; Lecture Notes in Computer Science; Springer: Berlin, Germany, 2003. [Google Scholar]
- Han, T.S. A uniqueness of shannon’s information distance and related nonnegativity problems. J. Comb. Inf. Syst. Sci. 1981, 6, 320–331. [Google Scholar]
- Li, C.; Walsh, J.M.; Weber, S. Matroid bounds on the region of en- tropic vectors. In Proceedings of the 2013 51st Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 2–4 October 2013; pp. 796–803. [Google Scholar]
- Zhang, Z.; Yeung, R. On characterization of entropy function via information inequalities. IEEE Trans. Inf. Theory 1998, 44, 1140–1452. [Google Scholar]
- Yeung, R.W. Information Theory and Network Coding; Springer: Berlin, Germany, 2008. [Google Scholar]
- Matúš, F. On Equivalence of Markov Properties over Undirected Graphs. J. Appl. Probab. 1992, 29, 745–749. [Google Scholar] [CrossRef]
- Matúš, F. Probabilistic conditional independence structures and matroid theory: Background. Int. J. Gen. Syst. 1994, 22, 185–196. [Google Scholar] [CrossRef]
- Abbe, E. Randomness and dependencies extraction via polarization, with applications to Slepian-Wolf coding and secrecy. IEEE Trans. Inf. Theory 2015, 61, 2388–2398. [Google Scholar] [CrossRef]
- Abbe, E. Mutual information, matroids and extremal dependencies. arXiv 2010, arXiv:1012.4755. [Google Scholar]
- Kahn, J.; Seymour, P. On forbidden minors for GF(3). Proc. Am. Math. Soc. 1988, 102, 437–440. [Google Scholar]
- Geelen, J.F.; Gerards, A.; Kapoor, A. The excluded minors for GF(4)-representable matroids. J. Comb. Theory Ser. B 2000, 79, 247–299. [Google Scholar] [CrossRef]
- Kahn, J. On the uniqueness of matroid representations over GF(4). Bull. Lond. Math. Soc. 1988, 20, 5–10. [Google Scholar] [CrossRef]
- Kung, J.P.; Oxley, J.G. Combinatorial geometries representable over GF(3) and GF(q). ii. dowling geometries. Gr. Comb. 1988, 4, 323–332. [Google Scholar] [CrossRef]
- Kung, J.P. Combinatorial geometries representable over GF(3) and GF(q). i. the number of points. Discret. Comput. Geom. 1990, 5, 83–95. [Google Scholar] [CrossRef]
- Whittle, G. On matroids representable over GF(3) and other fields. Trans. Am. Math. Soc. 1997, 349, 579–603. [Google Scholar] [CrossRef]
- Apte, J.; Li, C.; Walsh, J.M. Algorithms for computing network coding rate regions via single element extensions of matroids. In Proceedings of the 2014 IEEE International Symposium on Information Theory, Honolulu, HI, USA, 29 June–4 July 2014; pp. 2306–2310. [Google Scholar]
- Salimi, A.; Médard, M.; Cui, S. On the representability of integer poly- matroids: Applications in linear code construction. In Proceedings of the 2015 53rd Annual Allerton Conference on Communication, Control, and Computing (Aller- ton), Monticello, IL, USA, 29 September–2 October 2015; pp. 504–508. [Google Scholar]
- Chan, T.; Grant, A.; Kern, D. Existence of new inequalities for repre- sentable polymatroids. In Proceedings of the 2010 IEEE International Symposium on Information Theory, Austin, TX, USA, 13–18 June 2010; pp. 1364–1368. [Google Scholar]
- Chan, T.; Grant, A.; Pfluger, D. Truncation technique for charac- terizing linear polymatroids. IEEE Trans. Inf. Theory 2011, 57, 6364–6378. [Google Scholar] [CrossRef]
- Matúš, F. Classes of matroids closed under minors and principal extensions. Combinatorica 2018, 38, 935–954. [Google Scholar] [CrossRef]
- Seymour, P. On secret-sharing matroids. J. Comb. Theory Ser. B 1992, 56, 69–73. [Google Scholar] [CrossRef]
- Beimel, A.; Livne, N.; Padro, C. Matroids can be far from ideal secret sharing. In Theory of Cryptography Conference; Springer: Berlin/Heidelberg, Germany, 2008; pp. 194–212. [Google Scholar]
- Martin, S.; Padro, C.; Yang, A. Secret sharing, rank inequalities, and information inequalities. IEEE Trans. Inf. Theory 2015, 62, 599–609. [Google Scholar] [CrossRef]
- Brickell, E.F.; Daniel, M.D. On the classification of ideal secret sharing schemes. J. Cryptol. 1991, 4, 123–134. [Google Scholar] [CrossRef]
- Blakley, G.R. Safeguarding Cryptographic Keys. In Proceedings of the 1979 AFIPS National Computer Conference, Monval, NJ, USA, 4–7 June 1979; Volume 48, pp. 313–317. [Google Scholar]
- Shamir, A. How to share a secret. Commun. ACM 1979, 22, 612–613. [Google Scholar] [CrossRef]
- Martí-Farré, J.; Padró, C. On secret sharing schemes, matroids and polymatroids. In Theory of Cryptography Conference; Springer: Berlin/Heidelberg, Germany, 2007; pp. 273–290. [Google Scholar]
- Simonis, J.; Alexei, A. Almost affine codes. Des. Codes Cryptogr. 1998, 14, 179–197. [Google Scholar] [CrossRef]
- Tutte, W.T. A homotopy theorem for matroids II. Trans. Am. Math. Soc. 1958, 88, 144–174. [Google Scholar]
- Seymour, P. Matroid representation over GF(3). J. Comb. Theory Ser. B 1979, 26, 159–173. [Google Scholar] [CrossRef][Green Version]
- Bixby, R.E. On Reid’s characterization of the ternary matroids. J. Comb. Theory Ser. B 1979, 26, 174–204. [Google Scholar] [CrossRef]
- Pegg, E., Jr. Math Games: The Fano Plane. Available online: http://www.mathpuzzle.com/MAA/47-Fano/mathgames_05_30_06.html (accessed on 23 September 2019).
- Abbe, E.; Telatar, E. Polar codes for the m-user multiple access channel. IEEE Trans. Inf. Theory 2012, 58, 5437–5448. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abbe, E.; Spirkl, S. Entropic Matroids and Their Representation. Entropy 2019, 21, 948. https://doi.org/10.3390/e21100948
Abbe E, Spirkl S. Entropic Matroids and Their Representation. Entropy. 2019; 21(10):948. https://doi.org/10.3390/e21100948
Chicago/Turabian StyleAbbe, Emmanuel, and Sophie Spirkl. 2019. "Entropic Matroids and Their Representation" Entropy 21, no. 10: 948. https://doi.org/10.3390/e21100948
APA StyleAbbe, E., & Spirkl, S. (2019). Entropic Matroids and Their Representation. Entropy, 21(10), 948. https://doi.org/10.3390/e21100948




