Abstract
Derived from Lorenz-Haken equations, this paper presents a new 4D chaotic laser system with three equilibria and only two quadratic nonlinearities. Dynamics analysis, including stability of symmetric equilibria and the existence of coexisting multiple Hopf bifurcations on these equilibria, are investigated, and the complex coexisting behaviors of two and three attractors of stable point and chaotic are numerically revealed. Moreover, a conducted research on the complexity of the laser system reveals that the complexity of the system time series can locate and determine the parameters and initial values that show coexisting attractors. To investigate how much a chaotic system with multistability behavior is suitable for cryptographic applications, we generate a pseudo-random number generator (PRNG) based on the complexity results of the laser system. The randomness test results show that the generated PRNG from the multistability regions fail to pass most of the statistical tests.
1. Inroduction
The chaotic behavior as a rich nonlinear phenomenon has been detected in many non-natural and natural systems, and usually plays an important role in their performance [1,2]. Chaotic systems are complicated and have many interesting features, such as unpredictability, topological mixing, and high sensitivity to their initial conditions and parameters [3,4]. Therefore, chaotic systems have received significant attention from various fields including cryptography [5,6], secure communications [7,8], laser applications [9,10], biomedical engineering [11,12], and many others.
Existing chaotic systems can be classified into two categories: systems with self-excited attractors and systems with hidden attractors [13]. The chaotic system with self-excited attractors has a basin of attraction that is intersected with an unstable equilibrium, whereas the chaotic system with hidden attractors has a basin of attraction which does not intersect with any open neighborhoods of equilibria [14,15]. According to the above definition, most of the classical chaotic attractors are self-excited [16,17]. Meanwhile, it has been demonstrated that the attractors in dynamical systems with no equilibria [18,19], stable equilibria [20], lines of equilibria [21], and curves of equilibria [22] are hidden attractors.
However, with further investigation of chaos, it was unexpected to find that many systems with self-excited and hidden attractors have more than one attractor for a given set of parameters and different initial values. This phenomenon is known as multistability or coexisting attractors. The clear evidence of multistability was first experimentally manifested in a Q-switched gas laser [23], since then chaotic systems with multistability behaviors have been extensively reported. Munoz et al. presented a fractional-order chaotic system with multiple coexisting attractors [24]. Wang et al. established a 2D chaotic map with no-equilibria generating a pair of chaotic attractors [25]. Li et al. introduced a new method for constructing self-reproducing chaotic systems with extreme multistability [26]. In fact, multistability as a new research direction in chaos theory requires further research, especially, how to determine and locate this complicated nonlinear phenomenon in the chaotic systems.
Since the in-depth analysis of the local bifurcation is required to clarify the evolution of the chaotic state from the steady state, the scope of studying the bifurcation of the equilibria in the chaotic systems is of considerable interest [27]. Hopf bifurcation is one of an important local dynamic bifurcation, and is considered as the emergence of a limit cycle from an equilibrium point. Furthermore, the Hopf bifurcation plays a crucial role in analyzing the stability of the equilibria of the high-dimensional system [28,29]. Therefore, Hopf bifurcation is beneficial to analyzing the dynamic behavior of high-dimensional chaotic systems, as well as to the applications of controlling chaos [30].
Complexity of nonlinear dynamical systems has attracted attention in recent years due to its importance for measuring the predictability and randomness of the system time series [31,32]. The time series with high complexity led to a chaotic attractor, hence, the complexity is able to determine and locate the chaotic and periodic attractors in nonlinear systems [33,34]. Motivated by this observation, this paper applies Sample Entropy contour plot to determine multistability regions of a new 4D chaotic laser system, which is derived from Lorenz-Haken equations. The new chaotic system has one unstable equilibrium and symmetric stable equilibria, hence the chaotic attractor of the presented system is generally self-excited, meanwhile, the possible existence of a hidden chaotic attractor is an open problem.
The main contributions of this research work are as follows:
- (i)
- We derive a new 4D chaotic laser system with three equilibria from Lorenz-Haken equations;
- (ii)
- We investigate the stability of the symmetric equilibria, and the existence of coexisting multiple Hopf bifurcations on these equilibria;
- (iii)
- We analyze the presence of complex coexisting behaviors in the laser system;
- (iv)
- We use the complexity of the laser system time series to locate the regions of coexisting attractors when the parameters and initial values vary;
- (v)
- Based on the complexity of the system time series, we study the randomness of multistability regions.
The rest of this paper is organized as follows: Section 2 introduces the new 4D chaotic laser system and studies its dynamical properties. Section 3 investigates the existence of Hopf bifurcation in the laser system. Section 4 provides the details about the multistability of the laser system. In Section 5, we use SamEn to locate the regions of the coexisting attractors, as well as to demonstrate the randomness of these regions. The conclusions are presented in Section 6.
2. A New 4D Chaotic Laser System From Lorenz-Haken Model
In this section, we discuss the dynamics of a new 4D chaotic laser system which is derived from the well-known Lorenz-Haken equations [35]. In the standard notation of Reference [36], the Lorenz-Haken equations is given by
In the optical language, x is proportional to the electric field, y is proportional to the induced macroscopic polarization, denotes the inversion, , and . Here, represents the optical field, is the induced polarization, and denotes the inversion parameter. Meanwhile, the parameter governs the coupling between amplitude and phase variations, and q is known as the linewidth enhancement factor.
Since both x and z can be chosen to be real [37], the dynamics of Equation (1) can be investigated by considering the following linear transformation
Consequently, the new 4D chaotic laser system is defined as
where are state variables and and b are parameters.
2.1. Chaotic Behavior Regions
To examine the dynamic characteristics of the system (2), Figure 1a,b depicts its bifurcation diagram and Lyapunov exponents, respectively, in which the parameters are set as , , , and . This figure clearly shows chaotic attractors for , quasi-periodic (when ) and periodic attractors for . To demonstrate the chaotic behavior of the system (2), Figure 2 plots its phase portraits with , , , and for the initial values . As can be observed in Figure 2, the system (2) has a two-scroll chaotic attractor.
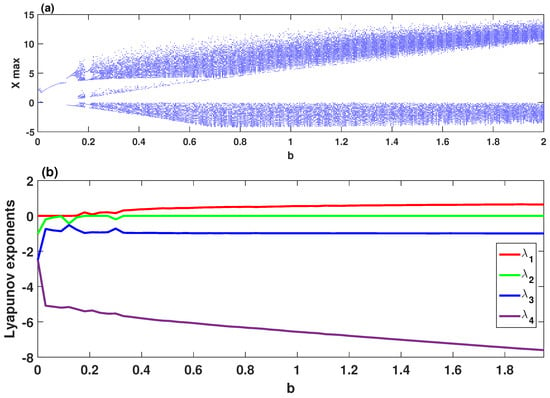
Figure 1.
Dynamics of the system (2) versus the parameter b for the initial values and with , , : (a) bifurcation diagram; (b) Lyapunov exponents.
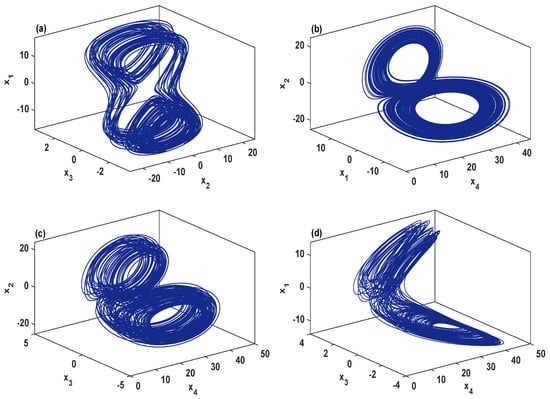
Figure 2.
Different orientations on a two-scroll chaotic attractor of the system (2) for the initial values and with the parameters , , , . (a) space; (b) space; (c) space; (d) space.
2.2. Dissipation and Symmetry
The divergence of system (2) is defined as
Thus, the system (2) becomes dissipative when . This means each volume element of system (2) shrinks to zero as at an exponential rate .
Additionally, the system (2) has invariance under the coordinate transformation
Consequently, the system (2) has rotational symmetry around the -axis.
2.3. Equilibria and Stability
Suppose that the parameters , , and , then the equilibria of the system (2) can be calculated by solving the following equations
From the above equations, it can be obtained that the equilibria of the system (2) have the following form:
where k is either 0 or . The system (2) has one real equilibrium when , whereas it has three real equilibria if
Using the Jacobian matrix, the system (2) is linearized at the equilibrium as follows
Since the equilibria are symmetric about the axis, then they will have the same characteristics. Therefore, the characteristic equation of Jacobian matrix at the equilibrium with can be written as
where
It is obvious that Equation (3) always has one eigenvalue with negative real part which is , whereas the real parts of the other eigenvalues are not always negative. It is well-known that a system is asymptotically stable when all eigenvalues have negative real parts; otherwise, the system is unstable. By Routh–Hurwitz criterion, the real parts of all the eigenvalues of the system (2) are negative if and only if
By choosing the parameters and , these inequalities lead to the following condition:
Thus, if the above conditions are satisfied, then the equilibrium is an asymptotically stable.
3. Local Bifurcation Analysis and Numerical Simulations
This section reviews the Hopf bifurcation using the bifurcation theories. In addition, the existence of coexisting symmetric Hopf bifurcations in the system (2) will be investigated with the variation of parameter .
3.1. Hopf Bifurcation
Hopf bifurcation is the source of a limit cycle, which usually appears when the stability of the equilibrium point changes at some critical parameter value. To illustrate the Hopf bifurcation of a dynamical system on the equilibrium point, consider a vector field as follows
where and represent the phase variables and the parameters, respectively. The vector field undergoes a Hopf bifurcation when the following conditions are satisfied simultaneously [38]:
- (A)
- nondegeneracy condition: the Jacobian matrix has one pair of purely imaginary roots, and other roots have nonzero real parts;
- (B)
- transversality condition: the real part of differentiation characteristic equation with respect to the parameter satisfy
- (C)
- the first Lyapunov coefficient is nonzero.
In order to derive the first Lyapunov coefficient , suppose that Equation (2) has an equilibrium point at . By denoting , we can write
as
where A is the Jacobian matrix, and B and C are symmetric multilinear vector functions which are defined as
Suppose that A possesses a pair of purely imaginary eigenvalues , meanwhile, the other eigenvalues have nonzero real part. Let be an eigenvectors of A satisfying the following three conditions
By means of an immersion of the form , the 2D center manifold associated to the eigenvalues is parameterized, where has a Taylor expansion of the following form
with and . By substituting Equation (12) into (8), one has
Defined by the coefficients , the complex vectors can be obtained by solving Equation (13). On the chart for a center manifold, the system (13) can be written as
Thus, the first Lyapunov coefficient can be defined as
where and .
3.2. Numerical Simulations
To investigate the existence of Hopf bifurcation in the system (2) at the equilibrium , we will examine the conditions (A), (B) and (C) one by one.
Firstly, we assume that the characteristic Equation (3) has a pair of purely imaginary eigenvalues . By substituting into (4), one has
which leads to:
Thus, one can obtain that
which are equivalent to
where . It is worth noting that when , the characteristic Equation (3) can be written as
Therefore, the four eigenvalues of the system (2) are as follows
Consequently, the nondegeneracy condition (A) is satisfied when .
Secondly, let , by substituting into Equation (10) and differentiate the both sides with respect to r, one obtains
which leads to:
Thus, one has
where , , and . Consequently, the transversality condition (B) is also verified.
At last, we will calculate the first Lyapunov coefficient under the above fixed parameters. The Jacobian matrix J on the equilibrium point is given by
The proper eigenvectors q and p are obtained by straightforward calculations
where the above eigenvectors q and p satisfy the three conditions (11), namely
Thus, one obtains
Therefore, the Hopf bifurcation of the system (2) at equilibrium point is nondegenerate and supercritical. Furthermore, the equilibria and are symmetric about the axis, hence, the system (2) should also undergo a Hopf bifurcation at . Two numerical simulations are given in Figure 3. For , the orbit of the system (2) with the initial values is attracted to the stable equilibrium point , whereas the orbit with the initial values is attracted to the other stable equilibrium point , as illustrated in Figure 3a. In Figure 3b, by choosing with the initial values and , the orbits of the system are attracted to stable limit cycles emerging from and , respectively.
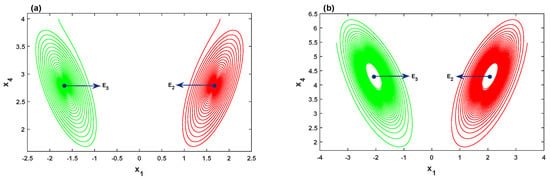
Figure 3.
Hopf bifurcation of the system (2): (a) , the orbit of the system is attracted to the stable symmetric equilibria and ; (b) , the orbit of the system is attracted to a stable limit cycle emerging from the symmetric equilibria and .
According to Reference [39], , and times standard deviation (SD) of the time series. In our experiment, we fix , and .
4. Multistability Behavior
A nonlinear dynamical system with multistability behavior can generate two or more attractors simultaneously depending on the initial values of the system. This section investigates the existence of multistability behavior in the system (2).
When we fix the parameters , , and select r as bifurcation parameter for over the range , the coexisting bifurcation models of the state variable are depicted in Figure 4a. In this figure, the attractor colored in blue is initiated from , meanwhile the attractor colored in red begins with the initial conditions . As can be observed in Figure 4a, the system (2) shows coexisting multiple chaotic attractors as well as the coexistence of multiple quasi-periodic attractors. To show the coexistence of multiple chaotic attractors visually, Figure 5 plots different orientations of the phase portraits of the system (2) when its parameters are set as , , , and .
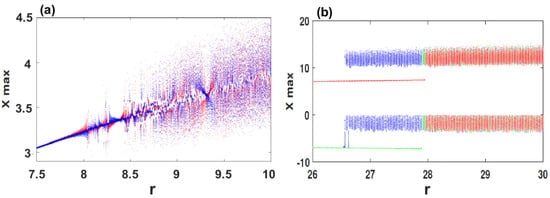
Figure 4.
Bifurcation diagrams versus parameter r for illustrating the two and three coexisting attractors of the system (2): (a) , , for the initial values (red) and (blue); (b) , , for the initial values (blue), (red) and (green).
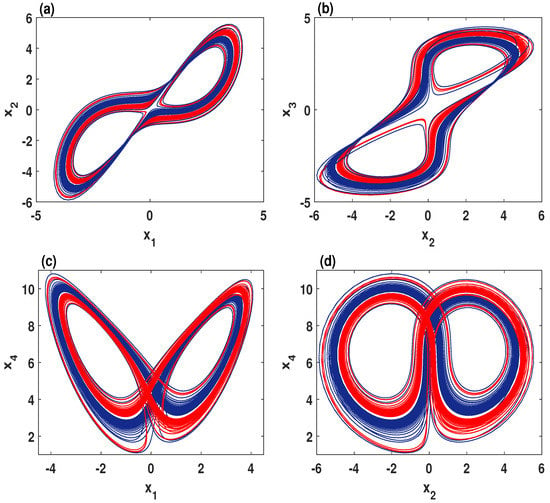
Figure 5.
Multiple coexisting chaotic attractors of the system (2) when , , , for the initial values (red) and (blue). (a) – plane; (b) – plane; (c) – plane; (d) – plane.
In addition, when we set , , with , Figure 4b shows that the chaotic attractor with two stable fixed-point attractors coexist for the initial values . For the orbit colored in blue, the evolution begins from attracting to the stable equilibrium within the range , and then the system shows chaotic behavior when . For (red), the system converges to the stable equilibrium when , and then exhibits chaotic behavior when . For the initial values (green), the system attracts to the stable equilibrium when , meanwhile the chaotic behavior is shown when . Selecting , an interesting dynamic is observed in the system (2) by plotting different orientations of the phase portraits with the corresponding time series, as shown in Figure 6. These portraits confirm the coexistence of three different attractors: (a) blue butterfly attractors surrounds the symmetric equilibria and ; (b) the red stable fixed-point attractor for , and the green stable fixed-point attractor for .
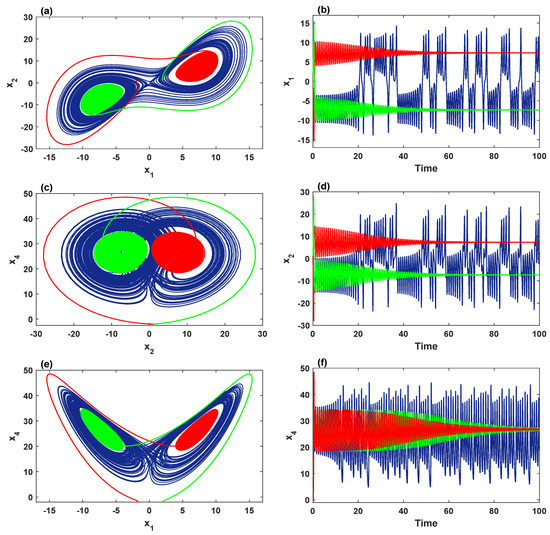
Figure 6.
Three coexisting attractors with , , , : (a,c,e) different perspectives on the coexistence of the chaotic and two stable fixed-point attractors for the initial values (blue), (red) and (green); (b,d,f) the corresponding time series of the state variables , and , respectively.
5. Complexity and Randomness of Multistability Regions
This section discusses determining and locating the parameters and initial values that show multistability behaviors, as well as investigates the randomness of the multistability regions.
5.1. Sample Entropy
Sample Entropy (SamEn) is a mathematical algorithm proposed by Richman [40]. It is used to provide a quantitative explanation about the complexity of nonlinear dynamical systems. Obviously, a system with bigger SamEn values indicates that it requires additional information to predict its attractor, hence, it is a chaotic system. Suppose that the time series of a dynamical system with a length of M, then the SamEn algorithm can be calculated by the following steps:
- (A)
- Reconstructing phase-space: for a given embedding dimension m and time delay , the reconstruction sequences are given bywhere .
- (B)
- Counting the vector pairs: let be the number of vector such thatwhere r is the tolerance parameter, and is the distance between and , which is defined by
- (C)
- Calculating probability: according to the obtained number of vector pairs, we can obtainthen calculate the probability by
- (D)
- Calculating SamEn: repeating the above steps we can obtain , then SamEn is given by
According to Reference [39], , and times standard deviation (SD) of the time series. In our experiment, we fix , and .
It is well-known that the cross-section of the basins of attraction can determine the dynamical system behaviors when its initial values vary. However, it is interesting to ask if there is any technique that can determine the behaviors of a dynamical system when its initial values and parameters vary. Therefore, SamEn based contour plots are applied to locate the regions of chaotic and periodic state, and hence, to determine the parameters and initial values that show multistability behaviors. To locate those parameters and initial values in the system (2), we designed the following experiments: (1) consider r as bifurcation parameter and set , and ; (2) let be the initial values; (3) calculate SamEn versus varying the parameter r and one of an initial value; (4) calculate SamEn versus varying two of the initial values.
Figure 7 plots SamEn of the system (2) in a two-dimensional plane when and different initial values. It can be observed from Figure 7a–d that four cases are analyzed when the initial values are set as , , and , respectively. From Figure 7, it can be seen that the parameter r and the initial values in the blue regions have smaller SamEn values, which means that the system (2) shows periodic state, whereas, those in the yellow and green regions lead to a chaotic state. Furthermore, Figure 8 shows the chaotic and periodic regions of system (2) when two of the initial values vary simultaneously.
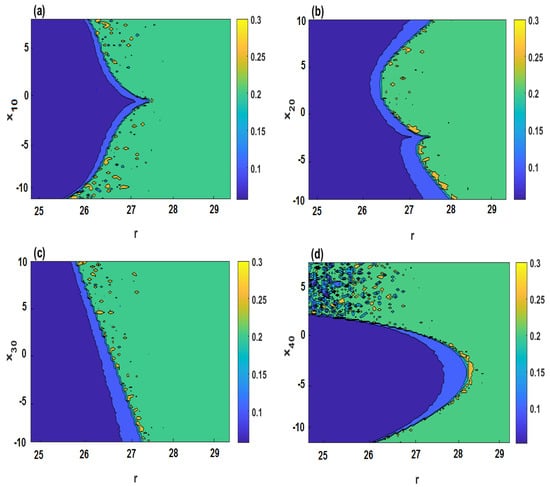
Figure 7.
SamEn in the parameter r-initial value plane for , , : (a) plane; (b) plane; (c) plane; (d) plane.
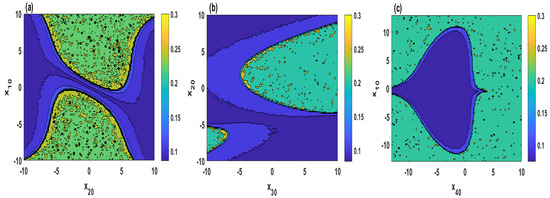
Figure 8.
SamEn versus varying two of the initial values for , , , : (a) ; (b) ; (c) .
5.2. Chaos-Based PRNG
Many chaotic systems have been applied to generate pseudorandom number generator (PRNG). The need of PRNG arises in many cryptographic applications, e.g., common cryptosystems employ keys, data hiding, and auxiliary quantities used in generating digital signatures [41,42]. However, secret keys of most chaos-based cryptographic schemes are generated by parameters and initial values of the employed chaotic systems [43]. Those parameters and initial values might be from multistability regions; it is therefore important to investigate the randomness of the trajectories generating from multistability regions.
To investigate the randomness of blue-green regions (multistability behaviors) and green regions (chaotic), which is shown in Figure 7d, we use here a simple chaos-based PRNG as an example. The generation procedures of the chaos-based PRNG are shown in Algorithm 1, for which , , and generates 1,000,000 bits binary string.
Several statistical tests can be employed to test the randomness of PRNG. Our experiment uses the highest standards of statistical packages which is NIST-800-22 [42]. The NIST-800-22 consists of 16 empirical statistical tests that provide true evaluation for the randomness of PRNG. Each test is developed to detect the non-random areas of a binary sequence from different sides, and then to derive a p-value. According to the recommendations in [24,44], we set the confidence level , and we use a binary sequence with length of 1,000,000 bit as the testing input. Since the confidence level of each test in NIST is set to be 1%, then the sequence is considered to be random with a confidence of 99% when the obtained p-value is bigger than .
According to Algorithm 1, we can obtain four PRNG from the trajectory of , , and when the initial values are considered as input. For , , and with the initial values , the SamEn values of the selected parameters and initial values are within the blue-green regions (multistability), as shown in Figure 7d. The randomness of the corresponding PRNG that generated from the trajectory of , , and can be visually shown by depicting the NIST-800-22 test results, as seen in Figure 9. As can be observed from Figure 9, the four PRNG generating from multistability regions fail to pass most of the statistical tests. On the other hand, when , , and with the initial values , the SamEn values are within the green region (chaotic), as shown in Figure 7d. Table 1 lists the corresponding NIST-800-22 results for each of the four PRNG. It is obvious that the four PRNG can pass all the statistical tests.
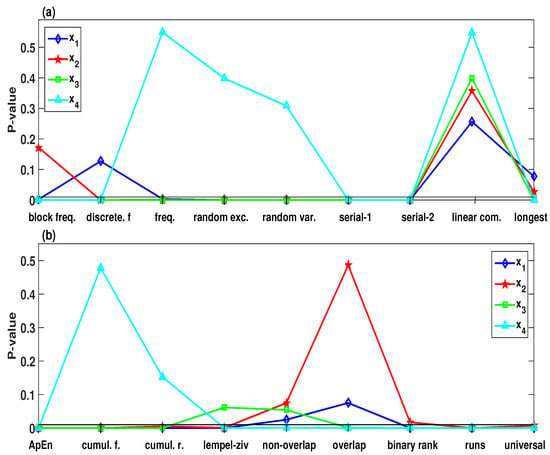
Figure 9.
The statistical tests NIST SP800-22 of the pseudorandom number generator (PRNG) that generated by , , , of the system (2) with , , , and for the initial values . (a) Block-Frequency, Discrete Fourier Transform, Frequency (Monobit), Random Excursions, Random Excursions Variant, Serial-1, Serial-2, Linear Complexity, and Longest Run of Ones, respectively; (b) Approximate Entropy, Cumulative Sums (Forward), Cumulative Sums (Reverse), Lempel-ziv Compression, Non-overlapping Template, Overlapping Template, Binary Matrix Rank, Runs, and Universal Statistical.

Table 1.
NIST-800-22 tests results of binary sequences generated by PRNG of , , and outputs.
| Algorithm 1 The generation of chaos-based PRNG |
Input: The initial values of system (2).
|
6. Conclusions
This paper has introduced a new 4D chaotic laser system, which is derived from Lorenz-Haken equations. The new chaotic laser system has three equilibria and only two quadratic nonlinearities. The dynamics of the new system have been studied deeply, in which the system shows coexisting multiple Hopf bifurcations, and complex coexisting behaviors of two and three attractors. In addition, we applied SamEn contour plots for measuring the complexity of the system when its initial values and parameters vary. Simulation results have shown that multistability regions can be easily determined and located using SamEn contour plots. To examine the randomness of PRNG that generate from the multistability regions, we used the NIST-800-22 tests. Statistical test results demonstrate that the generated PRNG from multistability regions are non-random. This means that although the multistability behaviors indicate high sensitivity of chaotic systems, they might be unsuitable for cryptographic applications.
Author Contributions
H.N. designed the study and wrote the paper. M.R.M.S. and N.M.G.A-S. contributed to the methodology, simulations and algorithm design. A.K. undertook the theoretical analysis. All authors read and approved the manuscript.
Funding
This research was funded by Universiti Putra Malaysia Grant under the grant code (GP. 2018/9595200).
Acknowledgments
The authors would like to thank the Research Management Center (RMC) of Universiti Putra Malaysia for supporting this work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Banerjee, S.; Rondoni, L.; Mukhopadhyay, S.; Misra, A.P. Synchronization of spatiotemporal semiconductor lasers and its application in color image encryption. Opt. Commun. 2011, 284, 2278–2291. [Google Scholar] [CrossRef]
- Valli, D.; Banerjee, S.; Ganesan, K.; Muthuswamy, B.; Subramaniam, C.K. Chaotic time delay systems and field programmable gate array realization. In Chaos, Complexity and Leadership 2012; Springer: Dordrecht, The Netherlands, 2014; pp. 9–16. [Google Scholar]
- Banerjee, S.; Saha, P.; Chowdhury, A.R. Chaotic scenario in the Stenflo equations. Phys. Scr. 2001, 63, 177. [Google Scholar] [CrossRef]
- Natiq, H.; Banerjee, S.; He, S.; Said, M.R.M.; Kilicman, A. Designing an M-dimensional nonlinear model for producing hyperchaos. Chaos Solitons Fractals 2018, 114, 506–515. [Google Scholar] [CrossRef]
- Ghosh, D.; Banerjee, S.; Chowdhury, A.R. Synchronization between variable time-delayed systems and cryptography. Europhys. Lett. 2007, 80, 30006. [Google Scholar] [CrossRef]
- Banerjee, S. (Ed.) Chaos Synchronization and Cryptography for Secure Communications: Applications for Encryption; IGI Global: Hershey, PA, USA, 2010. [Google Scholar]
- Saha, P.; Banerjee, S.; Chowdhury, A.R. Chaos, signal communication and parameter estimation. Phys. Lett. A 2004, 326, 133–139. [Google Scholar] [CrossRef]
- Fataf, N.A.A.; Palit, S.K.; Mukherjee, S.; Said, M.R.M.; Son, D.H.; Banerjee, S. Communication scheme using a hyperchaotic semiconductor laser model: Chaos shift key revisited. Eur. Phys. J. Plus 2017, 132, 492. [Google Scholar] [CrossRef]
- Banerjee, S.; Pizzi, M.; Rondoni, L. Modulation of output power in the spatio-temporal analysis of a semi conductor laser. Opt. Commun. 2012, 285, 1341–1346. [Google Scholar] [CrossRef]
- Rondoni, L.; Ariffin, M.R.K.; Varatharajoo, R.; Mukherjee, S.; Palit, S.K.; Banerjee, S. Optical complexity in external cavity semiconductor laser. Opt. Commun. 2017, 387, 257–266. [Google Scholar] [CrossRef]
- Mukherjee, S.; Palit, S.K.; Banerjee, S.; Ariffin, M.R.K.; Rondoni, L.; Bhattacharya, D.K. Can complexity decrease in congestive heart failure? Phys. A Stat. Mech. Appl. 2015, 439, 93–102. [Google Scholar] [CrossRef]
- Banerjee, S.; Palit, S.K.; Mukherjee, S.; Ariffin, M.R.K.; Rondoni, L. Complexity in congestive heart failure: A time-frequency approach. Chaos Interdiscip. J. Nonlinear Sci. 2016, 26, 033105. [Google Scholar] [CrossRef]
- Pham, V.-T.; Vaidyanathan, S.; Volos, C.K.; Jafari, S. Hidden attractors in a chaotic system with an exponential nonlinear term. Eur. Phys. J. Spec. Top. 2015, 224, 1507–1517. [Google Scholar] [CrossRef]
- Leonov, G.A.; Kuznetsov, N.V. Hidden attractors in dynamical systems. From hidden oscillations in Hilbert–Kolmogorov, Aizerman, and Kalman problems to hidden chaotic attractor in Chua circuits. Int. J. Bifurc. Chaos 2013, 23, 1330002. [Google Scholar] [CrossRef]
- Pham, V.T.; Volos, C.; Jafari, S.; Wang, X.; Vaidyanathan, S. Hidden hyperchaotic attractor in a novel simple memristive neural network. Optoelectron. Adv. Mater. Rapid Commun. 2014, 8, 1157–1163. [Google Scholar]
- Dudkowski, D.; Jafari, S.; Kapitaniak, T.; Kuznetsov, N.V.; Leonov, G.A.; Prasad, A. Hidden attractors in dynamical systems. Phys. Rep. 2016, 637, 1–50. [Google Scholar] [CrossRef]
- Tlelo-Cuautle, E.; de la Fraga, L.G.; Pham, V.T.; Volos, C.; Jafari, S.; de Jesus Quintas-Valles, A. Dynamics, FPGA realization and application of a chaotic system with an infinite number of equilibrium points. Nonlinear Dyn. 2017, 89, 1129–1139. [Google Scholar] [CrossRef]
- Pham, V.-T.; Volos, C.; Gambuzza, L.V. A memristive hyperchaotic system without equilibrium. Sci. World J. 2014, 2014, 368986. [Google Scholar] [CrossRef] [PubMed]
- Natiq, H.; Said, M.R.M.; Ariffin, M.R.K.; He, S.; Rondoni, L.; Banerjee, S. Self-excited and hidden attractors in a novel chaotic system with complicated multistability. Eur. Phys. J. Plus 2018, 133, 557. [Google Scholar] [CrossRef]
- Wang, X.; Pham, V.T.; Jafari, S.; Volos, C.; Munoz-Pacheco, J.M.; Tlelo-Cuautle, E. A new chaotic system with stable equilibrium: From theoretical model to circuit implementation. IEEE Access 2017, 5, 8851–8858. [Google Scholar] [CrossRef]
- Jafari, S.; Sprott, J.C. Simple chaotic flows with a line equilibrium. Chaos Solitons Fractals 2013, 57, 79–84. [Google Scholar] [CrossRef]
- Pham, V.T.; Jafari, S.; Volos, C.; Giakoumis, A.; Vaidyanathan, S.; Kapitaniak, T. A chaotic system with equilibria located on the rounded square loop and its circuit implementation. IEEE Trans. Circuits Syst. II Express Briefs 2016, 63, 878–882. [Google Scholar] [CrossRef]
- Arecchi, F.; Meucci, R.; Puccioni, G.; Tredicce, J. Experimental evidence of subharmonic bifurcations, multistability, and turbulence in a q-switched gas laser. Phys. Rev. Lett. 1982, 49, 1217. [Google Scholar] [CrossRef]
- Munoz-Pacheco, J.; Zambrano-Serrano, E.; Volos, C.; Jafari, S.; Kengne, J.; Rajagopal, K. A new fractional-order chaotic system with different families of hidden and self-excited attractors. Entropy 2018, 20, 564. [Google Scholar] [CrossRef]
- Wang, C.; Ding, Q. A New Two-Dimensional Map with Hidden Attractors. Entropy 2018, 20, 322. [Google Scholar] [CrossRef]
- Li, C.; Sprott, J.C.; Hu, W.; Xu, Y. Infinite multistability in a self-reproducing chaotic system. Int. J. Bifurc. Chaos 2017, 27, 1750160. [Google Scholar] [CrossRef]
- Sparrow, C. The Lorenz Equations: Bifurcations, Chaos, and Strange Attractors; Springer Science & Business Media: New York, NY, USA, 2012; Volume 41. [Google Scholar]
- Pereira, U.; Coullet, P.; Tirapegui, E. The Bogdanov—Takens normal form: A minimal model for single neuron dynamics. Entropy 2015, 17, 7859–7874. [Google Scholar] [CrossRef]
- Zhan, X.; Ma, J.; Ren, W. Research entropy complexity about the nonlinear dynamic delay game model. Entropy 2017, 19, 22. [Google Scholar] [CrossRef]
- Han, Z.; Ma, J.; Si, F.; Ren, W. Entropy complexity and stability of a nonlinear dynamic game model with two delays. Entropy 2016, 18, 317. [Google Scholar] [CrossRef]
- Dang, T.S.; Palit, S.K.; Mukherjee, S.; Hoang, T.M.; Banerjee, S. Complexity and synchronization in stochastic chaotic systems. Eur. Phys. J. Spec. Top. 2016, 225, 159–170. [Google Scholar] [CrossRef]
- He, S.; Sun, K.; Wang, H. Complexity analysis and DSP implementation of the fractional-order Lorenz hyperchaotic system. Entropy 2015, 17, 8299–8311. [Google Scholar] [CrossRef]
- Ma, J.; Ma, X.; Lou, W. Analysis of the Complexity Entropy and Chaos Control of the Bullwhip Effect Considering Price of Evolutionary Game between Two Retailers. Entropy 2016, 18, 416. [Google Scholar] [CrossRef]
- He, S.; Li, C.; Sun, K.; Jafari, S. Multivariate Multiscale Complexity Analysis of Self-Reproducing Chaotic Systems. Entropy 2018, 20, 556. [Google Scholar] [CrossRef]
- Haken, H. Analogy between higher instabilities in fluids and lasers. Phys. Lett. A 1975, 53, 77–78. [Google Scholar] [CrossRef]
- Banerjee, S.; Saha, P.; Chowdhury, A.R. Chaotic aspects of lasers with host-induced nonlinearity and its control. Phys. Lett. A 2001, 291, 103–114. [Google Scholar] [CrossRef]
- Van Tartwijk, G.H.M.; Agrawal, G.P. Nonlinear dynamics in the generalized Lorenz-Haken model. Opt. Commun. 1997, 133, 565–577. [Google Scholar] [CrossRef]
- Kuznetsov, Y.A. Numerical Analysis of Bifurcations. In Elements of Applied Bifurcation Theory; Springer: New York, NY, USA, 2004; pp. 505–585. [Google Scholar]
- Kaffashi, F.; Foglyano, R.; Wilson, C.G.; Loparo, K.A. The effect of time delay on approximate & sample entropy calculations. Phys. D Nonlinear Phenom. 2008, 237, 3069–3074. [Google Scholar]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef] [PubMed]
- Volos, C.K.; Kyprianidis, I.M.; Stouboulos, I.N. Fingerprint images encryption process based on a chaotic true random bits generator. Int. J. Multimedia Intell. Secur. 2010, 1, 320–335. [Google Scholar] [CrossRef]
- Rukhin, A.; Soto, J.; Nechvatal, J.; Smid, M.; Barker, E. A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications; Booz-Allen and Hamilton Inc.: Mclean, VA, USA, 2001. [Google Scholar]
- Natiq, H.; Al-Saidi, N.M.G.; Said, M.R.M.; Kilicman, A. A new hyperchaotic map and its application for image encryption. Eur. Phys. J. Plus 2018, 133, 6. [Google Scholar] [CrossRef]
- Rodríguez-Orozco, E.; García-Guerrero, E.; Inzunza-Gonzalez, E.; López-Bonilla, O.; Flores-Vergara, A.; Cárdenas-Valdez, J.; Tlelo-Cuautle, E. FPGA-based Chaotic Cryptosystem by Using Voice Recognition as Access Key. Electronics 2018, 7, 414. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).