Time-Shift Multiscale Fuzzy Entropy and Laplacian Support Vector Machine Based Rolling Bearing Fault Diagnosis
Abstract
1. Introduction
2. Time Shift Multiscale Fuzzy Entropy and Related Theories
2.1. Multiscale Entropy Method
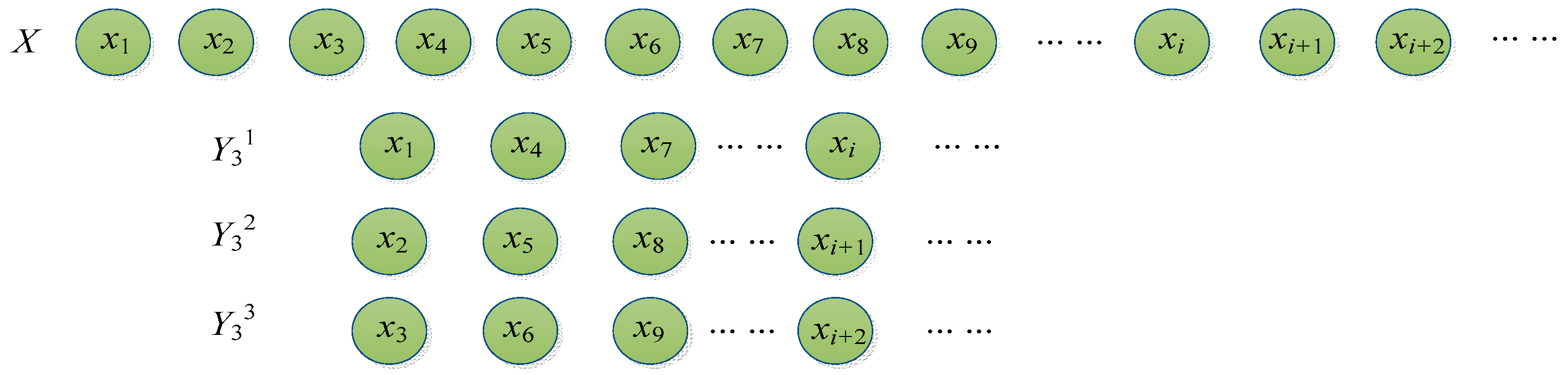
2.2. Time Shift Multiscale Sample Entropy
2.3. Time Shift Multiscale Fuzzy Entropy
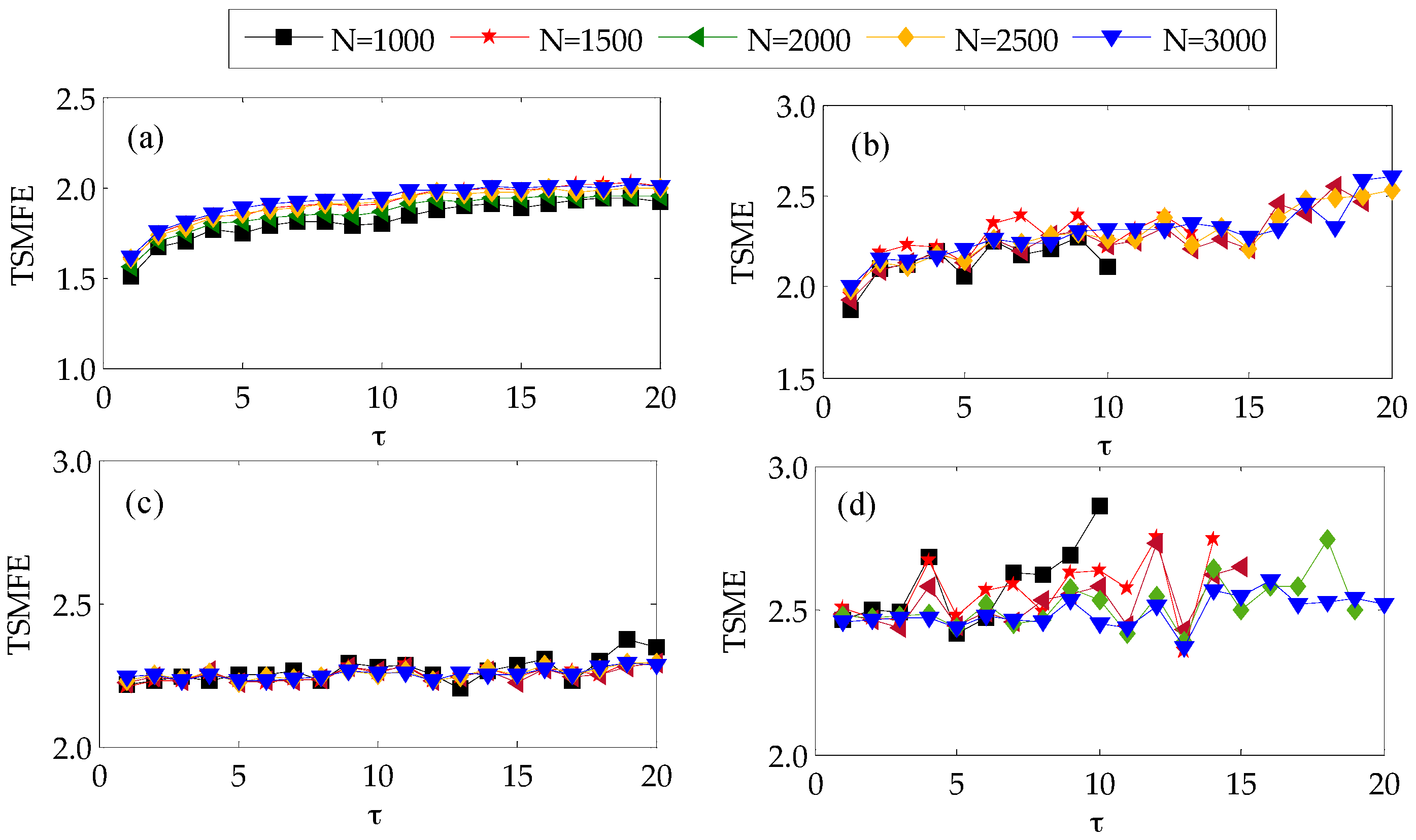
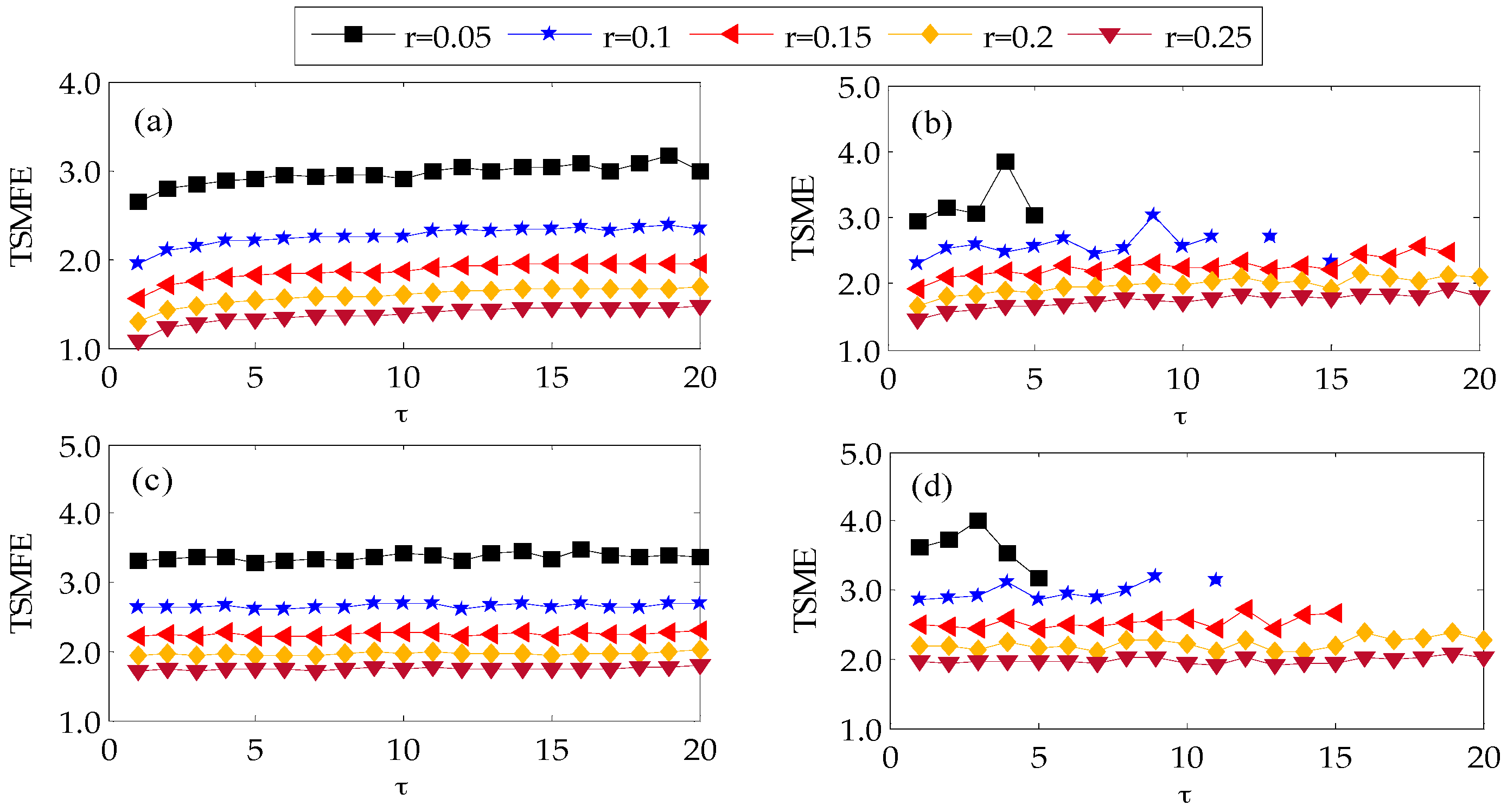
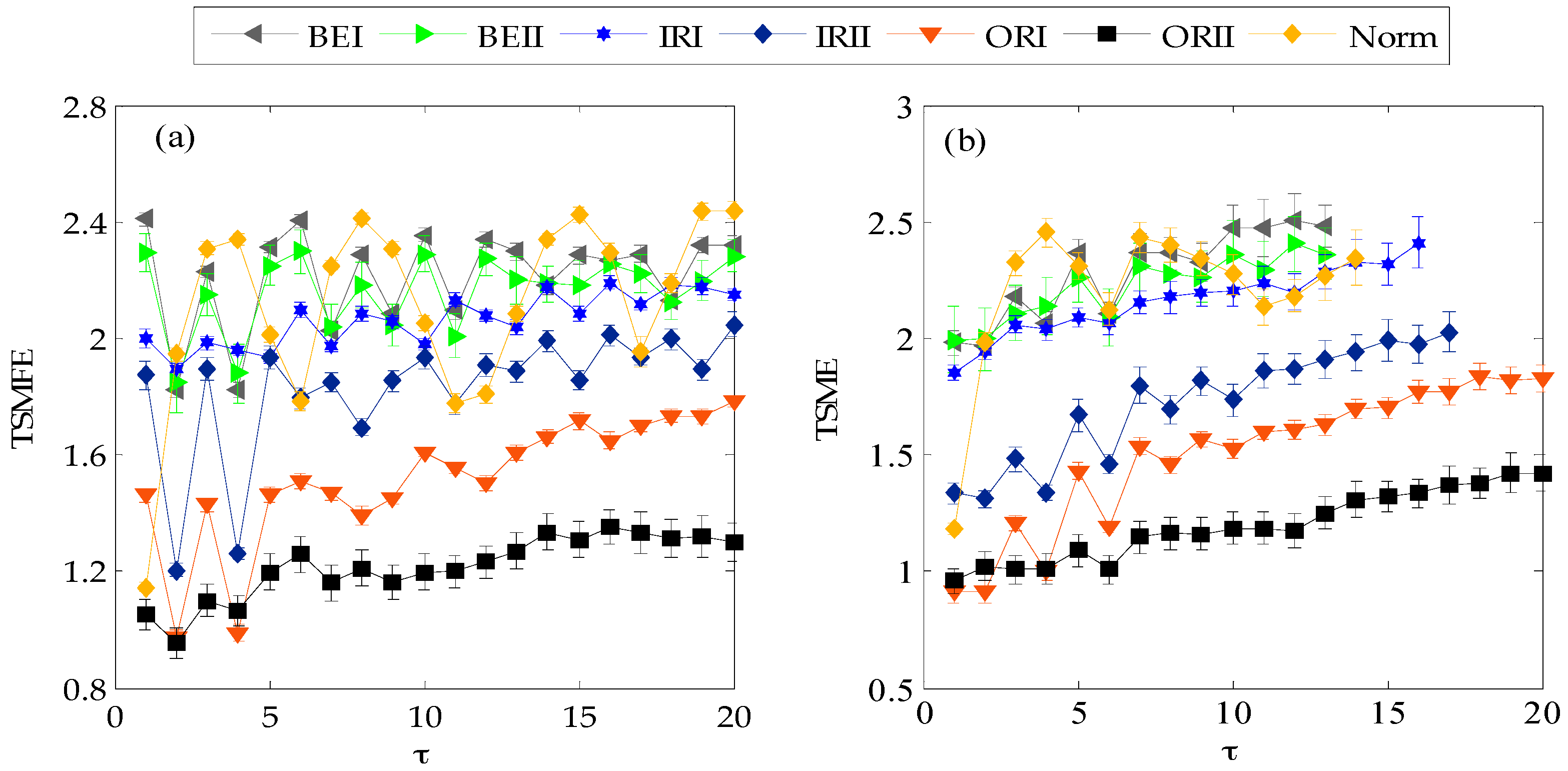
3. Comparison of TSME and TSMFE
3.1. Parameter Selection
3.2. Simulation Analysis
4. TSMFE and LapSVM Based Fault Diagnosis Method for Rolling Bearing
4.1. LapSVM Algorithm
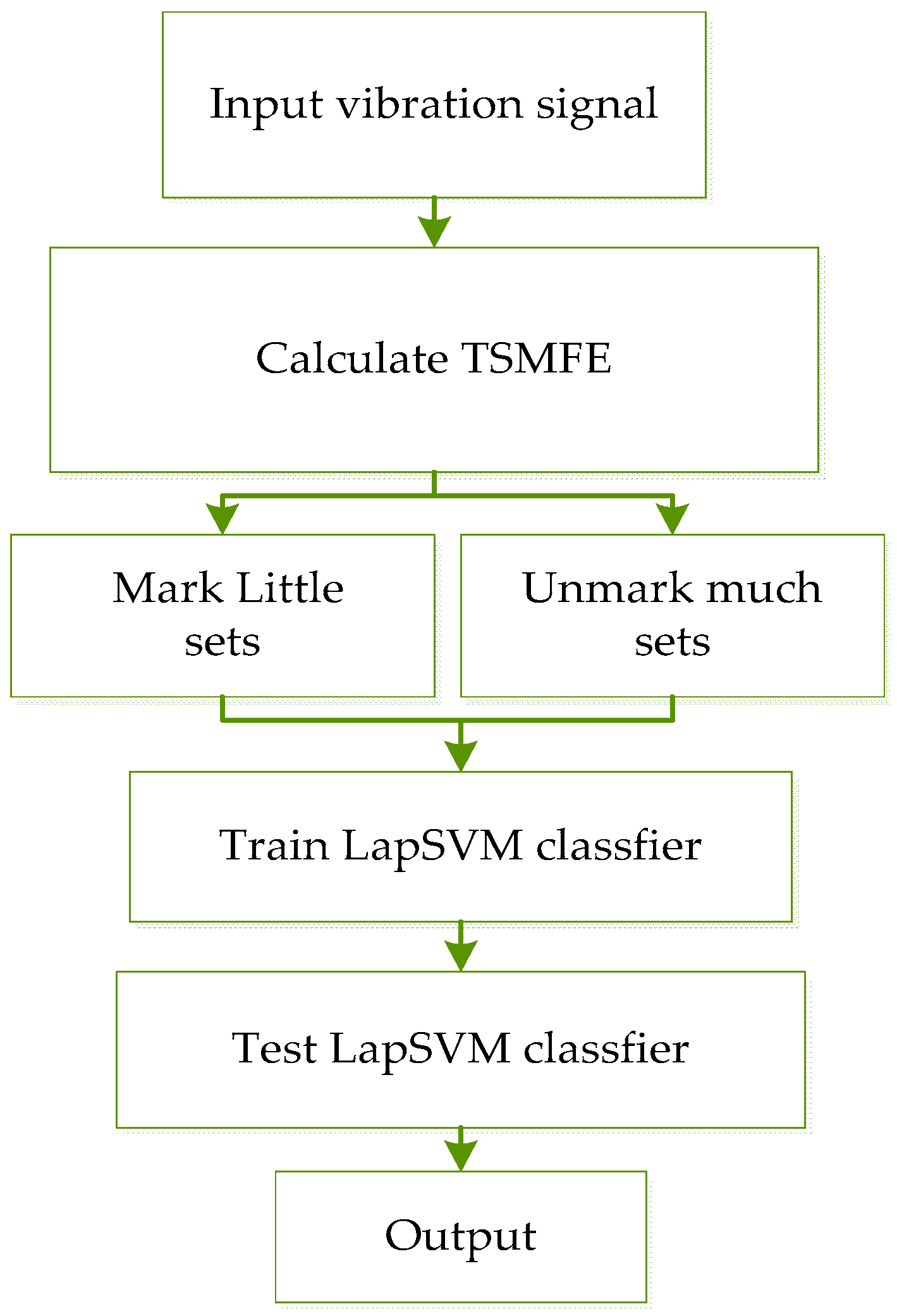
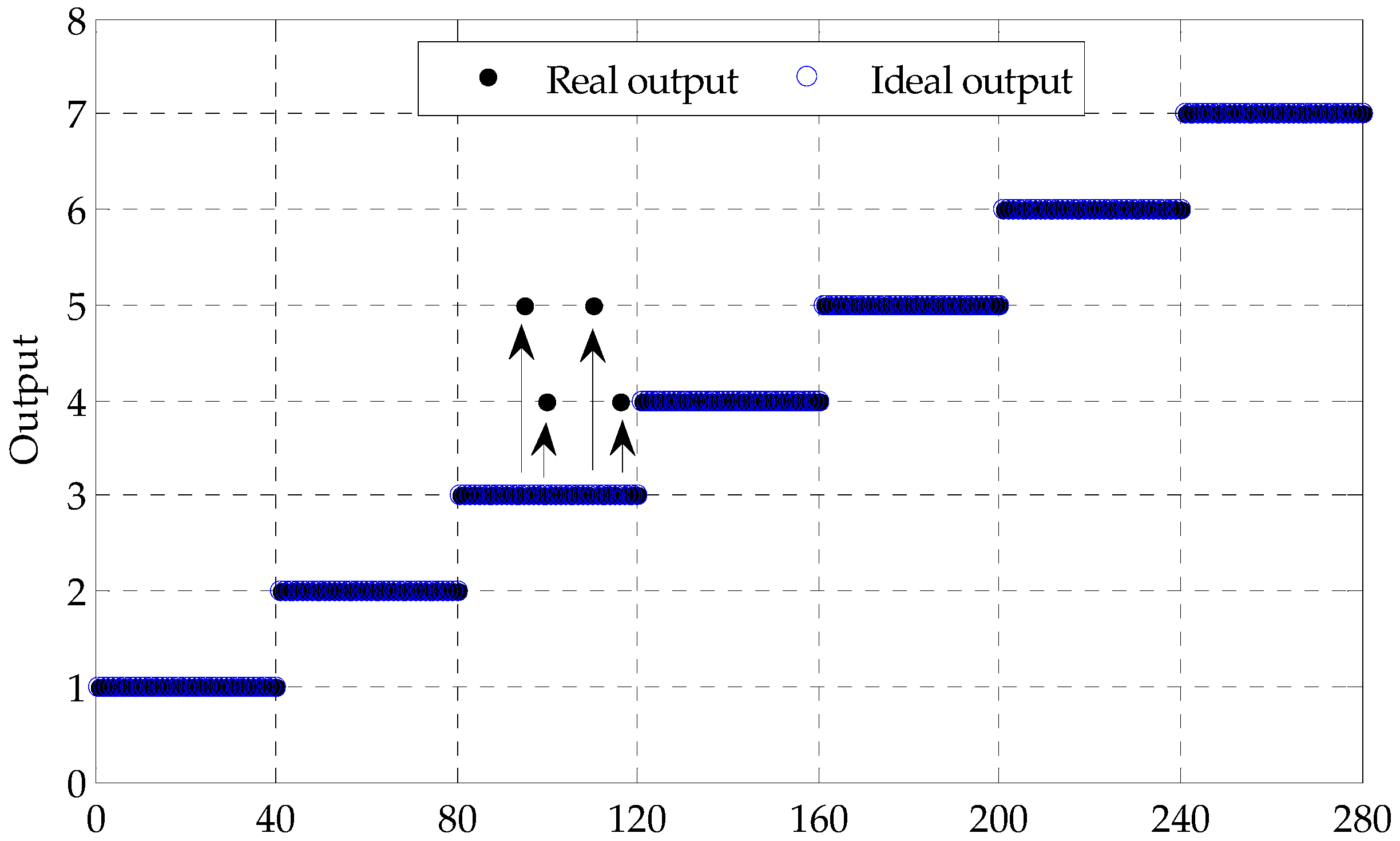
4.2. The Proposed Fault Diagnosis Method
- (1)
- For given p kinds of states of rolling bearing, each state has mp samples and thus the number of whole samples is ;
- (2)
- TSMFE of all the M samples are calculated and the feature sets , are obtained, where represents the p-th feature sets;
- (3)
- The mp samples of the p-th state are randomly divided into h as marked sample sets, i.e., and (mp − h) as unmarked sample sets, i.e., ;
- (4)
- The sensitive fault features sets of training samples: both and are input to the LapSVM classifier for training, learning and testing.
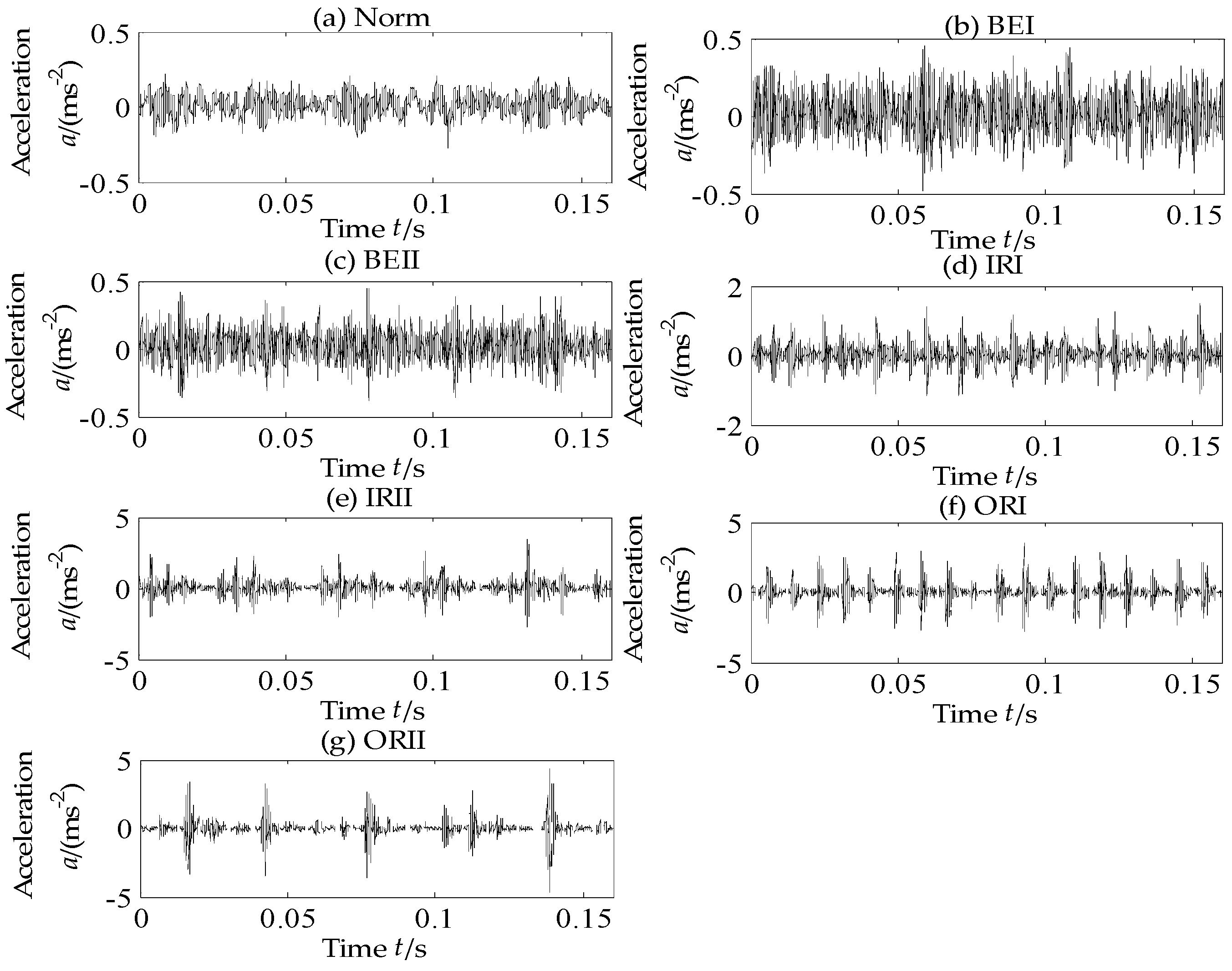
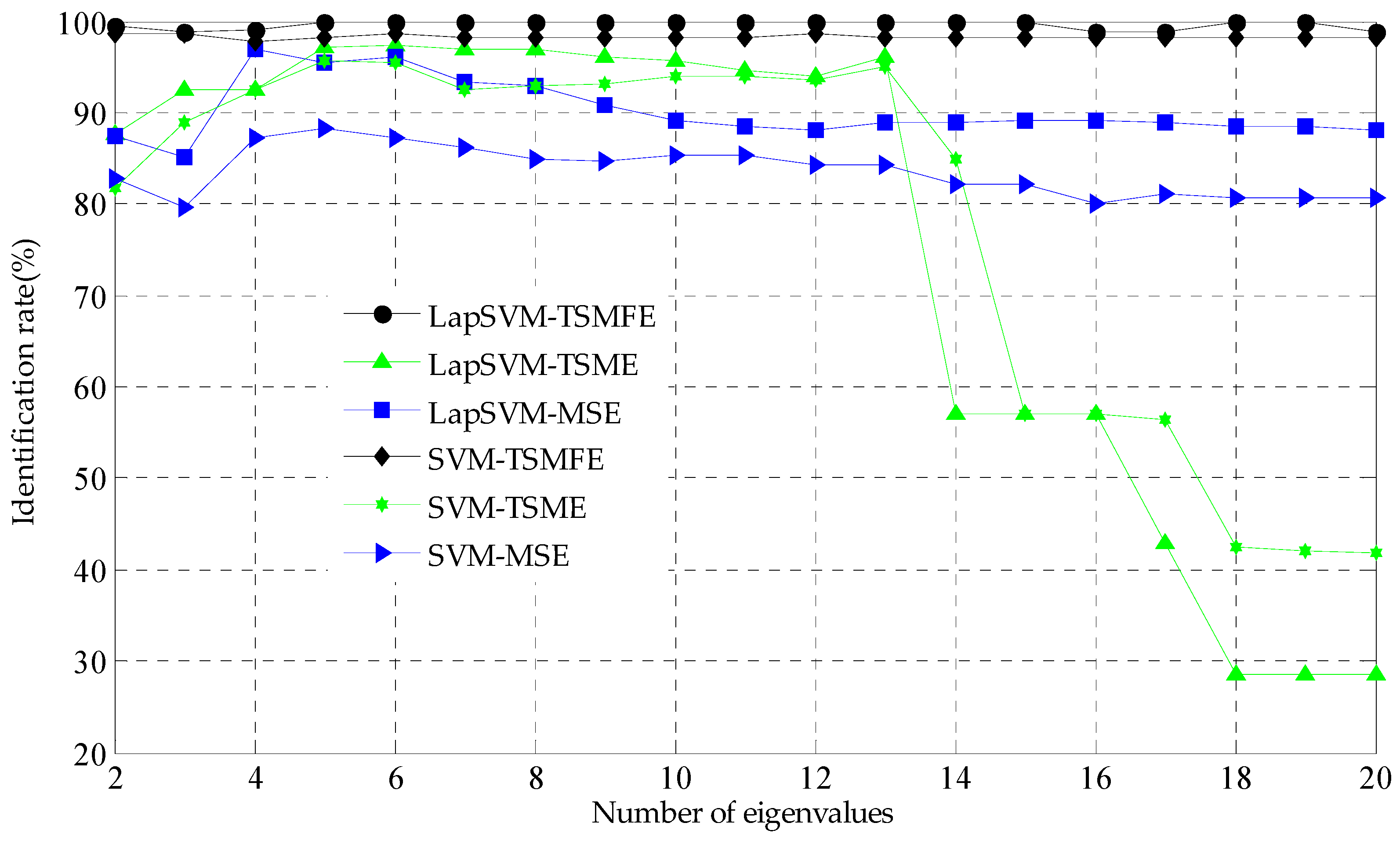
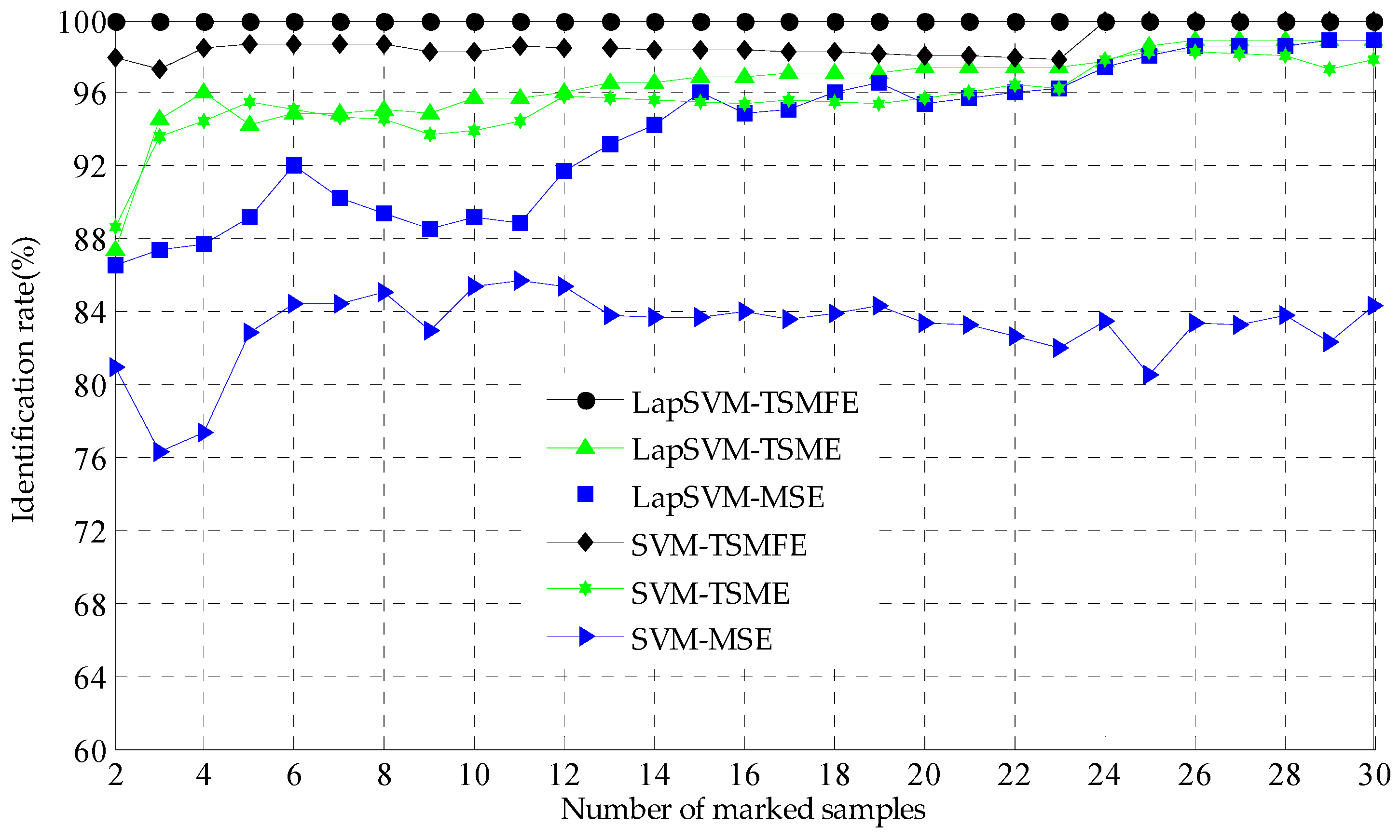
4.3. Experimental Data Analysis
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| Nomenclature | |||
| AppEn | Approximate entropy | Time scale | |
| SampEn | Sample entropy | X | Initial time series |
| MSE | Multiscale sample entropy | N | Length of data |
| SVM | Support vector machine | Embedding dimension | |
| LapSVM | Laplace support vector machine | r | Similar tolerances |
| FuzzyEn | Fuzzy entropy | k | Initial time point |
| TSMFE | Time shift multiscale fuzzy entropy | Interval time | |
| TSME | Time shift multiscale entropy | Upper rounding boundary | |
| Norm | Normal rolling bearing | l | Number of given marked samples |
| ORI | Outer race fault under fault diameters 0.1778 mm | u | Number of given unmarked samples |
| BEI | Ball element under fault diameters 0.1778 mm | Manifold regularization item | |
| IRI | Inner race fault under fault diameters 0.1778 mm | Manifold regularization framework | |
| ORII | Outer race fault under fault diameters 0.5334 mm | Quadratic planning | |
| BEII | Ball element under fault diameters 0.5334 mm | p | Number of rolling bearing states |
| IRII | Inner race fault under fault diameters 0.5334 mm | M | Total number of samples |
| SD | Standard deviation | p-th feature sets | |
| L | Laplacian | Marked sample sets | |
| V | Hinge loss function | Unmarked sample sets | |
References
- Lin, J.; Chen, Q. Fault diagnosis of rolling bearings based on multifractal detrended fluctuation analysis and Mahalanobis distance criterion. Mech. Syst. Signal Process. 2013, 38, 515–533. [Google Scholar] [CrossRef]
- Randall, R.B.; Antoni, J. Rolling element bearing diagnostics–A tutorial. Mech. Syst. Signal Process. 2011, 25, 485–520. [Google Scholar] [CrossRef]
- Cui, L.; Gong, X.; Zhang, J.; Wang, H. Double-dictionary matching pursuit for fault extent evaluation of rolling bearing based on the Lempel–Ziv complexity. J. Sound. Vib. 2016, 385, 372–388. [Google Scholar] [CrossRef]
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef] [PubMed]
- Xie, H.B.; Gao, Z.M.; Liu, H. Classification of ventricular tachycardia and fibrillation using fuzzy similarity-based approximate entropy. Expert Syst. Appl. 2011, 38, 3973–3981. [Google Scholar] [CrossRef]
- Richman, J.S.; Lake, D.E.; Moorman, J.R. Sample entropy. Methods Enzymol. 2004, 384, 172–184. [Google Scholar] [PubMed]
- Alcaraz, R.; Rieta, J.J. A review on sample entropy applications for the non-invasive analysis of atrial fibrillation electrocardiograms. Biomed. Signal Process. 2010, 5, 1–14. [Google Scholar] [CrossRef]
- Avci, E.; Avci, D. An expert system based on fuzzy entropy for automatic threshold selection in image processing. Expert Syst. Appl. 2009, 36, 3077–3085. [Google Scholar] [CrossRef]
- Xie, H.B.; Sivakumar, B.; Boonstra, T.W.; Mengersen, K. Fuzzy entropy and its application for enhanced subspace filtering. IEEE. Trans. Fuzzy Syst. 2017, 99, 1970–1982. [Google Scholar] [CrossRef]
- Mahajan, R.; Morshed, B.I. Unsupervised eye blink artifact denoising of EEG data with modified multiscale sample entropy, Kurtosis, and wavelet-ICA. IEEE. J. Biomed. Health Inform. 2014, 19, 158–165. [Google Scholar] [CrossRef] [PubMed]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale entropy to distinguish physiologic and synthetic RR time series. Comput. Cardiol. 2002, 29, 137–140. [Google Scholar] [PubMed]
- Yan, R.; Gao, R.X. Approximate Entropy as a diagnostic tool for machine health monitoring. Mech. Syst. Signal Process. 2007, 21, 824–839. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, L.; Hu, J.; Xiong, G. Bearing fault diagnosis using a novel classifier ensemble based on lifting wavelet packet transforms and sample entropy. Shock Vib. 2016, 2016, 1–13. [Google Scholar] [CrossRef]
- Zhong, X.Y.; Zhao, C.H.; Dong, H.J.; Liu, X.M.; Zeng, L.C. Rolling bearing fault diagnosis using sample entropy and 1.5 dimension spectrum based on EMD. Appl. Mech. Mater. 2013, 278–280, 1027–1031. [Google Scholar] [CrossRef]
- Chen, W.; Zhuang, J.; Yu, W.; Wang, Z. Measuring complexity using FuzzyEn, ApEn, and SampEn. Med. Eng. Phys. 2009, 31, 61–68. [Google Scholar] [CrossRef] [PubMed]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale entropy analysis of complex physiologic time series. Phys. Rev. Lett. 2002, 89, 068102. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Xiong, G.; Liu, H.; Zou, H.; Guo, W. Bearing fault diagnosis using multi-scale entropy and adaptive neuro-fuzzy inference. Expert Syst. Appl. 2010, 37, 6077–6085. [Google Scholar] [CrossRef]
- Aouabdi, S.; Taibi, M.; Bouras, S.; Boutasseta, N. Using multi-scale entropy and principal component analysis to monitor gears degradation via the motor current signature analysis. Mech. Syst. Signal Process. 2017, 90, 298–316. [Google Scholar] [CrossRef]
- Chen, W.; Wang, Z.; Xie, H.; Yu, W. Characterization of surface EMG signal based on fuzzy entropy. IEEE Trans. Neural Syst. Rehabil. Eng. 2007, 15, 266–272. [Google Scholar] [CrossRef] [PubMed]
- Pham, T.D. Time-shift multiscale entropy analysis of physiological signals. Entropy 2017, 19, 257. [Google Scholar] [CrossRef]
- Satone, M.; Kharate, G. Face recognition technique using PCA, Wavelet and SVM. Int. J. Comput. Sci. Eng. 2014, 6, 58–62. [Google Scholar]
- Foody, G.M.; Mathur, A. A relative evaluation of multiclass image classification by support vector machines. IEEE. Trans. Geosci. Remote Sens. 2004, 42, 1335–1343. [Google Scholar] [CrossRef]
- Mahmud, M.N.; Ibrahim, M.N.; Osman, M.K.; Hussain, Z. Support vector machine (SVM) for fault classification in radial distribution network. Adv. Sci. Lett. 2017, 23, 4124–4128. [Google Scholar] [CrossRef]
- Belkin, M.; Niyogi, P.; Sindhwani, V. Manifold regularization: A geometric framework for learning from labeled and unlabeled examples. J. Mach. Learn. Res. 2006, 7, 2399–2434. [Google Scholar]
- Melacci, S.; Belkin, M. Laplacian support vector machines trained in the primal. J. Mach. Learn. Res. 2011, 12, 1149–1184. [Google Scholar]
- Sun, S. Multi-view Laplacian support vector machines. Appl. Intell. 2013, 41, 209–222. [Google Scholar]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale entropy analysis of biological signals. Phys. Rev. E 2005, 71, 021906. [Google Scholar] [CrossRef] [PubMed]
- Richman, J.; Moorman, J. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart. Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef] [PubMed]
- Zheng, J.; Pan, H.; Cheng, J. Rolling bearing fault detection and diagnosis based on composite multiscale fuzzy entropy and ensemble support vector machines. Mech. Syst. Signal Process. 2017, 85, 746–759. [Google Scholar] [CrossRef]
- Higuchi, T. Approach to an irregular time series on the basis of the fractal theory. Physica D 1998, 31, 277–283. [Google Scholar] [CrossRef]
- Tong, S.; Koller, D. Support vector machine active learning with applications to text classification. J. Mach. Learn. Res. 2008, 2, 999–1006. [Google Scholar]
- Sakthivel, N.R.; Sugumaran, V.; Nair, B.B. Application of support vector machine (SVM) and proximal support vector machine (PSVM) for fault classification of monoblock centrifugal pump. Int. J. Data Anal. Tech. Strat. 2010, 2, 38–61. [Google Scholar] [CrossRef]
- Bordoloi, D.J.; Tiwari, R. Support vector machine based optimization of multi-fault classification of gears with evolutionary algorithms from time–frequency vibration data. Measurement 2014, 55, 1–14. [Google Scholar] [CrossRef]
- Wu, J.S.; Zhou, Z.H. Sequence-based prediction of microrna-binding residues in proteins using cost-sensitive Laplacian support vector machines. IEEE-ACM Trans. Comput. Biol. 2013, 10, 752–759. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.; Park, C.; Koo, J.Y. Feature selection in the Laplacian support vector machine. Computat. Stat. Data Anal. 2011, 55, 567–577. [Google Scholar] [CrossRef]
- Gomez-Chova, L.; Camps-Valls, G.; Munoz-Mari, J.; Caple, J. Semi-supervised image classification with Laplacian support vector machines. IEEE. Geosci. Remote Sens. 2008, 5, 336–340. [Google Scholar] [CrossRef]
- Bearing Data Center of the Case Western Reserve University. Available online: http://csegroups.Case.Edu/bearingdatacenter/pages/download-data-file (accessed on 20 August 2017).


| Sample Sets | Faults | LapSVM1 | LapSVM2 | LapSVM3 | LapSVM4 | LapSVM5 | LapSVM6 |
|---|---|---|---|---|---|---|---|
| T1~T50 | Norm | +1(50) | |||||
| T51~T100 | BEI | −1(50) | +1(50) | ||||
| T101~T150 | BEII | −1(50) | −1(50) | +1(50) | |||
| T151~T200 | IRI | −1(50) | −1(50) | −1(50) | +1(50) | ||
| T201~T250 | IRII | −1(50) | −1(50) | −1(50) | −1(50) | +1(50) | |
| T251~T300 | ORI | −1(50) | −1(50) | −1(50) | −1(50) | −1(50) | +1(50) |
| T301~T350 | ORII | −1(50) | −1(50) | −1(50) | −1(50) | −1(50) | −1(50) |
| Sample Sets | Faults | SVM1 | SVM2 | SVM3 | SVM4 | SVM5 | SVM6 |
|---|---|---|---|---|---|---|---|
| T1~T50 | Norm | +1(40) | |||||
| T51~T100 | BEI | −1(40) | +1(40) | ||||
| T101~T150 | BEII | −1(40) | −1(40) | +1(36) | |||
| T151~T200 | IRI | −1(40) | −1(40) | −1(42) | +1(40) | ||
| T201~T250 | IRII | −1(40) | −1(40) | −1(42) | −1(40) | +1(40) | |
| T251~T300 | ORI | −1(40) | −1(40) | −1(40) | −1(40) | −1(40) | +1(40) |
| T301~T350 | ORII | −1(40) | −1(40) | −1(40) | −1(40) | −1(40) | −1(40) |
| Methods | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 4 | MSE | 86.85 | 96.57 | 96.85 | 96.85 | 97.42 | 97.42 | 97.14 | 96.85 | 97.42 | 97.42 |
| TSME | 86 | 91.43 | 92 | 92.57 | 93.43 | 96 | 95.71 | 96.29 | 96.29 | 96.87 | |
| TSMFE | 99.14 | 99.14 | 99.14 | 99.14 | 99.14 | 99.14 | 99.14 | 99.14 | 99.14 | 99.14 | |
| 8 | MSE | 88.28 | 92.85 | 92.85 | 92.85 | 93.71 | 94.57 | 95.42 | 95.42 | 94.85 | 94.85 |
| TSME | 96.29 | 96.57 | 96.29 | 96.86 | 97.14 | 97.43 | 97.43 | 97.71 | 97.71 | 97.71 | |
| TSMFE | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | |
| 12 | MSE | 87.14 | 89.14 | 87.42 | 88 | 89.14 | 92.85 | 94.57 | 95.42 | 95.71 | 95.71 |
| TSME | 92.85 | 93.42 | 93.42 | 94 | 94.28 | 94.57 | 95.14 | 95.71 | 96.57 | 96.28 | |
| TSMFE | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | |
| 16 | MSE | 87.71 | 89.71 | 88.57 | 89.14 | 89.14 | 90.57 | 92.85 | 92.85 | 94 | 95.42 |
| TSME | 57.14 | 57.14 | 57.14 | 57.14 | 57.14 | 57.14 | 57.14 | 57.14 | 57.14 | 57.14 | |
| TSMFE | 98.86 | 98.86 | 98.86 | 98.86 | 98.86 | 98.86 | 98.86 | 98.86 | 98.86 | 98.86 | |
| 20 | MSE | 87.14 | 90 | 88.28 | 88 | 88.85 | 89.42 | 91.14 | 91.71 | 95.14 | 95.42 |
| TSME | 28.57 | 28.57 | 28.57 | 28.57 | 28.57 | 28.57 | 28.57 | 28.57 | 28.57 | 28.57 | |
| TSMFE | 98.86 | 98.86 | 98.86 | 98.86 | 98.86 | 98.86 | 98.86 | 98.86 | 98.86 | 98.86 |
| Methods | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 4 | MSE | 78.26 | 87.01 | 87.07 | 87.14 | 86.84 | 85.31 | 84.87 | 84.82 | 85.23 | 87.24 |
| TSME | 86.95 | 93.18 | 93.87 | 92.50 | 90.97 | 92.85 | 91.59 | 92.41 | 93.80 | 93.36 | |
| TSMFE | 97.51 | 97.72 | 97.61 | 97.85 | 98.12 | 98.41 | 98.31 | 98.21 | 98.09 | 97.95 | |
| 8 | MSE | 79.81 | 84.41 | 83.33 | 85.00 | 84.21 | 84.52 | 84.45 | 83.92 | 85.23 | 85.20 |
| TSME | 95.03 | 95.45 | 94.21 | 92.85 | 95.48 | 96.03 | 95.79 | 96.42 | 96.66 | 96.42 | |
| TSMFE | 98.44 | 98.70 | 98.29 | 98.21 | 98.49 | 98.41 | 98.31 | 98.21 | 98.02 | 97.88 | |
| 12 | MSE | 77.32 | 84.74 | 85.37 | 84.28 | 85.71 | 83.73 | 84.03 | 83.48 | 83.80 | 84.18 |
| TSME | 93.16 | 94.15 | 94.55 | 93.57 | 94.73 | 95.23 | 94.95 | 95.53 | 96.19 | 95.91 | |
| TSMFE | 98.13 | 98.70 | 98.63 | 98.57 | 98.49 | 98.41 | 98.31 | 98.21 | 98.09 | 97.95 | |
| 16 | MSE | 77.32 | 83.11 | 81.63 | 80.00 | 81.95 | 83.73 | 84.45 | 83.48 | 83.33 | 82.65 |
| TSME | 79.81 | 57.14 | 57.14 | 57.14 | 57.14 | 57.14 | 68.48 | 57.14 | 57.14 | 57.14 | |
| TSMFE | 97.82 | 98.37 | 98.29 | 98.21 | 98.49 | 98.41 | 98.31 | 98.21 | 98.09 | 97.95 | |
| 20 | MSE | 77.01 | 78.57 | 79.59 | 80.71 | 81.57 | 79.36 | 81.09 | 80.35 | 82.85 | 81.12 |
| TSME | 47.20 | 41.88 | 41.83 | 41.78 | 47.74 | 41.66 | 41.59 | 28.57 | 28.57 | 36.22 | |
| TSMFE | 97.82 | 98.37 | 98.29 | 98.21 | 98.49 | 98.01 | 98.31 | 98.21 | 98.09 | 97.95 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, X.; Zheng, J.; Pan, H.; Bao, J.; Zhang, Y. Time-Shift Multiscale Fuzzy Entropy and Laplacian Support Vector Machine Based Rolling Bearing Fault Diagnosis. Entropy 2018, 20, 602. https://doi.org/10.3390/e20080602
Zhu X, Zheng J, Pan H, Bao J, Zhang Y. Time-Shift Multiscale Fuzzy Entropy and Laplacian Support Vector Machine Based Rolling Bearing Fault Diagnosis. Entropy. 2018; 20(8):602. https://doi.org/10.3390/e20080602
Chicago/Turabian StyleZhu, Xiaolong, Jinde Zheng, Haiyang Pan, Jiahan Bao, and Yifang Zhang. 2018. "Time-Shift Multiscale Fuzzy Entropy and Laplacian Support Vector Machine Based Rolling Bearing Fault Diagnosis" Entropy 20, no. 8: 602. https://doi.org/10.3390/e20080602
APA StyleZhu, X., Zheng, J., Pan, H., Bao, J., & Zhang, Y. (2018). Time-Shift Multiscale Fuzzy Entropy and Laplacian Support Vector Machine Based Rolling Bearing Fault Diagnosis. Entropy, 20(8), 602. https://doi.org/10.3390/e20080602






