A Maximum-Entropy Method to Estimate Discrete Distributions from Samples Ensuring Nonzero Probabilities
Abstract
1. Introduction
2. The NZ Method
2.1. Method Description
- there are only two possible outcomes of each trial,
- the probability of success for each trial is constant, and
- all trials are independent.
2.2. Properties
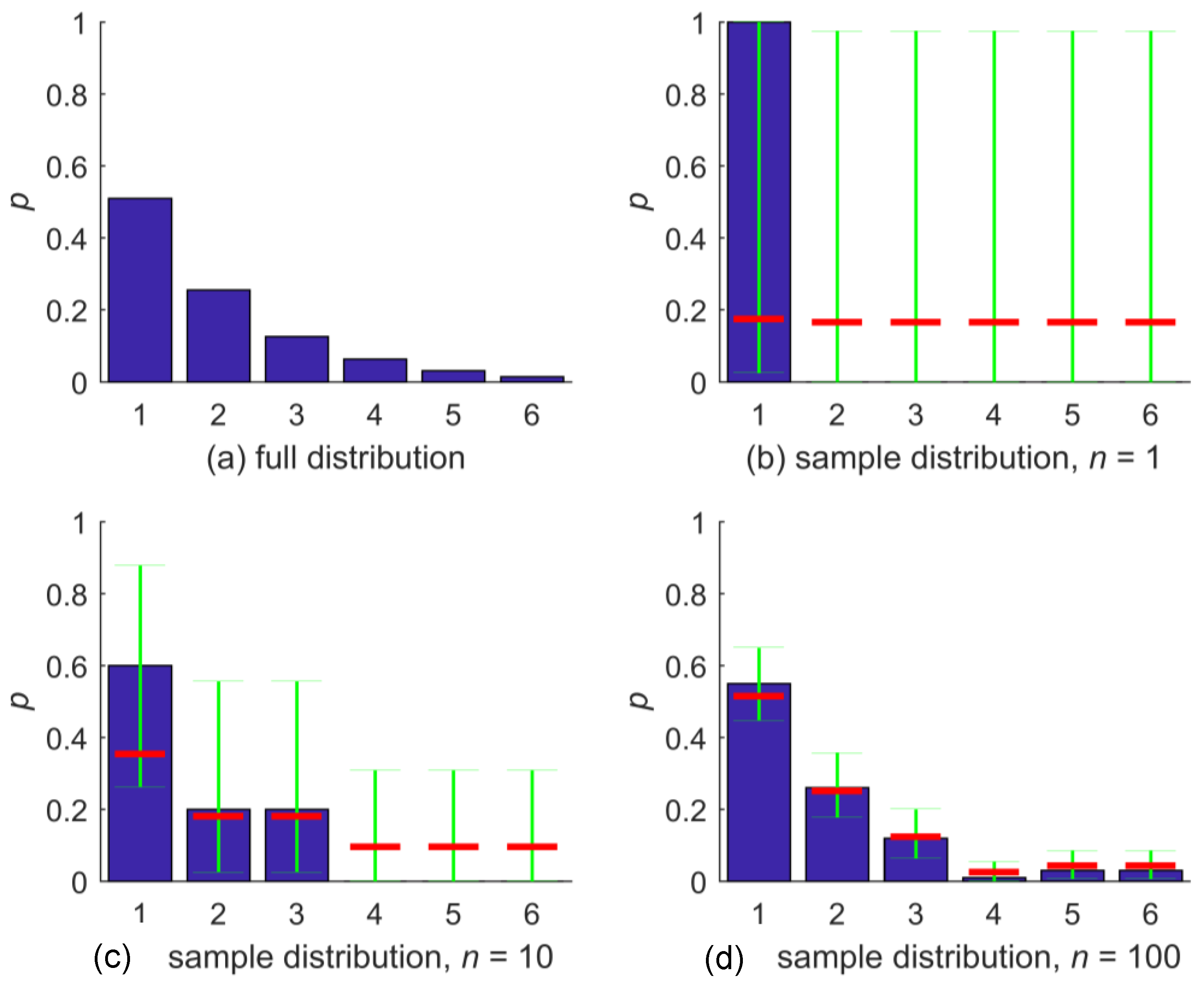
- Maximum Entropy by default: For an increasing number of zero probability bins in , converges towards a uniform distribution. For any zero probability bin we get , assign the same confidence interval, and, hence, the same NZ estimate. Consequently, estimating on a size-zero sample results in a uniform distribution with for all , which is a maximum-entropy (or minimum-assumption) estimate. For small samples, the NZ estimate is close to a uniform distribution.
- Positivity: As probabilities are restricted to the interval , and it always holds , the mean value of the confidence interval is strictly positive. This also applies to the normalized mean. This is the main property we were seeking to be guaranteed by .
- Convergence: Since is a consistent estimator (Reference [21], Section 5.2), it converges in probability towards for growing sample size . Moreover, the ranges of the confidence intervals approach zero with increasing sample size (Reference [19], Figures 4 and 5) and hence, the estimates converge towards .
- As described above, due to the normalization in the method, the NZ estimate does not exactly equal the mean of the confidence interval. However, the interval’s mean tends towards with growing and, hence, the normalizing sum in the denominator tends towards one. Consequently, for growing sample size , the effect of the normalization is of less and less influence.
2.3. Illustration of Properties
3. Comparison to Alternative Distribution Estimators
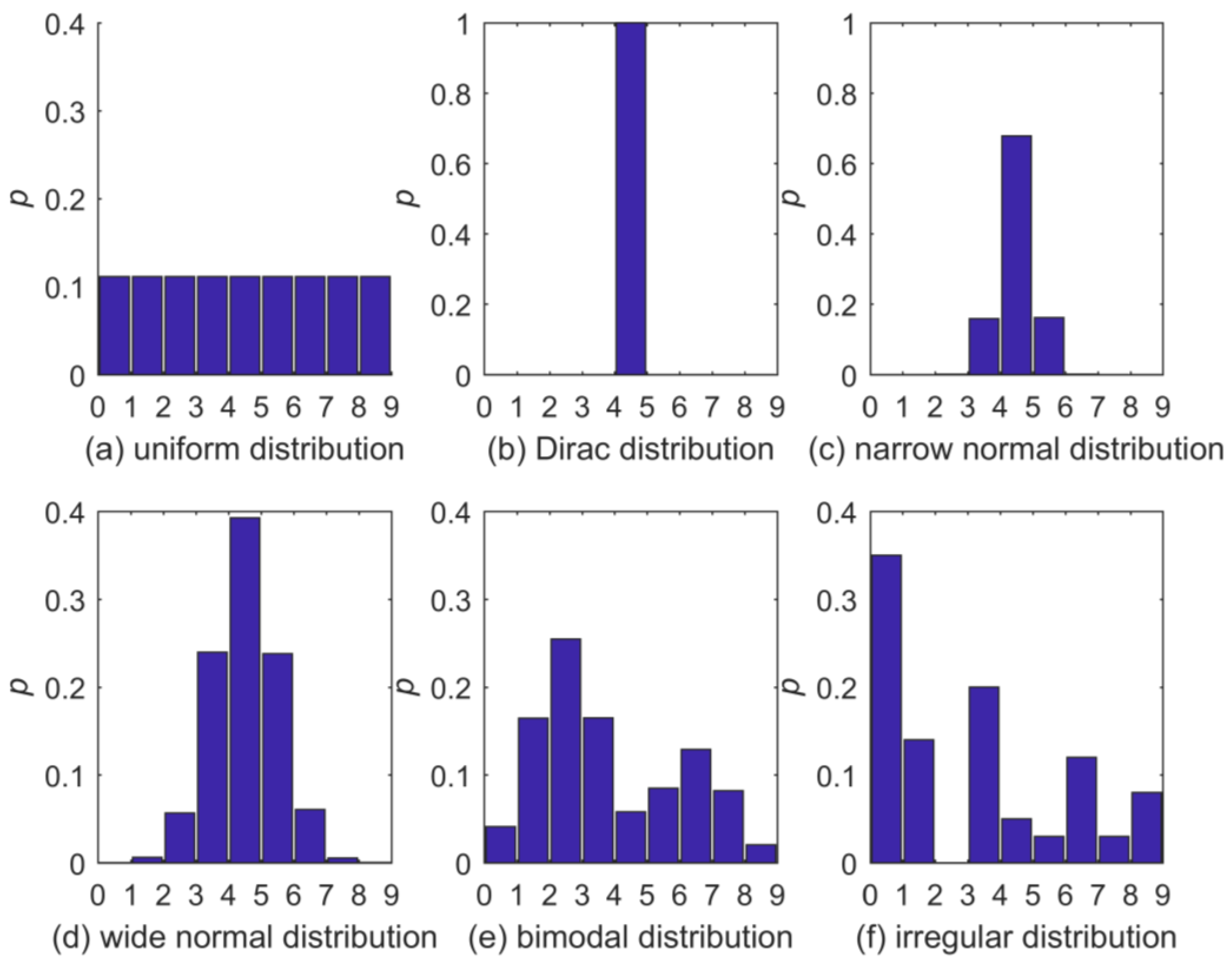
3.1. Test Setup
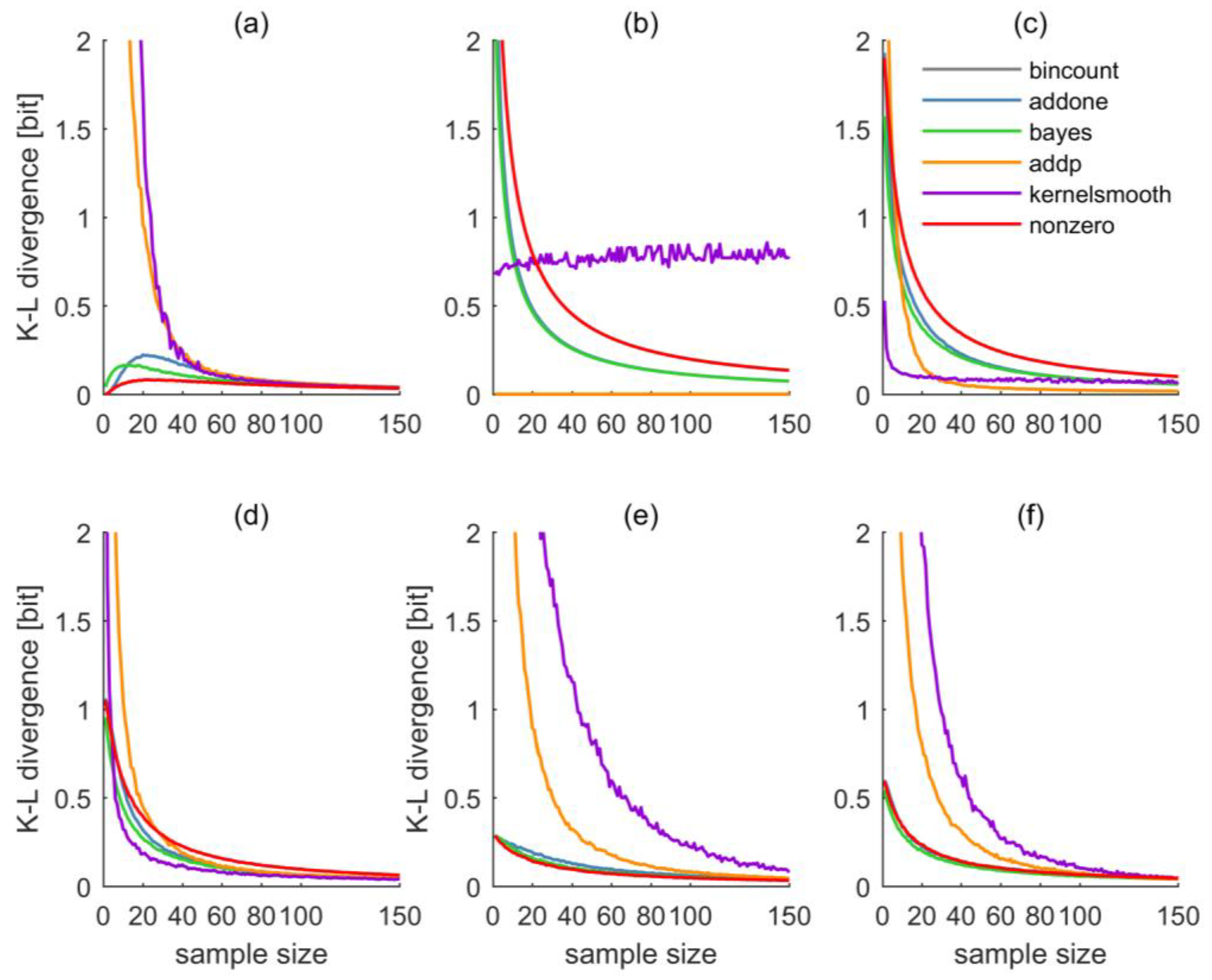
- BC: The full probability distribution is estimated by the normalized BC frequencies of the sample taken from the full data set. This method is just added for completeness, and as it does not guarantee NZ bin probabilities its divergences are often infinite, especially for small sample sizes.
- Add one (AO): With a sample taken from the full distribution, a histogram is constructed. Any empty bin in the histogram is additionally filled with one counter before converting it to a pdf by normalization. The impact of each added counter is therefore dependent on sample size.
- BAY: This approach to NZ bin-probability estimation places a Dirichlet prior on the distribution of bin probabilities and updates to a posterior distribution in the light of the given sample via a multinomial-likelihood function [22]. We use a flat uniform prior (with the Dirichlet distribution parameter alpha taking a constant value of one over all bins) as a maximum-entropy approach, which can be interpreted as a prior count of one per bin. Since the Dirichlet distribution is a conjugate prior to the multinomial-likelihood function, the posterior again is a Dirichlet distribution with analytically known updated parameters. We take the posterior mean probabilities as distribution estimate and, for our choice of prior, they correspond to the observed bin counts increased by the prior count of one. Hence, BAY is very similar to AO with the difference that a count of one is added to all bins instead of only to empty bins; like for AO, the impact of the added counters is dependent on sample size. Like the NZ method, BAY is by default a strictly positive and convergent maximum-entropy estimator (see Section 2.2).
- Add (AP): With a sample taken from the full distribution, a histogram is constructed and normalized to yield a pdf. Afterwards, each zero-probability bin is filled with a small probability mass (here: 0.0001) and the entire pdf is then renormalized. Unlike in the “AO” procedure, the impact of each probability mass added is therefore virtually independent of .
- KDS: We used the Matlab Kernel density function ksdensity as implemented in Matlab R2017b with a normal kernel function, support limited to [0, 9.001], which is the range of the test distributions, and an iterative adjustment of the bandwidth: Starting from an initially very low value of 0.05, the bandwidth (and with it the degree of smoothing across bins) was increased in 0.001 increments until each bin had NZ probability. We adopted this scheme to avoid unnecessarily strong smoothing while at the same time guaranteeing NZ bin probabilities.
- NZ: We applied the NZ method as described in Section 2.1.
3.2. Results and Discussion
4. Summary and Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. The Clopper–Pearson Method
- (a)
- for:
- (i)
- is thequantile of the beta distribution,
- (ii)
- is thequantile of the beta distribution;
- (b)
- for:
- (i)
- ,
- (ii)
- ;
- (c)
- for:
- (i)
- ,
- (ii)
- .
References
- Kullback, S.; Leibler, R.A. On Information and Sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Beck, J.L.; Au, S.-K. Bayesian Updating of Structural Models and Reliability using Markov Chain Monte Carlo Simulation. J. Eng. Mech. 2002, 128, 380–391. [Google Scholar] [CrossRef]
- Au, S.K.; Beck, J.L. Important sampling in high dimensions. Struct. Saf. 2003, 25, 139–163. [Google Scholar] [CrossRef]
- Kavetski, D.; Kuczera, G.; Franks, S.W. Bayesian analysis of input uncertainty in hydrological modeling: 1. Theory. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Pechlivanidis, I.G.; Jackson, B.; McMillan, H.; Gupta, H.V. Robust informational entropy-based descriptors of flow in catchment hydrology. Hydrol. Sci. J. 2016, 61, 1–18. [Google Scholar] [CrossRef]
- Knuth, K.H. Optimal Data-Based Binning for Histograms. arXiv, 2013; arXiv:physics/0605197v2. [Google Scholar]
- Fraser, A.M.; Swinney, H.L. Independent coordinates for strange attractors from mutual information. Phys. Rev. A 1986, 33, 1134–1140. [Google Scholar] [CrossRef]
- Darbellay, G.A.; Vajda, I. Estimation of the information by an adaptive partitioning of the observation space. IEEE Trans. Inf. Theory 1999, 45, 1315–1321. [Google Scholar] [CrossRef]
- Kraskov, A.; Stögbauer, H.; Grassberger, P. Estimating mutual information. Phys. Rev. E 2004, 69, 066138. [Google Scholar] [CrossRef] [PubMed]
- Blower, G.; Kelsall, J.E. Nonlinear Kernel Density Estimation for Binned Data: Convergence in Entropy. Bernoulli 2002, 8, 423–449. [Google Scholar]
- Simonoff, J.S. Smoothing Methods in Statistics; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Good, I.J. The Population Frequencies of Species and the Estimation of Population Parameters. Biometrika 1953, 40, 237–264. [Google Scholar] [CrossRef]
- Blaker, H. Confidence curves and improved exact confidence intervals for discrete distributions. Can. J. Stat. 2000, 28, 783–798. [Google Scholar] [CrossRef]
- Agresti, A.; Min, Y. On Small-Sample Confidence Intervals for Parameters in Discrete Distributions. Biometrics 2001, 57, 963–971. [Google Scholar] [CrossRef] [PubMed]
- Vollset, S.E. Confidence intervals for a binomial proportion. Stat. Med. 1993, 12, 809–824. [Google Scholar] [CrossRef] [PubMed]
- Escobar, M.D.; West, M. Bayesian Density Estimation and Inference Using Mixtures. J. Am. Stat. Assoc. 1995, 90, 577–588. [Google Scholar] [CrossRef]
- Argiento, R.; Guglielmi, A.; Pievatolo, A. Bayesian density estimation and model selection using nonparametric hierarchical mixtures. Comput. Stat. Data Anal. 2010, 54, 816–832. [Google Scholar] [CrossRef]
- Leemis, L.M.; Trivedi, K.S. A Comparison of Approximate Interval Estimators for the Bernoulli Parameter. Am. Stat. 1996, 50, 63–68. [Google Scholar]
- Clopper, C.J.; Pearson, E.S. The Use of Confidence or Fiducial Limits Illustrated in the Case of the Binomial. Biometrika 1934, 26, 404–413. [Google Scholar] [CrossRef]
- Larson, H.J. Introduction to Probability Theory and Statistical Inference; Wiley: Hoboken, NJ, USA, 1982. [Google Scholar]
- Bickel, P.J.; Doksum, K.A. Mathematical Statistics; CRC Press: Boca Raton, FL, USA, 2015; Volume 1. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Brown, L.D.; Cai, T.T.; DasGupta, A. Interval estimation for a binomial proportion. Stat. Sci. 2001, 16, 101–133. [Google Scholar]
- Blyth, C.R. Approximate binomial confidence limits. J. Am. Stat. Assoc. 1986, 81, 843–855. [Google Scholar] [CrossRef]
- Johnson, N.L.; Kemp, A.W.; Kotz, S. Univariate Discrete Distributions; Wiley Series in Probability and Statistics; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- Olver, F.W.; Lozier, D.W.; Boisvert, R.F.; Clark, C.W. NIST Handbook of Mathematical Functions, 1st ed.; Cambridge University Press: New York, NY, USA, 2010. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Darscheid, P.; Guthke, A.; Ehret, U. A Maximum-Entropy Method to Estimate Discrete Distributions from Samples Ensuring Nonzero Probabilities. Entropy 2018, 20, 601. https://doi.org/10.3390/e20080601
Darscheid P, Guthke A, Ehret U. A Maximum-Entropy Method to Estimate Discrete Distributions from Samples Ensuring Nonzero Probabilities. Entropy. 2018; 20(8):601. https://doi.org/10.3390/e20080601
Chicago/Turabian StyleDarscheid, Paul, Anneli Guthke, and Uwe Ehret. 2018. "A Maximum-Entropy Method to Estimate Discrete Distributions from Samples Ensuring Nonzero Probabilities" Entropy 20, no. 8: 601. https://doi.org/10.3390/e20080601
APA StyleDarscheid, P., Guthke, A., & Ehret, U. (2018). A Maximum-Entropy Method to Estimate Discrete Distributions from Samples Ensuring Nonzero Probabilities. Entropy, 20(8), 601. https://doi.org/10.3390/e20080601





