Investigation of Finite-Size 2D Ising Model with a Noisy Matrix of Spin-Spin Interactions
Abstract
1. Introduction
2. Essential Expressions, the Equation of State
2.1. The Effect of the Finite Grid Dimension
2.2. The Effect of Noise
2.3. Evaluating the Spectral Density
3. The Experiment Description
4. Experimental Results
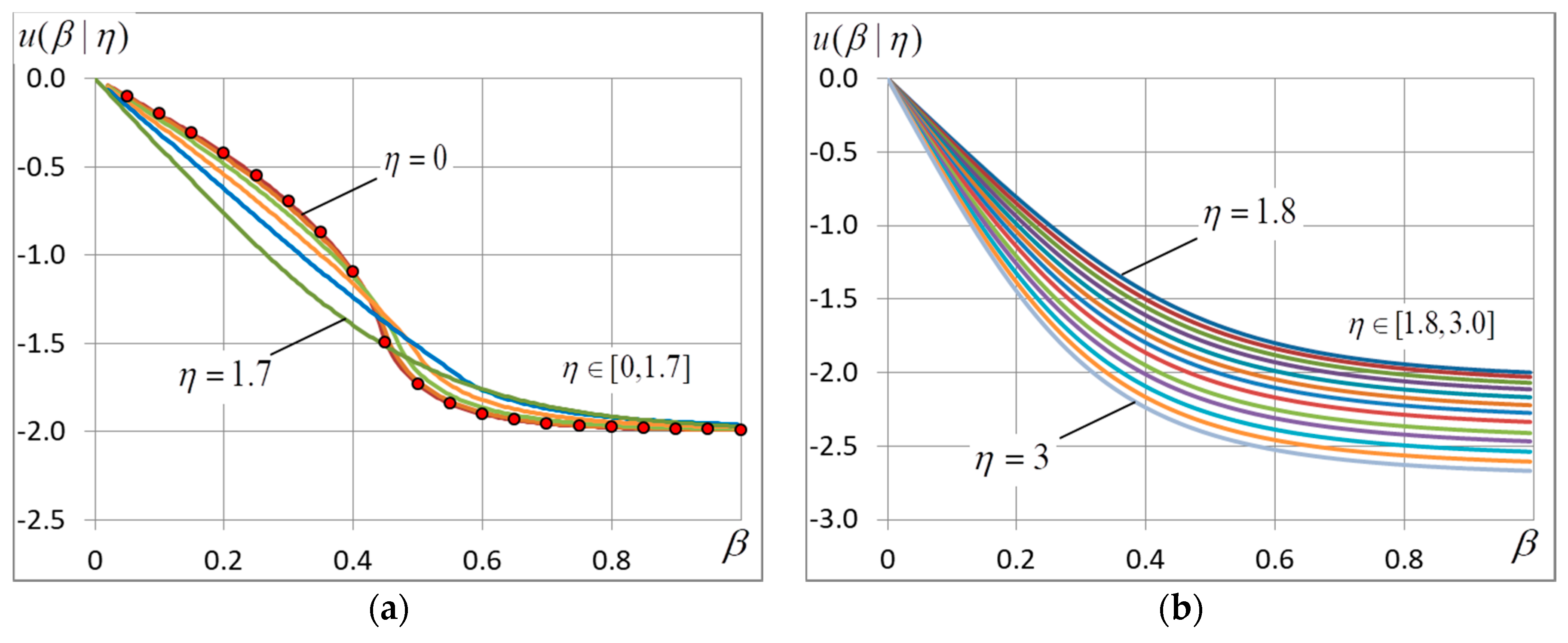
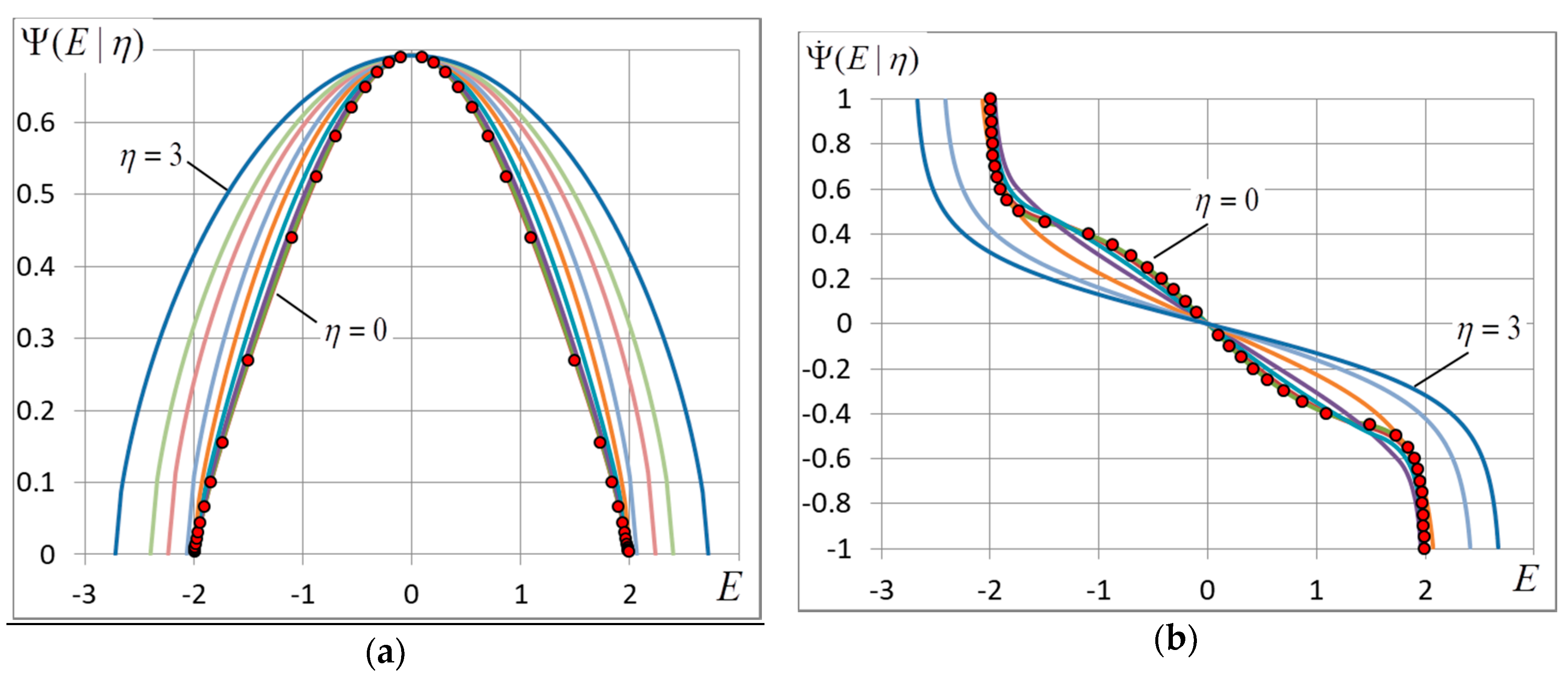
4.1. The Free and Internal Energy
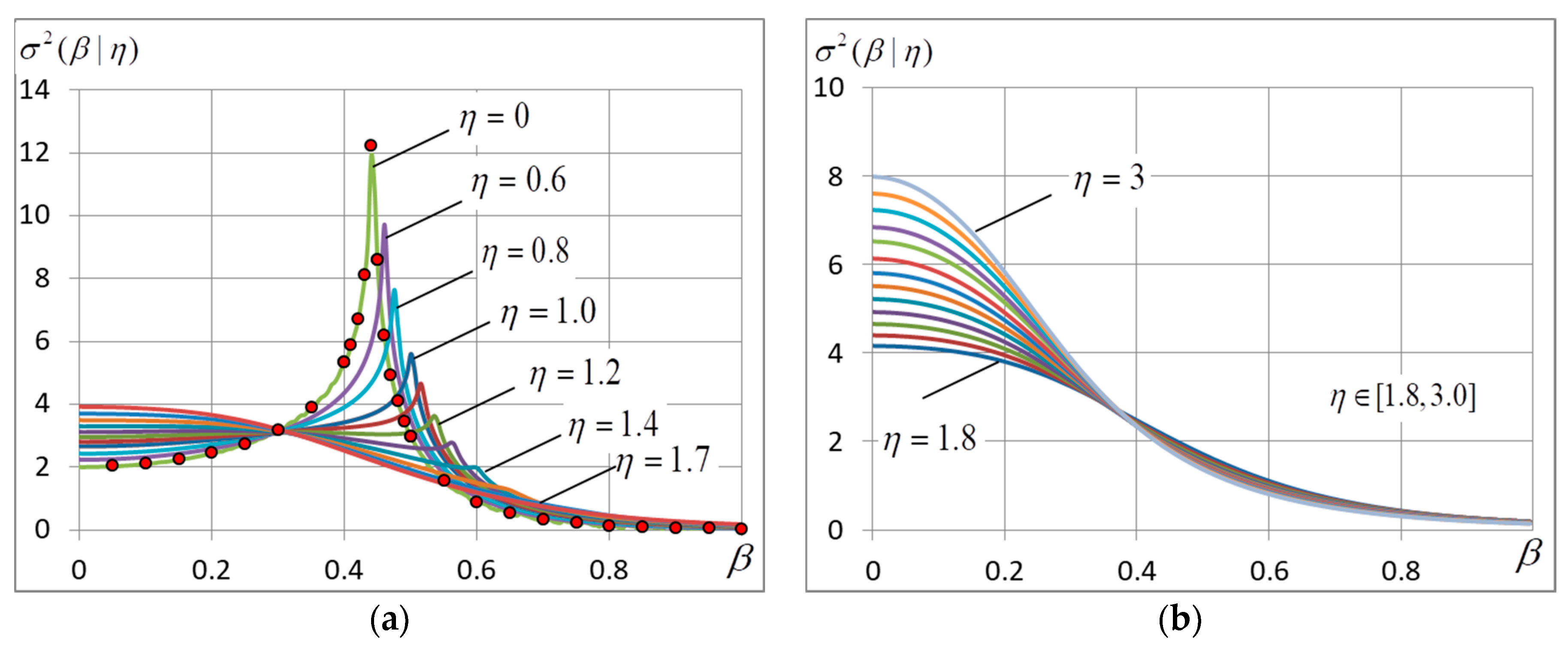
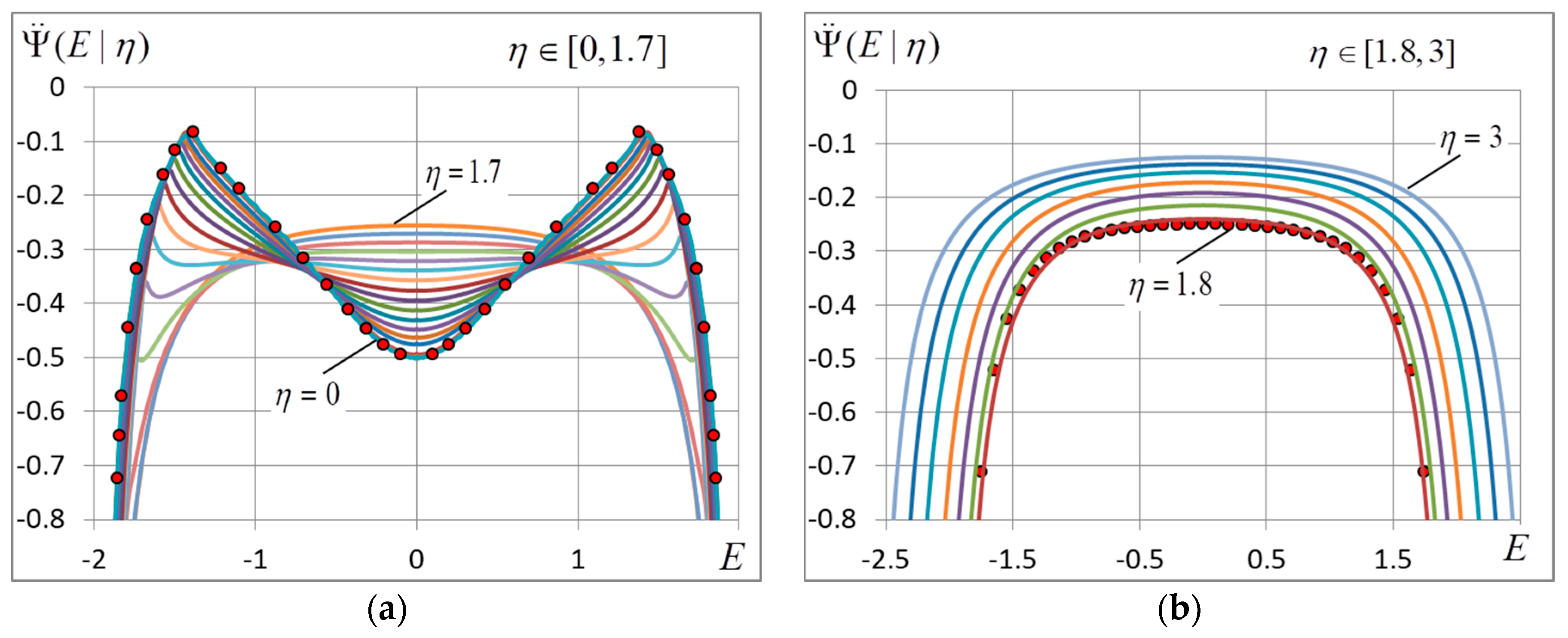
4.2. The Energy Variance
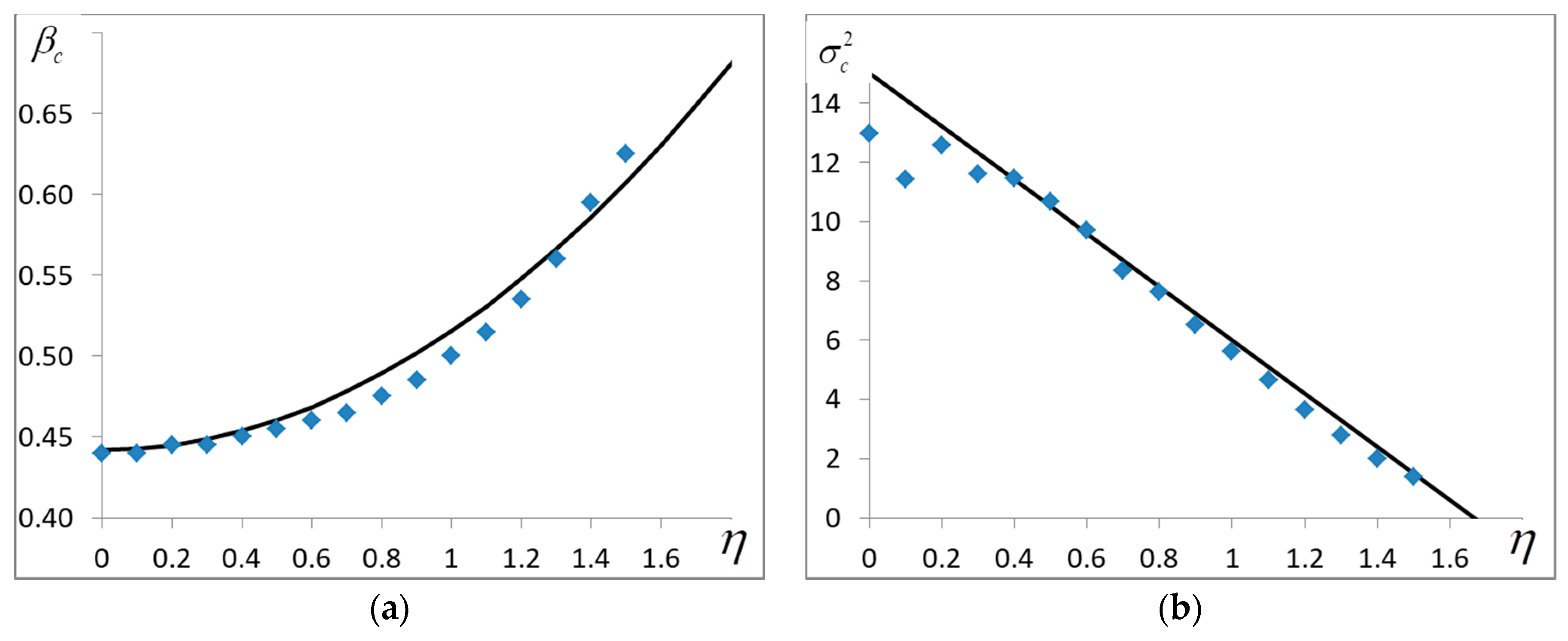
4.3. The Critical Temperature
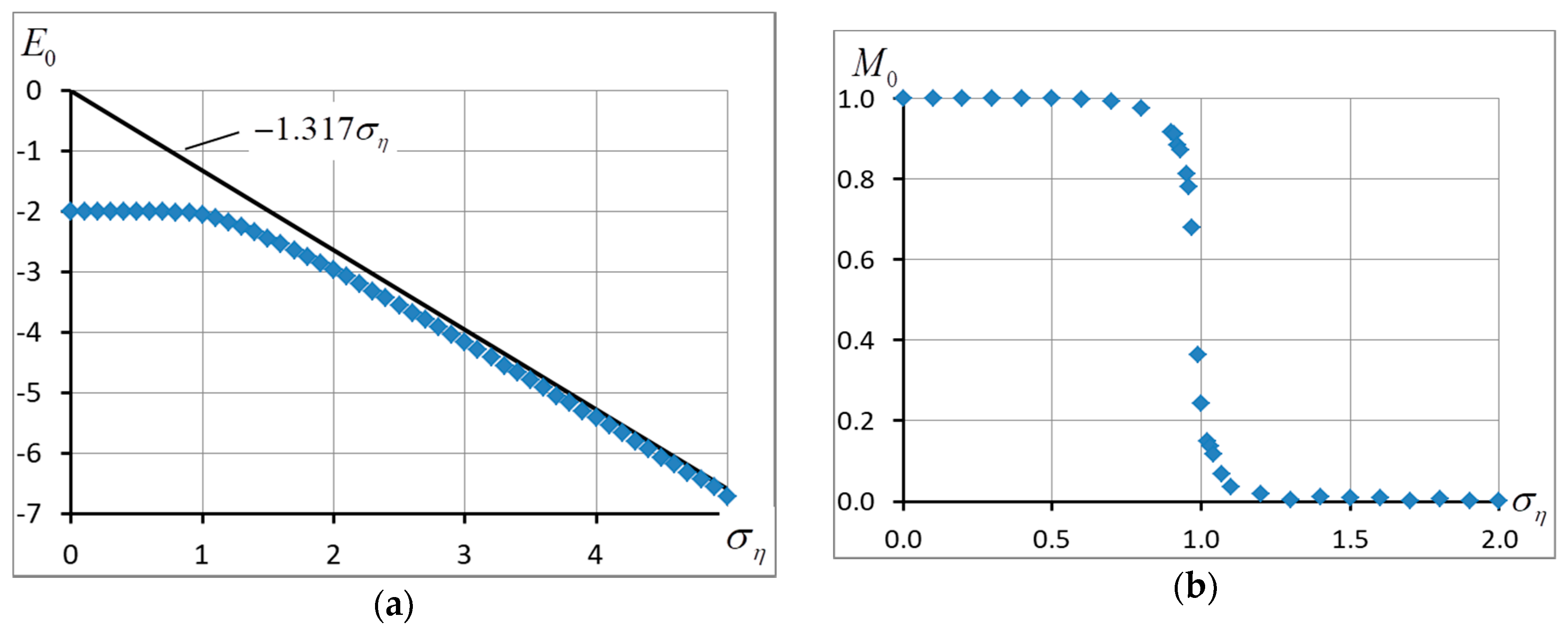
4.4. The Ground State
4.5. The Entropy
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Baxter, R.J. Exactly Solved Models in Statistical Mechanics; Academic Press: London, UK, 1982. [Google Scholar]
- Stanley, H. Introduction to Phase Transitions and Critical Phenomena; Clarendon Press: Oxford, UK, 1971. [Google Scholar]
- Becker, R.; Doring, W. Ferromagnetism; Springer: Berlin, Germany, 1939. [Google Scholar]
- Huang, K. Statistical Mechanics; Wiley: New York, NY, USA, 1987. [Google Scholar]
- Kubo, R. An analytic method in statistical mechanics. Busserion Kenk. 1943, 1, 1–13. [Google Scholar]
- Dixon, J.M.; Tuszynski, J.A.; Clarkson, P. From Nonlinearity to Coherence, Universal Features of Nonlinear Behaviour in Many-Body Physics; Clarendon Press: Oxford, UK, 1997. [Google Scholar]
- Onsager, L. Crystal statistics. A two-dimensional model with an order–disorder transition. Phys. Rev. 1944, 65, 117–149. [Google Scholar] [CrossRef]
- Edwards, S.F.; Anderson, P.W. Theory of spin glasses. J. Phys. F Met. Phys. 1975, 5, 965. [Google Scholar] [CrossRef]
- Sherrington, D.; Kirkpatrick, P. Solvable model of a spin-glass. Phys. Rev. Lett. 1975, 35, 1792. [Google Scholar] [CrossRef]
- Metropolis, N.; Ulam, S. The Monte Carlo Method. J. Am. Stat. Assoc. 1949, 44, 335–341. [Google Scholar] [CrossRef] [PubMed]
- Fishman, G.S. Monte Carlo: Concepts, Algorithms, and Applications; Springer: Berlin, Germnay, 1996. [Google Scholar]
- Bielajew, A.F. Fundamentals of the Monte Carlo Method for Neutral and Charged Particle Transport; The University of Michigan: Ann Arbor, MI, USA, 2001. [Google Scholar]
- Foulkes, W.M.C.; Mitas, L.; Needs, R.J.; Rajagopal, G. Quantum Monte Carlo simulations of solids. Rev. Mod. Phys. 2001, 73, 33. [Google Scholar] [CrossRef]
- Lyklema, J.W. Monte Carlo study of the one-dimensional quantum Heisenberg ferromagnet near = 0. Phys. Rev. B 1983, 27, 3108–3110. [Google Scholar] [CrossRef]
- Marcu, M.; Muller, J.; Schmatzer, F.-K. Quantum Monte Carlo simulation of the one-dimensional spin-S xxz model. II. High precision calculations for S = ½. J. Phys. A 1985, 18, 3189–3203. [Google Scholar] [CrossRef]
- Häggkvist, R.; Rosengren, A.; Lundow, P.H.; Markström, K.; Andren, D.; Kundrotas, P. On the Ising model for the simple cubic lattice. Adv. Phys. 2007, 5, 653–755. [Google Scholar] [CrossRef]
- Binder, K. Finite Size Scaling Analysis of Ising Model Block Distribution Functions. Z. Phys. B Condens. Matter 1981, 43, 119–140. [Google Scholar] [CrossRef]
- Binder, K.; Luijten, E. Monte Carlo tests of renormalization-group predictions for critical phenomena in Ising models. Phys. Rep. 2001, 344, 179–253. [Google Scholar] [CrossRef]
- Kasteleyn, P. Dimer statistics and phase transitions. J. Math. Phys. 1963, 4, 287–293. [Google Scholar] [CrossRef]
- Fisher, M. On the dimer solution of planar Ising models. J. Math. Phys. 1966, 7, 1776–1781. [Google Scholar] [CrossRef]
- Karandashev, Y.M.; Malsagov, M.Y. Polynomial algorithm for exact calculation of partition function for binary spin model on planar graphs. Opt. Mem. Neural Netw. (Inf. Opt.) 2017, 26, 87–95. [Google Scholar] [CrossRef]
- Schraudolph, N.; Kamenetsky, D. Efficient Exact Inference in Planar Ising Models. In NIPS. 2008. Available online: https://arxiv.org/abs/0810.4401 (accessed on 24 October 2008).
- Amit, D.; Gutfreund, H.; Sompolinsky, H. Statistical Mechanics of Neural Networks near Saturation. Ann. Phys. 1987, 173, 30–67. [Google Scholar] [CrossRef]
- Kohring, G.A. A High Precision Study of the Hopfield Model in the Phase of Broken Replica Symmetry. J. Stat. Phys. 1990, 59, 1077–1086. [Google Scholar] [CrossRef]
- Van Hemmen, J.L.; Kuhn, R. Collective Phenomena in Neural Networks. In Models of Neural Networks; Domany, E., van Hemmen, J.L., Shulten, K., Eds.; Springer: Berlin, Germany, 1992. [Google Scholar]
- Martin, O.C.; Monasson, R.; Zecchina, R. Statistical mechanics methods and phase transitions in optimization problems. Theor. Comput. Sci. 2001, 265, 3–67. [Google Scholar] [CrossRef]
- Karandashev, I.; Kryzhanovsky, B.; Litinskii, L. Weighted patterns as a tool to improve the Hopfield model. Phys. Rev. E 2012, 85, 041925. [Google Scholar] [CrossRef] [PubMed]
- Kryzhanovsky, B.V.; Litinskii, L.B. Generalized Bragg-Williams Equation for Systems with Arbitrary Long-Range Interaction. Dokl. Math. 2014, 90, 784–787. [Google Scholar] [CrossRef]
- Yedidia, J.S.; Freeman, W.T.; Weiss, Y. Constructing free-energy approximations and generalized belief propagation algorithms. IEEE Trans. Inf. Theory 2005, 51, 2282–2312. [Google Scholar] [CrossRef]
- Wainwright, M.J.; Jaakkola, T.; Willsky, A.S. A new class of upper bounds on the log partition function. IEEE Trans. Inf. Theory 2005, 51, 2313–2335. [Google Scholar] [CrossRef]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the dimensionality of data with neural networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef] [PubMed]
- Hinton, G.E.; Osindero, S.; Teh, Y.W. A fast learning algorithm for deep belief nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef] [PubMed]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436. [Google Scholar] [CrossRef] [PubMed]
- Lin, H.W.; Tegmark, M.; Rolnick, D. Why does deep and cheap learning work so well? J. Stat. Phys. 2017, 168, 1223–1247. [Google Scholar] [CrossRef]
- Wang, C.; Komodakis, N.; Paragios, N. Markov random field modeling, inference & learning in computer vision & image understanding: A survey. Comput. Vis. Image Understand. 2013, 117, 1610–1627. [Google Scholar]
- Krizhevsky, A.; Hinton, G.E. Using Very Deep Autoencoders for Content-Based Image Retrieval. In Proceedings of the 9th European Symposium on Artificial Neural Networks ESANN-2011, Bruges, Belgium, 27–29 April 2011. [Google Scholar]
- Gorban, A.N.; Gorban, P.A.; Judge, G. Entropy: The Markov Ordering Approach. Entropy 2010, 12, 1145–1193. [Google Scholar] [CrossRef]
- Dotsenko, V.S. Physics of the spin-glass state. Phys.-Uspekhi 1993, 36, 455–485. [Google Scholar] [CrossRef]
- Karandashev, I.M.; Kryzhanovsky, B.V.; Malsagov, M.Y. The Analytical Expressions for a Finite-Size 2D Ising Model. Opt. Mem. Neural Netw. 2017, 26, 165–171. [Google Scholar] [CrossRef]
- Häggkvist, R.; Rosengren, A.; Andrén, D.; Kundrotas, P.; Lundow, P.H.; Markström, K. Computation of the Ising partition function for 2-dimensional square grids. Phys. Rev. E 2004, 69, 046104. [Google Scholar] [CrossRef] [PubMed]
- Beale, P.D. Exact distribution of energies in the two-dimensional Ising model. Phys. Rev. Lett. 1996, 76, 78–81. [Google Scholar] [CrossRef] [PubMed]
- Kryzhanovsky, B.; Malsagov, M. The Spectra of Local Minima in Spin-Glass Models. Opt. Mem. Neural Netw. (Inf. Opt.) 2016, 25, 1–15. [Google Scholar] [CrossRef]
- Colangeli, M.; Giardinà, C.; Giberti, C.; Vernia, C. Nonequilibrium two-dimensional Ising model with stationary uphill diffusion. Phys. Rev. E 2018, 97, 030103. [Google Scholar] [CrossRef] [PubMed]
- Bodineau, T.; Presutti, E. Surface Tension and Wulff Shape for a Lattice Model without Spin Flip Symmetry. Ann. Henri Poincaré 2003, 4, 847–896. [Google Scholar] [CrossRef]
- Ohzeki, M.; Nishimori, H. Analytical evidence for the absence of spin glass transition on self-dual lattices. J. Phys. A Math. Theor. 2009, 42, 332001. [Google Scholar] [CrossRef]
- Thomas, C.K.; Katzgraber, H.G. Simplest model to study reentrance in physical systems. Phys. Rev. E 2011, 84, 040101. [Google Scholar] [CrossRef] [PubMed]
- Izmailian, N. Finite size and boundary effects in critical two-dimensional free-fermion models. Eur. Phys. J. B 2017, 90, 160. [Google Scholar] [CrossRef]

| 0 | −1.995 | 1 | 0.442 | −0.6931 | −1.978 × 105 | 12.958 |
| 0.1 | −1.995 | 1 | 0.443 | −0.6931 | −1.986 × 105 | 11.427 |
| 0.2 | −1.995 | 1 | 0.444 | −0.6932 | −0.0101 | 12.566 |
| 0.3 | −1.995 | 1 | 0.445 | −0.6932 | −0.0103 | 11.627 |
| 0.4 | −1.996 | 1 | 0.452 | −0.6933 | −0.0211 | 11.476 |
| 0.5 | −1.994 | 1 | 0.454 | −0.6934 | −0.0324 | 10.666 |
| 0.6 | −1.993 | 1 | 0.459 | −0.6936 | −0.0447 | 9.719 |
| 0.7 | −1.994 | 1 | 0.465 | −0.6939 | −0.0581 | 8.328 |
| 0.8 | −1.996 | 1 | 0.476 | −0.6946 | −0.0849 | 7.642 |
| 0.9 | −1.996 | 1 | 0.484 | −0.6957 | −0.1143 | 6.518 |
| 1.0 | −1.993 | 1 | 0.503 | −0.6979 | −0.1599 | 5.603 |
| 1.1 | −1.996 | 0.9998 | 0.515 | −0.7010 | −0.2109 | 4.656 |
| 1.2 | −1.995 | 0.9987 | 0.536 | −0.7065 | −0.2815 | 3.629 |
| 1.3 | −1.994 | 0.9943 | 0.562 | −0.7156 | −0.3747 | 2.775 |
| 1.4 | −1.996 | 0.9839 | 0.591 | −0.7327 | −0.5107 | 1.998 |
| 1.5 | −2.002 | 0.9602 | 0.623 | −0.7527 | −0.6414 | 1.380 |
| 1.6 | −2.014 | 0.9060 | - | - | - | - |
| 1.7 | −2.033 | 0.2155 | - | - | - | - |
| 1.8 | −2.065 | 0.0312 | - | - | - | - |
| 1.9 | −2.098 | 0.0241 | - | - | - | - |
| 2.0 | −2.139 | 0.0058 | - | - | - | - |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kryzhanovsky, B.; Malsagov, M.; Karandashev, I. Investigation of Finite-Size 2D Ising Model with a Noisy Matrix of Spin-Spin Interactions. Entropy 2018, 20, 585. https://doi.org/10.3390/e20080585
Kryzhanovsky B, Malsagov M, Karandashev I. Investigation of Finite-Size 2D Ising Model with a Noisy Matrix of Spin-Spin Interactions. Entropy. 2018; 20(8):585. https://doi.org/10.3390/e20080585
Chicago/Turabian StyleKryzhanovsky, Boris, Magomed Malsagov, and Iakov Karandashev. 2018. "Investigation of Finite-Size 2D Ising Model with a Noisy Matrix of Spin-Spin Interactions" Entropy 20, no. 8: 585. https://doi.org/10.3390/e20080585
APA StyleKryzhanovsky, B., Malsagov, M., & Karandashev, I. (2018). Investigation of Finite-Size 2D Ising Model with a Noisy Matrix of Spin-Spin Interactions. Entropy, 20(8), 585. https://doi.org/10.3390/e20080585





