A Novel Index Based on Binary Entropy to Confirm the Spatial Expansion Degree of Urban Sprawl
Abstract
1. Introduction
2. Materials and Methods
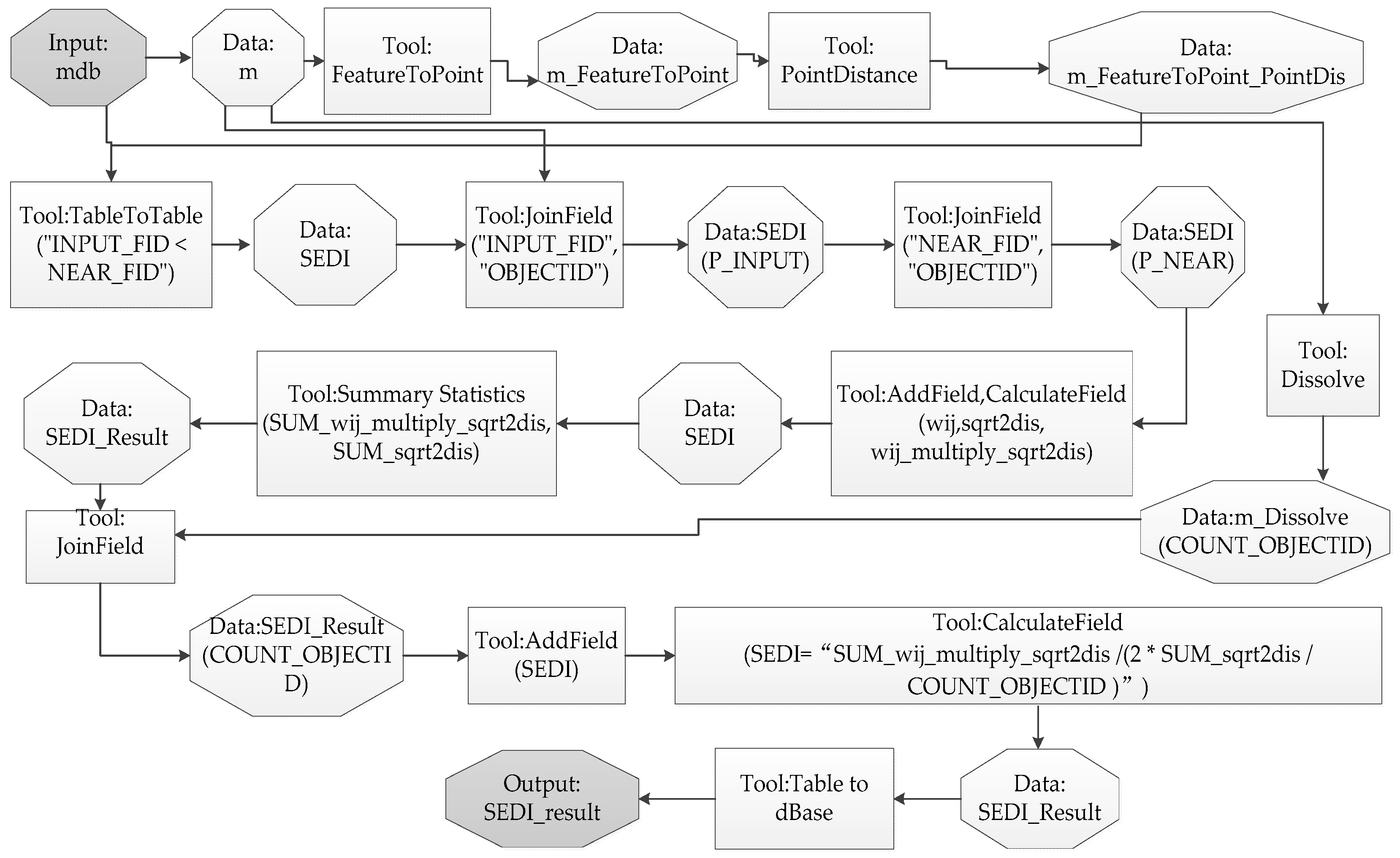
2.1. Building Spatial Expansion Degree Index (SEDI)
2.1.1. Choosing the Spatial Analysis Method and Determining Dimensions of SEDUS
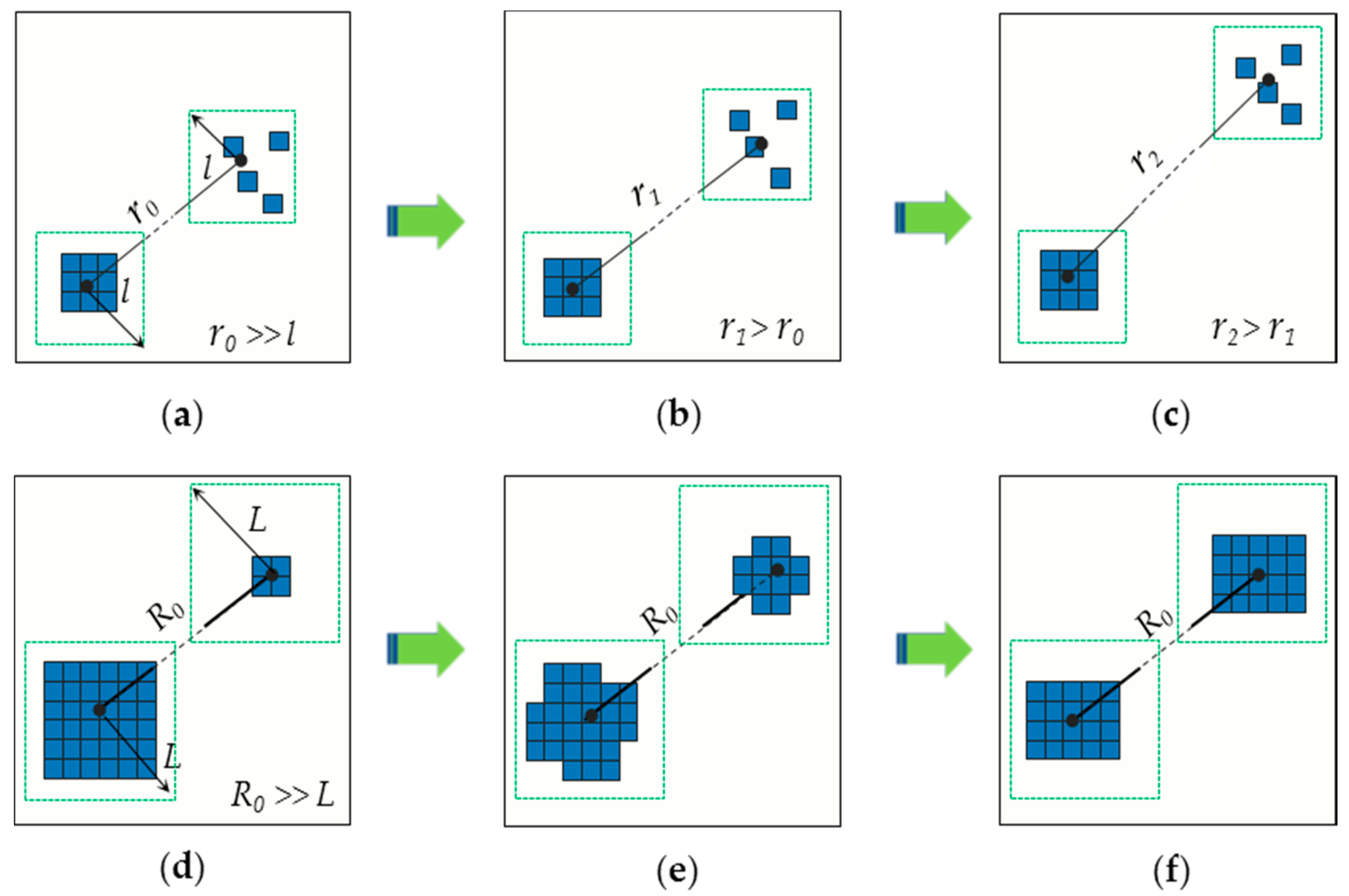
2.1.2. Defining the Point-Pair Entropy Distance
2.1.3. Giving Weights to Point-Pair Entropy Distance and Optimizing
2.1.4. Constructing Spatial Expansion Degree Index (SEDI)
2.2. Study Case
3. Results
4. Discussion
4.1. Comparsion with Commonly Used Indices of SEDUS
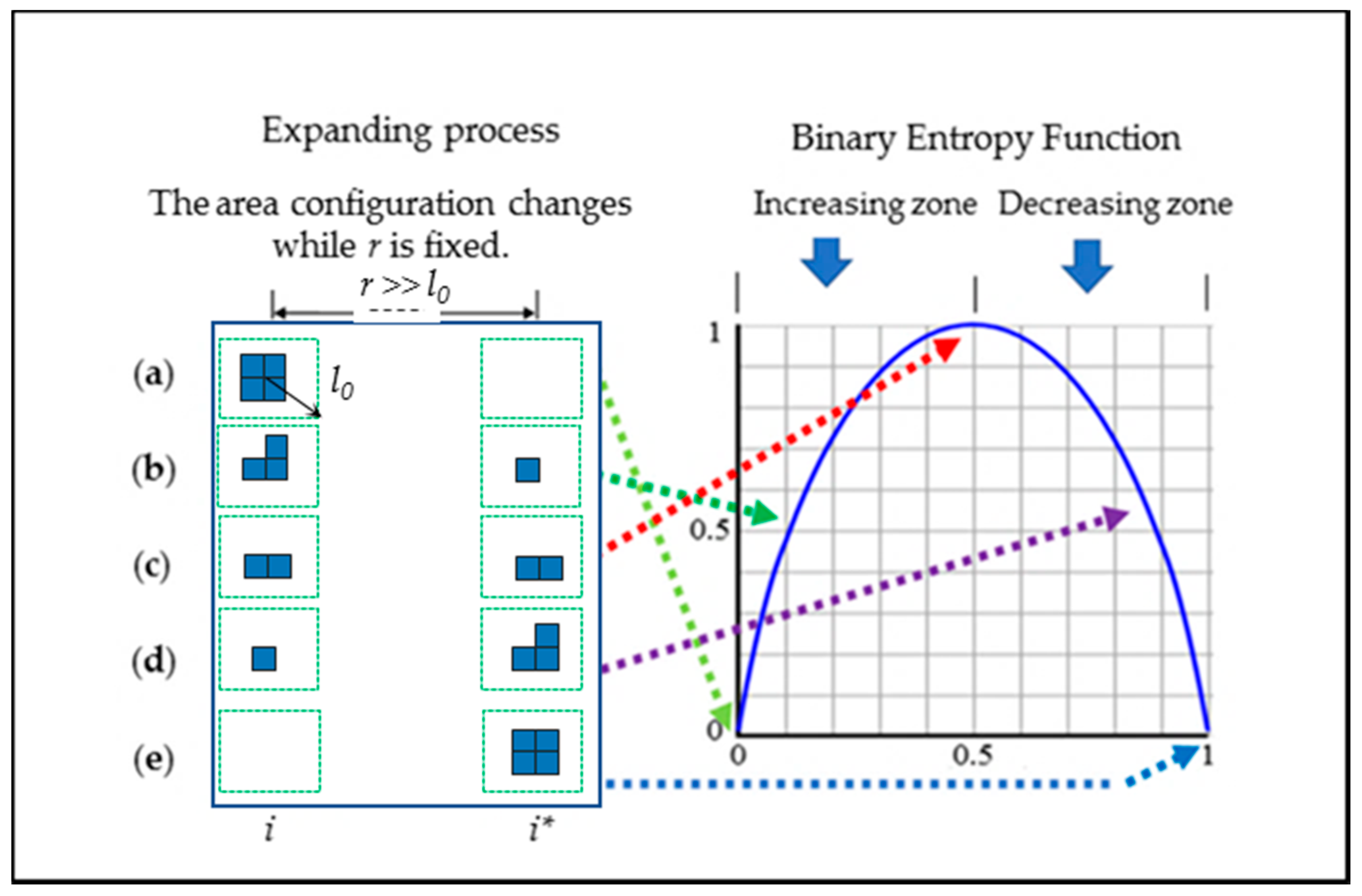
4.2. The Extreme Value and Certainty of SEDI
4.3. The New Index Deepening the Understanding of the Concept of Second-Order Metrics
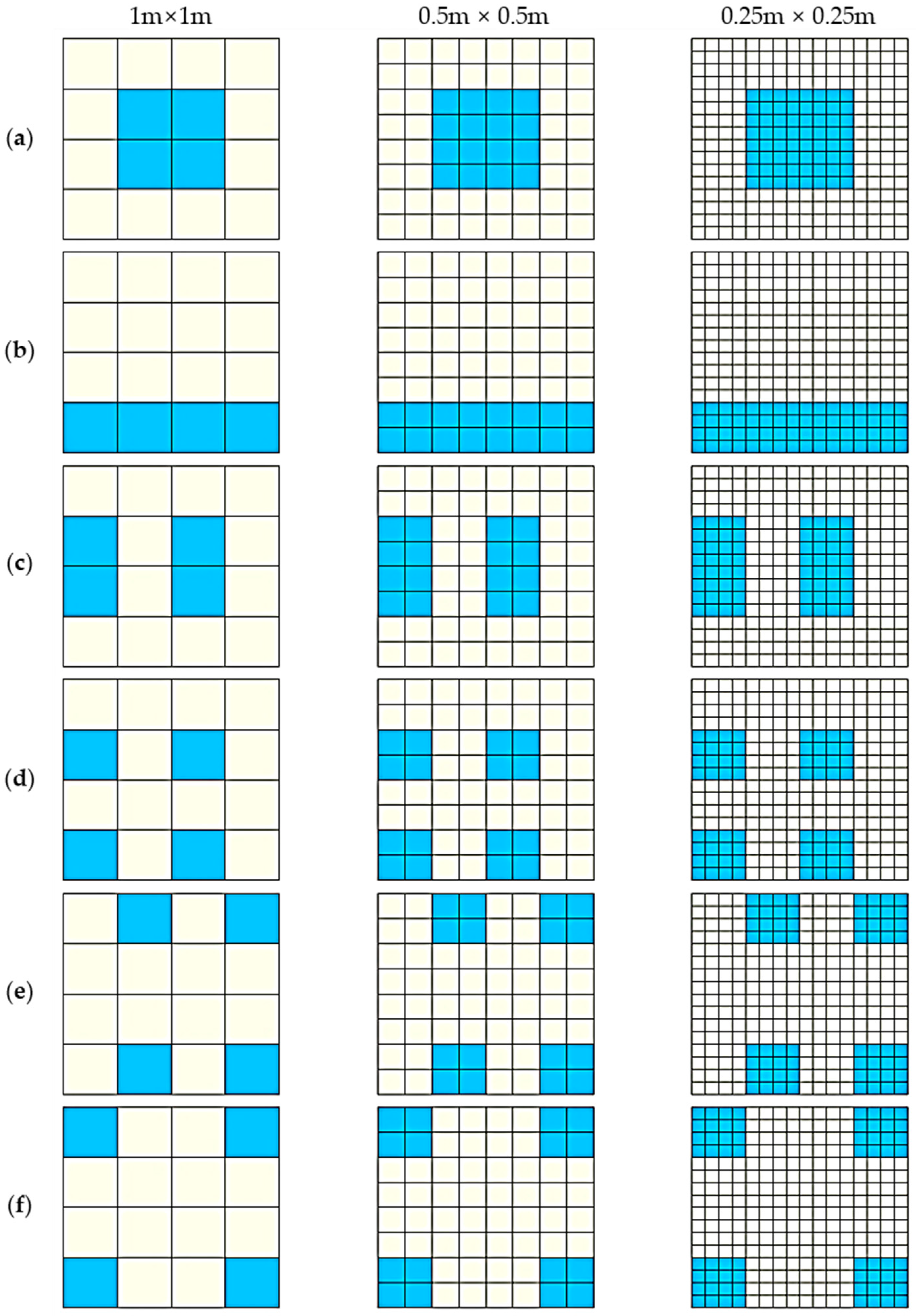
4.4. Effect of Partitioning Method on SEDI
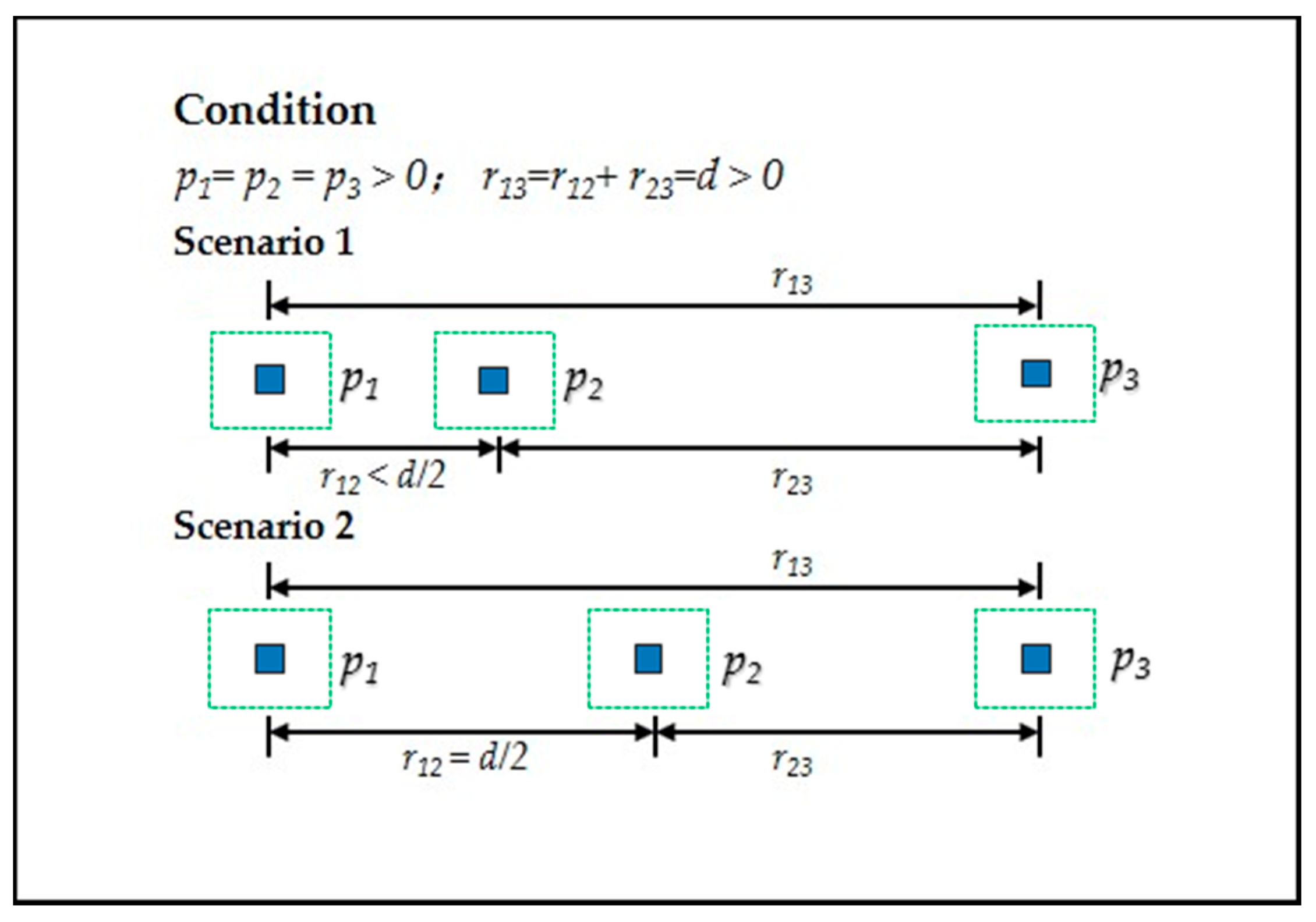
4.5. Relativity of SEDI in Measuring Urban Sprawl
4.6. Future Work
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Pielke, R.A. Land use and climate change. Science 2005, 310, 1625–1626. [Google Scholar] [CrossRef] [PubMed]
- Seto, K.C.; Michail, F.; Burak, G.; Reilly, M.K. A meta-analysis of global urban land expansion. PLoS ONE 2011, 6, e23777. [Google Scholar] [CrossRef] [PubMed]
- Visalatchi, A.; Padmanaban, R. Land Use and Land Cover Mapping and Shore Line Changes Studies in Tuticorin Coastal Area Using Remote Sensing. Int. J. Remote Sens. 2012, 1, 1–12. [Google Scholar]
- Monishiya, B.G.; Padmanaban, R. Mapping and change detection analysis of marine resources in Tuicorin and Vembar group of Islands using remote sensing. Int. J. Adv. For. Sci. Manag. 2012, 1, 1–16. [Google Scholar]
- Ewing, R. Is Los Angeles-style sprawl desirable? J. Am. Plan. Assoc. 1997, 1, 107–126. [Google Scholar] [CrossRef]
- Bhatta, B.; Saraswati, S.; Bandyopadhyay, D. Urban sprawl measurement from remote sensing data remote sensing data. Appl. Geogr. 2010, 30, 731–740. [Google Scholar] [CrossRef]
- Jaeger, J.A.; Bertiller, R.; Schwick, C.; Cavens, D.; Kienast, F. Urban permeation of landscapes and sprawl per capita: New measures of urban sprawl. Ecol. Indic. 2010, 10, 427–441. [Google Scholar] [CrossRef]
- Wilson, E.H.; Hurd, J.D.; Civco, D.L.; Prisloe, M.P.; Arnold, C. Development of a geospatial model to quantify, describe and map urban growth. Remote Sens. Environ. 2003, 86, 275–285. [Google Scholar] [CrossRef]
- Peter, G.; Harry, W.R. Are compact cities a desirable planning goal? J. Am. Plan. Assoc. 1997, 63, 95–106. [Google Scholar]
- Miller, M.D. The impacts of Atlanta’s urban sprawl on forest cover and fragmentation. Appl. Geogr. 2012, 34, 171–179. [Google Scholar] [CrossRef]
- Tan, M.; Li, X.; Xie, H.; Lu, C. Urban land expansion and arable land loss in China-a case study of Beijing-Tianjin-Hebei region. Land Use Policy 2005, 22, 187–196. [Google Scholar] [CrossRef]
- Cabral, P.; Feger, C.; Levrel, H.; Chambolle, M.; Basque, D. Assessing the impact of land-cover changes on ecosystem services: A first step toward integrative planning in Bordeaux, France. Ecosyst. Serv. 2016, 22, 318–327. [Google Scholar] [CrossRef]
- Padmanaban, R.; Bhowmik, A.K.; Cabral, P.; Zamyatin, A.; Almegdadi, O.; Wang, S. Modelling Urban Sprawl Using Remotely Sensed Data: A Case Study of Chennai City, Tamilnadu. Entropy 2017, 19, 164. [Google Scholar] [CrossRef]
- Sun, H.; Forsythe, W.; Waters, N. Modeling Urban Land Use Change and Urban Sprawl: Calgary, AB, Canada. Netw. Spat. Econ. 2007, 7, 353–376. [Google Scholar] [CrossRef]
- Stow, D.A.; Hope, A.; McGuire, D.; Verbyla, D.; Gamon, J.; Huemmrich, F.; Houston, S.; Racine, C.; Sturm, M.; Tape, K.; et al. Remote sensing of vegetation and land-cover change in Arctic Tundra Ecosystems. Remote Sens. Environ. 2004, 89, 281–308. [Google Scholar] [CrossRef]
- Arribas-Bel, D.; Nijkamp, P.; Scholten, H. Multidimensional urban sprawl in Europe: A self-organizing map approach. Comput. Env. Syst. 2011, 35, 263–275. [Google Scholar] [CrossRef]
- Sudhira, H.S.; Ramachandra, T.V.; Jagdish, K.S. Urban sprawl: Metrics, dynamics and modeling using GIS. Int. J. Appl. Earth. Obs. Geoinform. 2004, 5, 29–39. [Google Scholar] [CrossRef]
- Galster, G.; Hanson, R.; Ratcliffe, M.R.; Wolman, H.; Coleman, S.; Freihage, J. Wrestling sprawl to the ground: Defining and measuring an elusive concept. Hous. Policy Debate 2001, 12, 681–717. [Google Scholar] [CrossRef]
- Hamidi, S.; Ewing, R. A longitudinal study of changes in urban sprawl between 2000 and 2010 in the united states. Landsc. Urban Plan. 2014, 128, 72–82. [Google Scholar] [CrossRef]
- Tsai, Y. Quantifying urban form: Compactness versus ‘sprawl’. Urban Stud. 2005, 42, 141–161. [Google Scholar] [CrossRef]
- Jaeger, J.A.; Bertiller, R.; Schwick, C.; Kienast, F. Suitability criteria for measures of urban sprawl. Ecol. Indic. 2010, 10, 397–406. [Google Scholar] [CrossRef]
- Hasse, J.E.; Lathrop, R.G. Land resource impact indicators of urban sprawl. Appl. Geogr. 2003, 23, 159–175. [Google Scholar] [CrossRef]
- Herold, M.; Couclelis, H.; Clarke, K.C. The role of spatial metrics in the analysis and modeling of urban change. Comput. Env. Syst. 2005, 29, 339–369. [Google Scholar]
- Padmanaban, R. Integrating of urban growth modelling and utility management system using Spatiotemporal data mining. Int. J. Adv. Earth Sci. Eng. 2012, 1, 13–15. [Google Scholar]
- Jat, M.K.; Garg, P.K.; Khare, D. Monitoring and modelling of urban sprawl using remote sensing and GIS techniques. Int. J. Appl. Earth Obs. Geoinform. 2008, 10, 26–43. [Google Scholar] [CrossRef]
- Aithal, B.H.; Ramachandra, T.V. Visualization of Urban Growth Pattern in Chennai Using Geoinformatics and Spatial Metrics. J. Indian Soc. Remote Sens. 2016, 44, 617–633. [Google Scholar] [CrossRef]
- Jayaprakash, M.; Senthil Kumar, R.; Giridharan, L.; Sujitha, S.B.; Sarkar, S.K.; Jonathan, M.P. Bioaccumulation of metals in fish species from water and sediments in macrotidal Ennore creek, Chennai, SE coast of India: A metropolitan city effect. Ecotoxicol. Environ. Saf. 2015, 120, 243–255. [Google Scholar] [CrossRef] [PubMed]
- Gowri, V.S.; Ramachandran, S.; Ramesh, R.; Pramiladevi, I.R.; Krishnaveni, K. Application of GIS in the study of mass transport of pollutants by Adyar and Cooum Rivers in Chennai, Tamilnadu. Environ. Monit. Assess. 2008, 138, 41–49. [Google Scholar] [CrossRef] [PubMed]
- Yeh, A.G.O.; Li, X. Measurement and monitoring of urban sprawl in a rapidly growing region using entropy. Photogramm. Eng. Remote Sens. 2001, 67, 83–90. [Google Scholar]
- Ferdinent, J.; Padmanaban, R. Development of a Methodology to Estimate Biomass from Tree Height Using Airborne Digital Image. Int. J. Adv. Remote Sens. GIS 2013, 2, 49–58. [Google Scholar]
- Frankel, A.; Ashkenazi, M. Measuring urban sprawl: How can we deal with it? Environ. Plan. B 2008, 35, 56–79. [Google Scholar] [CrossRef]
- Frenkel, A.; Orenstein, D.E. Can urban growth management work in an era of political and economic change? J. Am. Plan. Assoc. 2012, 78, 16–33. [Google Scholar] [CrossRef]
- Dewan, A.M.; Humayun, K.; Nahar, M.K.; Rahman, Z. Urbanisation and environmental degradation in Dhaka Metropolitan Area of Bangladesh. Environ. Sustain. Dev. 2012, 11, 118–147. [Google Scholar] [CrossRef]
- Riitters, K.H.; O’Neill, R.V.; Hunsaker, C.T.; Wickham, J.D.; Yankee, D.H.; Timmins, S.P.; Jones, K.B.; Jackson, B.L. A factor analysis of landscape pattern and structure metrics. Landsc. Ecol. 1995, 10, 23–39. [Google Scholar] [CrossRef]
- Herold, M.; Goldstein, N.C.; Clarke, K.C. The spatiotemporal form of urban growth: Measurement, analysis and modeling. Remote Sens. Environ. 2003, 86, 286–302. [Google Scholar] [CrossRef]
- Openshaw, S. Optimal zoning systems for spatial interaction models. Environ. Plan. B 1977, 9, 169–184. [Google Scholar] [CrossRef]
- Jelinski, D.E.; Wu, J. The modifiable areal unit problem and implications for landscape ecology. Landsc. Ecol. 1996, 11, 129–140. [Google Scholar] [CrossRef]
- Fan, Y.; Yu, G.; He, Z.; Yu, H.; Bai, R.; Yang, L.; Wu, D. Entropies of the Chinese Land Use/Cover Change from 1990 to 2010 at a County Level. Entropy 2017, 19, 51. [Google Scholar] [CrossRef]
- Torrens, P.M. A toolkit for measuring sprawl. Appl. Spat. Anal. Policy 2008, 1, 5–36. [Google Scholar] [CrossRef]
- Tewolde, M.G.; Cabral, P. Urban sprawl analysis and modeling in Asmara, Eritrea. Remote Sens. 2011, 3, 2148–2165. [Google Scholar] [CrossRef]
- Yue, W.; Liu, Y.; Fan, P. Measuring urban sprawl and its drivers in large Chinese cities: The case of Hangzhou. Land Use Policy 2013, 31, 358–370. [Google Scholar] [CrossRef]
- Sabet Sarvestani, M.; Ibrahim, A.L.; Kanaroglou, P. Three decades of urban growth in the city of Shiraz, Iran: A remote sensing and geographic information systems application. Cities 2011, 28, 320–329. [Google Scholar] [CrossRef]
- Dewan, A.M.; Corner, R.J. Spatiotemporal Analysis of Urban Growth, Sprawl and Structure. In Dhaka Megacity: Geospatial Perspectives on Urbanization, Environment and Health; Dewan, A., Corner, R.J., Eds.; Springer Science and Business Media: Dordretch, The Netherlands, 2014; pp. 99–121. [Google Scholar]
- Cabral, P.; Augusto, G.; Tewolde, M.; Araya, Y. Entropy in urban systems. Entropy 2013, 15, 5223–5236. [Google Scholar] [CrossRef]
- Clausius, R. The Mechanical Theory of Heat: With its Applications to the Steam-Engine and to the Physical Properties of Bodies; J. Van Voorst: London, UK, 1867; p. 376. [Google Scholar]
- Uffink, J. Bluff your way in the second law of thermodynamics. Stud. Hist. Philos. Sci. Part B Stud. Hist. Philos. Mod. Phys. 2001, 32, 305–394. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Wilson, A. Entropy in urban and regional modelling: Retrospect and prospect. Geogr. Anal. 2010, 42, 364–394. [Google Scholar] [CrossRef]
- Leopold, L.B.; Langbein, W.B. The Concept of Entropy in Landscape Evolution; United States Geological Survey: Washington, DC, USA, 1962.
- Thomas, R.W. Information Statistics in Geography; Headey Brothers Ltd., The Invicta Press: Ashford, UK, 1981. [Google Scholar]
- O’Sullivan, D.; Unwin, D.J. Point Pattern Analysis. In Geographic Information Analysis, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NY, USA, 2010; pp. 121–156. ISBN 9780470549094. [Google Scholar]
- O’Sullivan, D.; Unwin, D.J. Practical Point Pattern Analysis. In Geographic Information Analysis, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NY, USA, 2010; pp. 157–186. ISBN 9780470288573. [Google Scholar]
- Perry, G.L.W.; Miller, B.P.; Enright, N.J. A comparison of methods for the statistical analysis of spatial point patterns in plant ecology. Plant. Ecol. 2006, 187, 59–82. [Google Scholar] [CrossRef]
- Wikipedia. Available online: https://en.wikipedia.org/wiki/Binary_entropy_function (accessed on 17 May 2018).
- Wu, J.G. Landscape Ecology-Pattern, Process, Scale and Hierarchy, 2nd ed.; Higher Education Press: Beijing, China, 2007; pp. 107–116. ISBN 978–7-04-020879-5. (In Chinese) [Google Scholar]
- Jiang, F.; Liu, S.; Yuan, H.; Zhang, Q. Measuring urban sprawl in Beijing with geo-spatial indices. J. Geoginform. Sci. 2007, 17, 469–478. [Google Scholar] [CrossRef]
- Dietzel, C.; Oguz, H.; Hemphill, J.J.; Clarke, K.C.; Gazulis, N. Diffusion and coalescence of the Houston metropolitan area: Evidence supporting a new urban theory. Environ. Plan. B 2005, 32, 231–236. [Google Scholar] [CrossRef]
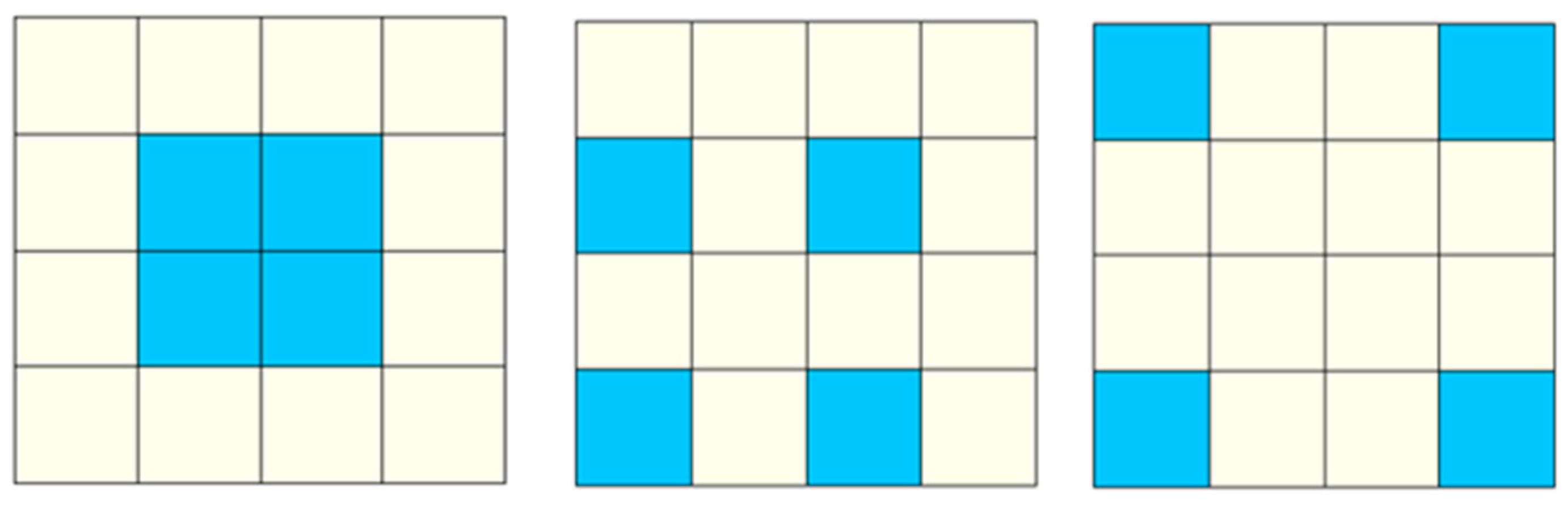

| Index | Mathematical Expression | Explanation |
|---|---|---|
| PSI | P denotes the perimeter of the polygon measured, and A is its area. The greater the value, the greater the SEDUS [26]. | |
| GI | i, j refer to different subzones, respectively; refer to the area proportions of built-up lands of subzones i, j over total area, respectively; X is the mean value of all subzones; is the reciprocal of the distance between the centroids of subzones i, j. The lower the value of GI is, the higher the SEDUS [16]. | |
| RS | is the proportion of different land use in grid cells, and n is the total number of subzones. Values of the index range from 0 to 1. The greater the value, the greater the SEDUS [3]. | |
| LPI | denotes “leapfrog area”, is the total area of built-up land. The higher the value, the greater the SEDUS [20]. |
| Indices | The Resulting Values of the Different Scenarios in Figure 6 | |||||
|---|---|---|---|---|---|---|
| Subplot (a) | Subplot (b) | Subplot (c) | Subplot (d) | Subplot (e) | Subplot (f) | |
| PSI | 1.0000 | 1.2500 | 1.5000 | 2.0000 | 2.0000 | 2.0000 |
| GI | 1.0770 | 0.8203 | 1.0697 | 1.0493 | 0.9768 | 0.9108 |
| RS | 0.5000 | 0.5000 | 0.5000 | 0.5000 | 0.5000 | 0.5000 |
| LPI | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 |
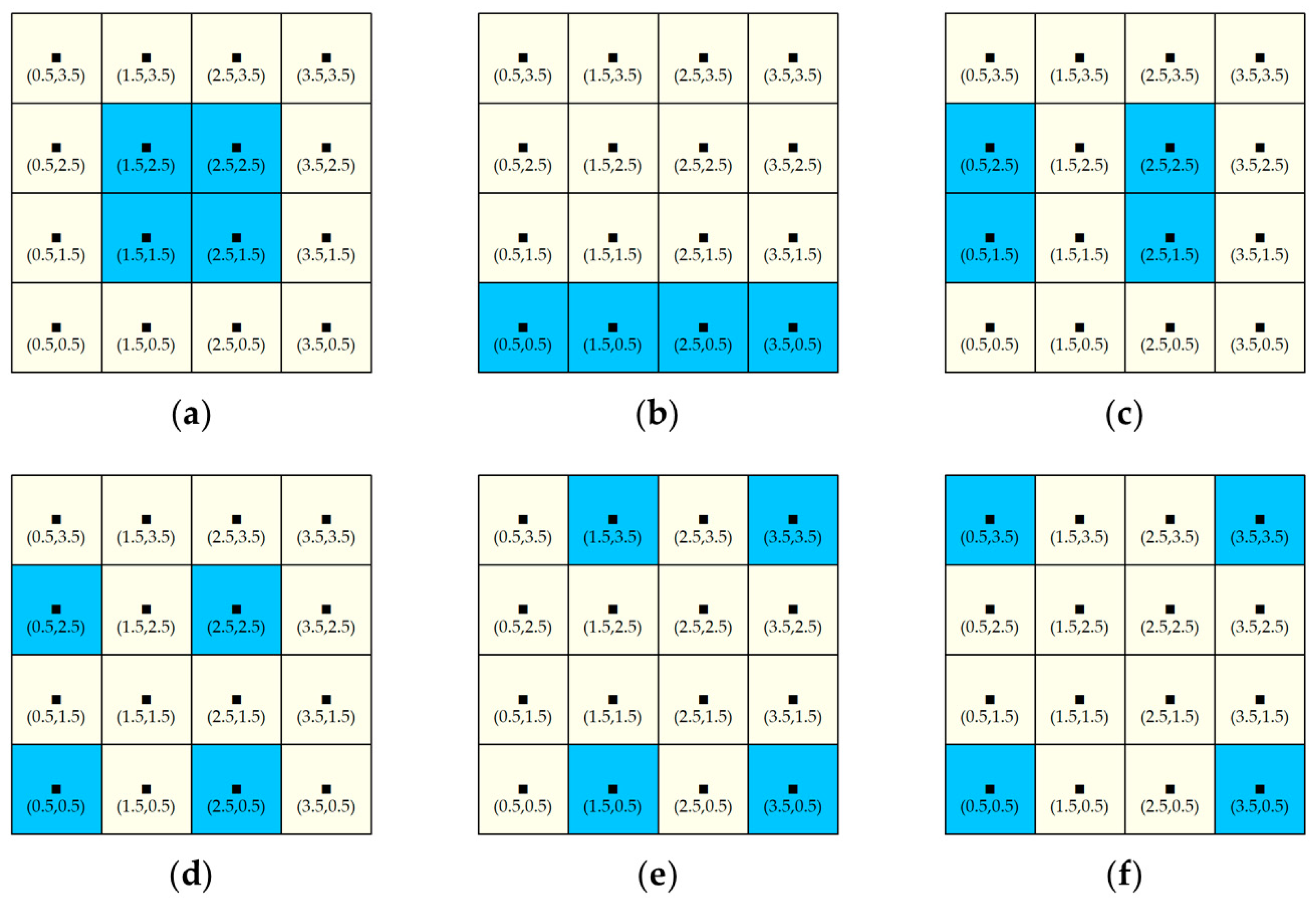
| SEDI | 0.1484 | 0.1759 | 0.1820 | 0.2099 | 0.2348 | 0.2571 |
| Indices | The Resulting Values of the Different Scenarios in Figure 7 | |||||
|---|---|---|---|---|---|---|
| Subplot (a) | Subplot (b) | Subplot (c) | Subplot (d) | Subplot (e) | Subplot (f) | |
| PSI | 1.0000 | 1.4142 | 1.4434 | 1.5000 | 1.5652 | 1.4289 |
| GI | 0.8356 | 1.0364 | 1.0669 | 1.0768 | 1.0501 | 1.0036 |
| RS | 0.0000 | 0.2500 | 0.3962 | 0.5000 | 0.5805 | 0.6462 |
| LPI | 0.0000 | 0.5000 | 0.6667 | 0.7500 | 0.8000 | 0.8333 |
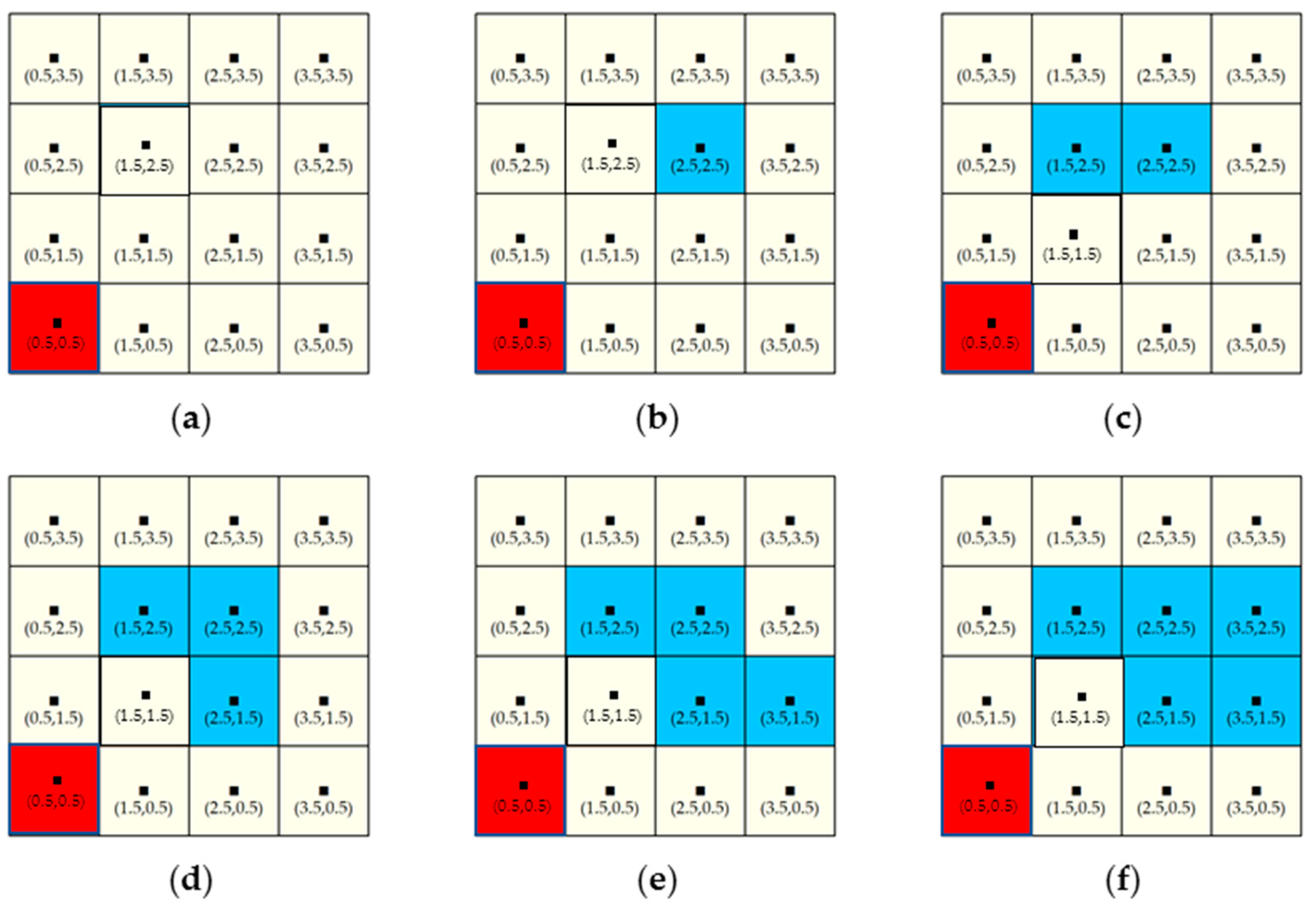
| SEDI | 0.0000 | 0.0783 | 0.1296 | 0.1830 | 0.2481 | 0.3076 |
| Scale | Subplot (a) | Subplot (b) | Subplot (c) | Subplot (d) | Subplot (e) | Subplot (f) |
|---|---|---|---|---|---|---|
| 1 m × 1 m | 0.1484 | 0.1759 | 0.1820 | 0.2099 | 0.2348 | 0.2571 |
| 0. 5 m × 0.5 m | 0.1714 | 0.1976 | 0.2032 | 0.2296 | 0.2536 | 0.2750 |
| 0.25 m × 0.25 m | 0.1757 | 0.2016 | 0.2070 | 0.2332 | 0.2570 | 0.2783 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Zhou, Y.; Jin, X. A Novel Index Based on Binary Entropy to Confirm the Spatial Expansion Degree of Urban Sprawl. Entropy 2018, 20, 559. https://doi.org/10.3390/e20080559
Chen Z, Zhou Y, Jin X. A Novel Index Based on Binary Entropy to Confirm the Spatial Expansion Degree of Urban Sprawl. Entropy. 2018; 20(8):559. https://doi.org/10.3390/e20080559
Chicago/Turabian StyleChen, Zhen, Yinkang Zhou, and Xiaobin Jin. 2018. "A Novel Index Based on Binary Entropy to Confirm the Spatial Expansion Degree of Urban Sprawl" Entropy 20, no. 8: 559. https://doi.org/10.3390/e20080559
APA StyleChen, Z., Zhou, Y., & Jin, X. (2018). A Novel Index Based on Binary Entropy to Confirm the Spatial Expansion Degree of Urban Sprawl. Entropy, 20(8), 559. https://doi.org/10.3390/e20080559




