Ensemble Estimation of Information Divergence †
Abstract
1. Introduction
- We propose the first information divergence estimator, referred to as EnDive, that is based on ensemble methods. The ensemble estimator takes a weighted average of an ensemble of weak kernel density plug-in estimators of divergence where the weights are chosen to improve the MSE convergence rate. This ensemble construction makes it very easy to implement EnDive.
- We prove that the proposed ensemble divergence estimator achieves the optimal parametric MSE rate of , where N is the sample size when the densities are sufficiently smooth. In particular, EnDive achieves these rates without explicitly performing boundary correction which is required for most other estimators. Furthermore, we show that the convergence rates are uniform.
- We prove that EnDive obeys a central limit theorem and thus, can be used to perform inference tasks on the divergence such as testing that two populations have identical distributions or constructing confidence intervals.
1.1. Related Work
1.2. Organization and Notation
2. The Divergence Functional Weak Estimator
2.1. The Kernel Density Plug-in Estimator
2.2. Convergence Rates
2.3. Optimal MSE Rate
2.4. Proof Sketches of Theorems 1 and 2
3. Weighted Ensemble Estimation
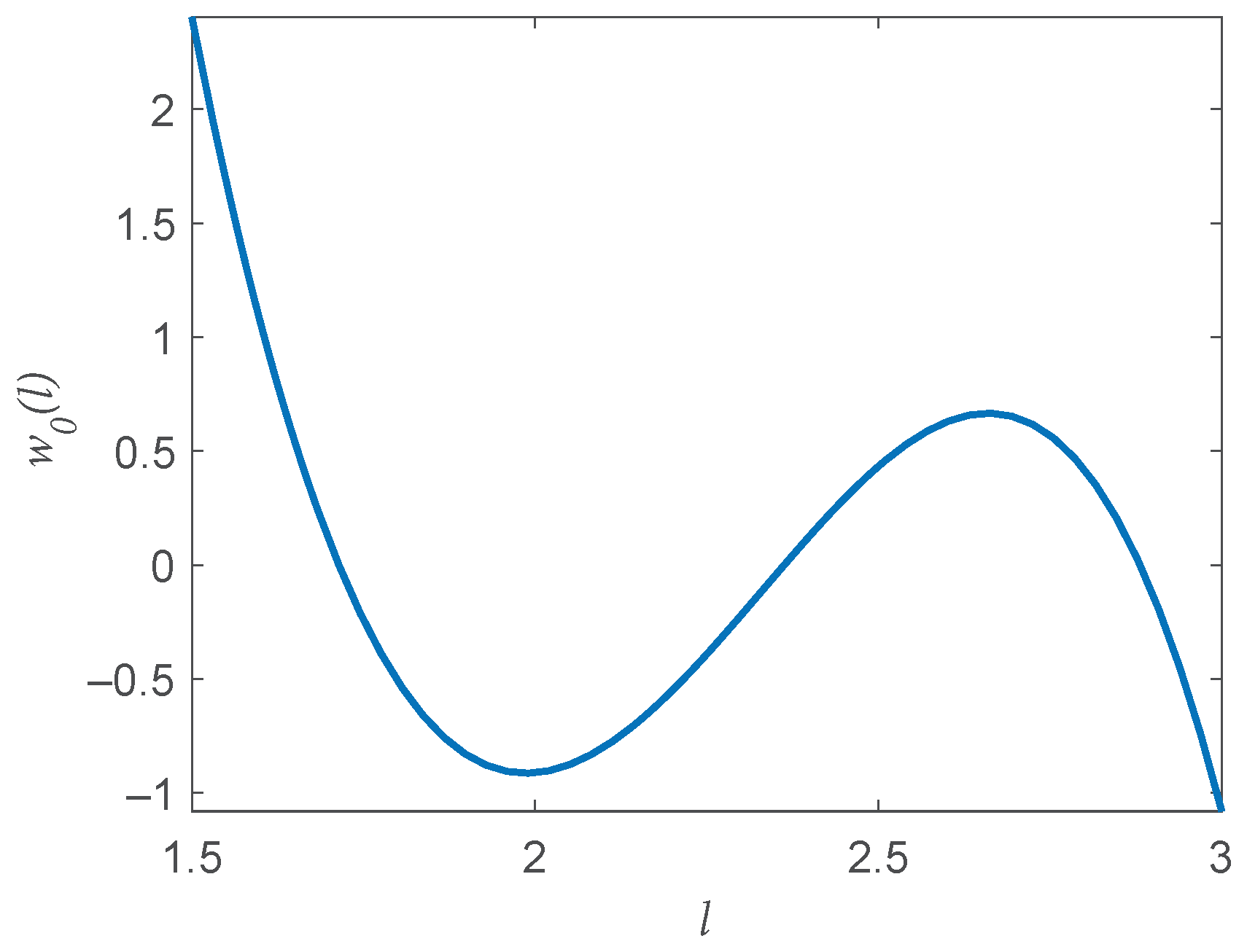
3.1. Finding the Optimal Weight
- The bias is expressible aswhere are constants that depend on the underlying density and are independent of N and l, is a finite index set with , and are basis functions depending only on parameter l and not on the sample size (N).
- The variance is expressible as
3.2. The EnDive Estimator
3.3. Central Limit Theorem
3.4. Uniform Convergence Rates
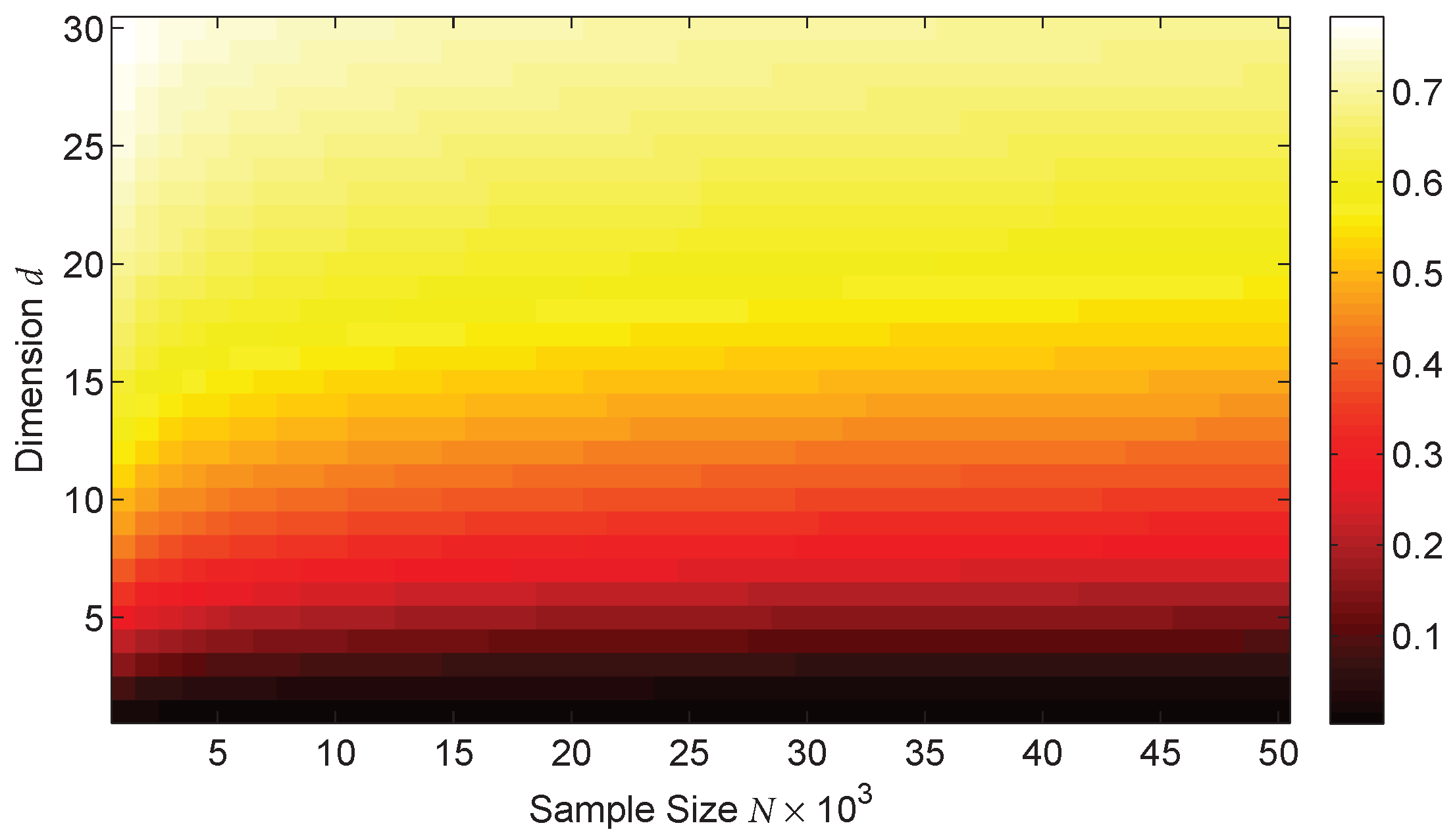
4. Experimental Results
4.1. Tuning Parameter Selection
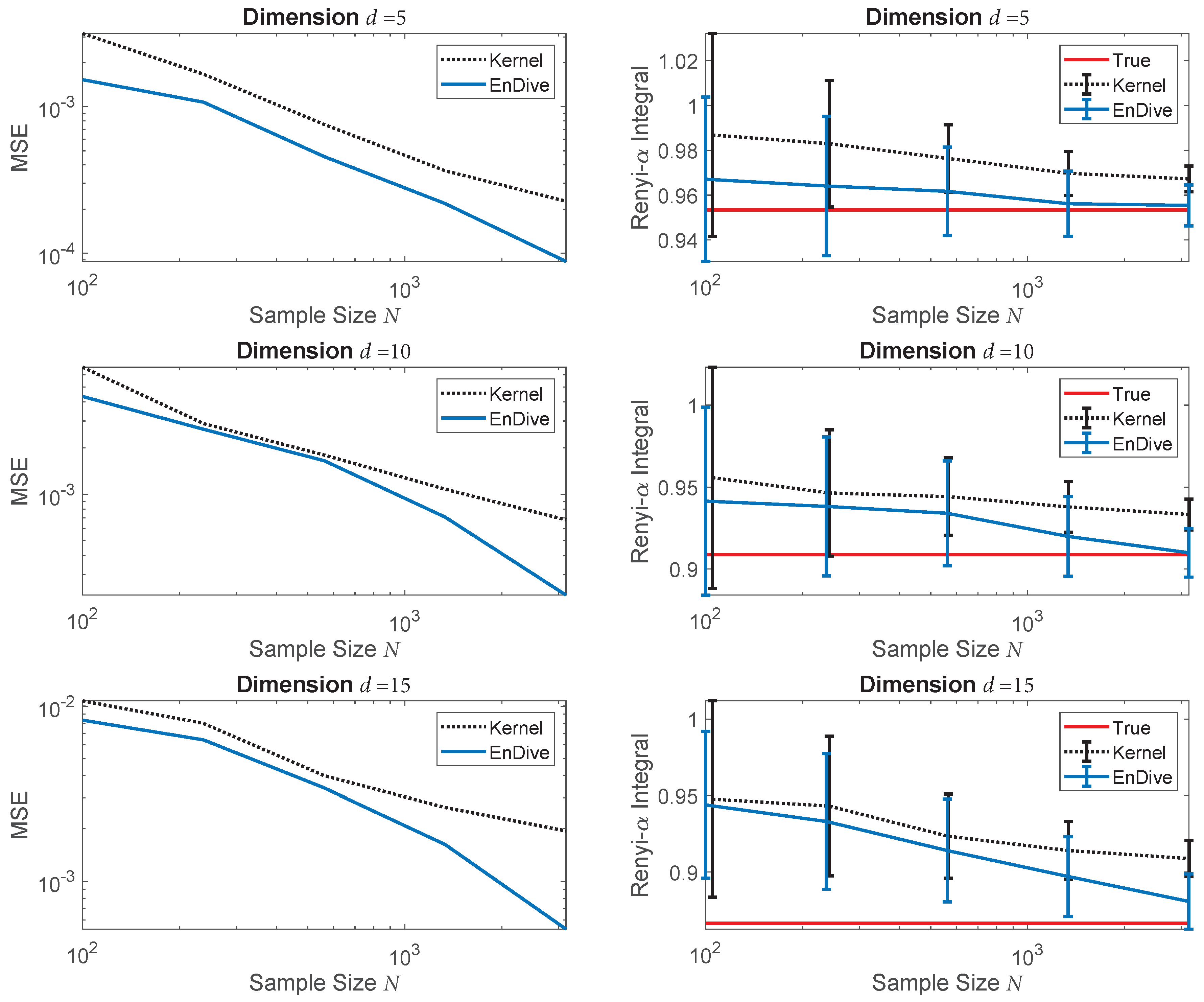
4.2. Convergence Rates Validation: Rényi- Divergence
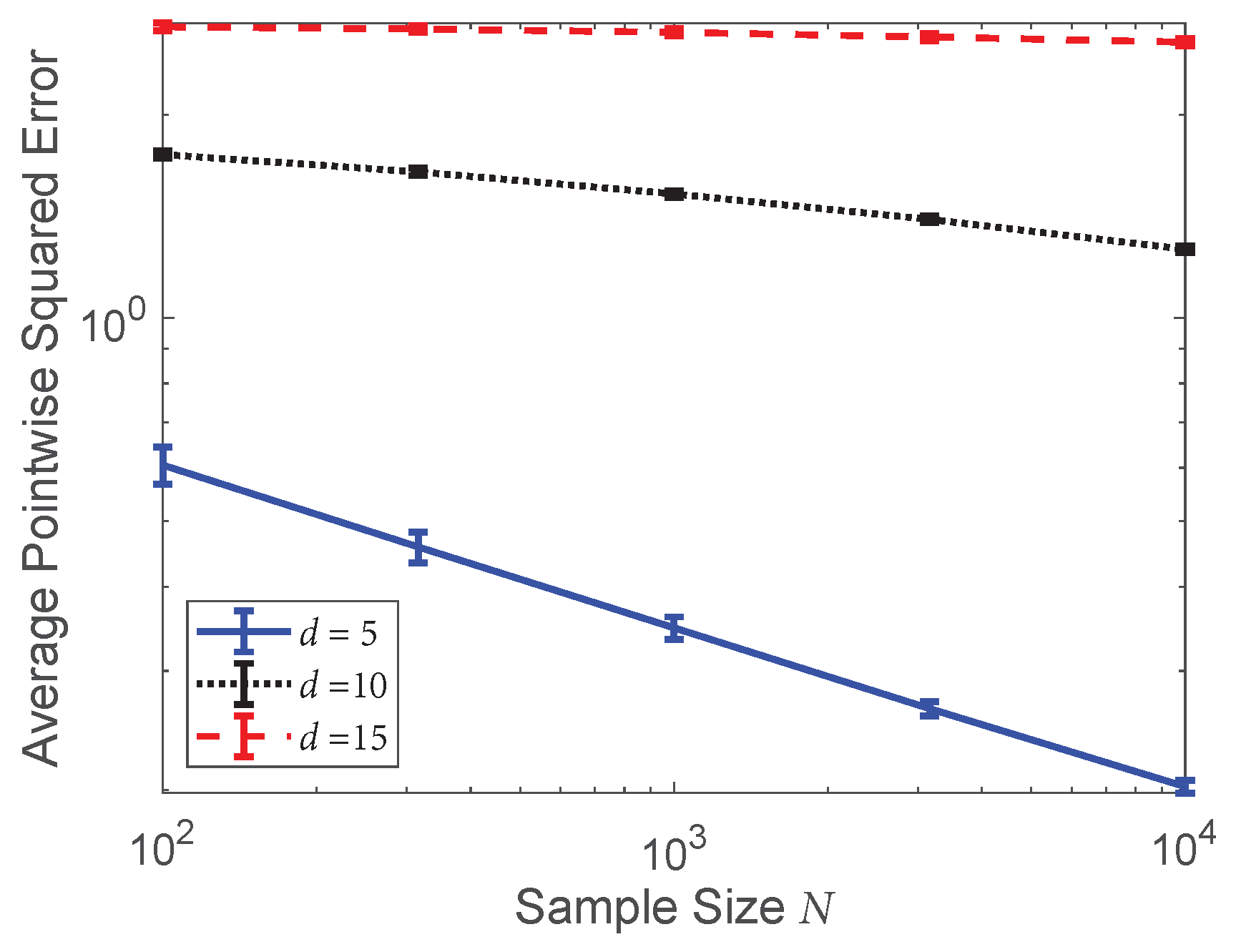
4.3. Central Limit Theorem Validation: KL Divergence
4.4. Bayes Error Rate Estimation on Single-Cell Data
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| KL | Kullback–Leibler |
| MSE | Mean squared error |
| SVM | Support vector machine |
| KDE | kernel density estimator |
| EnDive | Ensemble Divergence |
| BER | Bayes error rate |
| scRNA-seq | Single-cell RNA-sequencing |
| HP | Henze–Penrose |
Appendix A. Bias Assumptions
- : Assume that the kernel K is symmetric, is a product kernel, and has bounded support in each dimension.
- : Assume there exist constants , such that
- : Assume that the densities are in the interior of with .
- : Assume that g has an infinite number of mixed derivatives.
- ): Assume that , are strictly upper bounded for .
- : Assume the following boundary smoothness condition: Let be a polynomial in u of order whose coefficients are a function of x and are times differentiable. Then, assume thatwhere admits the expansionfor some constants .
Appendix B. Modified EnDive
| Algorithm A1: The Modified EnDive Estimator |
|
Appendix C. General Results
Appendix D. Proof of Theorem A1 (Boundary Conditions)
Appendix D.1. Single Coordinate Boundary Point
Appendix D.2. Multiple Coordinate Boundary Point
Appendix E. Proof of Theorem A3 (Bias)
Appendix F. Proof of Theorem A4 (Variance)
Appendix G. Proof of Theorem 4 (CLT)
Appendix H. Proof of Theorem 5 (Uniform MSE)
References
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; John Wiley & Sons: New York, NY, USA, 2012. [Google Scholar]
- Avi-Itzhak, H.; Diep, T. Arbitrarily tight upper and lower bounds on the Bayesian probability of error. IEEE Trans. Pattern Anal. Mach. Intell. 1996, 18, 89–91. [Google Scholar] [CrossRef]
- Hashlamoun, W.A.; Varshney, P.K.; Samarasooriya, V. A tight upper bound on the Bayesian probability of error. IEEE Trans. Pattern Anal. Mach. Intell. 1994, 16, 220–224. [Google Scholar] [CrossRef]
- Moon, K.; Delouille, V.; Hero, A.O., III. Meta learning of bounds on the Bayes classifier error. In Proceedings of the 2015 IEEE Signal Processing and Signal Processing Education Workshop (SP/SPE), Salt Lake City, UT, USA, 9–12 August 2015; pp. 13–18. [Google Scholar]
- Chernoff, H. A measure of asymptotic efficiency for tests of a hypothesis based on the sum of observations. Ann. Math. Stat. 1952, 23, 493–507. [Google Scholar] [CrossRef]
- Berisha, V.; Wisler, A.; Hero, A.O., III; Spanias, A. Empirically Estimable Classification Bounds Based on a New Divergence Measure. IEEE Trans. Signal Process. 2016, 64, 580–591. [Google Scholar] [CrossRef] [PubMed]
- Moon, K.R.; Hero, A.O., III. Multivariate f-Divergence Estimation With Confidence. In Proceedings of the 27th International Conference on Neural Information Processing Systems (NIPS 2014), Montreal, QC, Canada, 8–13 December 2014; pp. 2420–2428. [Google Scholar]
- Gliske, S.V.; Moon, K.R.; Stacey, W.C.; Hero, A.O., III. The intrinsic value of HFO features as a biomarker of epileptic activity. In Proceedings of the 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, 20–25 March 2016. [Google Scholar]
- Loh, P.-L. On Lower Bounds for Statistical Learning Theory. Entropy 2017, 19, 617. [Google Scholar] [CrossRef]
- Póczos, B.; Schneider, J.G. On the estimation of alpha-divergences. In Proceedings of the 22nd International Conference on Artificial Intelligence and Statistics, Fort Lauderdale, FL, USA, 11–13 April 2011; pp. 609–617. [Google Scholar]
- Oliva, J.; Póczos, B.; Schneider, J. Distribution to distribution regression. In Proceedings of the 30th International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013; pp. 1049–1057. [Google Scholar]
- Szabó, Z.; Gretton, A.; Póczos, B.; Sriperumbudur, B. Two-stage sampled learning theory on distributions. In Proceeding of The 18th International Conference on Artificial Intelligence and Statistics, San Diego, CA, USA, 9–12 May 2015. [Google Scholar]
- Moon, K.R.; Delouille, V.; Li, J.J.; De Visscher, R.; Watson, F.; Hero, A.O., III. Image patch analysis of sunspots and active regions. II. Clustering via matrix factorization. J. Space Weather Space Clim. 2016, 6, A3. [Google Scholar] [CrossRef]
- Moon, K.R.; Li, J.J.; Delouille, V.; De Visscher, R.; Watson, F.; Hero, A.O., III. Image patch analysis of sunspots and active regions. I. Intrinsic dimension and correlation analysis. J. Space Weather Space Clim. 2016, 6, A2. [Google Scholar] [CrossRef]
- Dhillon, I.S.; Mallela, S.; Kumar, R. A divisive information theoretic feature clustering algorithm for text classification. J. Mach. Learn. Res. 2003, 3, 1265–1287. [Google Scholar]
- Banerjee, A.; Merugu, S.; Dhillon, I.S.; Ghosh, J. Clustering with Bregman divergences. J. Mach. Learn. Res. 2005, 6, 1705–1749. [Google Scholar]
- Lewi, J.; Butera, R.; Paninski, L. Real-time adaptive information-theoretic optimization of neurophysiology experiments. In Proceedings of the 19th International Conference on Neural Information Processing Systems (NIPS 2006), Vancouver, BC, Canada, 4–9 December 2006; pp. 857–864. [Google Scholar]
- Bruzzone, L.; Roli, F.; Serpico, S.B. An extension of the Jeffreys-Matusita distance to multiclass cases for feature selection. IEEE Trans. Geosci. Remote Sens. 1995, 33, 1318–1321. [Google Scholar] [CrossRef]
- Guorong, X.; Peiqi, C.; Minhui, W. Bhattacharyya distance feature selection. In Proceedings of the 13th International Conference on Pattern Recognition, Vienna, Austria, 25–29 August 1996; Volume 2, pp. 195–199. [Google Scholar]
- Sakate, D.M.; Kashid, D.N. Variable selection via penalized minimum φ-divergence estimation in logistic regression. J. Appl. Stat. 2014, 41, 1233–1246. [Google Scholar] [CrossRef]
- Hild, K.E.; Erdogmus, D.; Principe, J.C. Blind source separation using Renyi’s mutual information. IEEE Signal Process. Lett. 2001, 8, 174–176. [Google Scholar] [CrossRef]
- Mihoko, M.; Eguchi, S. Robust blind source separation by beta divergence. Neural Comput. 2002, 14, 1859–1886. [Google Scholar] [CrossRef] [PubMed]
- Vemuri, B.C.; Liu, M.; Amari, S.; Nielsen, F. Total Bregman divergence and its applications to DTI analysis. IEEE Trans. Med. Imaging 2011, 30, 475–483. [Google Scholar] [CrossRef] [PubMed]
- Hamza, A.B.; Krim, H. Image registration and segmentation by maximizing the Jensen-Rényi divergence. In Proceedings of the 4th International Workshop Energy Minimization Methods in Computer Vision and Pattern Recognition (EMMCVPR 2003), Lisbon, Portugal, 7–9 July 2003; pp. 147–163. [Google Scholar]
- Liu, G.; Xia, G.; Yang, W.; Xue, N. SAR image segmentation via non-local active contours. In Proceedings of the 2014 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Quebec City, QC, Canada, 13–18 July 2014; pp. 3730–3733. [Google Scholar]
- Korzhik, V.; Fedyanin, I. Steganographic applications of the nearest-neighbor approach to Kullback-Leibler divergence estimation. In Proceedings of the 2015 Third International Conference on Digital Information, Networking, and Wireless Communications (DINWC), Moscow, Russia, 3–5 February 2015; pp. 133–138. [Google Scholar]
- Basseville, M. Divergence measures for statistical data processing–An annotated bibliography. Signal Process. 2013, 93, 621–633. [Google Scholar] [CrossRef]
- Cichocki, A.; Amari, S. Families of alpha-beta-and gamma-divergences: Flexible and robust measures of similarities. Entropy 2010, 12, 1532–1568. [Google Scholar] [CrossRef]
- Csiszar, I. Information-type measures of difference of probability distributions and indirect observations. Stud. Sci. Math. Hungar. 1967, 2, 299–318. [Google Scholar]
- Ali, S.M.; Silvey, S.D. A general class of coefficients of divergence of one distribution from another. J. R. Stat. Soc. Ser. B Stat. Methodol. 1966, 28, 131–142. [Google Scholar]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Rényi, A. On measures of entropy and information. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 20 June–30 July 1960; University of California Press: Berkeley, CA, USA, 1961; pp. 547–561. [Google Scholar]
- Hellinger, E. Neue Begründung der Theorie quadratischer Formen von unendlichvielen Veränderlichen. J. Rein. Angew. Math. 1909, 136, 210–271. (In German) [Google Scholar]
- Bhattacharyya, A. On a measure of divergence between two multinomial populations. Indian J. Stat. 1946, 7, 401–406. [Google Scholar]
- Silva, J.F.; Parada, P.A. Shannon entropy convergence results in the countable infinite case. In Proceedings of the 2012 IEEE International Symposium on Information Theory Proceedings (ISIT), Cambridge, MA, USA, 1–6 July 2012; pp. 155–159. [Google Scholar]
- Antos, A.; Kontoyiannis, I. Convergence properties of functional estimates for discrete distributions. Random Struct. Algorithms 2001, 19, 163–193. [Google Scholar] [CrossRef]
- Valiant, G.; Valiant, P. Estimating the unseen: An n/log (n)-sample estimator for entropy and support size, shown optimal via new CLTs. In Proceedings of the 43rd Annual ACM Symposium on Theory of Computing, San Jose, CA, USA, 6–8 June 2011; pp. 685–694. [Google Scholar]
- Jiao, J.; Venkat, K.; Han, Y.; Weissman, T. Minimax estimation of functionals of discrete distributions. IEEE Trans. Inf. Theory 2015, 61, 2835–2885. [Google Scholar] [CrossRef] [PubMed]
- Jiao, J.; Venkat, K.; Han, Y.; Weissman, T. Maximum likelihood estimation of functionals of discrete distributions. IEEE Trans. Inf. Theory 2017, 63, 6774–6798. [Google Scholar] [CrossRef]
- Valiant, G.; Valiant, P. The power of linear estimators. In Proceedings of the 2011 IEEE 52nd Annual Symposium on Foundations of Computer Science (FOCS), Palm Springs, CA, USA, 22–25 October 2011; pp. 403–412. [Google Scholar]
- Paninski, L. Estimation of entropy and mutual information. Neural Comput. 2003, 15, 1191–1253. [Google Scholar] [CrossRef]
- Paninski, L. Estimating entropy on m bins given fewer than m samples. IEEE Trans. Inf. Theory 2004, 50, 2200–2203. [Google Scholar] [CrossRef]
- Alba-Fernández, M.V.; Jiménez-Gamero, M.D.; Ariza-López, F.J. Minimum Penalized ϕ-Divergence Estimation under Model Misspecification. Entropy 2018, 20, 329. [Google Scholar] [CrossRef]
- Ahmed, N.A.; Gokhale, D. Entropy expressions and their estimators for multivariate distributions. IEEE Trans. Inf. Theory 1989, 35, 688–692. [Google Scholar] [CrossRef]
- Misra, N.; Singh, H.; Demchuk, E. Estimation of the entropy of a multivariate normal distribution. J. Multivar. Anal. 2005, 92, 324–342. [Google Scholar] [CrossRef]
- Gupta, M.; Srivastava, S. Parametric Bayesian estimation of differential entropy and relative entropy. Entropy 2010, 12, 818–843. [Google Scholar] [CrossRef]
- Li, S.; Mnatsakanov, R.M.; Andrew, M.E. K-nearest neighbor based consistent entropy estimation for hyperspherical distributions. Entropy 2011, 13, 650–667. [Google Scholar] [CrossRef]
- Wang, Q.; Kulkarni, S.R.; Verdú, S. Divergence estimation for multidimensional densities via k-nearest-neighbor distances. IEEE Trans. Inf. Theory 2009, 55, 2392–2405. [Google Scholar] [CrossRef]
- Darbellay, G.A.; Vajda, I. Estimation of the information by an adaptive partitioning of the observation space. IEEE Trans. Inf. Theory 1999, 45, 1315–1321. [Google Scholar] [CrossRef]
- Silva, J.; Narayanan, S.S. Information divergence estimation based on data-dependent partitions. J. Stat. Plan. Inference 2010, 140, 3180–3198. [Google Scholar] [CrossRef]
- Le, T.K. Information dependency: Strong consistency of Darbellay–Vajda partition estimators. J. Stat. Plan. Inference 2013, 143, 2089–2100. [Google Scholar] [CrossRef]
- Wang, Q.; Kulkarni, S.R.; Verdú, S. Divergence estimation of continuous distributions based on data-dependent partitions. IEEE Trans. Inf. Theory 2005, 51, 3064–3074. [Google Scholar] [CrossRef]
- Hero, A.O., III; Ma, B.; Michel, O.; Gorman, J. Applications of entropic spanning graphs. IEEE Signal Process. Mag. 2002, 19, 85–95. [Google Scholar] [CrossRef]
- Moon, K.R.; Hero, A.O., III. Ensemble estimation of multivariate f-divergence. In Proceedings of the 2014 IEEE International Symposium on Information Theory (ISIT), Honolulu, HI, USA, 29 June–4 July 2014; pp. 356–360. [Google Scholar]
- Moon, K.R.; Sricharan, K.; Greenewald, K.; Hero, A.O., III. Improving convergence of divergence functional ensemble estimators. In Proceedings of the 2016 IEEE International Symposium on Information Theory (ISIT), Barcelona, Spain, 10–15 July 2016; pp. 1133–1137. [Google Scholar]
- Nguyen, X.; Wainwright, M.J.; Jordan, M.I. Estimating divergence functionals and the likelihood ratio by convex risk minimization. IEEE Trans. Inf. Theory 2010, 56, 5847–5861. [Google Scholar] [CrossRef]
- Krishnamurthy, A.; Kandasamy, K.; Poczos, B.; Wasserman, L. Nonparametric Estimation of Renyi Divergence and Friends. In Proceedings of the 31st International Conference on Machine Learning, Beijing, China, 21–26 June 2014; pp. 919–927. [Google Scholar]
- Singh, S.; Póczos, B. Generalized exponential concentration inequality for Rényi divergence estimation. In Proceedings of the 31st International Conference on Machine Learning (ICML-14), Beijing, China, 21–26 June 2014; pp. 333–341. [Google Scholar]
- Singh, S.; Póczos, B. Exponential Concentration of a Density Functional Estimator. In Proceedings of the 27th International Conference on Neural Information Processing Systems (NIPS 2014), Montreal, QC, Canada, 8–13 December 2014; pp. 3032–3040. [Google Scholar]
- Kandasamy, K.; Krishnamurthy, A.; Poczos, B.; Wasserman, L.; Robins, J. Nonparametric von Mises Estimators for Entropies, Divergences and Mutual Informations. In Proceedings of the 28th International Conference on Neural Information Processing Systems (NIPS 2015), Montreal, QC, Canada, 7–12 December 2015; pp. 397–405. [Google Scholar]
- Härdle, W. Applied Nonparametric Regression; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Berlinet, A.; Devroye, L.; Györfi, L. Asymptotic normality of L1-error in density estimation. Statistics 1995, 26, 329–343. [Google Scholar] [CrossRef]
- Berlinet, A.; Györfi, L.; Dénes, I. Asymptotic normality of relative entropy in multivariate density estimation. Publ. l’Inst. Stat. l’Univ. Paris 1997, 41, 3–27. [Google Scholar]
- Bickel, P.J.; Rosenblatt, M. On some global measures of the deviations of density function estimates. Ann. Stat. 1973, 1, 1071–1095. [Google Scholar] [CrossRef]
- Sricharan, K.; Wei, D.; Hero, A.O., III. Ensemble estimators for multivariate entropy estimation. IEEE Trans. Inf. Theory 2013, 59, 4374–4388. [Google Scholar] [CrossRef] [PubMed]
- Berrett, T.B.; Samworth, R.J.; Yuan, M. Efficient multivariate entropy estimation via k-nearest neighbour distances. arXiv 2017, arXiv:1606.00304. [Google Scholar]
- Kozachenko, L.; Leonenko, N.N. Sample estimate of the entropy of a random vector. Probl. Peredachi Inf. 1987, 23, 9–16. [Google Scholar]
- Hansen, B.E.; (University of Wisconsin, Madison, WI, USA). Lecture Notes on Nonparametrics. 2009. [Google Scholar]
- Budka, M.; Gabrys, B.; Musial, K. On accuracy of PDF divergence estimators and their applicability to representative data sampling. Entropy 2011, 13, 1229–1266. [Google Scholar] [CrossRef]
- Efron, B.; Stein, C. The jackknife estimate of variance. Ann. Stat. 1981, 9, 586–596. [Google Scholar] [CrossRef]
- Wisler, A.; Moon, K.; Berisha, V. Direct ensemble estimation of density functionals. In Proceedings of the 2018 International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018. [Google Scholar]
- Moon, K.R.; Sricharan, K.; Greenewald, K.; Hero, A.O., III. Nonparametric Ensemble Estimation of Distributional Functionals. arXiv 2016, arXiv:1601.06884v2. [Google Scholar]
- Paul, F.; Arkin, Y.; Giladi, A.; Jaitin, D.A.; Kenigsberg, E.; Keren-Shaul, H.; Winter, D.; Lara-Astiaso, D.; Gury, M.; Weiner, A.; et al. Transcriptional heterogeneity and lineage commitment in myeloid progenitors. Cell 2015, 163, 1663–1677. [Google Scholar] [CrossRef] [PubMed]
- Kanehisa, M.; Goto, S. KEGG: Kyoto encyclopedia of genes and genomes. Nucleic Acids Res. 2000, 28, 27–30. [Google Scholar] [CrossRef] [PubMed]
- Kanehisa, M.; Sato, Y.; Kawashima, M.; Furumichi, M.; Tanabe, M. KEGG as a reference resource for gene and protein annotation. Nucleic Acids Res. 2015, 44, D457–D462. [Google Scholar] [CrossRef] [PubMed]
- Kanehisa, M.; Furumichi, M.; Tanabe, M.; Sato, Y.; Morishima, K. KEGG: New perspectives on genomes, pathways, diseases and drugs. Nucleic Acids Res. 2016, 45, D353–D361. [Google Scholar] [CrossRef] [PubMed]
- Van Dijk, D.; Sharma, R.; Nainys, J.; Yim, K.; Kathail, P.; Carr, A.J.; Burdsiak, C.; Moon, K.R.; Chaffer, C.; Pattabiraman, D.; et al. Recovering Gene Interactions from Single-Cell Data Using Data Diffusion. Cell 2018, 174, 716–729. [Google Scholar] [CrossRef] [PubMed]
- Moon, K.R.; Sricharan, K.; Hero, A.O., III. Ensemble Estimation of Distributional Functionals via k-Nearest Neighbors. arXiv 2017, arXiv:1707.03083. [Google Scholar]
- Durrett, R. Probability: Theory and Examples; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Gut, A. Probability: A Graduate Course; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Munkres, J. Topology; Prentice Hall: Englewood Cliffs, NJ, USA, 2000. [Google Scholar]
- Evans, L.C. Partial Differential Equations; American Mathematical Society: Providence, RI, USA, 2010. [Google Scholar]
- Gilbarg, D.; Trudinger, N.S. Elliptic Partial Differential Equations of Second Order; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
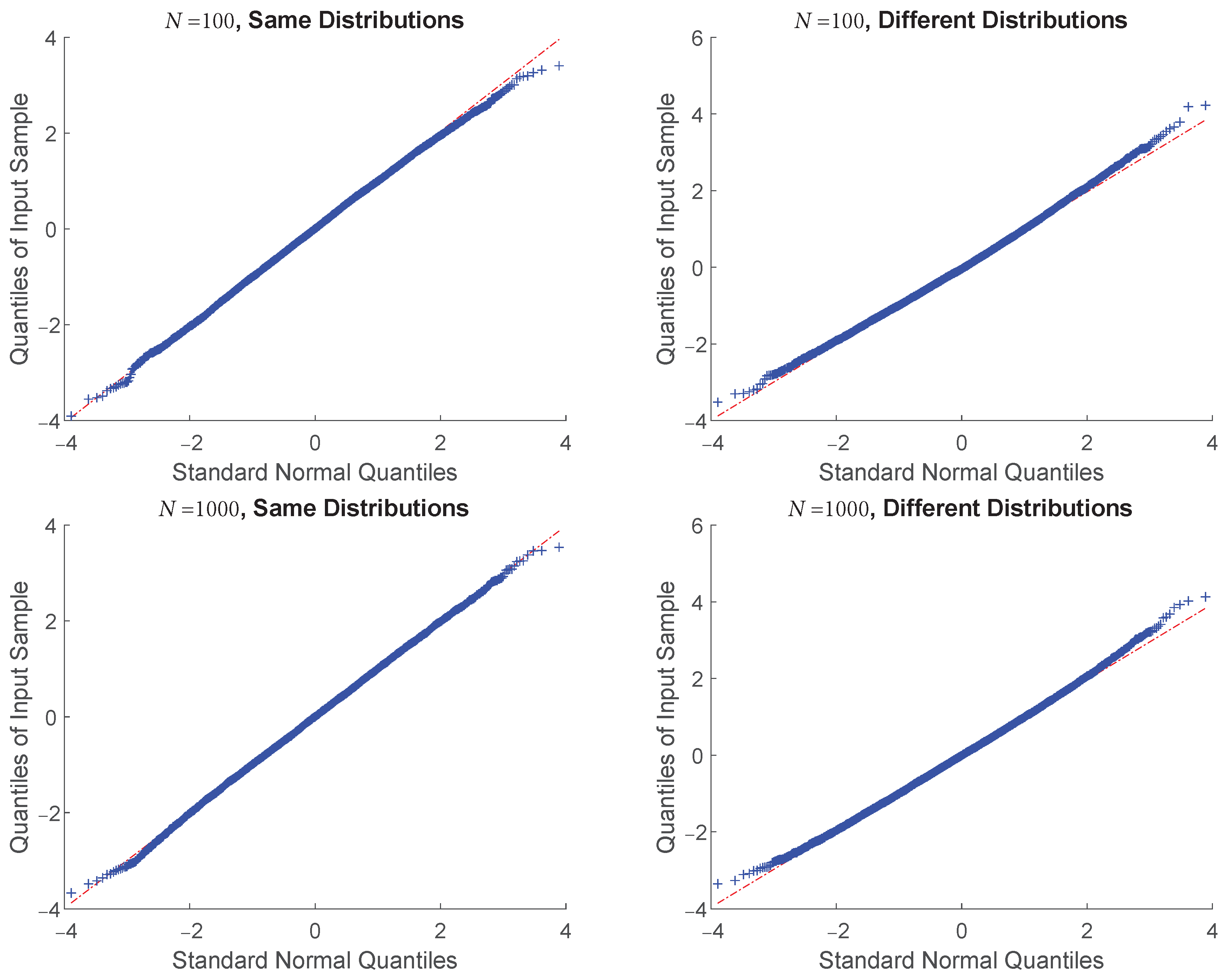
| Estimator | |||
|---|---|---|---|
| N | Same | Different | ||
|---|---|---|---|---|
| 100 | ||||
| 500 | ||||
| 1000 | ||||
| 5000 | ||||
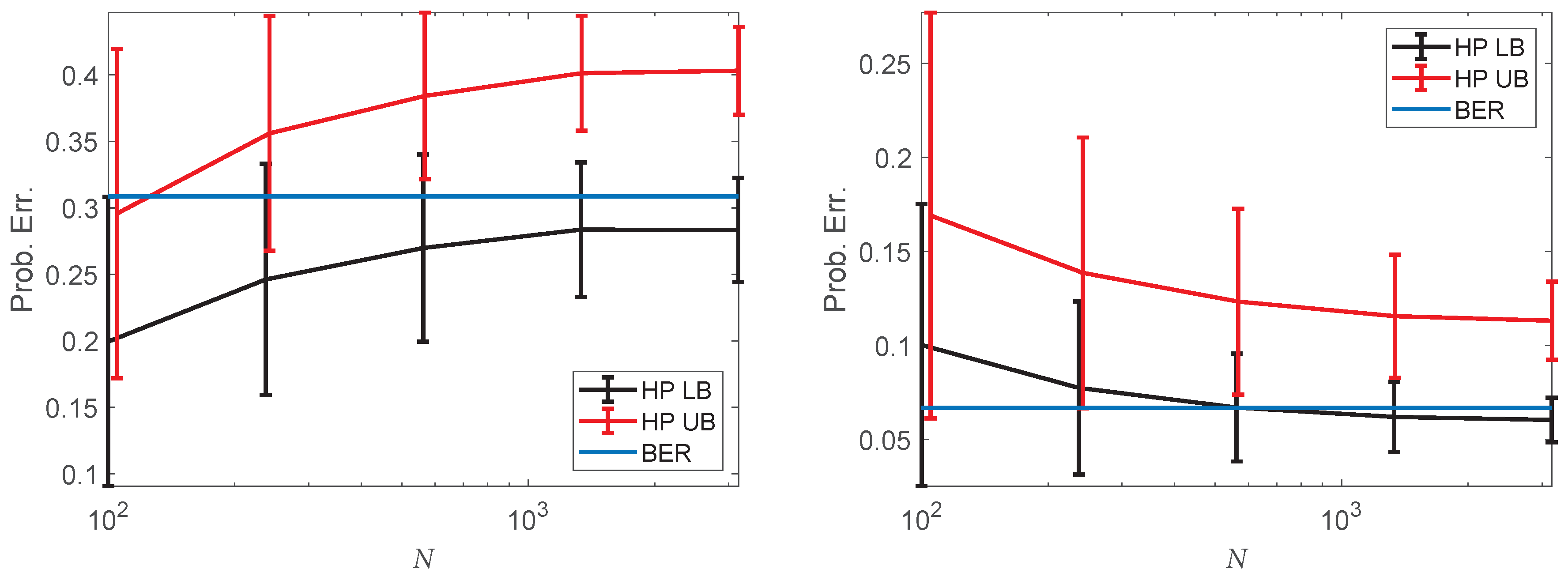
| Platelets | Erythrocytes | Neutrophils | Macrophages | Random | |
|---|---|---|---|---|---|
| Eryth. vs. Mono., LB | |||||
| Eryth. vs. Mono., UB | |||||
| Eryth. vs. Mono., Prob. Error | |||||
| Eryth. vs. Baso., LB | |||||
| Eryth. vs. Baso., UB | |||||
| Eryth. vs. Baso., Prob. Error | |||||
| Baso. vs. Mono., LB | |||||
| Baso. vs. Mono., UB | |||||
| Baso. vs. Mono., Prob. Error |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moon, K.R.; Sricharan, K.; Greenewald, K.; Hero, A.O., III. Ensemble Estimation of Information Divergence †. Entropy 2018, 20, 560. https://doi.org/10.3390/e20080560
Moon KR, Sricharan K, Greenewald K, Hero AO III. Ensemble Estimation of Information Divergence †. Entropy. 2018; 20(8):560. https://doi.org/10.3390/e20080560
Chicago/Turabian StyleMoon, Kevin R., Kumar Sricharan, Kristjan Greenewald, and Alfred O. Hero, III. 2018. "Ensemble Estimation of Information Divergence †" Entropy 20, no. 8: 560. https://doi.org/10.3390/e20080560
APA StyleMoon, K. R., Sricharan, K., Greenewald, K., & Hero, A. O., III. (2018). Ensemble Estimation of Information Divergence †. Entropy, 20(8), 560. https://doi.org/10.3390/e20080560





