Magnetocaloric Effect in Non-Interactive Electron Systems: “The Landau Problem” and Its Extension to Quantum Dots
Abstract
1. Introduction
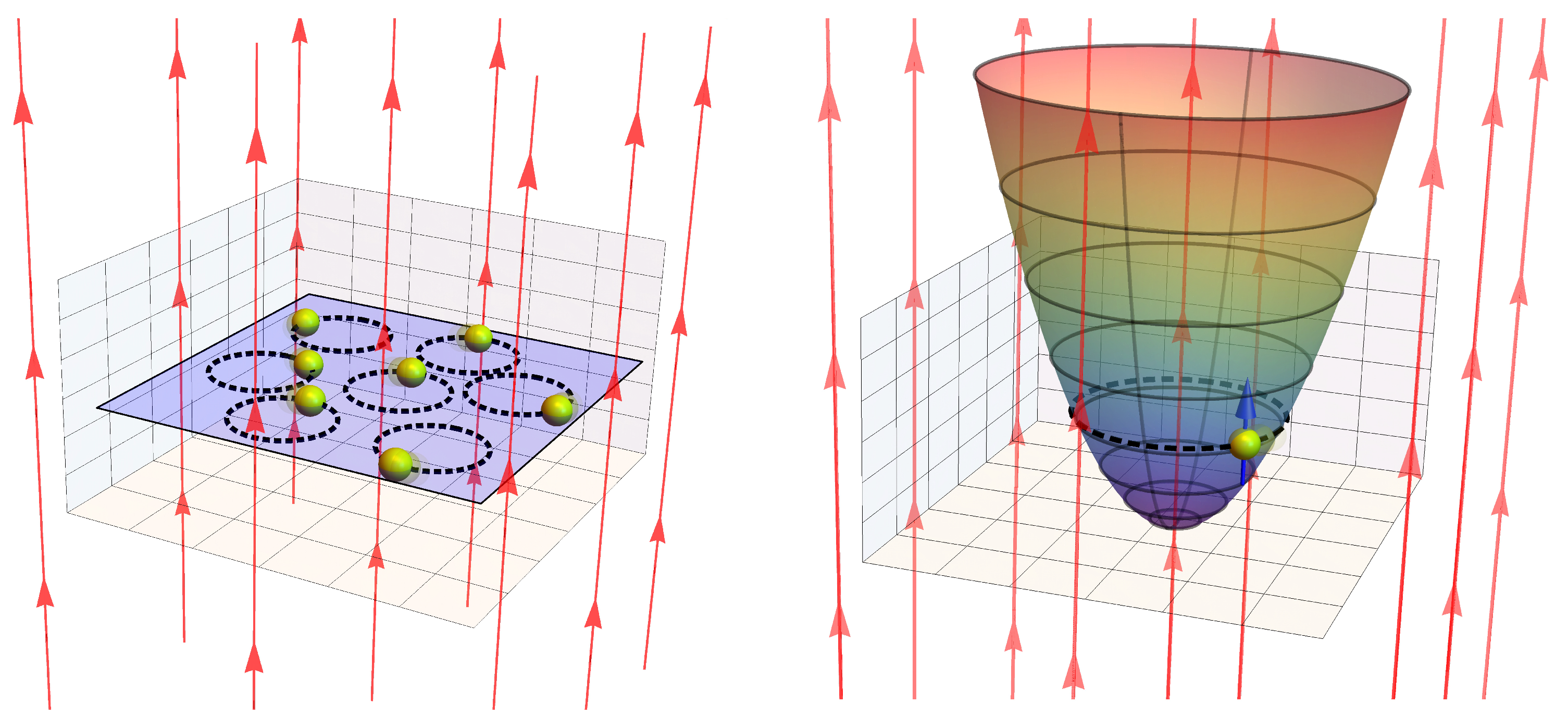
2. Model
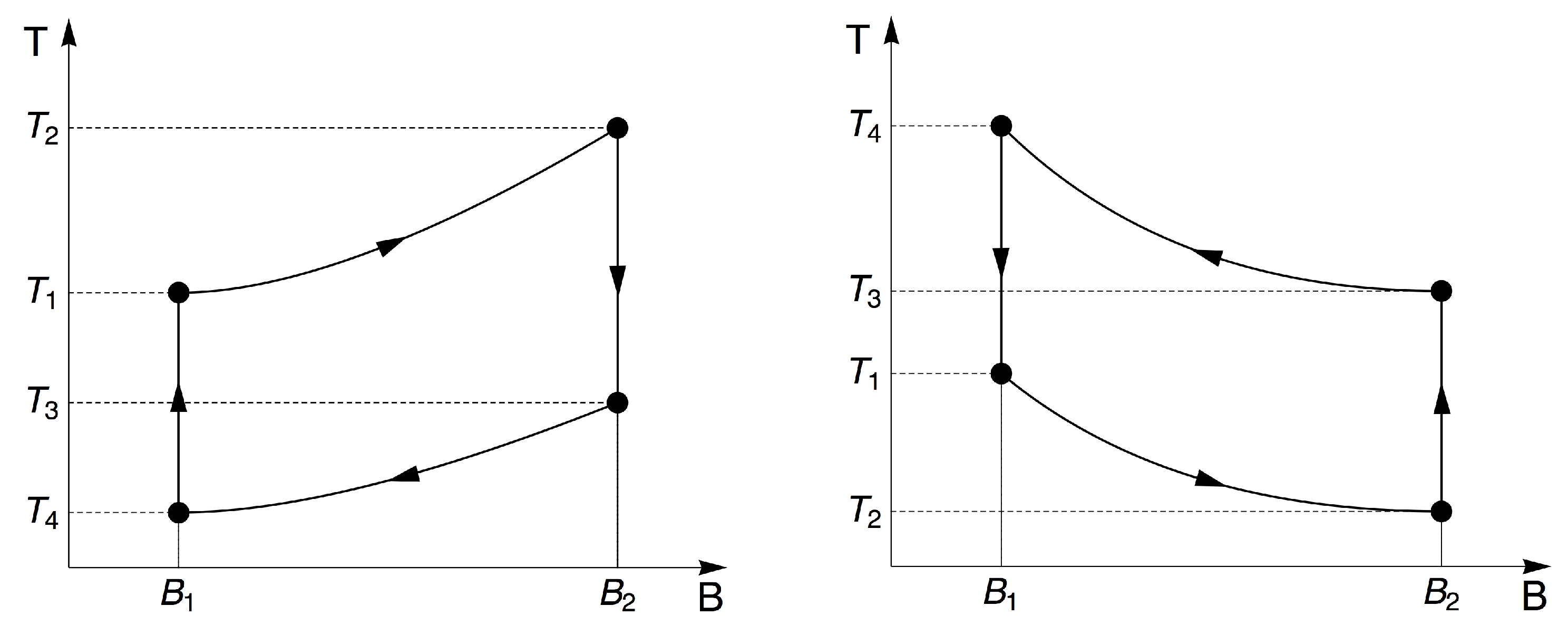
Magnetocaloric Observables
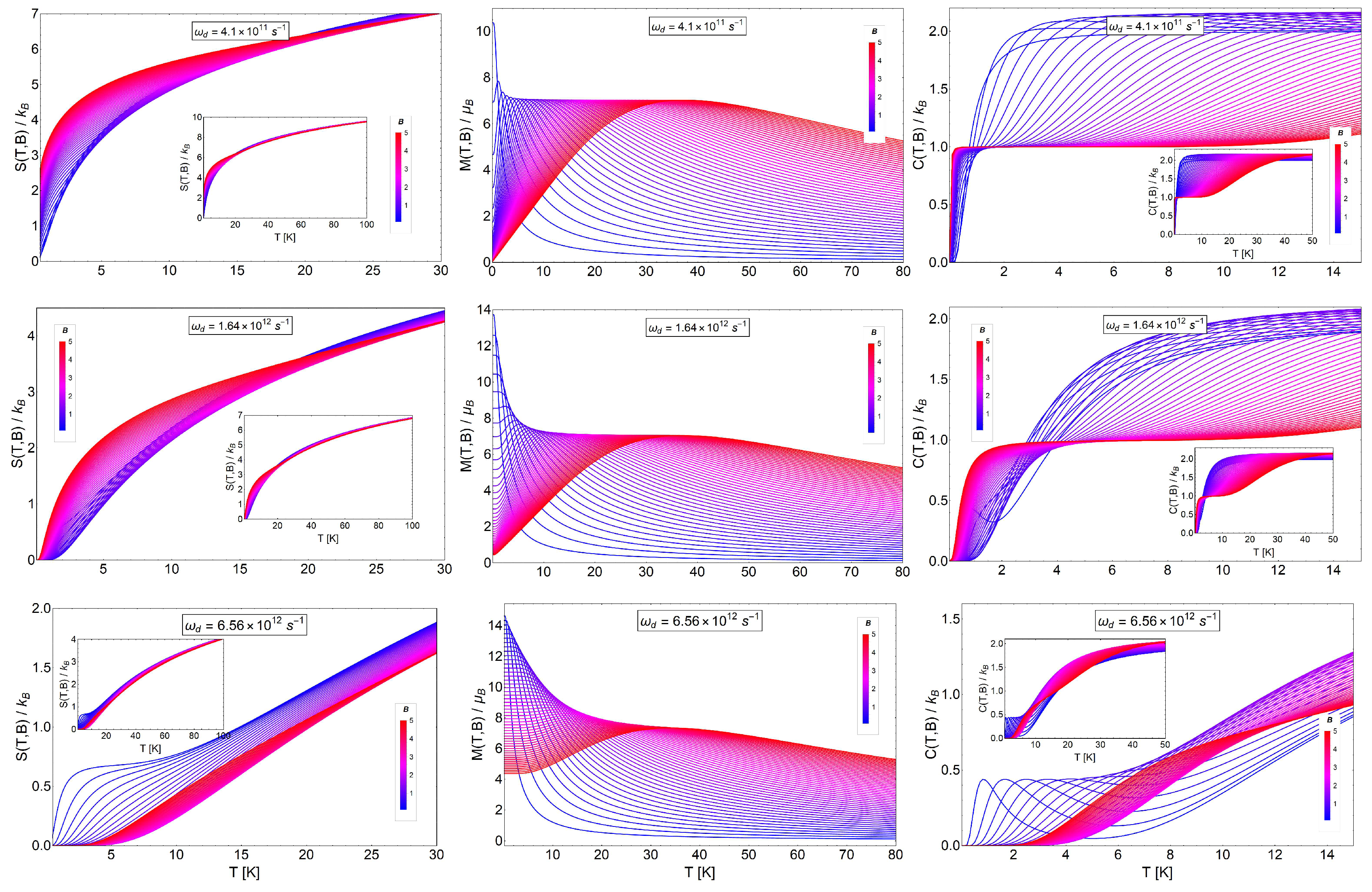
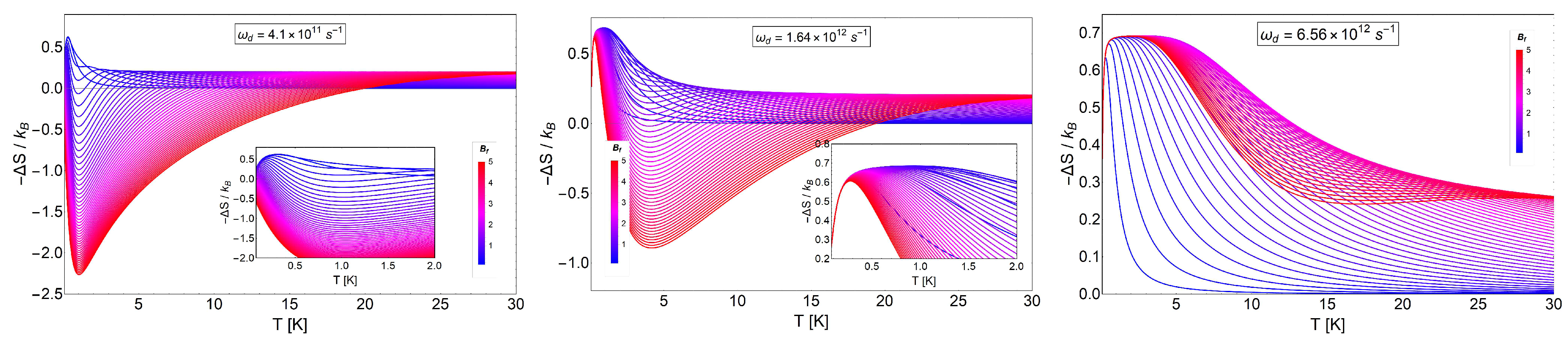
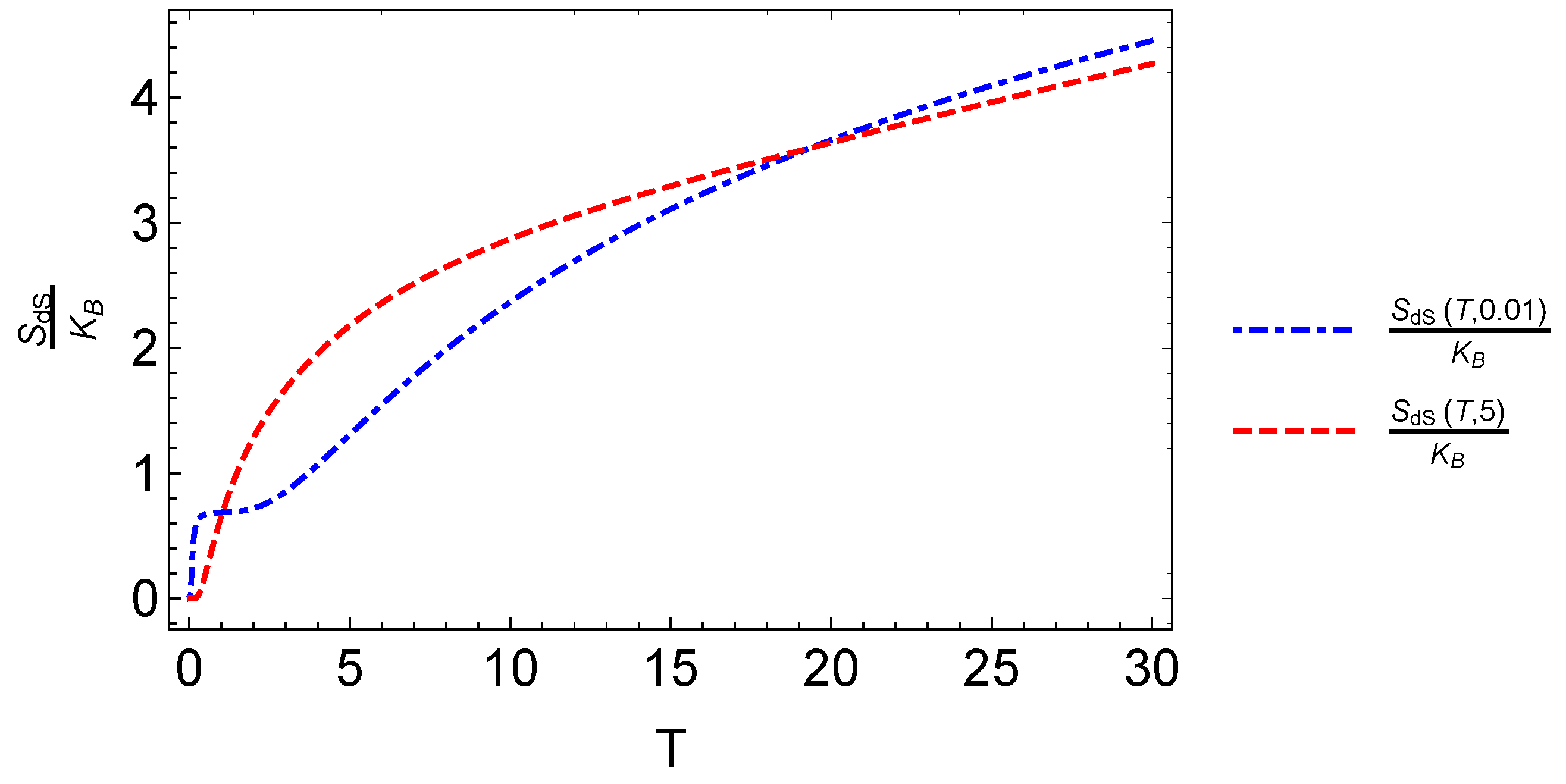
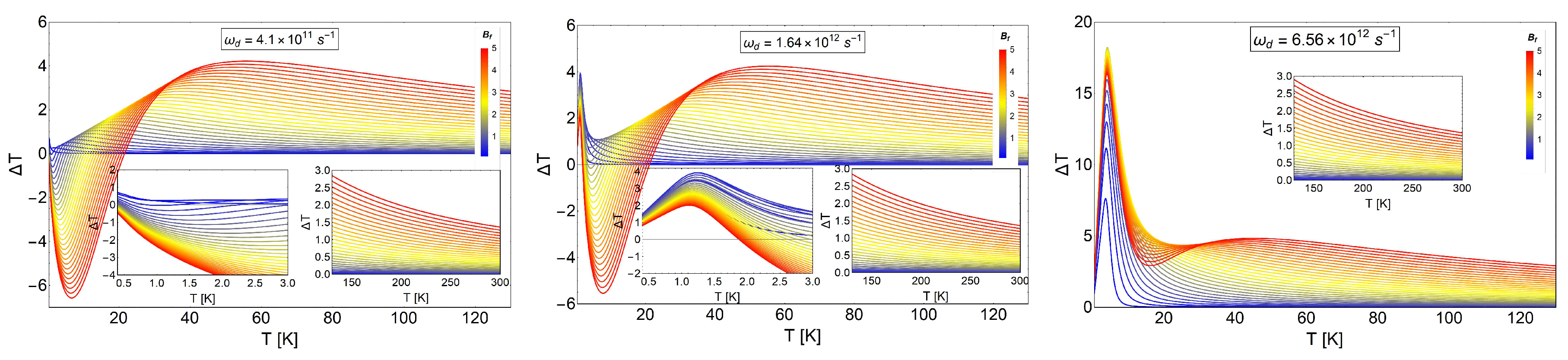
3. Results and Discussion
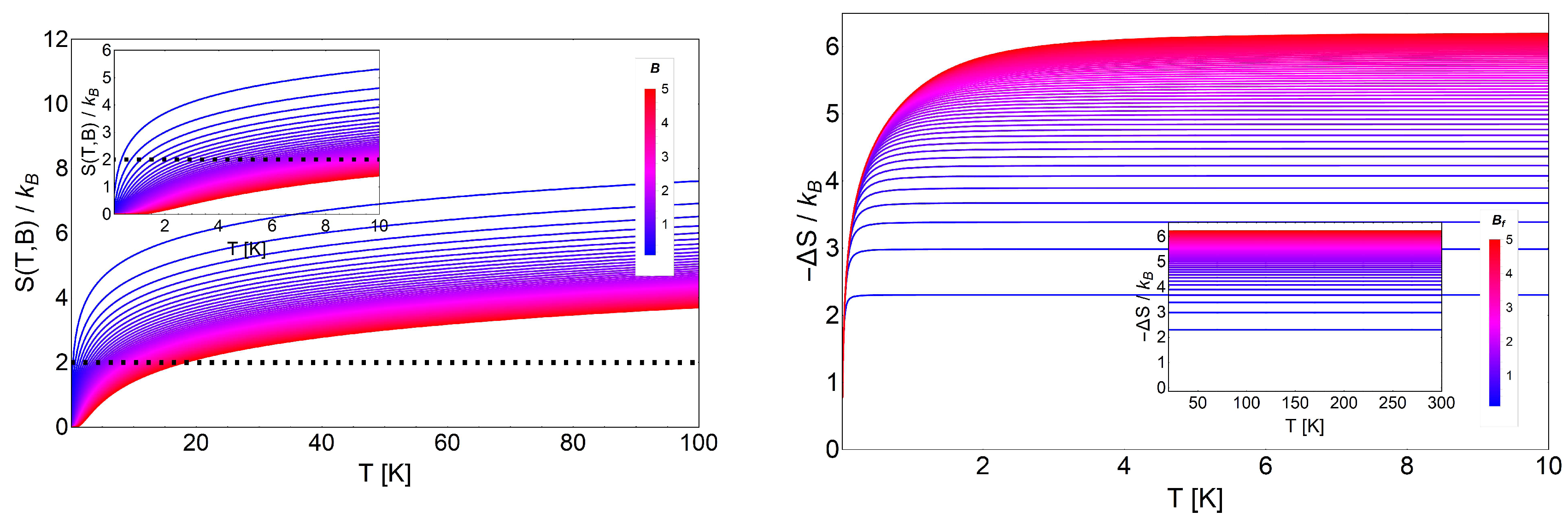
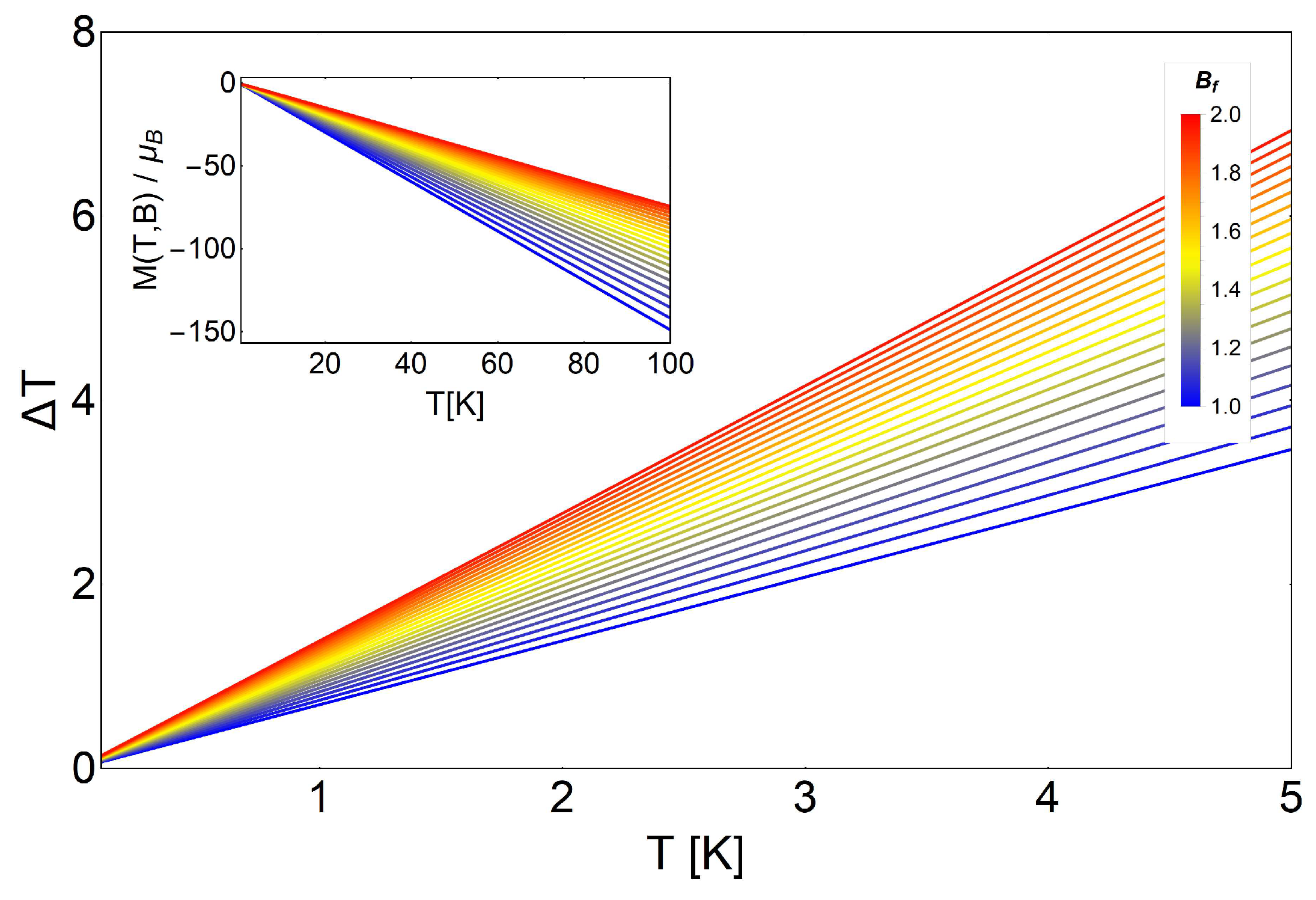
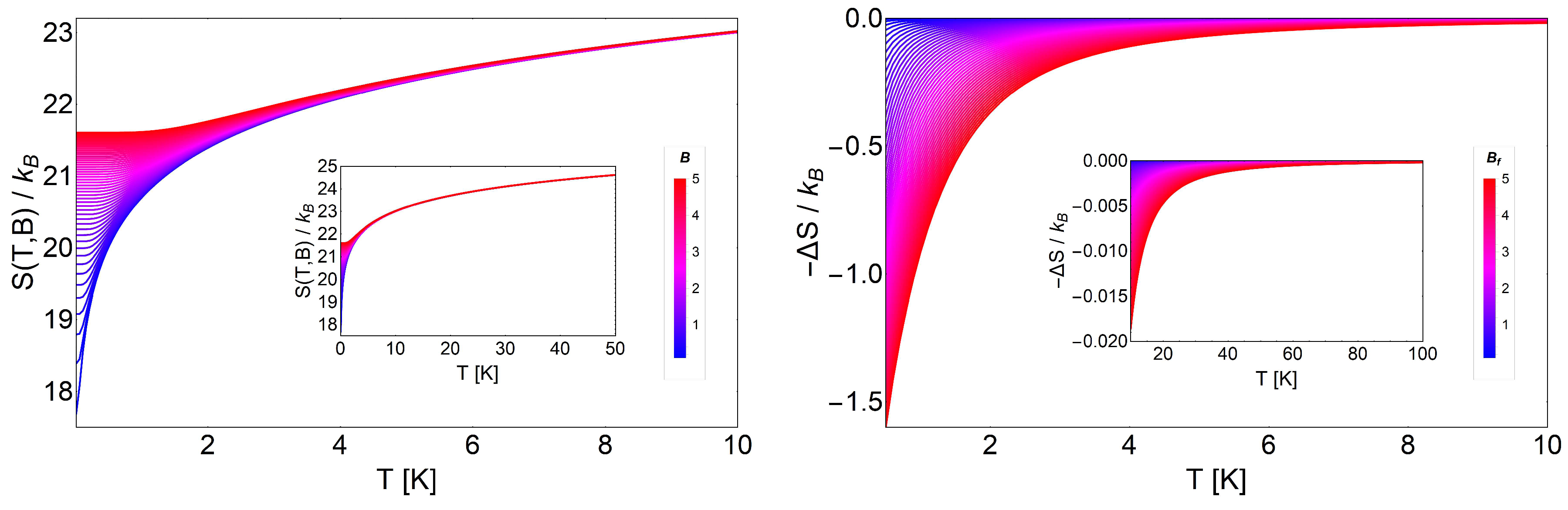
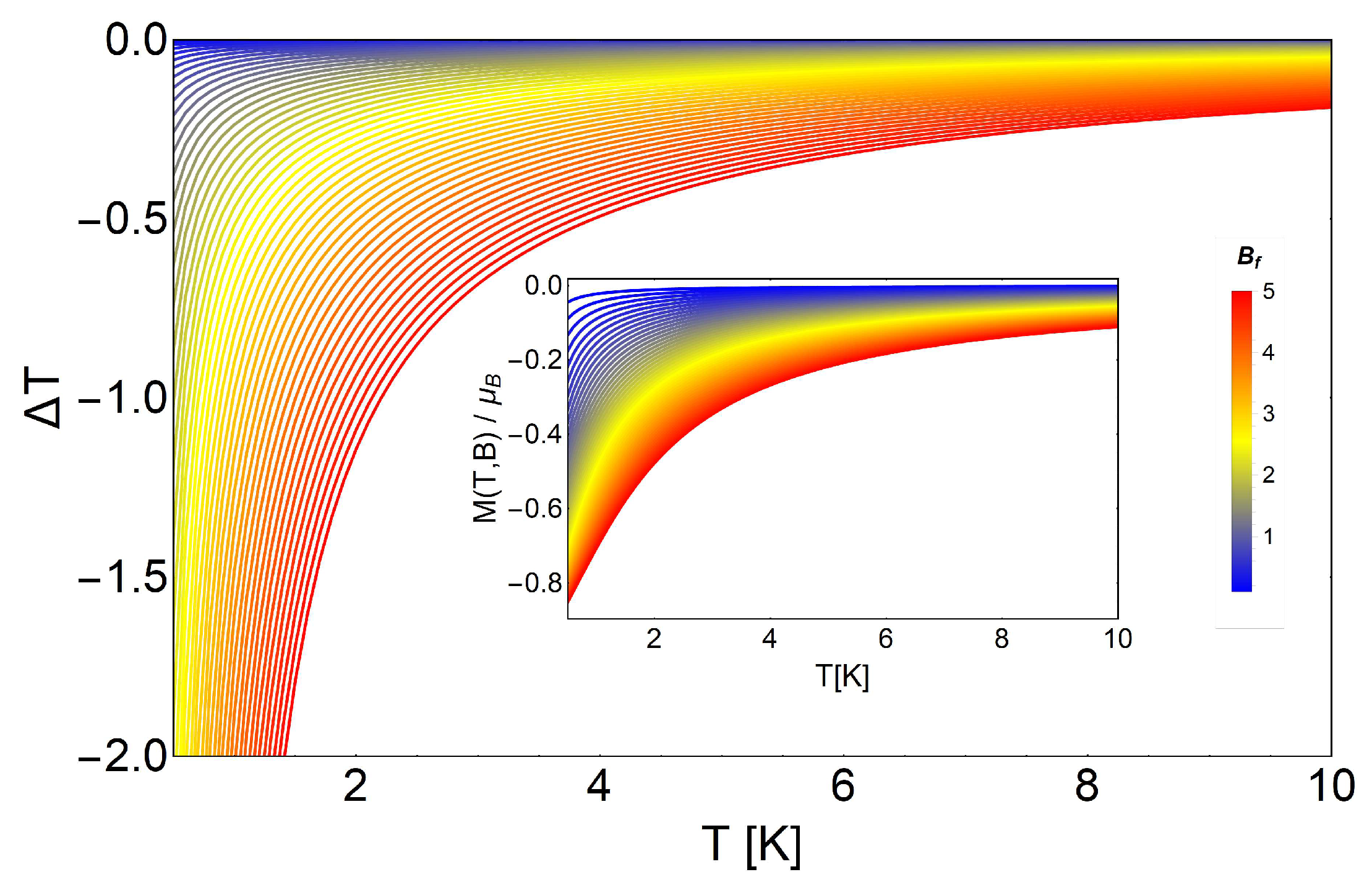
3.1. Landau Problem: Influence of Energy Degeneracy on the MCE
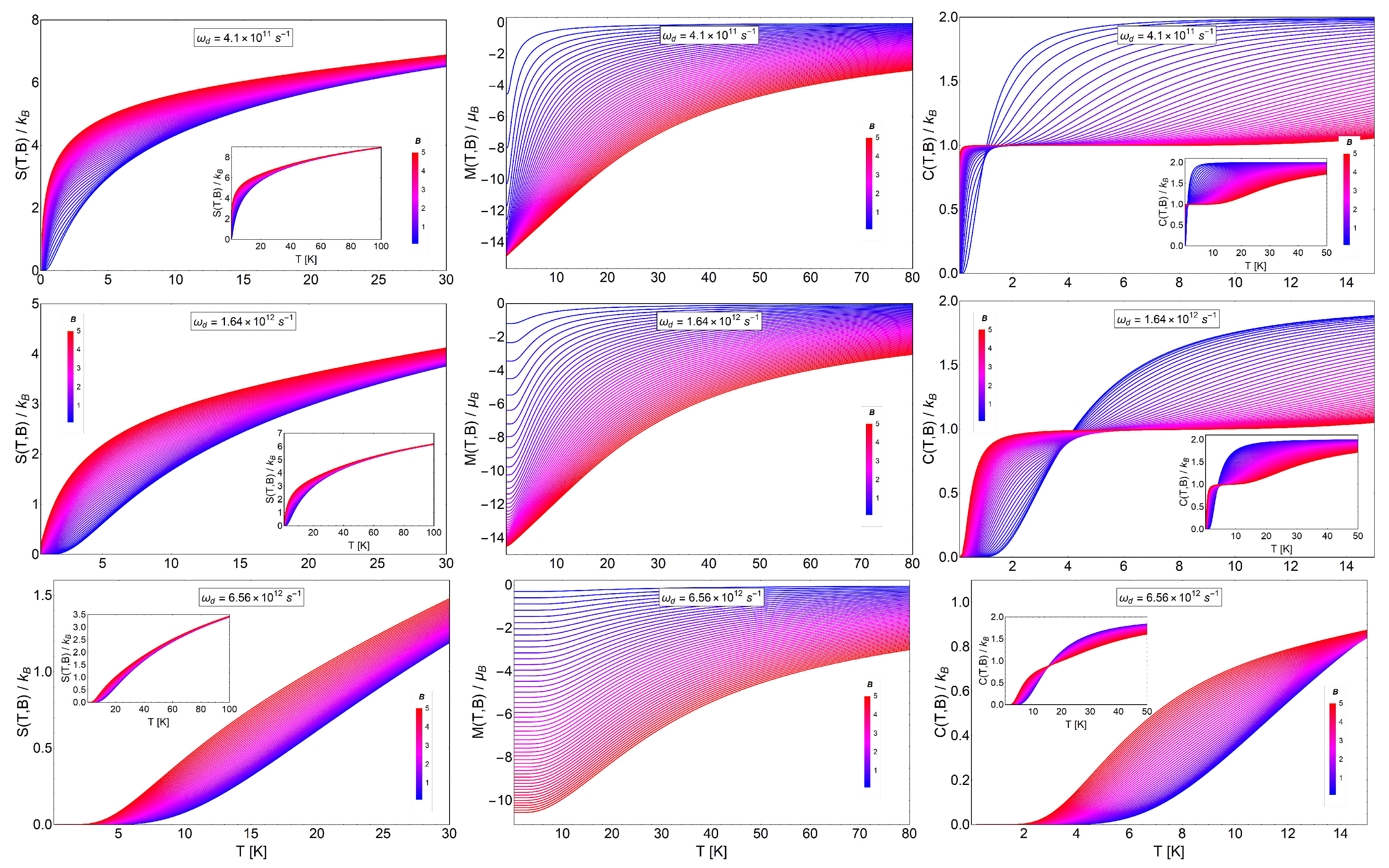
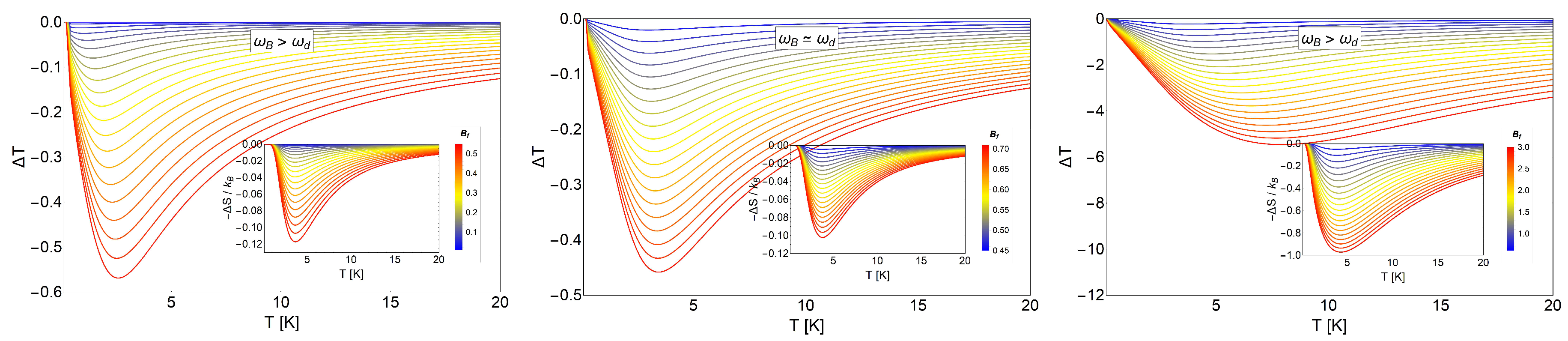
3.2. MCE for Electrons Trapped in a Quantum Dot
3.3. MCE for Electrons with Spin Trapped in a Quantum Dot
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Warburg, E. Magnetische Untersuchungen. Ueber einige Wirkungen der Coërcitivkraft. Ann. Phys. (Leipzig) 1881, 249, 141–164. (In German) [Google Scholar] [CrossRef]
- Weiss, P.; Piccard, A. Le pheénoméne magnétocalorique. J. Phys. (Paris) 1917, 7, 103–109. (In French) [Google Scholar]
- Weiss, P.; Piccard, A. Sur un nouveau phénoméne magnétocalorique. Comptes Rendus 1918, 166, 352–354. (In French) [Google Scholar]
- Debye, P. Einige Bemerkungen zur Magnetisierung bei tiefer Temperatur. Ann. Phys. 1926, 81, 1154–1160. (In Germany) [Google Scholar] [CrossRef]
- Giauque, W.F.; Macdougall, D.P. The Production of Temperatures below One Degree Absolute by Adiabatic Demagnetization of Gadolinium Sulfate. J. Am. Chem. Soc. 1935, 57, 1175–1185. [Google Scholar] [CrossRef]
- Brown, G.V. Magnetic heat pumping near room temperature. J. Appl. Phys. 1976, 47, 3673–3680. [Google Scholar] [CrossRef]
- Pecharsky, V.K.; Gschneidner, K.A., Jr. Giant Magnetocaloric Effect in Gd5(Si2Ge2). Phys. Rev. Lett. 1997, 78, 4494–4497. [Google Scholar] [CrossRef]
- Pathak, A.K.; Gschneidner, K.A.; Pecharsky, V.K. Negative to positive magnetoresistance and magnetocaloric effect in Pr0.6Er0.4Al2. J. Alloys Compd. 2015, 621, 411–414. [Google Scholar] [CrossRef]
- Florez, J.M.; Vargas, P.; Garcia, C.; Ross, C.A. Magnetic entropy change plateau in a geometrically frustrated layered system: FeCrAs-like iron-pnictide structure as a magnetocaloric prototype. J. Phys. Condens. Matter 2013, 25, 226004. [Google Scholar] [CrossRef] [PubMed]
- Hudl, M.; Campanini, D.; Caron, L.; Hoglin, V.; Sahlberg, M.; Nordblad, P.; Rydh, A. Thermodynamics around the first-order ferromagnetic phase transition of Fe2P single crystals. Phys. Rev. B 2014, 90, 144432. [Google Scholar] [CrossRef]
- Miao, X.F.; Caron, L.; Roy, P.; Dung, N.H.; Zhang, L.; Kockelmann, W.A.; De Grootm, R.A.; Van Dijk, N.H.; Brück, E. Tuning the phase transition in transition-metal-based magnetocaloric compounds. Phys. Rev. B 2014, 89, 174429. [Google Scholar] [CrossRef]
- Sosin, S.; Prozorova, L.; Smirnov, A.; Golov, A.; Berkutov, I.; Petrenko, O.; Balakrishnan, G.; Zhitomirsky, M.E. Magnetocaloric effect in pyrochlore antiferromagnet Gd2Ti2O7. Phys. Rev. B 2005, 71, 2005094413. [Google Scholar] [CrossRef]
- Wang, F.; Yuan, F.-Y.; Wang, J.-Z.; Feng, T.-F.; Hu, G.-Q. Conventional and inverse magnetocaloric effect in Pr2CuSi3 and Gd2CuSi3 compounds. J. Alloys Compd. 2014, 592, 63–66. [Google Scholar] [CrossRef]
- Du, Q.; Chen, G.; Yang, W.; Wei, J.; Hua, M.; Du, H.; Wang, C.; Liu, S.; Han, J.; Zhang, Y.; et al. Magnetic frustration and magnetocaloric effect in AlFe2−xMnxB2 (x = 0–0.5) ribbons. J. Phys. D-Appl. Phys. 2015, 48, 335001. [Google Scholar] [CrossRef]
- Balli, M.; Fruchart, D.; Zach, R. Negative and conventional magnetocaloric effects of a MnRhAs single crystal. J. Appl. Phys. 2014, 115, 203909. [Google Scholar] [CrossRef]
- Kolat, V.S.; Izgi, T.; Kaya, A.O.; Bayri, N.; Gencer, H.; Atalay, S. Metamagnetic transition and magnetocaloric effect in charge-ordered Pr0.68Ca0.32−xSrxMnO3 (x = 0, 0.1, 0.18, 0.26 and 0.32) compounds. J. Magn. Magn. Mater. 2010, 322, 427433. [Google Scholar] [CrossRef]
- Phan, M.H.; Morales, M.B.; Bingham, N.S.; Srikanth, H.; Zhang, C.L.; Cheong, S.-W. Phase coexistence and magnetocaloric effect in La5/8−yPryCa3/8MnO3(y = 0.275). Phys. Rev. B 2010, 81, 094413. [Google Scholar] [CrossRef]
- Patra, M.; Majumdar, S.; Giri, S.; Iles, G.N.; Chatterji, T. Anomalous magnetic field dependence of magnetocaloric effect at low temperature in Pr0.52Sr0.48MnO3 single crystal. J. Appl. Phys. 2010, 107, 076101. [Google Scholar] [CrossRef]
- Szalowski, K.; Balcerzak, T. Normal and inverse magnetocaloric effect in magnetic multilayers with antiferromagnetic interlayer coupling. J. Phys. Condens. Matter 2014, 26, 386003. [Google Scholar] [CrossRef] [PubMed]
- Midya, A.; Khan, N.; Bhoi, D.; Mandal, P. Giant magnetocaloric effect in magnetically frustrated EuHo2O4 and EuDy2O4 compounds. Appl. Phys. Lett. 2012, 101, 132415. [Google Scholar] [CrossRef]
- Moya, X.; Kar-Narayan, S.; Mathur, N.D. Caloric materials near ferroic phase transitions. Nat. Mater. 2014, 13, 439–450. [Google Scholar] [CrossRef] [PubMed]
- Guillou, F.; Porcari, G.; Yibole, H.; van Dijk, N.; Bruck, E. Taming the First-Order Transition in Giant Magnetocaloric Materials. Adv. Mater. 2014, 26, 2671–2675. [Google Scholar] [CrossRef] [PubMed]
- Gong, Y.-Y.; Wang, D.-H.; Cao, Q.-Q.; Liu, E.-K.; Liu, J.; Du, Y.-W. Electric Field Control of the Magnetocaloric Effect. Adv. Mater. 2014, 27, 801–805. [Google Scholar] [CrossRef] [PubMed]
- Nalbandyan, V.B.; Zvereva, E.A.; Nikulin, A.Y.; Shukaev, I.L.; Whangbo, M.-H.; Koo, H.-J.; Abdel-Hafiez, M.; Chen, X.J.; Koo, C.; Vasiliev, A.N.; et al. New Phase of MnSb2O6 Prepared by Ion Exchange: Structural, Magnetic, and Thermodynamic Properties. Inorg. Chem. 2015, 54, 1705–1711. [Google Scholar] [CrossRef] [PubMed]
- Tkac, V.; Orendacova, A.; Cizmar, E.; Orendac, M.; Feher, A.; Anders, A.G. Giant reversible rotating cryomagnetocaloric effect in KEr(MoO4)2 induced by a crystal-field anisotropy. Phys. Rev. B 2015, 92, 024406. [Google Scholar] [CrossRef]
- Tamura, R.; Ohno, T.; Kitazawa, H. A generalized magnetic refrigeration scheme. Appl. Phys. Lett. 2014, 104, 052415. [Google Scholar] [CrossRef]
- Tamura, R.; Tanaka, S.; Ohno, T.; Kitazawa, H. Magnetic ordered structure dependence of magnetic refrigeration efficiency. J. Appl. Phys. 2014, 116, 053908. [Google Scholar] [CrossRef]
- Li, G.; Wang, J.; Cheng, Z.; Ren, Q.; Fang, C.; Dou, S. Large entropy change accompanying two successive magnetic phase transitions in TbMn2Si2 for magnetic refrigeration. Appl. Phys. Lett. 2015, 106, 182405. [Google Scholar] [CrossRef]
- Von Ranke, J.P.; Alho, B.P.; Nóbrega, B.P.; de Oliveira, N.A. Understanding the inverse magnetocaloric effect through a simple theoretical model. Phys. B 2009, 404, 056004. [Google Scholar] [CrossRef]
- Von Ranke, J.P.; de Oliveira, N.A.; Alho, B.P.; Plaza, E.J.R.; de Sousa, V.S.R.; Caron, L.; Reis, M.S. Understanding the inverse magnetocaloric effect in antiferro- and ferrimagnetic arrangements. J. Phys. Condens. Matter 2009, 21, 3045–3047. [Google Scholar] [CrossRef] [PubMed]
- Reis, M.S. Oscillating adiabatic temperature change of diamagnetic materials. Solid State Commun. 2012, 152, 921–923. [Google Scholar] [CrossRef]
- Reis, M.S. Oscillating magnetocaloric effect on graphenes. Appl. Phys. Lett. 2012, 101, 222405. [Google Scholar] [CrossRef]
- Reis, M.S. Step-like features on caloric effects of graphenes. Phys. Lett. A 2014, 378, 918–921. [Google Scholar] [CrossRef]
- Reis, M.S. Magnetocaloric cycle with six stages: Possible application of graphene at low temperature. Appl. Phys. Lett. 2015, 107, 102401. [Google Scholar] [CrossRef]
- Alisultanov, Z.Z.; Reis, M.S. Oscillating magneto- and electrocaloric effects on bilayer graphenes. Solid State Commun. 2015, 206, 17–21. [Google Scholar] [CrossRef]
- Ma, N.; Reis, M.S. Barocaloric effect on graphene. Sci. Rep. 2017, 7, 13257. [Google Scholar] [CrossRef] [PubMed]
- Peña, F.J.; González, A.; Nunez, A.S.; Orellana, P.A.; Rojas, R.G.; Vargas, P. Magnetic Engine for the Single-Particle Landau Problem. Entropy 2017, 19, 639. [Google Scholar] [CrossRef]
- Mehta, V.; Johal, R.S. Quantum Otto engine with exchange coupling in the presence of level degeneracy. Phys. Rev. E 2017, 96, 032110. [Google Scholar] [CrossRef] [PubMed]
- Azimi, M.; Chorotorlisvili, L.; Mishra, S.K.; Vekua, T.; Hübner, W.; Berakdar, J. Quantum Otto heat engine based on a multiferroic chain working substance. New J. Phys. 2014, 16, 063018. [Google Scholar] [CrossRef]
- Chotorlishvili, L.; Azimi, M.; Stagraczyński, S.; Toklikishvili, Z.; Schüler, M.; Berakdar, J. Superadiabatic quantum heat engine with a multiferroic working medium. Phys. Rev. E 2016, 94, 032116. [Google Scholar] [CrossRef] [PubMed]
- Dong, C.D.; Lefkidis, G.; Hübner, W. Quantum Isobaric Process in Ni2. J. Supercond. Nov. Magn. 2013, 26, 1589–1594. [Google Scholar] [CrossRef]
- Dong, C.D.; Lefkidis, G.; Hübner, W. Quantum Magnetic quantum diesel in Ni2. Phys. Rev. B 2013, 88, 214421. [Google Scholar] [CrossRef]
- Hübner, W.; Lefkidis, G.; Dong, C.D.; Chaudhuri, D. Spin-dependent Otto quantum heat engine based on a molecular substance. Phys. Rev. B 2014, 90, 024401. [Google Scholar] [CrossRef]
- Abah, O.; Roßnagel, J.; Deffner, S.; Schmidth-Kaler, F.; Singer, K.; Lutz, E. Single-Ion Heat Engine at Maximum Power. Phys. Rev. Lett. 2012, 109, 2033006. [Google Scholar] [CrossRef] [PubMed]
- Mani, R.G.; Smet, J.H.; von Klitzing, K.; Narayanamurti, V.; Johnson, W.B.; Umansky, V. Zero-resistance states induced by electromagnetic-wave excitation in GaAs/AlGaAs heterostructures. Nature 2002, 420, 646–650. [Google Scholar] [CrossRef] [PubMed]
- Prance, J.R.; Smith, C.G.; Griffiths, J.P.; Chorley, S.J.; Anderson, D.; Jones, G.A.C.; Farrer, I.; Ritchie, D.A. Electronic Refrigeration of a Two-Dimensional Electron Gas. Phys. Rev. Lett. 2009, 102, 146602. [Google Scholar] [CrossRef] [PubMed]
- Hübel, A.; Held, K.; Weis, J.; Klitzing, K.V. Correlated electron tunneling through two separate quantum dot systems with strong capacitive interdot coupling. Phys. Rev. Lett. 2008, 101, 186804. [Google Scholar] [CrossRef] [PubMed]
- Hübel, A.; Weis, J.; Dietsche, W.; Klitzing, K.V. Two laterally arranged quantum dot systems with strong capacitive interdot coupling. Appl. Phys. Lett. 2007, 91, 102101. [Google Scholar] [CrossRef]
- Donsa, S.; Andergassen, S.; Held, K. Double quantum dot as a minimal thermoelectric generator. Phys. Rev. B 2014, 89, 125103. [Google Scholar] [CrossRef]
- Muñoz, E.; Peña, F.J.; González, A. Magnetically-Driven Quantum Heat Engines: The Quasi-Static Limit of Their Efficiency. Entropy 2016, 18, 173. [Google Scholar] [CrossRef]
- Muñoz, E.; Peña, F.J. Magnetically driven quantum heat engine. Phys. Rev. E 2014, 89, 052107. [Google Scholar] [CrossRef] [PubMed]
- Peña, F.J.; Muñoz, E. Magnetostrain-driven quantum heat engine on a graphene flake. Phys. Rev. E 2015, 91, 052152. [Google Scholar] [CrossRef] [PubMed]
- Kumar, J.; Sreeram, P.A.; Dattagupta, S. Low-temperature thermodynamics in the context of dissipative diamagnetism. Phys. Rev. E 2009, 79, 021130. [Google Scholar] [CrossRef] [PubMed]
- Jacak, L.; Hawrylak, P.; W’ojs, A. Quantum Dots; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Muñoz, E.; Barticevic, Z.; Pacheco, M. Electronic spectrum of a two-dimensional quantum dot array in the presence of electric and magnetic fields in the Hall configuration. Phys. Rev. B 2005, 71, 165301. [Google Scholar] [CrossRef]
- Reis, M.S. Oscillating magnetocaloric effect. Appl. Phys. Lett. 2011, 99, 052511. [Google Scholar] [CrossRef]
- Grujić, M.; Zarenia, M.; Chaves, A.; Tadić, M.; Farias, G.A.; Peeters, F.M. Electronic and optical properties of a circular graphene quantum dot in a magnetic field: Influence of the boundary conditions. Phys. Rev. B 2011, 84, 205441. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Negrete, O.A.; Peña, F.J.; Florez, J.M.; Vargas, P. Magnetocaloric Effect in Non-Interactive Electron Systems: “The Landau Problem” and Its Extension to Quantum Dots. Entropy 2018, 20, 557. https://doi.org/10.3390/e20080557
Negrete OA, Peña FJ, Florez JM, Vargas P. Magnetocaloric Effect in Non-Interactive Electron Systems: “The Landau Problem” and Its Extension to Quantum Dots. Entropy. 2018; 20(8):557. https://doi.org/10.3390/e20080557
Chicago/Turabian StyleNegrete, Oscar A., Francisco J. Peña, Juan M. Florez, and Patricio Vargas. 2018. "Magnetocaloric Effect in Non-Interactive Electron Systems: “The Landau Problem” and Its Extension to Quantum Dots" Entropy 20, no. 8: 557. https://doi.org/10.3390/e20080557
APA StyleNegrete, O. A., Peña, F. J., Florez, J. M., & Vargas, P. (2018). Magnetocaloric Effect in Non-Interactive Electron Systems: “The Landau Problem” and Its Extension to Quantum Dots. Entropy, 20(8), 557. https://doi.org/10.3390/e20080557







