Multivariate Multiscale Complexity Analysis of Self-Reproducing Chaotic Systems
Abstract
1. Introduction
2. Designing the Complexity Measuring Algorithms
2.1. Data Processing and Quantification
- Step 1:
- Normalization of time series. For given time series , where d is the number of time series or the dimension of the chaotic system. Since amplitudes of different time series are different, normalization processing is necessary. The normalization function is given by:
- Step 2:
- Coarse graining. To design multiscale complexity measuring algorithms, the multiscale coarse-grained processing should be carried out firstly. For the j-th time series, its consecutive coarse-grained time series is constructed by [23]:where and is the scale factor that represents the length of the non-overlapping windows.
- Step 3:
- Data quantification. For the given k and scale factor , [, , ⋯, ] can be modeled as a pattern by introducing the idea of the Bandt–Pompe pattern [26]. Obviously, there are possible patterns. Let the pattern space be given by , and thus, a pattern series can be obtained. Moreover, let ; we can get a quantification pattern series, which is given by .
2.2. Complexity Measuring Algorithms
2.2.1. Multiscale Multivariate Permutation Entropy
2.2.2. Multiscale Multivariate Lempel–Ziv Complexity
- Step 1:
- Suppose that the quantification pattern series is . Let S and Q be two character strings.
- Step 2:
- For the step n , let , and or , then we get:or:Define:or:If there exist an and the following relationship is satisfied:it means that Q is a duplicate of . Then, the size of Q should increase by one, and the above operation is carried out again until . When Q does not belong to , we call Q an “insertion”. When an “insertion” is found, we place a “·” behind S. Repeat the above operations until .
- Step 3:
- In Step 2, we obtained a series of dots; thus, we can calculate the number of dots and denote the complexity as .
- Step 4:
- According to [27], Lempel–Ziv complexity will reach a stable value, which is given by:where is the stable complexity measure value of a finite long time series. Thus, the normalized multiscale multivariate Lempel–Ziv complexity is defined as:
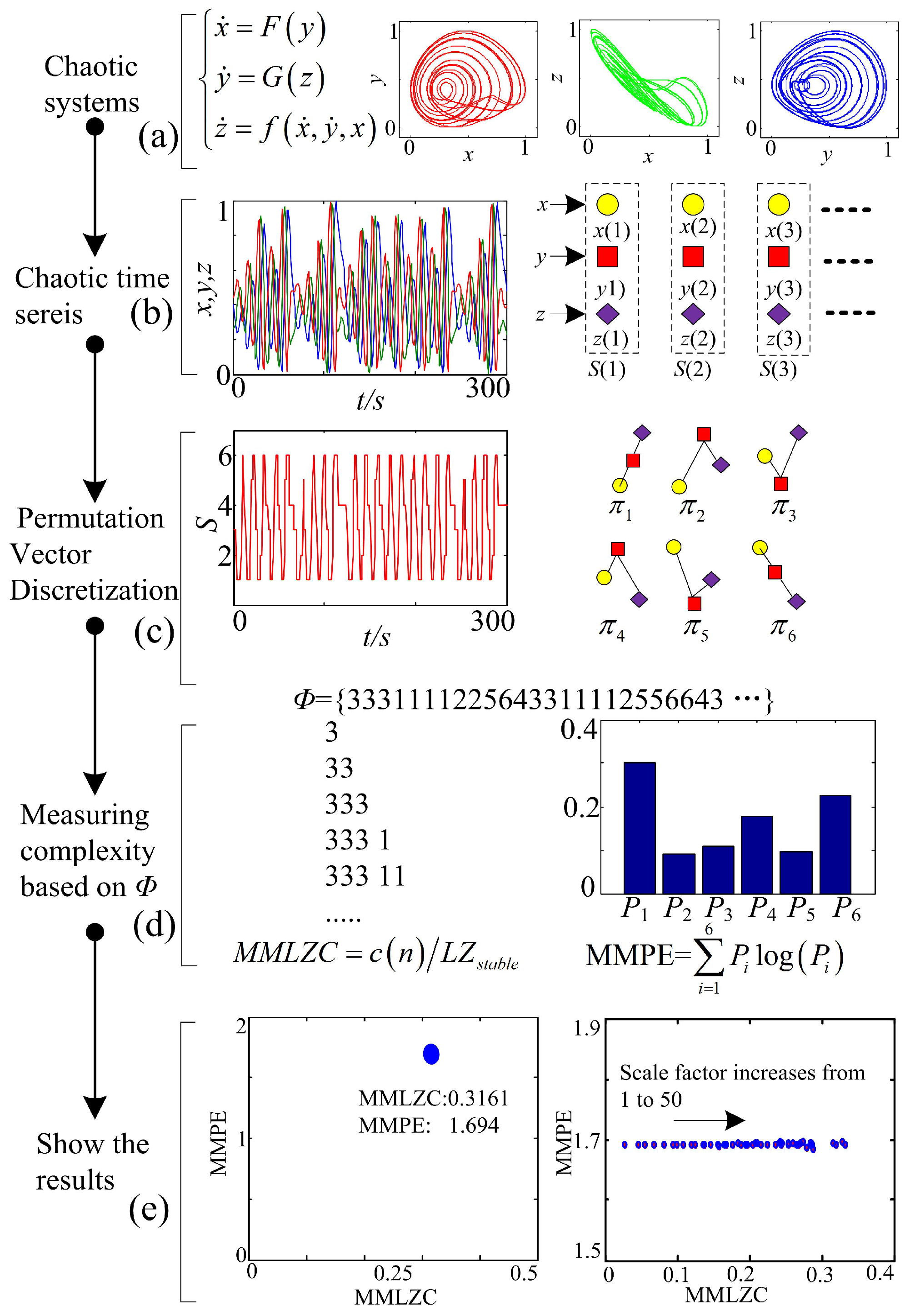
2.2.3. Process for Complexity Measuring
- Step 1:
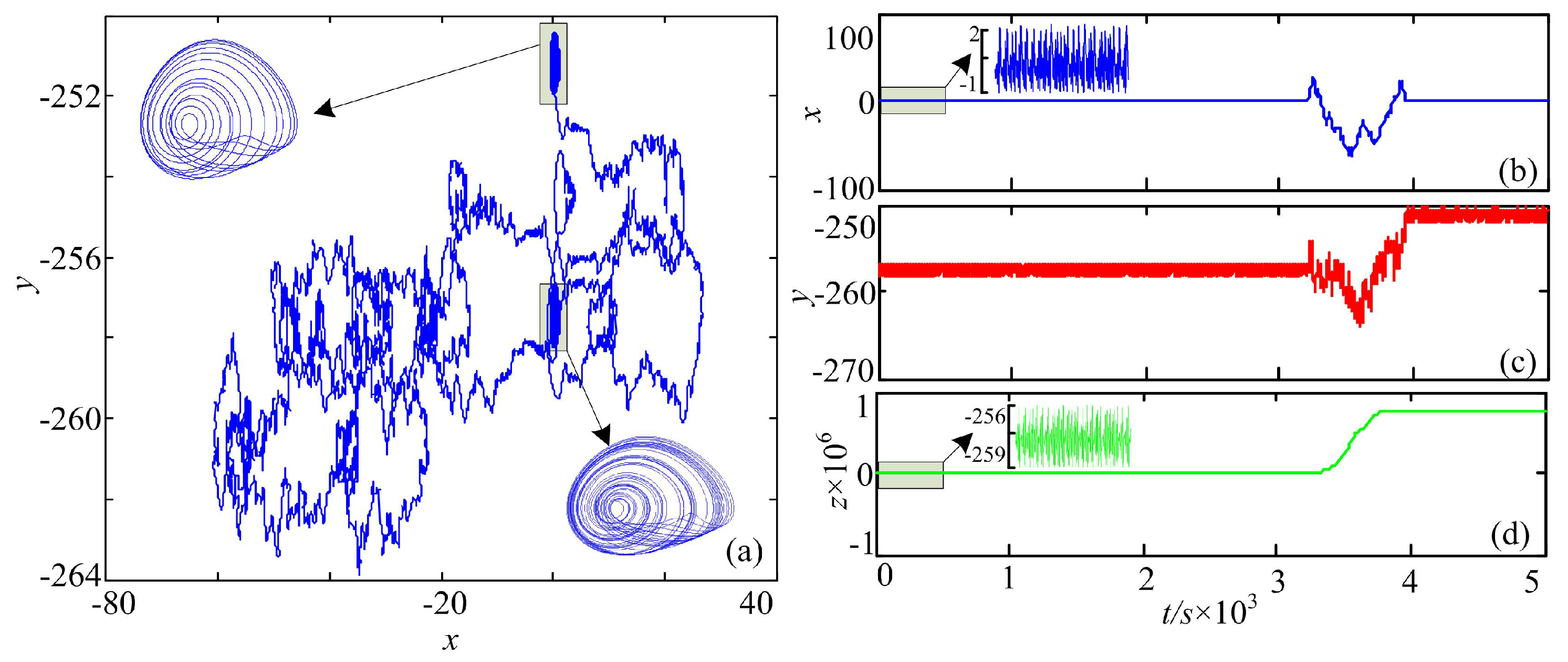
- Figure 1a. Solve the chaotic system and observe the state of the system based on the phase diagrams, preliminarily.
- Step 2:
- Figure 1b. Cut three segments of chaotic time series, which are the three state variables of the 3D chaotic system. Data processing and coarse graining are carried out by employing the method given in the Section 2.1.
- Step 3:
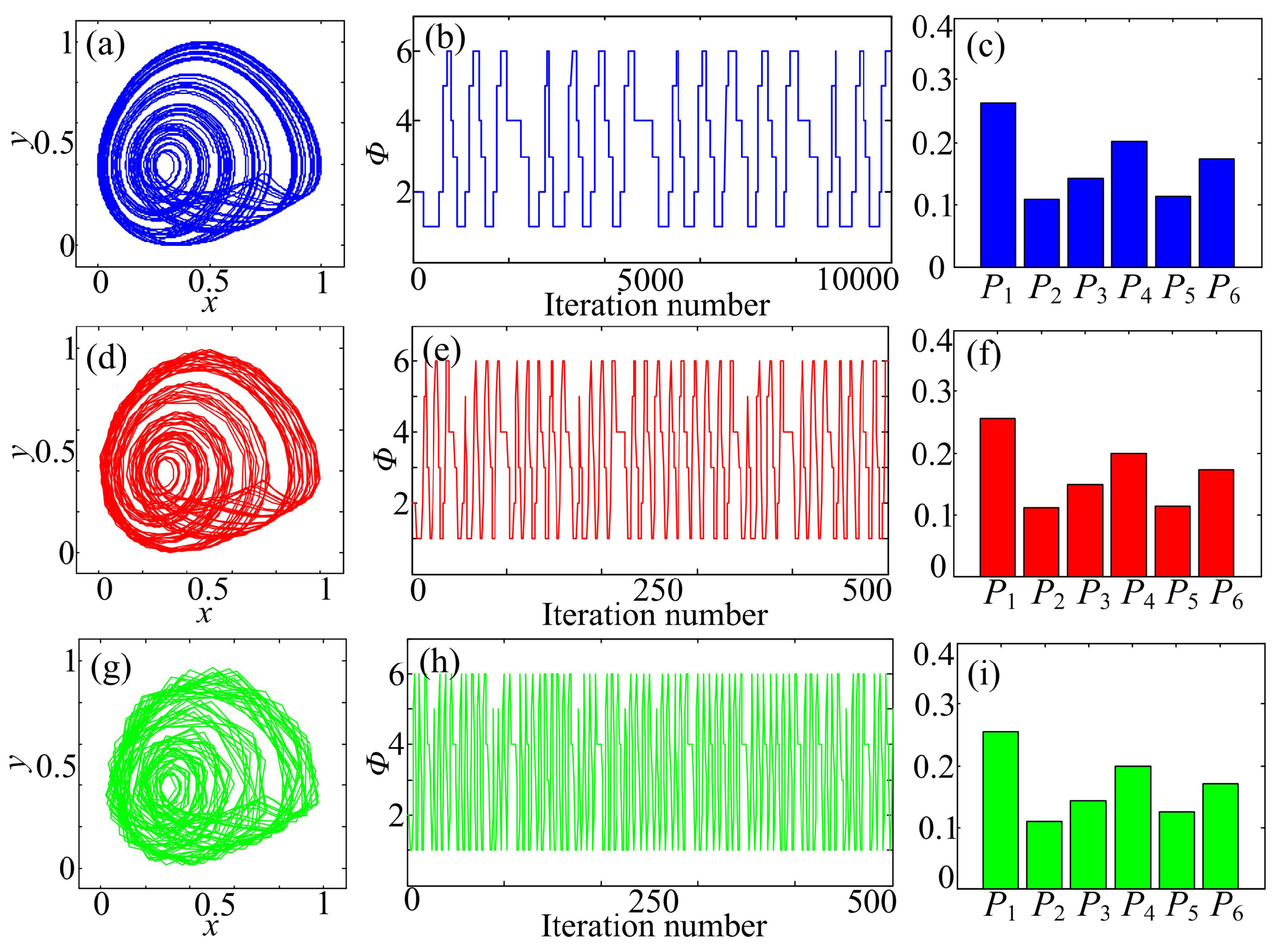
- Figure 1c. Quantize the scaled time series using the Bandt–Pompe approach; thus, a symbol time series is obtained.
- Step 4:
- Figure 1d. Estimate the MMLZC and MMPE according to the obtained sequence, where the steps of MMPE and MMLZC are shown in Section 2.2.1 and Section 2.2.2, respectively.
- Step 5:
- Figure 1e. Illustrate the complexity measuring results with different figures. Here, the two measures are shown in the MMPLC-MMPE plane.Note that we also illustrate the complexity with MMLZC and MMPE as shown by the curve and surfaces for comparison.
3. Complexity Analysis of Self-Reproducing Chaotic Systems
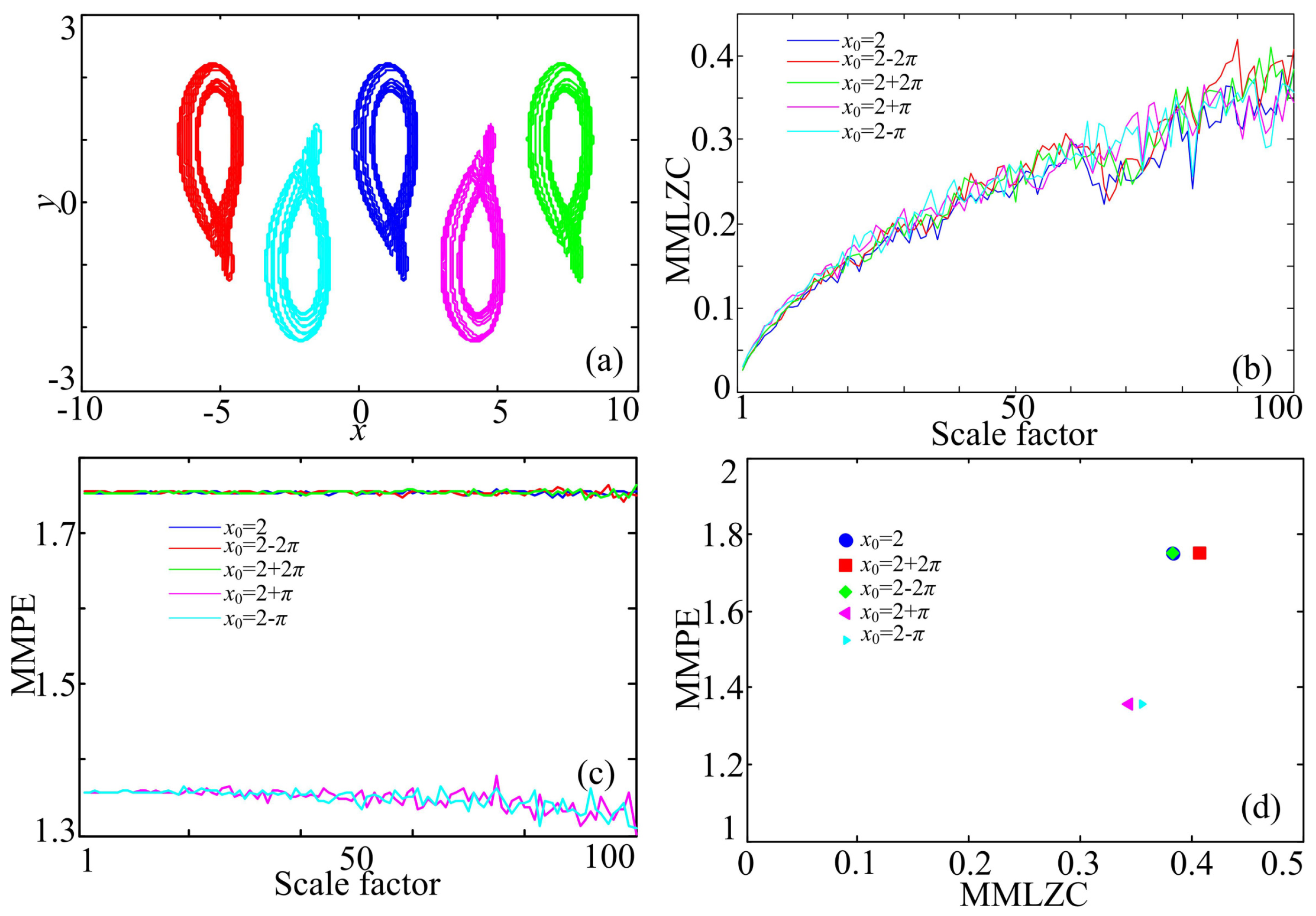
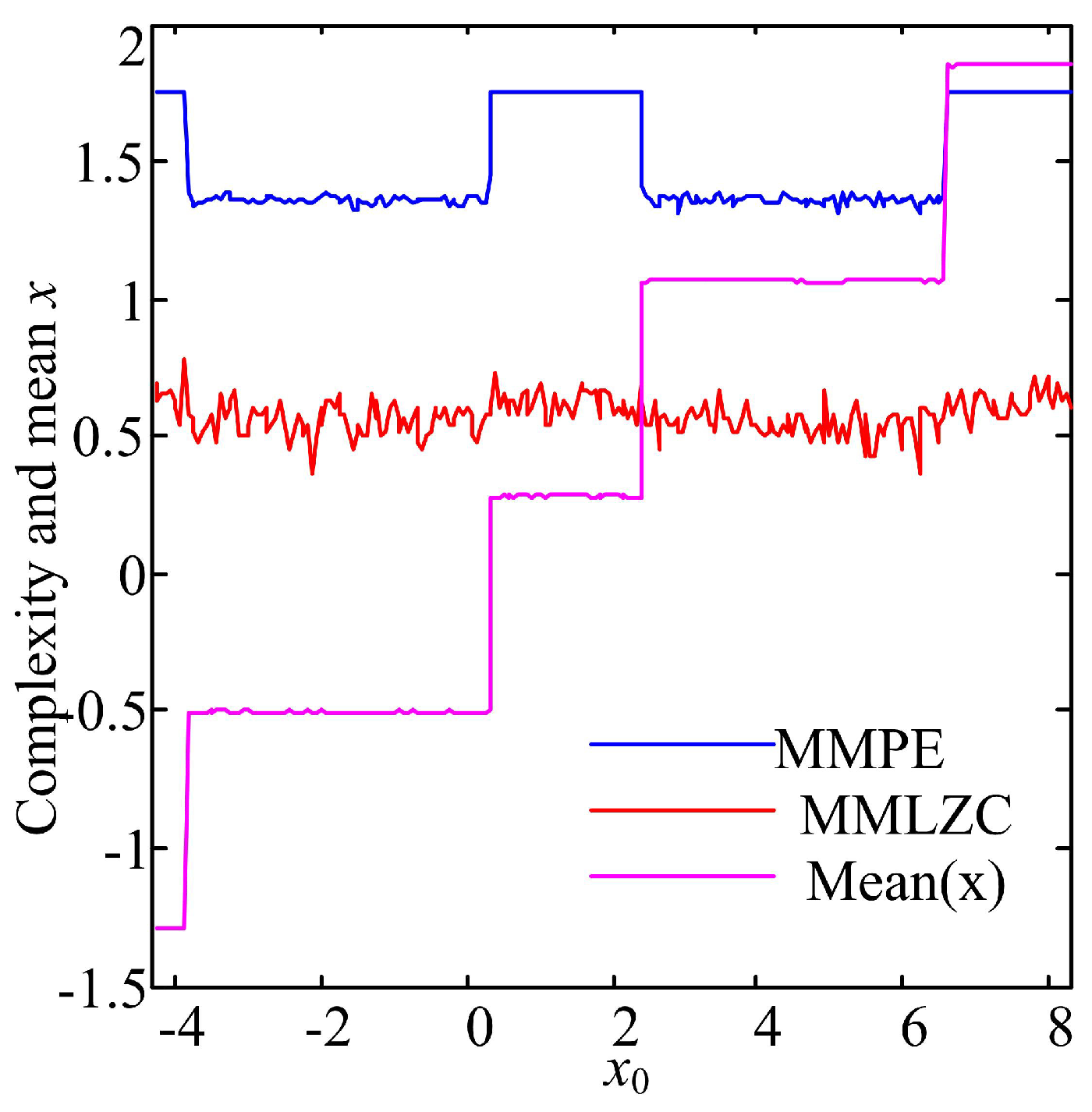
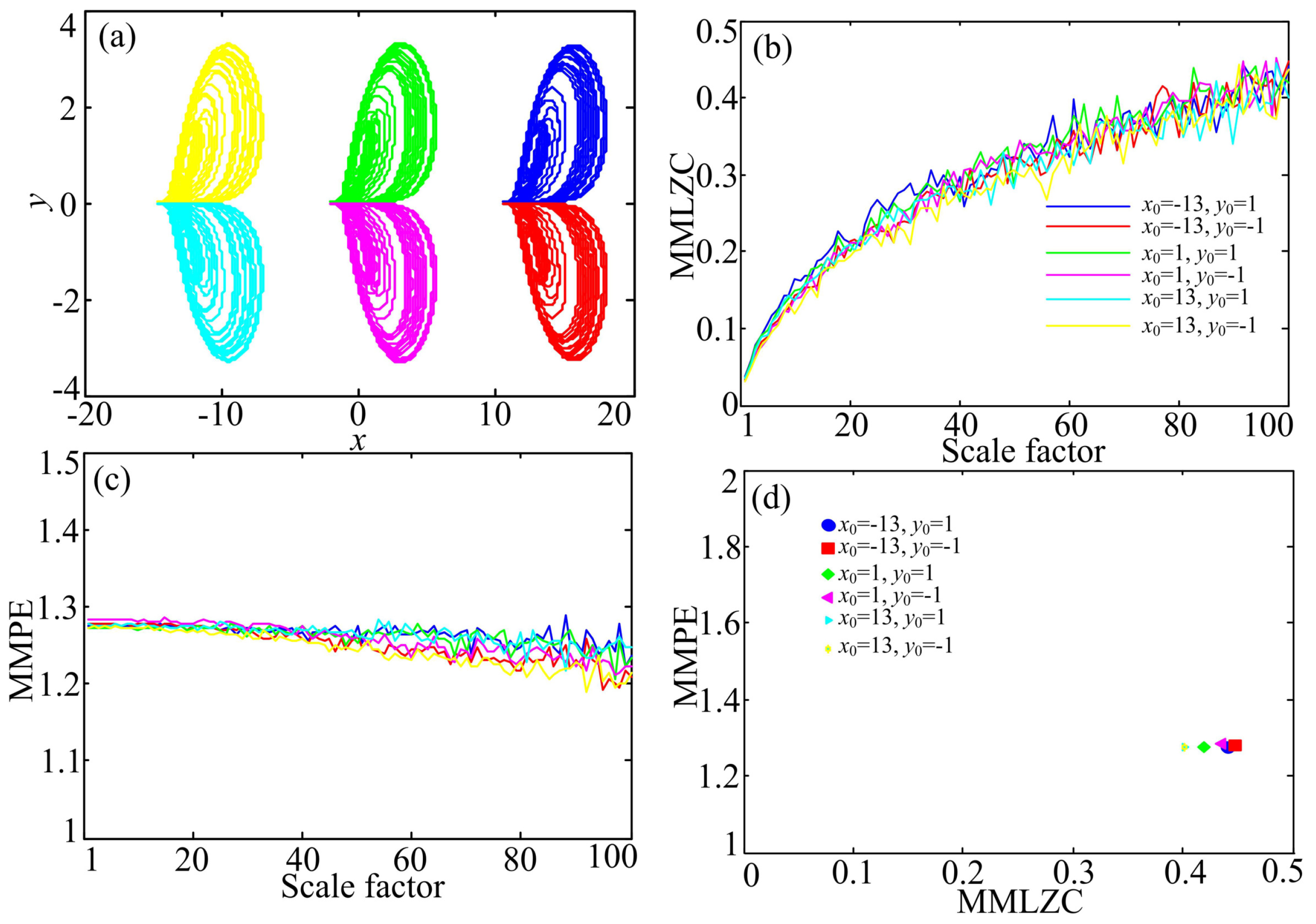
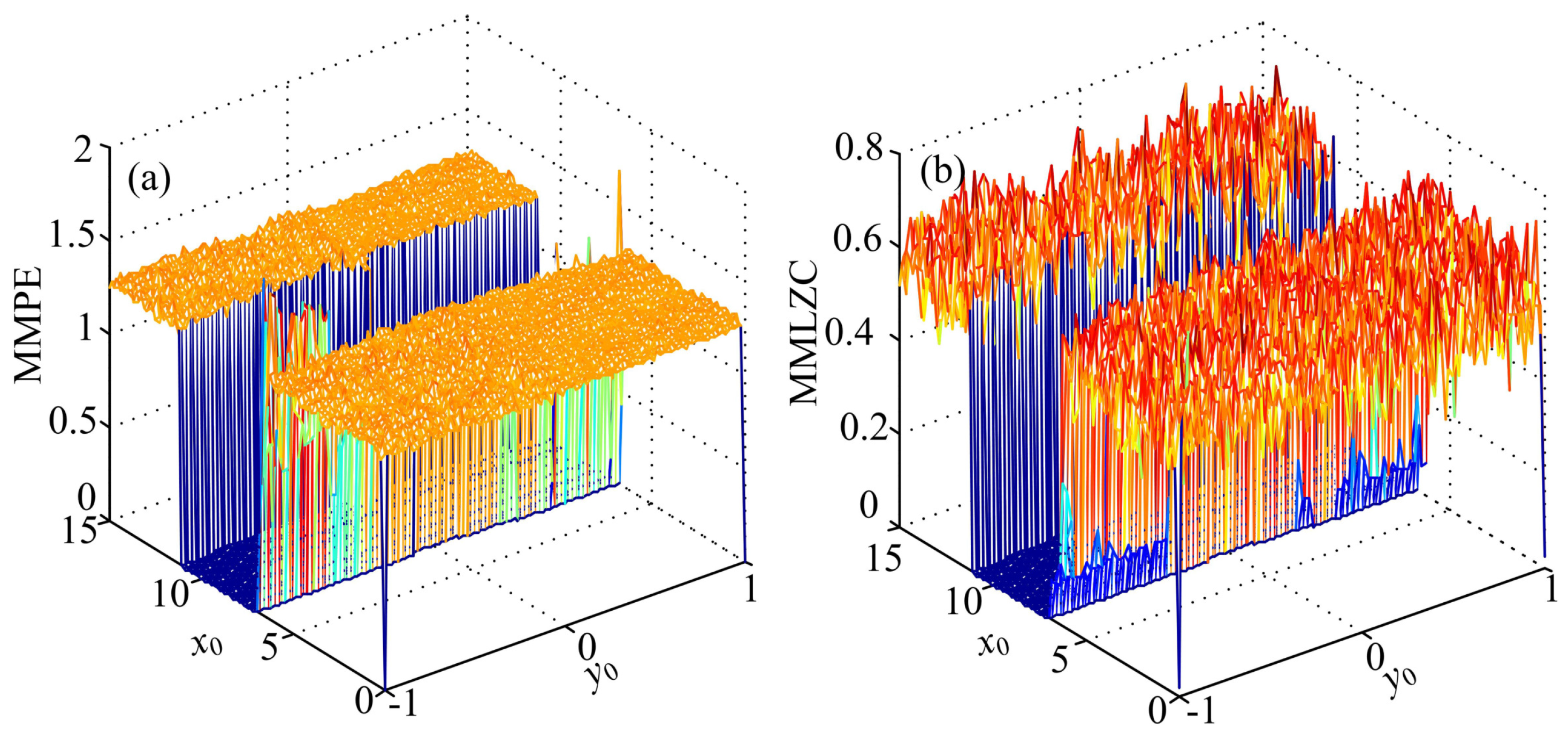
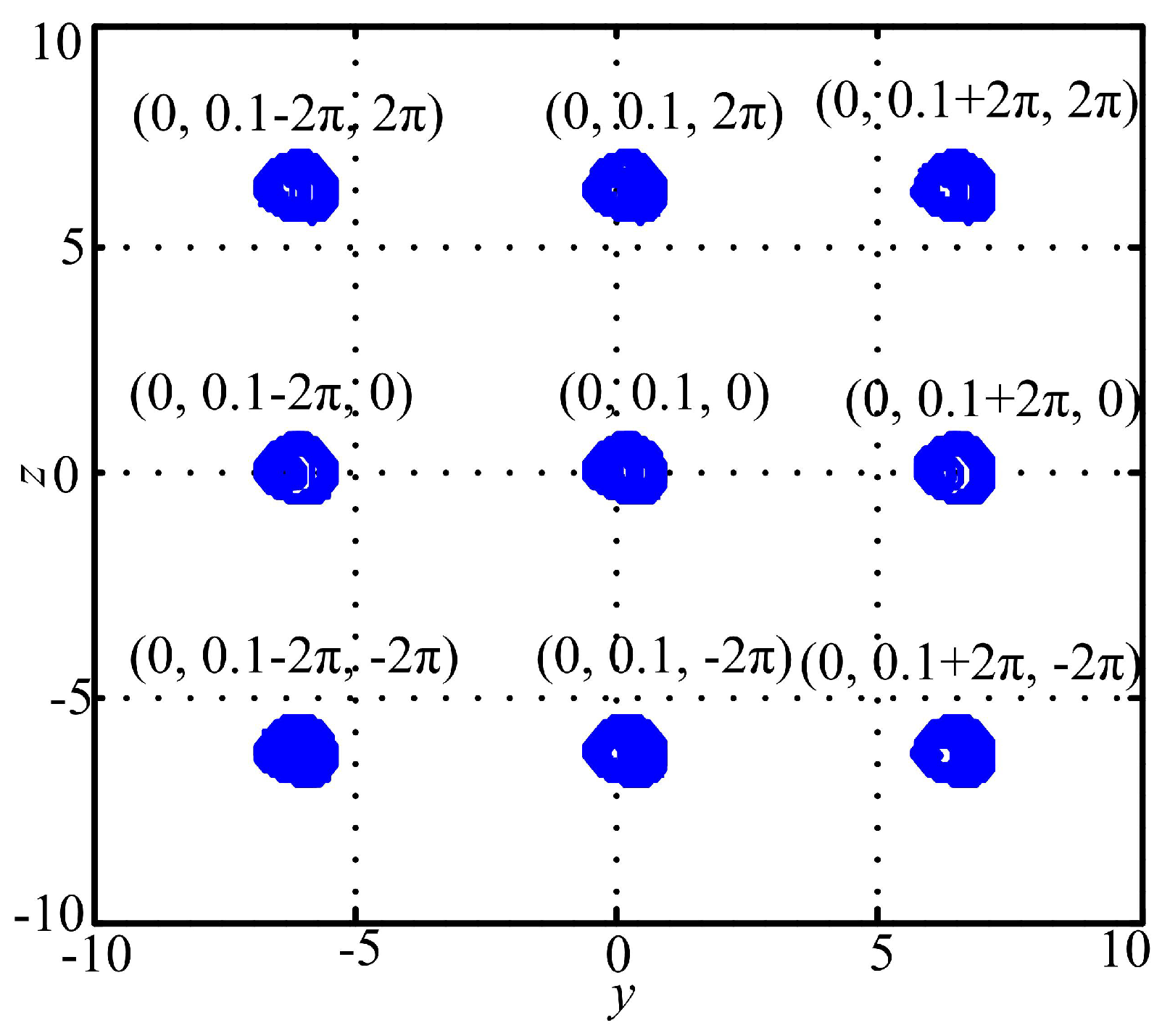
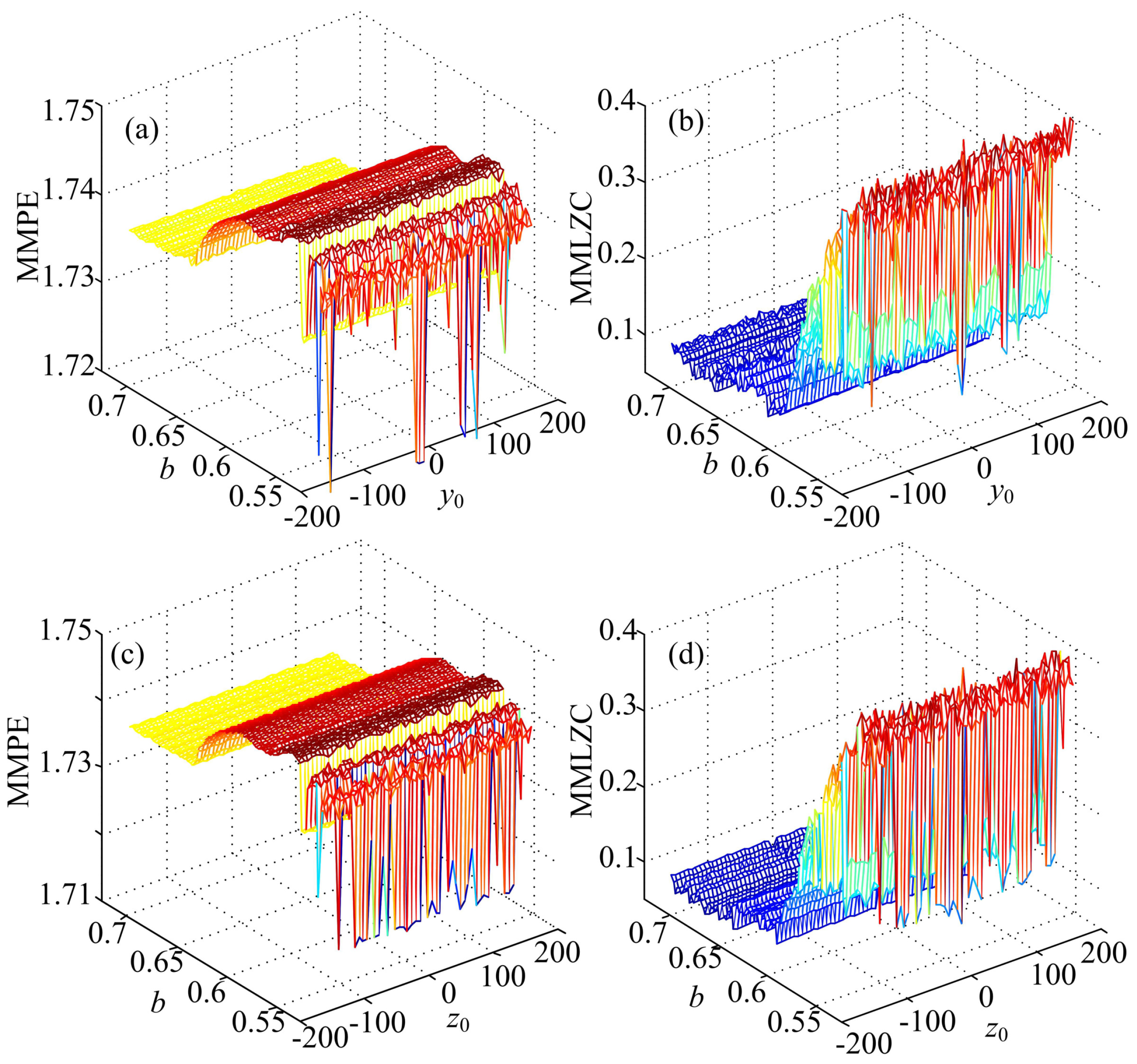
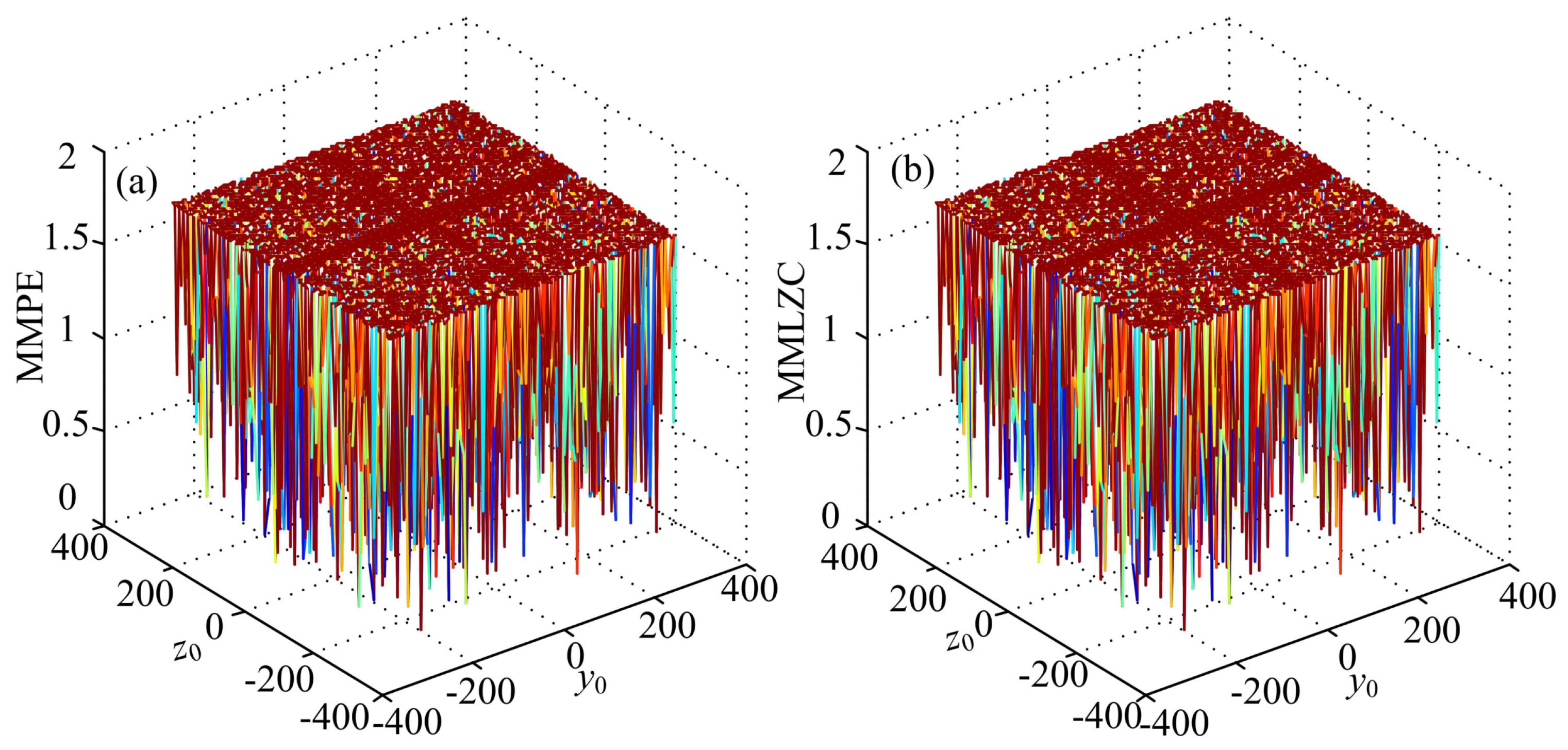
3.1. Case A: One-Directional Self-Reproducing System
3.2. Case B: Two-Directional Self-Reproducing System
4. Discussion
4.1. Comparison with the Corresponding Original Systems
4.2. Comparison of MMPE and MMLZC
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Feudel, U.; Kraut, S. Complex dynamics in multistable systems. Int. J. Bifur. Chaos 2008, 18, 1607–1626. [Google Scholar] [CrossRef]
- Singh, J.P.; Roy, B.K. Multistability and hidden chaotic attractors in a new simple 4-D chaotic system with chaotic 2-torus behaviour. Int. J. Dyn. Control 2017, 6, 529–538. [Google Scholar] [CrossRef]
- Li, C.B.; Hu, W.; Sprott, J.C.; Wang, X. Multistability in symmetric chaotic systems. Eur. Phys. J. Spec. Top. 2015, 224, 1493–1506. [Google Scholar] [CrossRef]
- Liu, Y.; Chávez, J.P. Controlling multistability in a vibro-impact capsule system. Nonlinear Dyn. 2017, 88, 1289–1304. [Google Scholar] [CrossRef]
- Zhusubaliyev, Z.T.; Mosekilde, E.; Rubanov, V.G.; Nabokov, R.A. Multistability and hidden attractors in a relay system with hysteresis. Phys. D 2015, 306, 6–15. [Google Scholar] [CrossRef]
- Bao, B.C.; Li, Q.D.; Wang, N.; Xu, Q. Multistability in Chua’s circuit with two stable node-foci. Chaos 2016, 26, 043111. [Google Scholar] [CrossRef] [PubMed]
- Hu, A.; Xu, Z. Multi-stable chaotic attractors in generalized synchronization. Commun. Nonl. Sci. Num. Simul. 2011, 16, 3237–3244. [Google Scholar] [CrossRef]
- Peng, G.; Min, F. Multistability analysis, circuit implementations and application in image encryption of a novel memristive chaotic circuit. Nonlinear Dyn. 2017, 90, 1607–1625. [Google Scholar] [CrossRef]
- Shih, C.W. Multistability in recurrent neural networks. SIAM J. Appl. Math. 2006, 66, 1301–1320. [Google Scholar]
- Lai, Q.; Chen, S. Research on a new 3D autonomous chaotic system with coexisting attractors. Optik 2016, 127, 3000–3004. [Google Scholar] [CrossRef]
- Li, C.B.; Sprott, J.C.; Hu, W.; Xu, Y. Infinite multistability in a self-reproducing chaotic system. Int. J. Bifur. Chaos 2017, 27, 1750160. [Google Scholar] [CrossRef]
- Li, C.B.; Sprott, J.C.; Mei, Y. An infinite 2-D lattice of strange attractors. Nonlinear Dyn. 2017, 89, 2629–2639. [Google Scholar] [CrossRef]
- Kreinovich, V.; Kunin, I.A. Kolmogorov complexity and chaotic phenomena. Int. J. Eng. Sci. 2003, 41, 483–493. [Google Scholar] [CrossRef]
- Micco, L.D.; Fernández, J.G.; Larrondo, H.A.; Plastino, A.; Rosso, O.A. Sampling period, statistical complexity, and chaotic attractors. Phys. A 2012, 391, 2564–2575. [Google Scholar] [CrossRef]
- Balasubramanian, K.; Nair, S.S.; Nagaraj, N. Classification of periodic, chaotic and random sequences using approximate entropy and Lempel–Ziv complexity measures. Pramana 2015, 84, 365–372. [Google Scholar] [CrossRef]
- Makark, S.A.; Starodubov, A.V.; Kalinin, Y.A. Application of permutation entropy method in the analysis of chaotic, noisy, and chaotic noisy series. Tech. Phys. 2017, 62, 1714–1719. [Google Scholar] [CrossRef]
- He, S.B.; Sun, K.H.; Wang, H.H. Complexity Analysis and DSP Implementation of the Fractional-Order Lorenz Hyperchaotic System. Entropy 2015, 17, 8299–8311. [Google Scholar] [CrossRef]
- He, S.B.; Sun, K.H.; Wang, H.H. Modified multiscale permutation entropy algorithm and its application for multiscroll chaotic systems. Complexity 2016, 21, 52–58. [Google Scholar]
- Mukherjee, S.; Palit, S.K.; Banerjee, S.; Ariffin, M.R.K.; Rondoni, L.; Bhattacharya, D.K. Can complexity decrease in congestive heart failure? Phys. A 2015, 439, 93–102. [Google Scholar] [CrossRef]
- Ahmed, M.U.; Mandic, D.P. Multivariate multiscale entropy: A tool for complexity analysis of multichannel data. Phys. Rev. E 2011, 84, 061918. [Google Scholar] [CrossRef] [PubMed]
- Richman, J.S. Multivariate neighborhood sample entropy: A method for data reduction and prediction of complex data. Meth. Enzymol. 2011, 487, 397–408. [Google Scholar] [PubMed]
- He, S.B.; Sun, K.; Wang, H. Multivariate permutation entropy and its application for complexity analysis of chaotic systems. Phys. A 2016, 461, 812–823. [Google Scholar] [CrossRef]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale entropy analysis of biological signals. Phys. Rev. E 2005, 71, 021906. [Google Scholar] [CrossRef] [PubMed]
- Humeauheurtier, A. The Multiscale entropy algorithm and its variants: A review. Entropy 2015, 17, 3110–3123. [Google Scholar] [CrossRef]
- Yu, S.N.; Lee, M.Y. Wavelet-Based Multiscale Sample Entropy and Chaotic Features for Congestive Heart Failure Recognition Using Heart Rate Variability. J. Med. Biol. Eng. 2015, 35, 338–347. [Google Scholar] [CrossRef]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef] [PubMed]
- Lempel, A.; Ziv, J. On the complexity of finite sequences. IEEE Trans. Inform. Theory 1976, 22, 75–81. [Google Scholar] [CrossRef]
- Zozor, S.; Mateos, D.; Lamberti, P.W. Mixing Bandt-Pompe and Lempel–Ziv approaches: Another way to analyze the complexity of continuous-state sequences. Eur. Phys. J. B 2014, 87, 107. [Google Scholar] [CrossRef]
- Hong, H.; Liang, M. Fault severity assessment for rolling element bearings using the Lempel–Ziv complexity and continuous wavelet transform. J. Sound Vib. 2009, 320, 452–468. [Google Scholar] [CrossRef]
- Li, C.B.; Sprott, J.C.; Xing, H. Crisis in amplitude control hides in multistability. Inter. J. Bifur. Chaos 2017, 26, 1650233. [Google Scholar] [CrossRef]
- Li, C.B.; Sprott, J.C.; Xing, H. Constructing chaotic systems with conditional symmetry. Nonlinear Dyn. 2016, 87, 1351–1358. [Google Scholar] [CrossRef]
- Kengne, J.; Njitacke, Z.T.; Fotsin, H.B. Dynamical analysis of a simple autonomous jerk system with multiple attractors. Nonlinear Dyn. 2016, 83, 751–765. [Google Scholar] [CrossRef]
| (Original, New) | MMPE | MMLZC | |
|---|---|---|---|
| (Sys(16), Sys(13)) | (0.0363, 0.0285) | (1.3805, 1.5579) | (0.5402, 0.5376) |
| (Sys(17), Sys(14)) | (0.1149, 0.1101) | (1.1610, 1.2657) | (0.5402, 0.5907) |
| (Sys(18), Sys(15)) | (0.0938, 0.0890) | (1.7435, 1.7414) | (0.6483, 0.6976) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, S.; Li, C.; Sun, K.; Jafari, S. Multivariate Multiscale Complexity Analysis of Self-Reproducing Chaotic Systems. Entropy 2018, 20, 556. https://doi.org/10.3390/e20080556
He S, Li C, Sun K, Jafari S. Multivariate Multiscale Complexity Analysis of Self-Reproducing Chaotic Systems. Entropy. 2018; 20(8):556. https://doi.org/10.3390/e20080556
Chicago/Turabian StyleHe, Shaobo, Chunbiao Li, Kehui Sun, and Sajad Jafari. 2018. "Multivariate Multiscale Complexity Analysis of Self-Reproducing Chaotic Systems" Entropy 20, no. 8: 556. https://doi.org/10.3390/e20080556
APA StyleHe, S., Li, C., Sun, K., & Jafari, S. (2018). Multivariate Multiscale Complexity Analysis of Self-Reproducing Chaotic Systems. Entropy, 20(8), 556. https://doi.org/10.3390/e20080556






