2.1. Introductory Example
Suppose two players play the following bimatrix game:
Let us consider the case that Players 1 and 2 are not aware of the third strategy of their opponent. That is, Player 1 views the game in the form
whereas Player 2 perceives that the game is of the form
Further, suppose that each player finds that their third strategy is hidden from the opponent. In other words, each player finds that the other player is considering the following game:
Moreover, the higher order views (for example, the view
that Player 1 finds that Player 2 finds that Player 1 is considering) are associated with Equation (
4), i.e.,
for
.
The problem presented above is an example of a strategic-form game with unawareness that can be formally described by a family of games
where
. The set
(with typical element
v) consists of the relevant views. The view
corresponds to the modeler’s game—the actual game played by the players. In our example, this is the game in Equation (
1).
A basic solution concept is a Nash equilibrium (see Definition 2). One can check that the game in Equation (
1) has the unique equilibrium payoff profile
generated, for example, by the strategy profile
. Although both players are aware of their own strategies, they are not aware of the whole game in Equation (
1), and, apart from that, they perceive the game seen by the other player in different ways. Thus, it is not evident that the game ends with outcome (2, 2). Since Player 1 finds that Player 2 perceives the game in Equation (
4), she may deduce that Player 2 plays according to the unique Nash equilibrium
of Equation (
4). Therefore, Player 1’s best reply to
is
as she perceives Equation (
2).
In the same manner, Player 2 deduces that Player 1 plays the equilibrium strategy
in Equation (
4). Since Player 2 views the game in Equation (
3), his best reply to
is
. As a result, the strategy profile
with the worst possible payoffs for the players is predicted to be a reasonable outcome in the game
described by Equations (
1)–(
4).
The game result
can be directly determined by the extended Nash equilibrium [
17]—a counterpart of the notion of Nash equilibrium in games with unawareness. The formal definition is presented in
Section 2.3. Here, we simply provide the result of applying the extended Nash equilibrium to Equations (
1)–(
4). The unique equilibrium is a family of strategy profiles
defined as follows:
The profiles in Equation (
5) coincide with the reasoning we already used to determine the outcome
. The result of the game corresponds to the modeler’s view
. The result
seen from Player 1’s point of view corresponds to the view
. Player 2 predicts the outcome
corresponding to the view
.
2.2. Strategic-Form Games with Unawareness
Let be a strategic form game. This is the game considered by the modeler. Each player may not be aware of the full description of G. Hence, denotes Player ’s view of the game for . That is, the Player views the set of players, the sets of players’ strategies, and the payoff functions as , and , respectively. In general, each player also considers how each of the other players views the game. Formally, with a finite sequence of players , there is associated a game . This is the game that Player considers that Player considers that …Player is considering. A sequence v is called a view. The empty sequence is assumed to be the modeler’s view, i.e., . We denote an action profile in , where by . The concatenation of two views followed by is defined to be . The set of all potential views is where and .
Definition 1. A collection where is a collection of finite sequences of players is called a strategic-form game with unawareness and the collection of views is called its set of relevant views if the following properties are satisfied:
- 1.
- 2.
- 3.
If , then - 4.
For every strategy profile , there exists a completion to a strategy profile such that
The first condition says what views are, in fact, relevant. If, for example, the set of players perceived by Player 1 does not contain, say, Player 3, i.e., , the view what Player 1 thinks that Player 3 is considering is not relevant to strategic position of Player 1. Therefore, .
The second condition, in particular, states that if, Player 1 finds that Player 2 is considering a player or a strategy as a part of the game, he himself considers those elements in the game he perceives.
The third condition requires that if a player finds a game , he also finds that he has that perception, i.e., . More generally, if Player 1 finds that Player 2 finds that Player 1 is considering a given game, then Player 1 is aware that Player 2 knows that he finds that Player 1 is considering that game.
Games corresponding to some views and the modeler’s game may differ with respect to the number of players. Since the payoffs are the result of strategies chosen by all the players, the payoffs in a restricted game (with possibly a smaller number of players) may not be uniquely determined. The fourth condition says that the payoffs in a restricted game are the payoffs in the game with more players by adding some strategy profile of these players. In other words, a restricted game does not contain new payoffs.
2.3. Extended Nash Equilibrium
A basic solution concept for predicting players’ behavior is a Nash equilibrium [
19].
Definition 2. A strategy profile is a Nash equilibrium if for each Player and each strategy of Player iwhere . To define the Nash-type equilibrium for a strategic-form game with unawareness, it is needed to redefine the notion of strategy profile.
Definition 3. Let be a strategic-form game with unawareness. An extended strategy profile (ESP) in this game is a collection of (pure or mixed) strategy profiles , where is a strategy profile in the game such that for every holds To illustrate Equation (
11), let us take the game
—the game that Player 1 thinks that Player 2 is considering. If Player 1 assumes that Player 2 plays strategy
in the game
, she must assume the same strategy in the game
that she considers, i.e.,
. In our introductory example, Player 1 finds that Player 2 is considering strategy
. Thus, Player 1 considers that strategy in her game
while preparing a best reply to that strategy. The next step is to extend rationalizability from strategic-form games to the games with unawareness.
Definition 4. An ESP in a game with unawareness is called extended rationalizable if for every strategy is a best reply to in the game .
Consider a strategic-form game with unawareness . For every relevant view , the relevant views as seen from v are defined to be . Then, the game with unawareness as seen from v is defined by .
We are now in a position to define the Nash equilibrium in the strategic-form games with unawareness.
Definition 5. An ESP in a game with unawareness is called an extended Nash equilibrium (ENE) if it is rationalizable and for all such that we have .
The first part of the definition (rationalizability) is similar to the standard Nash equilibrium, where it is required that each strategy in the equilibrium is a best reply to the other strategies of that profile. According to Definition 4, Player 2’s strategy in the game of Player 1 has to be a best reply to Player 1’s strategy in the game . On the other hand, in contrast to the concept of Nash equilibrium, does not have to a best reply to but to strategy .
We saw in
Section 2.1 that for
we have
. It follows that
. The second part of ENE implies that
. The following proposition [
17] shows that the notion of extended Nash equilibrium coincides with the standard one for strategic-form games when all views share the same perception of the game. It is therefore useful for determining ENE.
Proposition 1. Let G be a strategic-form game and a strategic-form game with unawareness such that, for some , we have for every such that . Let σ be a strategy profile in G. Then,
- 1.
σ is rationalizable for G if and only if is part of an extended rationalizable profile in .
- 2.
σ is a Nash equilibrium for G if and only if is part of on an ENE for and this ENE also satisfies .
Remark 1. We see from Equations (8) and (11) that, for every , a normal-form game and a strategy profile determine the games and profiles in the form and , respectively, for example, determines . Hence, in general, a game with unawareness and an extended strategy profile are defined by and , where Then, we get from by setting for and . For this reason, we often restrict ourselves to throughout the paper.
2.4. The Role of the Notion of Games with Unawareness in Quantum Game Theory
The notion of games with unawareness is designed to model game theory problems in which players’ perceptions of the game are restricted. It was shown in [
17] that the novel structure extends the existing forms of games. Although it is possible to represent games with unawareness with the use of games with incomplete information (by using probability equal to 0 to the situations that a player is not aware of), the extended Nash equilibrium does not map to any known solution concept of incomplete information games. In particular, the set of extended Nash equilibria forms a strict subset of the Bayesian Nash equilibria.
Once we know that games with unawareness is a new game form, it is natural to study that type of games in the quantum domain. Having given a quantum game scheme that maps a classical game G to the quantum one , and having given a family of games , a family of quantum games can be constructed in a natural way. Then, we can study if, and to what extent, quantum strategies compensate restricted perception of players.
Besides
, the notion of game with unawareness allows one to expand the theory of quantum games by defining a family
, where each quantum game
corresponds to a specific perception of players about the quantum game
. In this case players may have restricted perception of how a quantum game is defined. A good example of that quantum game theory problem is the quantum PQ Penny Flip game [
3]: one of the players is aware of having all the quantum strategies, the other player perceives two unitary strategies identified with the classical Penny Flip game. We provide a detail exposition of that problem in [
18].
Another example of applying the notion of games with unawareness concerns the case when playing a quantum game is not common knowledge among the players. The quantum game is to be played with the aid of objects that behave according to the laws of quantum mechanics, in particular, the players may share an entangled two-qubit state on which they apply unitary strategies.
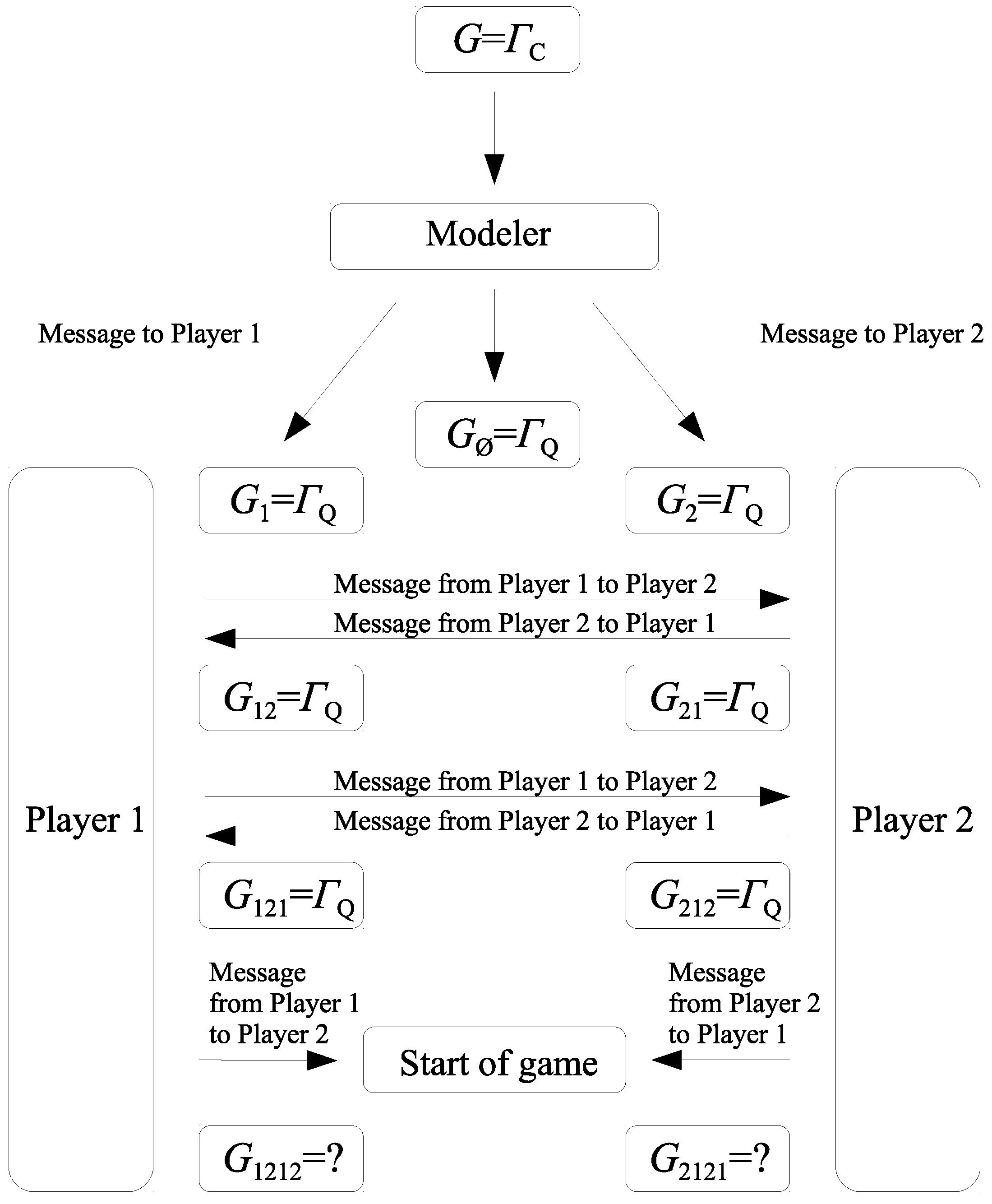
Under this scenario (see
Figure 1), Players 1 and 2 can be far apart, and a third party, say a modeler, is to prepare the game. After the modeler prepares the quantum game based on its classical counterpart, she sends the message to Players 1 and 2 so that they know they are to play the quantum game rather than the classical one. When the players receive the message, each Player
i perceives the game as being quantum, i.e.,
for
. However, this fact is not common knowledge among Players 1 and 2. Recall that a fact is common knowledge among the players of a game if for any finite sequence of players
Player
knows that Player
knows …that Player
knows the fact. In our case, each of the players cannot be certain that the other player finds the quantum game (receives the message from the modeler) until he or she receives a confirmation from that player. According to the scheme in
Figure 1, Players 1 and 2 send a message to each other about their own current state of knowledge. In this way, Player 1 receiving the message from Player 2 finds that Player 2 is considering the quantum game, i.e.,
. Similarly, Player 2 after receiving the message finds that Player 1 is also considering the quantum game, i.e.,
. The players continue to send messages to each other informing about their own knowledge. After receiving the message, Player 1 learns that Player 2 finds that Player 1 is considering the quantum game. As a result, Player 1 perceives the game
as
. In the same manner we can see that the game
that Player 2 finds that Player 1 finds that Player 2 is considering is
.
Two rounds of sending messages are still insufficient to say that
is common knowledge among the players. At the time the game starts, the games
corresponding to higher order views
are still unknown for the players, and either the classical game
or the quantum game
may be associated with
and
. As a result, the players face a game with unawareness described by a family of games
consisting of two types of games:
and
. An example of the game being in line with the scheme in
Figure 1 is a family of games
, where
We show below that whether a quantum game is common knowledge considerably affects the result of game.