Geometry and Entanglement of Two-Qubit States in the Quantum Probabilistic Representation
Abstract
1. Introduction
2. Qubit and Qutrit States in Quantum Geometric Representation
2.1. Qubit Case
2.2. Qutrit Case
3. Separability Properties of the Two-Qubit Composite Systems
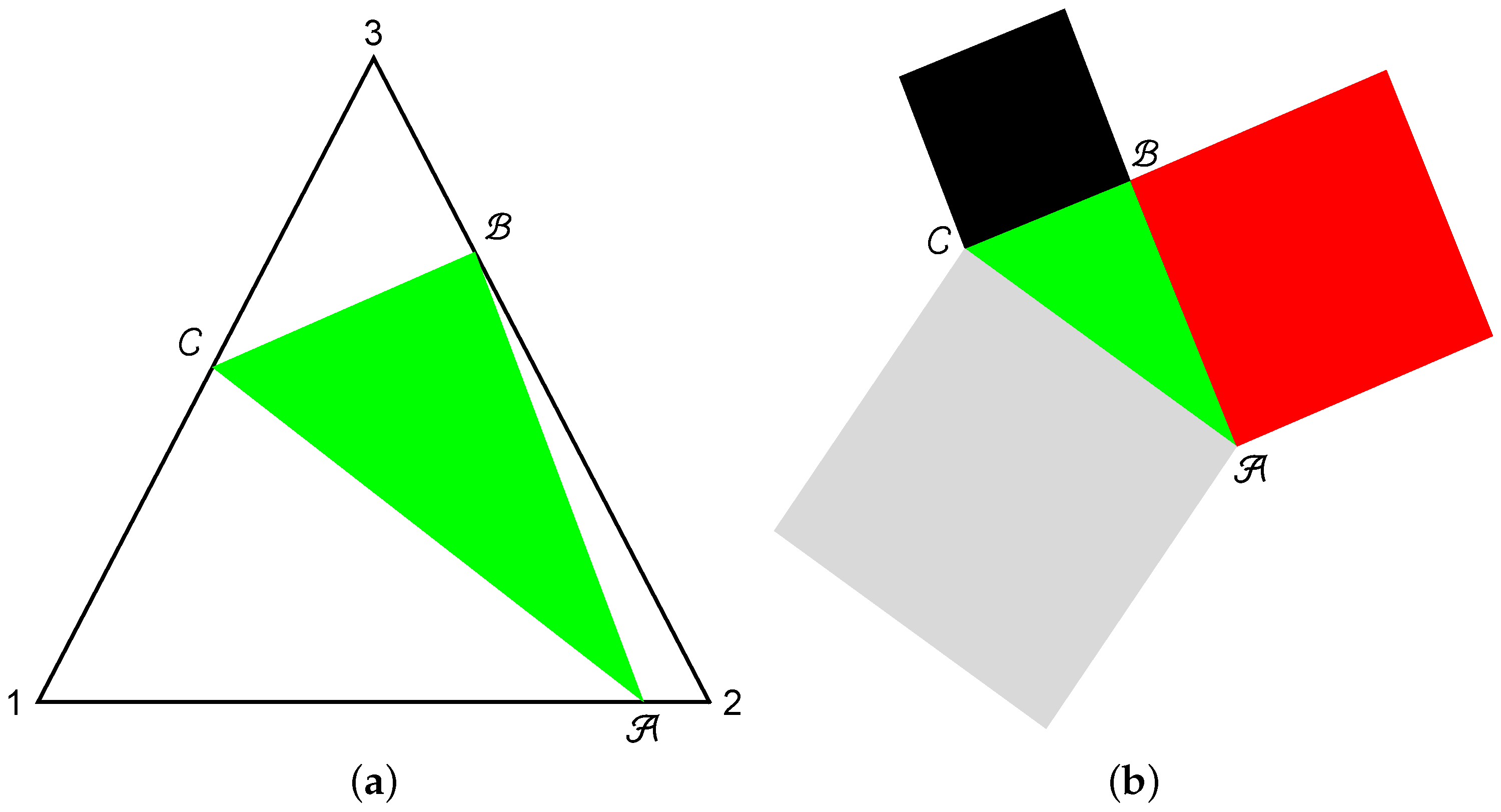
3.1. Two Inaccessible States
3.2. One Inaccessible State
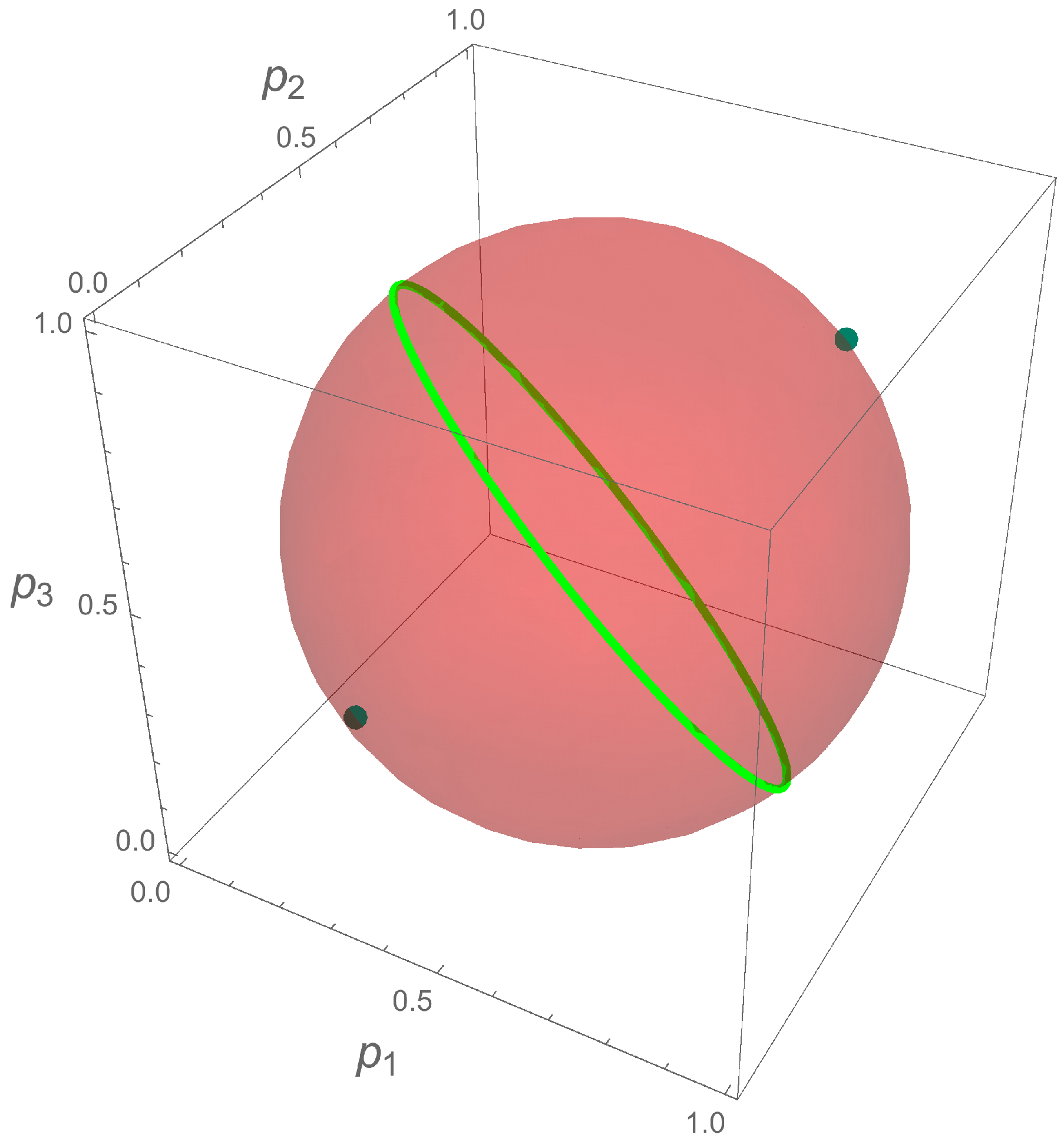
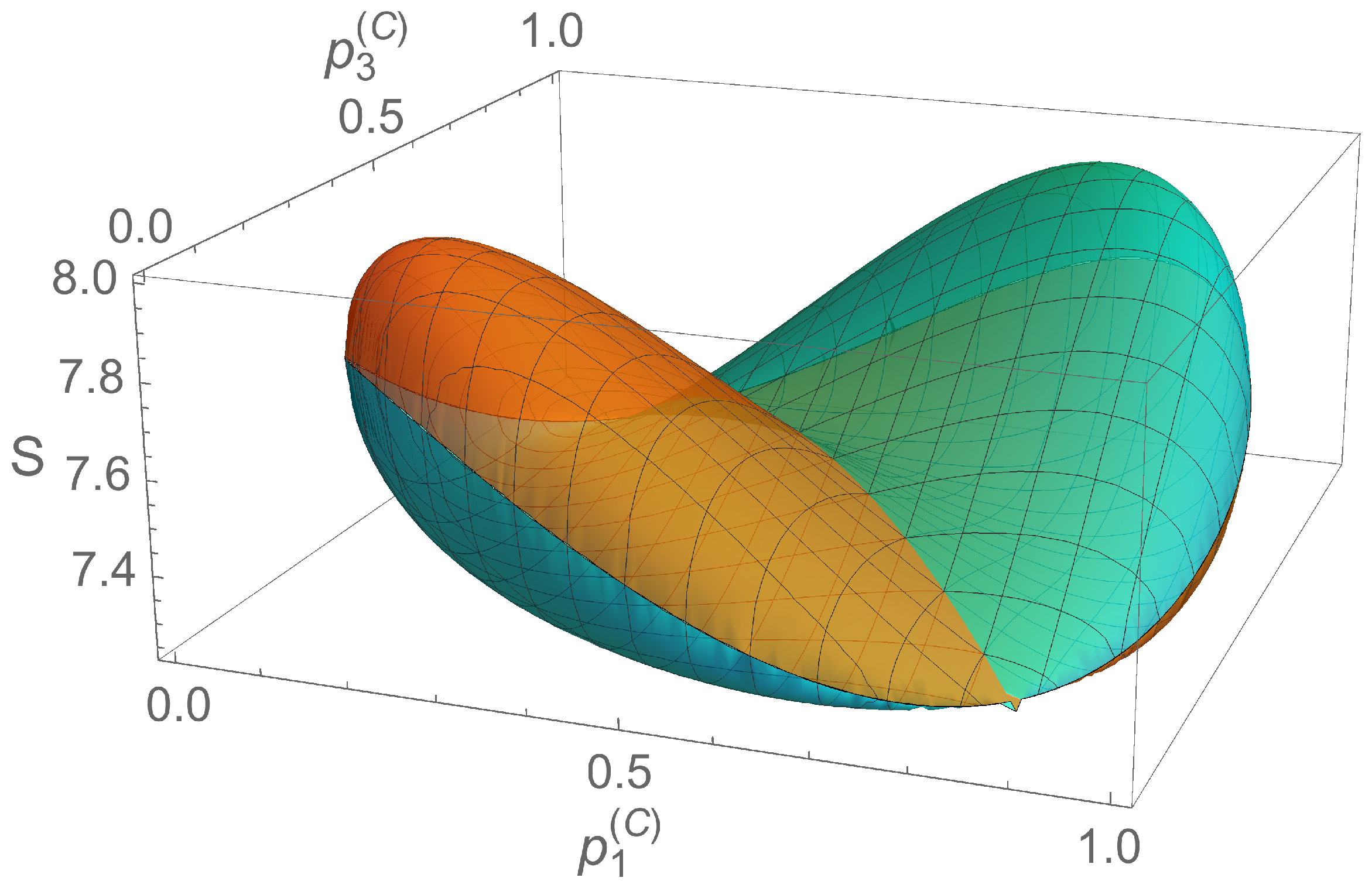
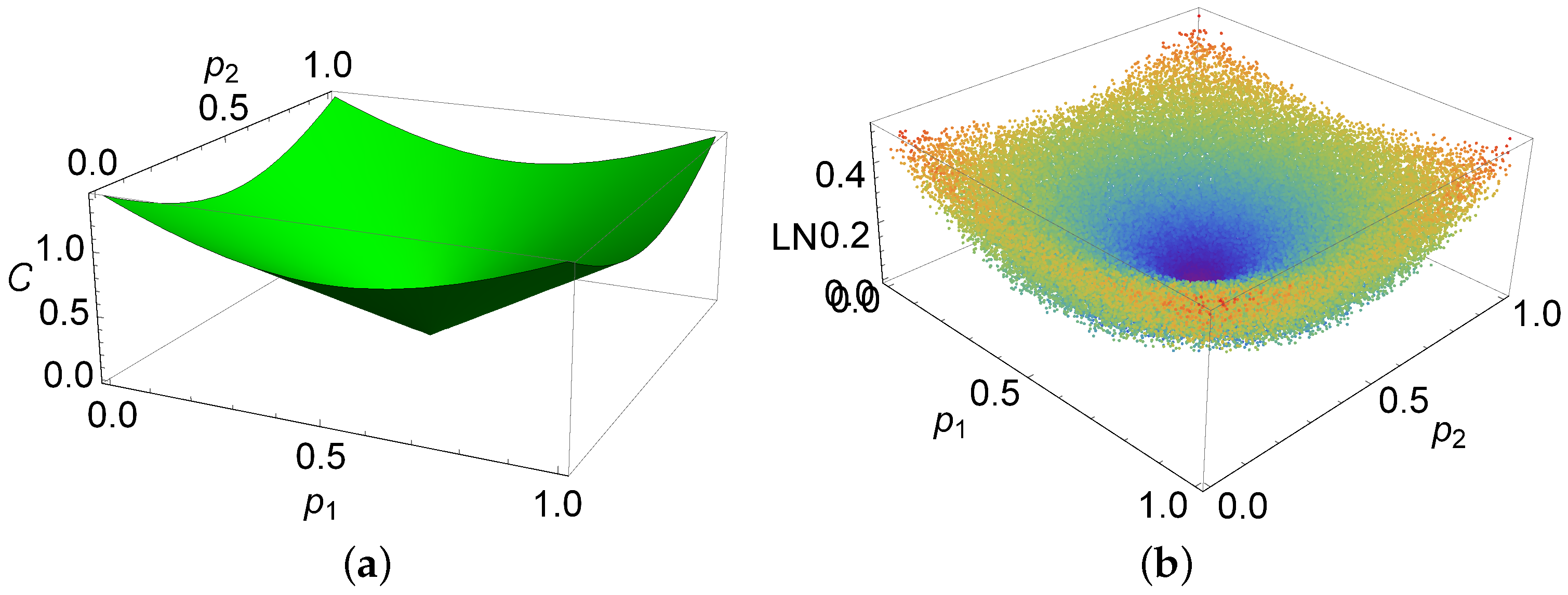
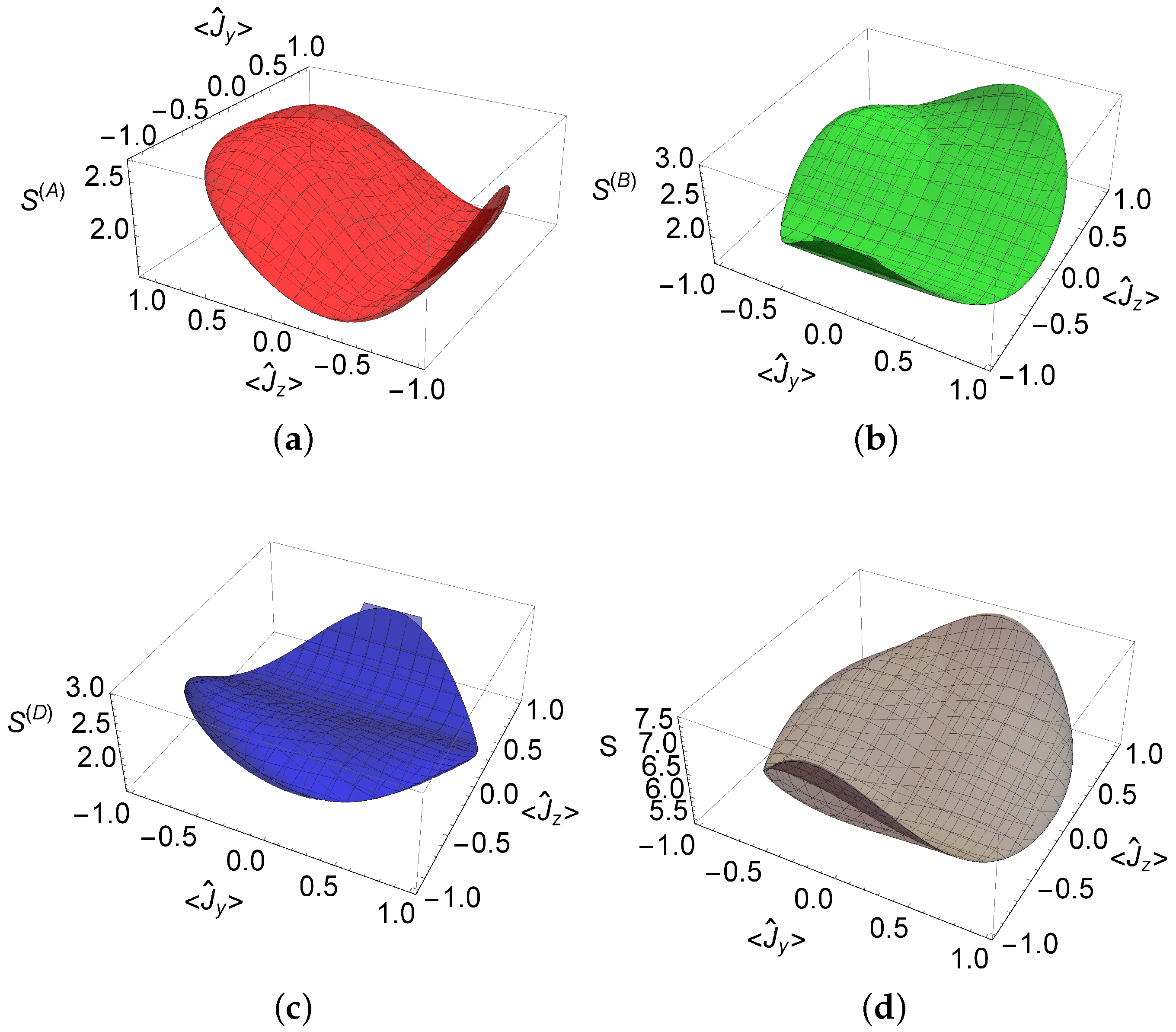
4. Example
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Appendix A. Upper Bound for the Sum of the Square Areas
References
- Schrödinger, E. Quantisierung als Eigenwertproblem (Erste Mitteilung). Ann. Phys. 1926, 384, 361–376. [Google Scholar] [CrossRef]
- Schrödinger, E. Quantisierung als Eigenwertproblem (Zweite Mitteilung). Ann. Phys. 1926, 384, 489–527. [Google Scholar] [CrossRef]
- Landau, L. Das Da¨mpfungsproblem in der Wellenmechanik. Z. Phys. 1927, 45, 430–441. [Google Scholar] [CrossRef]
- Von Neumann, J. Wahrscheinlichkeitstheoretischer Aufbau der Quantenmechanik. Gött. Nach. 1927, 1, 245–272. [Google Scholar]
- Dirac, P.A.M. The Principles of Quantum Mechanics; Clarendon Press: Oxford, UK, 1981; ISBN 9780198520115. [Google Scholar]
- Wigner, E. On the Quantum Correction For Thermodynamic Equilibrium. Phys. Rev. 1932, 40, 749–759. [Google Scholar] [CrossRef]
- Husimi, K. Some Formal Properties of the Density Matrix. Proc. Phys. Math. Soc. Jpn. 1940, 22, 264–314. [Google Scholar] [CrossRef]
- Glauber, R.J. Coherent and Incoherent States of the Radiation Field. Phys. Rev. 1963, 131, 2766–2788. [Google Scholar] [CrossRef]
- Sudarshan, E.C.G. Equivalence of Semiclassical and Quantum Mechanical Descriptions of Statistical Light Beams. Phys. Rev. Lett. 1963, 10, 277–279. [Google Scholar] [CrossRef]
- Stratonovich, R.L. On Distributions in Representation Space. J. Exp. Theor. Phys. 1957, 4, 891–898. [Google Scholar]
- Wootters, W.K. Quantum mechanics without probability amplitudes. Found. Phys. 1986, 16, 391–405. [Google Scholar] [CrossRef]
- Mielnik, B. Geometry of quantum states. Commun. Math. Phys. 1968, 9, 55–80. [Google Scholar] [CrossRef]
- Mancini, S.; Man’ko, V.I.; Tombesi, P. Symplectic tomography as classical approach to quantum systems. Phys. Lett. A 1996, 213, 1–6. [Google Scholar] [CrossRef]
- Dodonov, V.V.; Man’ko, V.I. Positive distribution description for spin states. Phys. Lett. A 1997, 229, 335–339. [Google Scholar] [CrossRef]
- Man’ko, V.I.; Man’ko, O.V. Spin state tomography. J. Exp. Theor. Phys. 1997, 85, 430–434. [Google Scholar] [CrossRef]
- Chernega, V.N.; Man’ko, O.V.; Man’ko, V.I. Triangle Geometry of the Qubit State in the Probability Representation Expressed in Terms of the Triada of Malevich’s Squares. J. Russ. Laser Res. 2017, 38, 141–149. [Google Scholar] [CrossRef]
- Chernega, V.N.; Man’ko, O.V.; Man’ko, V.I. Probability Representation of Quantum Observables and Quantum States. J. Russ. Laser Res. 2017, 38, 324–333. [Google Scholar] [CrossRef]
- Chernega, V.N.; Man’ko, O.V.; Man’ko, V.I. Triangle Geometry for Qutrit States in the Probability Representation. J. Russ. Laser Res. 2017, 38, 416–425. [Google Scholar] [CrossRef]
- Chernega, V.N.; Man’ko, O.V.; Man’ko, V.I. Quantum suprematism picture of Malevich’s squares triada for spin states and the parameteric oscillator evolution in the probability representation of quantum mechanics. J. Phys. Conf. Ser. 2018, in press. [Google Scholar]
- Carinena, J.F.; Ibort, A.; Marmo, G.; Morandi, G. Geometry from Dynamics, Classical and Quantum; Springer: Dordrecht, The Netherlands, 2015; ISBN 9789401792202. [Google Scholar]
- Bengtsson, I.; Zyczkowski, K. Geometry of Quantum States: An Introduction to Quantum Entanglement; Cambridge University Press: Cambridge, UK, 2008; ISBN 9781107026254. [Google Scholar]
- Man’ko, V.I.; Marmo, G.; Ventriglia, F.; Vitale, P. Metric on the space of quantum states from relative entropy. Tomographic reconstruction. J. Phys. A 2017, 50, 335302. [Google Scholar] [CrossRef]
- Grabowski, J.; Kuś, M.; Marmo, G. Geometry of quantum systems: Density states and entanglement. J. Phys. A 2005, 38, 10217. [Google Scholar] [CrossRef]
- Rexiti, M.; Felice, D.; Mancini, S. The volume of two-qubit states by information geometry. Entropy 2018, 20, 146. [Google Scholar] [CrossRef]
- Jordan, P. Der Zusammenhang der symmetrischen und linearen Gruppen und das Mehrkörperproblem. Z. Phys. 1935, 94, 531–535. [Google Scholar] [CrossRef]
- Schwinger, J. Quantum Theory of Angular Momentum; Biedenharn, L.C., Van Dam, H., Eds.; Academic Press Inc.: Cambridge, UK, 1965; ISBN 9780120960569. [Google Scholar]
- Dumitrescu, E.F.; McCaskey, A.J.; Hagen, G.; Jansen, G.R.; Morris, T.D.; Papenbrock, T.; Pooser, R.C.; Dean, D.J.; Lougovski, P. Cloud Quantum Computing of an Atomic Nucleus. Phys. Rev. Lett. 2018, 120, 210501. [Google Scholar] [CrossRef] [PubMed]
- Filippov, S.N.; Man’ko, V.I. Symmetric informationally complete positive operator valued measure and probability representation of quantum mechanics. J. Russ. Laser Res. 2010, 31, 211–231. [Google Scholar] [CrossRef]
- Castaños, O.; Lopez-Peña, R.; Man’ko, M.A.; Man’ko, V.I. Squeeze tomography of quantum states. J. Phys. A 2004, 37, 8529–8544. [Google Scholar] [CrossRef]
- Man’ko, M.A.; Man’ko, V.I. Properties of Nonnegative Hermitian Matrices and New Entropic Inequalities for Noncomposite Quantum Systems. Entropy 2015, 17, 2876–2894. [Google Scholar] [CrossRef]
- Asorey, M.; Ibort, A.; Marmo, G.; Ventriglia, F. Quantum Tomography twenty years later. Phys. Scr. 2015, 90, 074031. [Google Scholar] [CrossRef]
- Khrennikov, A. Quantum-like Representation Algorithm: Transformation of Probabilistic Data into vectors on Bloch’s Sphere. arXiv, 2008; arXiv:0803.1391v1. [Google Scholar] [CrossRef]
- Khrennikov, A. The Principle of Supplementarity: A Contextual Probabilistic Viewpoint to Complementarity, the Interference of Probabilities and Incompatibility of Variables in Quantum Mechanics. Found. Phys. 2005, 35, 1655–1693. [Google Scholar] [CrossRef]
- Khrennikov, A. Interference of probabilities and number field structure of quantum models. Ann. Phys. 2003, 12, 575–585. [Google Scholar] [CrossRef]
- Khrennikov, A. Contextual Approach to Quantum Formalism; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2009; ISBN 9781402095924. [Google Scholar]
- Chernega, V.N.; Man’ko, O.V.; Man’ko, V.I. God Plays Coins or Superposition Principle for Classical Probabilities in Quantum Suprematism Representation of Qubit States. J. Russ. Laser Res. 2018, 39, 128–139. [Google Scholar] [CrossRef]
- Man’ko, M.A.; Man’ko, V.I. From quantum carpets to quantum suprematism—The probability representation of qudit states and hidden correlations. Phys. Scr. 2018, 93, 084002. [Google Scholar] [CrossRef]
- Shatskikh, A. Black Square: Malevich and the Origin of Suprematism; Yale University Press: New Haven, NH, USA, 2012; ISBN 0300140894. [Google Scholar]
- Zeilinger, A. Light for the quantum. Entangled photons and their applications: A very personal perspective. Phys. Scr. 2017, 92, 072501. [Google Scholar] [CrossRef]
- Peres, A. Separability Criterion for Density Matrices. Phys. Rev. Lett. 1996, 77, 1413–1415. [Google Scholar] [CrossRef] [PubMed]
- Horodecki, M.; Horodecki, P.; Horodecki, R. Separability of mixed states: Necessary and sufficient conditions. Phys. Lett. A 1996, 223, 1–8. [Google Scholar] [CrossRef]
- López-Saldívar, J.A.; Castaños, O.; Man’ko, M.A.; Man’ko, V.I. New entropic inequalities for qubit and unimodal Gaussian states. Physica A 2018, 491, 64–70. [Google Scholar] [CrossRef]
- Gell-Mann, M. Symmetries of Baryons and Mesons. Phys. Rev. 1962, 125, 1067–1084. [Google Scholar] [CrossRef]
- Zyczkowski, K.; Horodecki, P.; Sanpera, A.; Lewenstein, M. Volume of the set of separable states. Phys. Rev. A 1998, 58, 883–892. [Google Scholar] [CrossRef]
- Hill, S.; Wootters, W.K. Entanglement of a Pair of Quantum Bits. Phys. Rev. Lett. 1997, 78, 5022–5025. [Google Scholar] [CrossRef]
- Wootters, W.K. Entanglement of Formation of an Arbitrary State of Two Qubits. Phys. Rev. Lett. 1998, 80, 2245–2248. [Google Scholar] [CrossRef]
- Radcliffe, J.M. Some properties of coherent spin states. J. Phys. A 1971, 4, 313–323. [Google Scholar] [CrossRef]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
López-Saldívar, J.A.; Castaños, O.; Nahmad-Achar, E.; López-Peña, R.; Man’ko, M.A.; Man’ko, V.I. Geometry and Entanglement of Two-Qubit States in the Quantum Probabilistic Representation. Entropy 2018, 20, 630. https://doi.org/10.3390/e20090630
López-Saldívar JA, Castaños O, Nahmad-Achar E, López-Peña R, Man’ko MA, Man’ko VI. Geometry and Entanglement of Two-Qubit States in the Quantum Probabilistic Representation. Entropy. 2018; 20(9):630. https://doi.org/10.3390/e20090630
Chicago/Turabian StyleLópez-Saldívar, Julio Alberto, Octavio Castaños, Eduardo Nahmad-Achar, Ramón López-Peña, Margarita A. Man’ko, and Vladimir I. Man’ko. 2018. "Geometry and Entanglement of Two-Qubit States in the Quantum Probabilistic Representation" Entropy 20, no. 9: 630. https://doi.org/10.3390/e20090630
APA StyleLópez-Saldívar, J. A., Castaños, O., Nahmad-Achar, E., López-Peña, R., Man’ko, M. A., & Man’ko, V. I. (2018). Geometry and Entanglement of Two-Qubit States in the Quantum Probabilistic Representation. Entropy, 20(9), 630. https://doi.org/10.3390/e20090630






