Photons Probe Entropic Potential Variation during Molecular Confinement in Nanocavities
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. 157 nm Laser
2.3. AFM Imaging
2.4. Fractal Analysis
2.4.1. Cube Counting
2.4.2. Triangulation
2.4.3. Variance Method
2.4.4. Power Spectrum
2.5. Nanoindentation
2.6. Water Contact Angle
2.7. WLRS
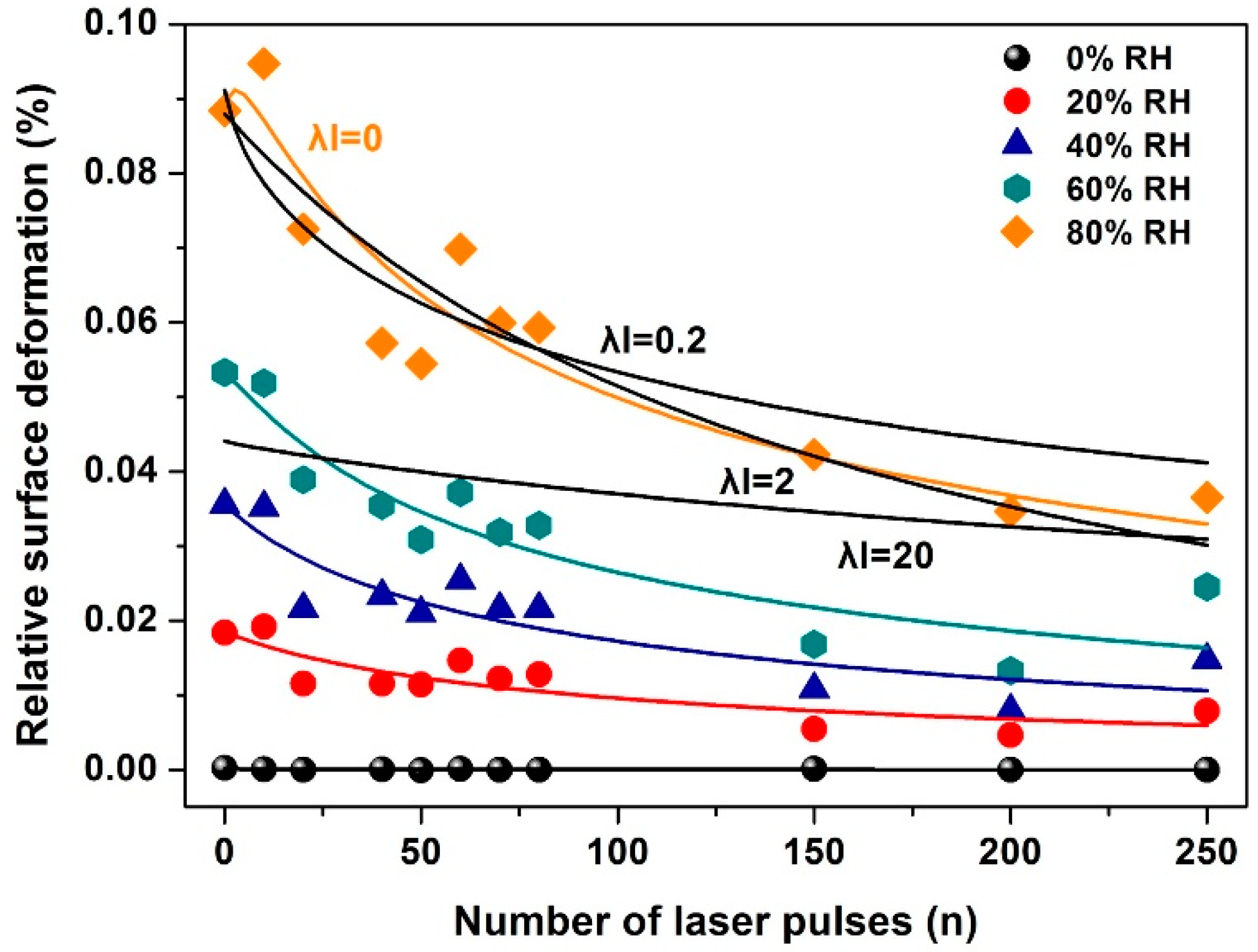
3. Results
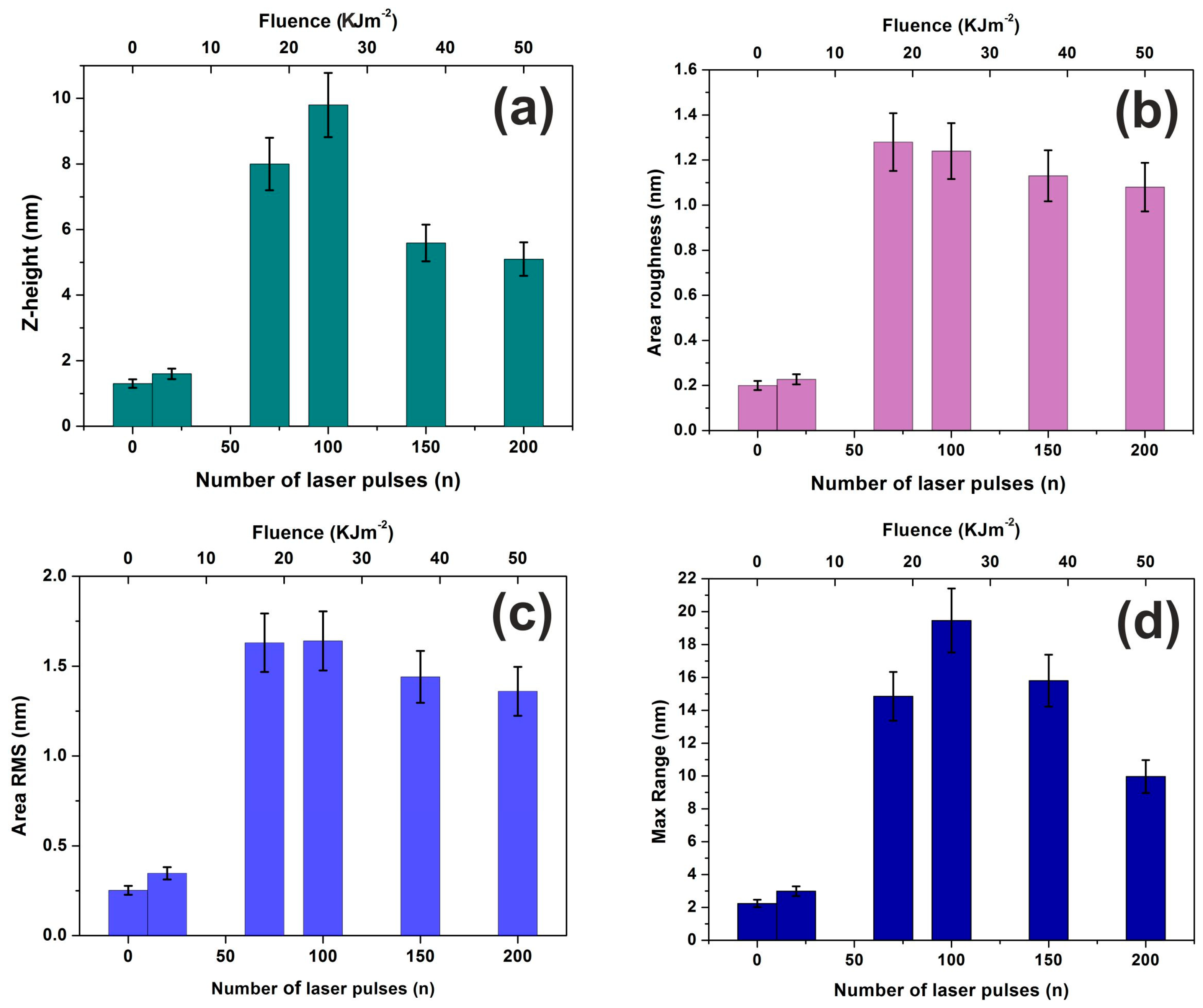
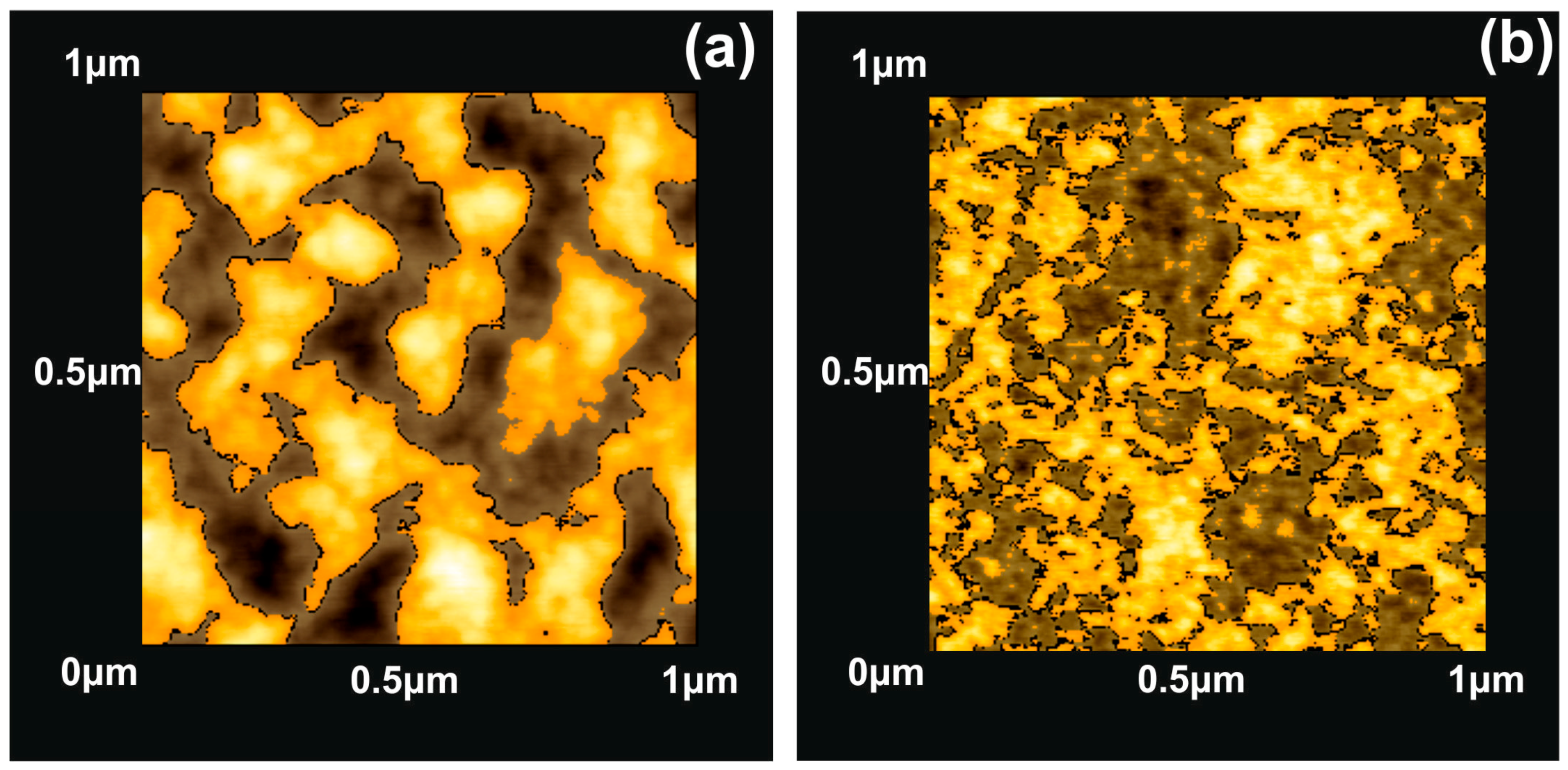
3.1. Surface Morphological Characteristics of 157 nm Photon Processed PHEMA Polymeric Matrixes
3.2. Surface Analysis
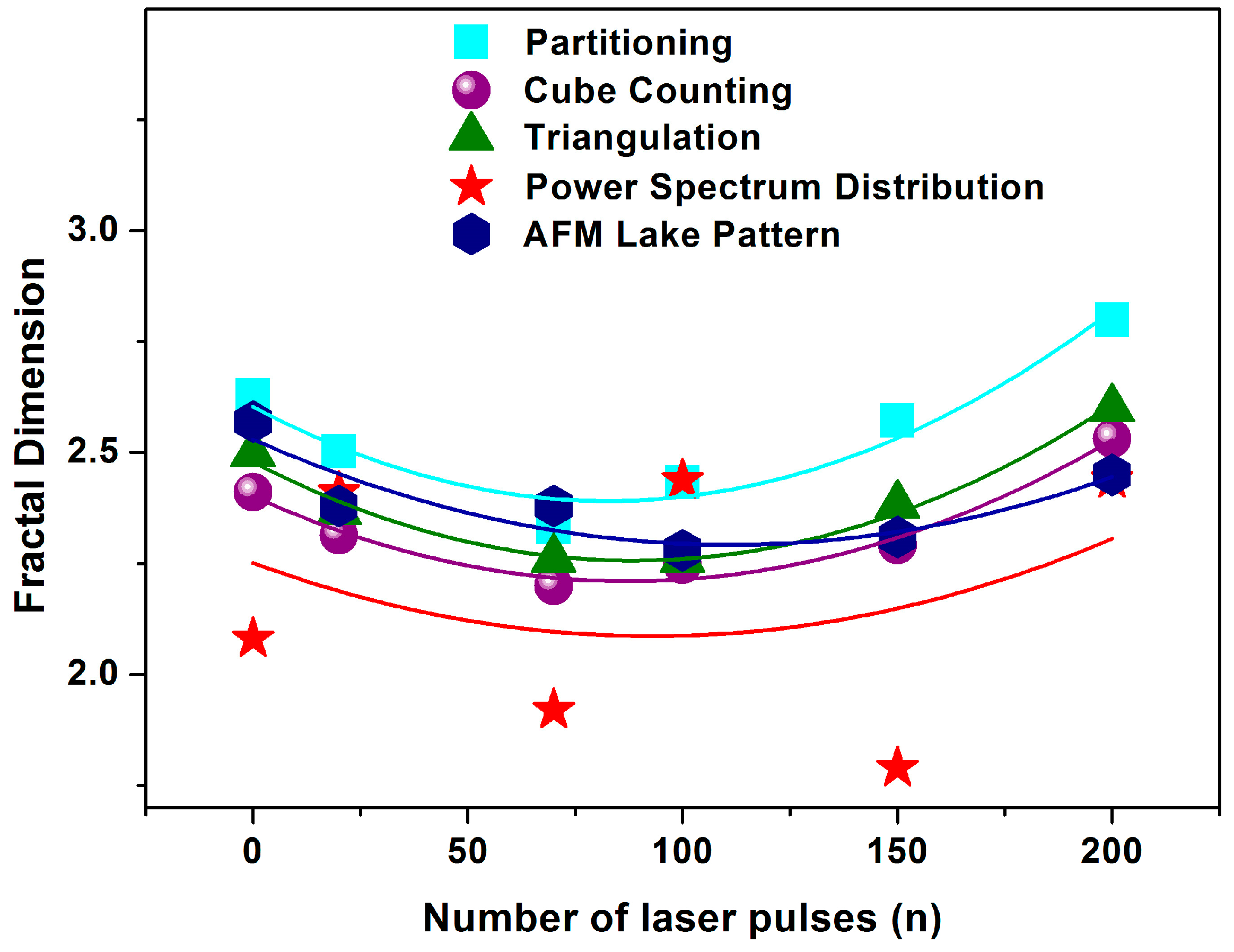
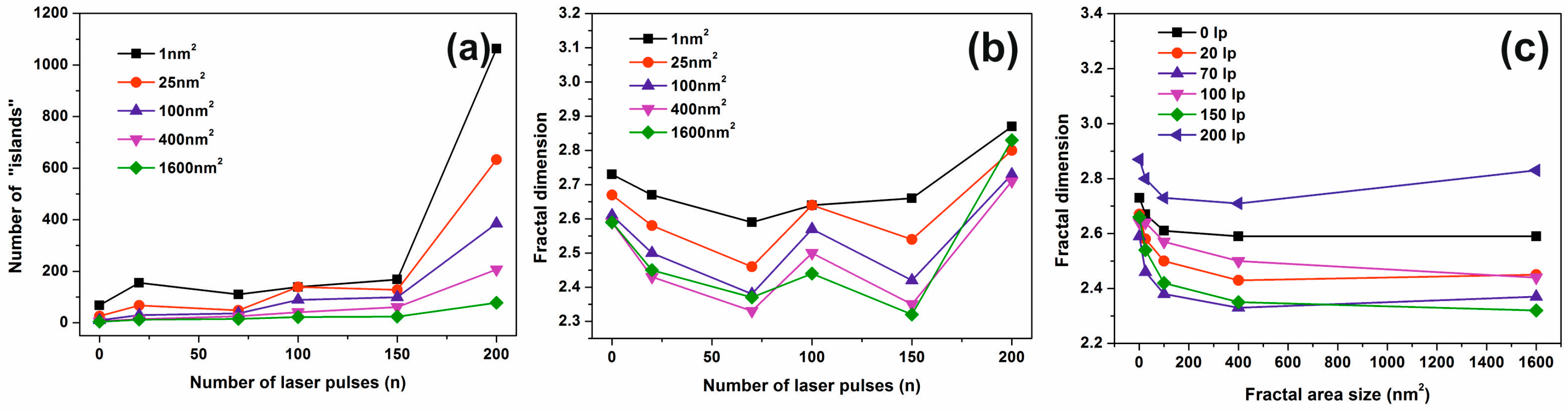
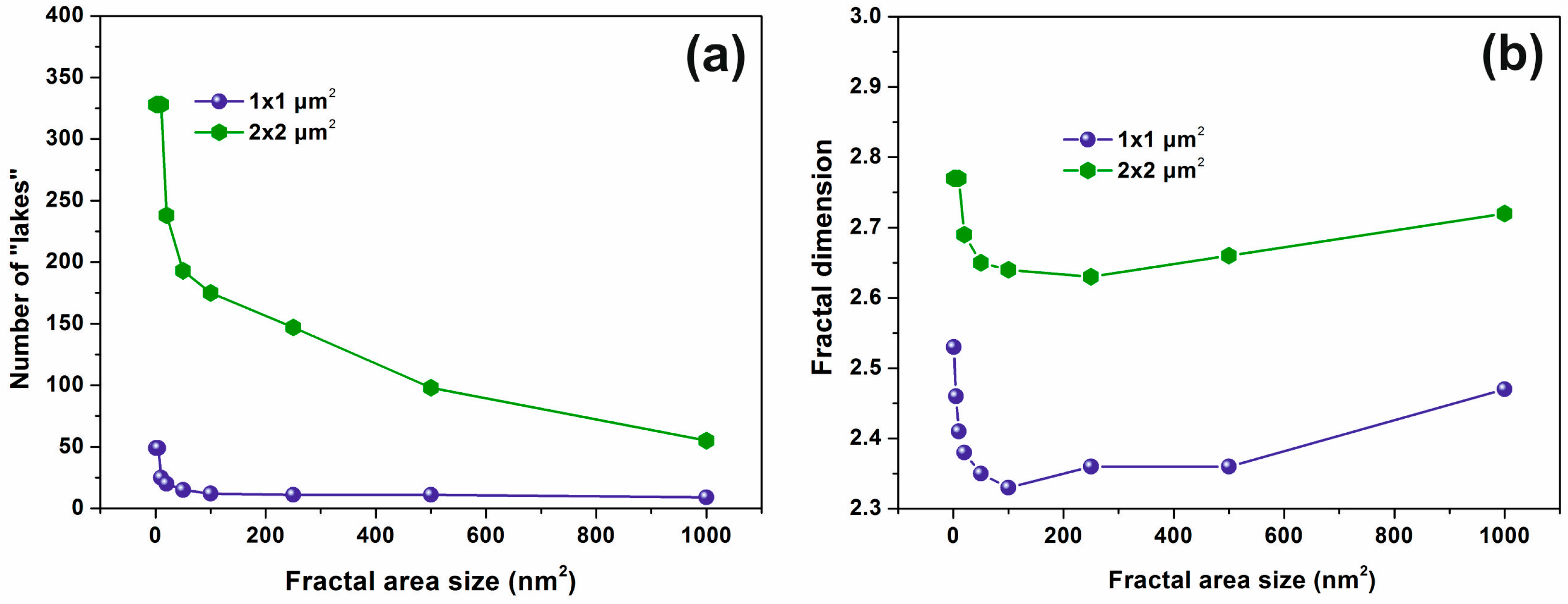
3.3. Fractal Characteristics of 157 nm Photon Processed PHEMA Polymeric Matrixes
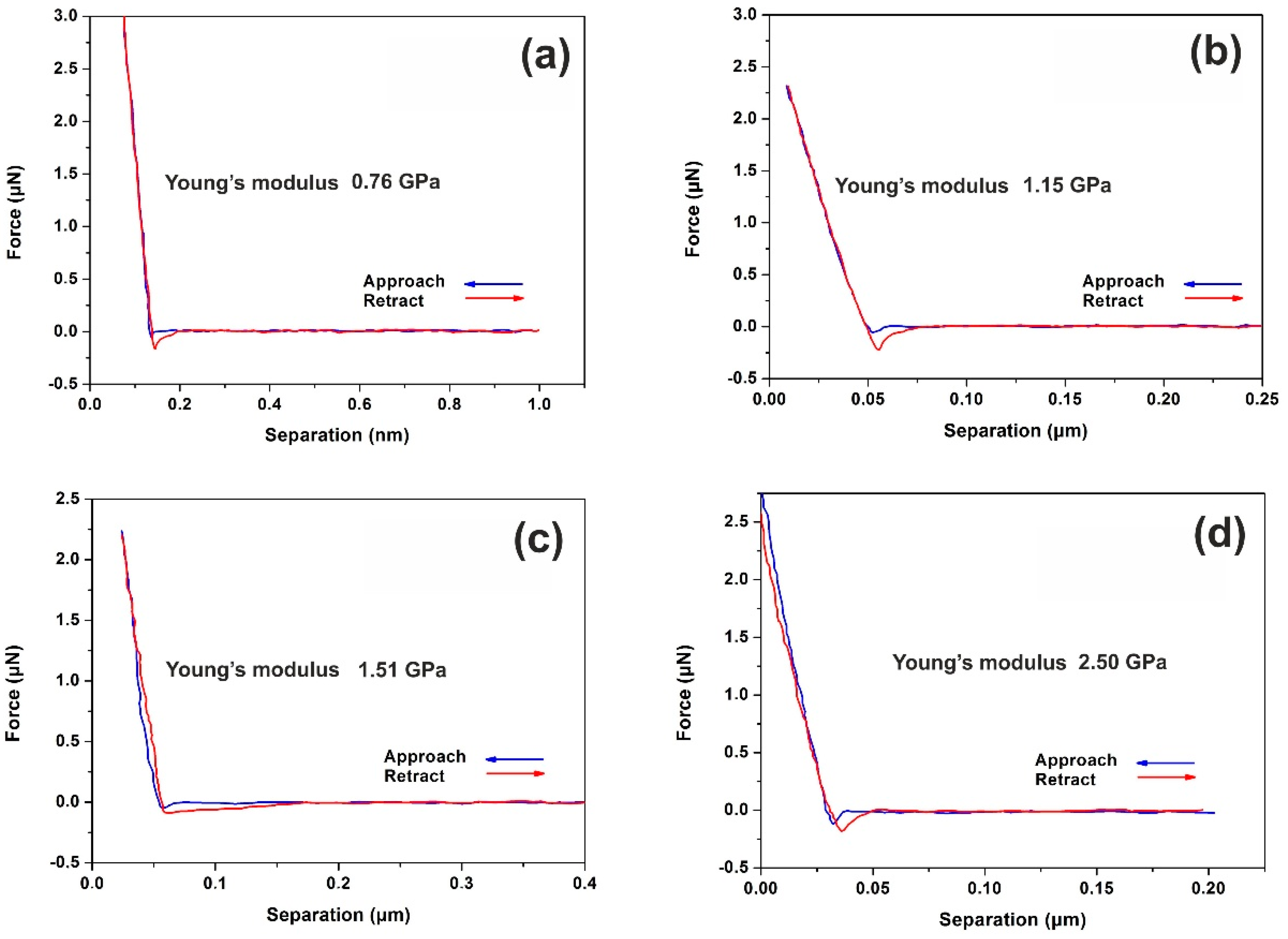
3.4. Nanoindentation
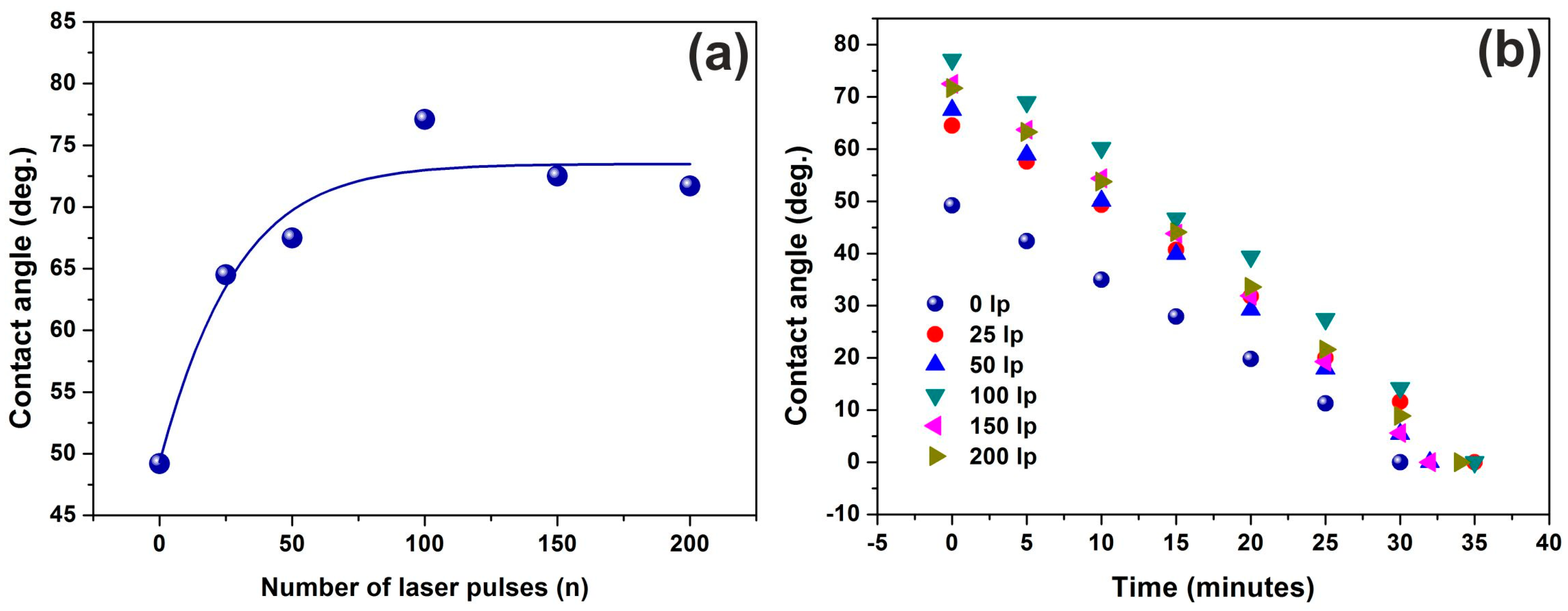
3.5. Water Contact Angle
3.6. WLRS
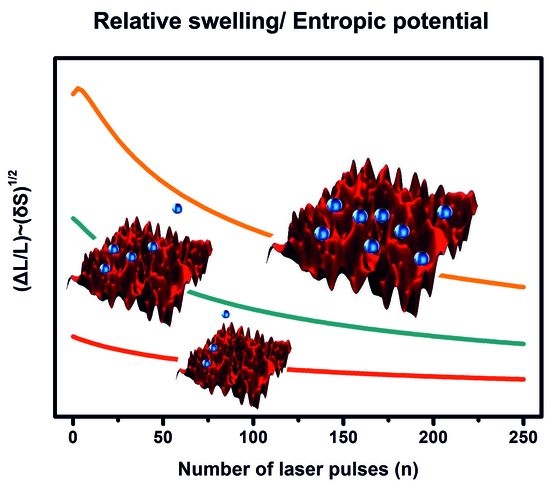
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hill, T.L. A Different Approach to Nanothermodynamics. Nano Lett. 2001, 1, 273–275. [Google Scholar] [CrossRef]
- Giebultowicz, T. Nanothermodynamics: Breathing life into an old model. Nature 2000, 408, 299–301. [Google Scholar] [CrossRef] [PubMed]
- Delogu, F. Thermodynamics on the Nanoscale. J. Phys. Chem. B 2005, 109, 21938–21941. [Google Scholar] [CrossRef] [PubMed]
- Alivisatos, P. Nanothermodynamics: A Personal Perspective by Terrell Hill. Nano Lett. 2001, 1, 109. [Google Scholar] [CrossRef]
- Fan, G.; Huang, Z.; Wang, T. Size effect on thermodynamic properties of CaMoO4 micro/nano materials and reaction systems. Solid State Sci. 2013, 16, 121–124. [Google Scholar] [CrossRef]
- Strom, B.A.; Simon, J.-M.; Schnell, S.K.; Kjelstrup, S.; He, J.; Bedeaux, D. Size and shape effects on the thermodynamic properties of nanoscale volumes of water. Phys. Chem. Chem. Phys. 2017, 19, 9016–9027. [Google Scholar] [CrossRef] [PubMed]
- Chamberlin, R. The Big World of Nanothermodynamics. Entropy 2015, 17, 52–73. [Google Scholar] [CrossRef]
- Li, Z.H.; Truhlar, D.G. Nanothermodynamics of metal nanoparticles. Chem. Sci. 2014, 5, 2605–2624. [Google Scholar] [CrossRef]
- Wang, C.X.; Yang, G.W. Thermodynamics of metastable phase nucleation at the nanoscale. Mater. Sci. Eng. R Rep. 2005, 49, 157–202. [Google Scholar] [CrossRef]
- Hill, T.L. Extension of Nanothermodynamics to Include a One-Dimensional Surface Excess. Nano Lett. 2001, 1, 159–160. [Google Scholar] [CrossRef]
- Schnell, S.K.; Liu, X.; Simon, J.M.; Bardow, A.; Bedeaux, D.; Vlugt, T.J.H.; Kjelstrup, S. Calculating Thermodynamic Properties from Fluctuations at Small Scales. J. Phys. Chem. B 2011, 115, 10911–10918. [Google Scholar] [CrossRef] [PubMed]
- Schnell, S.K.; Vlugt, T.J.H.; Simon, J.M.; Bedeaux, D.; Kjelstrup, S. Thermodynamics of a small system in a μT reservoir. Chem. Phys. Lett. 2011, 504, 199–201. [Google Scholar] [CrossRef]
- Moscatelli, A. Nanothermodynamics: The Power of One Atom. 2016. Available online: https://www.nature.com/articles/nnano.2016.102#article-info (accessed on 23 July 2018).
- Lucia, U. A Link between Nano- and Classical Thermodynamics: Dissipation Analysis (The Entropy Generation Approach in Nano-Thermodynamics). Entropy 2015, 17, 1309–1328. [Google Scholar] [CrossRef]
- Rasaiah, J.C.; Garde, S.; Hummer, G. Water in Nondipole Confinement: From Nanotubes to Proteins and Beyond. Annu. Rev. Phys. Chem. 2008, 59, 713–740. [Google Scholar] [CrossRef] [PubMed]
- Chaban, V.V.; Prezhdo, V.V.; Prezhdo, O.V. Confinement by Carbon Nanotubes Drastically Alters the Boiling and Critical Behavior of Water Droplets. ACS Nano 2012, 6, 2766–2773. [Google Scholar] [CrossRef] [PubMed]
- Cefalas, A.C.; Sarantopoulou, E.; Kollia, Z.; Kitsara, M.; Raptis, I.; Bakalis, E. Entropic nanothermodynamic potential from molecular trapping within photon induced nano-voids in photon processed PDMS layers. Soft Matter 2012, 8, 5561–5574. [Google Scholar] [CrossRef]
- Gadomski, A.; Rubi, J.M. On the two principal curvatures as potential barriers in a model of complex matter agglomeration. Chem. Phys. 2003, 293, 169–177. [Google Scholar] [CrossRef]
- Gadomski, A. Polymorphic phase transitions in systems evolving in a two-dimensional discrete space. Phys. Rev. E 1999, 60, 1252–1261. [Google Scholar] [CrossRef]
- Cefalas, A.C.; Kollia, Z.; Spyropoulos-Antonakakis, N.; Cavriil, V.; Christofilos, D.; Kourouklis, G.; Semashko, V.; Pavlov, V.; Sarantopoulou, E. Surface profile gradient in Ta2O5 semiconductive layers regulates nanoscale electric current stability. Appl. Surf. Sci. 2017, 396, 1000–1019. [Google Scholar] [CrossRef]
- Stefi, A.L.; Sarantopoulou, E.; Kollia, Z.; Spyropoulos-Antonakakis, N.; Bourkoula, A.; Petrou, P.S.; Kakabakos, S.; Soras, G.; Trohopoulos, P.N.; Nizamutdinov, A.S.; et al. Nanothermodynamics Mediates Drug Delivery. In GeNeDis 2014; Vlamos, P., Alexiou, A., Eds.; Springer: Cham, Switzerland, 2015; pp. 213–220. [Google Scholar]
- Mahadevan, L.; Rica, S. Self-Organized Origami. Science 2005, 307, 1740. [Google Scholar] [CrossRef] [PubMed]
- Guvendiren, P.; Messersmith, P.B.; Shull, K.R. Self-Assembly and Adhesion of DOPA-Modified Methacrylic Triblock Hydrogels. Biomacromolecules 2008, 9, 122–128. [Google Scholar] [CrossRef] [PubMed]
- Nicolis, S.J. Dynamics of Hierarchical Systems: An Evolutionary Approach; Springer: Berlin/Heidelberg, Germany, 1986; ISBN-13: 978-3-642-69694-7. [Google Scholar]
- Bowden, N.; Brittain, S.; Evans, A.G.; Hutcinson, J.W.; Whitesides, M. Spontaneous formation of ordered structures in thin films of metals supported on an elastomeric polymer. Nature 1998, 393, 146–149. [Google Scholar] [CrossRef]
- Cefalas, A.C.; Kobe, S.; Dražic, G.; Sarantopoulou, E.; Kollia, Z.; Stražišar, J.; Medend, A. Nanocrystallization of CaCO3 at solid/liquid interfaces in magnetic field: A quantum approach. Appl. Surf. Sci. 2008, 254, 6715–6724. [Google Scholar] [CrossRef]
- Koch, K.; Bhushan, B.; Jung, Y.C.; Barthhlot, W. Fabrication of artificial Lotus leaves and significance of hierarchical structure for superhydrophobicity and low adhesion. Soft Matter 2009, 5, 1386–1393. [Google Scholar] [CrossRef]
- Schnell, S.K.; Vlugt, T.J.H.; Simon, J.M.; Bedeaux, D.; Kjelstrup, S. Thermodynamics of small systems embedded in a reservoir: A detailed analysis of finite size effects. Mol. Phys. 2012, 110, 1069–1079. [Google Scholar] [CrossRef]
- Reguera, D.; Luque, A.; Burada, P.S.; Schmid, G.; Rubi, J.M.; Hänggi, P. Entropic splitter for particle separation. Phys. Rev. Lett. 2012, 108, 020604. [Google Scholar] [CrossRef] [PubMed]
- Zwanzig, R. Diffusion past an entropy barrier. J. Phys. Chem. 1992, 96, 3926–3930. [Google Scholar] [CrossRef]
- Bauer, W.R.; Nadler, W. Thermodynamics of Competitive Molecular Channel Transport: Application to Artificial Nuclear Pores. PLoS ONE 2010, 5, e15160. [Google Scholar] [CrossRef] [PubMed]
- Pascal, T.A.; Goddard, W.A.; Jung, Y. Entropy and the driving force for the filling of carbon nanotubes with water. Proc. Natl. Acad. Sci. USA 2011, 108, 11794–11798. [Google Scholar] [CrossRef] [PubMed]
- Gorshunov, B.P.; Zhukova, E.S.; Torgashev, V.I.; Lebedev, V.V.; Shakurov, G.S.; Kremer, R.K.; Pestrjakov, E.V.; Thomas, V.G.; Fursenko, D.A.; Dressel, M. Quantum Behavior of Water Molecules Confined to Nanocavities in Gemstones. J. Phys. Chem. Lett. 2013, 4, 2015–2020. [Google Scholar] [CrossRef] [PubMed]
- Farsari, M.; Chichkov, B.N. Materials processing: Two-photon fabrication. Nat. Photonics 2009, 3, 450–452. [Google Scholar] [CrossRef]
- Sarantopoulou, E.; Petrou, P.S.; Kollia, Z.; Palles, D.; Spyropoulos-Antonakakis, N.; Kakabakos, S.; Cefalas, A.C. Protein immobilization and detection on laser processed polystyrene surfaces. J. Appl. Phys. 2011, 110, 064309. [Google Scholar] [CrossRef]
- Sarantopoulou, E.; Kollia, Z.; Cefalas, A.C.; Siokou, A.E.; Argitis, P.; Bellas, V.; Kobe, S. Surface modification of polyhedral oligomeric silsesquioxane block copolymer films by 157 nm laser light. J. Appl. Phys. 2009, 105, 114305. [Google Scholar] [CrossRef]
- Sarantopoulou, E.; Kollia, Z.; Cefalas, A.C.; Manoli, K.; Sanopoulou, M.; Goustouridis, D.; Chatzandroulis, S.; Raptis, I. Surface nano/micro functionalization of PMMA thin films by 157nm irradiation for sensing applications. Appl. Surf. Sci. 2008, 254, 1710–1719. [Google Scholar] [CrossRef]
- Douvas, A.M.; Petrou, P.S.; Kakabakos, S.E.; Misiakos, K.; Argitis, P.; Sarantopoulou, E.; Kollia, Z.; Cefalas, A.C. 157 nm Laser ablation of polymeric layers for fabrication of biomolecule microarrays. Anal. Bioanal. Chem. 2005, 381, 1027–1032. [Google Scholar] [CrossRef] [PubMed]
- Ligon, S.C.; Liska, R.; Stampfl, J.; Gurr, M.; Mülhaupt, R. Polymers for 3D Printing and Customized Additive Manufacturing. Chem. Rev. 2017, 117, 10212–10290. [Google Scholar] [CrossRef] [PubMed]
- Zhou, X.; Hou, Y.; Lin, J. A review on the processing accuracy of two-photon polymerization. AIP Adv. 2015, 5, 030701. [Google Scholar] [CrossRef]
- Laraoui, A.; Aycock-Rizzo, H.; Gao, Y.; Lu, X.; Riedo, E.; Meriles, C.A. Imaging thermal conductivity with nanoscale resolution using a scanning spin probe. Nat. Commun. 2015, 6, 8954. [Google Scholar] [CrossRef] [PubMed]
- Vitry, P.; Bourillot, E.; Plassard, C.; Lacroute, Y.; Tetard, L.; Lesniewska, E. Advances in quantitative nanoscale subsurface imaging by mode-synthesizing atomic force microscopy. Appl. Phys. Lett. 2014, 105, 053110. [Google Scholar] [CrossRef]
- Baffou, G.; Quidant, R.; Girard, C. Heat generation in plasmonic nanostructures: Influence of morphology. Appl. Phys. Lett. 2009, 94, 153109. [Google Scholar] [CrossRef]
- Baffou, G.; Quidant, R.; Girard, C. Thermoplasmonics modeling: A Green’s function approach. Phys. Rev. B 2010, 82, 165424. [Google Scholar] [CrossRef]
- Myers, A.L.; Monson, P.A. Adsorption in Porous Materials at High Pressure: Theory and Experiment. Langmuir 2002, 18, 10261–10273. [Google Scholar] [CrossRef]
- Dubbeldam, D.; Calero, S.; Ellis, D.E.; Snurr, R.Q. RASPA: Molecular simulation software for adsorption and diffusion in flexible nanoporous materials. Mol. Simul. 2016, 42, 81–101. [Google Scholar] [CrossRef]
- Torres-Knoop, A.; Poursaeidesfahani, A.; Vlugt, T.J.H.; Dubbeldam, D. Behavior of the Enthalpy of Adsorption in Nanoporous Materials Close to Saturation Conditions. J. Chem. Theory Comput. 2017, 13, 3326–3339. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.; Wu, S.; Yi, Z.; Zeng, F.; Wu, W.; Qiao, Y.; Zhao, X.; Cheng, X.; Tian, Y. Hydrogel-Based Fluorescent Dual pH and Oxygen Sensors Loaded in 96-Well Plates for High-Throughput Cell Metabolism Studies. Sensors 2018, 18, 564. [Google Scholar] [CrossRef] [PubMed]
- Wilhelmsen, Ø.; Trinh, T.T.; Kjelstrup, S.; Bedeaux, D. Influence of Curvature on the Transfer Coefficients for Evaporation and Condensation of Lennard-Jones Fluid from Square-Gradient Theory and Nonequilibrium Molecular Dynamics. J. Phys. Chem. C 2015, 119, 8160–8173. [Google Scholar] [CrossRef]
- McCarthy, J.R.; Jaffer, F.A.; Weissleder, R. Macrophage-targeted theranostic nanoparticle for biomedical applications. Small 2006, 2, 983–987. [Google Scholar] [CrossRef] [PubMed]
- Giglio, E.D.; Cafagna, D.; Giangregorio, M.M.; Domingos, M.; Mattioli-Belmonte, M.; Cometa, S. PHEMA-based thin hydrogel films for biomedical applications. J. Bioact. Compat. Polym. 2011, 26, 420–434. [Google Scholar] [CrossRef]
- Zainuddin; Chirila, T.V.; Barnard, Z.; Watson, G.S.; Toh, C.; Blakey, I.; Whittaker, A.K.; Hill, D.J.T. F2 excimer laser (157 nm) radiation modification and surface ablation of PHEMA hydrogels and the effects on bioactivity: Surface attachment and proliferation of human corneal epithelial cells. Radiat. Phys. Chem. 2011, 80, 219–229. [Google Scholar] [CrossRef]
- Spyropoulos-Antonakakis, N.; Sarantopoulou, E.; Trohopoulos, P.N.; Stefi, A.L.; Kollia, Z.; Gavriil, V.E.; Bourkoula, A.; Petrou, P.S.; Kakabakos, S.; Semashko, V.V.; et al. Selective aggregation of PAMAM dendrimer nanocarriers and PAMAM/ZnPc nanodrugs on human atheromatous carotid tissues: A photodynamic therapy for atherosclerosis. Nanoscale Res. Lett. 2015, 10, 210. [Google Scholar] [CrossRef] [PubMed]
- Douketis, C.; Wang, Z.; Haslett, T.L.; Moskovits, M. Fractal character of cold-deposited silver films determined by low-temperature scanning tunnelling microscopy. Phys. Rev. B 1995, 51, 11022–11031. [Google Scholar] [CrossRef]
- Zahn, W.; Zösch, A. The dependence of fractal dimension on measuring conditions of scanning probe microscopy. Fresenius J. Anal. Chem. 1999, 365, 168–172. [Google Scholar] [CrossRef]
- Van Put, A.; Vertes, A.; Wegrzynek, D.; Treiger, B.; Van Grieken, R. Quantitative characterization of individual particle surfaces by fractal analysis of scanning electron microscope images. Fresenius J. Anal. Chem. 1994, 350, 440–447. [Google Scholar] [CrossRef]
- Mannelquist, A.; Almquist, N.; Fredriksson, S. Influence of tip geometry on fractal analysis of atomic force microscopy images. Appl. Phys. A 1998, 66, S891–S895. [Google Scholar] [CrossRef]
- Zahn, W.; Zösch, A. Characterization of thin film surfaces by fractal geometry. Fresenius J. Anal. Chem. 1997, 358, 119–121. [Google Scholar] [CrossRef]
- Nečas, D.; Klapetek, P. Gwyddion: An open-source software for SPM data analysis. Cent. Eur. J. Phys. 2012, 10, 181–188. [Google Scholar] [CrossRef]
- Opdahl, A.; Kim, S.H.; Koffas, T.S.; Marmo, C.; Somorjai, G.A. Surface mechanical properties of PHEMA contact lenses: Viscoelastic and adhesive property changes on exposure to controlled humidity. J. Biomed. Mater. Res. A 2003, 67, 350–356. [Google Scholar] [CrossRef] [PubMed]
- González Martínez, J.F.; Nieto-Carvajal, I.; Abad, J.; Colchero, J. Nanoscale measurement of the power spectral density of surface roughness: How to solve a difficult experimental challenge. Nanoscale Res. Lett. 2012, 7, 174. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Zhang, X. Beyond Indentation Hardness and Modulus: Recent Advances in Nanoindentation Techniques: Part I. JOM 2017, 69, 2227–2228. [Google Scholar] [CrossRef]
- Díez-Pascual, A.M.; Gómez-Fatou, M.A.; Ania, F.; Flores, A. Nanoindentation in polymer nanocomposites. Prog. Mater. Sci. 2015, 67, 1–94. [Google Scholar] [CrossRef]
- Selby, A.; Maldonado-Codina, C.; Derby, B. Influence of specimen thickness on the nanoindentation of hydrogels: Measuring the mechanical properties of soft contact lenses. J. Mech. Behav. Biomed. Mater. 2014, 35, 144–156. [Google Scholar] [CrossRef] [PubMed]
- Grosman, A.; Ortega, C. Influence of elastic deformation of porous materials in adsorption-desorption process: A thermodynamic approach. Phys. Rev. B 2008, 78, 085433. [Google Scholar] [CrossRef]
- Wohlert, J.; Edholm, O. The range and shielding of dipole-dipole interactions in phospholipid bilayers. Biophys. J. 2004, 87, 2433–2445. [Google Scholar] [CrossRef] [PubMed]


© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gavriil, V.; Chatzichristidi, M.; Kollia, Z.; Cefalas, A.-C.; Spyropoulos-Antonakakis, N.; Semashko, V.V.; Sarantopoulou, E. Photons Probe Entropic Potential Variation during Molecular Confinement in Nanocavities. Entropy 2018, 20, 545. https://doi.org/10.3390/e20080545
Gavriil V, Chatzichristidi M, Kollia Z, Cefalas A-C, Spyropoulos-Antonakakis N, Semashko VV, Sarantopoulou E. Photons Probe Entropic Potential Variation during Molecular Confinement in Nanocavities. Entropy. 2018; 20(8):545. https://doi.org/10.3390/e20080545
Chicago/Turabian StyleGavriil, Vassilios, Margarita Chatzichristidi, Zoe Kollia, Alkiviadis-Constantinos Cefalas, Nikolaos Spyropoulos-Antonakakis, Vadim V. Semashko, and Evangelia Sarantopoulou. 2018. "Photons Probe Entropic Potential Variation during Molecular Confinement in Nanocavities" Entropy 20, no. 8: 545. https://doi.org/10.3390/e20080545
APA StyleGavriil, V., Chatzichristidi, M., Kollia, Z., Cefalas, A.-C., Spyropoulos-Antonakakis, N., Semashko, V. V., & Sarantopoulou, E. (2018). Photons Probe Entropic Potential Variation during Molecular Confinement in Nanocavities. Entropy, 20(8), 545. https://doi.org/10.3390/e20080545