Modelling of Behavior for Inhibition Corrosion of Bronze Using Artificial Neural Network (ANN)
Abstract
:1. Introduction
2. Experimental
3. Artificial Neural Network Methodology
3.1. Database Preparation
3.2. Normalization Input Data
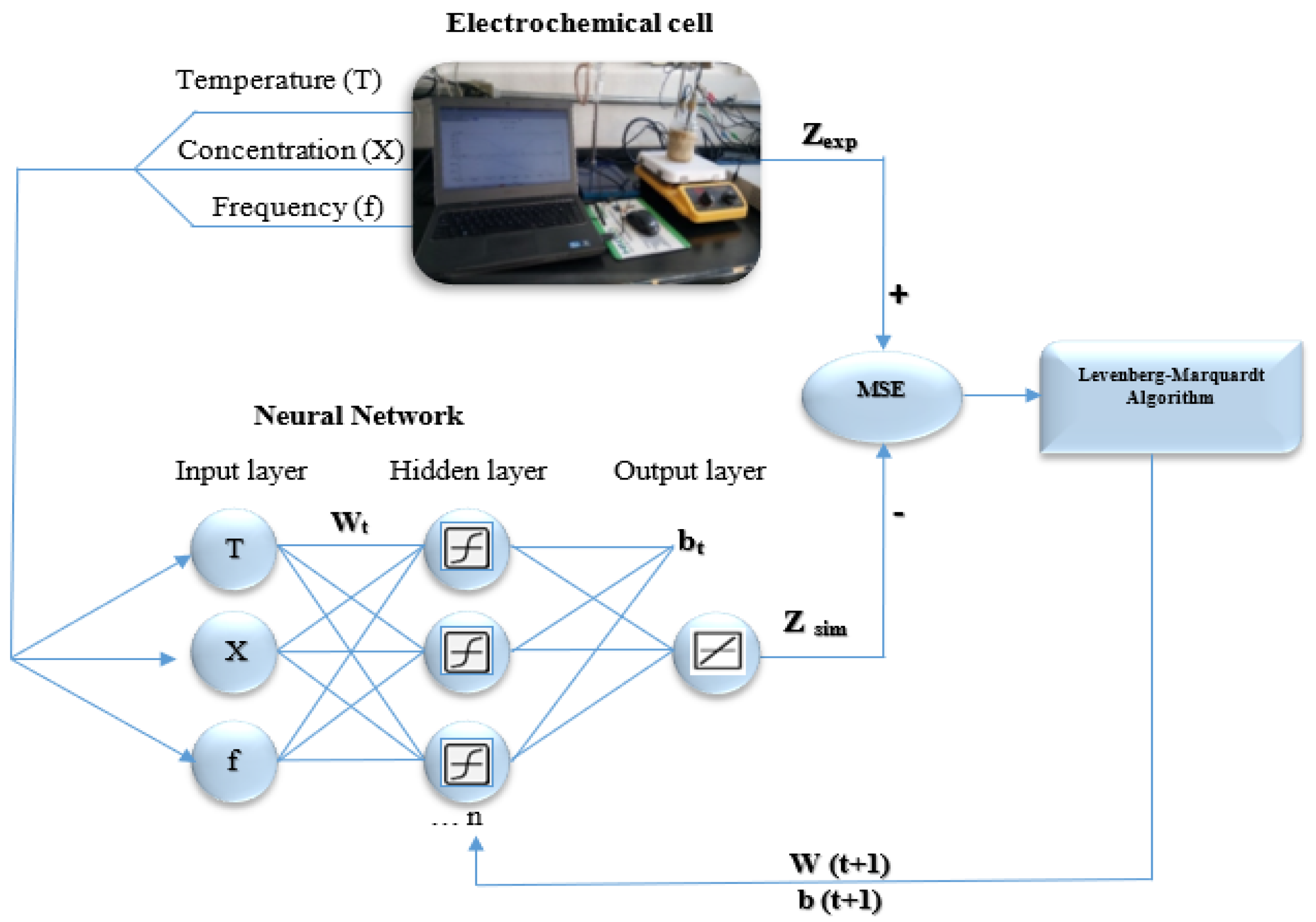
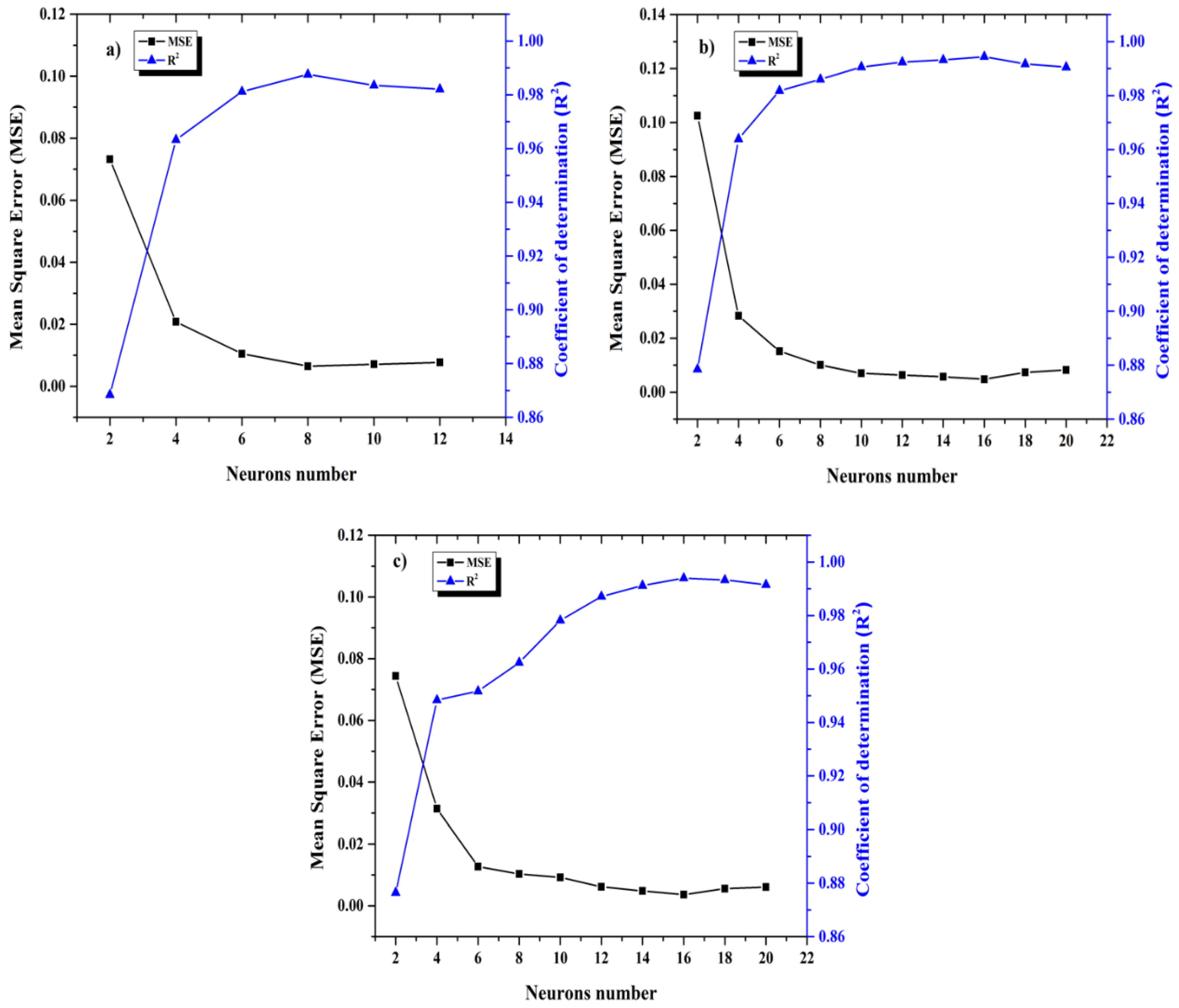
3.3. Development of ANN Models
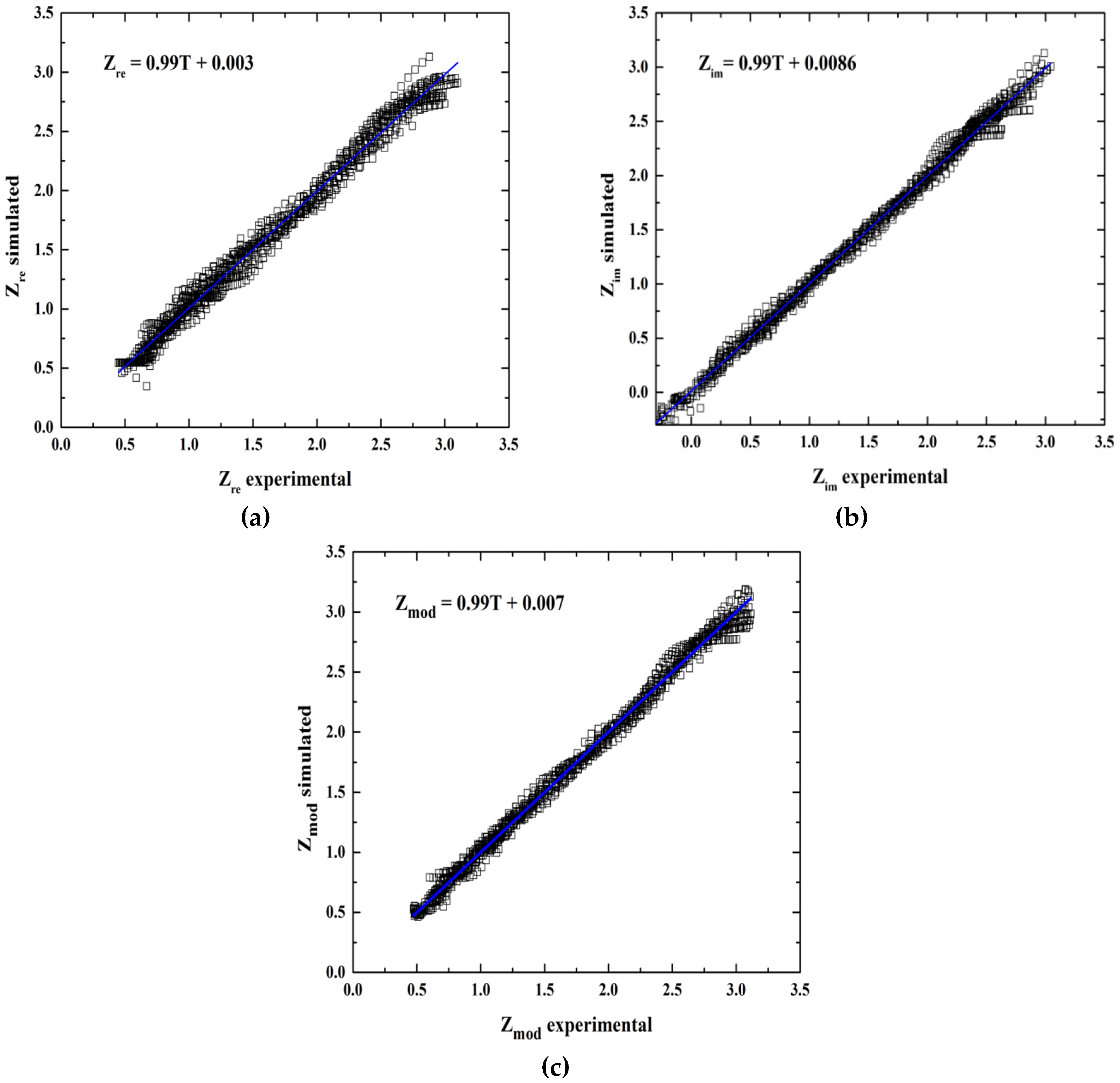
3.4. Statistical Analysis of Experimental and Predicted Data
3.5. Sensitivity Analysis
4. Results and Discussion
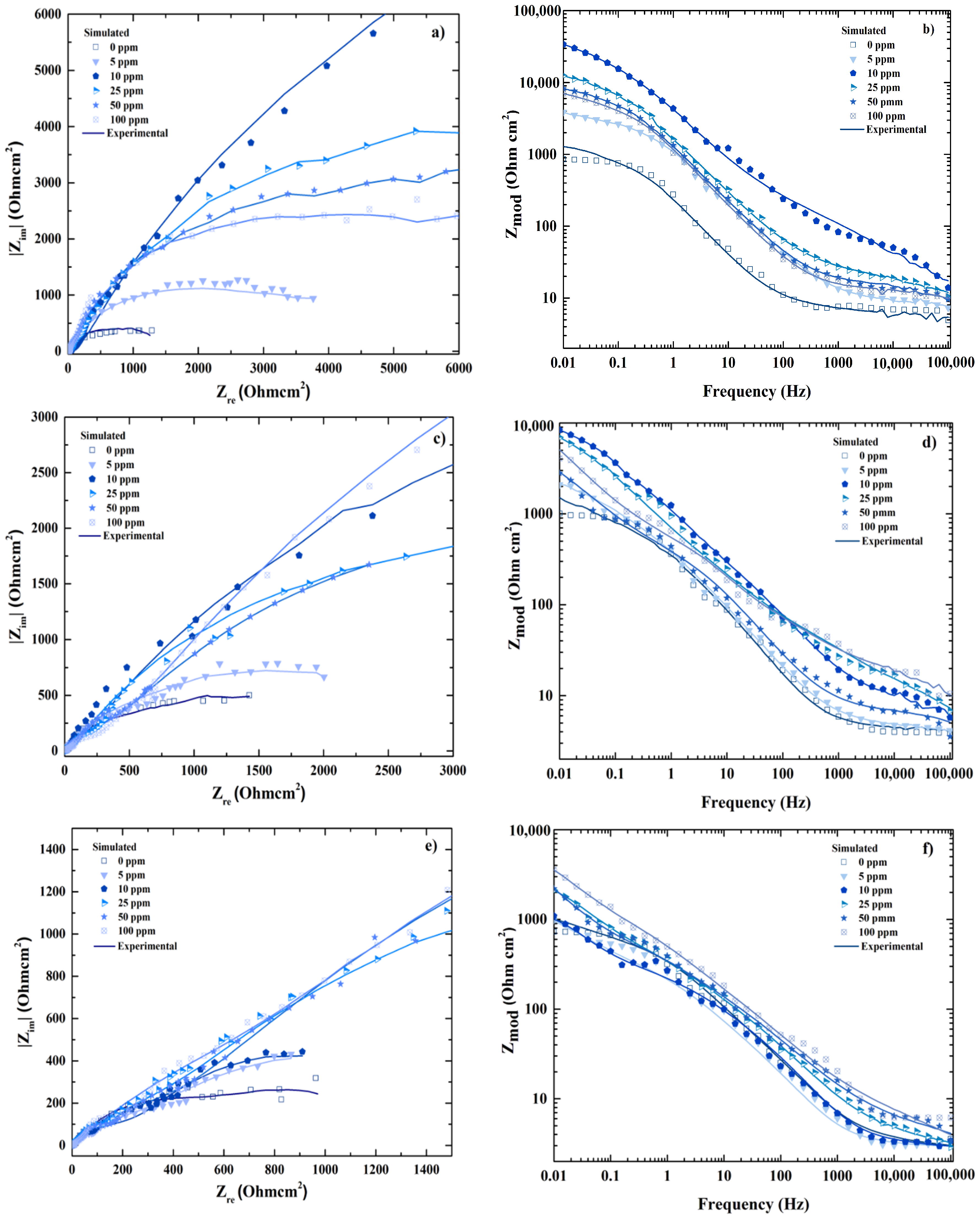
4.1. ANN Model
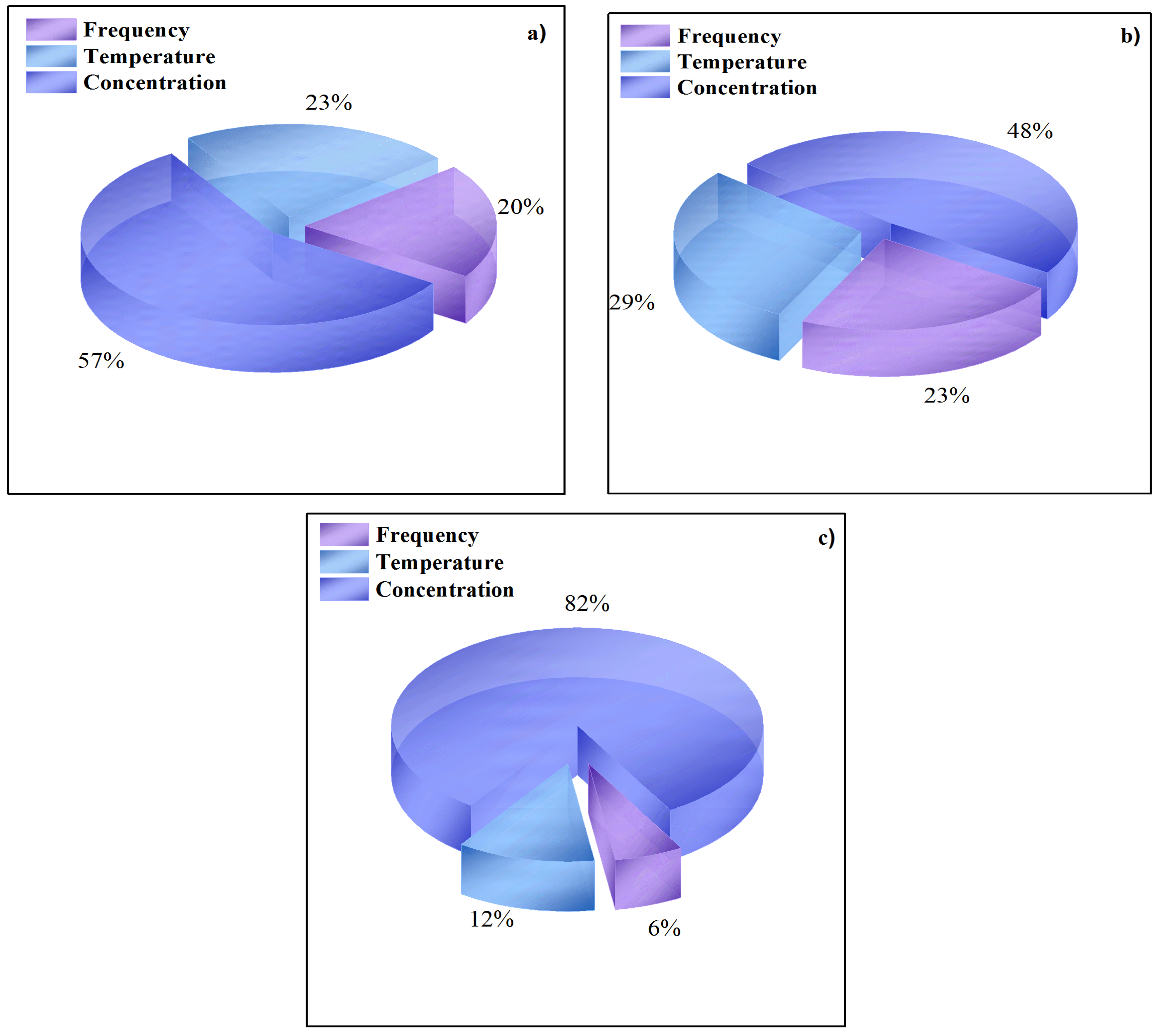
4.2. Sensitive Analysis of Input Variables
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sherif, E.M.; Park, S.M. 2-Amino-5-ethyl-1, 3, 4-thiadiazole as a corrosion inhibitor for copper in 3.0% NaCl solutions. Corros. Sci. 2006, 48, 4065–4079. [Google Scholar] [CrossRef]
- Tian, H.; Cheng, Y.F.; Li, W.; Hou, B. Triazolyl-acylhydrazone derivatives as novel inhibitors for copper corrosion in chloride solutions. Corros. Sci. 2015, 100, 341–352. [Google Scholar] [CrossRef]
- Porcayo-Calderón, J.; Martínez de la Escalera, L.M.; Canto, J.; Casales-Díaz, M. Imidazoline Derivatives Based on Coffee Oil as CO2 Corrosion Inhibitor. Int. J. Electrochem. Sci 2015, 10, 3160–3176. [Google Scholar]
- Finšgar, M.; Milošev, I. Inhibition of copper corrosion by 1, 2, 3-benzotriazole: A review. Corros. Sci. 2010, 52, 2737–2749. [Google Scholar] [CrossRef]
- Otmačić, H.; Stupnišek-Lisac, E. Copper corrosion inhibitors in near neutral media. Electrochim. Acta 2003, 48, 985–991. [Google Scholar] [CrossRef]
- Marusic, K.; Otmačić-Curkovic, H.; Takenout, H. Inhibiting effect of 4-methyl-1-p-tolylimidazole to the corrosion of bronze patinated in sulphate medium. Electrochim. Acta 2011, 56, 7491–7502. [Google Scholar] [CrossRef]
- Gece, G. Drugs: A review of promising novel corrosion inhibitors. Corros. Sci. 2011, 53, 3873–3898. [Google Scholar] [CrossRef]
- Tüken, T.; Giray, E.S.; Fındıkkıran, G.; Sıg, G. A new corrosion inhibitor for copper protection. Corros. Sci. 2014, 84, 21–29. [Google Scholar]
- Petrovic, M.B.; Antonijevic, M.M. Copper Corrosion Inhibitors. A review. Int. J. Electrochem. Sci. 2015, 10, 1027–1053. [Google Scholar] [CrossRef]
- Quraishi, M.A.; Sardar, R. Hector bases—A new class of heterocyclic corrosion inhibitors for mild steel in acid solutions. J. Appl. Electrochem. 2003, 33, 1163–1168. [Google Scholar] [CrossRef]
- Millan-Ocampo, D.E.; Hernandez-Perez, J.A.; Porcayo-Calderon, J.; Flores-De Los Ríos, J.P.; Landeros-Martínez, L.L.; Salinas-Bravo, V.M.; Gonzalez-Rodriguez, J.G.; Martinez, L. Experimental and Theoretical Study of Ketoconazole as Corrosion Inhibitor for Bronze in NaCl + Na2SO4 Solution. Int. J. Electrochem. Sci. 2017, 1212, 11428–1144522. [Google Scholar] [CrossRef]
- Chen, F.F.; Breedon, M.; White, P.; Chu, C.; Dwaipayan, M.; Thomas, S.; Sapper, E.; Cole, I. Correlation between molecular features and electrochemical properties using an artificial neural network. Mater. Des. 2016, 112, 410–418. [Google Scholar]
- Ndukwe, A.I.; Anyakwo, C.N. Modelling of Corrosion Inhibition of Mild Steel in Hydrochloric Acid by Crushed Leaves of Sida Acuta (Malvaceae). Int. J. Eng. Sci. 2017, 6, 22–33. [Google Scholar] [CrossRef]
- Khaled, K.F.; Mobarak, N.A. A Predictive Model for Corrosion Inhibition of Mild Steel by Thiophene and Its Derivatives Using Artificial Neural Network. Int. J. Electrochem. Sci. 2012, 7, 1045–1059. [Google Scholar]
- Khaled, K.F. Studies of iron corrosion inhibition using chemical, electrochemical and computer simulation techniques. Electrochim. Acta 2010, 55, 6523–6532. [Google Scholar] [CrossRef]
- Colorado-Garrido, D.; Ortega-Toledo, D.M.; Hernández, J.A.; González-Rodríguez, J.G.; Uruchurtu, J. Neural networks for Nyquist plots prediction during corrosion inhibition of a pipeline steel. J. Solid State Electrochem. 2009, 13, 1715–1722. [Google Scholar] [CrossRef]
- Efimov, A.A.; Moskvin, L.N.; Pykhteev, O.Y.; Epimakhov, T.V. Simulation of corrosion processes in the closed system steel-water coolant. Radiochemistry 2011, 53, 19–25. [Google Scholar] [CrossRef]
- Hernández, M.; Genescá, J.; Uruchurtu, J.; Barba, A. Correlation between electrochemical impedance and noise measurements of waterborne coatings. Corros. Sci. 2009, 51, 499–510. [Google Scholar] [CrossRef]
- Mareci, D.; Suditu, G.D.; Chelariu, R.; Trincă, L.C.; Curteanu, S. Prediction of corrosion resistance of some dental metallic materials applying artificial neural networks. Mater. Corros. 2016, 67, 1213–1219. [Google Scholar] [CrossRef]
- Komijani, H.; Rezaeihassanabadi, S.; Parsaei, M.R.; Maleki, S. Radial basis function neural network for electrochemical impedance prediction at presence of corrosion inhibitor. Period. Polytech. Chem. Eng. 2017, 61, 128–132. [Google Scholar] [CrossRef]
- Kumar, G.; Buchheit, R.G. Use of Artificial Neural Network Models to Predict Coated Component Life from Short-Term Electrochemical Impedance Spectroscopy Measurements. Corrosion 2008, 64, 241–254. [Google Scholar] [CrossRef]
- Chelariu, R.; Suditu, G.D.; Mareci, D.; Bolat, G.; Cimpoesu, N.; Leon, F.; Curteanu, S. Prediction of Corrosion Resistance of Some Dental Metallic Materials with an Adaptive Regression Model. JOM 2015, 67, 767–774. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Y.; Jungwirth, S.; Seely, N.; Fan, Y.; Shi, X. Corrosion inhibitors for metals in maintenance equipment: Introduction and recent developments. Corros. Rev. 2014, 32, 163–181. [Google Scholar] [CrossRef]
- Shi, X.; Liu, Y.; Mooney, M.; Berry, M.; Hubbard, B.; Nguyen, T.A. Laboratory investigation and neural networks modeling of deicer ingress into portlan cement concret and its corrosion implications. Corros. Rev. 2010, 28, 105–154. [Google Scholar] [CrossRef]
- Cristea, M.; Varvara, S.; Muresan, L. Popescu Neural networks approach for simul ation of electroc he mical impedance diagrams. Indian J. Chem. 2003, 42A, 764–768. [Google Scholar]
- Ciucci, F.; Chen, C. Analysis of electrochemical impedance spectroscopy data using the distribution of relaxation times: A Bayesian and hierarchical Bayesian approach. Electrochim. Acta 2015, 167, 439–454. [Google Scholar] [CrossRef]
- Bonora, P.; Deflorian, F.; Fedrizzi, L. Electrochemical impedance spectroscopy as a tool for investigating underpaint corrosion. Electrochim. Acta 1996, 41, 1073–1082. [Google Scholar] [CrossRef]
- Boukhari, Y.; Boucherit, M.N.; Zaabat, M.; Amzert, S.; Brahimi, K. Artificial intelligence to predict inhibition performance of pitting corrosion. J. Fundam. Appl. Sci. 2017, 9, 308–332. [Google Scholar] [CrossRef]
- Macdonald, D.D. Reflections on the history of electrochemical impedance spectroscopy. Electrochim. Acta 2006, 51, 1376–1388. [Google Scholar] [CrossRef]
- Sola, J.; Sevilla, J. Importance of input data normalization for the application of neural networks to complex industrial problems. IEEE Trans. Nucl. Sci. 1997, 44, 1464–1468. [Google Scholar] [CrossRef]
- Bassam, A.; Conde-Gutierrez, R.A.; Castillo, J.; Laredo, G.; Hernandez, J.A. Direct neural network modeling for separation of linear and branched paraffins by adsorption process for gasoline octane number improvement. Fuel 2014, 124, 158–167. [Google Scholar] [CrossRef]
- Khataee, A.R.; Kasiri, M.B. Artificial neural networks modeling of contaminated water treatment processes by homogeneous and heterogeneous nanocatalysis. J. Mol. Catal. A Chem. 2010, 331, 86–100. [Google Scholar] [CrossRef]
- Hernández, J.A.; Colorado, D. Uncertainty analysis of COP prediction in a water purification system integrated into a heat transformer using several artificial neural networks. Desalination Water Treat. 2013, 51, 1443–1456. [Google Scholar] [CrossRef]
- Ghorbani, M.A.; Khatibi, R.; Hosseini, B.; Bilgili, M. Relative importance of parameters affecting wind speed prediction using artificial neural networks. Theor. Appl. Climatol. 2013, 114, 107–114. [Google Scholar] [CrossRef]
- Razvarz, S.; Jafari, R. ICA and ANN Modeling for Photocatalytic Removal of Pollution in Wastewater. Math. Comput. Appl. 2017, 22, 38. [Google Scholar] [CrossRef]
| Variable | Interval | Units | |
|---|---|---|---|
| Input | Frequency (f) | 0.01–100,000 | Hz |
| Temperature (T) | 25, 40 and 60 | °C | |
| Concentration (X) | 0, 5, 10, 25, 50 and 100 | ppm | |
| Output | Zre | 2.43–30,730.92 | Ω·cm2 |
| Zim | 0.06–14,635.77 | Ω·cm2 | |
| Zmod | 2.54–34,028.29 | Ω·cm2 | |
| Number of Neurons (S) | Weigths | Bias | ||||
|---|---|---|---|---|---|---|
| Hidden Layer (S = 8, K = 3), Wi = (S, K) | Output Layer (l = 1) | b1 (S) | b2 (l = 1) | |||
| Temperature (K = 2) | Concentration (K = 3) | Frequency (K = 1) | Wo (S) | |||
| 1 | −33.646 | −20.438 | 0.787 | −2747.15 | 38.4 | 3852.324 |
| 2 | −0.083 | −0.218 | −14,401.331 | 10,146.758 | 1440 | - |
| 3 | −35.456 | 20.288 | −0.783 | 2747.545 | 9.26 | - |
| 4 | 29.495 | 212.895 | 237.096 | 3870.101 | −43.1 | - |
| 5 | −0.084 | −0.222 | −14,575.934 | −3403.786 | 1460 | - |
| 6 | −3.519 | 20.429 | −0.783 | −2747.269 | −4.93 | - |
| 7 | 0.285 | −0.118 | −184.512 | 978.928 | 14.4 | - |
| 8 | −55.035 | −20.405 | 0.783 | −2747.447 | 10.8 | - |
| Number of Neurons (S) | Weigths | Bias | ||||
|---|---|---|---|---|---|---|
| Hidden Layer (S = 16, K = 3), Wi = (S, K) | Output Layer (l = 1) | b1 (S) | b2 (l = 1) | |||
| Temperature (K = 2) | Concentration (K = 3) | Frequency (K = 1) | Wo (S) | |||
| 1 | 6.614 | −23.974 | 0 | −764.894 | −3.78 | 650.218 |
| 2 | −0.036 | −0.011 | 9166.232 | −1805.728 | −915 | - |
| 3 | −0.191 | 0.322 | 21.357 | −102.331 | 0.665 | - |
| 4 | −332.336 | −192.892 | 0.786 | −363.086 | 329 | - |
| 5 | −135.744 | −142.424 | 0.003 | 650.751 | 142 | - |
| 6 | 1302.857 | 1486.882 | 361.305 | 368.812 | −1950 | - |
| 7 | −1.379 | −4.616 | −188.514 | 247.849 | 16.9 | - |
| 8 | 236.332 | −946.128 | 93.239 | 97.318 | 173 | - |
| 9 | 11.089 | −9.867 | −0.003 | −585.071 | 0.621 | - |
| 10 | 6.134 | −3.169 | −0.371 | −21.576 | 0.216 | - |
| 11 | −14.635 | −17.402 | −0.018 | −291.533 | 10.9 | - |
| 12 | −0.316 | 0.135 | −262.205 | 187.906 | 23.3 | - |
| 13 | −0.042 | −0.012 | 9380.565 | 629.753 | −937 | - |
| 14 | −4.066 | 2.754 | 0.02 | −396.08 | −0.54 | - |
| 15 | 5.255 | −17.41 | −0.015 | 287.948 | 2.15 | - |
| 16 | 1.68 | 3.64 | 169.097 | 510.83 | −14.6 | - |
| Number of Neurons (S) | Weigths | Bias | ||||
|---|---|---|---|---|---|---|
| Hidden Layer (S = 16, K = 3), Wi = (S, K) | Output Layer (l = 1) | b1 (S) | b2 (l = 1) | |||
| Temperature (K = 2) | Concentration (K = 3) | Frequency (K = 1) | Wo (S) | |||
| 1 | −33.176 | 17.960 | 0.012 | −547.000 | −17.189 | 552.201 |
| 2 | 3.805 | −69.199 | 1271.784 | 527.000 | −61.965 | - |
| 3 | 0.083 | 1.466 | 251.299 | −107.000 | −22.409 | - |
| 4 | −0.018 | −0.092 | −6863.647 | −1800.000 | 685.730 | - |
| 5 | −0.944 | 25.642 | −0.678 | −235.000 | −7.706 | - |
| 6 | −22.081 | −11.516 | 0.534 | −49.100 | 23.759 | - |
| 7 | −0.017 | −0.100 | −7271.011 | 654.000 | 726.734 | - |
| 8 | −33.898 | −11.118 | 0.529 | 49.200 | 34.268 | - |
| 9 | −0.940 | 21.966 | −0.679 | 236.000 | −6.602 | - |
| 10 | −0.601 | −0.365 | 37.056 | −168.000 | 0.104 | - |
| 11 | 4.029 | 145.354 | 114.095 | 547.000 | −22.550 | - |
| 12 | −17.393 | −10.582 | 15.370 | 0.084 | 8.632 | - |
| 13 | 20.647 | −2.031 | 1124.730 | −117.000 | −110.286 | - |
| 14 | −272.457 | −176.891 | 278.738 | −0.078 | 123.102 | - |
| 15 | −0.020 | −0.083 | −6356.422 | 2930.000 | 634.291 | - |
| 16 | −1982.569 | 417.592 | −660.569 | 0.112 | 735.831 | - |
| Output Variable | Architecture | R2 | MSE | Intercept Slope Test | |||
|---|---|---|---|---|---|---|---|
| amin | amax | bmax | bmin | ||||
| Zre | 3:8:1 | 0.9875 | 0.00659 | 0.0251 | −0.0079 | 1.0049 | 0.9862 |
| Zim | 3:16:1 | 0.9944 | 0.00475 | 0.0186 | −0.0013 | 1.0002 | 0.9878 |
| Zmod | 3:16:1 | 0.9876 | 0.00686 | 0.0198 | −0.0059 | 1.0009 | 0.9873 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Millán-Ocampo, D.E.; Parrales-Bahena, A.; González-Rodríguez, J.G.; Silva-Martínez, S.; Porcayo-Calderón, J.; Hernández-Pérez, J.A. Modelling of Behavior for Inhibition Corrosion of Bronze Using Artificial Neural Network (ANN). Entropy 2018, 20, 409. https://doi.org/10.3390/e20060409
Millán-Ocampo DE, Parrales-Bahena A, González-Rodríguez JG, Silva-Martínez S, Porcayo-Calderón J, Hernández-Pérez JA. Modelling of Behavior for Inhibition Corrosion of Bronze Using Artificial Neural Network (ANN). Entropy. 2018; 20(6):409. https://doi.org/10.3390/e20060409
Chicago/Turabian StyleMillán-Ocampo, D. Elusaí, Arianna Parrales-Bahena, J. Gonzalo González-Rodríguez, Susana Silva-Martínez, Jesús Porcayo-Calderón, and J. Alfredo Hernández-Pérez. 2018. "Modelling of Behavior for Inhibition Corrosion of Bronze Using Artificial Neural Network (ANN)" Entropy 20, no. 6: 409. https://doi.org/10.3390/e20060409
APA StyleMillán-Ocampo, D. E., Parrales-Bahena, A., González-Rodríguez, J. G., Silva-Martínez, S., Porcayo-Calderón, J., & Hernández-Pérez, J. A. (2018). Modelling of Behavior for Inhibition Corrosion of Bronze Using Artificial Neural Network (ANN). Entropy, 20(6), 409. https://doi.org/10.3390/e20060409







