On f-Divergences: Integral Representations, Local Behavior, and Inequalities
Abstract
1. Introduction
- (1)
- (2)
- Inequalities which rely on a characterization of the exact locus of the joint range of f-divergences [29];
- (3)
- (4)
- Sharp f-divergence inequalities by using numerical tools for maximizing or minimizing an f-divergence subject to a finite number of constraints on other f-divergences [33];
- (5)
- (6)
- (7)
- (8)
- (9)
- Bounds among f-divergences (or functions of f-divergences such as the Rényi divergence) via integral representations of these divergence measures [22] Section 8;
- (10)
- Inequalities which rely on variational representations of f-divergences (e.g., [54] Section 2).
2. Preliminaries and Notation
- (1)
- (2)
- there exists a constantsuch that
- (1)
- Relative entropy:with
- (2)
- (3)
- Some of the significance of the Hellinger divergence stems from the following facts:
- -
- The analytic extension of at yields
- -
- The chi-squared divergence [61] is the second order Hellinger divergence (see, e.g., [62] p. 48), i.e.,Note that, due to Proposition 1,where can be defined as
- -
- -
- -
- The Rényi divergence of order is a one-to-one transformation of the Hellinger divergence of the same order [11] (14):
- -
- The Alpha-divergence of order , as it is defined in [64] and ([65] (4)), is a generalized relative entropy which (up to a scaling factor) is equal to the Hellinger divergence of the same order . More explicitly,where denotes the Alpha-divergence of order . Note, however, that the Beta and Gamma-divergences in [65], as well as the generalized divergences in [66,67], are not f-divergences in general.
- (4)
- Specifically, for , letand the total variation distance is expressed as an f-divergence:
- (5)
- Note that
- (6)
- The special case of (41) with gives the Jensen-Shannon divergence (a.k.a. capacitory discrimination):
- (7)
- (8)
- The following relation to the total variation distance holds:and the DeGroot statistical information and the divergence are related as follows [22] (384):
3. New Integral Representations of -Divergences
- (1)
- Let
- -
- be differentiable on;
- -
- be the non-negative weight function given, for, by
- -
- the functionbe given by
Then, - (2)
- More generally, for an arbitrary, letbe a modified real-valued function defined asThen,
- (1)
- We first assume an additional requirement that f is strictly convex at 1. In view of Lemma 2,Since by assumption is differentiable on and strictly convex at 1, the function g in (54) is differentiable on . In view of (84) and (85), substituting in (60) for implies thatwhere is given byfor , where (88) follows from (54). Due to the monotonicity properties of g in Lemma 1, (87) implies that for , and for . Hence, the weight function in (79) satisfiesWe now extend the result in (81) when is differentiable on , but not necessarily strictly convex at 1. To that end, let be defined asThis implies that is differentiable on , and it is also strictly convex at 1. In view of the proof of (81) when f is strict convexity of f at 1, the application of this result to the function s in (90) yieldsIn view of (6), (22), (23), (25) and (90),from (79), (89), (90) and the convexity and differentiability of , it follows that the weight function satisfiesfor . Furthermore, by applying the result in (81) to the chi-squared divergence in (25) whose corresponding function for is strictly convex at 1, we obtain
- (2)
- (1)
- Relative entropy [22] (219):
- (2)
- Hellinger divergence of order [22] (434) and (437):
- (3)
- Rényi divergence [22] (426) and (427): For ,
- (4)
- divergence: For
- (5)
- DeGroot statistical information:
- (6)
- Triangular discrimination:
- (7)
- Lin’s measure: For ,where denotes the binary entropy function. Specifically, the Jensen-Shannon divergence admits the integral representation:
- (8)
- Jeffrey’s divergence:
- (9)
- divergence: For ,
- is a continuously differentiable function of γ on , and ;
- the sets and determine, respectively, the relative information spectrum on and ;
- for ,
- is a continuously differentiable function of ω on ,and is, respectively, non-negative or non-positive on and ;
- the sets and determine, respectively, the relative information spectrum on and ;
- forforand
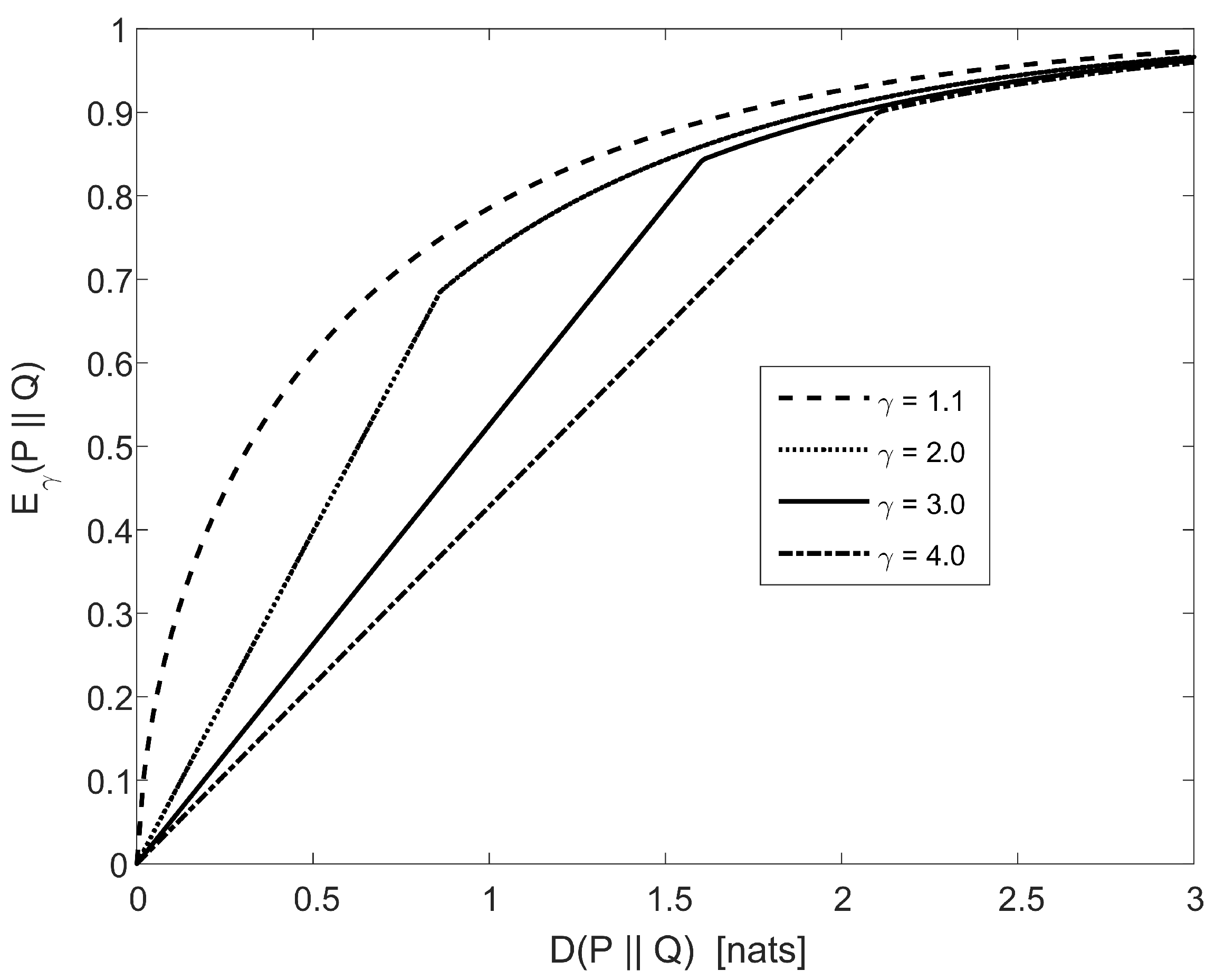
4. New -Divergence Inequalities
Bayesian Binary Hypothesis Testing
- (1)
- (2)
- (1)
- for ,
- (2)
- for ,
5. Local Behavior of f-Divergences
- be a sequence of probability measures on a measurable space ;
- the sequence converge to a probability measure Q in the sense thatwhere for all sufficiently large n;
- have continuous second derivatives at 1 and .
- P and Q be probability measures defined on a measurable space , , and suppose that
- , and be continuous at 1.
Acknowledgments
Conflicts of Interest
Appendix A. Proof of Theorem 2
- (1)
- (2)
- Hellinger divergence: In view of (22), for , the weight function in (79) which corresponds to in (23) can be verified to be equal tofor . In order to simplify the integral representation of the Hellinger divergence , we apply Theorem 1-(1). From (A3), setting in (82) implies that is given byfor . Hence, substituting (80) and (A4) into (83) yieldsThis proves (99). We next consider the following special cases:
- (3)
- (4)
- (5)
- DeGroot statistical information: In view of (50)–(51), since the function is not differentiable at the point for , Theorem 1 cannot be applied directly to get an integral representation of the DeGroot statistical information. To that end, for , consider the family of convex functions given by (see [3] (55))for . These differentiable functions also satisfywhich holds due to the identitiesThe application of Theorem 1-(1) to the set of functions withyieldsfor , andwith as defined in (80), and . From (A15) and (A18), it follows thatfor . In view of (50), (51), (80), (A14), (A19) and (A20), and the monotone convergence theorem,for . We next simplify (A23) as follows:
- -
- if , then and (A23) yields
- -
- (6)
- (7)
- (8)
- (9)
- divergence: Let , and let satisfy ; hence, . From (53), we getThe second line in the right side of (107) yields
References
- Basseville, M. Divergence measures for statistical data processing—An annotated bibliography. Signal Process. 2013, 93, 621–633. [Google Scholar] [CrossRef]
- Liese, F.; Vajda, I. Convex Statistical Distances. In Teubner-Texte Zur Mathematik; Springer: Leipzig, Germany, 1987; Volume 95. [Google Scholar]
- Liese, F.; Vajda, I. On divergences and informations in statistics and information theory. IEEE Trans. Inf. Theory 2006, 52, 4394–4412. [Google Scholar] [CrossRef]
- Reid, M.D.; Williamson, R.C. Information, divergence and risk for binary experiments. J. Mach. Learn. Res. 2011, 12, 731–817. [Google Scholar]
- Tsybakov, A.B. Introduction to Nonparametric Estimation; Springer: New York, NY, USA, 2009. [Google Scholar]
- Vapnik, V.N. Statistical Learning Theory; John Wiley & Sons: Hoboken, NJ, USA, 1998. [Google Scholar]
- Verdú, S. Information Theory. Unpublished work. 2018. [Google Scholar]
- Csiszár, I. Axiomatic characterization of information measures. Entropy 2008, 10, 261–273. [Google Scholar] [CrossRef]
- Ali, S.M.; Silvey, S.D. A general class of coefficients of divergence of one distribution from another. J. R. Stat. Soc. Ser. B 1966, 28, 131–142. [Google Scholar]
- Csiszár, I. Eine Informationstheoretische Ungleichung und ihre Anwendung auf den Bewis der Ergodizität von Markhoffschen Ketten. Magyer Tud. Akad. Mat. Kutato Int. Koezl. 1963, 8, 85–108. [Google Scholar]
- Csiszár, I. A note on Jensen’s inequality. Stud. Sci. Math. Hung. 1966, 1, 185–188. [Google Scholar]
- Csiszár, I. Information-type measures of difference of probability distributions and indirect observations. Stud. Sci. Math. Hung. 1967, 2, 299–318. [Google Scholar]
- Csiszár, I. On topological properties of f-divergences. Stud. Sci. Math. Hung. 1967, 2, 329–339. [Google Scholar]
- Morimoto, T. Markov processes and the H-theorem. J. Phys. Soc. Jpn. 1963, 18, 328–331. [Google Scholar] [CrossRef]
- Liese, F. φ-divergences, sufficiency, Bayes sufficiency, and deficiency. Kybernetika 2012, 48, 690–713. [Google Scholar]
- DeGroot, M.H. Uncertainty, information and sequential experiments. Ann. Math. Stat. 1962, 33, 404–419. [Google Scholar] [CrossRef]
- Cohen, J.E.; Kemperman, J.H.B.; Zbăganu, G. Comparisons of Stochastic Matrices with Applications in Information Theory, Statistics, Economics and Population; Springer: Berlin, Germany, 1998. [Google Scholar]
- Feldman, D.; Österreicher, F. A note on f-divergences. Stud. Sci. Math. Hung. 1989, 24, 191–200. [Google Scholar]
- Guttenbrunner, C. On applications of the representation of f-divergences as averaged minimal Bayesian risk. In Proceedings of the Transactions of the 11th Prague Conferences on Information Theory, Statistical Decision Functions, and Random Processes, Prague, Czechoslovakia, 26–31 August 1992; pp. 449–456. [Google Scholar]
- Österreicher, F.; Vajda, I. Statistical information and discrimination. IEEE Trans. Inf. Theory 1993, 39, 1036–1039. [Google Scholar] [CrossRef]
- Torgersen, E. Comparison of Statistical Experiments; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Sason, I.; Verdú, S. f-divergence inequalities. IEEE Trans. Inf. Theory 2016, 62, 5973–6006. [Google Scholar] [CrossRef]
- Gibbs, A.L.; Su, F.E. On choosing and bounding probability metrics. Int. Stat. Rev. 2002, 70, 419–435. [Google Scholar] [CrossRef]
- Anwar, M.; Hussain, S.; Pecaric, J. Some inequalities for Csiszár-divergence measures. Int. J. Math. Anal. 2009, 3, 1295–1304. [Google Scholar]
- Simic, S. On logarithmic convexity for differences of power means. J. Inequal. Appl. 2007, 2007, 37359. [Google Scholar] [CrossRef]
- Simic, S. On a new moments inequality. Stat. Probab. Lett. 2008, 78, 2671–2678. [Google Scholar] [CrossRef]
- Simic, S. On certain new inequalities in information theory. Acta Math. Hung. 2009, 124, 353–361. [Google Scholar] [CrossRef]
- Simic, S. Moment Inequalities of the Second and Third Orders. Preprint. Available online: http://arxiv.org/abs/1509.0851 (accessed on 13 May 2016).
- Harremoës, P.; Vajda, I. On pairs of f-divergences and their joint range. IEEE Trans. Inf. Theory 2011, 57, 3230–3235. [Google Scholar] [CrossRef]
- Sason, I.; Verdú, S. f-divergence inequalities via functional domination. In Proceedings of the 2016 IEEE International Conference on the Science of Electrical Engineering, Eilat, Israel, 16–18 November 2016; pp. 1–5. [Google Scholar]
- Taneja, I.J. Refinement inequalities among symmetric divergence measures. Aust. J. Math. Anal. Appl. 2005, 2, 1–23. [Google Scholar]
- Taneja, I.J. Seven means, generalized triangular discrimination, and generating divergence measures. Information 2013, 4, 198–239. [Google Scholar] [CrossRef]
- Guntuboyina, A.; Saha, S.; Schiebinger, G. Sharp inequalities for f-divergences. IEEE Trans. Inf. Theory 2014, 60, 104–121. [Google Scholar] [CrossRef]
- Endres, D.M.; Schindelin, J.E. A new metric for probability distributions. IEEE Trans. Inf. Theory 2003, 49, 1858–1860. [Google Scholar] [CrossRef]
- Kafka, P.; Östreicher, F.; Vincze, I. On powers of f-divergences defining a distance. Stud. Sci. Math. Hung. 1991, 26, 415–422. [Google Scholar]
- Lu, G.; Li, B. A class of new metrics based on triangular discrimination. Information 2015, 6, 361–374. [Google Scholar] [CrossRef]
- Vajda, I. On metric divergences of probability measures. Kybernetika 2009, 45, 885–900. [Google Scholar]
- Gilardoni, G.L. On Pinsker’s and Vajda’s type inequalities for Csiszár’s f-divergences. IEEE Trans. Inf. Theory 2010, 56, 5377–5386. [Google Scholar] [CrossRef]
- Topsøe, F. Some inequalities for information divergence and related measures of discrimination. IEEE Trans. Inf. Theory 2000, 46, 1602–1609. [Google Scholar] [CrossRef]
- Sason, I.; Verdú, S. Upper bounds on the relative entropy and Rényi divergence as a function of total variation distance for finite alphabets. In Proceedings of the 2015 IEEE Information Theory Workshop, Jeju Island, Korea, 11–15 October 2015; pp. 214–218. [Google Scholar]
- Dragomir, S.S. Upper and lower bounds for Csiszár f-divergence in terms of the Kullback-Leibler divergence and applications. In Inequalities for Csiszár f-Divergence in Information Theory, RGMIA Monographs; Victoria University: Footscray, VIC, Australia, 2000. [Google Scholar]
- Dragomir, S.S. Upper and lower bounds for Csiszár f-divergence in terms of Hellinger discrimination and applications. In Inequalities for Csiszár f-Divergence in Information Theory, RGMIA Monographs; Victoria University: Footscray, VIC, Australia, 2000. [Google Scholar]
- Dragomir, S.S. An upper bound for the Csiszár f-divergence in terms of the variational distance and applications. In Inequalities for Csiszár f-Divergence in Information Theory, RGMIA Monographs; Victoria University: Footscray, VIC, Australia, 2000. [Google Scholar]
- Dragomir, S.S.; Gluščević, V. Some inequalities for the Kullback-Leibler and χ2-distances in information theory and applications. Tamsui Oxf. J. Math. Sci. 2001, 17, 97–111. [Google Scholar]
- Dragomir, S.S. Bounds for the normalized Jensen functional. Bull. Aust. Math. Soc. 2006, 74, 471–478. [Google Scholar] [CrossRef]
- Kumar, P.; Chhina, S. A symmetric information divergence measure of the Csiszár’s f-divergence class and its bounds. Comp. Math. Appl. 2005, 49, 575–588. [Google Scholar] [CrossRef]
- Taneja, I.J. Bounds on non-symmetric divergence measures in terms of symmetric divergence measures. J. Comb. Inf. Syst. Sci. 2005, 29, 115–134. [Google Scholar]
- Binette, O. A note on reverse Pinsker inequalities. Preprint. Available online: http://arxiv.org/abs/1805.05135 (accessed on 14 May 2018).
- Gilardoni, G.L. On the minimum f-divergence for given total variation. C. R. Math. 2006, 343, 763–766. [Google Scholar] [CrossRef]
- Gilardoni, G.L. Corrigendum to the note on the minimum f-divergence for given total variation. C. R. Math. 2010, 348, 299. [Google Scholar] [CrossRef]
- Gushchin, A.A. The minimum increment of f-divergences given total variation distances. Math. Methods Stat. 2016, 25, 304–312. [Google Scholar] [CrossRef]
- Sason, I. Tight bounds on symmetric divergence measures and a refined bound for lossless source coding. IEEE Trans. Inf. Theory 2015, 61, 701–707. [Google Scholar] [CrossRef]
- Sason, I. On the Rényi divergence, joint range of relative entropies, and a channel coding theorem. IEEE Trans. Inf. Theory 2016, 62, 23–34. [Google Scholar] [CrossRef]
- Liu, J.; Cuff, P.; Verdú, S. Eγ-resolvability. IEEE Trans. Inf. Theory 2017, 63, 2629–2658. [Google Scholar]
- Csiszár, I.; Shields, P.C. Information Theory and Statistics: A Tutorial. Found. Trends Commun. Inf. Theory 2004, 1, 417–528. [Google Scholar] [CrossRef]
- Pardo, M.C.; Vajda, I. On asymptotic properties of information-theoretic divergences. IEEE Trans. Inf. Theory 2003, 49, 1860–1868. [Google Scholar] [CrossRef]
- Polyanskiy, Y.; Poor, H.V.; Verdú, S. Channel coding rate in the finite blocklength regime. IEEE Trans. Inf. Theory 2010, 56, 2307–2359. [Google Scholar] [CrossRef]
- Bretagnolle, J.; Huber, C. Estimation des densités: Risque minimax. Probab. Theory Relat. Fields 1979, 47, 119–137. [Google Scholar]
- Vajda, I. Note on discrimination information and variation. IEEE Trans. Inf. Theory 1970, 16, 771–773. [Google Scholar] [CrossRef]
- Jeffreys, H. An invariant form for the prior probability in estimation problems. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1946, 186, 453–461. [Google Scholar] [CrossRef]
- Pearson, K. On the criterion that a given system of deviations from the probable in the case of a correlated system of variables is such that it can be reasonably supposed to have arisen from random sampling. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1900, 50, 157–175. [Google Scholar] [CrossRef]
- Le Cam, L. Asymptotic Methods in Statistical Decision Theory; Springer: New York, NY, USA, 1986. [Google Scholar]
- Kailath, T. The divergence and Bhattacharyya distance measures in signal selection. IEEE Trans. Commun. Technol. 1967, 15, 52–60. [Google Scholar] [CrossRef]
- Amari, S.I.; Nagaoka, H. Methods of Information Geometry; Oxford University Press: New York, NY, USA, 2000. [Google Scholar]
- Cichocki, A.; Amari, S.I. Families of Alpha- Beta- and Gamma-divergences: Flexible and robust measures of similarities. Entropy 2010, 12, 1532–1568. [Google Scholar] [CrossRef]
- Cichocki, A.; Cruces, S.; Amari, S.I. Generalized Alpha-Beta divergences and their application to robust nonnegative matrix factorization. Entropy 2011, 13, 134–170. [Google Scholar] [CrossRef]
- Cichocki, A.; Cruces, S.; Amari, S.I. Log-determinant divergences revisited: Alpha-Beta and Gamma log-det divergences. Entropy 2015, 17, 2988–3034. [Google Scholar] [CrossRef]
- Lin, J. Divergence measures based on the Shannon entropy. IEEE Trans. Inf. Theory 1991, 37, 145–151. [Google Scholar] [CrossRef]
- Polyanskiy, Y.; Wu, Y. Dissipation of information in channels with input constraints. IEEE Trans. Inf. Theory 2016, 62, 35–55. [Google Scholar] [CrossRef]
- Kullback, S. A lower bound for discrimination information in terms of variation. IEEE Trans. Inf. Theory 1967, 13, 126–127. [Google Scholar] [CrossRef]
- Kemperman, J.H.B. On the optimal rate of transmitting information. Ann. Math. Stat. 1969, 40, 2156–2177. [Google Scholar] [CrossRef]
- Corless, R.M.; Gonnet, G.H.; Hare, D.E.; Jeffrey, D.J.; Knuth, D.E. On the Lambert W function. Adv. Comput. Math. 1996, 5, 329–359. [Google Scholar] [CrossRef]
- Van Erven, T.; Harremoës, P. Rényi divergence and Kullback-Leibler divergence. IEEE Trans. Inf. Theory 2014, 60, 3797–3820. [Google Scholar] [CrossRef]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sason, I. On f-Divergences: Integral Representations, Local Behavior, and Inequalities. Entropy 2018, 20, 383. https://doi.org/10.3390/e20050383
Sason I. On f-Divergences: Integral Representations, Local Behavior, and Inequalities. Entropy. 2018; 20(5):383. https://doi.org/10.3390/e20050383
Chicago/Turabian StyleSason, Igal. 2018. "On f-Divergences: Integral Representations, Local Behavior, and Inequalities" Entropy 20, no. 5: 383. https://doi.org/10.3390/e20050383
APA StyleSason, I. (2018). On f-Divergences: Integral Representations, Local Behavior, and Inequalities. Entropy, 20(5), 383. https://doi.org/10.3390/e20050383