Chaotic Attractors with Fractional Conformable Derivatives in the Liouville–Caputo Sense and Its Dynamical Behaviors
Abstract
1. Introduction
2. Mathematical Preliminaries
- , for all .
- , for all
- , if is a constant.
- .
- .
3. Adams–Moulton Scheme for Fractional Conformable Derivatives
4. Application and Numerical Examples
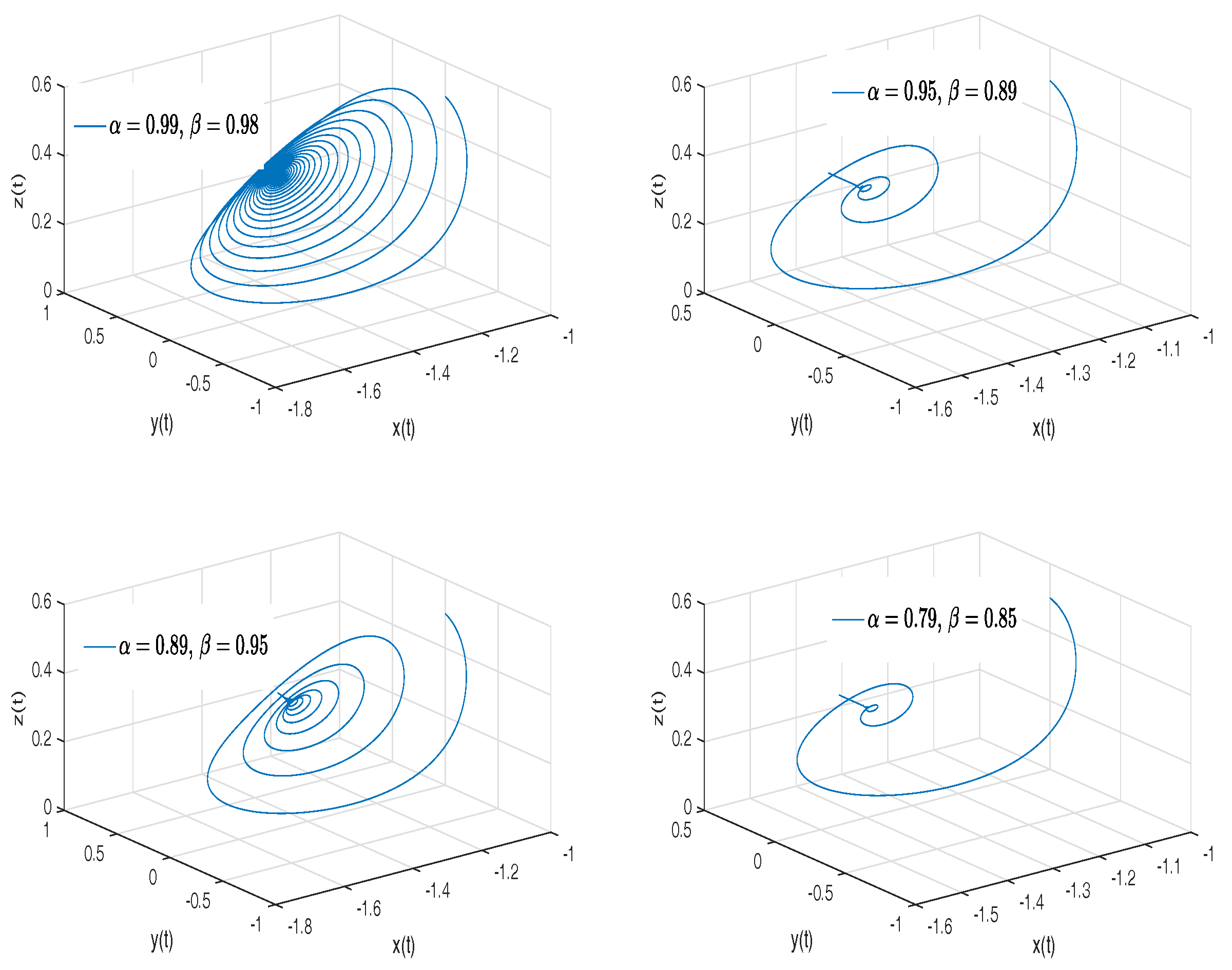
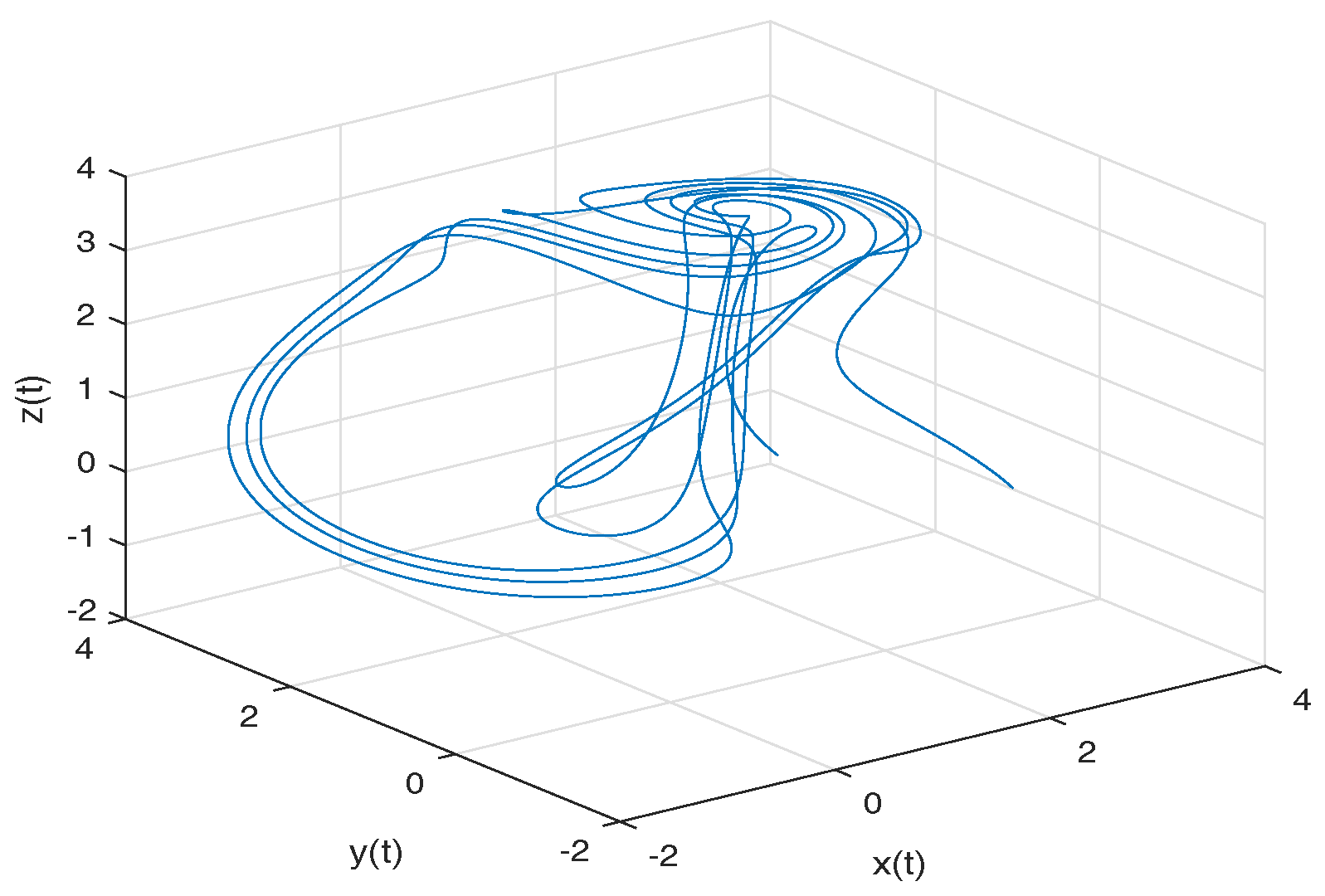
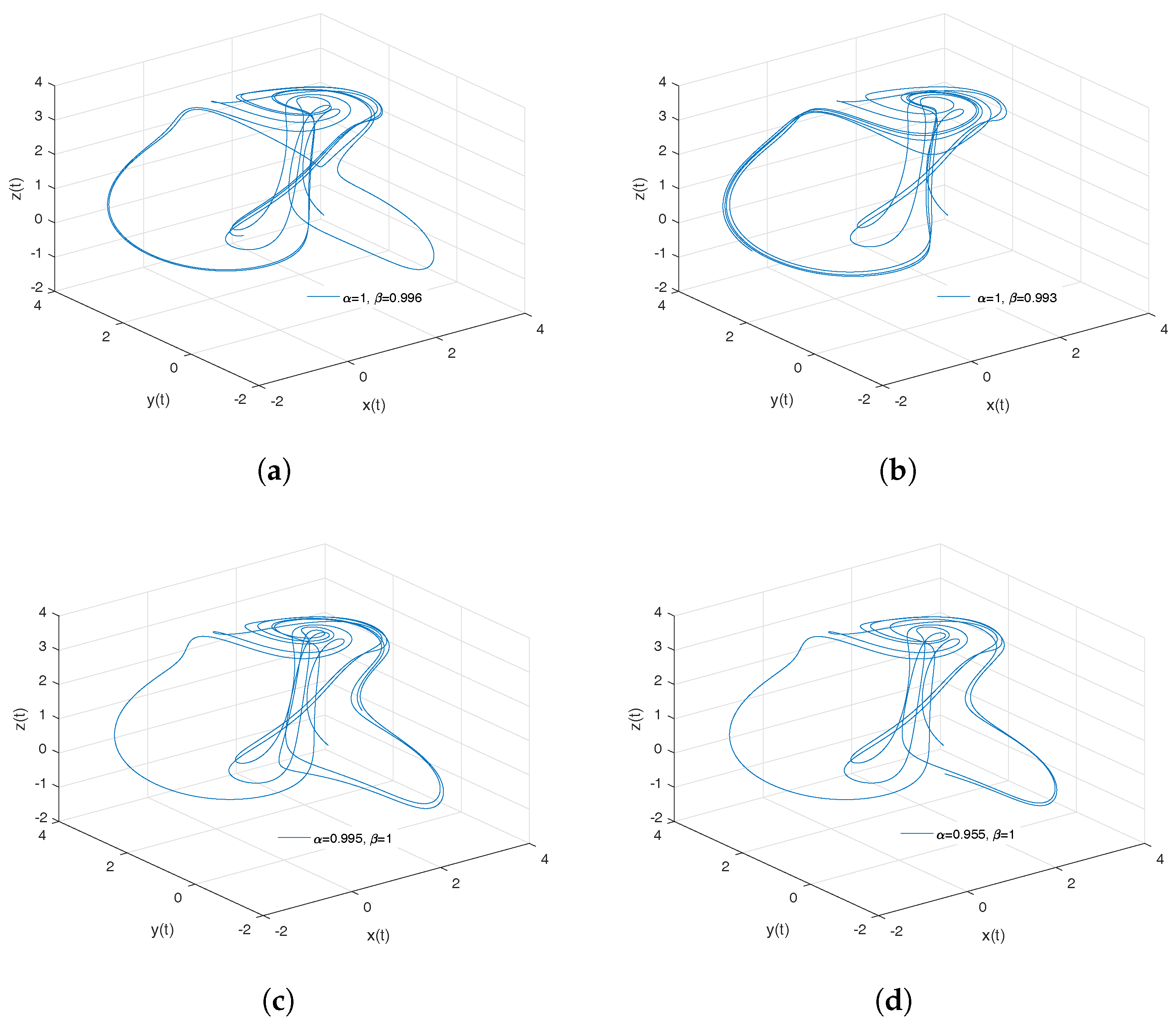
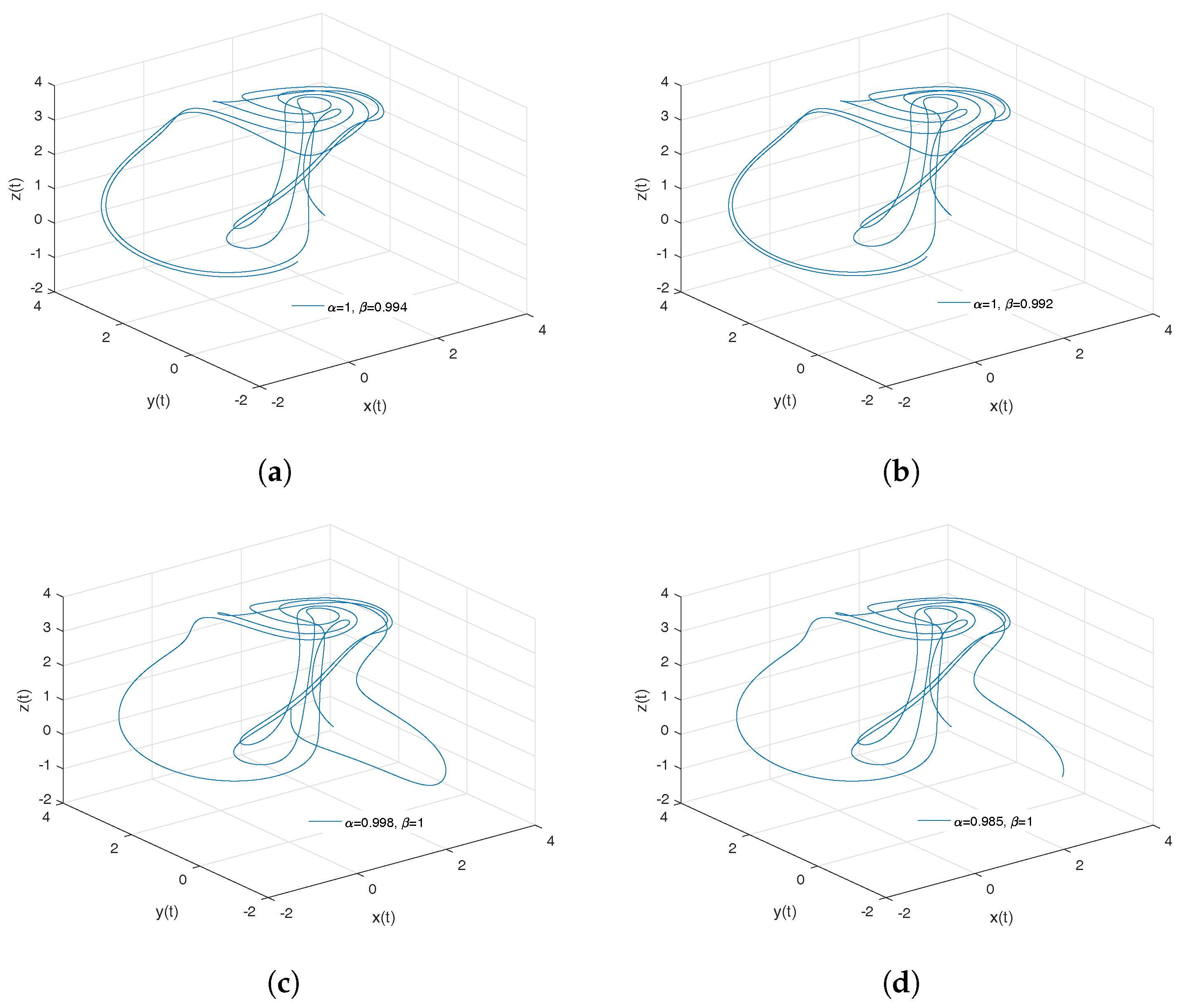
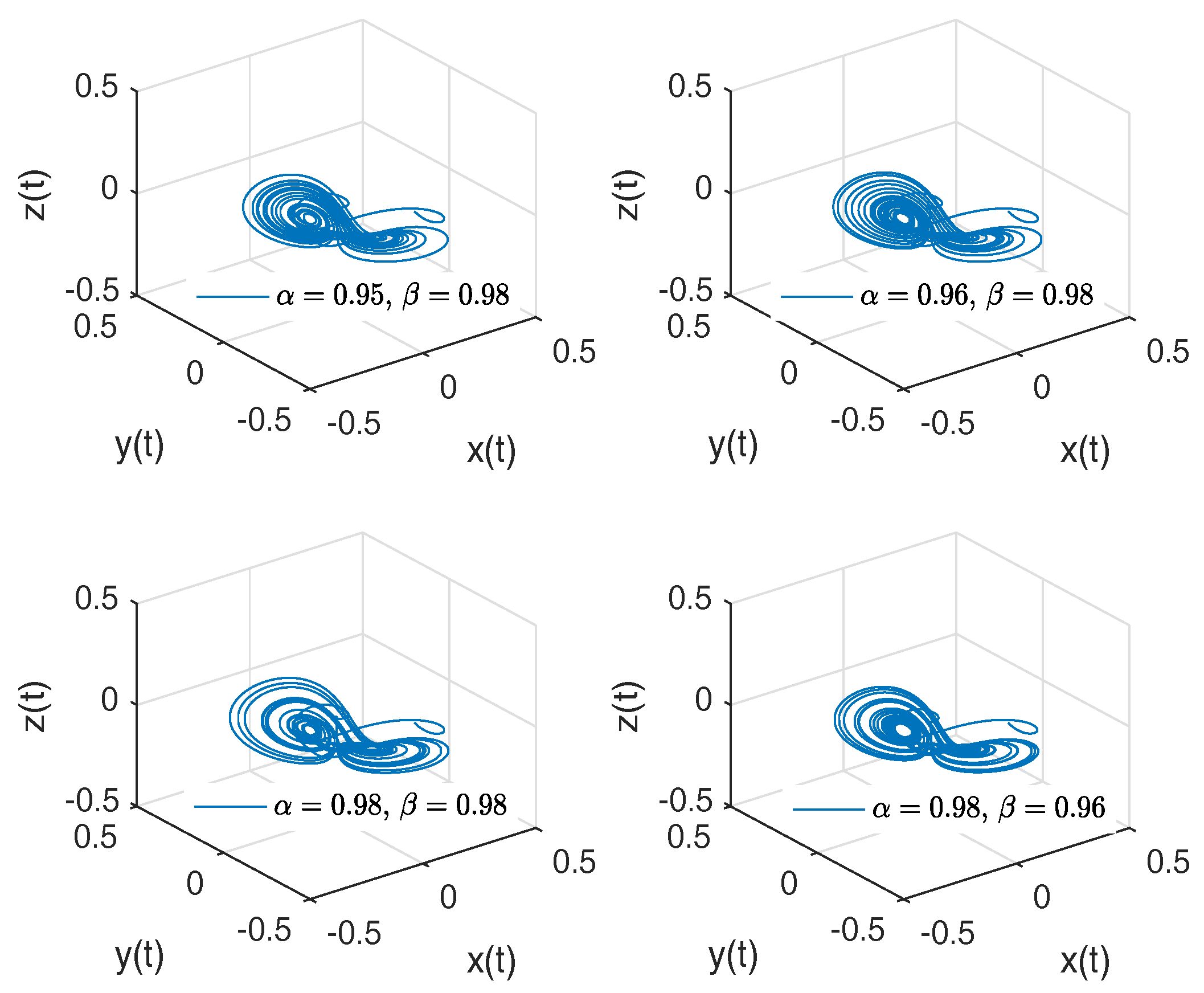
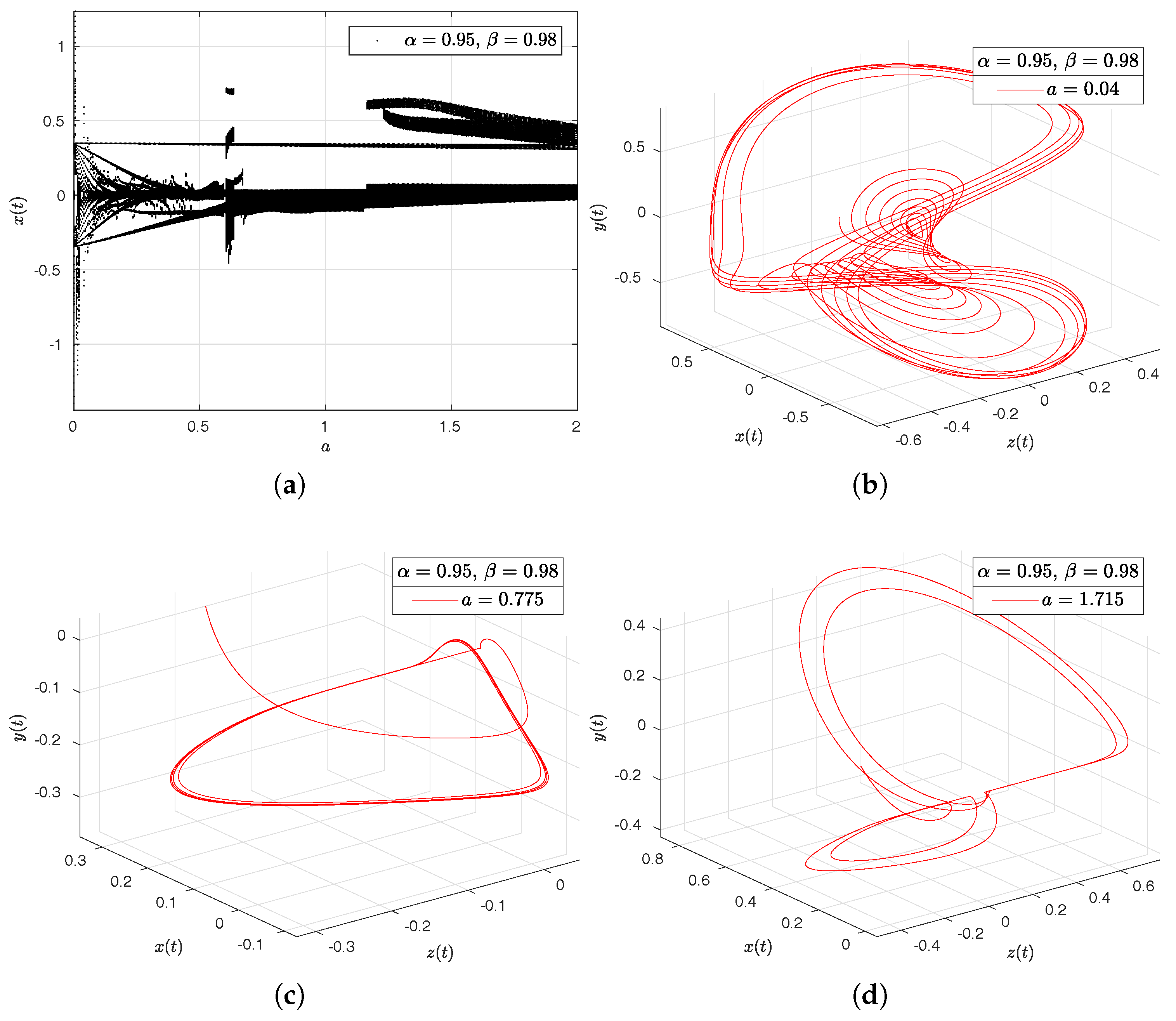
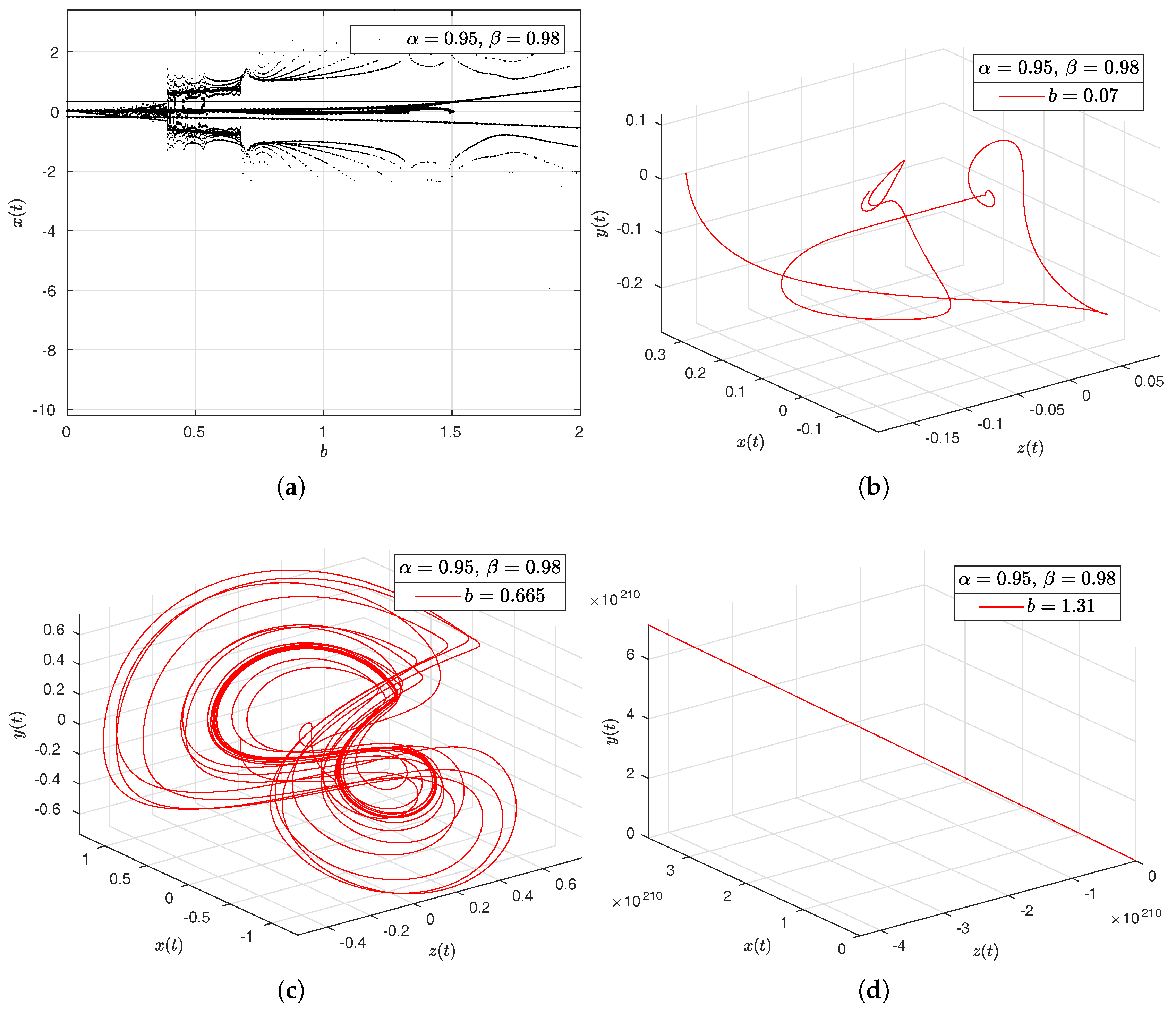
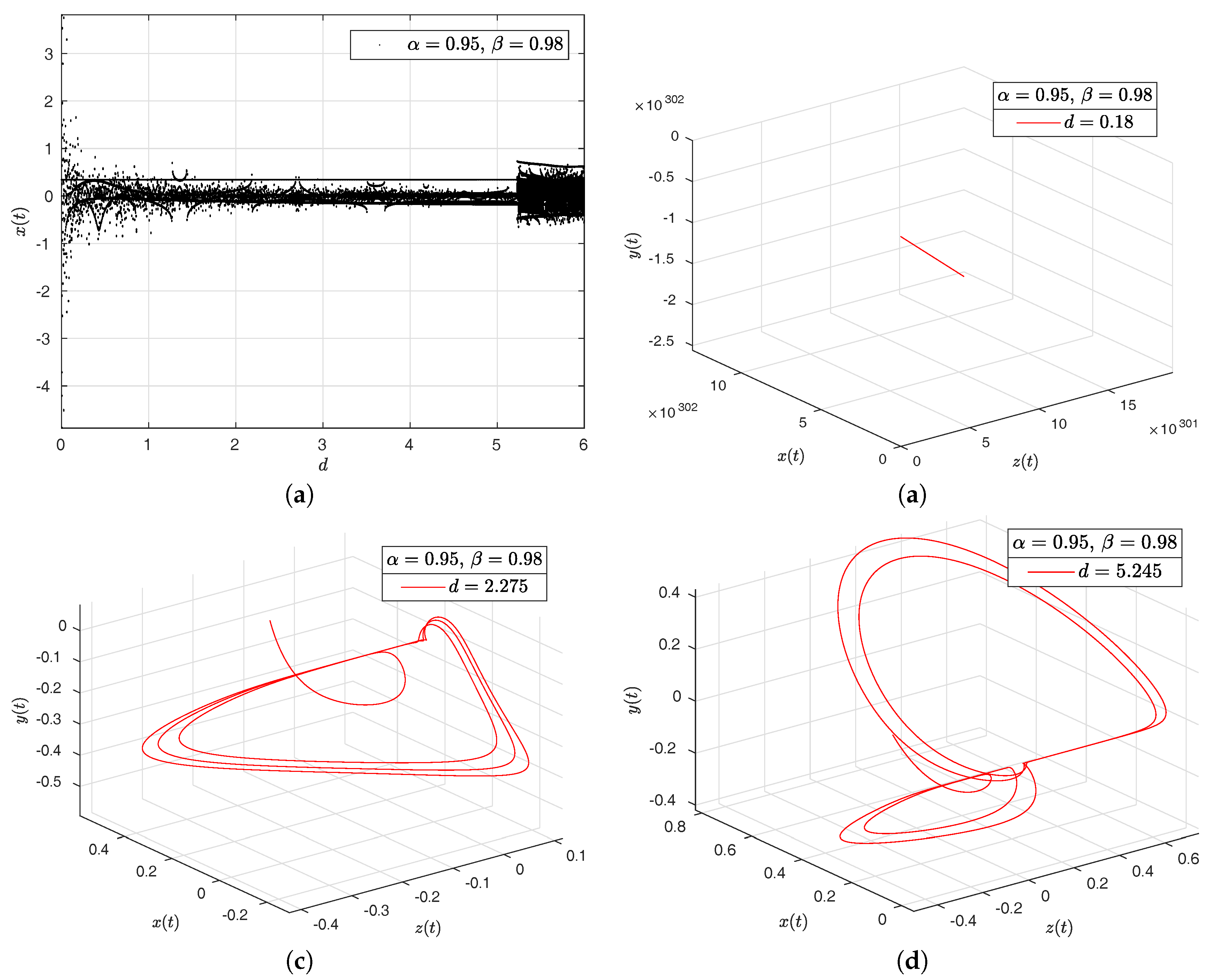
- Rabinovich–Fabrikant attractor. The model of Rabinovich–Fabrikant [44] was initially designed as a physical model describing the stochasticity arising from the modulation instability in a non-equilibrium dissipative medium. The Rabinovich–Fabrikant system is described by the following equations:where . The system (16) is chaotic for some values of a and b, but for , the system is dissipative.
- Observation. In the case when , we obtain the numerical solution of the Rabinovich–Fabrikant attractor in the Liouville–Caputo sense.
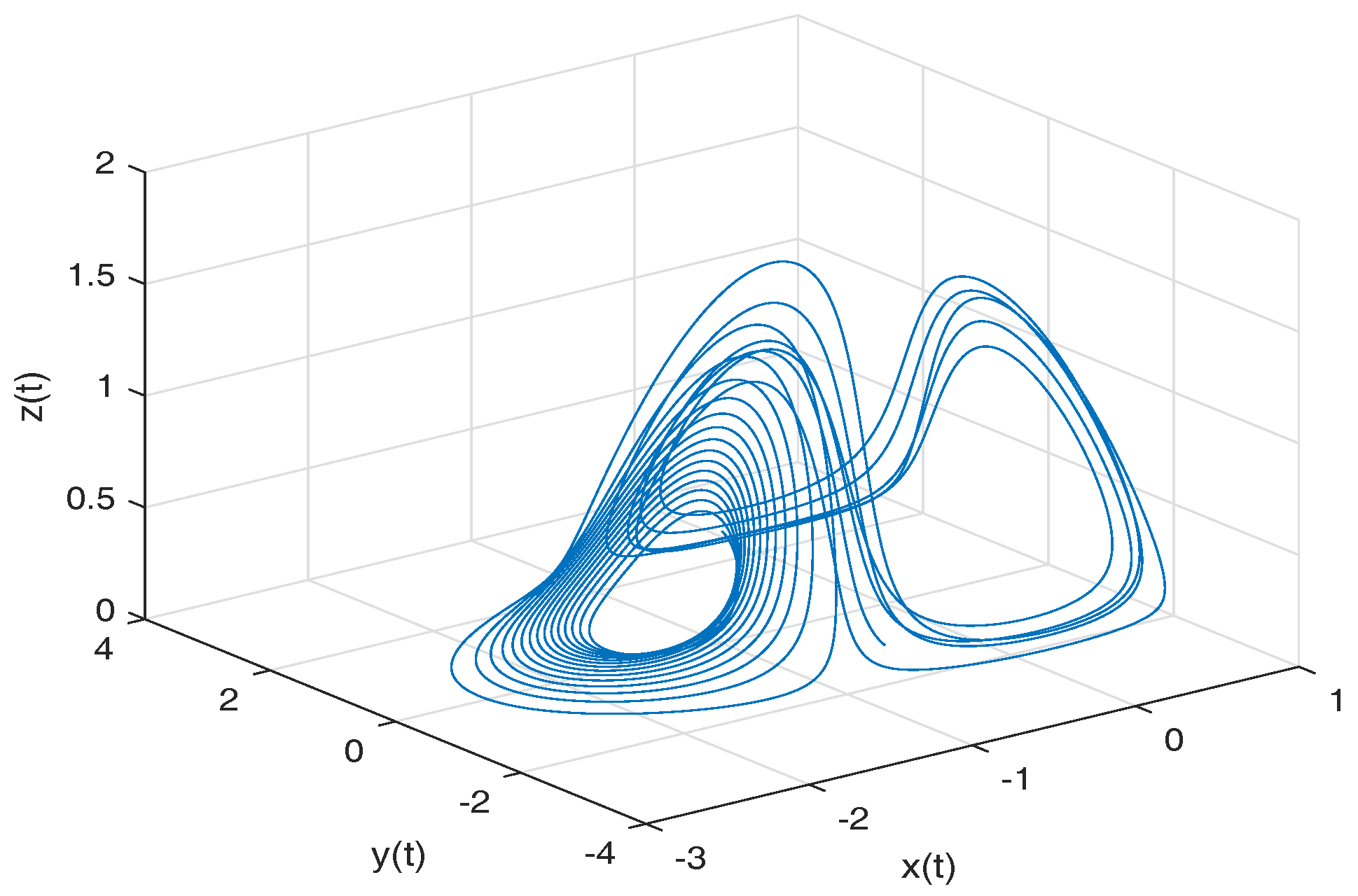
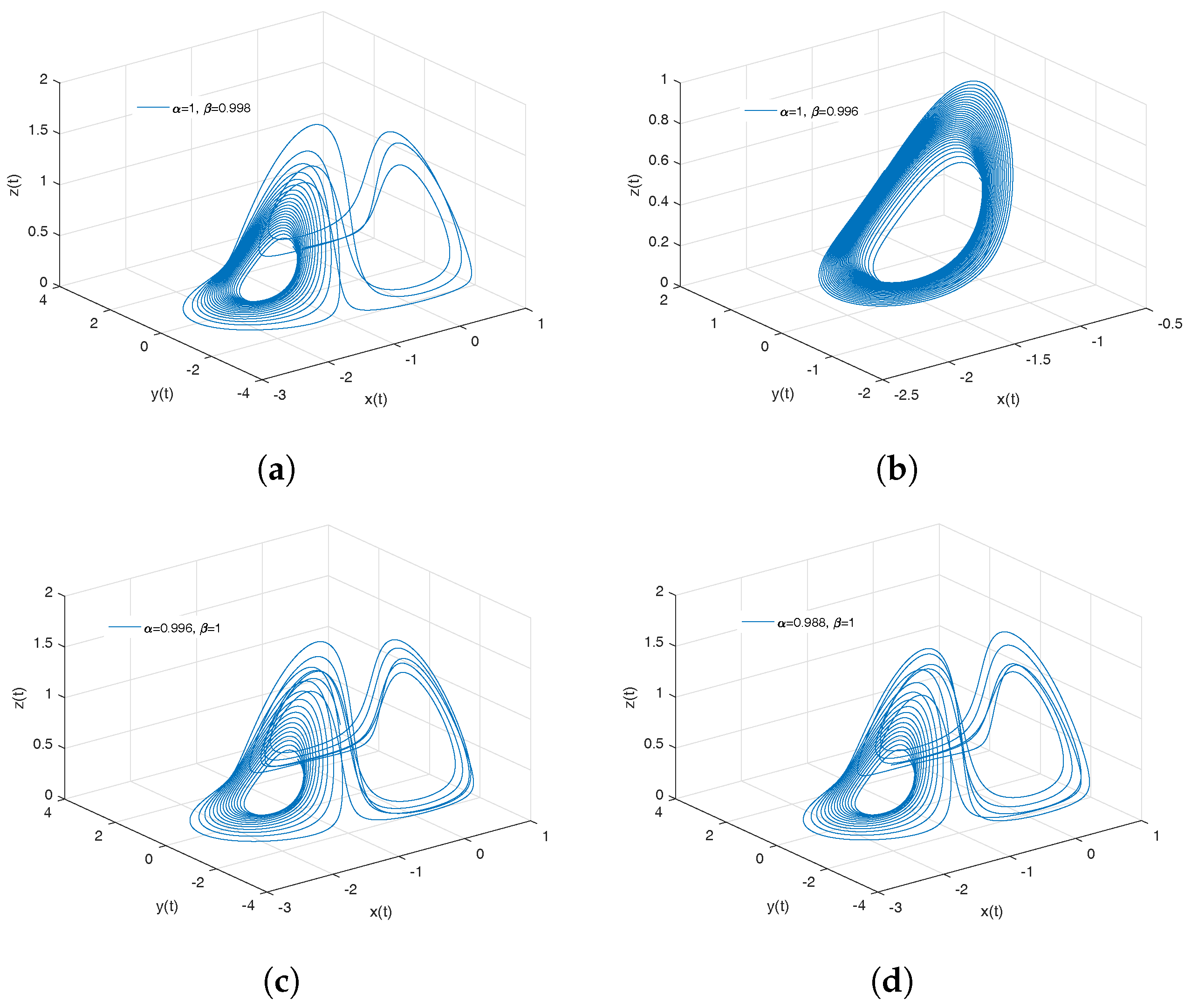
- Thomas’ cyclically symmetric attractor. Thomas in [45] proposed a mathematically three-dimensional cyclically symmetric attractor. This system is cyclically symmetric in the variables x, y, and z and considers a frictional damping b. The Thomas’ cyclically symmetric attractor is described by the following equations:where b can be considered a frictional damping for a particle moving in a three-dimensional lattice [46]. This attractor is tuned by a single value in any dimension of range 2 to 3; it also has the quality of transition from a dissipative system to a conservative system.
- Observation. In the case when , we obtain the numerical solution of the Thomas’ cyclically symmetric attractor in the Liouville–Caputo sense.
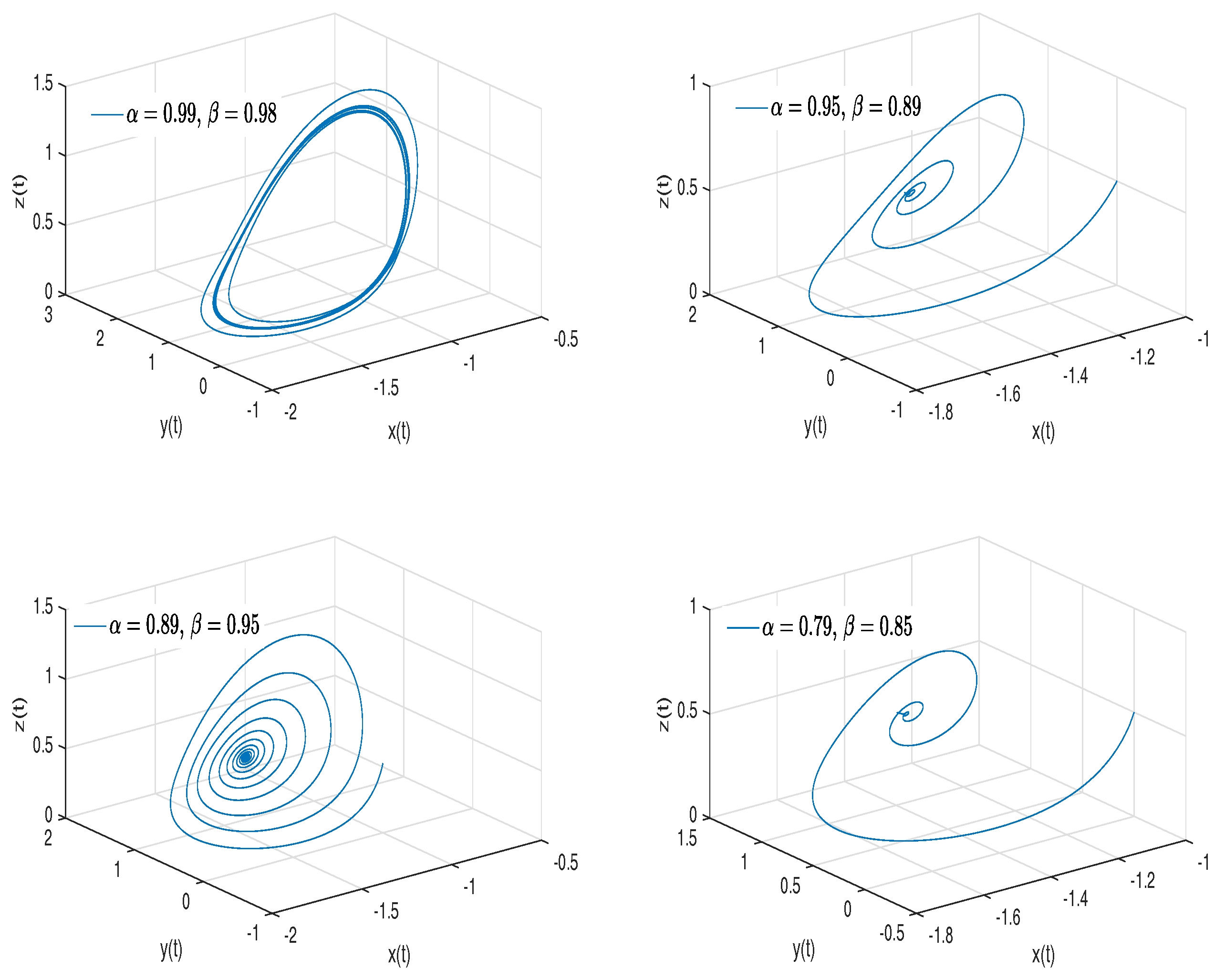
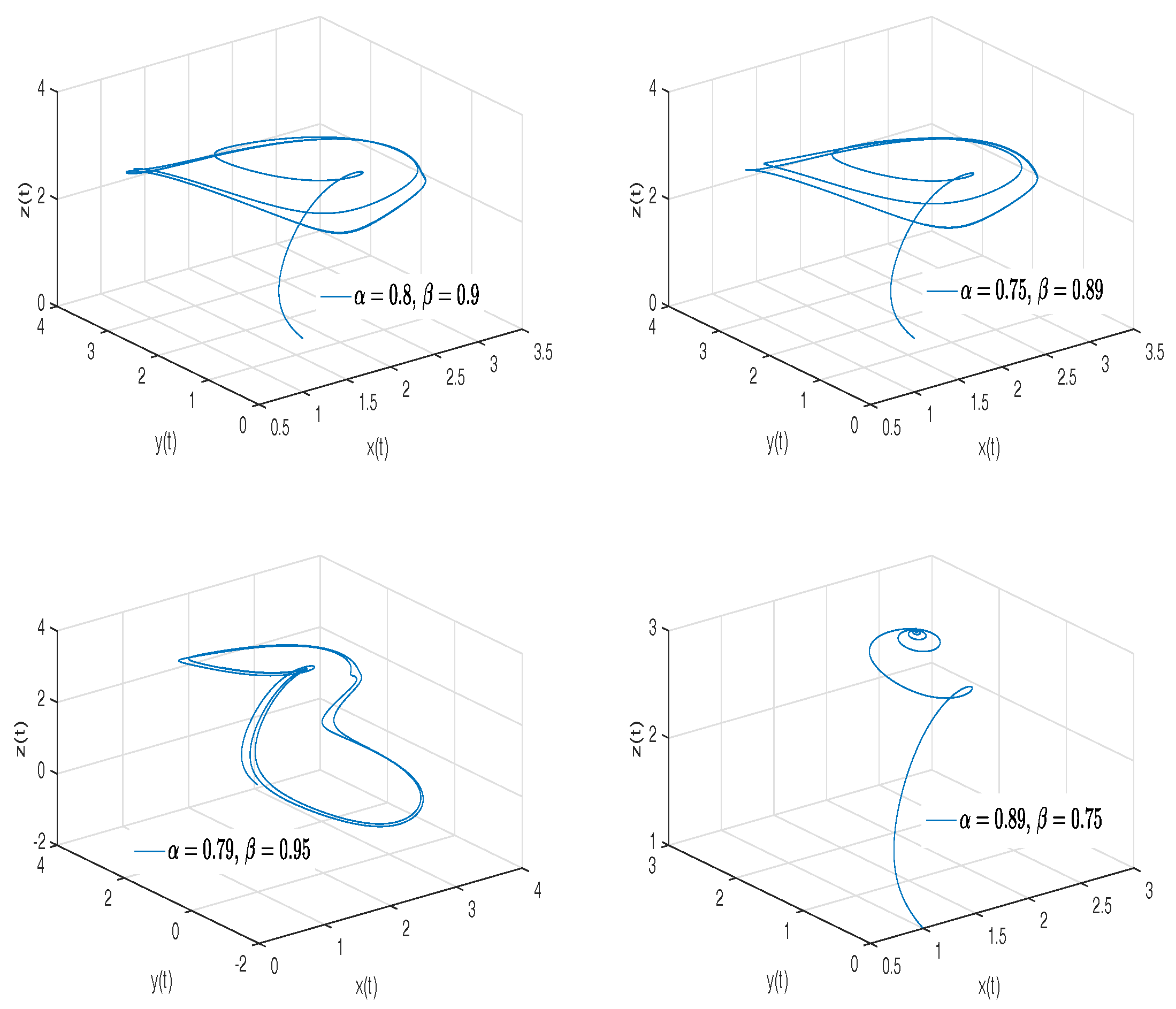
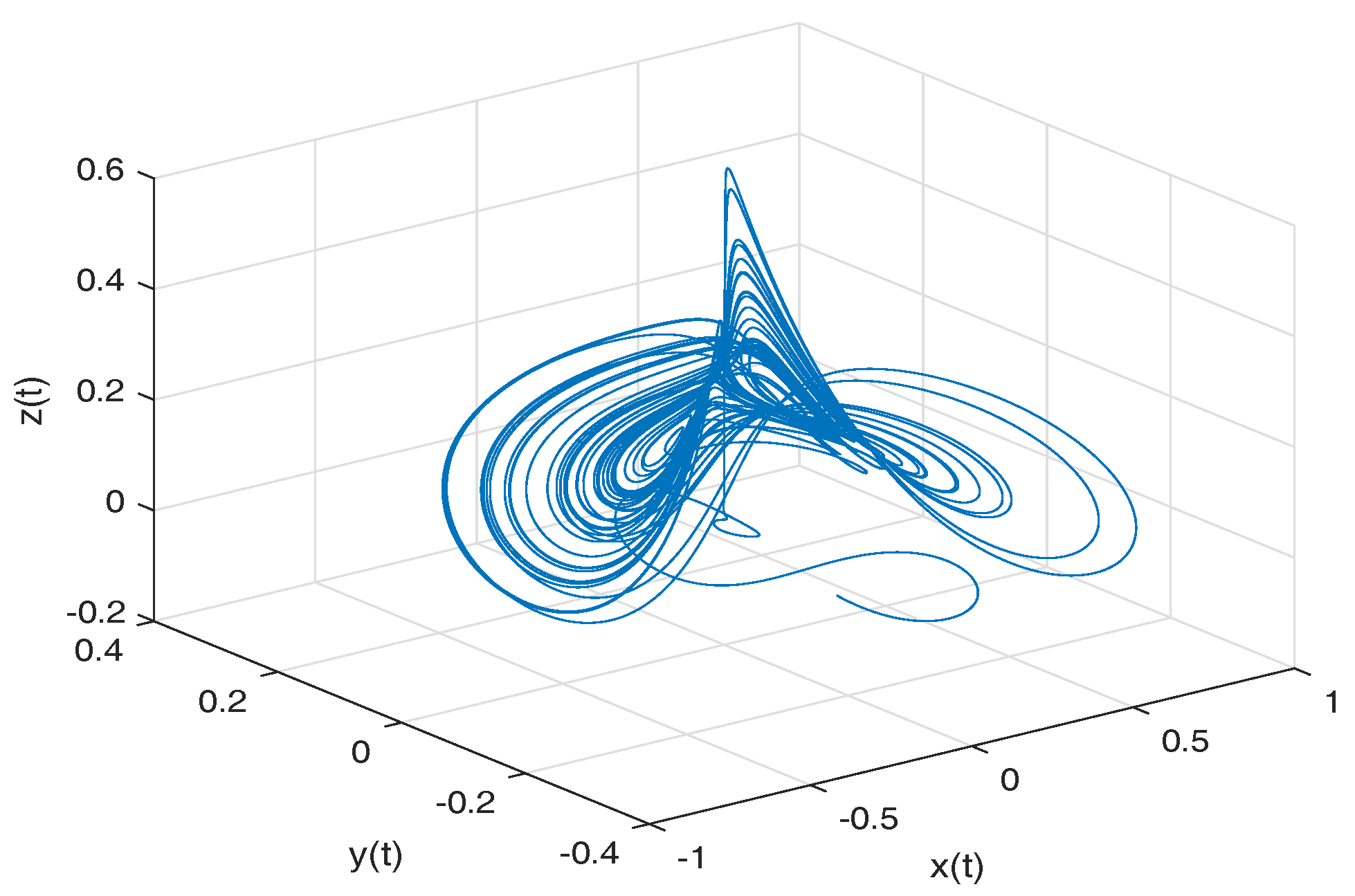
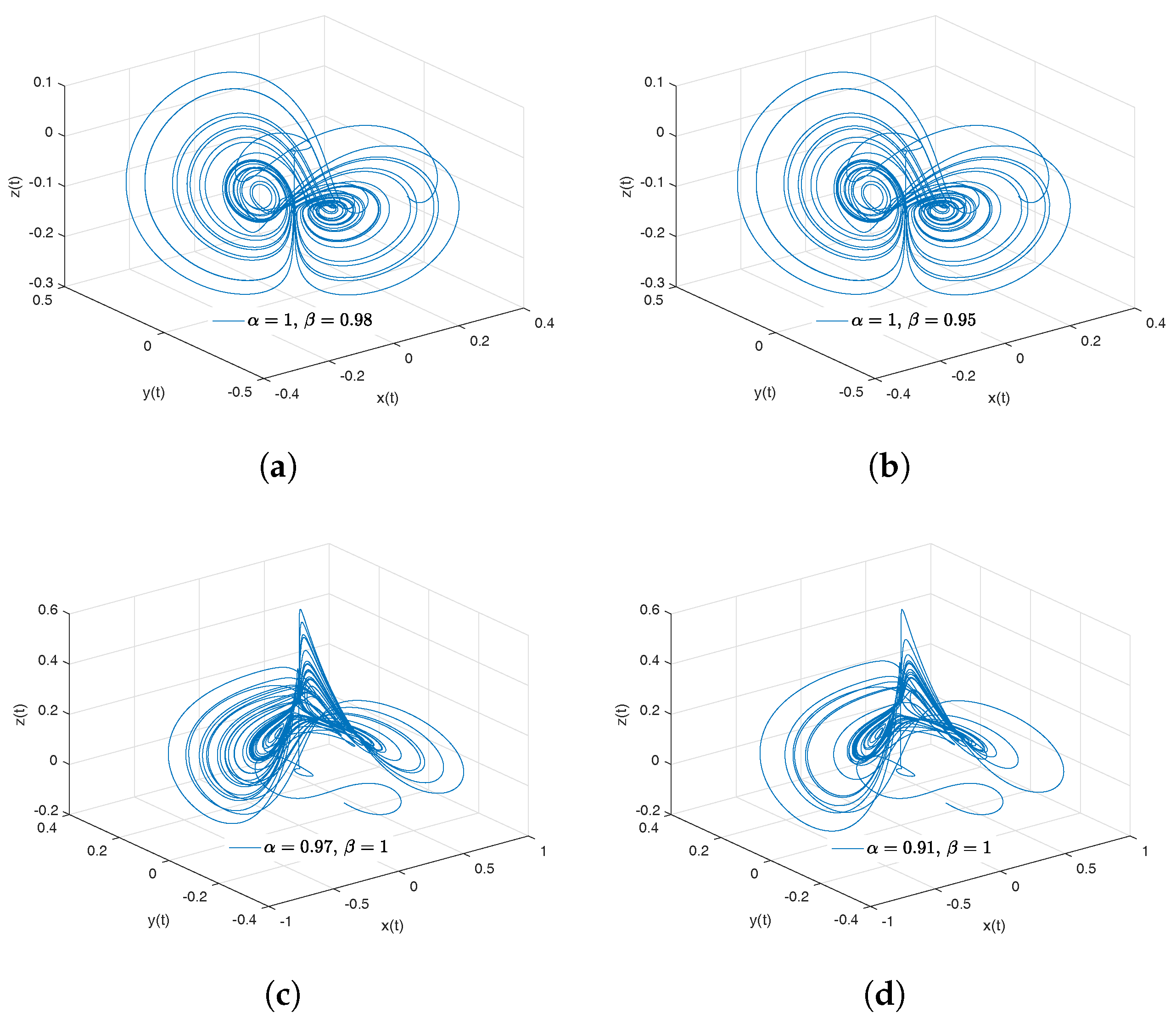
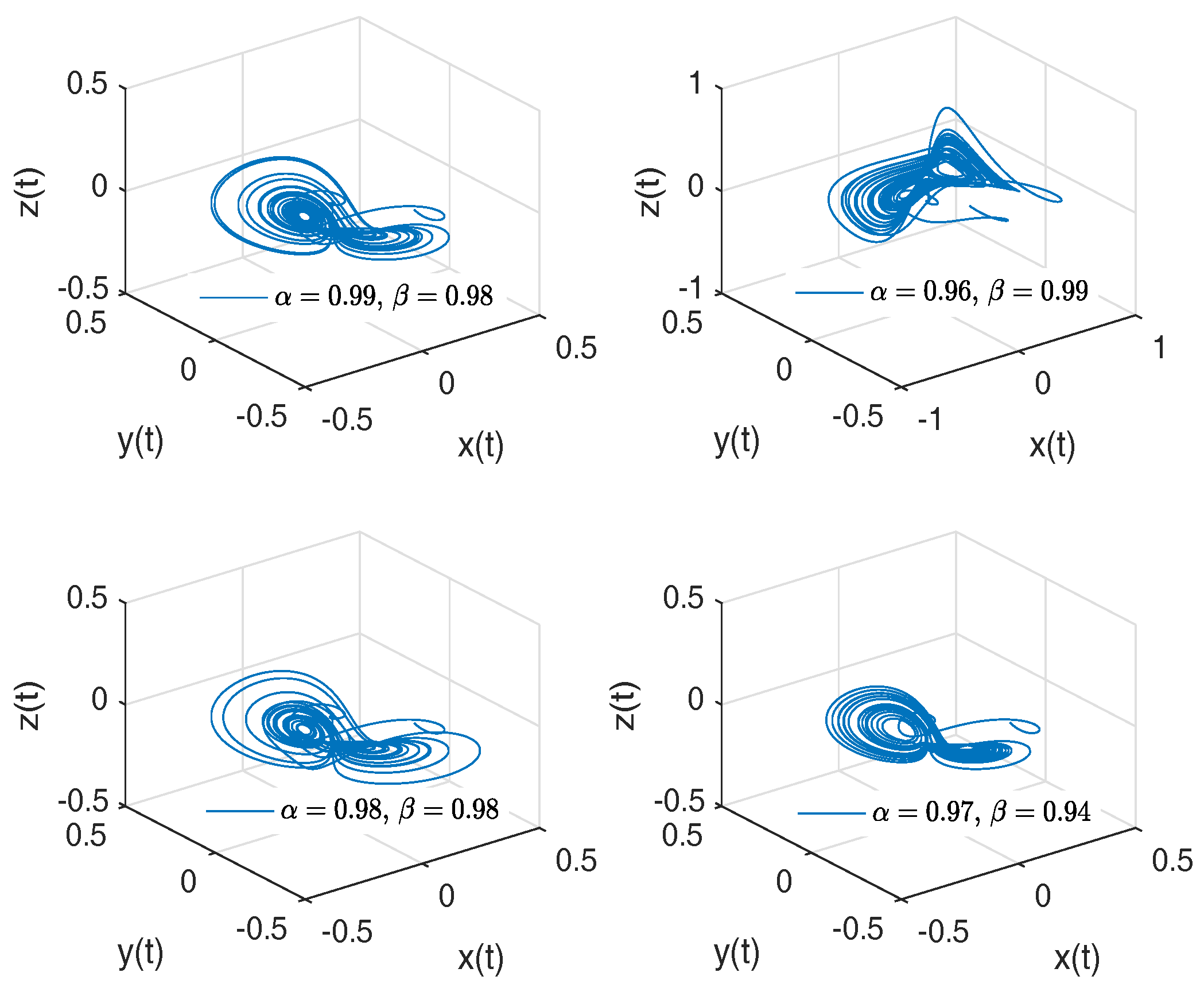
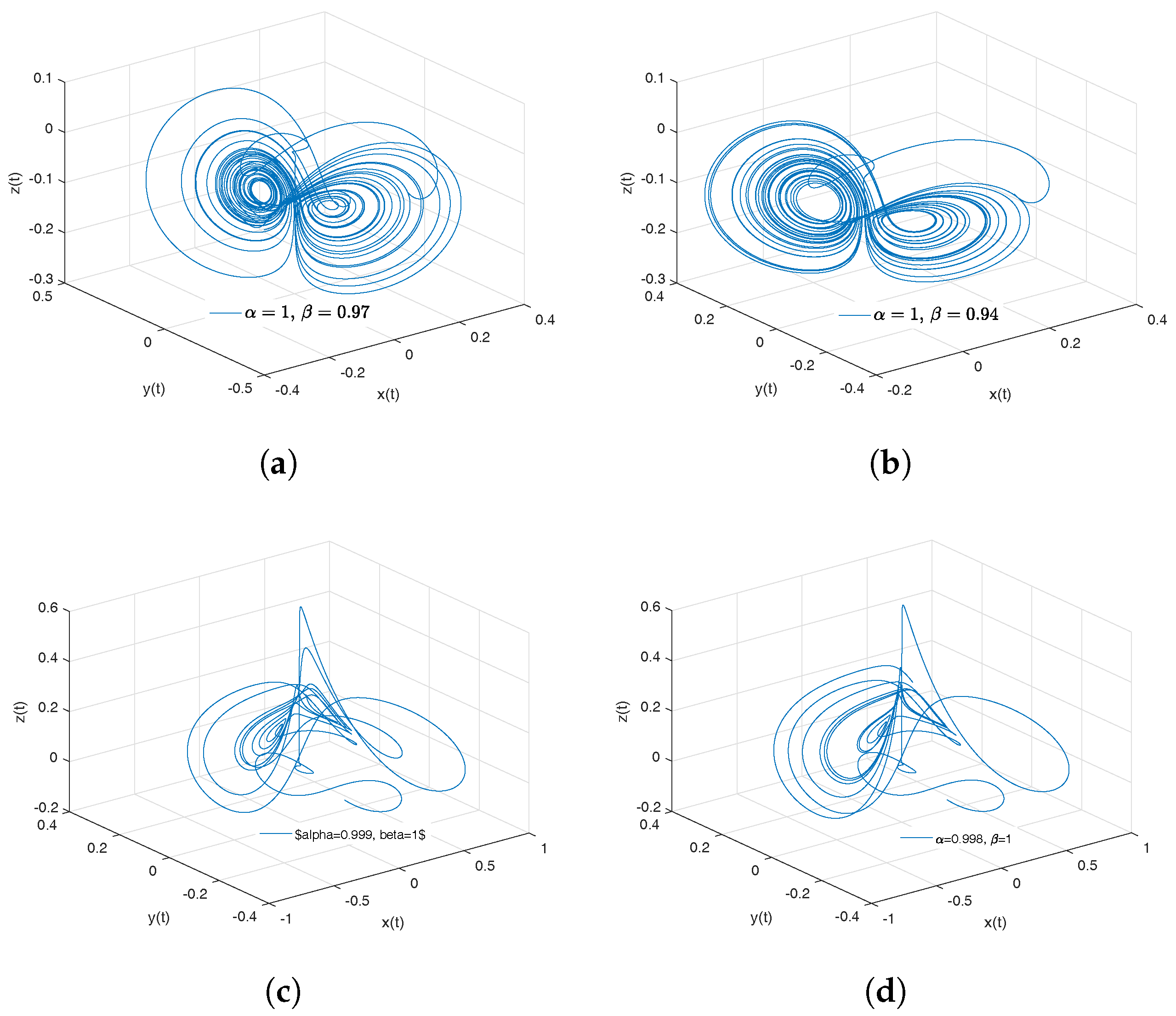
- Newton–Leipnik attractor. The Newton–Leipnik system model was obtained by modifying Euler’s rigid body equations with the addition of a linear feedback in 1981. For this example, we consider a 3D system of fractional order nonlinear autonomous differential equations known as Newton–Leipnik attractor [47,48]:where .
- Observation. In the case when , we obtain the numerical solution of the Newton–Leipnik attractor in the Liouville–Caputo sense.
- If the distance between two points is larger than 0we assume that the dynamics of the system (27) are different; therefore, said system is susceptible to the change of initial conditions.
- The distance between two points is equal to 0, if and only if two points are overlappedwich means that the dynamics of the system are the same in that initial condition.
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Kumar, D.; Singh, J.; Kumar, S. A fractional model of Navier-Stokes equation arising in unsteady flow of a viscous fluid. J. Assoc. Arab Univ. Basic Appl. Sci. 2015, 17, 14–19. [Google Scholar] [CrossRef]
- Bhrawy, A.H.; Zaky, M.A.; Baleanu, D. New numerical approximations for space-time fractional Burgers’ equations via a Legendre spectral-collocation method. Rom. Rep. Phys. 2015, 67, 340–349. [Google Scholar]
- Liu, L.; Zheng, L.; Liu, F.; Zhang, X. Anomalous convection diffusion and wave coupling transport of cells on comb frame with fractional Cattaneo-Christov flux. Commun. Nonlinear Sci. Numer. Simul. 2016, 38, 45–58. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, X.; Li, Y.; Huang, X. Stability and Hopf Bifurcation of Fractional-Order Complex-Valued Single Neuron Model with Time Delay. Int. J. Bifurc. Chaos 2017, 27, 1–13. [Google Scholar] [CrossRef]
- Vastarouchas, C.; Tsirimokou, G.; Freeborn, T.J.; Psychalinos, C. Emulation of an electrical-analogue of a fractional-order human respiratory mechanical impedance model using OTA topologies. AEU-Int. J. Electron. Commun. 2017, 78, 201–208. [Google Scholar] [CrossRef]
- Tsirimokou, G.; Psychalinos, C. Ultra-low voltage fractional-order circuits using current mirrors. Int. J. Circuit Theory Appl. 2016, 44, 109–126. [Google Scholar] [CrossRef]
- Wang, Z.; Huang, X.; Shi, G. Analysis of nonlinear dynamics and chaos in a fractional order financial system with time delay. Comput. Math. Appl. 2011, 62, 1531–1539. [Google Scholar] [CrossRef]
- Tarasov, V.E. Fractal electrodynamics via non-integer dimensional space approach. Phys. Lett. A 2015, 379, 2055–2061. [Google Scholar] [CrossRef]
- Gómez-Aguilar, J.F.; Yépez-Martínez, H.; Calderón-Ramón, C.; Benavidez-Cruz, M.; Morales-Mendoza, L.J. Fractional electromagnetic waves in conducting media. J. Electromagn. Waves Appl. 2016, 30, 259–271. [Google Scholar] [CrossRef]
- Wang, B.; Xue, J.; Wu, F.; Zhu, D. Stabilization conditions for fuzzy control of uncertain fractional order nonlinear systems with random disturbances. IET Control Theory Appl. 2016, 10, 637–647. [Google Scholar] [CrossRef]
- Nojavanzadeh, D.; Badamchizadeh, M. Adaptive fractional-order non-singular fast terminal sliding mode control for robot manipulators. IET Control Theory Appl. 2016, 10, 1565–1572. [Google Scholar] [CrossRef]
- Aslam, M.S.; Raja, M.A.Z. A new adaptive strategy to improve online secondary path modeling in active noise control systems using fractional signal processing approach. Signal Process. 2015, 107, 433–443. [Google Scholar] [CrossRef]
- Liu, D.Y.; Laleg-Kirati, T.M. Robust fractional order differentiators using generalized modulating functions method. Signal Process. 2015, 107, 395–406. [Google Scholar] [CrossRef]
- Rihan, F.A.; Lakshmanan, S.; Hashish, A.H.; Rakkiyappan, R.; Ahmed, E. Fractional-order delayed predator-prey systems with Holling type-II functional response. Nonlinear Dyn. 2015, 80, 777–789. [Google Scholar] [CrossRef]
- Sharma, M.; Ali, M.F.; Jain, R. Advanced generalized fractional kinetic equation in astrophysics. Prog. Fract. Differ. Appl. 2015, 1, 65–71. [Google Scholar]
- Iyiola, O.S.; Nwaeze, E.R. Some new results on the new conformable fractional calculus with application using D’Alambert approach. Progr. Fract. Differ. Appl. 2016, 2, 115–122. [Google Scholar] [CrossRef]
- Avcı, D.; Eroglu, B.B.I.; Özdemir, N. Conformable Fractional Wave-Like Equation on a Radial Symmetric Plate. In Theory and Applications of Non-integer Order Systems; Springer: Cham, Switzerland; Zakopane, Poland, 2017. [Google Scholar]
- Ziaei, E.; Farahi, M.H.; Safaie, E. The approximate solution of nonlinear fractional optimal control problems by measure theory approach. Progr. Fract. Differ. Appl. 2018, 4, 1–13. [Google Scholar]
- Yavuz, M.; Özdemir, N. European Vanilla Option Pricing Model of Fractional Order without Singular Kernel. Fractal Fract. 2018, 2, 3. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and some of Their Applications; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- M Caputo, M.F. A New Definition of Fractional Derivative without Singular Kernel. Prog. Fract. Differ. Appl. 2015, 1, 73–85. [Google Scholar]
- Atangana, A.; Baleanu, D. New Fractional Derivatives with Nonlocal and Non-Singular Kernel: Theory and Application to Heat Transfer Model. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef]
- Khalil, R.; al Horani, M.; Yousef, A.; Sababheh, M. A new definition of fractional derivative. J. Comput. Appl. Math. 2014, 264, 65–70. [Google Scholar] [CrossRef]
- Atangana, A. A novel model for the lassa hemorrhagic fever: deathly disease for pregnant women. Neural Comput. Appl. 2015, 26, 1895–1903. [Google Scholar] [CrossRef]
- Cenesiz, Y.; Baleanu, D.; Kurt, A.; Tasbozan, O. New exact solutions of Burgers’ type equations with conformable derivative. Waves Random Complex Media 2016, 27, 103–116. [Google Scholar] [CrossRef]
- He, S.; Sun, K.; Mei, X.; Yan, B.; Xu, S. Numerical analysis of a fractional-order chaotic system based on conformable fractional-order derivative. Eur. Phys. J. Plus 2017, 132, 36. [Google Scholar] [CrossRef]
- Abdeljawad, T. On conformable fractional calculus. J. Comput. Appl. Math. 2015, 279, 57–66. [Google Scholar] [CrossRef]
- Atangana, A.; Alsaedi, D.B.A. New properties of conformable derivative. Open Math. 2015, 13, 889–898. [Google Scholar] [CrossRef]
- Chung, W.S. Fractional Newton mechanics with conformable fractional derivative. J. Comput. Appl. Math. 2015, 290, 150–158. [Google Scholar] [CrossRef]
- Cenesiz, Y.; Kurt, A. The new solution of time fractional wave equation with conformable fractional derivative definition. J. New Theory 2015, 7, 79–85. [Google Scholar]
- Atangana, A.; Ünlü, C. New groundwater flow equation with its exact solution. Scientia Iranica. Trans. B Mech. Eng. 2016, 23, 1837–1843. [Google Scholar]
- Atangana, A.; Baleanu, D.; Alsaedi, A. Analysis of time-fractional Hunter-Saxton equation: A model of neumatic liquid crystal. Open Phys. 2016, 14, 145–149. [Google Scholar] [CrossRef]
- Koca, I.; Atangana, A. Analysis of a nonlinear model of interpersonal relationships with time fractional derivative. J. Math. Anal. 2016, 7, 1–11. [Google Scholar]
- Atangana, A.; Alkahtani, B.S.T. Modeling the spread of Rubella disease using the concept of with local derivative with fractional parameter. Complexity 2016, 21, 442–451. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D. On modeling the groundwater flow within a confined aquifer. Rom. J. Phys. 2015, 60, 573–582. [Google Scholar]
- Jarad, F.; Ugurlu, E.; Abdeljawad, T.; Baleanu, D. On a new class of fractional operators. Adv. Differ. Equ. 2017, 2017, 1–16. [Google Scholar] [CrossRef]
- Morales-Delgado, V.F.; Gómez-Aguilar, J.F.; Taneco-Hernández, M.A. Analytical solutions of electrical circuits described by fractional conformable derivatives in Liouville–Caputo sense. AEU-Int. J. Electron. Commun. 2018, 85, 108–117. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J.; Freed, A.D. Detailed Error Analysis for a Fractional Adams Method. Numer. Algorithms 2004, 36, 31–52. [Google Scholar] [CrossRef]
- Li, C.; Peng, G. Chaos in chen’s system with a fractional order. Chaos Solitons Fractals 2004, 22, 443–450. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J.; Freed, A.D. A predictor-corrector approach for the numerical solution of fractional differential equations. Nonlinear Dyn. 2002, 29, 3–22. [Google Scholar] [CrossRef]
- Galeone, L.; Garrappa, R. Fractional Adams–Moulton methods. Math. Comput. Simul. 2008, 79, 1358–1367. [Google Scholar] [CrossRef]
- Zayernouri, M.; Matzavinos, A. Fractional Adams-Bashforth/Moulton methods: An application to the fractional Keller-Segel chemotaxis system. J. Comput. Phys. 2016, 317. [Google Scholar] [CrossRef]
- Baskonus, H.M.; Bulut, H. On the numerical solutions of some fractional ordinary differential equations by fractional Adams-Bashforth-Moulton method. Open Math. 2015, 13, 547–556. [Google Scholar] [CrossRef]
- Rabinovich, M.I.; Fabrikant, A.L. Nonlinear waves in nonequilibrium media. Radiophys. Quantum Electron. 1976, 19, 508–543. [Google Scholar]
- Thomas, R. Deterministic chaos seen in terms of feedback circuits: Analysis, synthesis, labyrinth chaos. Int. J. Bifurc. Chaos 1999, 9, 1889–1905. [Google Scholar] [CrossRef]
- Sprott, J.C.; Chlouverakis, K.E. Labyrinth chaos. Int. J. Bifurc. Chaos 2007, 17, 2097–2108. [Google Scholar] [CrossRef]
- Leipnik, R.B.; Newton, T.A. Double strange attractors in rigid body motion with linear feedback control. Phys. Lett. A 1981, 86, 63–67. [Google Scholar] [CrossRef]
- Sheu, L.J.; Chen, H.K.; Chen, J.H.; Tam, L.M.; Chen, W.C.; Lin, K.T.; Kang, Y. Chaos in the Newton–Leipnik system with fractional order. Chaos Solitons Fractals 2008, 36, 98–103. [Google Scholar] [CrossRef]
- Tusset, A.M.; Piccirillo, V.; Bueno, A.M.; Balthazar, J.M.; Sado, D.; Felix, J.L.P.; Brasil, R.M.L. Chaos control and sensitivity analysis of a double pendulum arm excited by an RLC circuit based nonlinear shaker. J. Vib. Control 2016, 22, 3621–3637. [Google Scholar] [CrossRef]
- Peruzzi, N.J.; Chavarette, F.R.; Balthazar, J.M.; Tusset, A.M.; Perticarrari, A.L.P.M.; Brasil, R.M.L. The dynamic behavior of a parametrically excited time-periodic MEMS taking into account parametric errors. J. Vib. Control 2016, 22, 4101–4110. [Google Scholar] [CrossRef]






© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pérez, J.E.S.; Gómez-Aguilar, J.F.; Baleanu, D.; Tchier, F. Chaotic Attractors with Fractional Conformable Derivatives in the Liouville–Caputo Sense and Its Dynamical Behaviors. Entropy 2018, 20, 384. https://doi.org/10.3390/e20050384
Pérez JES, Gómez-Aguilar JF, Baleanu D, Tchier F. Chaotic Attractors with Fractional Conformable Derivatives in the Liouville–Caputo Sense and Its Dynamical Behaviors. Entropy. 2018; 20(5):384. https://doi.org/10.3390/e20050384
Chicago/Turabian StylePérez, Jesús Emmanuel Solís, José Francisco Gómez-Aguilar, Dumitru Baleanu, and Fairouz Tchier. 2018. "Chaotic Attractors with Fractional Conformable Derivatives in the Liouville–Caputo Sense and Its Dynamical Behaviors" Entropy 20, no. 5: 384. https://doi.org/10.3390/e20050384
APA StylePérez, J. E. S., Gómez-Aguilar, J. F., Baleanu, D., & Tchier, F. (2018). Chaotic Attractors with Fractional Conformable Derivatives in the Liouville–Caputo Sense and Its Dynamical Behaviors. Entropy, 20(5), 384. https://doi.org/10.3390/e20050384






