1. Introduction
Glass, such as naturally-occurring obsidian, pumice, etc., or man-made Venetian glass, window glass, etc., is a well-known class of materials that has captured our fascination forever. We can now make a defect-free glass in the laboratory for a variety of scientific and technological applications. Crudely speaking, it is an almost solid-like amorphous material that possesses no long-range atomic order and, upon heating, gradually softens as it turns into its molten state (also known as the supercooled liquid) as it passes through the glass transition region normally denoted by a suitable chosen single temperature
in this region [
1,
2,
3,
4]. For the purpose of this article, a glass is treated merely as a nonequilibrium (NEQ) state of matter, which can be made quite homogeneous so to a good approximation, it can be treated as a thermodynamic system that is in internal equilibrium (IEQ), but not in equilibrium (EQ), as explained later (at present, it suffices to say that the entropy in an IEQ state is a state function of its state variables that now include some NEQ state variables (commonly known as internal variables) [
1,
2,
3,
4] besides those needed to specify EQ states; see also [
5,
6,
7]). This means that a glass will exhibit relaxation as it strives to come to equilibrium. The relaxation time is known to be large enough close to
that at much lower temperatures, one can usually treat a glass as in an almost frozen state over experimental time scale
, the time period over which successive observations are made. We refer the reader to an excellent monograph by Debenedetti [
3] on these issues. We will primarily focus on the thermodynamics of glasses and supercooled liquid in this work and treat them as NEQ states. Therefore, our discussion will mostly consider a NEQ system, which we denote by
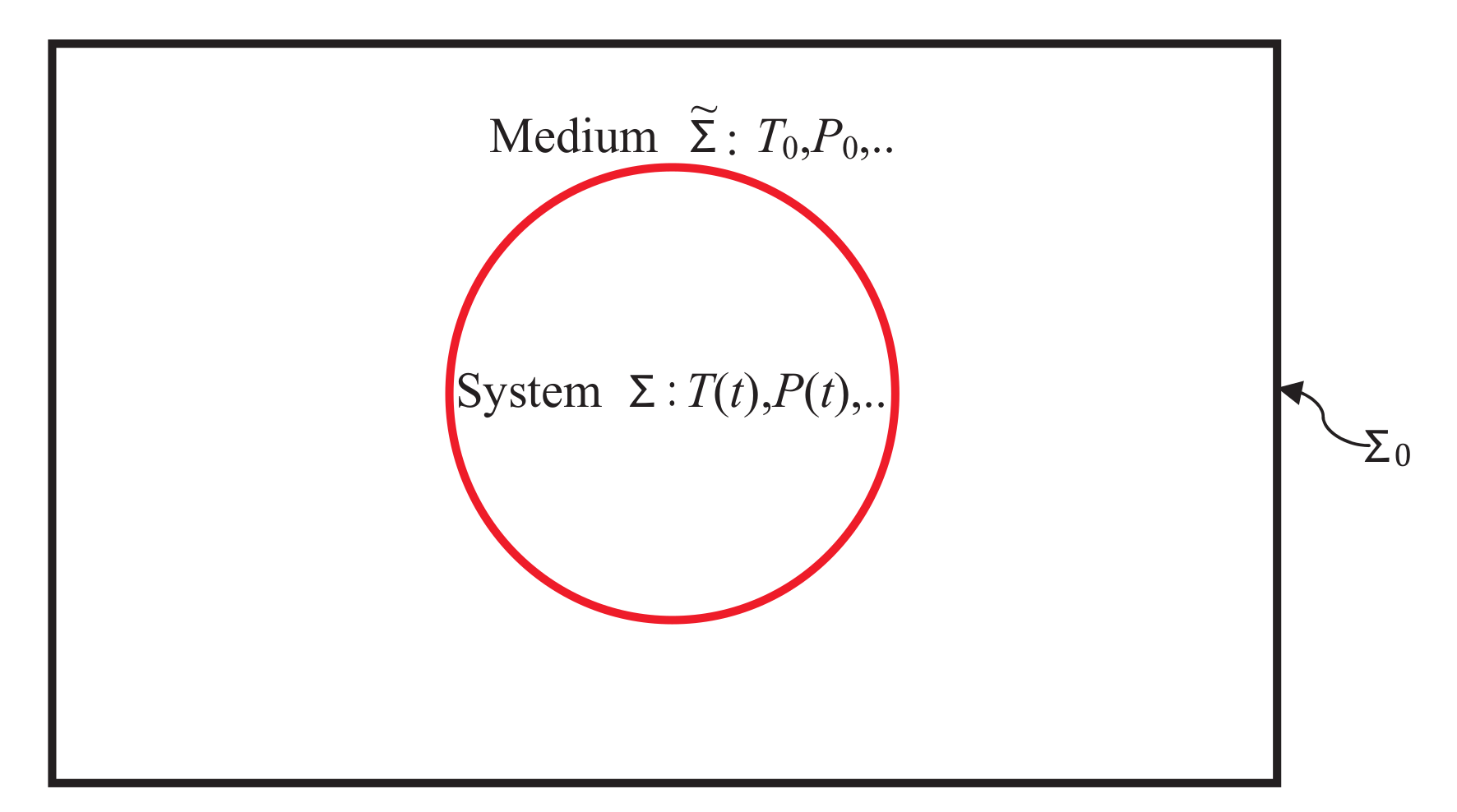
in an extensively large medium
as shown in
Figure 1.
Definition 1. As we will not consider a system in isolation in this work, we will always use EQ or “equilibrium” to mean “equilibrium with respect to the medium .” We will not reserve EQ for the entire system only. We will also use it for a part of the system, part of the state variables or part of the degrees of freedom such as vibrational degrees of the system, if they are in equilibrium with . On the other hand, we will reserve the use of IEQ for the entire system; see also [5]. It is a well-known fact that in glasses, the vibrational modes come to equilibrium very fast, even though the glass is out of equilibrium. Similarly, in a sinusoidal variation of
T, some degrees of freedom would equilibrate after a cycle; others would not and would control the temporal behavior of the system. It seems natural that the sinusoidal variation would give rise to a distribution of relaxation times. Thus, in general, one of the most important consequences of the rate of variation of the external stimuli such as the temperature or pressure is the possibility that the state of the system may be so far away from equilibrium that the dynamics becomes too complex, involving multiple relaxation time scales
, in supercooled liquids [
1,
3,
8,
9]. The relaxation time is defined as the time required for the corresponding dynamical variable to come to equilibrium with the medium; see Equation (
7) for the proper definition of the relaxation time. It should be emphasized that this interpretation of the relaxation time is dictated by the experimental setup, but does not depend on any particular mathematical form of the relaxation. An interplay between
and relaxation times
’s becomes crucial in determining the thermodynamics of the system and plays a major role in our discussion here. In fact, one of the following cases for a given
will be usually encountered in experiments:
- Relax 1
: In this situation, the k-th relaxing dynamical variable has equilibrated and does not have to be accounted for in the NEQ thermodynamics.
- Relax 2
: In this situation, the k-th dynamical variable will continue to relax towards equilibrium during and must be accounted for as the system approaches equilibrium.
- Relax 3
: In this situation, the k-th dynamical variable will not fully relax and will strongly affect the behavior of the system. The corresponding dynamical variable is said to be “frozen-in” over .
When there are several relaxation times, it is possible that different
’s will correspond to different cases above. Thus, care must be exercised in dealing with different relaxation times. The need for such care has been recognized in vitrification for a long time [
10]. Relaxation is a universal phenomenon when a system drives itself towards a more stable state such as an EQ state. In liquids or glasses, relaxations involving changes of the atomic or molecular positions are generally known as structural relaxations [
11]. Recent experimentation advances have made it possible to directly measure these relaxation processes at the molecular level simultaneously [
12]. At sufficiently low temperatures, the characteristic time for structural relaxations becomes comparable to the time scale of a macroscopic observation
100 s. For shorter time scales, the supercooled liquid (SCL) exhibits solid-like properties, while for longer times, it shows liquid-like properties. Even the dynamics in these cases is not so trivial, but has been investigated for a long time [
1,
3,
8,
9] with tremendous success. The glass transition being an “NEQ transition,” its description will require extensive internal variables, collectively denoted by a vector
that are independent of the set
of extensive observables (
) [
13] whenever the system is out of equilibrium [
2,
4,
14,
15,
16,
17,
18,
19,
20,
21,
22,
23,
24,
25]. We denote their collection by
in this work. The investigations of the glass transition invariably assume that the entropy
S is a state function
of the state variables in the extended state space
spanned by
; here,
is the state space of the observables. There is a memory of the initial state, and it requires the entire history of how the state is prepared to uniquely describe the preparation. Such a memory in some cases can be described by
. One example is residual stresses [
26]: if particle configurations in a glass cannot fully relax to equilibrium, some of the stresses that build up during flow in the melt persist in the glass; these stresses cannot be captured by
. We will say that such a state is an incompletely described state in terms of
. but a completely described state in terms of
. In contrast, the EQ state
is a completely (i.e., uniquely) described state by
and has no memory of the initial state. This means that in equilibrium,
is no longer independent of
.
The consideration of dynamics resulting from the simple connectivity of the sample (also known as the microstate or phase) space has played a pivotal role in developing the kinetic theory of gases [
27,
28,
29], where the interest is at high temperatures [
7,
30,
31,
32]. As the dynamics is very fast here, it is well known that the ensemble averages agree with temporal averages. However, at low temperatures, where dynamics becomes sluggish as in a glass [
3,
33,
34,
35], the system can be confined into disjoint components. The confinement occurs under NEQ conditions, when the observational time scale
becomes shorter than the equilibration time
, such as in glasses, whose behavior and properties have been extensively studied. These components are commonly known as basins in the energy landscape picture [
36,
37]. The entropy of confinement at absolute zero is known as the residual entropy and can be observed in glasses or disordered crystals; see below.
The existence of a nonzero residual entropy does not violate Nernst’s postulate, as the latter is applicable only to EQ states [
7] (Section 64). The observation of residual entropy is very common in Nature. Indeed, Tolman [
38] (Section 137) devotes an entire section on this issue for crystals in his seminal work, while Sethna provides an illuminating discussion for glasses [
39] (Section 5.2.2). In addition, the existence of the residual entropy has been demonstrated rigorously for glasses by Pauli and Tolman [
40] and for a very general spin model by Chow and Wu [
41]; see the references in these works for other cases where the residual entropy is shown to exist rigorously. The numerical simulation carried out by Bowles and Speedy for glassy dimers [
42] also supports the existence of a residual entropy. We refer the reader to consult various publications [
38,
43,
44]. Experiment evidence for a nonzero residual entropy is abundant as discussed by several authors [
30,
35,
42,
45,
46,
47,
48,
49,
50,
51]; various textbooks [
2,
4] also discuss this issue.
We introduce useful notation and concepts in the next section. In the following section, we introduce the concept of internal equilibrium (IEQ) states for which the entropy is a state function in the extended state space
.
Definition 2. As we are not interested in ordering phenomena (such as crystallization), we define an NEQ state with respect to an EQ state that is also disordered, i.e., with respect to SCL. This is formally done by considering only disordered configurations and discarding all ordered configurations in our discussion. We warn the reader that this is different from the conventional approach in which the equilibrium state is always taken to be the perfectly crystalline state. This point should not be forgotten. We then discuss the nature of the nonequilibrium state variables in in Proposition 1. The affinity corresponding to ξ is defined so that it vanishes in SCL, the equilibrium state in our approach.
The concept of a hierarchy of relaxation times is introduced in
Section 4, which forms a central part of the paper. A given
determines a particular time window, which provides a justification for Proposition 1. We find that internal variable
that has equilibrated plays no role thermodynamically since the affinity vanishes during
. In
Section 5, we discuss the first law in terms of the new notation, identify the irreversible work and the IEQ thermodynamics to be used in the next two sections on the entropy bound in vitrification and the residual entropy (
Section 6) and on the properties of the isothermal relaxation (
7). In
Section 8, we find that
still indirectly affects the thermodynamics as it is required to have a thermodynamic temperature, pressure, etc., for the system. The final section contains a brief discussion of the results.
2. Notation
Below is a brief introduction to the notation and the significance of various modern terminology [
19,
21] for readers who are unfamiliar with them. As usual,
and
form an isolated system
. Extensive quantities associated with
and
carry a tilde
and a suffix 0, respectively. As
is very large compared to
and is in equilibrium, all its conjugate fields
etc., carry a suffix 0 as they are the same as for
, and there is no irreversibility in
. Any irreversibility is ascribed to the system
[
19,
21] and is caused by processes such as dissipation due to viscosity, internal inhomogeneities, etc., that are internal to the system. Quantities without any suffix refer to the system. Throughout this work, we will assume that
and
are spatially disjoint and statistically quasi-independent [
25,
52,
53] so that their volumes, masses and entropies are additive at each instant. In particular,
, since
remains constant for
. We define a quantity to be a system-intrinsic (SI) quantity if it depends only on the property of the system alone and nothing else. For example, if
P is the pressure of
and
that of
, then
is the SI work done by the system, but
is not as the latter also depends on
through
. However,
is the work done by the medium, and this work can be identified as a medium-intrinsic (MI) quantity. Any extensive SI quantity
of
can undergo two distinct kinds of changes in time: one due to the exchange with the medium and another one due to internal processes. Following modern notation [
19,
21], exchanges of
with the medium and changes within the system carry the suffixes e and i, respectively:
For
and
, we must replace
by
and
, respectively, so that
and
. We will assume additivity so that:
For this to hold, we need to assume that
and
interact so weakly that their interactions can be neglected. As there is no irreversibility within
, we must have
for any medium quantity
and:
It follows from additivity that:
This means that any irreversibility in
is ascribed to
, and not to
. In a reversible change,
. For example, the entropy change:
for
; here,
is the entropy exchange with the medium and
is the irreversible entropy generation due to internal processes within
; the latter is also the entropy change
of
; see Equation (
3). Similarly, if
and
represent the work done by and the heat change of the system, then:
Here,
and
are the work exchange and heat exchange with the medium, respectively, and
and
are irreversible work done and heat generation due to internal processes in
. For an isolated system such as
, the exchange quantity vanishes so that:
We have introduced the pressure-volume work. We identify
and
. In the absence of any chemical reaction,
for the
k-th species of the particles; otherwise,
is its change due to the chemical reaction within
. As the energy of
can only change due to exchange with
,
We now explain the concept of the relaxation time used in this work, which is a simple generalization of its common usage, but which proves useful here. Consider some dynamical variable
as a function of time. Its dependence on
is suppressed. Let
denote its limiting value as
; thus, it also represents its EQ value. In reality, we do not have to wait an infinite amount of time as we cannot distinguish between a nonzero difference
, which is smaller than some small cutoff value so that for all purposes it is no different than zero, or a zero difference. Let us introduce a normalized ratio:
to account for this cutoff value, which we denote by
; the cutoff is primarily determined by the experimental setup. We say that the dynamical variable
has equilibrated when
equals the cutoff
. The relaxation time
is defined by:
It is clear that for a given choice
, the relaxation time
can be used to describe how rapidly a quantity effectively reaches its equilibrium value. Usually, one assumes for
an exponential form:
or a stretched exponential form:
also known as the Kohlrausch–Williams–Watts form, which reduces to the simple exponential for
. The relaxation time is:
and reduces to
for
, the exponential form. In this work, we do not make any particular choice for the decay behavior of
; thus, we do not make any distinction between the two forms of relaxation given above or any other form. We use a similar cutoff to identify the equilibration time
. In reality, the stretched exponential is very common in glassy dynamics, but its origin is far from clear at present, even though attempts have been made to express it as a superposition of simple exponentials with different
’s [
54,
55]. It is, therefore, treated as empirical in nature. The origin for the exponential relaxation, on the other hand, is well known as the Debye dynamics. For us, what is important is the existence of
through Equation (
7) and not the actual form of
.
We find it very useful in this work to divide all internal variables in
into non-overlapping groups
indexed by
, such that all internal variables in
have the same relaxation time
so that they equilibrate and are no longer independent of
for
, and that all groups have distinct relaxation times (
for
). We supplement
by introducing a new group
with relaxation time
in order to compactify our notation so that
. We also introduce the concept of hierarchy of relaxation times
associated with
, and state spaces
, where
, is spanned by all
, with relaxation times
. Physically, the hierarchy of relaxation times means that the longest relaxation time in
is
corresponding to
, and the shortest relaxation time is
corresponding to
. Thus, if
, any
, with relaxation time shorter than
, has already equilibrated (i.e., is no longer independent of
) and does not have to be used to specify the NEQ state. Thus,
is the state space needed to specify the NEQ state for
. However, as
is changed, both
and
can change as shown in
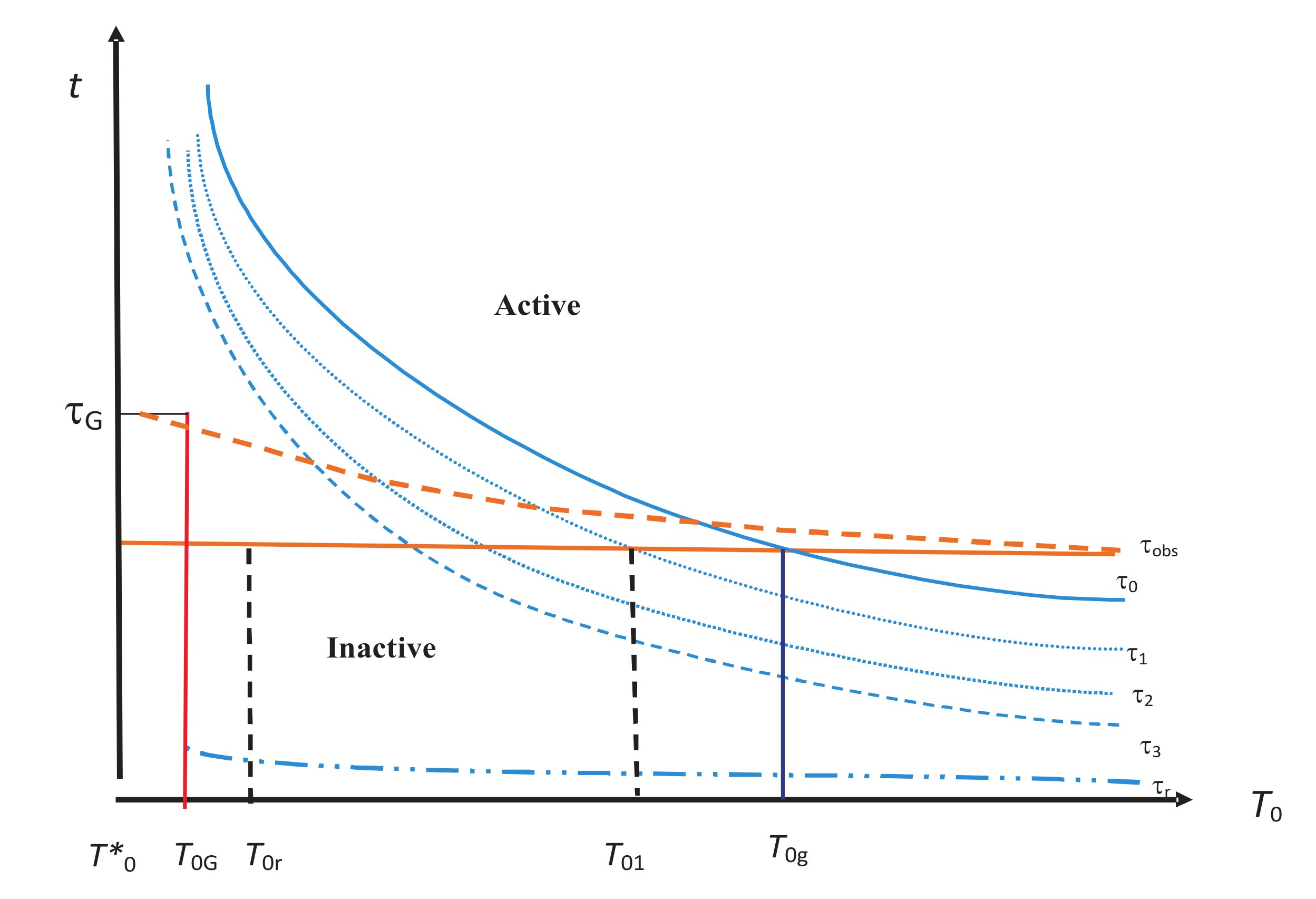
Figure 2. This then affects the choice of the required state space
. Thus, the hierarchy becomes a central concept in our analysis.
One of the most important sets of internal variables is that associated with the vibrational modes in the system. We denote it by
, and it seems to have the property that it is always inactive. This is shown by the lowest lying relaxation time curve corresponding to
in
Figure 2. This is because we expect these modes to always come to equilibrium with the medium for any reasonable
.
4. Hierarchy among Relaxation Times and Enlarged State
Spaces
We now classify state variables in a hierarchical manner as below. In IEQ states,
has had enough time
for
to emerge. However, for
, the states in
have not had enough time for
to emerge so that their entropy is a non-state function, which will continue to increase if the system is left isolated until it reaches
and becomes a state function. The affinity
corresponding to
is nonzero in
. If there were other internal variables
in the system, with relaxation times
, respectively, that are distinct from
, then these must have equilibrated during
so that their affinities
have vanished, implying that they are no longer independent of
(
). This means that the entropy does not depend on them. It is clear that
forms an upper bound for the relaxation times
. Thus, they play no role in
. When the process is carried out somewhat faster (
) than that required for obtaining
, then
has not had enough time to “equilibrate”, as we have discussed earlier [
52,
53] and
.
Even if
S does not depend on
, we will see in
Section 8 that they affect the thermodynamics of the system indirectly, a fact that does not seem to have been appreciated. For the moment, we will not consider the internal variables
. We will consider them later and will denote them collectively by
.
The discussion below is somewhat abstract and intricate and requires patience on the part of the reader. The set-theoretic notation is perfectly suited for the abstract nature of the discussion. Some readers may find the set-theoretic notation cumbersome, but this is the price we must pay to make the discussion comprehensive, but compact.
To simplify our discussion, we assume that all internal variables in
are divided into non-overlapping groups
indexed by
. We further assume that all internal variables in
have the same relaxation time
so that they equilibrate and are no longer independent of
for
. The relaxation times depend strongly on
. Let us also define
in order to compactify our notation below. Because of this, we can include
whenever we speak of internal variables from now on, unless clarity is needed. The groups
are indexed by
n so that
’s appear in a decreasing order (with
):
The relaxation times form a discrete set and not a continuum for simplicity. It is important that the set has a finite though large number of elements for a physically sensible thermodynamic description of the system; having an enormous number of elements will make the description unnecessarily too complex and completely useless for thermodynamics.
We now introduce the sequence of state spaces
, where
, is spanned by the union:
of all
, with relaxation times
, with
(not to be confused with
) denoting an empty set, so that:
Thus, , formed by , is relevant when . Similarly, , formed by is relevant when , and so on.
It is clear from the construction that the state spaces
, are ordered with increasing dimensions:
The longest relaxation time in
is
corresponding to
and the shortest relaxation time is
corresponding to
. Any
with relaxation time shorter than
need not be considered as it has already equilibrated and does not affect any state in
. We can summarize this conclusion as follows:
Proposition 2. The additional internal variable in relative to equilibrates and plays no role (i.e., is absent) in any smaller state spaces , but participates in all state spaces larger than , i.e., .
Proof. See the discussion above. ☐
Let us consider some observation time
used to observe a state M of an interacting system. We can always find a pair of neighboring state spaces
satisfying:
The two sides define a window in which must lie. As , no ’s, , have to be considered to describe the state M as they have already equilibrated (cf. the discussion of above); thus, , play no role in describing M. As , we need to consider all to describe M. We must, therefore, use to describe M for a in this window; we denote M by for clarity in this section. Among all the states in , there are IEQ states for which . This happens when , denoting the time required for to evolve into ; we will also use or simply to denote in if no confusion will arise. For , simply refers to .
There exists IEQ states
in
for which
is no longer independent of
; for these states,
. However,
as
even if
in
has not turned into
. As achieving internal equilibrium will take some additional time, we have
. We thus conclude that (with
representing
):
which will be assumed in this work.
We now consider the window:
As
,
has already equilibrated, so it need not be considered,
has not yet equilibrated. Thus, the entropy must be a function only of the observables
, which we must write as
, as it continues to vary. As
,
,
continues to increase until it finally reaches
; there is no explicit time dependence as all
’s,
, have equilibrated; see also Landau and Lifshitz [
7] and Wilks [
10], where NEQ states with respect to the medium are treated as IEQ states in
. This is the most common way NEQ states in the literature are treated when internal variables are not invoked. This is only possible when
satisfies Equation (
21).
We now consider the remaining case:
This situation corresponds to the quasistatic case so that even
has equilibrated to
, and we are dealing with an EQ state:
We know that
depend on the state of the system. In vitrification, which is of our primary interest here, they depend on the temperature
. It is commonly believed that
’s increase with decreasing
as shown in
Figure 2, where we show them as a function of
. From this figure, we observe that for a given
, drawn as a solid or broken line in red,
correspond to the internal variables that lie in the inactive zone lying below
(recall that
is now included in internal variables). They have all equilibrated. The active zone corresponds to internal variables that lie above
. They have not equilibrated. For higher temperatures (
), all internal variables are inactive. At lower temperatures, some of them become active and make the system out of equilibrium. At very low temperatures, all internal variables become active for their NEQ role. We will discuss this figure further in
Section 6.
6. Entropy Bound during Vitrification
We now apply the IEQ thermodynamics of the last section to the vitrification process, which is carried out at some cooling rate as follows. The discussion in this section is an elaboration and extension of our earlier discussion [
53,
64,
65,
66,
67,
68] and follows the approach first used by Bestul and Chang [
48] and later by Sethna and coworkers [
69,
70]. The temperature of the medium is isobarically changed by some small, but fixed
from the current value to the new value, and we wait for (not necessarily fixed) time
at the new temperature to make an instantaneous measurement on the system before changing the temperature again. At some temperature
, the relaxation time
, which continuously increases as the temperature is lowered (see
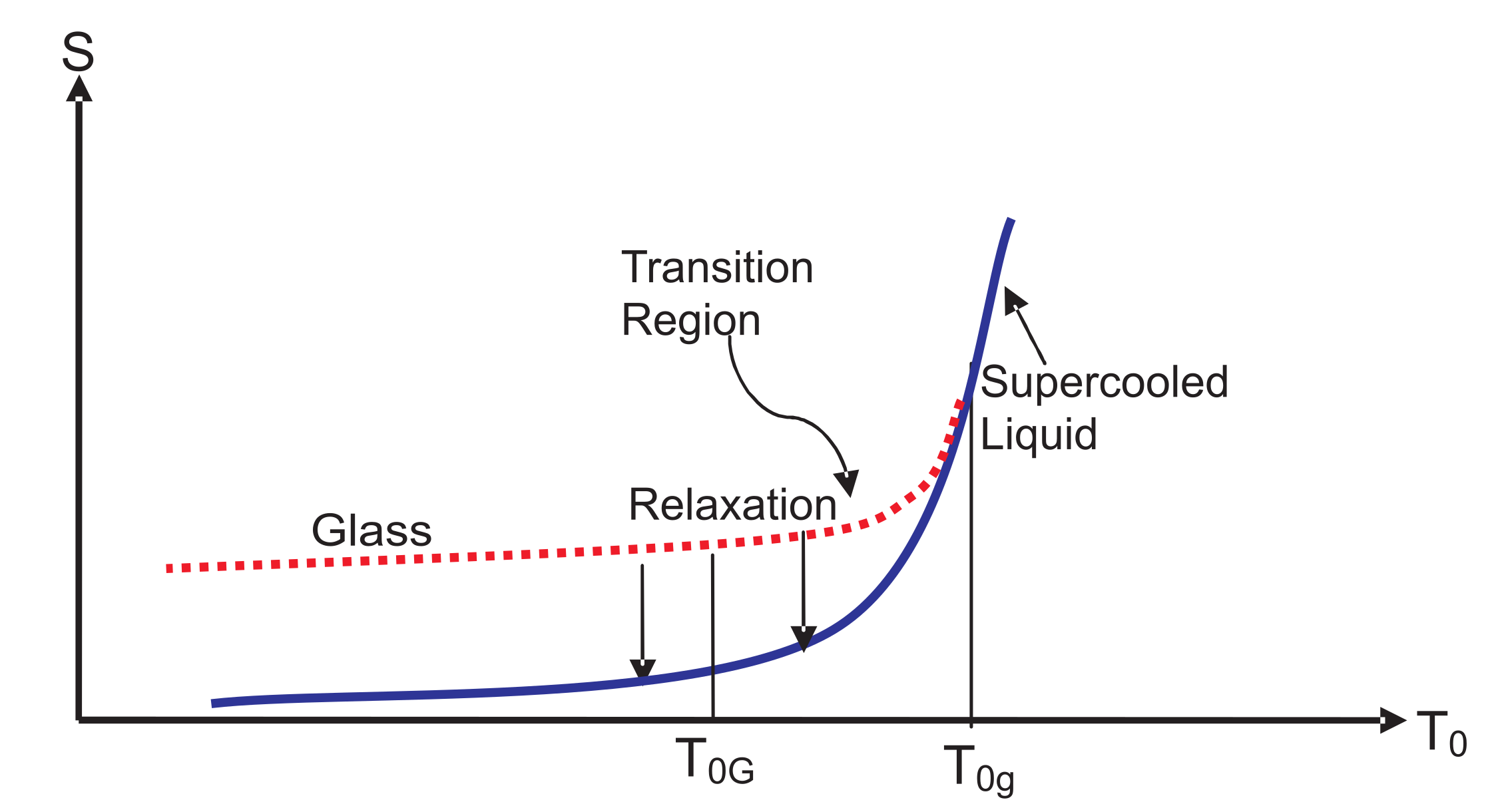
Figure 2), becomes equal to
, as shown in
Figure 3. The location of
depends on the rate of cooling, i.e., on
, which is clear from the figure. The crossing
is lower for the broken
than for the solid
. There are several other crossings at
(see
Figure 2), at which
crosses other relaxation curves for
, respectively. The crossing again depends on whether we take the solid or the broken curve for
. Let
denote the temperature of the last such crossing (not shown in the figure) before
. Just below
, the structures are not yet frozen; they “freeze” at a lower temperature
(not too far from
to form an amorphous solid with a viscosity
poise corresponding to some time scale
; see
Figure 3. This solid is identified as a glass determined by the choice of
or
. At
, the relaxation time
is at least
. Over the glass transition region between
and
in
Figure 3, the NEQ liquid gradually turns from an EQ supercooled liquid at or above
into a glass at or below
, a picture already known since Tammann [
2]; see also [
71]. Over this region, some dynamical properties such as the viscosity vary continuously, but very rapidly. However, thermodynamic quantities such as the volume or the enthalpy change continuously, but slowly. As is evident from
Figure 2, more and more internal variables become active as the temperature is reduced and will determine the thermodynamics in this region. Below
, all of these are almost “frozen” except those in the inactive zone such as
corresponding to the relaxation time
, representing localized oscillations within cells in the cell model [
72]; see the discussion in
Section 8 and
Section 9.
As the observation time
is increased, the equilibrated supercooled liquid continues to lower temperatures before the appearance of
. In the hypothetical limit
, it is believed that the equilibrated supercooled liquid will continue to lower temperatures without any interruption and is shown schematically by the solid blue curve in
Figure 3. We overlook the possibility of the supercooled liquid ending in a spinodal that has been seen theoretically [
73]. It is commonly believed that this entropy will vanish at absolute zero (
), as shown in the figure. As we are going to be interested in
over
, we must also acknowledge the possibility of an ideal glass transition in the system. If one believes in an ideal glass transition, then there would be a singularity in
at some positive temperature
below which the system will turn into an ideal glass whose entropy will also vanish at absolute zero [
34, see also the references cited there]. The possibility of an ideal glass transition, which has been discussed in a recent review elsewhere [
34], will not be discussed further in this work. All that will be relevant in our discussion here is the fact that the entropy vanishes in both situations (
). However, it should be emphasized that the actual value of
has no relevance for the theorems we derive below.
It is a common practice to think of the glass transition as occurring at a point that lies between
and
. We have drawn entropy curves (glass and SCL) in
Figure 3 for a process of vitrification in a cooling experiment. The entropy curves
for glass emerges out of
at
for a given
in such a way that it lies above that of SCL for
. At any nonzero temperature
,
approach
from above during isothermal (fixed temperature of the medium) relaxation; see the two downward vertical arrows. These relaxations are discussed in the next section.
The concept of internal equilibrium is also a common practice now-a-days for glasses [
2,
4]. Employing the concept of internal equilibrium provides us with an instantaneous Gibbs fundamental relation (see Equation (
32)), which determines instantaneous temperature, pressure, etc., of the system.
We now prove the entropy bounds:
in the form of Theorems 3 and 4. We will only consider isobaric cooling (we will not explicitly exhibit the pressure in this section), which is the most important situation for glasses. The process is carried out along some path from an initial state A at temperature
in the supercooled liquid state, which is still higher than
, to the state A
0 at absolute zero. The state A
0 depends on the path A→A
0, which is implicit in the following. The change
between two neighboring points along such a path is [
19,
21,
24,
25,
61]
; for an NEQ system, the two parts of
are path dependent. The component:
represents the reversible entropy exchange with the medium in terms of the heat
given out by the glass at time
t to the medium whose temperature at that instant is
. The component
represents the irreversible entropy generation in the irreversible process; see Equation (
29). In general, it contains, in addition to the contribution from the irreversible heat transfer with the medium, contributions from all sorts of viscous dissipation going on within the system and normally requires the use of internal variables [
19,
21,
24,
25,
61]. The equality in Equation (
29) holds for a reversible process, which we will no longer consider unless stated otherwise. The strict inequality
occurs only for an irreversible process such as in a glass.
Theorem 3. The experimentally-observed (extrapolated) non-zero entropy at absolute zero in a vitrification process is a strict lower bound of the residual entropy of any system: Proof. We have along A→A
0:
where we have assumed that there is no latent heat in the vitrification process. The first integral is easily determined experimentally since it is expressible in terms of the exchange heat:
The second integral in (
47) is always positive, but almost impossible to measure as it involves thermodynamic forces (see Equation (
37a)):
It involves knowing that since the residual entropy
is, by definition, the entropy
at absolute zero, we obtain the important result:
This proves Theorem 3. ☐
The irreversibility during vitrification does not allow for the determination of the entropy exactly, because evaluating the integral in Equation (
48) is not feasible [
2,
25]. The forward inequality:
is due to the irreversible entropy generation from all possible sources [
19,
21,
24,
25,
61]. The inequality is made strict as we are treating the NEQ glass with
and clearly establishes that the residual entropy at absolute zero must be strictly larger than the “experimentally- or calorimetrically-measured”
.
Theorem 4. The calorimetrically-measured (extrapolated) entropy during processes that occur when for any is larger than the hypothetical supercooled liquid entropy at absolutely zero: Proof. Let
be the rate of net heat loss by the system during
as it relaxes isothermally at some fixed
. For each temperature interval
below
, we have:
where
denotes the net heat loss by the system to come to equilibrium, i.e., become supercooled liquid during cooling at
. For
,
. Thus, the entropy loss observed experimentally with
is less than the entropy loss if the system is allowed to come to SCL at each temperature
. We thus conclude that:
This proves Theorem 4. ☐
The strict inequality above is the result of the fact that glass is an NEQ state. Otherwise, we will have for any arbitrary state.
The difference
would be larger the more irreversible the process is. The quantity
can be determined calorimetrically by performing a cooling experiment. We take
to be the melting temperature
and uniquely determine the entropy of the supercooled liquid at
by adding the entropy of melting to the crystal entropy
at
. The latter is obtained in a unique manner by integration along a reversible path from
to
:
here,
is the entropy of the crystal at absolute zero, which is traditionally taken to be zero in accordance with the third law, and
is the isobaric heat capacity of the crystal. This then uniquely determines the entropy of the liquid to be used in the right-hand side in Equation (
49). We will assume that
. Thus, an experimental determination of
is required to give the lower bound to the residual entropy in Equation (
45). Experimental evidence for a non-zero value of
is abundant as discussed by several authors [
35,
44,
45,
46,
74,
75,
76]; various textbooks [
2,
4] also discuss this issue. Goldstein [
44] gives a value of
J/K mol for
o-terphenyl from the value of its entropy at
K. However, Equation (
50) gives a mathematical justification of
. The strict inequality proves immediately that the residual entropy cannot vanish for glasses, which justifies the curve “Glass” in
Figure 3. The relevance of the residual entropy has been discussed by several authors in the literature [
30,
32,
38,
39,
40,
41,
44,
74,
75,
77].
By considering the state A
0 above to be a state A
0 of the glass in a medium at some arbitrary temperature
below
, we can get a generalization of Equation (
49):
We again wish to remind the reader that all quantities depend on the path A→A
0, which we have not exhibited. By replacing
by the melting temperature
and
by
, adding the entropy
of the medium on both sides in the above inequality and rearranging terms, we obtain (with
for the liquid):
where we have also included the equality for a reversible process. This provides us with an independent derivation of the inequality given by Sethna and coworkers [
69,
70].
It is also clear from the derivation of Equation (
50) that the inequality can be generalized to any temperature
with the result:
with
as
from below.
While we have only demonstrated the forward inequality, the excess
can be computed in NEQ thermodynamics [
19,
21,
24,
25,
61], which provides a clear prescription for calculating the irreversible entropy generation. The calculation will, of course, be system dependent and will require detailed information. Gutzow and Scmelzer [
74] provide such a procedure with a single internal variable, but under the assumption of equal temperature and pressure for the glass and the medium. However, while they comment that
, whose evaluation requires system-dependent properties, their main interest is to only show that it is negligible compared to
.
We have prove, Theorems 3 and 4 by considering only the system without paying any attention to the medium. For Theorem 3, we require the second law, i.e., Equation (
29). This is also true of Equation (
51). The proof of Theorem 4 requires the constraint
for any
, which leads to an NEQ state. The same is also true of Equation (
53).
We have focused on the system in this section. This does not mean that the conclusion would be any different had we brought the medium into our discussion. This is seen from the derivation of the inequality in Equation (
52) from Equation (
51).
7. Entropy and Enthalpy during Isothermal
Relaxation
We wish to consider isothermal relaxation in an isobaric cooling experiment carried out at a fixed pressure
. Let us assume that
is in equilibrium at some temperature
of some medium
. We change to a different medium
at
and bring
in its contact. Initially, the temperature
of
is
, so it is out of equilibrium with the new medium, and its temperature
will strive to get closer to
as we wait for
to come to equilibrium with
; see Equation (
15). The initial entropy
. If the system is now allowed to equilibrate, it will undergo spontaneous (isothermal) relaxation at fixed
so that
in the time during which its temperature changes. We assume that the relaxation times of
as a function of
are similar to those shown in
Figure 2; all we need to do is to replace
by
. During relaxation, the entropy of the glass is supposed to decrease. This is what we expect intuitively as the arrows show in
Figure 3. We now wish to consider such a relaxation and determine the behavior of thermodynamic functions such as the entropy, enthalpy, etc., using IEQ thermodynamics introduced above. We prove two additional theorems in this section. The theorems are general even though we have in mind NEQ states including glasses obtained under the condition
for any
. We consider the system to be in internal equilibrium with temperature
, pressure
, etc. We remind the reader that all processes that go on within the medium occur at constant temperature
, pressure
, etc. Thus, there will not be any irreversible process going on within the medium. All irreversible processes will go on within the system.
We will exploit below the strict inequalities in Equation (37) to derive a bound on the rate of entropy variation. For a system out of equilibrium, the instantaneous entropy
and volume
seem to play the role [
24] of “internal variables,” whose “affinities” are given by the corresponding thermodynamic forces
and
, respectively. This fact is not commonly appreciated in the glass literature to the best of our knowledge. Even during an isobaric vitrification, there is no fundamental reason to assume that the pressure
P of the system is always equal to the external pressure
. However, it is a common practice to assume the two to be the same, which may not be a poor approximation in most cases. We will not generally make such an approximation in this work.
We now state Theorem 5.
Theorem 5. The entropy of a glass reaches that of the supercooled liquid from above during relaxation at fixed of the mediums. Thus,so that the entropy variation in time has a unique direction as shown by the downward arrows in Figure 3. Proof. It follows from Equations (
15) and (
37a) that for any NEQ state during relaxation (fixed
):
the inequality turns into an equality once equilibrium is reached. In other words, during relaxation,
the plus symbol is again to indicate that the glass entropy reaches
from above. This completes the proof of Theorem 5. ☐
We have shown
in
to emphasize that the result is general during any relaxation. In the derivation, we have only used the second law. Being a general result, it should be valid for any real glass. Above
, the system is always in equilibrium with the medium so its temperature is the same as
. Below
, when the system is not in equilibrium with the medium, then
in accordance with Equation (
15) based on the experimental observation. Any theory, such as the one proposed in [
78,
79,
80,
81] and known as the entropy loss view of the glass transition, in which
drops below
, is such that:
In this case, during relaxation,
, so that
in direct conflict with Equation (
37a), a consequence of the second law. Such a theory then violates the second law as first pointed out by Goldstein [
44]; we will revisit this issue in the final section.
We now prove the following theorem:
Theorem 6. For a glass, we must have at all , where
Proof. According to Equations (
15) and (37b), we conclude that
(cf. Equation (
46)), while relaxation is going on and vanishes as
. It then follows from Equation (
43) that:
a result that is consistent with experimental observations [
1]. This completes the proof of the theorem. ☐
It follows from the behavior of the Gibbs free energy
during relaxation (
) that
, i.e.,
and:
The equality holds at
. We can also obtain Equation (
57a) using
.
From Equations (41) and (37), we also have:
The last bound is tighter than the bound in Equation (
57a) and reduces to the equality obtained earlier [
24] where
was neglected. This equality there was used to infer Equation (
54). We have just established that the conclusion remains unaltered even if we consider internal variables.
In summary, the isothermal relaxation originates from the tendency of the glass to come to thermal equilibrium during which its temperature
approaches
from above in time. The relaxation process results in the lowering of the corresponding Gibbs free energy in time, as expected due to the second law. However, it also results in the lowering of the corresponding entropy as shown in
Figure 3 and the enthalpy during vitrification; the latter is observed experimentally [
1].
8. Temperature Disparity due to Fast and Slow Variables: Tool–Narayanaswamy Equation
We have shown that for a given
, we can partition
into two distinct groups: one containing internal variable
whose affinity has vanished and the other one, which we now denote by
, that has not equilibrated and has a nonzero affinity
. These are the active internal variables. As
has equilibrated, its temperature, pressure, etc., must be those of the medium, that is
, etc. It is the inactive internal variable. On the other hand, the temperature, pressure, etc., associated with different components of
must not be those of the medium as there will be nonzero thermodynamic forces to bring each to equilibrium in due course. This raises a very interesting question. Because we are dealing with an IEQ state of the system, there is a well-defined and unique thermodynamic definition of its temperature
. This temperature also satisfies the identity
. How does
relate to the temperatures of
and
? To make some progress, we assume
and
to be quasi-independent over
. There is strong experimental evidence for this [
82,
83]. However, there are observables in
that also participate in relaxation. For example,
V will relax if
. Similarly,
E will relax if
. As we have discussed earlier [
24], one can treat
etc., in
as internal variables with their affinities
, etc., that vanish once equilibrium is reached. This is also seen from Equation (
14), where the first two terms have the same form as the last term involving
; recall that
. Therefore, in this section, we will continue to include
in
as we had done in
Section 4. This should not cause any confusion. We only have to be careful to always include
to specify the system even when
.
8.1. A Black Box Model
We consider a simple NEQ laboratory problem to model the above situation. Consider a system as a “black box” consisting of two parts at different temperatures
and
, but insulated from each other so that they cannot come to equilibrium. The two parts are like slow and fast motions in a glass or
and
, and the insulation allows us to treat them as independent, having different temperatures. We assume that there are no irreversible processes that go on within each part so that there is no irreversible heat
and
generated within each part. We wish to identify the temperature of the system, the black box. To do so, we imagine that to each part is added a certain infinitesimal amount of heat from outside, which we denote by
and
. We assume the entropy changes to be
and
. Then, we have for the net heat and entropy change:
We introduce the temperature
T by
. This makes it a thermodynamic temperature of the black box; see Equation (
33). Using
, we immediately find:
By introducing
, which is determined by the setup, we find that
T is given by:
As x is between zero and one, it is clear that T lies between and depending on the value of x. Thus, we see from this heuristic model calculation that the thermodynamic temperature T of the system is not the same as the temperature of either parts, a common property of a system not in equilibrium.
If the insulation between the parts is not perfect, there is going to be some energy transfer between the two parts, which would result in maximizing the entropy of the system. As a consequence, their temperatures will eventually become the same. During this period, T will also change until all three temperatures become equal.
8.2. Tool–Narayanaswamy Equation
We turn to the general case of the relaxation of thermodynamic properties. At high enough temperatures, the time variation of
as it relaxes towards
can be described as a single simple exponential with a characteristic time scale
. This happens when all internal variables have come to equilibrium during
, so no internal variables besides
are needed, a case discussed by Landau and Lifshitz [
7] and by Wilks [
10].
At low temperatures, this is not true. There are quasi-independent slow and fast internal variables
and
that are well known in glasses and supercooled liquids [
82,
83]. The situation is similar to the black box considered above. Both parts will strive to come to equilibrium with the medium, but they have widely separated relaxation times. As time goes on during relaxation, some of the groups in
introduced in
Section 4 become part of
after equilibration, as we have discussed there. We first assume, for simplicity, that all active internal variables in
have the same relaxation time
, i.e., they equilibrate together, but have not equilibrated. The quasi-independence of
and
immediately leads to the following partition of the
and
into two contributions, one from each kind:
For example, quasi-independence gives the additivity
, where
and
stand for
and
, etc. Here, we have introduced
as the volume difference
in terms of the free volume
in the cell model in which
allows for the molecules to move long distances (liquid-like slow motion) over
[
84]. Thus,
corresponds to the fast center of mass solid-like motion within the cells, which are in equilibrium with the medium; see also Zallen [
72].
Let us now introduce the “energy fraction”
as:
at a given
t, so that:
By definition, we have
, while
will have a temperature different from this. Assuming internal equilibrium, we can introduce a new temperature
by:
The following identity:
easily follows from considering
and using Equation (
59) for
and Equation (
61). This equation should be compared with (
58) obtained above using a black box model and is identical to the Tool–Narayanaswamy equation [
1] in form, except that we have given thermodynamic definitions of
in (
60) and
in Equation (
62).
It is easy to extend the above calculation to the case of different groups
belonging to
. The quasi-independence gives:
so that
with
and
as discussed above. For each
, we have its own temperature
using. It is now easy to see that Equation (
63) is extended to:
with
and
.
Let us now understand the significance of the above analysis. The partition in Equations (
59) and (
64) along with the fractions
and
shows that the partition satisfies a lever rule: the relaxing glass can be conceptually (but not physically) thought of as a “mixture” consisting of different “parts” corresponding to different temperatures and fractions. However, one of the temperatures is
of the medium, while
’s denote the temperature of the parts that are not equilibrated yet. As some of these parts equilibrate, their temperature becomes
, and they add to the weight
for the equilibrated internal variables. Thus, we see that while
may play no role in the IEQ thermodynamics, it still plays an important role in relating the thermodynamic temperature
with those of various groups of
. Thinking of a system conceptually as a “mixture” of “parts” is quite common in theoretical physics. One common example is that of a superfluid, which can be thought of as a “mixture” of a normal viscous “component” and a superfluid “component”. In reality, there exist two simultaneous motions, one of which is “normal”, and the other one is “superfluid”. A similar division can also be carried out in a superconductor: the total current is a sum of a “normal current” and a “superconducting current”.
Such an analysis has been carried out in detail earlier [
24], where a connection is made with the notion of the “fictive” temperature [
1], but in the absence of any internal variables (besides
). Here, we will summarize that discussion and refer the reader to this work for missing details. It is easy to first consider the simple case in Equation (
63). One can consider the part
of the energy fraction
at
to represent a “fictitious” SCL at temperature
. It is fictitious since the entire system does not consist of this part, so it is not in equilibrium as SCL is supposed to be; it is missing the part corresponding to the fraction
. We can supplement mentally the fictitious SCL by the same SCL of fraction
at the same temperature
to ensure that the entire system consists of
at
. This now represents an IEQ state at
, the left side of Equation (
63). Thus,
represents the thermodynamic temperature of this IEQ state, which can then be treated as an “unequilibrated” SCL, in thermal equilibrium with a medium at
(but not at
). We have identified it as an “unequilibrated” SCL since there is no reason for
corresponding to
to vanish in this SCL, whereas it is required to vanish in equilibrium. This SCL at
is also not identical to the glass as the latter has
at
, which is absent in this SCL. We can thus justify
as the fictive temperature.
This picture can be extended to Equation (
65) by introducing
as follows:
which converts it to Equation (
63). We can then introduce an equilibrated SCL, in equilibrium with a medium at
so that we can treat
as the fictive temperature.
Instead of considering a derivative of
S with
E, we can consider derivatives with respect to other state variables such as
V. In that case, a similar analysis can be carried out as done in [
24] to obtain a similar looking Tool–Narayanaswamy equation for
. We leave it to the reader to carry out this simple extension. The result for
is given in [
24].