Complexity and Entropy Analysis of a Multi-Channel Supply Chain Considering Channel Cooperation and Service
Abstract
1. Introduction
- (1)
- This paper builds a multi-channel supply chain model considering OSC and proposes a new perspective for multichannel research.
- (2)
- This paper discusses the effect of service cooperation on the multi-channel supply chain with OSC and provides decision references for enterprises.
- (3)
- This paper studies the complexity and characteristics of the multichannel service supply chain and puts forward management opinions.
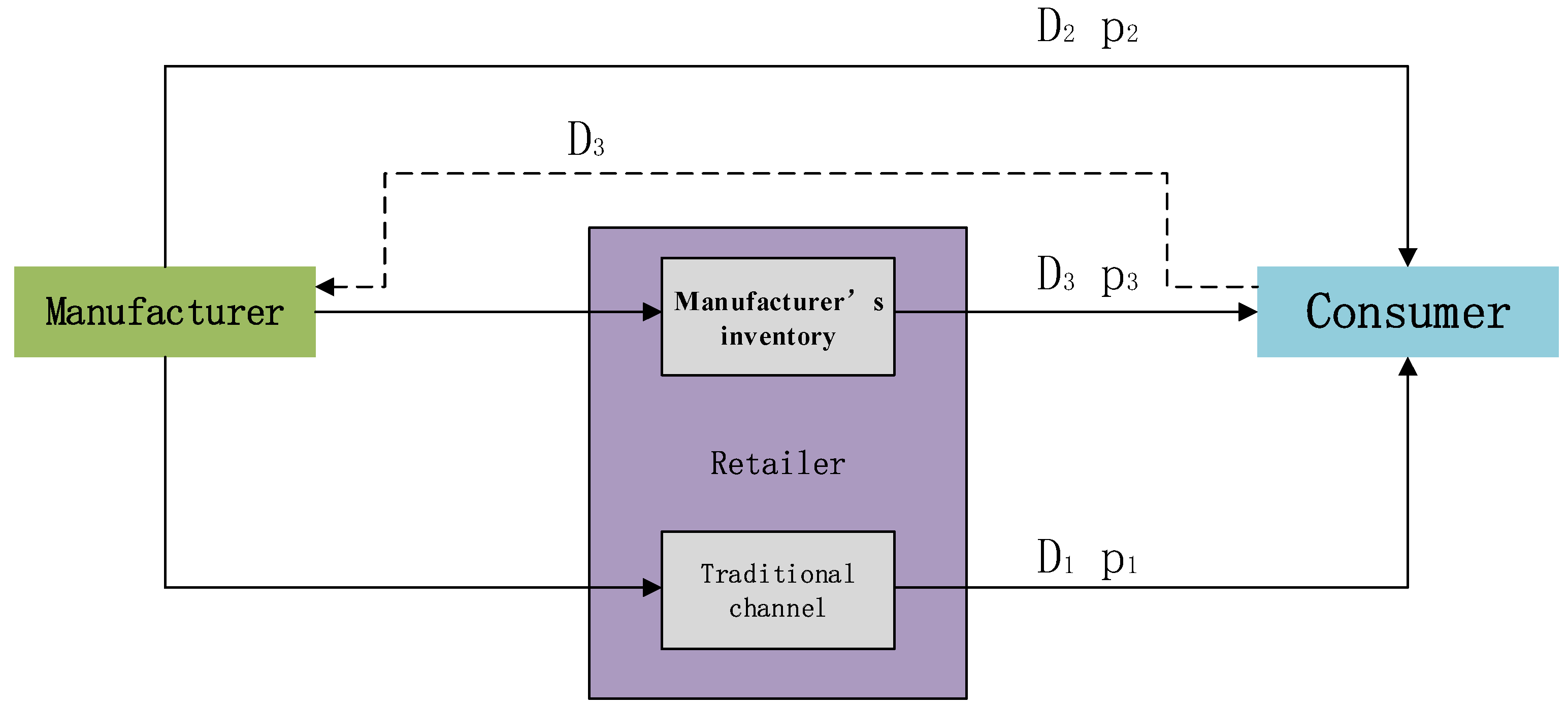
2. Model Description
2.1. Basic Model Description
2.2. Symbol Description
- : the size of the potential market
- : the wholesale price that the dual-channel manufacturer sets for the traditional retailer
- : the price sensitive coefficient
- : the influence of the substitute’s price
- : product demand at period t
- : product price at period t
- : the service level
- : the service sensitive coefficient
- e: influence of the substitute’s service
- : unit service cost
- : manufacturer’s profit at period t: retailer’s profit at period t
- : profit distribution rate
2.3. Profit Functions
3. The Nash Equilibrium Game Model
3.1. Model Construction
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- .
3.2. The Stability of the System (6)
3.2.1. System Equilibrium Points
3.2.2. Stability Analysis of the Equilibrium Points
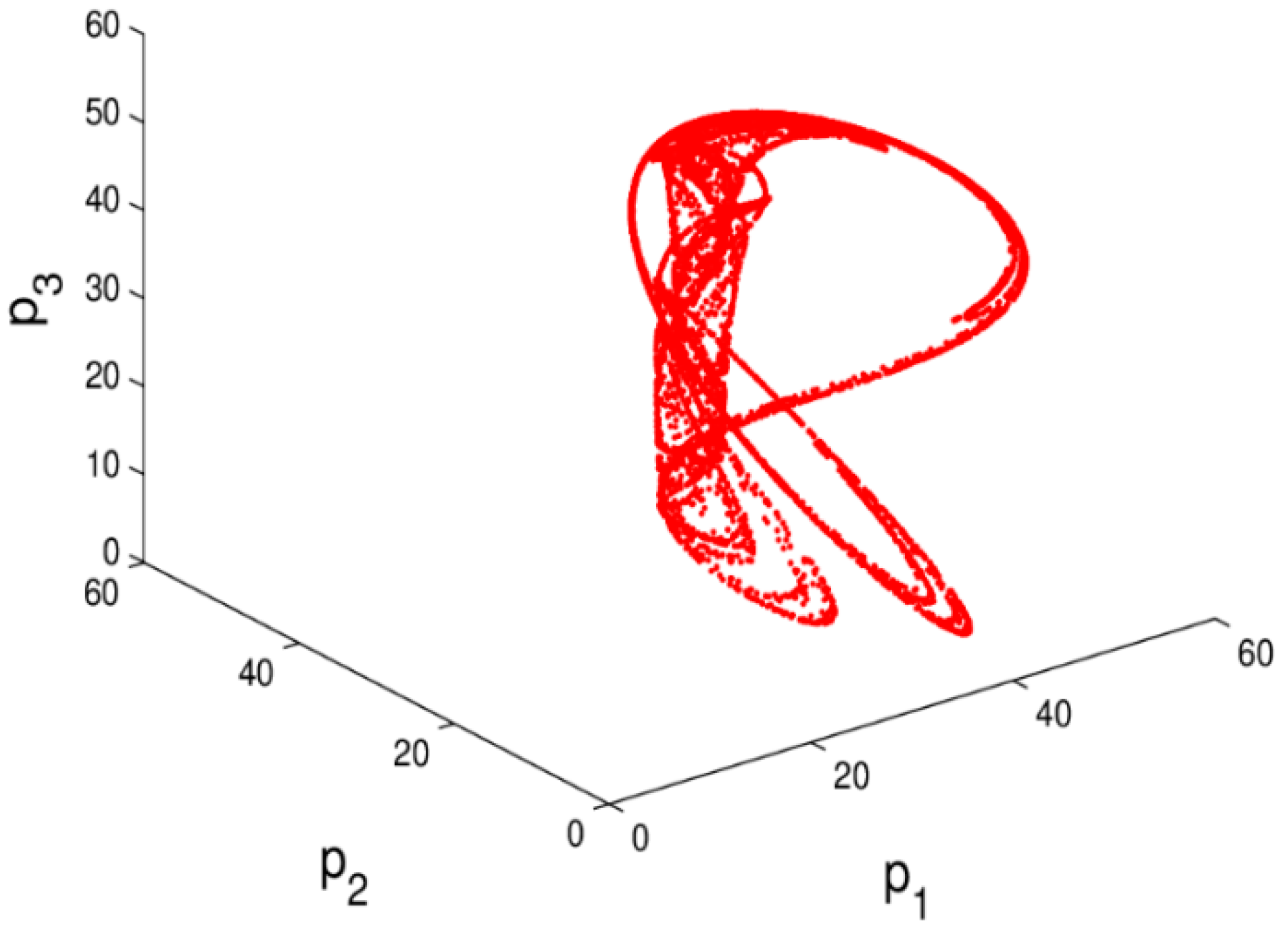
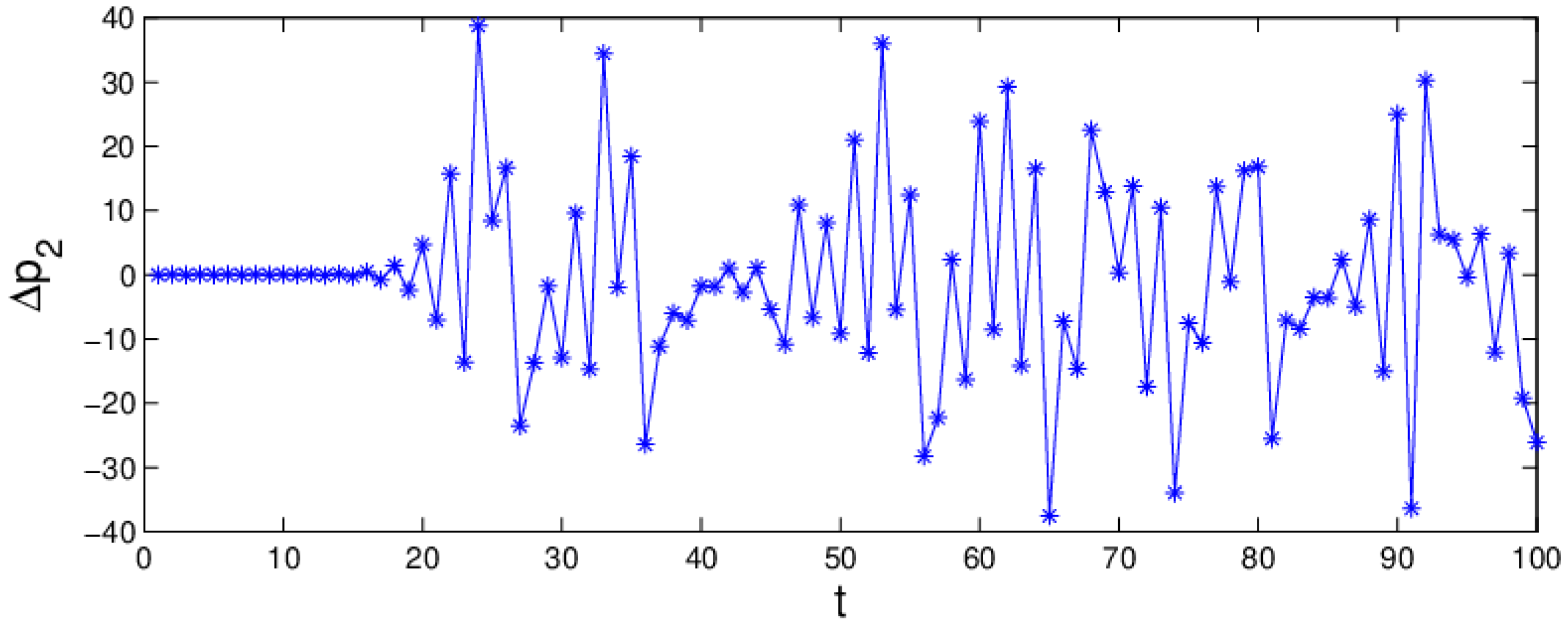
3.3. Numerical Simulation
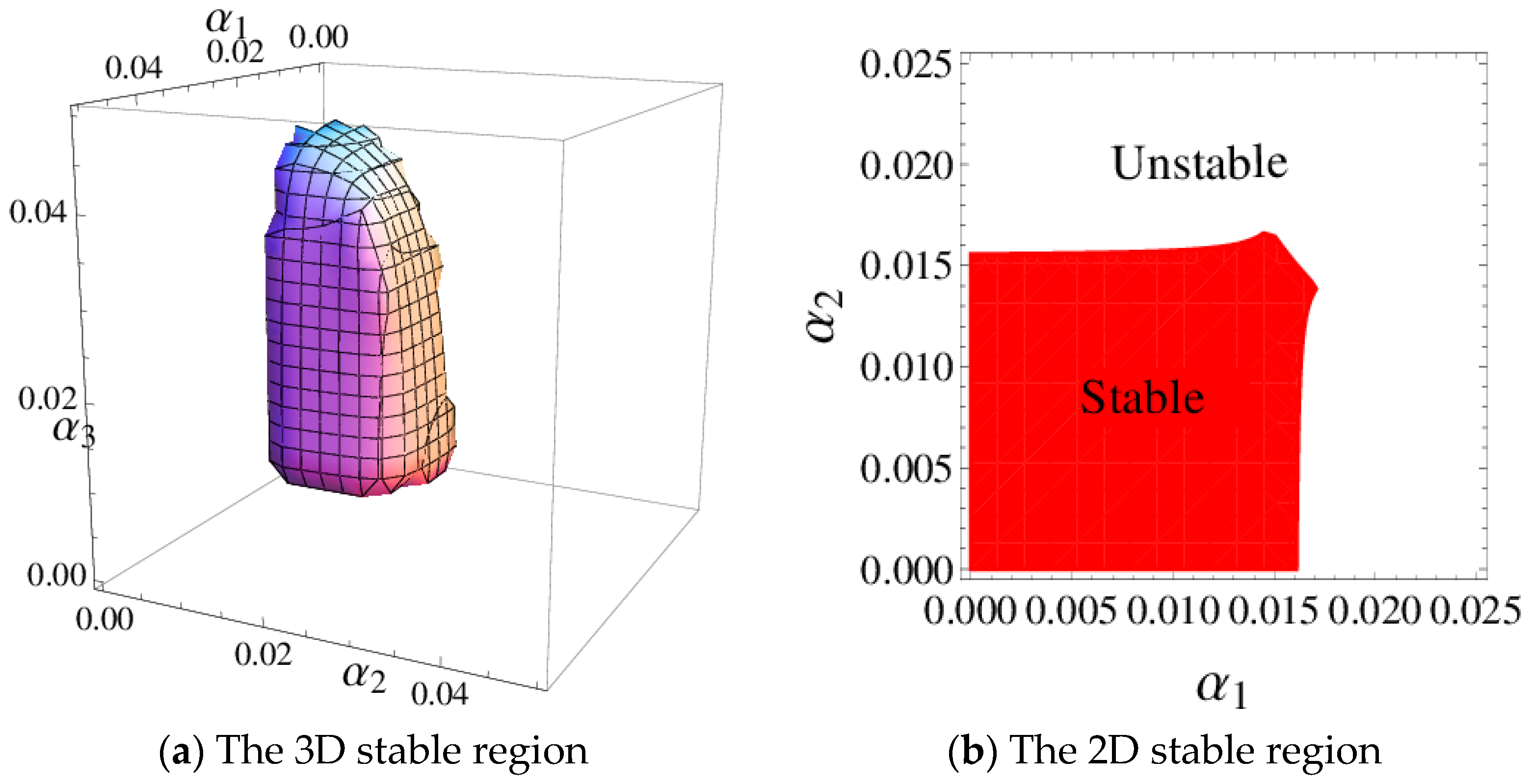
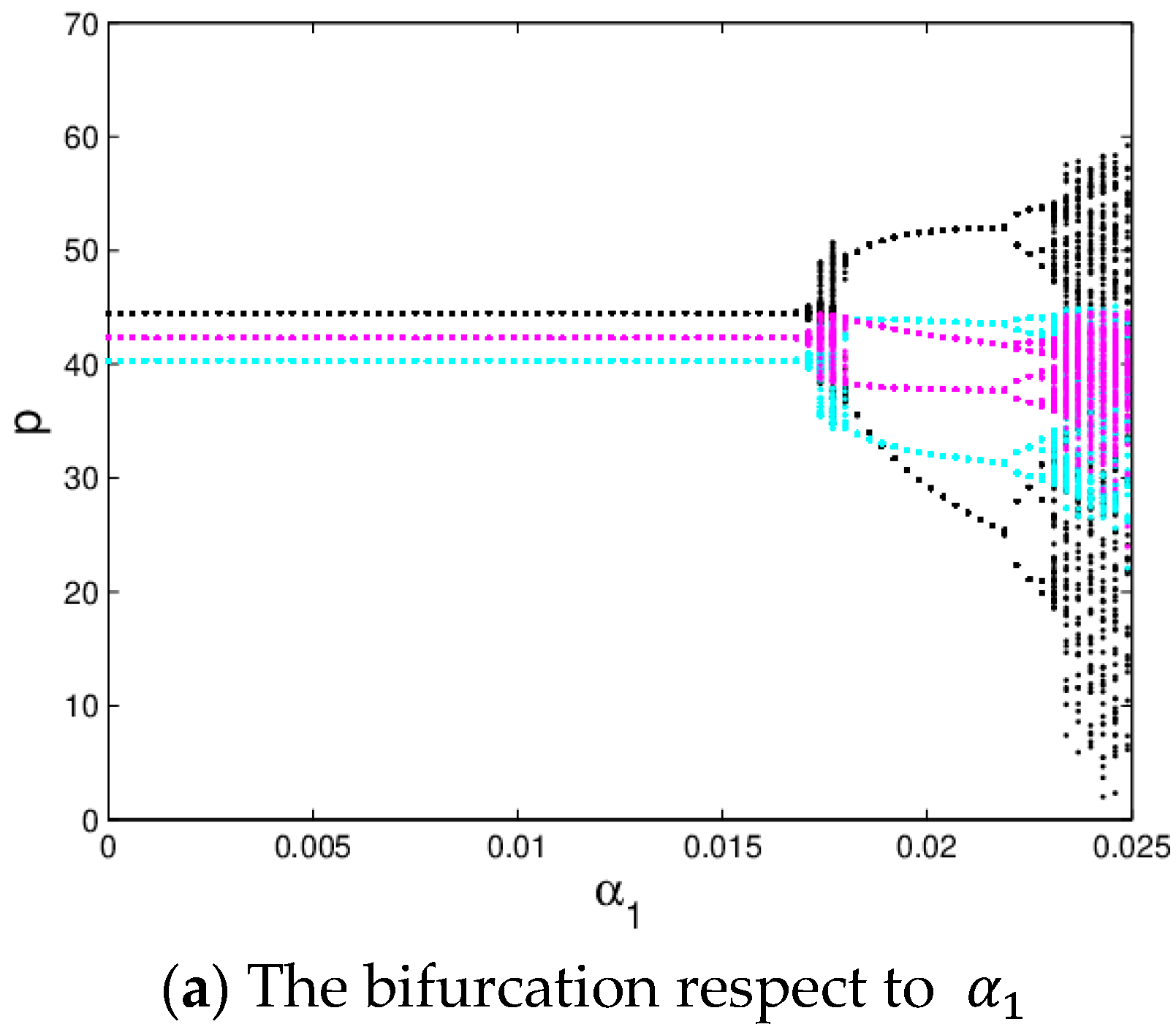
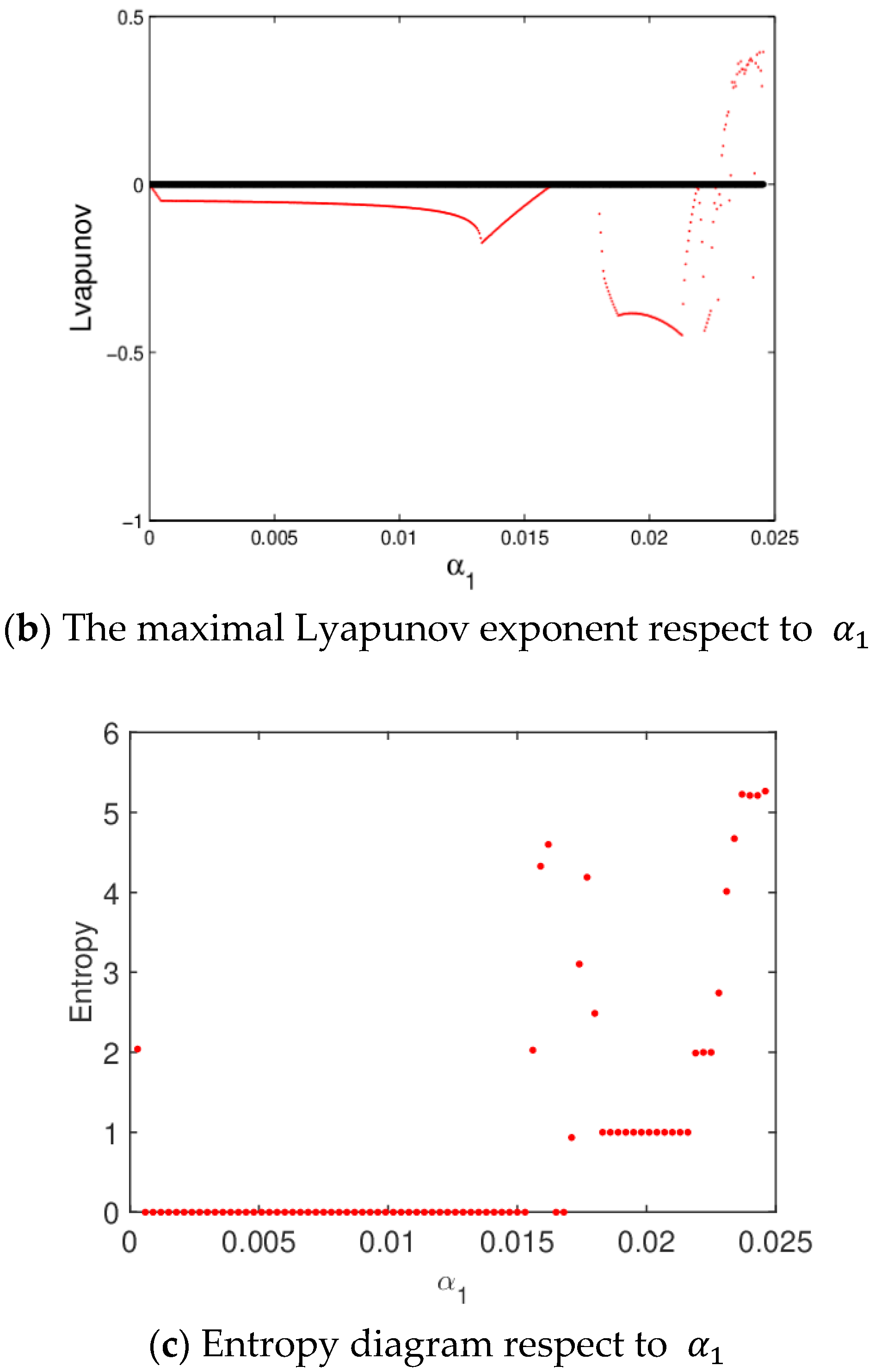
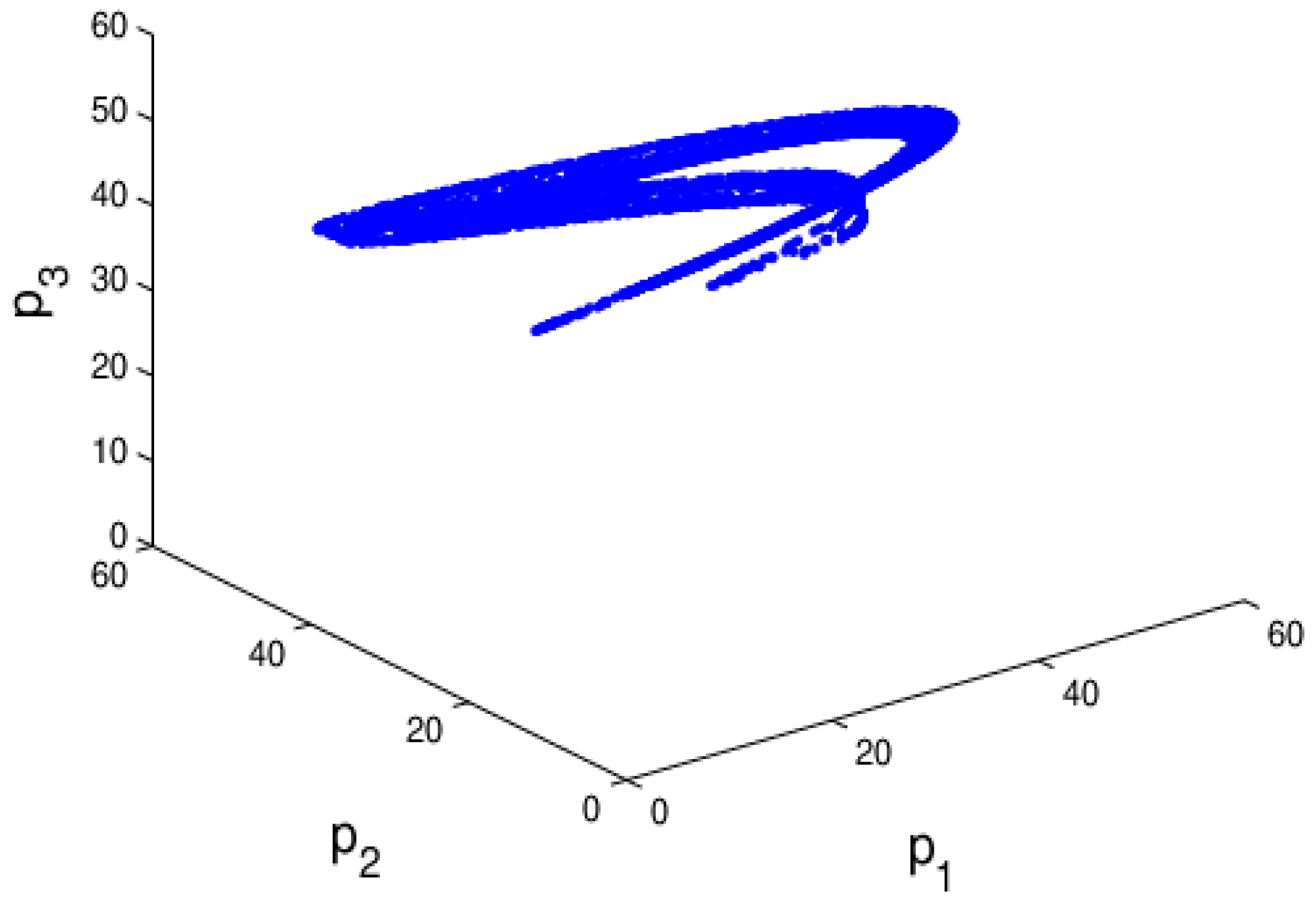
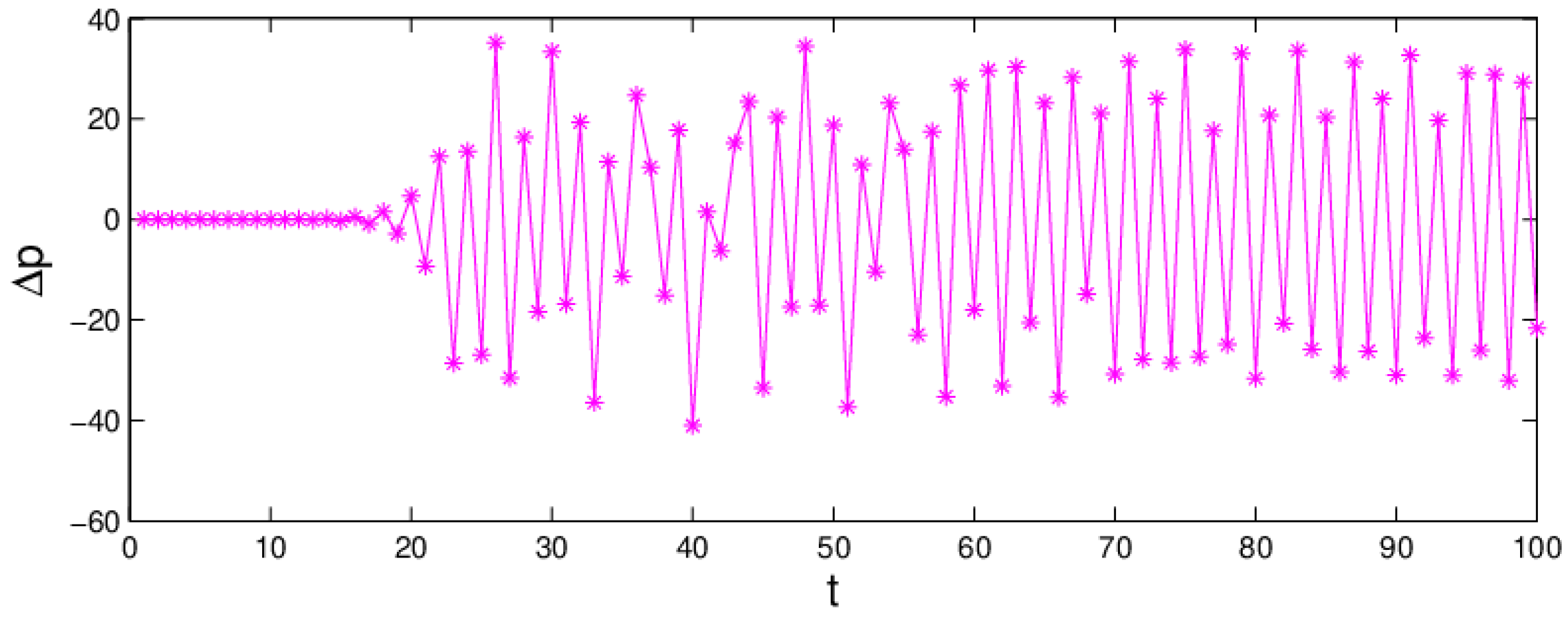
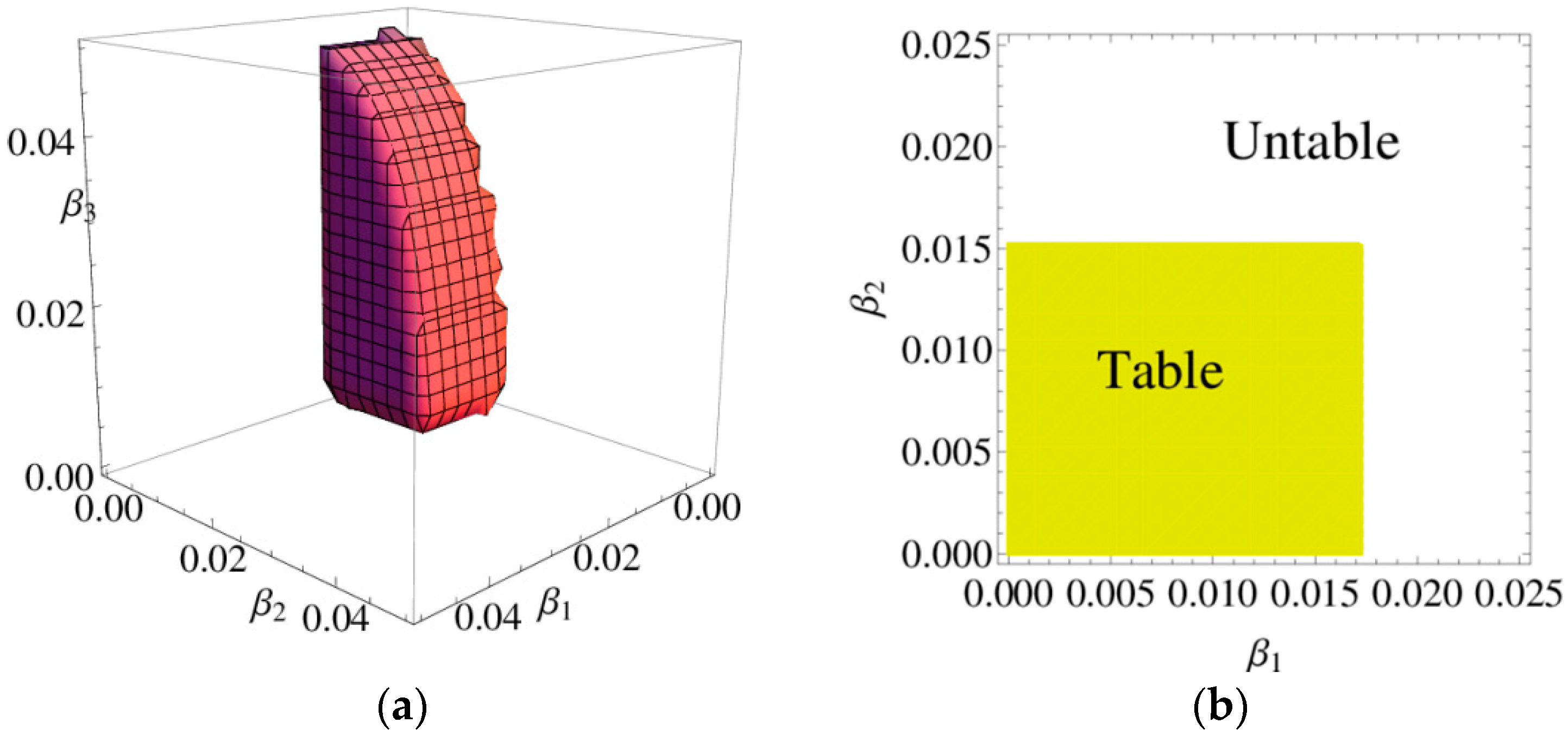
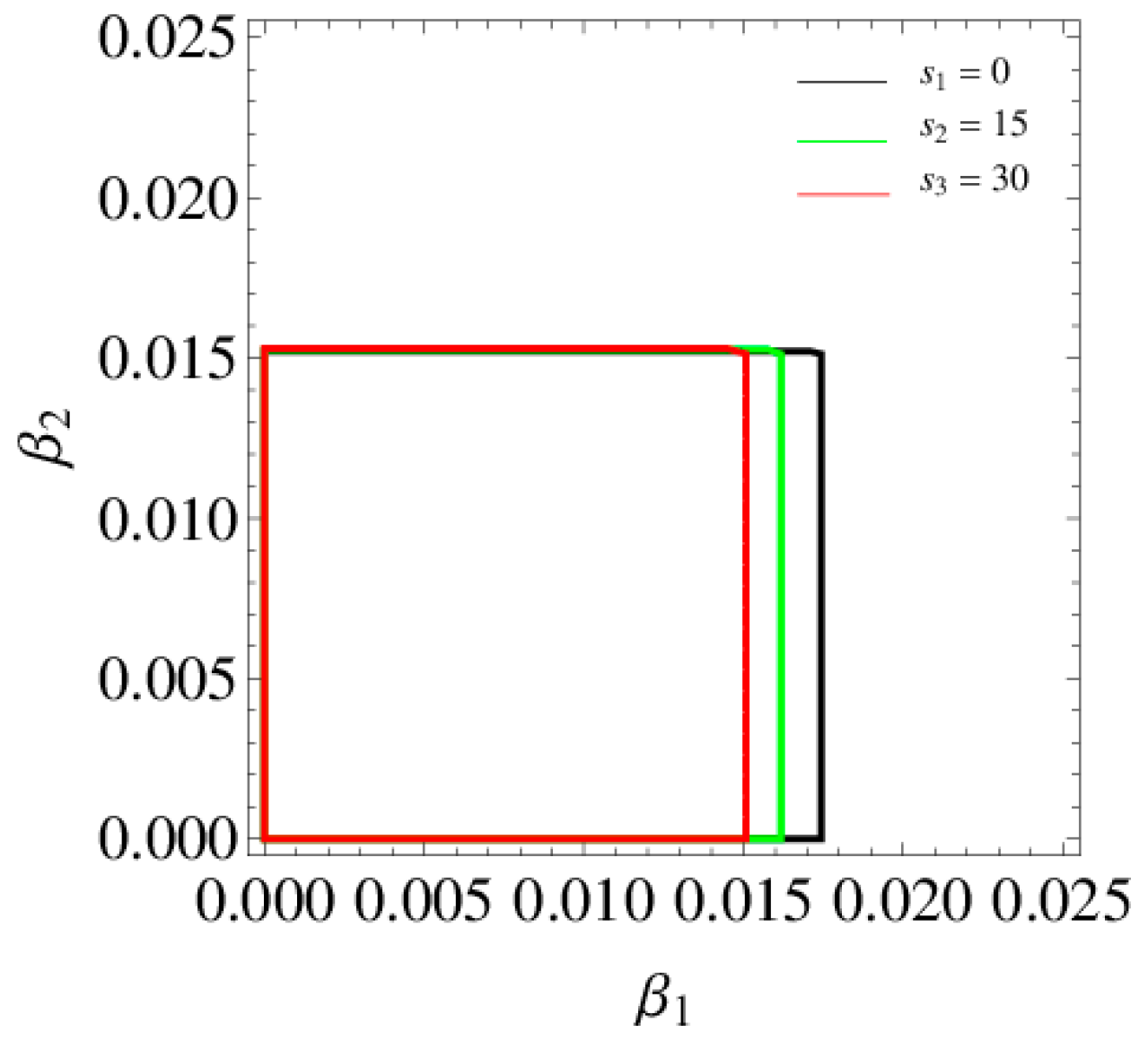
3.3.1. Stability Region of the System (6)
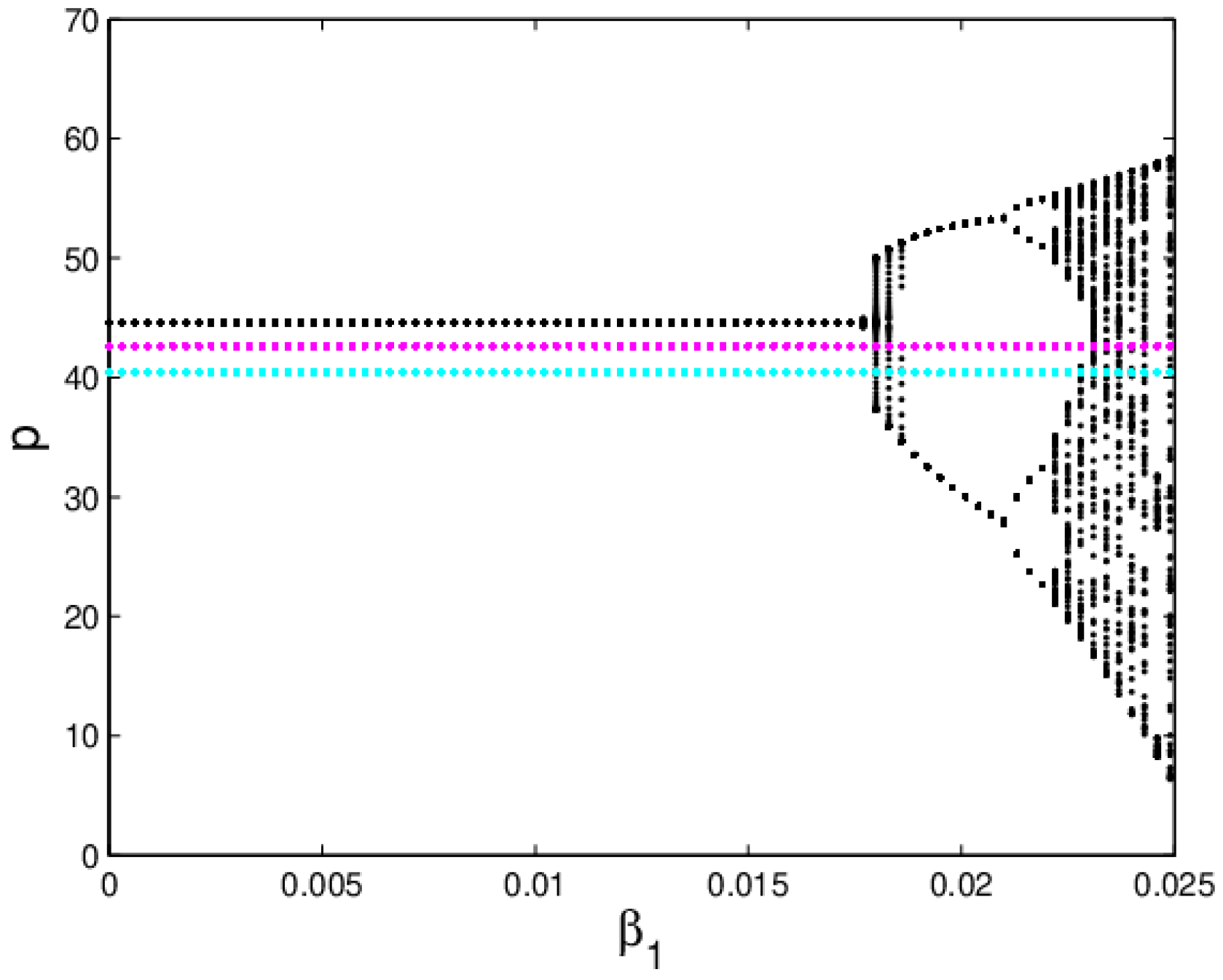
3.3.2. The Influence of the Price Adjustment Speed on the System Stability
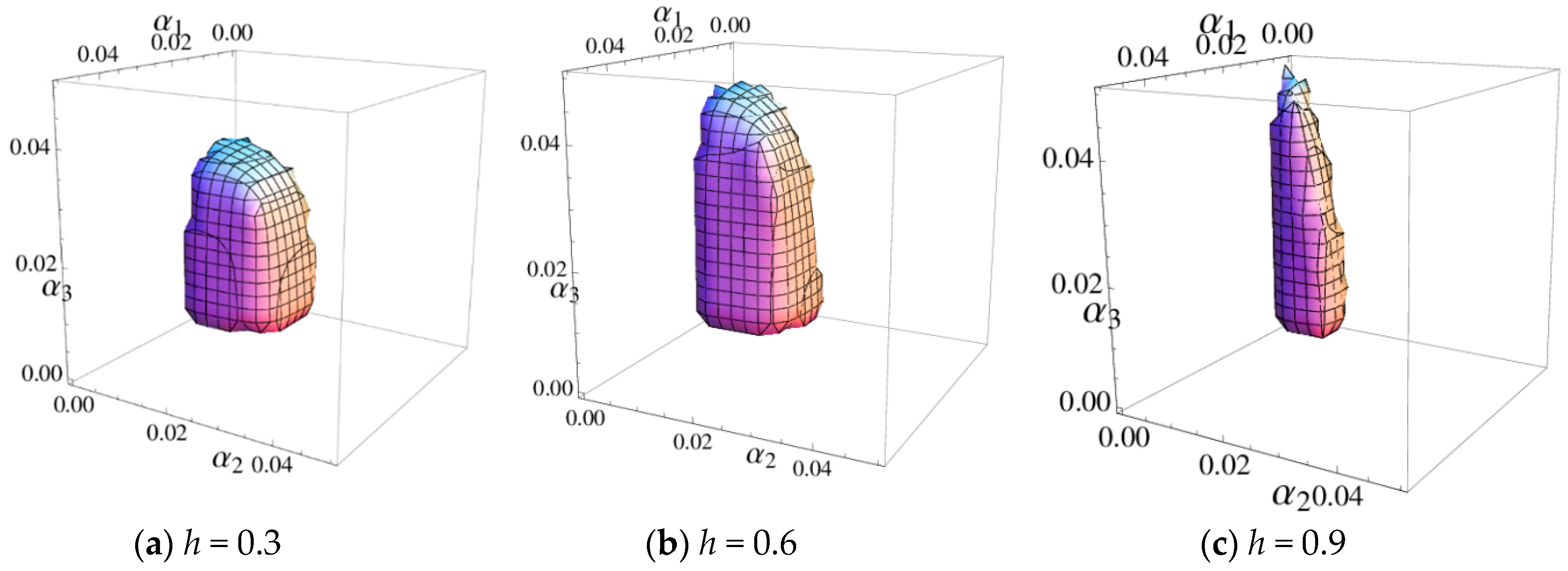
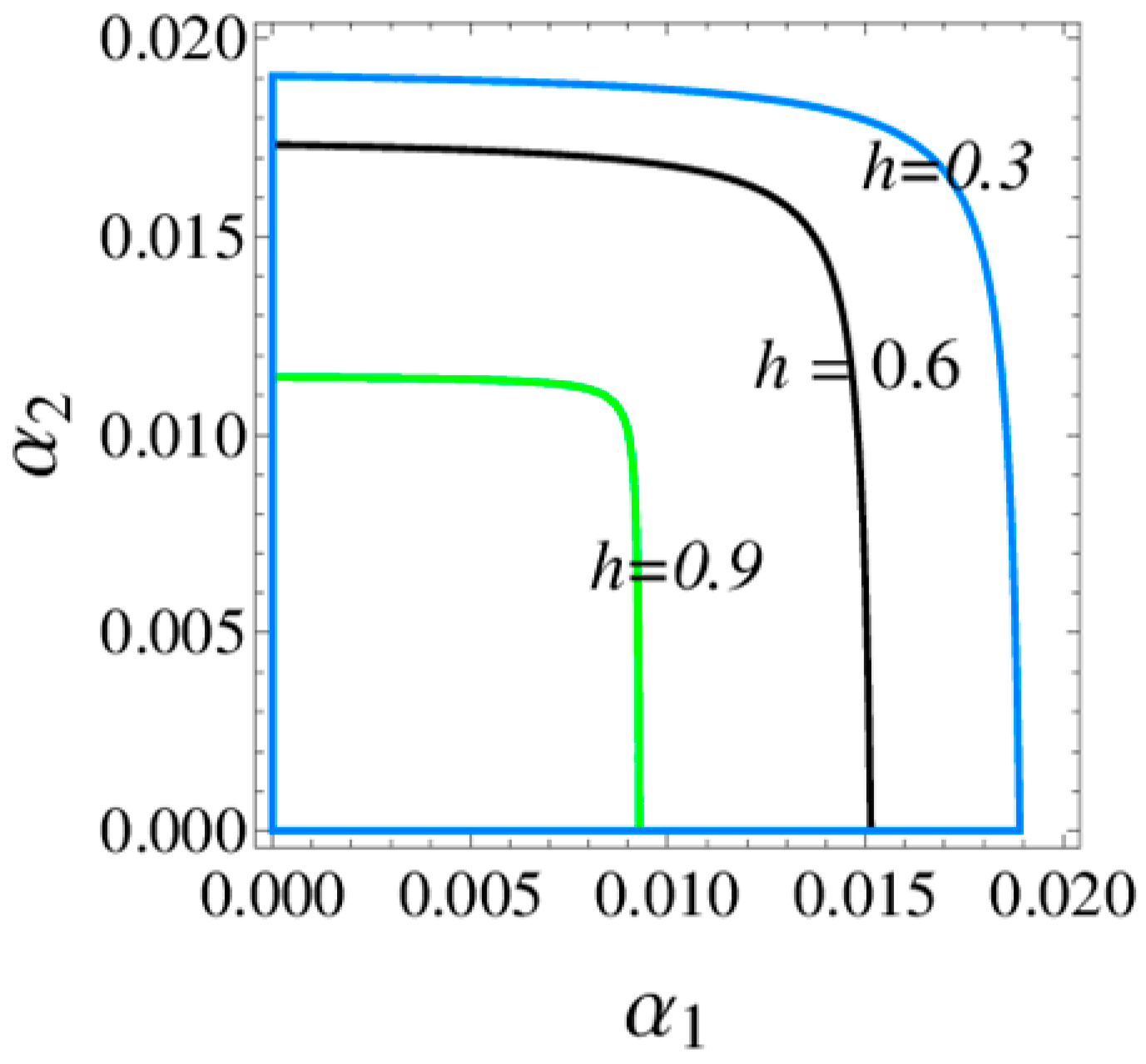
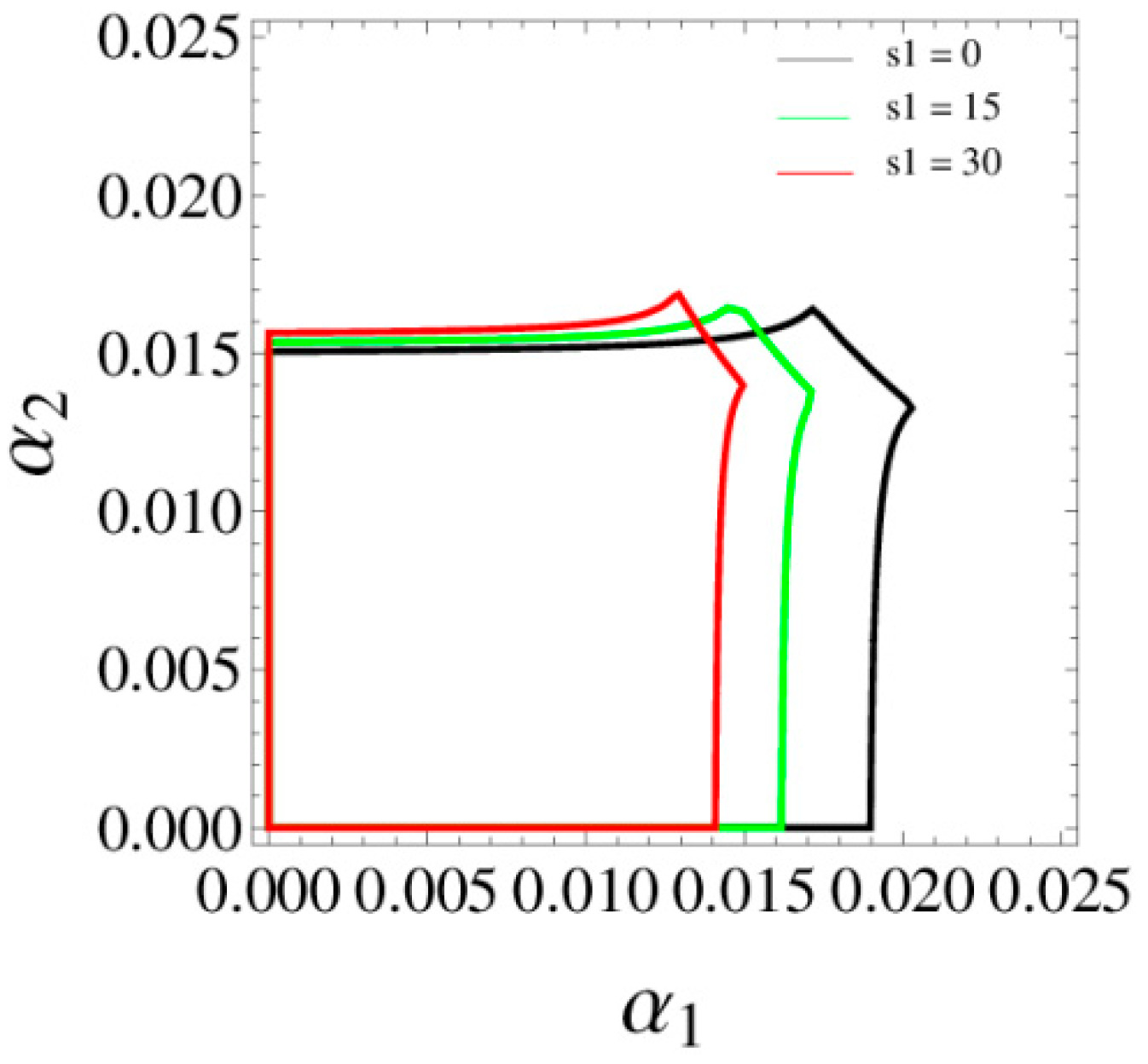
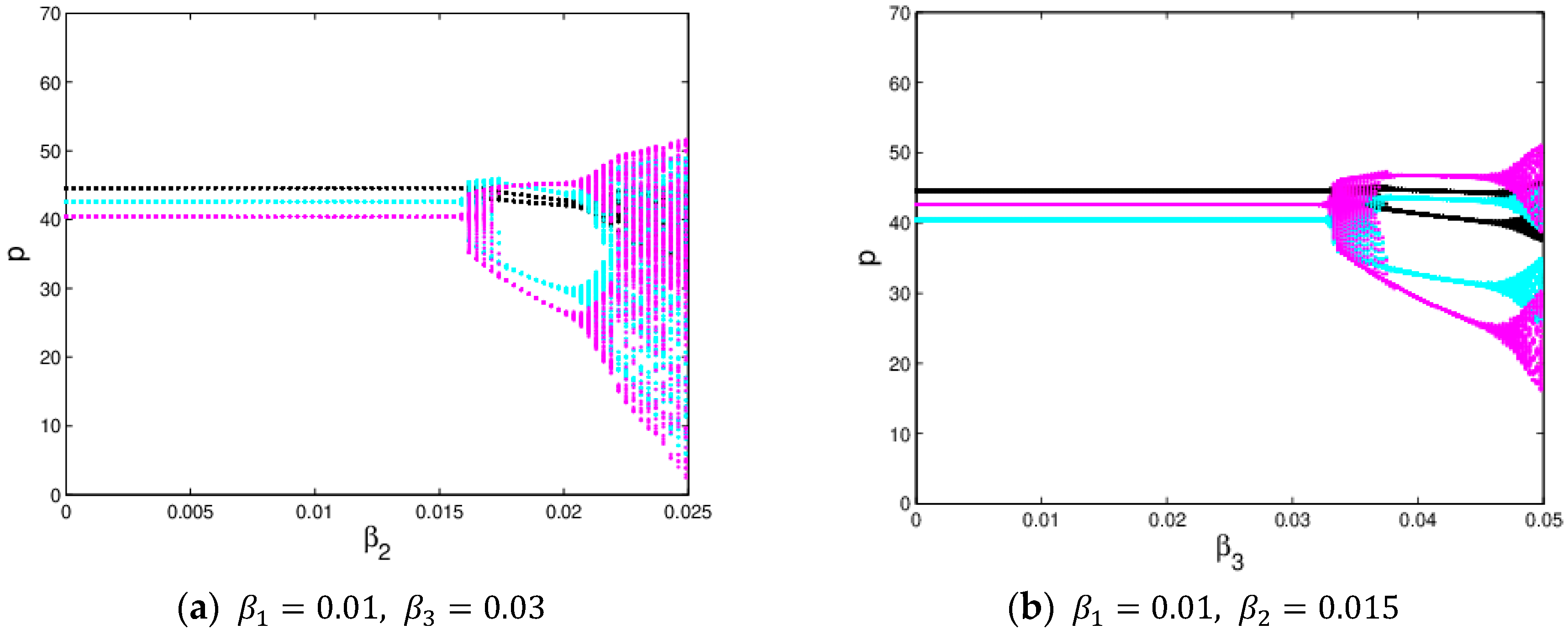
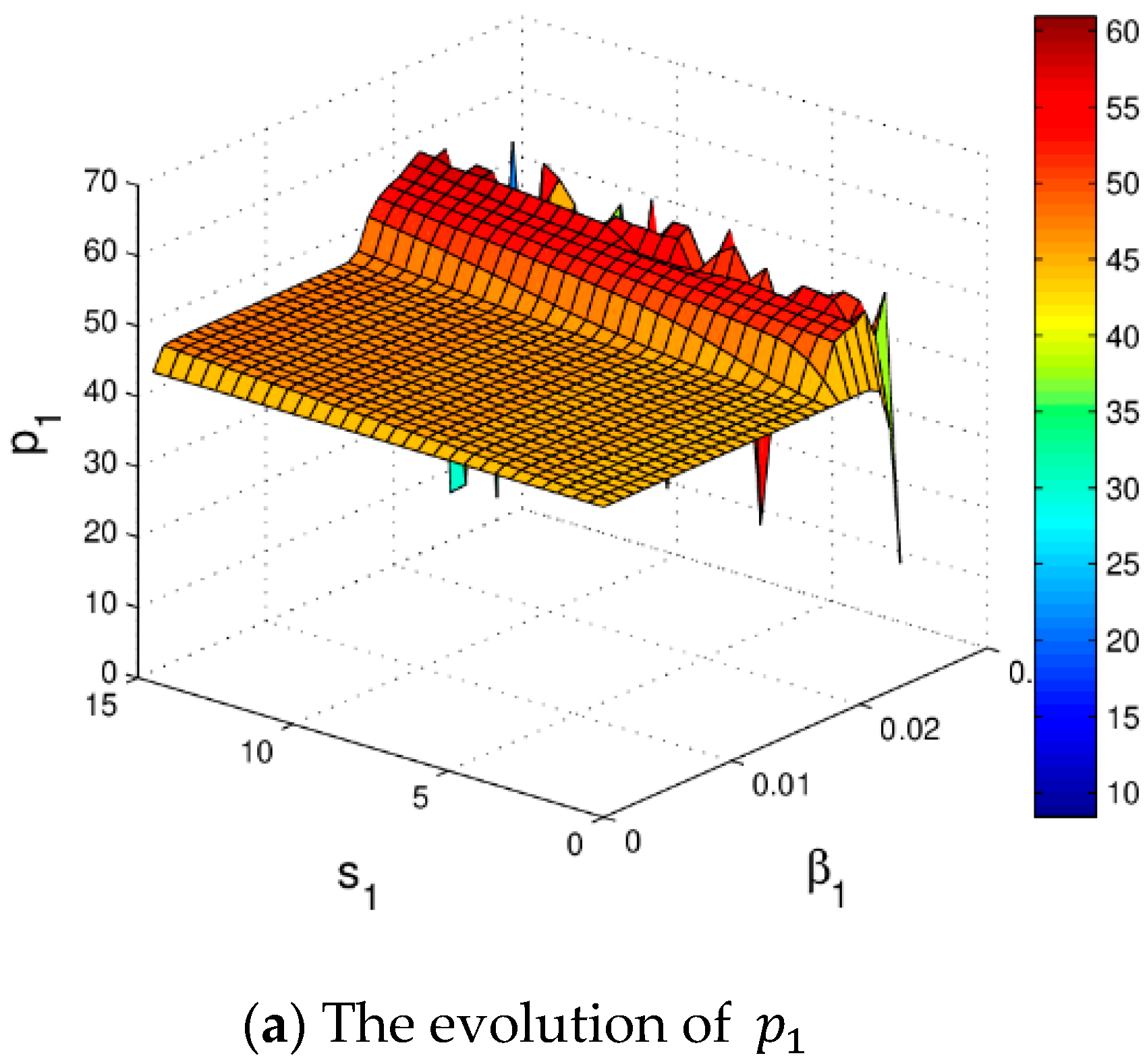
3.3.3. The Influence of Service Level on the System Stability
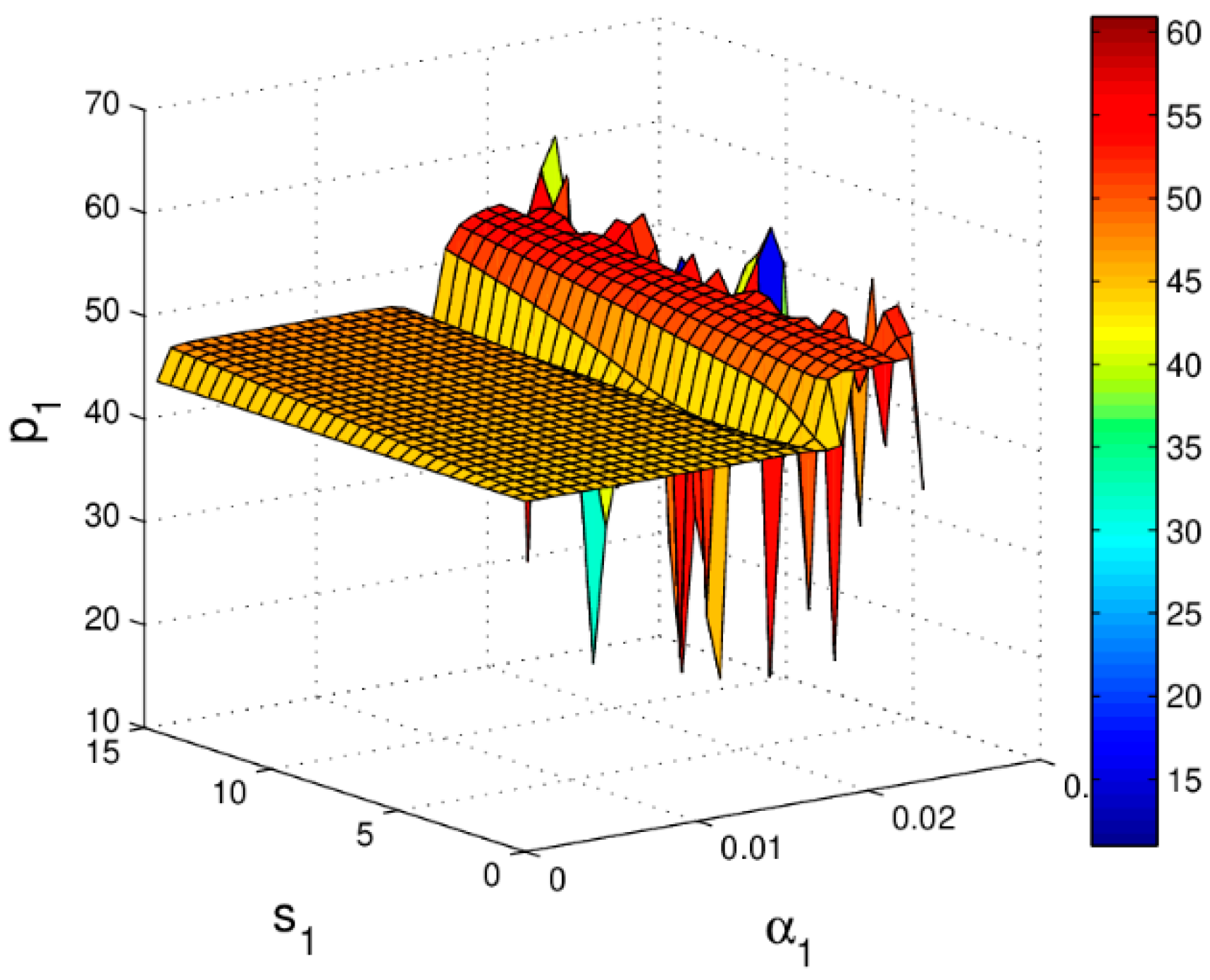
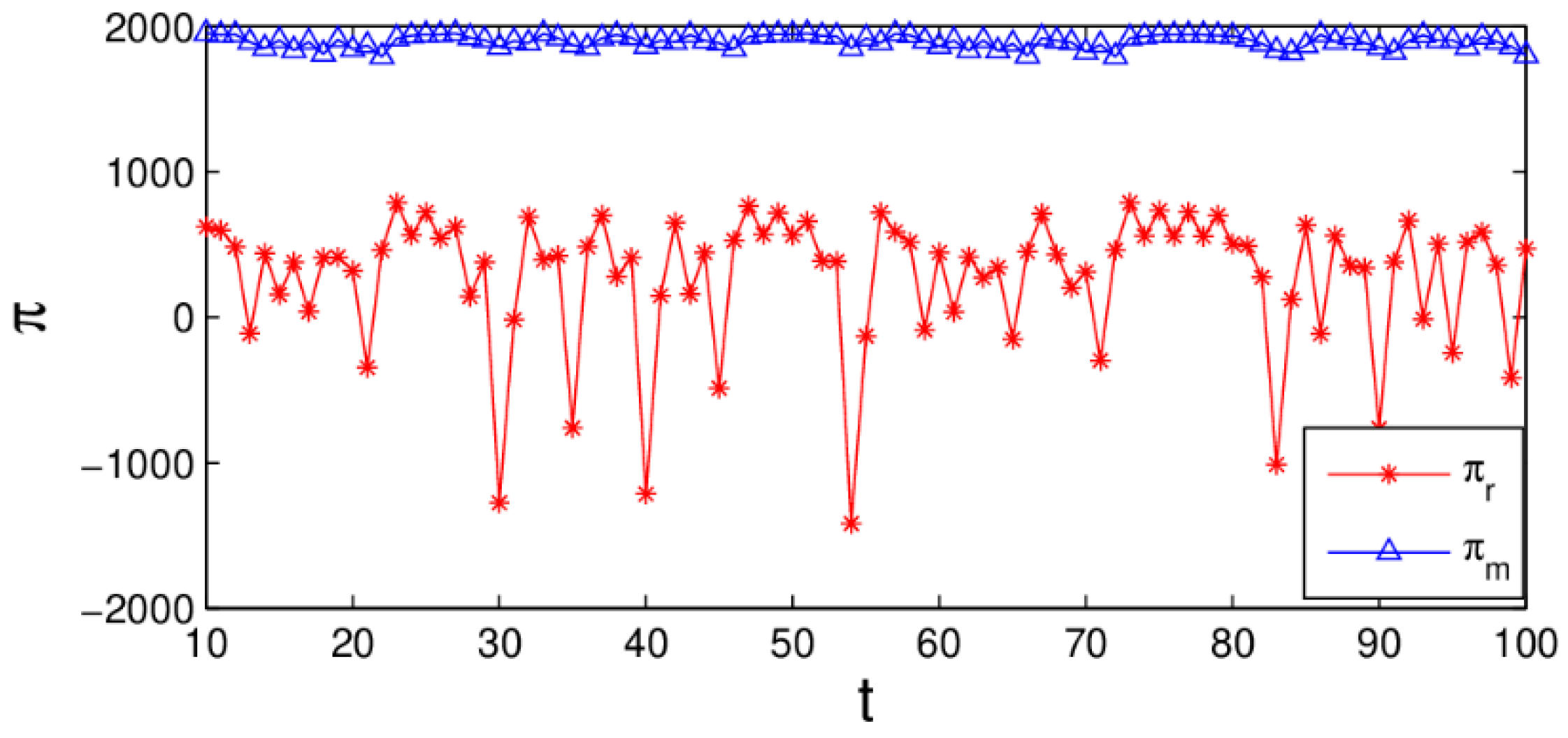
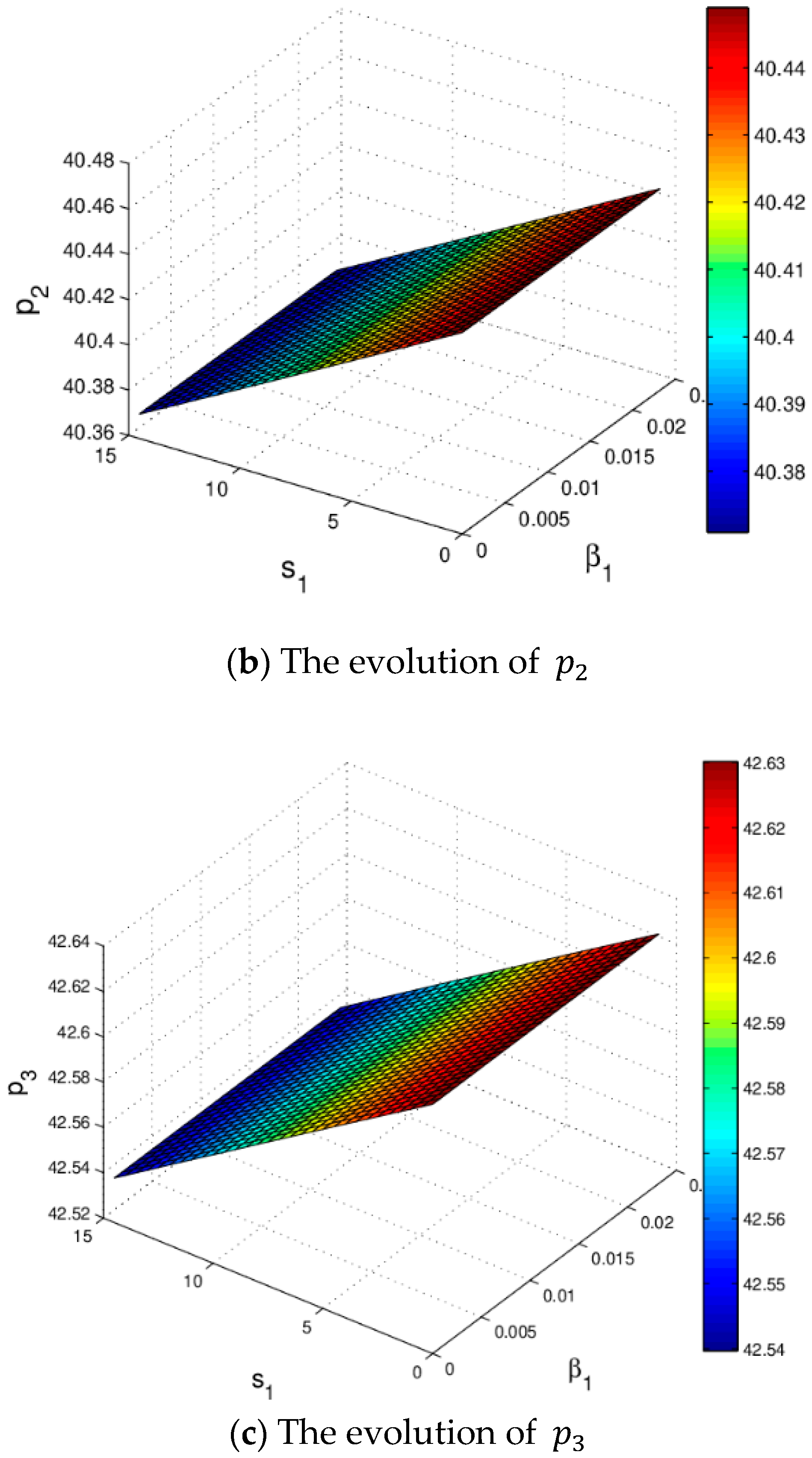
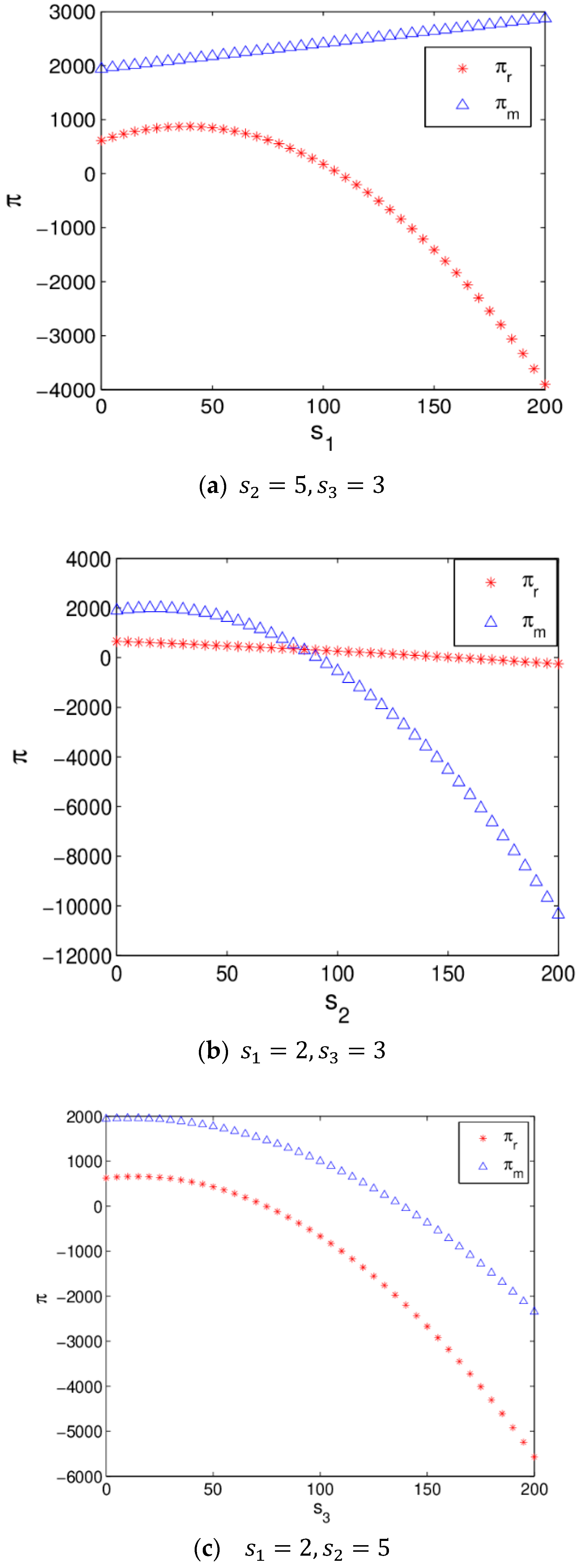
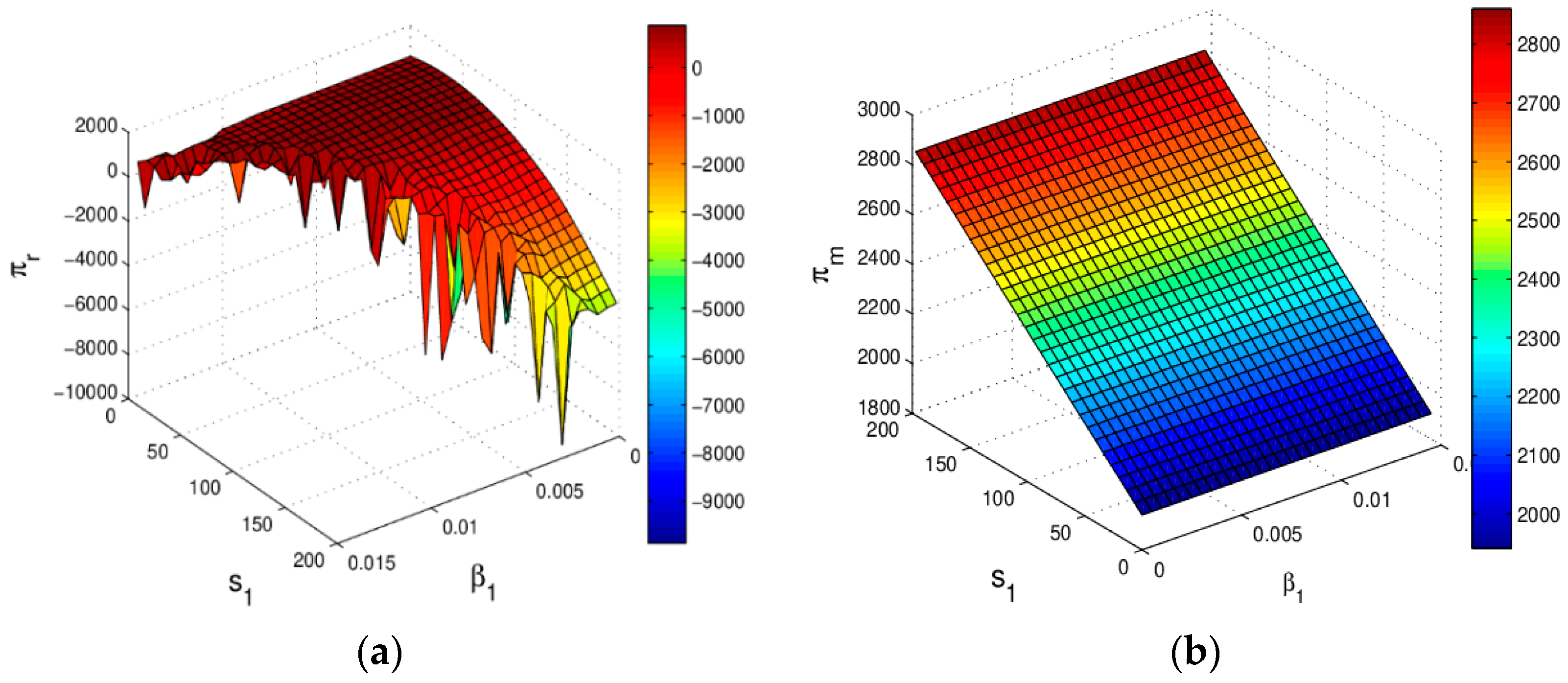
3.3.4. The Influence of the Service Level on System Profit
4. The Stackelberg Dynamic Game Model
4.1. The Model Construction
4.2. Equilibrium Points
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- .
4.3. Numerical Simulation
4.3.1. Stability Region of the System (11)
4.3.2. The Influence of the Price Adjustment Speed on the System Stability
4.3.3. The Influence of Service Level on the System Stability
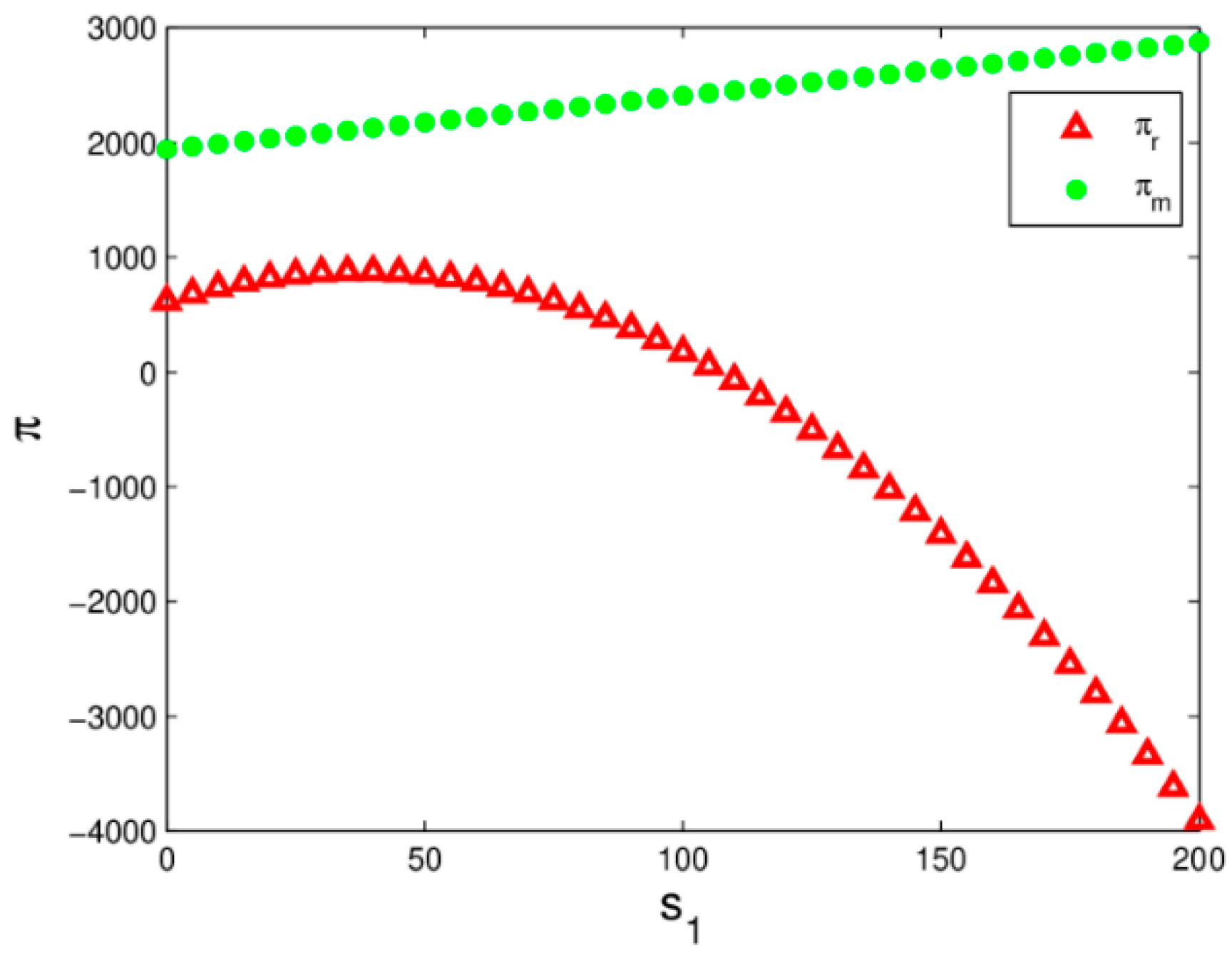
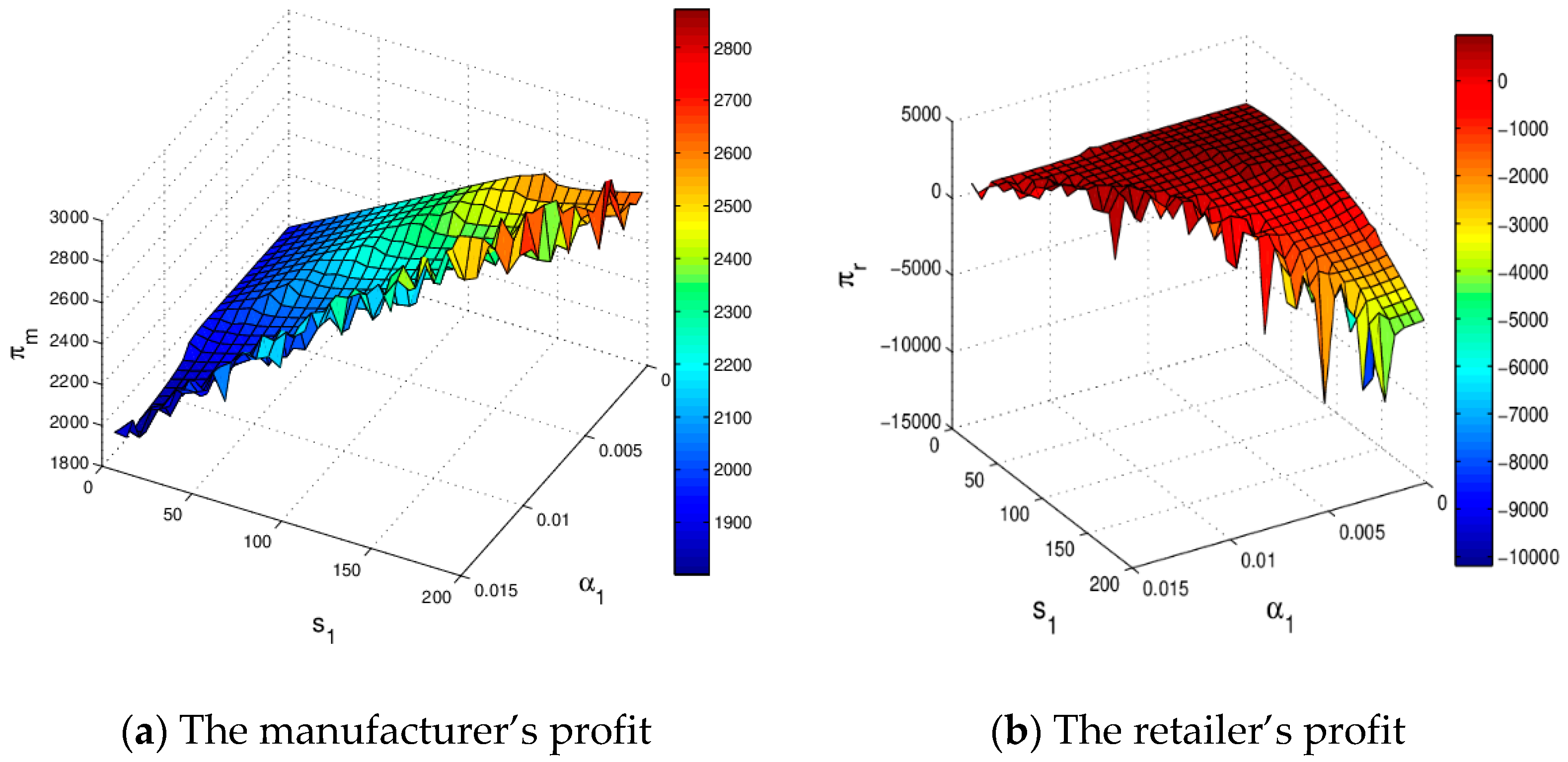
4.3.4. The Influence of Service Level on System Profit
5. Conclusions
- (1)
- the greater the service level and profit distribution rate are, the smaller the stability domain of the system is;
- (2)
- with the price adjustment speed gradually increasing, the price system gets unstable and finally becomes chaotic;
- (3)
- when the manufacturer or the retailer keeps service level in the appropriate value which is conducive to maximizing her/his profits;
- (4)
- in Nash game model, the stability of the system weakens than that in the Stackelberg game model.
Author Contributions
Acknowledgments
Conflicts of Interest
References
- China E-commerce Transaction Report. Available online: http://www.ec.com.cn/article/dsyj/dsbg/201807/299171.html (accessed on 18 July 2018).
- Hsieh, C.C.; Chang, Y.L.; Wu, C.H. Competitive pricing and ordering decisions in a multiple-channel supply chain. Int. J. Prod. Econ. 2014, 154, 156–165. [Google Scholar] [CrossRef]
- Liu, K.; Zhou, Y.; Zhang, Z. Capacitated location model with online demand pooling in a multi-channel supply chain. Eur. J. Oper. Res. 2010, 207, 218–231. [Google Scholar] [CrossRef]
- Lang, G. Multi-Channel Retail Supply Chain Management: Fulfillment systems in Multi-Channel Retailing—Customer Expectations and Economic Performance. In Proceedings of the 8th International Research Conference in Logistics and Supply Chain Management (RIRL), Bordeaux, France, 29 September–1 October 2010; pp. 1–25. [Google Scholar]
- Breugelmans, E.; Campo, K. Cross-Channel Effects of Price Promotions: An Empirical Analysis of the Multi-Channel Grocery Retail Sector. J. Retail. 2016, 92, 333–351. [Google Scholar] [CrossRef]
- Matsui, K. When and what wholesale and retail prices should be set in multi-channel supply chains? Eur. J. Oper. Res. 2018, 267, 540–554. [Google Scholar] [CrossRef]
- Yu, L.J.; Li, X.; Zhu, A.M. Coordination Pricing in Multi-Channels Supply Chain with Asymmetric Demand Information. Oper. Res. Manag. Sci. 2015, 2, 006. [Google Scholar]
- Esmaeilzadeh, A.; Taleizadeh, A.A. Pricing in a two-echelon supply chain with different market powers: Game theory approaches. J. Ind. Eng. Int. 2016, 12, 119–135. [Google Scholar] [CrossRef]
- Li, J.; Zhang, W.; Wu, J. Research on the Pricing of Multi-Channel Supply Chain under the Competition between the Traditional Brand and the Net Goods Brand. J. Ind. Technol. Econ. 2017, 36, 107–115. [Google Scholar]
- Dan, B.; Zhenjing, Q.U.; Liu, C.; Xumei, Z. Priceing Decision and Equilibrium Analysis in the Multi-Channel Supply Chain with the Strong Retailer. J. Syst. Manag. 2016, 25, 556–570. [Google Scholar]
- Ma, J.; Lou, W. Complex Characteristics of Multichannel Household Appliance Supply Chain with the Price Competition. Complexity 2017, 2017, 4327069. [Google Scholar] [CrossRef]
- Bai, Q.G.; Xu, X.H.; Pan, W. Joint pricing and inventory model for deteriorating items multi-channel distribution system. J. Ind. Eng. Eng. Manag. 2017, 31, 84–92. [Google Scholar]
- Cai, G.; Dai, Y.; Zhang, W. Modeling Multichannel Supply Chain Management with Marketing Mixes: A Survey; Social Science Electronic Publishing: Beijing, China, 2015. [Google Scholar]
- Du, K. The impact of multi-channel and multi-product strategies on firms’ risk-return performance. Decis. Support Syst. 2018, 109, 27–38. [Google Scholar] [CrossRef]
- Hübner, A.; Holzapfel, A.; Kuhn, H. Operations management in multi-channel retailing: An exploratory study. J. Oper. Manag. Res. 2015, 8, 84–100. [Google Scholar] [CrossRef]
- Luo, M.L.; Li, G.; Zhang, W. Channel Integration Strategy Based on E-coupon in a Multi-channel Supply Chain. Oper. Res. Manag. Sci. 2017, 26, 192–199. [Google Scholar]
- Dumrongsiri, A.; Fan, M.; Jain, A. A supply chain model with direct and retail channels. Eur. J. Oper. Res. 2008, 187, 691–718. [Google Scholar] [CrossRef]
- Ren, L.; He, Y.; Song, H. Price and Service Competition of Dual-Channel Supply Chain with Consumer Returns. Discret. Dyn. Nat. Soc. 2014, 2014, 565603. [Google Scholar] [CrossRef]
- Pei, Z.; Yan, R. Do channel members value supportive retail services? Why? J. Bus. Res. 2015, 68, 1350–1358. [Google Scholar] [CrossRef]
- Li, Q.H.; Li, B. Dual-channel supply chain equilibrium problems regarding retail services and fairness concerns. Appl. Math. Model. 2016, 40, 7349–7367. [Google Scholar] [CrossRef]
- Protopappa-Sieke, M.; Sieke, M.A.; Thonemann, U.W. Optimal two-period inventory allocation under multiple service level contracts. Eur. J. Oper. Res. 2016, 252, 145–155. [Google Scholar] [CrossRef]
- Zhou, Y.W.; Guo, J.; Zhou, W. Pricing/service strategies for a dual-channel supply chain with free riding and service-cost sharing. Int. J. Prod. Econ. 2018, 196, 198–210. [Google Scholar] [CrossRef]
- Sadjadi, S.J.; Asadi, H.; Sadeghian, R. Retailer Stackelberg game in a supply chain with pricing and service decisions and simple price discount contract. PLoS ONE 2018, 13, e0195109. [Google Scholar] [CrossRef]
- Chen, M.; Hu, Q.; Wei, H. Interaction of after-sales service provider and contract type in a supply chain. Int. J. Prod. Econ. 2017, 193, 514–527. [Google Scholar] [CrossRef]
- Jena, S.K.; Sarmah, S.P. Price and service co-opetiton under uncertain demand and condition of used items in a remanufacturing system. Int. J. Prod. Econ. 2016, 173, 1–21. [Google Scholar] [CrossRef]
- Zhang, F.; Wang, C. Dynamic pricing strategy and coordination in a dual-channel supply chain considering service value. Appl. Math. Model. 2017, 54, 722–742. [Google Scholar] [CrossRef]
- Ma, J.; Li, T.; Ren, W. Research on the Complexity of Dual-Channel Supply Chain Model in Competitive Retailing Service Market. Int. J. Bifurc. Chaos 2017, 27, 1750098. [Google Scholar] [CrossRef]
- Ghosh, S.K. Optimal Pricing Strategy of a Two-Echelon Supply Chain Consisting of One Manufacturer and Two Retailers with Price and Service Sensitive Demand. Int. J. Appl. Comput. Math. 2018, 4, 1. [Google Scholar] [CrossRef]
- Harré, M.S.; Bossomaier, T. Strategic islands in economic games: Isolating economies from better outcomes. Entropy 2014, 16, 5102–5121. [Google Scholar] [CrossRef]
- Dajka, J.; Łobejko, M.; Sładkowski, J. Payoffs and Coherence of a Quantum Two-Player Game in a Thermal Environment. Entropy 2015, 17, 7736–7751. [Google Scholar] [CrossRef]
- Huang, Y.; Chen, X.; Li, Q.; Ma, X. The complexity and entropy analysis for service game model based on different expectations and optimal pricing. Entropy 2018, 20, 858. [Google Scholar] [CrossRef]
- Han, Z.; Ma, J.; Si, F. Entropy Complexity and Stability of a Nonlinear Dynamic Game Model with Two Delays. Entropy 2016, 18, 317. [Google Scholar] [CrossRef]
- Levner, E.; Ptuskin, A. Entropy-based model for the ripple effect: Managing environmental risks in supply chains. Int. J. Prod. Res. 2018, 56, 2539–2551. [Google Scholar] [CrossRef]
- Yao, D.Q.; Yue, X.; Liu, J. Vertical cost information sharing in a supply chain with value-adding retailers. Omega 2008, 36, 838–851. [Google Scholar] [CrossRef]
- Zhao, J.; Wei, J.; Zhao, J. The coordinating contracts for a fuzzy supply chain with effort and price dependent demand. Appl. Math. Model. 2014, 38, 2476–2489. [Google Scholar] [CrossRef]
- Sarathi, G.P.; Sarmah, S.P.; Jenamani, M. An integrated revenue sharing and quantity discounts contract for coordinating a supply chain dealing with short life-cycle products. Appl. Math. Model. 2014, 38, 4120–4136. [Google Scholar] [CrossRef]
- Tsay, A.A.; Agrawal, N. Channel Dynamics under Price and Service Competition. Manuf. Serv. Oper. Manag. 2000, 2, 372–391. [Google Scholar] [CrossRef]
- Li, Q.; Zhang, Y.; Huang, Y. The complexity analysis in dual-channel supply chain based on fairness concern and different business objectives. Complexity 2018, 2018, 1–13. [Google Scholar]
- Huang, Y.; Li, Q. The Entropy Complexity of an Asymmetric Dual-Channel Supply Chain with Probabilistic Selling. Entropy 2018, 20, 543. [Google Scholar] [CrossRef]
- Huang, Y.; Liu, L.; Qi, E. The dynamic decision in risk-averse complementary product manufacturers with corporate social responsibility. J. Kybernetes. 2015, 45, 244–265. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Chen, X.; Huang, Y. Complexity and Entropy Analysis of a Multi-Channel Supply Chain Considering Channel Cooperation and Service. Entropy 2018, 20, 970. https://doi.org/10.3390/e20120970
Li Q, Chen X, Huang Y. Complexity and Entropy Analysis of a Multi-Channel Supply Chain Considering Channel Cooperation and Service. Entropy. 2018; 20(12):970. https://doi.org/10.3390/e20120970
Chicago/Turabian StyleLi, Qiuxiang, Xingli Chen, and Yimin Huang. 2018. "Complexity and Entropy Analysis of a Multi-Channel Supply Chain Considering Channel Cooperation and Service" Entropy 20, no. 12: 970. https://doi.org/10.3390/e20120970
APA StyleLi, Q., Chen, X., & Huang, Y. (2018). Complexity and Entropy Analysis of a Multi-Channel Supply Chain Considering Channel Cooperation and Service. Entropy, 20(12), 970. https://doi.org/10.3390/e20120970



