Flexibility of Boolean Network Reservoir Computers in Approximating Arbitrary Recursive and Non-Recursive Binary Filters
Abstract
1. Introduction
2. Materials and Methods
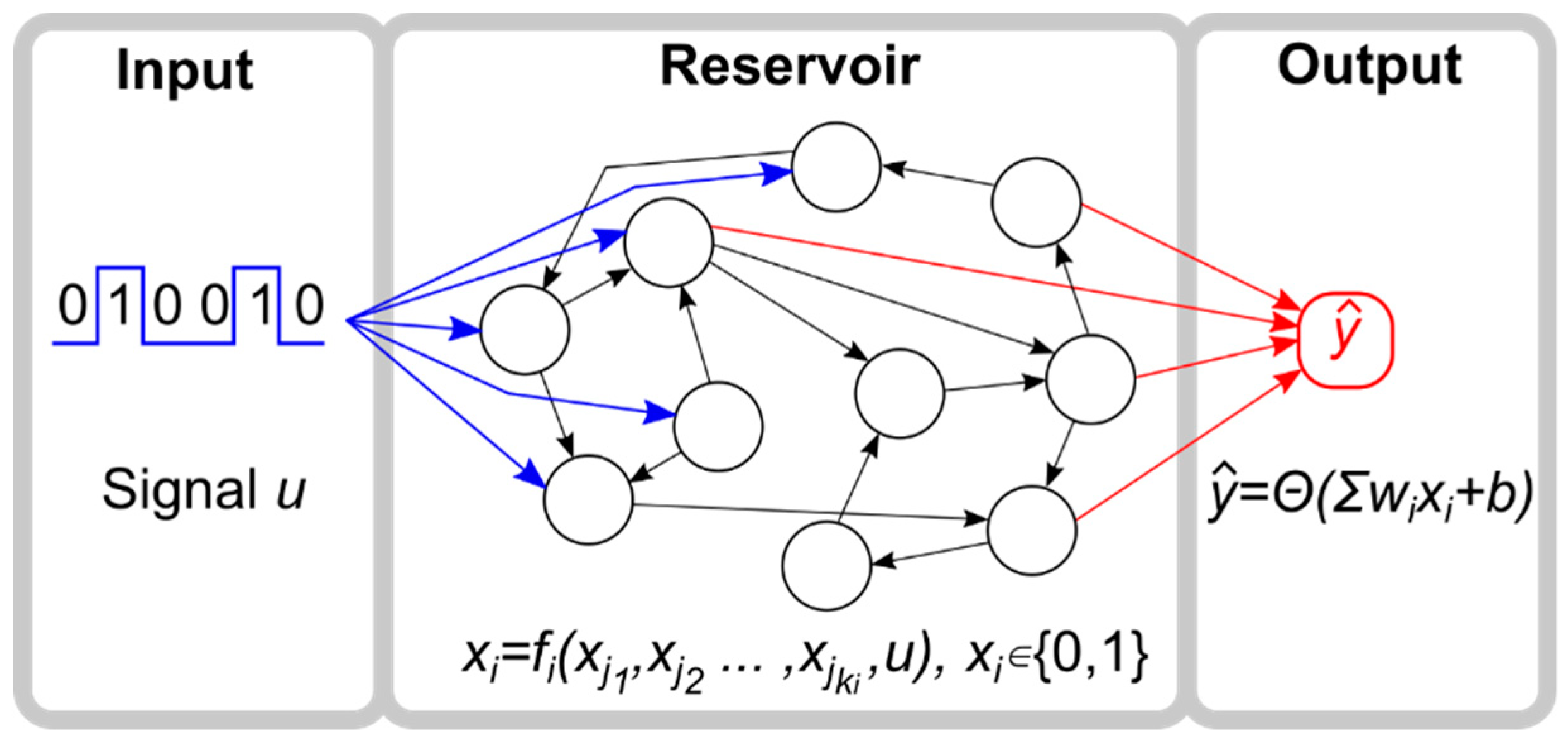
2.1. Reservoir Computer
2.2. Reservoir
2.3. Input
2.4. Output
2.5. Objective Functions
- Non-recursive functions, defined as
- Recursive functions, defined as
2.6. Training and Testing Algorithm
2.7. Overall Strategy
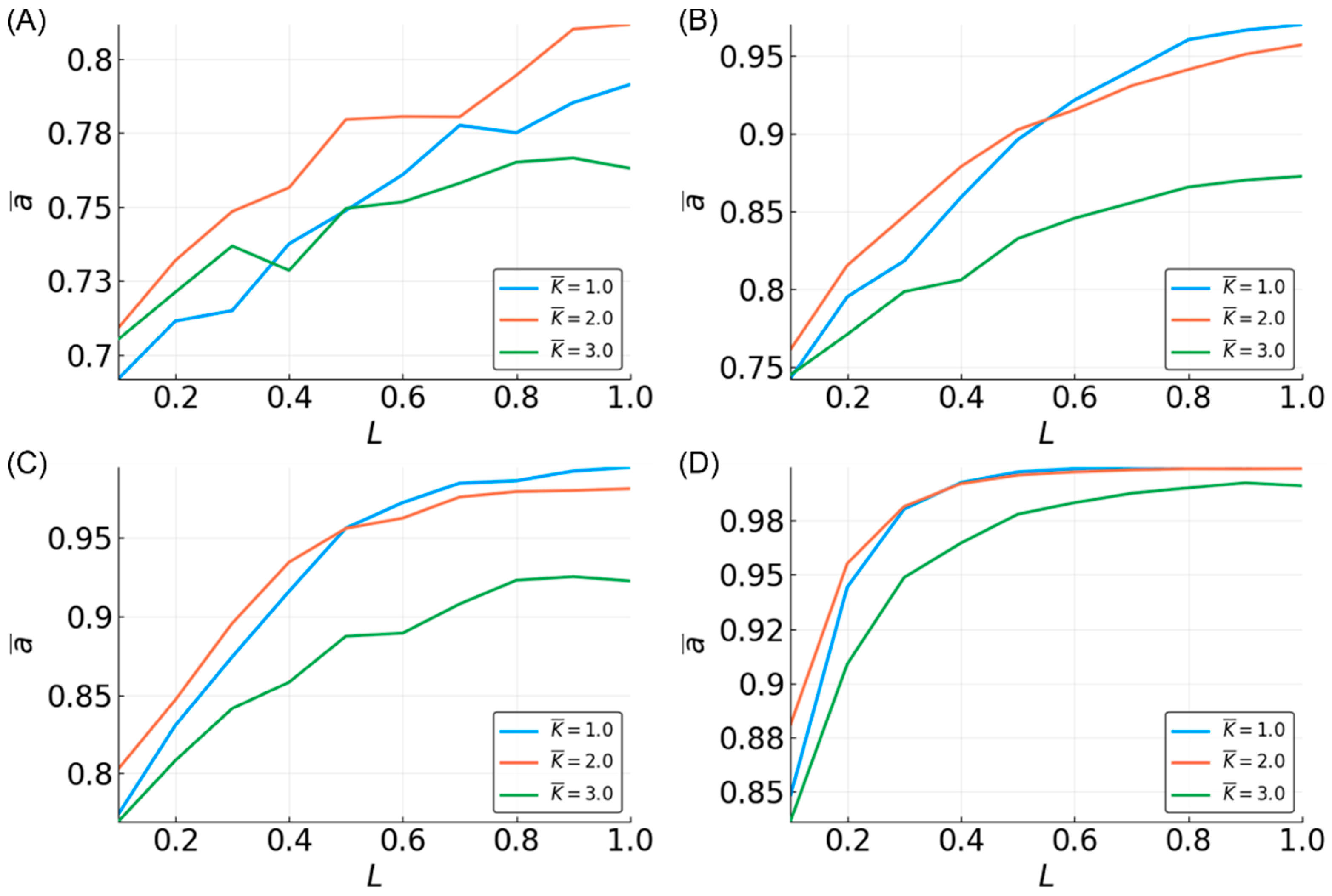
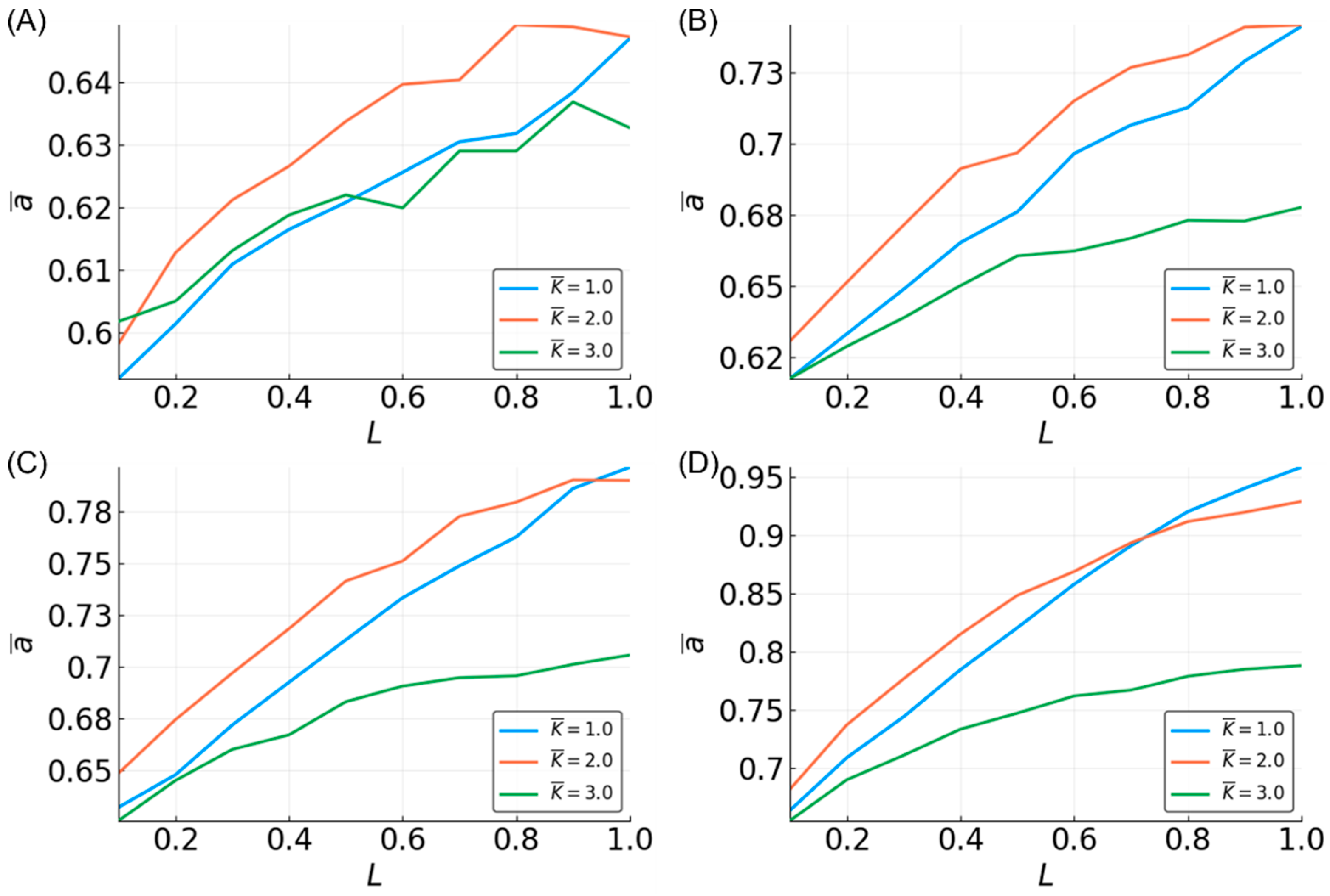
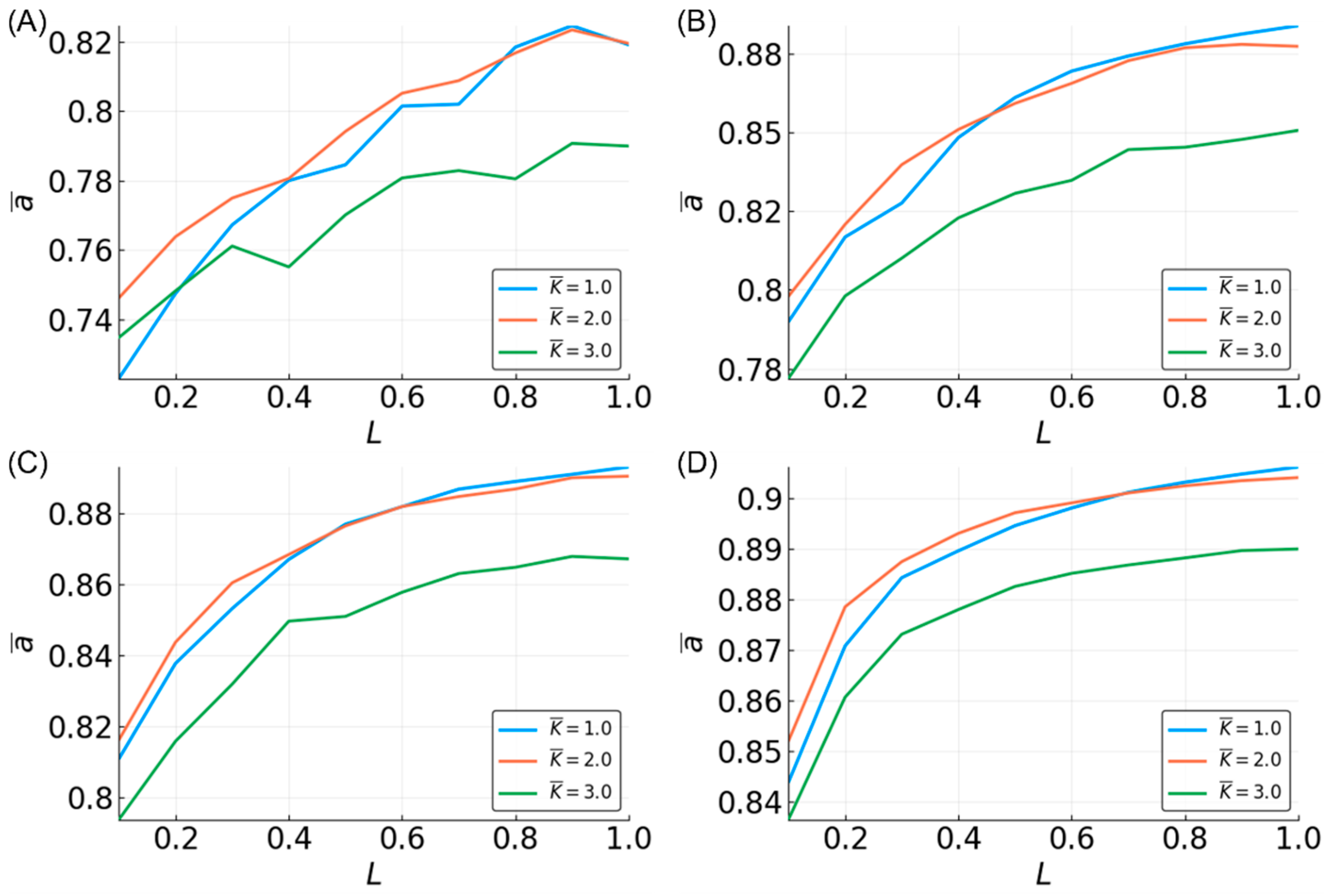
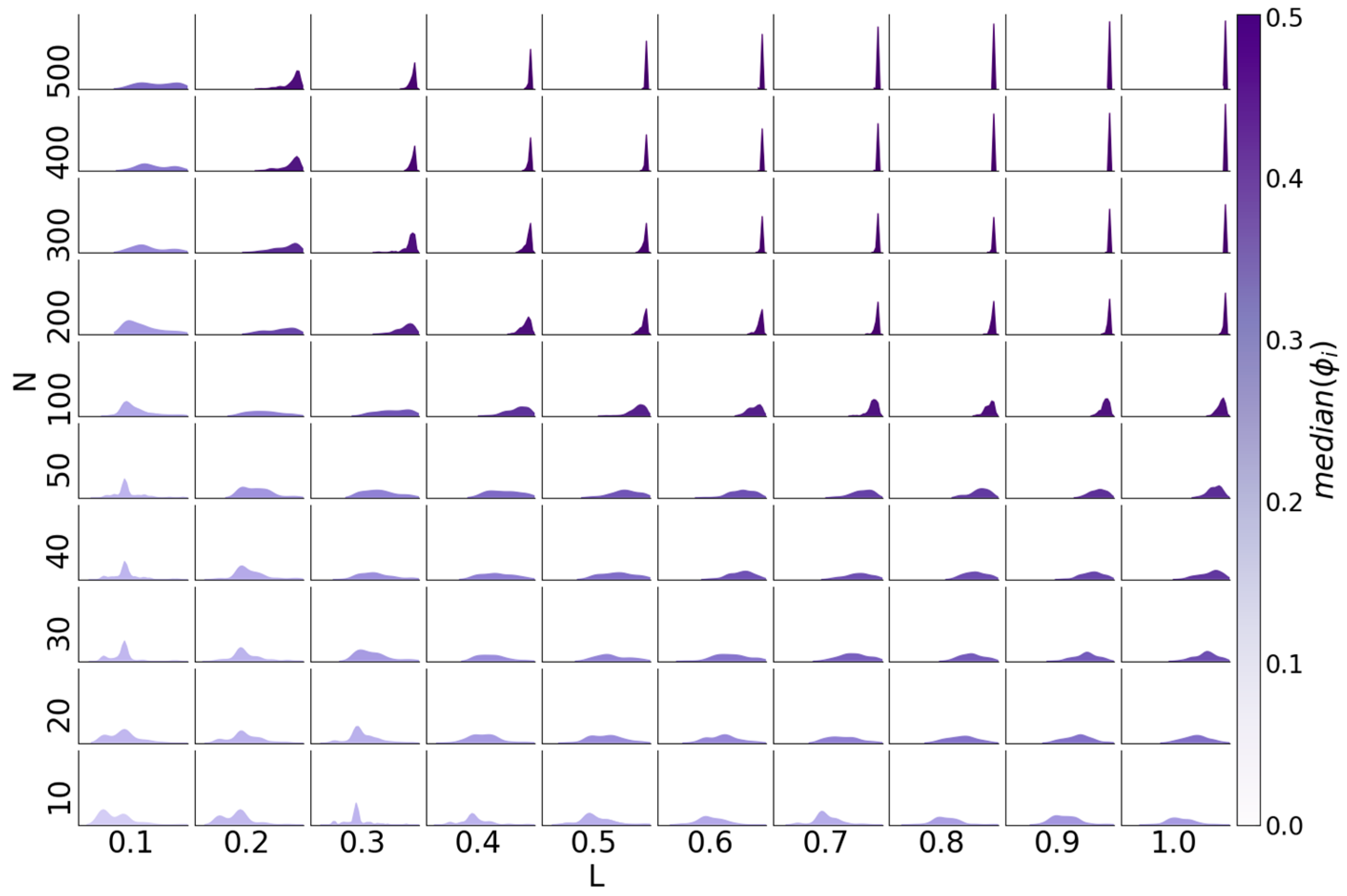
3. Results
3.1. Benchmark Functions: Median and Parity
3.2. Median
3.3. Parity
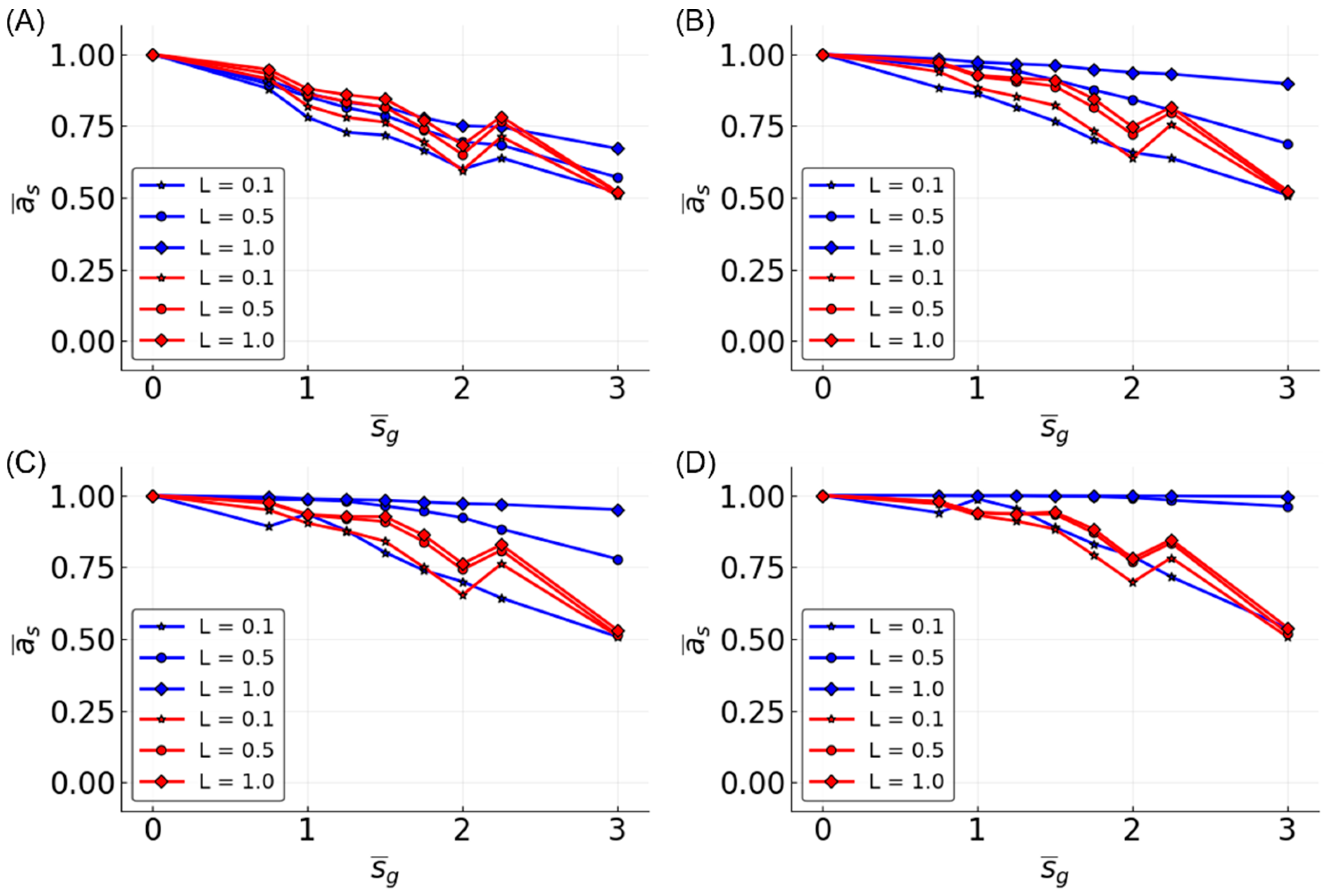
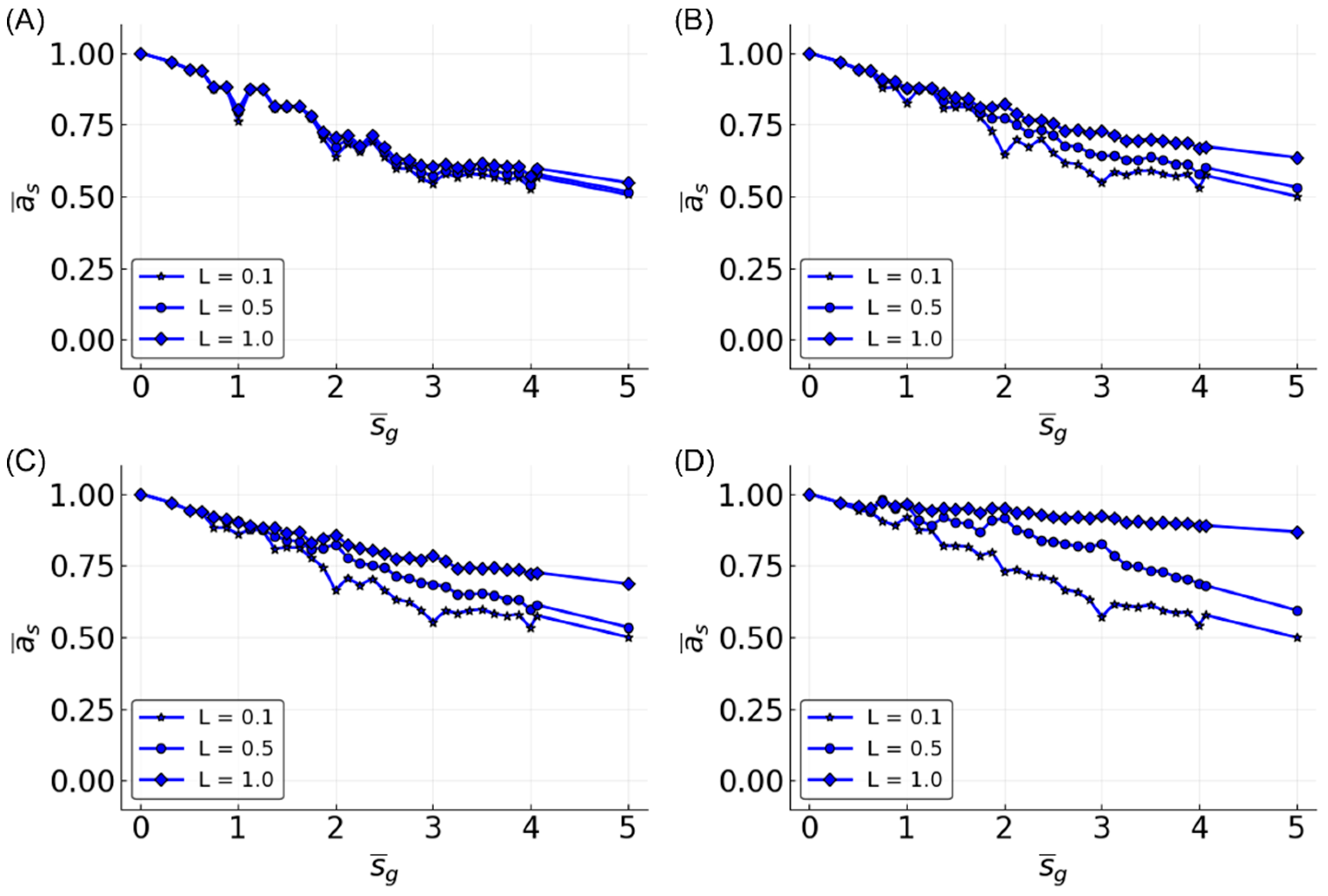
3.4. Estimating a Range of Functions
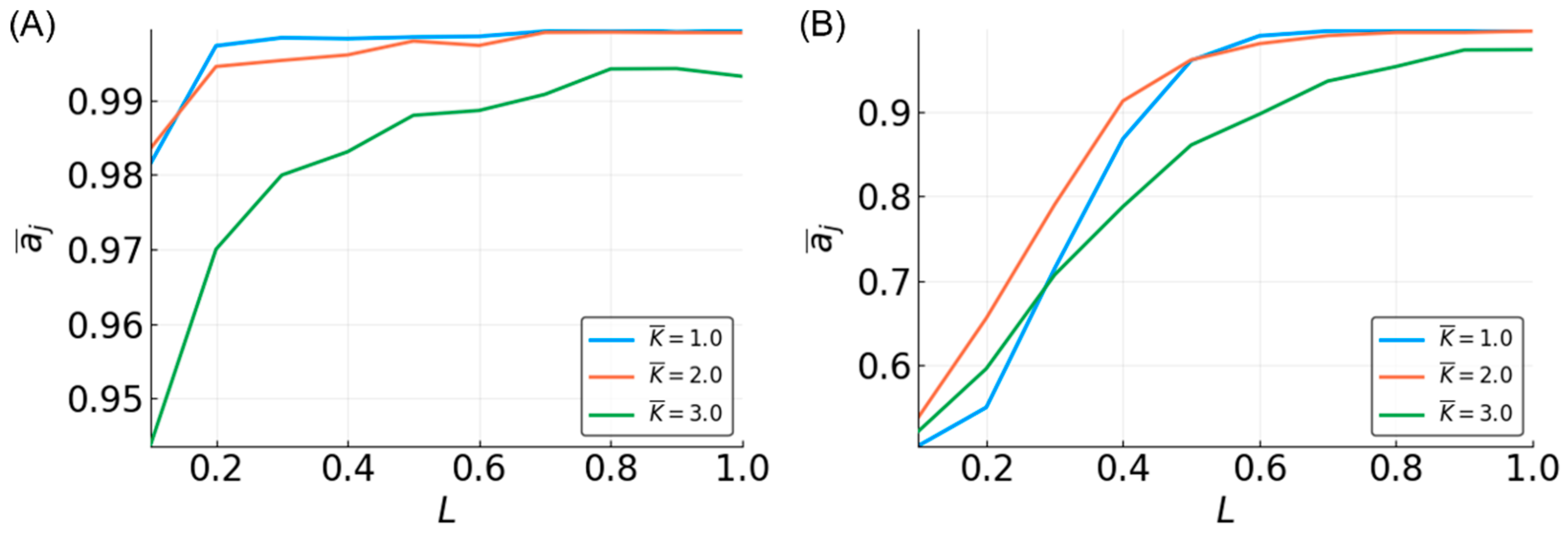
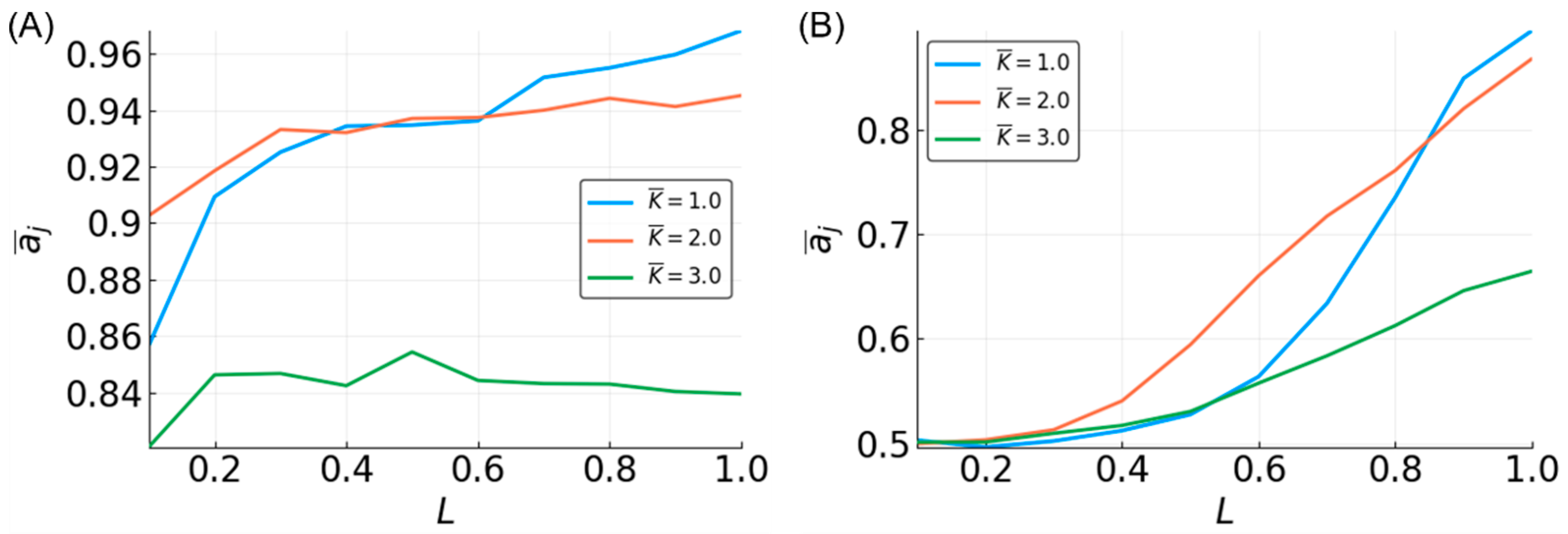
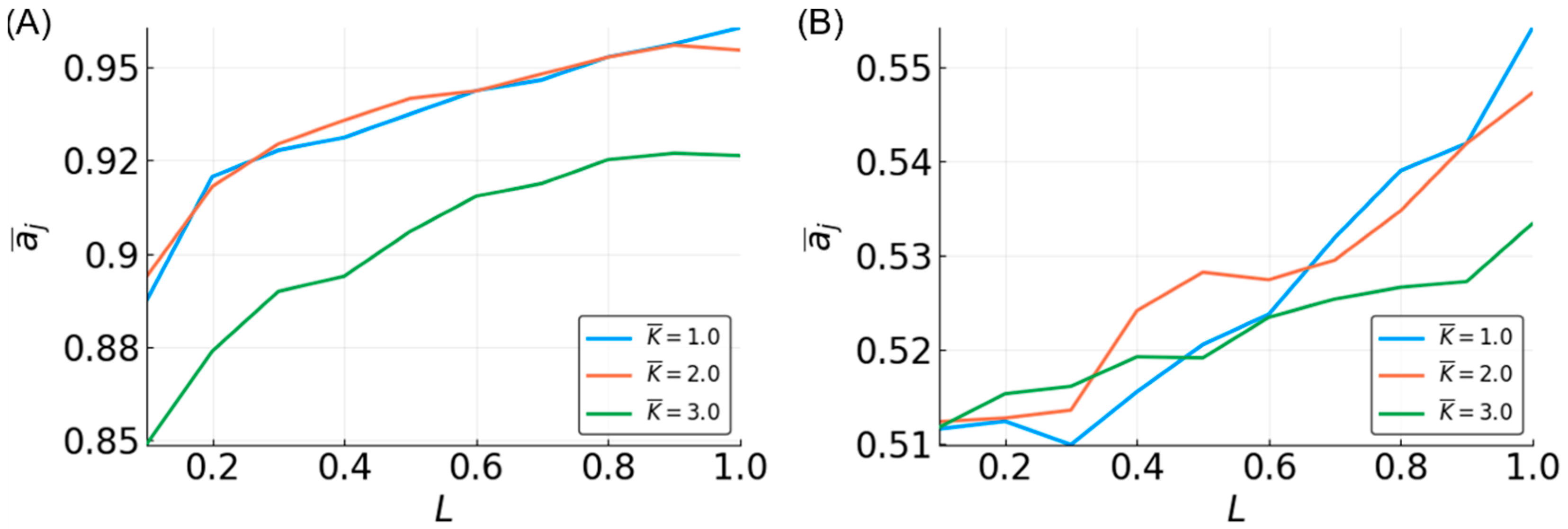
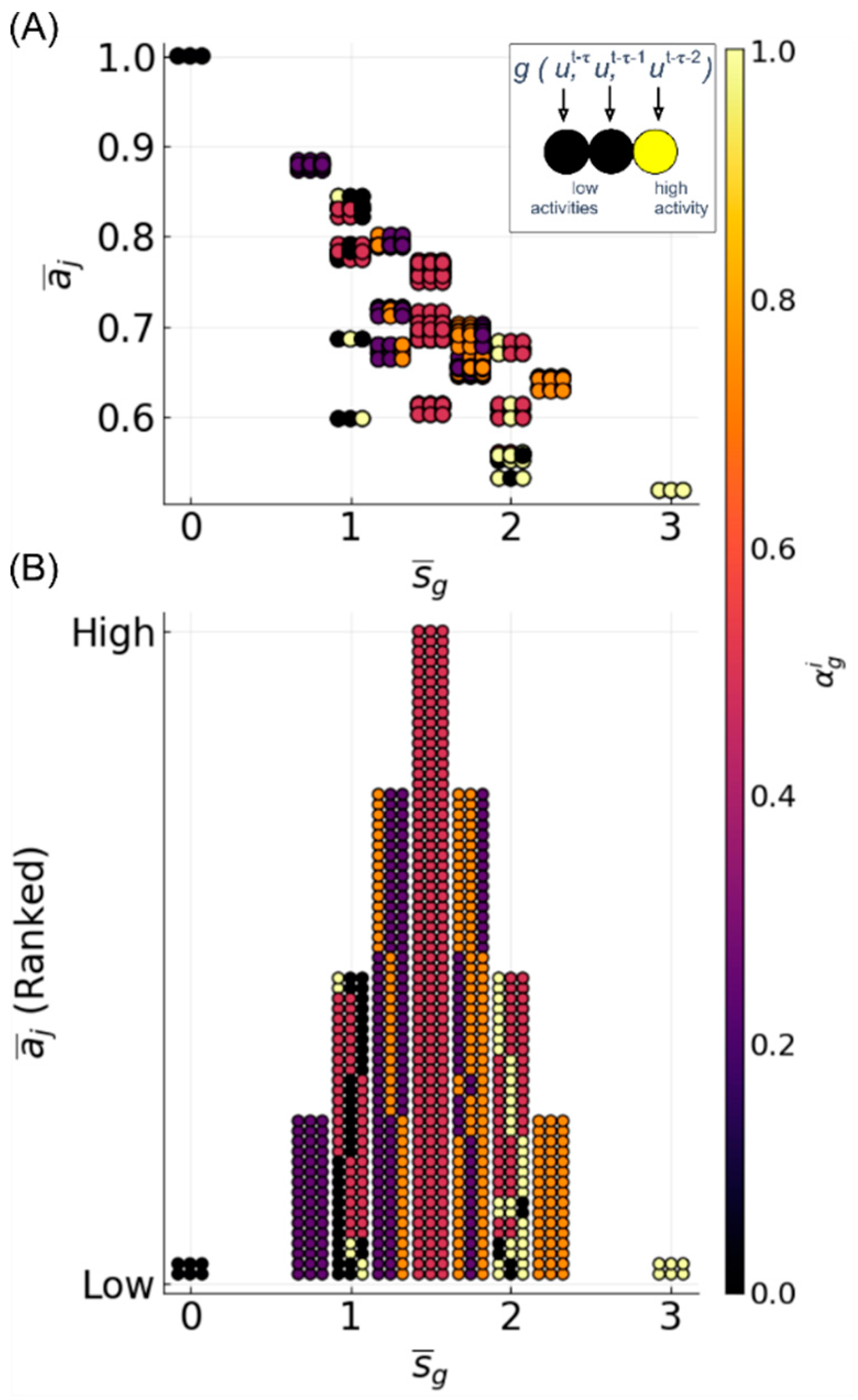
3.5. Reservoir Flexibility
3.6. Determinants of Difficulty
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Dasgupta, S.; Stevens, C.F.; Navlakha, S. A neural algorithm for a fundamental computing problem. Science 2017, 358, 793–796. [Google Scholar] [CrossRef] [PubMed]
- Jaeger, H. Adaptive Nonlinear System Identification with Echo State Networks. In Advances in Neural Information Processing Systems 15; Becker, S., Thrun, S., Obermayer, K., Eds.; MIT Press: Cambridge, MA, USA, 2003; pp. 609–616. [Google Scholar]
- Kitano, H. Systems biology: A brief overview. Science 2002, 295, 1662–1664. [Google Scholar] [CrossRef] [PubMed]
- Shivdasani, R.A. Limited gut cell repertoire for multiple hormones. Nat. Cell Biol. 2018, 20, 865–867. [Google Scholar] [CrossRef] [PubMed]
- Maass, W.; Natschläger, T.; Markram, H. Real-time computing without stable states: A new framework for neural computation based on perturbations. Neural Comput. 2002, 14, 2531–2560. [Google Scholar] [CrossRef] [PubMed]
- McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Lu, Z.; Pathak, J.; Hunt, B.; Girvan, M.; Brockett, R.; Ott, E. Reservoir observers: Model-free inference of unmeasured variables in chaotic systems. Chaos 2017, 27, 041102. [Google Scholar] [CrossRef] [PubMed]
- Pathak, J.; Lu, Z.; Hunt, R.B.; Girvan, M.; Ott, E. Using machine learning to replicate chaotic attractors and calculate Lyapunov exponents from data. Chaos 2017, 27, 121102. [Google Scholar] [CrossRef]
- Fonollosa, J.; Sheik, S.; Huerta, R.; Marco, S. Reservoir computing compensates slow response of chemosensor arrays exposed to fast varying gas concentrations in continuous monitoring. Sens. Actuators B Chem. 2015, 215, 618–629. [Google Scholar] [CrossRef]
- Caluwaerts, K.; D’Haene, M.; Verstraeten, D.; Schrauwen, B. Locomotion without a brain: Physical reservoir computing in tensegrity structures. Artif. Life 2013, 19, 35–66. [Google Scholar] [CrossRef]
- Aaser, P.; Knudsen, M.; Ramstad, H.O.; van de Wijdeven, R.; Nichele, S.; Sandvig, I.; Tufte, G.; Bauer, U.S.; Halaas, Ø.; Hendseth, S.; et al. Towards Making a Cyborg: A Closed-Loop Reservoir-Neuro System; MIT Press: Cambridge, MA, USA, 2016; pp. 430–437. [Google Scholar]
- Antonelo, A.E.; Schrauwen, B.; Van Campenhout, J. Generative Modeling of Autonomous Robots and their Environments using Reservoir Computing. Neural Process. Lett. 2007, 26. [Google Scholar] [CrossRef]
- Bianchi, F.M.; Santis, E.D.; Rizzi, A.; Sadeghian, A. Short-Term Electric Load Forecasting Using Echo State Networks and PCA Decomposition. IEEE Access 2015, 3, 1931–1943. [Google Scholar] [CrossRef]
- Gallicchio, C.; Micheli, A. A preliminary application of echo state networks to emotion recognition. In Fourth International Workshop EVALITA 2014; Pisa University Press: Pisa, Italy, 2014; pp. 116–119. [Google Scholar]
- Gallicchio, C. A Reservoir Computing Approach for Human Gesture Recognition from Kinect Data. In Proceedings of the Second Italian Workshop on Artificial Intelligence for Ambient Assisted Living (AI*AAL.it), Co-Located with the XV International Conference of the Italian Association for Artificial Intelligence (AI*IA 2016), Genova, Italy, 28 November 2016. [Google Scholar]
- Waibel, A. Modular Construction of Time-Delay Neural Networks for Speech Recognition. Neural Comput. 1989, 1, 39–46. [Google Scholar] [CrossRef]
- Triefenbach, F.; Jalalvand, A.; Schrauwen, B.; Martens, J.-P. Phoneme Recognition with Large Hierarchical Reservoirs. In Advances in Neural Information Processing Systems 23; Lafferty, J.D., Williams, C.K.I., Shawe-Taylor, J., Zemel, R.S., Culotta, A., Eds.; Curran Associates, Inc.: Nice, France, 2010; pp. 2307–2315. [Google Scholar]
- Palumbo, F.; Gallicchio, C.; Pucci, R.; Micheli, A. Human activity recognition using multisensor data fusion based on Reservoir Computing. J. Ambient. Intell. Smart Environ. 2016, 8, 87–107. [Google Scholar] [CrossRef]
- Luz, E.J.; Schwartz, W.R.; Cámara-Chávez, G.; Menotti, D. ECG-based heartbeat classification for arrhythmia detection: A survey. Comput. Methods Prog. Biomed. 2016, 127, 144–164. [Google Scholar] [CrossRef] [PubMed]
- Merkel, C.; Saleh, Q.; Donahue, C.; Kudithipudi, D. Memristive Reservoir Computing Architecture for Epileptic Seizure Detection. Procedia Comput. Sci. 2014, 41, 249–254. [Google Scholar] [CrossRef]
- Buteneers, P.; Verstraeten, D.; van Mierlo, P.; Wyckhuys, T.; Stroobandt, D.; Raedt, R.; Hallez, H.; Schrauwen, B. Automatic detection of epileptic seizures on the intra-cranial electroencephalogram of rats using reservoir computing. Artif. Intell. Med. 2011, 53, 215–223. [Google Scholar] [CrossRef]
- Ayyagari, S. Reservoir Computing Approaches to EEG-Based Detection of Microsleeps. Ph.D. Thesis, University of Canterbury, Christchurch, New Zealand, 2017. [Google Scholar]
- Kainz, P.; Burgsteiner, H.; Asslaber, M.; Ahammer, H. Robust Bone Marrow Cell Discrimination by Rotation-Invariant Training of Multi-class Echo State Networks. In Engineering Applications of Neural Networks; Springer International Publishing: Cham, Switzerland, 2015; pp. 390–400. [Google Scholar]
- Reid, D.; Barrett-Baxendale, M. Glial Reservoir Computing. In Proceedings of the Second UKSIM European Symposium on Computer Modeling and Simulation, Liverpool, UK, 8–10 September 2008; IEEE Computer Society: Washington, DC, USA, 2008; pp. 81–86. [Google Scholar]
- Enel, P.; Procyk, E.; Quilodran, R.; Dominey, P.F. Reservoir Computing Properties of Neural Dynamics in Prefrontal Cortex. PLoS Comput. Biol. 2016, 12, e1004967. [Google Scholar] [CrossRef]
- Yamazaki, T.; Tanaka, S. The cerebellum as a liquid state machine. Neural Netw. 2007, 20, 290–297. [Google Scholar] [CrossRef]
- Dai, X. Genetic Regulatory Systems Modeled by Recurrent Neural Network. In Advances in Neural Networks, Proceedings of the International Symposium on Neural Networks (ISNN 2004), Dalian, China, 19–21 August 2004; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2004; pp. 519–524. [Google Scholar]
- Jones, B.; Stekel, D.; Rowe, J.; Fernando, C. Is there a Liquid State Machine in the Bacterium Escherichia Coli? In Proceedings of the 2007 IEEE Symposium on Artificial Life, Honolulu, HI, USA, 1–5 April 2007. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression Shrinkage and Selection via the Lasso. J. R. Stat. Soc. Ser. B Stat. Methodol. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Lynn, P.A. Recursive digital filters for biological signals. Med. Biol. Eng. 1971, 9, 37–43. [Google Scholar] [CrossRef]
- Burian, A.; Kuosmanen, P. Tuning the smoothness of the recursive median filter. IEEE Trans. Signal Process. 2002, 50, 1631–1639. [Google Scholar] [CrossRef]
- Shmulevich, I.; Yli-Harja, O.; Egiazarian, K.; Astola, J. Output distributions of recursive stack filters. IEEE Signal Process. Lett. 1999, 6, 175–178. [Google Scholar] [CrossRef]
- Dambre, J.; Verstraeten, D.; Schrauwen, B.; Massar, S. Information processing capacity of dynamical systems. Sci. Rep. 2012, 2, 514. [Google Scholar] [CrossRef] [PubMed]
- Fernando, C.; Sojakka, S. Pattern Recognition in a Bucket. Advances in Artificial Life; Springer: Berlin/Heidelberg, Germany, 2003; pp. 588–597. [Google Scholar]
- Kulkarni, S.M.; Teuscher, C. Memristor-Based Reservoir Computing; ACM Press: Baltimore, MD, USA, 2009; pp. 226–232. [Google Scholar]
- Dale, M.; Miller, J.F.; Stepney, S.; Trefzer, M.A. Evolving Carbon Nanotube Reservoir Computers. In Proceedings of the UCNC 2016: Unconventional Computation and Natural Computation, Manchester, UK, 11–15 July 2016; Springer International Publishing: Cham, Switzerland, 2016; pp. 49–61. [Google Scholar]
- Kauffman, S.A. Metabolic stability and epigenesis in randomly constructed genetic nets. J. Theor. Biol. 1969, 22, 437–467. [Google Scholar] [CrossRef]
- Snyder, D.; Goudarzi, A.; Teuscher, C. Finding optimal random boolean networks for reservoir computing. In Proceedings of the Thirteenth International Conference on the Simulation and Synthesis of Living Systems (Alife’13), East Lansing, MI, USA, 19–22 July 2012. [Google Scholar]
- Derrida, B.; Pomeau, Y. Random networks of automata: A simple annealed approximation. EPL 1986, 1, 45. [Google Scholar] [CrossRef]
- Luque, B.; Solé, R.V. Lyapunov exponents in random Boolean networks. Phys. A Stat. Mech. Its Appl. 2000, 284, 33–45. [Google Scholar] [CrossRef]
- Van der Sande, G.; Brunner, D.; Soriano, M.C. Advances in photonic reservoir computing. Nanophotonics 2017, 6, 8672. [Google Scholar] [CrossRef]
- Shmulevich, I.; Dougherty, E.R.; Zhang, W. From Boolean to probabilistic Boolean networks as models of genetic regulatory networks. Proc. IEEE 2002, 90, 1778–1792. [Google Scholar] [CrossRef]
- De Jong, H. Modeling and Simulation of Genetic Regulatory Systems: A Literature Review. J. Comput. Biol. 2002, 9, 67–103. [Google Scholar] [CrossRef]
- Davidich, M.I.; Bornholdt, S. Boolean network model predicts cell cycle sequence of fission yeast. PLoS ONE 2008, 3, e1672. [Google Scholar] [CrossRef]
- Fumiã, H.F.; Martins, M.L. Boolean network model for cancer pathways: Predicting carcinogenesis and targeted therapy outcomes. PLoS ONE 2013, 8, e69008. [Google Scholar] [CrossRef] [PubMed]
- Serra, R.; Villani, M.; Barbieri, A.; Kauffman, S.A.; Colacci, A. On the dynamics of random Boolean networks subject to noise: Attractors, ergodic sets and cell types. J. Theor. Biol. 2010, 265, 185–193. [Google Scholar] [CrossRef] [PubMed]
- Helikar, T.; Konvalina, J.; Heidel, J.; Rogers, J.A. Emergent decision-making in biological signal transduction networks. Proc. Natl. Acad. Sci. USA 2008, 105, 1913–1918. [Google Scholar] [CrossRef] [PubMed]
- Thakar, J.; Pilione, M.; Kirimanjeswara, G.; Harvill, E.T.; Albert, R. Modeling systems-level regulation of host immune responses. PLoS Comput. Biol. 2007, 3, e109. [Google Scholar] [CrossRef] [PubMed]
- Damiani, C.; Kauffman, S.A.; Villani, M.; Colacci, A.; Serra, R. Cell–cell interaction and diversity of emergent behaviours. IET Syst. Biol. 2011, 5, 137–144. [Google Scholar] [CrossRef] [PubMed]
- Snyder, D.; Goudarzi, A.; Teuscher, C. Computational capabilities of random automata networks for reservoir computing. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2013, 87, 042808. [Google Scholar] [CrossRef]
- Bertschinger, N.; Natschläger, T. Real-time computation at the edge of chaos in recurrent neural networks. Neural Comput. 2004, 16, 1413–1436. [Google Scholar] [CrossRef]
- Balleza, E.; Alvarez-Buylla, E.R.; Chaos, A.; Kauffman, S.; Shmulevich, I.; Aldana, M. Critical dynamics in genetic regulatory networks: Examples from four kingdoms. PLoS ONE 2008, 3, e2456. [Google Scholar] [CrossRef]
- Goudarzi, A.; Teuscher, C.; Gulbahce, N.; Rohlf, T. Emergent criticality through adaptive information processing in boolean networks. Phys. Rev. Lett. 2012, 108, 128702. [Google Scholar] [CrossRef]
- Torres-Sosa, C.; Huang, S.; Aldana, M. Criticality is an emergent property of genetic networks that exhibit evolvability. PLoS Comput. Biol. 2012, 8, e1002669. [Google Scholar] [CrossRef]
- Muñoz, M.A. Colloquium: Criticality and dynamical scaling in living systems. Rev. Mod. Phys. 2018, 90, 031001. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Shmulevich, I.; Kauffman, S.A. Activities and sensitivities in boolean network models. Phys. Rev. Lett. 2004, 93, 048701. [Google Scholar] [CrossRef] [PubMed]
- Cook, S.; Dwork, C.; Reischuk, R. Upper and Lower Time Bounds for Parallel Random Access Machines without Simultaneous Writes. SIAM J. Comput. 1986, 15, 87–97. [Google Scholar] [CrossRef]
- Kahn, J.; Kalai, G.; Linial, N. The Influence of Variables on Boolean Functions. In Proceedings of the 29th Annual Symposium on Foundations of Computer Science, White Plains, NY, USA, 24–26 October 1998; IEEE Computer Society: Washington, DC, USA, 1988; pp. 68–80. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Echlin, M.; Aguilar, B.; Notarangelo, M.; Gibbs, D.L.; Shmulevich, I. Flexibility of Boolean Network Reservoir Computers in Approximating Arbitrary Recursive and Non-Recursive Binary Filters. Entropy 2018, 20, 954. https://doi.org/10.3390/e20120954
Echlin M, Aguilar B, Notarangelo M, Gibbs DL, Shmulevich I. Flexibility of Boolean Network Reservoir Computers in Approximating Arbitrary Recursive and Non-Recursive Binary Filters. Entropy. 2018; 20(12):954. https://doi.org/10.3390/e20120954
Chicago/Turabian StyleEchlin, Moriah, Boris Aguilar, Max Notarangelo, David L. Gibbs, and Ilya Shmulevich. 2018. "Flexibility of Boolean Network Reservoir Computers in Approximating Arbitrary Recursive and Non-Recursive Binary Filters" Entropy 20, no. 12: 954. https://doi.org/10.3390/e20120954
APA StyleEchlin, M., Aguilar, B., Notarangelo, M., Gibbs, D. L., & Shmulevich, I. (2018). Flexibility of Boolean Network Reservoir Computers in Approximating Arbitrary Recursive and Non-Recursive Binary Filters. Entropy, 20(12), 954. https://doi.org/10.3390/e20120954





