Irreversibility Analysis of Dissipative Fluid Flow Over A Curved Surface Stimulated by Variable Thermal Conductivity and Uniform Magnetic Field: Utilization of Generalized Differential Quadrature Method
Abstract
1. Introduction
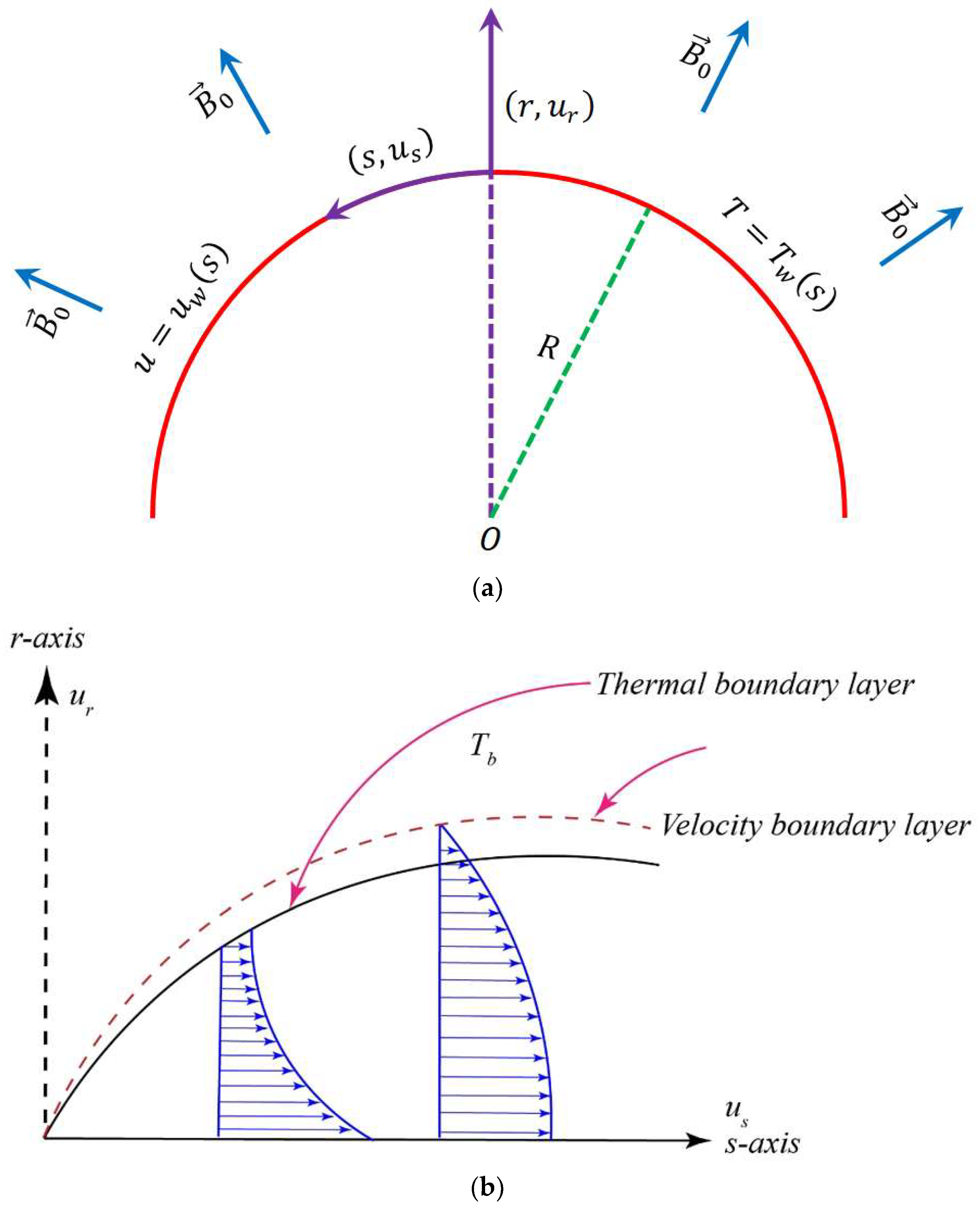
2. Problem Formulation
3. Analysis of Entropy Production
4. Solution Methodology
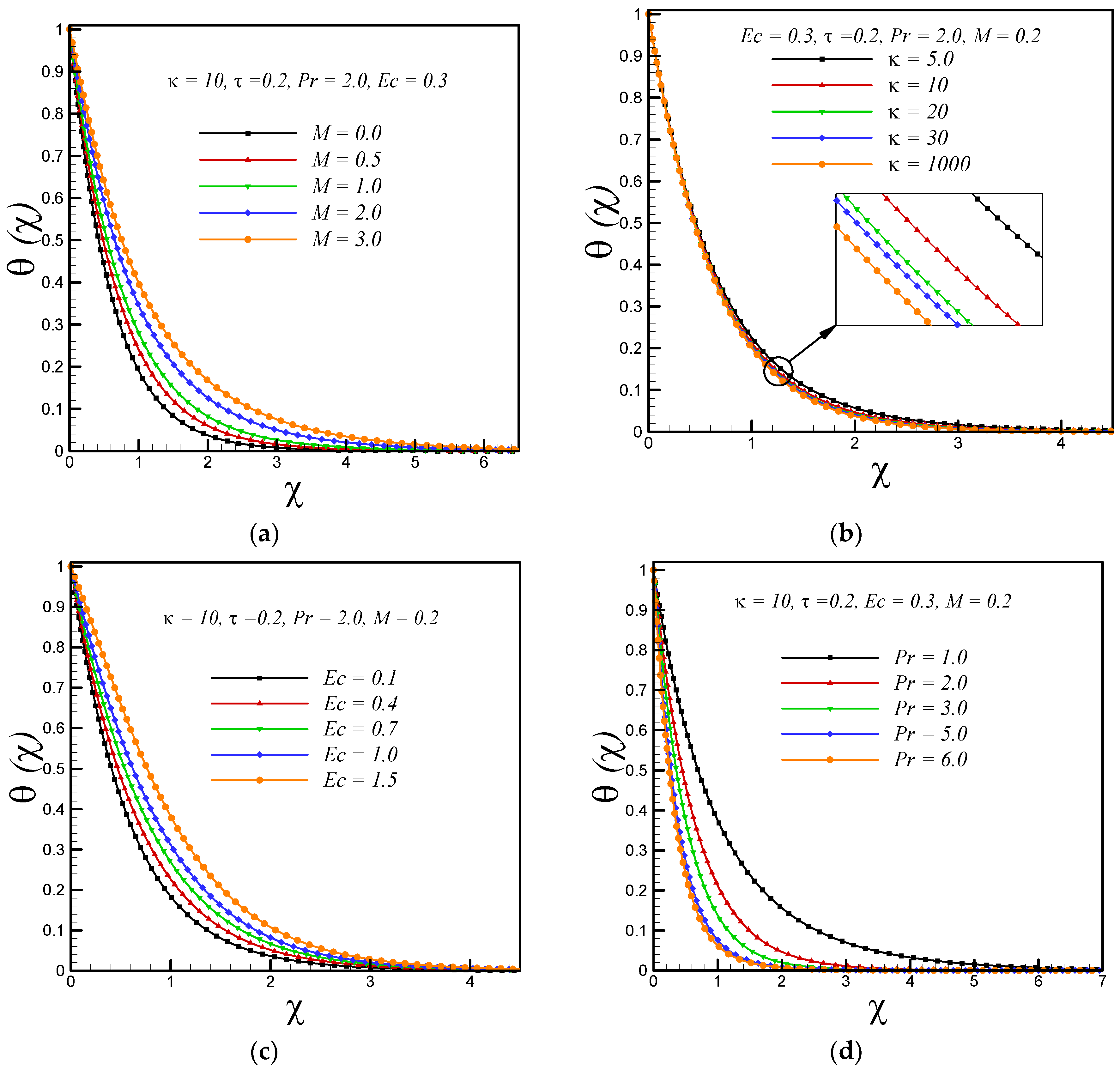
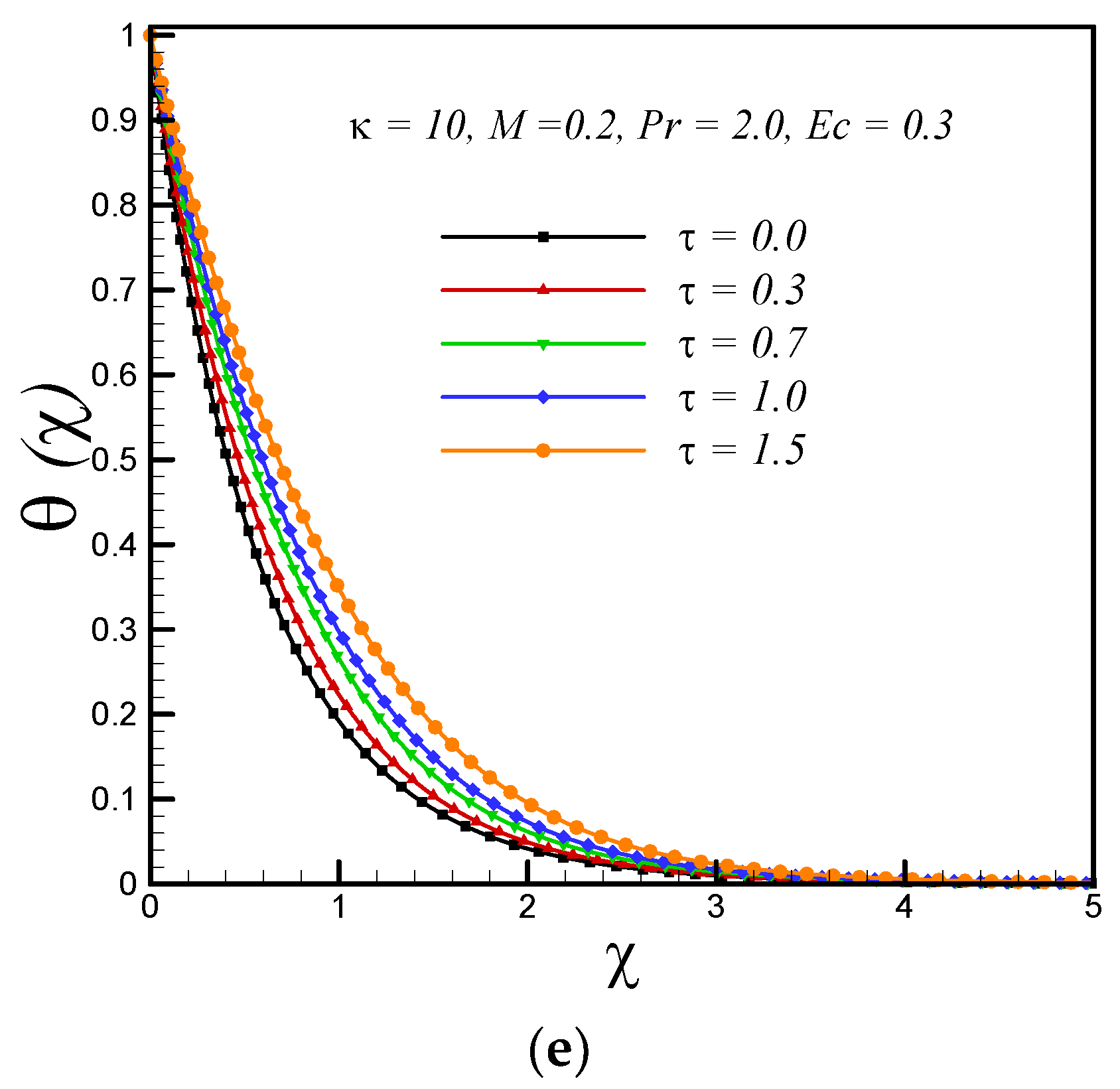
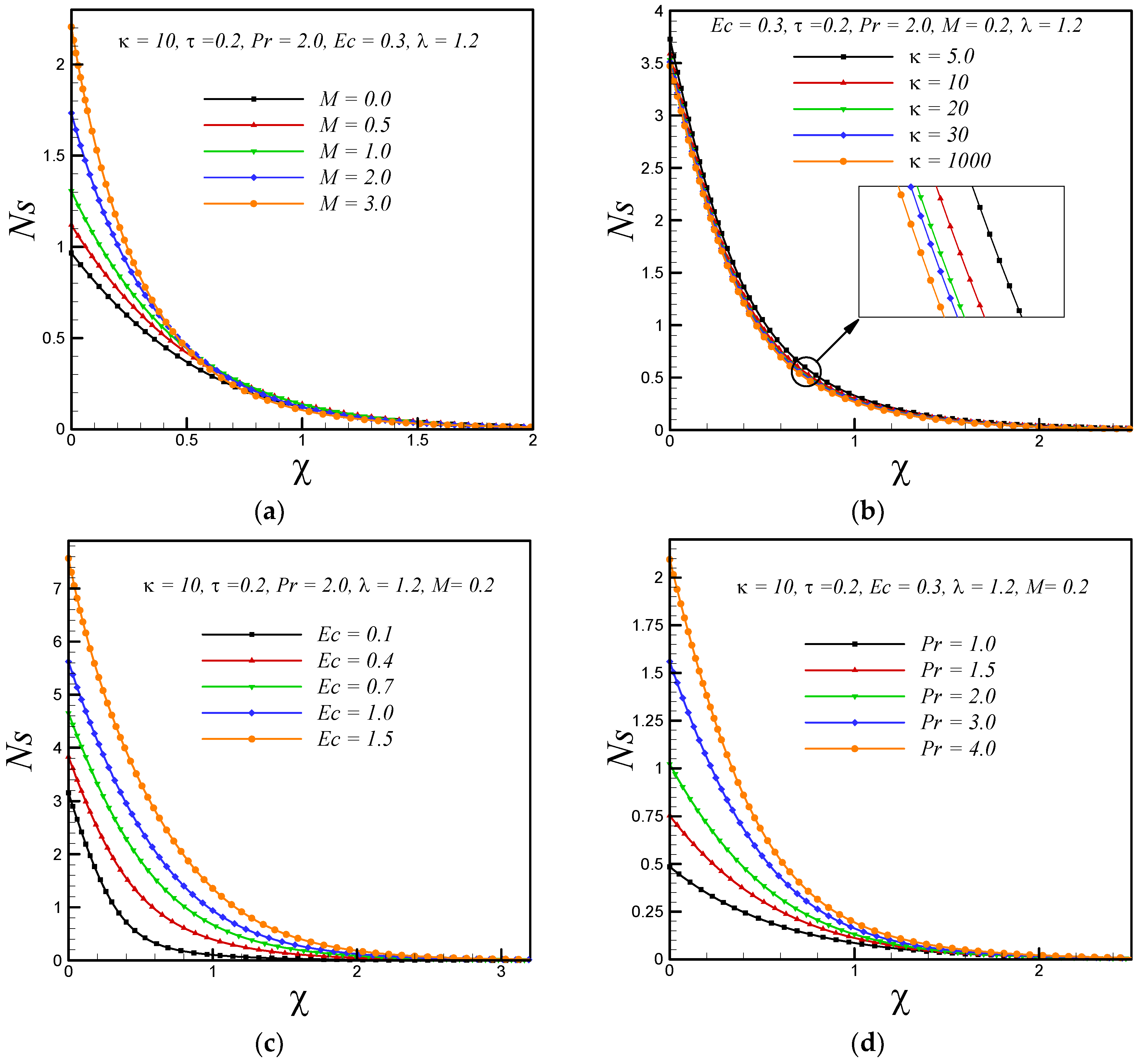
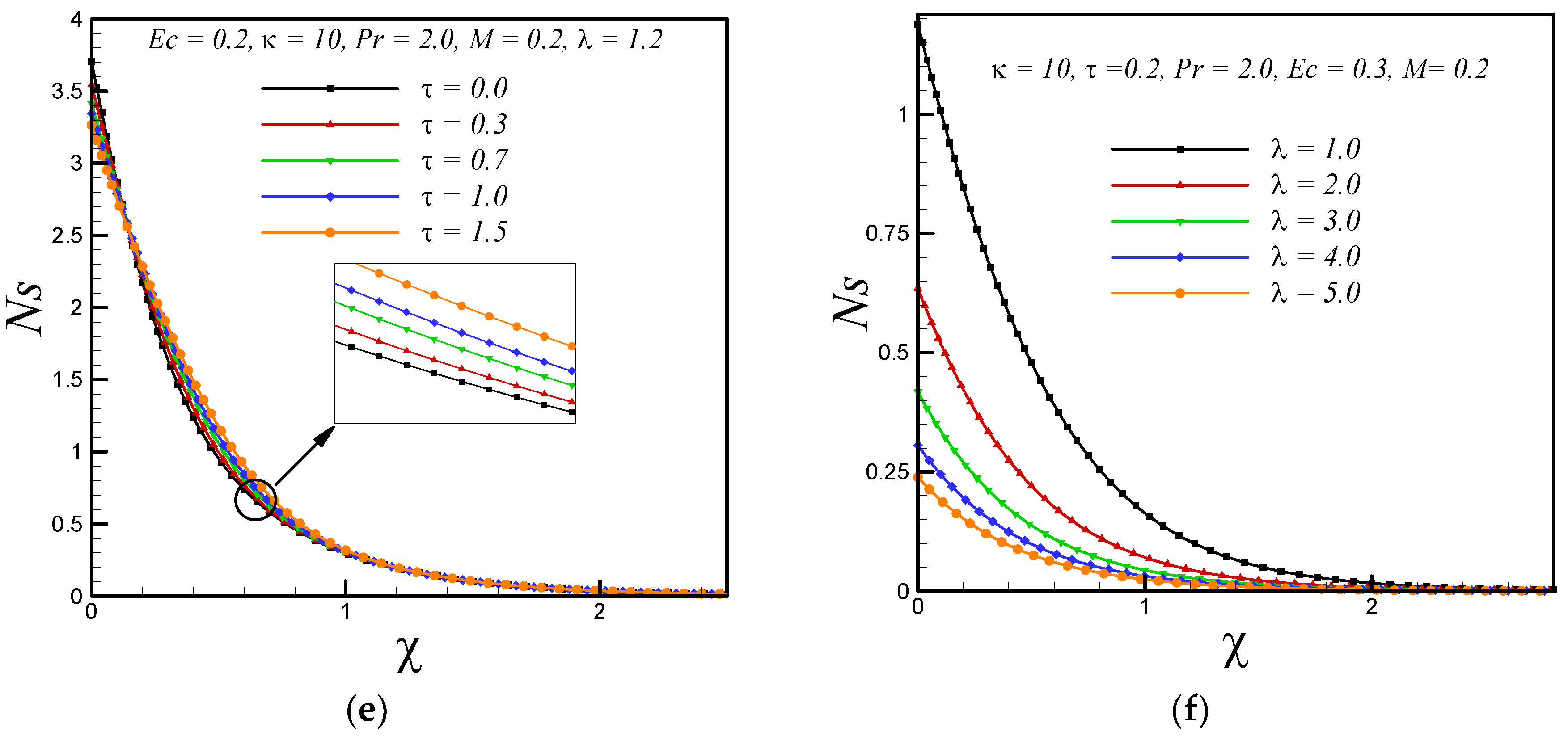
5. Results and Discussion
6. Closing Remarks
- The local skin friction coefficient enhances with magnetic parameter and reduces with increasing curvature parameter.
- With an increase in magnetic parameter, Eckert number and variable thermal conductivity parameter, the local Nusselt number reduces but it enhances with rising values of curvature parameter and Prandtl number.
- The fluid motion decelerates with increasing M and curvature parameter .
- With rising values of magnetic parameter, Eckert number and variable thermal conductivity parameter, the temperature of fluid rises whereas decrement in temperature is observed with increasing values of Prandtl number and curvature parameter.
- Less entropy is generated in the flow past over a flat stretching boundary as compared to the flow over a curved surface.
- By increasing the curvature and temperature difference parameter, the entropy generation reduces.
- With enhancing the values of magnetic parameter, Eckert number, Prandtl number and variable thermal conductivity parameter, Ns increases.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bejan, A. The method of entropy generation minimization. In Energy and the Environment; Springer: Berlin/Heidelberg, Germany, 1999; pp. 11–22. [Google Scholar]
- Afridi, M.I.; Tlili, I.; Qasim, M.; Khan, I. Nonlinear Rosseland thermal radiation and energy dissipation effects on entropy generation in CNTs suspended nanofluids flow over a thin needle. Bound. Value Probl. 2018, 2018, 148. [Google Scholar] [CrossRef]
- Makinde, O.D. Second law analysis for variable viscosity hydromagnetic boundary layer flow with thermal radiation and Newtonian heating. Entropy 2011, 13, 1446–1464. [Google Scholar] [CrossRef]
- Butt, A.S.; Munawar, S.; Ali, A.; Mehmood, A. Entropy generation in the Blasius flow under thermal radiation. Phys. Scr. 2012, 85, 1–6. [Google Scholar] [CrossRef]
- Afridi, M.I.; Qasim, M. Entropy generation in three dimensional flow of dissipative fluid. Int. J. Appl. Comput. Math. 2018, 4, 16. [Google Scholar] [CrossRef]
- Vasu, B.; Ram, R.C.; Murthy, P.; Gorla, R.S.R. Entropy generation analysis in nonlinear convection flow of thermally stratified fluid in saturated porous medium with convective boundary condition. J. Heat Transf. 2017, 139, 1–10. [Google Scholar] [CrossRef]
- Afridi, M.I.; Qasim, M.; Shafie, S. Entropy generation in hydromagnetic boundary flow under the effects of frictional and Joule heating: Exact solutions. Eur. Phys. J. Plus 2017, 132, 1–11. [Google Scholar] [CrossRef]
- Butt, A.S.; Ali, A.; Mehmood, A. Entropy generation effects in Cu water nano fluid flow and heat transfer over a radially stretching surface. J. Nanofluids 2016, 5, 471–478. [Google Scholar] [CrossRef]
- Makinde, O.D.; Eegunjobi, A.S. Entropy generation in a couple stress fluid flow through a vertical channel filled with saturated porous media. Entropy 2013, 15, 4589–4606. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Abelman, S.; Mehr, N.F. Entropy generation in steady MHD flow due to a rotating porous disk in a nanofluid. Int. J. Heat Mass Transf. 2013, 62, 515–525. [Google Scholar] [CrossRef]
- Schlichting, H.; Gersten, K. Boundary-Layer Theory; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Sakiadis, B.C. Boundary-layer behavior on continuous solid surfaces: I. Boundary-layer equations for two-dimensional and axisymmetric flow. AIChE J. 1961, 7, 26–28. [Google Scholar] [CrossRef]
- Crane, L.J. Flow past a stretching plate. J. Appl. Math. Phys. 1970, 21, 645–647. [Google Scholar] [CrossRef]
- Gupta, P.S.; Gupta, A.S. Heat and mass transfer on a stretching sheet with suction or blowing. Can. J. Chem. Eng. 1977, 55, 744–746. [Google Scholar] [CrossRef]
- Wang, C.Y. Fluid flow due to a stretching cylinder. Phys. Fluids 1988, 31, 466–468. [Google Scholar] [CrossRef]
- Wang, C.Y. Stretching a surface in a rotating fluid. J. Appl. Math. Phys. 1988, 39, 177–185. [Google Scholar] [CrossRef]
- Dandapat, B.S.; Santra, B.; Vajravelu, K. The effects of variable fluid properties and thermocapillarity on the flow of a thin film on an unsteady stretching sheet. Int. J. Heat Mass Transf. 2007, 50, 991–996. [Google Scholar] [CrossRef]
- Vajravelu, K.; Rollins, D. Hydromagnetic flow of a second grade fluid over a stretching sheet. Appl. Math. Comput. 2004, 148, 783–791. [Google Scholar] [CrossRef]
- Pal, D.; Mondal, H. Effects of temperature-dependent viscosity and variable thermal conductivity on MHD non-Darcy mixed convective diffusion of species over a stretching sheet. J. Egypt. Math. Soc. 2014, 22, 123–133. [Google Scholar] [CrossRef]
- Yazdi, M.H.; Hashim, I.; Sopian, K. Bin Slip boundary layer flow of a power-law fluid over moving permeable surface with viscous dissipation and prescribed surface temperature. Int. Rev. Mech. Eng. 2014, 8, 502–510. [Google Scholar]
- Hsiao, K.-L. MHD mixed convection of viscoelastic fluid over a stretching sheet with ohmic dissipation. J. Mech. 2008, 24, 29–34. [Google Scholar] [CrossRef]
- Vajravelu, K.; Prasad, K.V.; Vaidya, H. Influence of hall current on MHD flow and heat transfer over a slender stretching sheet in the presence of variable fluid properties. Commun. Numer. Anal. 2016, 2016, 17–36. [Google Scholar] [CrossRef]
- Vajravelu, K.; Prasad, K.V.; Vaidya, H.; Basha, N.Z.; Ng, C.-O. Mixed convective flow of a Casson fluid over a vertical stretching sheet. Int. J. Appl. Comput. Math. 2017, 3, 1619–1638. [Google Scholar] [CrossRef]
- Ali, F.; Sheikh, N.A.; Khan, I.; Saqib, M. Influence of a porous medium on the hydromagnetic free convection flow of micropolar fluid with radiative heat flux. J. Porous Media 2018, 21, 123–144. [Google Scholar] [CrossRef]
- Hsiao, K.-L. Conjugate heat transfer of magnetic mixed convection with radiative and viscous dissipation effects for second-grade viscoelastic fluid past a stretching sheet. Appl. Therm. Eng. 2007, 27, 1895–1903. [Google Scholar] [CrossRef]
- Pop, I.; Isa, S.S.P.M.; Arifin, N.M.; Nazar, R.; Bachok, N.; Ali, F.M. Unsteady viscous MHD flow over a permeable curved stretching/shrinking sheet. Int. J. Numer. Methods Heat Fluid Flow 2016, 26, 2370–2392. [Google Scholar] [CrossRef]
- Reddy, J.V.R.; Sugunamma, V.; Sandeep, N. Dual solutions for nanofluid flow past a curved surface with nonlinear radiation, Soret and Dufour effects. J. Phys. Conf. Ser. 2018, 1000, 12152. [Google Scholar] [CrossRef]
- Rudraswamy, N.G.; Kumar, K.G.; Gireesha, B.J.; Gorla, R.S.R. Soret and Dufour effects in three-dimensional flow of Jeffery nanofluid in the presence of nonlinear thermal radiation. J. Nanoeng. Nanomanuf. 2016, 6, 278–287. [Google Scholar] [CrossRef]
- Roşca, N.C.; Pop, I. Unsteady boundary layer flow over a permeable curved stretching/shrinking surface. Eur. J. Mech. 2015, 51, 61–67. [Google Scholar] [CrossRef]
- Rashad, A.M.; Rashidi, M.M.; Lorenzini, G.; Ahmed, S.E.; Aly, A.M. Magnetic field and internal heat generation effects on the free convection in a rectangular cavity filled with a porous medium saturated with Cu–water nanofluid. Int. J. Heat Mass Transf. 2017, 104, 878–889. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Vajravelu, K.; Rashidi, M.M. Forced convection heat transfer in a semi annulus under the influence of a variable magnetic field. Int. J. Heat Mass Transf. 2016, 92, 339–348. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Rashidi, M.M.; Ganji, D.D. Effect of non-uniform magnetic field on forced convection heat transfer of Fe3O4–water nanofluid. Comput. Methods Appl. Mech. Eng. 2015, 294, 299–312. [Google Scholar] [CrossRef]
- Shu, C. Differential Quadrature and Its Application in Engineering; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Baskaya, E.; Komurgoz, G.; Ozkol, I. Investigation of oriented magnetic field effects on entropy generation in an inclined channel filled with ferrofluids. Entropy 2017, 19, 377. [Google Scholar] [CrossRef]

| M | κ | Ec | Pr | τ | *GDQM | *RKFM | ||
|---|---|---|---|---|---|---|---|---|
| 0.0 | 10 | 0.3 | 2.0 | 0.2 | 1.0734886 | 1.0956346 | 1.0734886 | 1.0956346 |
| 0.5 | 1.3279849 | 1.0182902 | 1.3279849 | 1.0182902 | ||||
| 1.0 | 1.5302913 | 0.9433763 | 1.5302913 | 0.9433763 | ||||
| 2.0 | 1.8601286 | 0.7956016 | 1.8601286 | 0.7956016 | ||||
| 3.0 | 2.1338460 | 0.6495366 | 2.1338460 | 0.6495366 | ||||
| 0.2 | 5 | 0.3 | 2.0 | 0.2 | 1.2856525 | 1.0580225 | 1.2856526 | 1.0580225 |
| 10 | 1.1846573 | 1.0641428 | 1.1846573 | 1.0641428 | ||||
| 20 | 1.1386292 | 1.0659353 | 1.1386292 | 1.0659353 | ||||
| 30 | 1.1239341 | 1.0663482 | 1.1239341 | 1.0663482 | ||||
| 1000 | 1.0963201 | 1.0668915 | 1.0963201 | 1.0668915 | ||||
| 0.2 | 10 | 0.1 | 2.0 | 0.2 | 1.1846573 | 1.1176921 | 1.1846573 | 1.1176921 |
| 0.4 | 1.1846573 | 1.0339380 | 1.1846573 | 1.0339380 | ||||
| 0.7 | 1.1846573 | 0.9295582 | 1.1846573 | 0.9295582 | ||||
| 1.0 | 1.1846573 | 0.8044534 | 1.1846573 | 0.8044534 | ||||
| 1.5 | 1.1846573 | 0.5496236 | 1.1846573 | 0.5496236 | ||||
| 0.2 | 10 | 0.3 | 1.0 | 0.2 | 1.1846573 | 0.8221439 | 1.1846573 | 0.8221439 |
| 2.0 | 1.1846573 | 1.0641428 | 1.1846573 | 1.0641428 | ||||
| 3.0 | 1.1846573 | 1.1801381 | 1.1846573 | 1.1801381 | ||||
| 5.0 | 1.1846573 | 1.2499780 | 1.1846573 | 1.2499781 | ||||
| 6.0 | 1.1846573 | 1.2391867 | 1.1846573 | 1.2391866 | ||||
| 0.2 | 10 | 0.3 | 2.0 | 0.0 | 1.1846573 | 1.7356948 | 1.1846573 | 1.7356948 |
| 0.3 | 1.1846573 | 0.8201182 | 1.1846573 | 0.8201182 | ||||
| 0.7 | 1.1846573 | 0.1759590 | 1.1846573 | 0.1759590 | ||||
| 1.0 | 1.1846573 | −0.1120986 | 1.1846573 | −0.1120984 | ||||
| 1.5 | 1.1846573 | −0.4142181 | 1.1846573 | −0.4142179 | ||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Afridi, M.I.; Wakif, A.; Qasim, M.; Hussanan, A. Irreversibility Analysis of Dissipative Fluid Flow Over A Curved Surface Stimulated by Variable Thermal Conductivity and Uniform Magnetic Field: Utilization of Generalized Differential Quadrature Method. Entropy 2018, 20, 943. https://doi.org/10.3390/e20120943
Afridi MI, Wakif A, Qasim M, Hussanan A. Irreversibility Analysis of Dissipative Fluid Flow Over A Curved Surface Stimulated by Variable Thermal Conductivity and Uniform Magnetic Field: Utilization of Generalized Differential Quadrature Method. Entropy. 2018; 20(12):943. https://doi.org/10.3390/e20120943
Chicago/Turabian StyleAfridi, Muhammad Idrees, Abderrahim Wakif, Muhammad Qasim, and Abid Hussanan. 2018. "Irreversibility Analysis of Dissipative Fluid Flow Over A Curved Surface Stimulated by Variable Thermal Conductivity and Uniform Magnetic Field: Utilization of Generalized Differential Quadrature Method" Entropy 20, no. 12: 943. https://doi.org/10.3390/e20120943
APA StyleAfridi, M. I., Wakif, A., Qasim, M., & Hussanan, A. (2018). Irreversibility Analysis of Dissipative Fluid Flow Over A Curved Surface Stimulated by Variable Thermal Conductivity and Uniform Magnetic Field: Utilization of Generalized Differential Quadrature Method. Entropy, 20(12), 943. https://doi.org/10.3390/e20120943






