Ranking the Impact of Different Tests on a Hypothesis in a Bayesian Network
Abstract
:1. Introduction
2. Three Methods to Choose the Most Important Test
- One distinguished node that we call G; item A subset of terminal nodes, which we call ;
- A given state for all the other nodes of the network, which can be either fixed to one of their values, or unfixed.
2.1. The Expected Information Gain Method
2.2. The Tornado Method
2.3. The Single Missing Item Method
3. Comparison of the Methods
3.1. Comparison of the Expected Information Gain Method with the Tornado Method
3.2. Comparison of the Expected Information Gain Method with the Single Missing Item Method
3.3. Comparison of the Tornado and Single Missing Item Methods
4. The Bit Torrent Case
4.1. Description of the Case
4.2. Application of the Expected Information Gain Method
4.3. Application of the Tornado Method
4.4. Application of the Single Missing Item Method
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
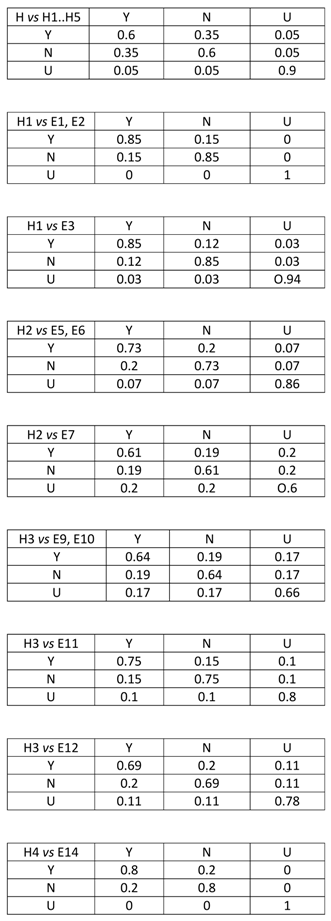
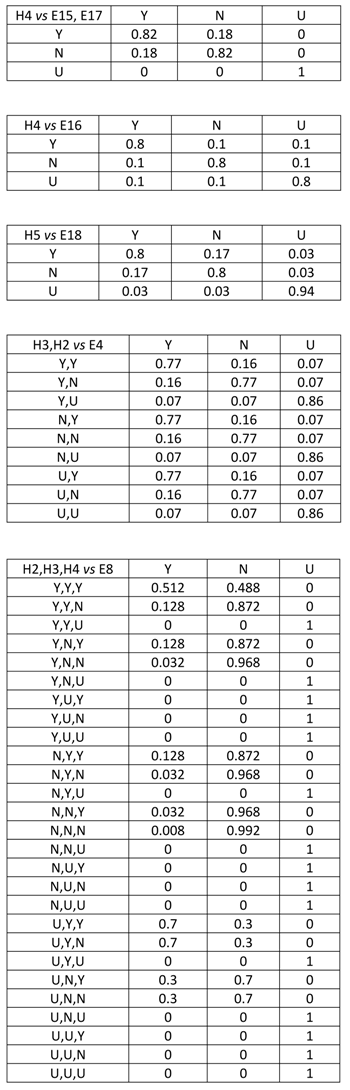
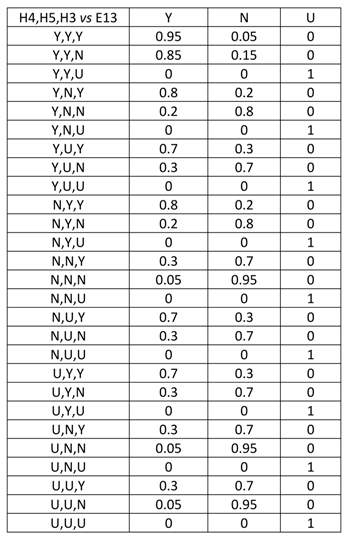
Appendix A
References
- Pearl, J. Probabilistic Reasoning in Intelligent Systems; Morgan Kaufmann: San Francisco, CA, USA, 1997. [Google Scholar]
- Nelson, J. Finding Useful Questions: On Bayesian Diagnosticity, Probability, Impact and Informtion Gain. Psychol. Rev. 2005, 112, 979–999. [Google Scholar] [CrossRef] [PubMed]
- Roche, W.; Shogenji, T. Information and Inaccuracy. Br. J. Philos. Sci. 2018, 69, 577–604. [Google Scholar] [CrossRef]
- Coenen, A.; Nelson, J.; Gureckis, T. Asking the right questions about the psychology of human inquiry: Nine open challenges. Psychon. Bull. Rev. 2018, 1–41. [Google Scholar] [CrossRef] [PubMed]
- Nielson, T.D.; Jensen, F.V. Bayesian Networks and Decision Graphs; Springer Science and Business Media: Berlin, Germany, 2018. [Google Scholar]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Howard, R. Decision Analysis: Practice and Promise. Manag. Sci. 1988, 34, 679–695. [Google Scholar] [CrossRef]
- Overill, R.; Chow, K.P. Measuring Evidential Weight in a Digital Forensic Investigations. In Proceedings of the 14th Annual IFIP WG11.9 International Conference on Digital Forensics, New Delhi, India, 3–5 January 2018; pp. 3–10. [Google Scholar]
- Kwan, Y.-K. The Research of Using Bayesian Inferential Network in Digital Forensic Analysis. Ph.D. Thesis, The University of Hong Kong, Hong Kong, China, 2011. [Google Scholar]
- Ming, C.N. Magistrates’ Court at Tuen Mun, Hong Kong Special Administrative Region v; TMCC 1268/2005: Hong Kong, China, 2005. [Google Scholar]
- Kwan, M.; Chow, K.-P.; Law, F.; Lai, P. Reasoning about Evidence using Bayesian Networks. In Proceedings of the IFIP WG11.9 International Conference on Digital Forensics, Tokyo, Japan, 27–30 January 2008; pp. 141–155. [Google Scholar]
- Fenton, N.; Neil, M. AgenaRisk Open Source Software, See Also AgenaRisk 7.0 User Manual. 2016. Available online: http://www.agenarisk.com/resources/AgenaRisk_User_Manual.pdf (accessed on 31 May 2018).
- Overill, R.E.; Kwan, Y.-K.; Chow, K.P.; Lai, K.-Y.; Law, Y.-W. A Cost-Effective Digital Forensics Investigation Model. In Proceedings of the 5th Annual IFIP WG 11.9 International Conference on Digital Forensics, Orlando, FL, USA, 25–28 January 2009; pp. 193–202. [Google Scholar]
- Overill, R.E. ‘Digital Forensonomics’—The Economics of Digital Forensics. In Proceedings of the 2nd International Workshop on Cyberpatterns (Cyberpatterns 2013), Abingdon, UK, 8–9 July 2013. [Google Scholar]
- Overill, R.E.; Silomon, J.A.M.; Kwan, Y.-K.; Chow, K.P.; Law, Y.-W.; Lai, K.Y. Sensitivity Analysis of a Bayesian Network for Reasoning about Digital Forensic Evidence. In Proceedings of the 2010 3rd International Conference on Human-Centric Computing, Cebu, Philippines, 11–13 August 2010; pp. 228–232. [Google Scholar]

| Test | Information Gain Method | Updated P (H = Yes) | Increase in P (H = Yes) |
|---|---|---|---|
| Prior | 0.3333 | ||
| 0.4083 | 0.6829 | 0.3496 | |
| 0.0463 | 0.7661 | 0.0832 | |
| 0.0198 | 0.8196 | 0.0535 | |
| 0.0060 | 0.8521 | 0.0325 | |
| 0.0044 | 0.8803 | 0.0282 | |
| 0.0029 | 0.8942 | 0.0139 | |
| 0.0018 | 0.9049 | 0.0107 | |
| 0.0014 | 0.9148 | 0.0099 |
| Test | Tornado Method Impact | Updated P (H = Yes) | Increase in P (H = Yes) |
|---|---|---|---|
| 0.2913 | 0.6250 | 0.2916 | |
| 0.1824 | 0.7226 | 0.0976 | |
| 0.1374 | 0.7878 | 0.0652 | |
| 0.0982 | 0.8208 | 0.0330 | |
| 0.0735 | 0.8481 | 0.0273 | |
| 0.0770 | 0.8790 | 0.0309 | |
| 0.0526 | 0.8904 | 0.0114 | |
| 0.0419 | 0.9026 | 0.0123 | |
| 0.0246 | 0.9095 | 0.0068 | |
| 0.0234 | 0.9148 | 0.0054 | |
| 0.0140 | 0.9182 | 0.0033 |
| Test | Information Gain Method | Updated P (H = Yes) | Increase in P (H = Yes) |
|---|---|---|---|
| 0.0633 | 0.5410 | 0.1347 | |
| 0.0265 | 0.6759 | 0.0832 | |
| 0.0146 | 0.7590 | 0.1283 | |
| 0.0097 | 0.7790 | 0.0199 | |
| 0.0097 | 0.7828 | 0.0039 | |
| 0.0021 | 0.8361 | 0.0533 | |
| 0.0013 | 0.8643 | 0.0245 | |
| 0.0012 | 0.8791 | 0.0152 | |
| 0.0012 | 0.8836 | 0.0046 | |
| 0.0011 | 0.9118 | 0.0305 | |
| 0.0088 | 0.9120 | 0.0003 | |
| 0.0071 | 0.9200 | 0.0003 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schneps, L.; Overill, R.; Lagnado, D. Ranking the Impact of Different Tests on a Hypothesis in a Bayesian Network. Entropy 2018, 20, 856. https://doi.org/10.3390/e20110856
Schneps L, Overill R, Lagnado D. Ranking the Impact of Different Tests on a Hypothesis in a Bayesian Network. Entropy. 2018; 20(11):856. https://doi.org/10.3390/e20110856
Chicago/Turabian StyleSchneps, Leila, Richard Overill, and David Lagnado. 2018. "Ranking the Impact of Different Tests on a Hypothesis in a Bayesian Network" Entropy 20, no. 11: 856. https://doi.org/10.3390/e20110856
APA StyleSchneps, L., Overill, R., & Lagnado, D. (2018). Ranking the Impact of Different Tests on a Hypothesis in a Bayesian Network. Entropy, 20(11), 856. https://doi.org/10.3390/e20110856





