Statistical Mechanics of On-Line Learning Under Concept Drift
Abstract
1. Introduction
1.1. Concept Drift and Continual Learning
1.2. Models of On-Line Learning Under Concept Drift
1.3. Relation to Earlier Work
1.4. Outline
2. Models and Mathematical Analysis
2.1. Learning Vector Quantization
2.1.1. Nearest Prototype Classification and Winner-Takes-All Training
2.1.2. Clustered Model Data
2.2. Soft Committee Machines
2.2.1. Network Definition
2.2.2. Regression Scheme and On-Line Gradient Descent
2.2.3. Student–Teacher Scenario and Model Data
2.3. The Dynamics of On-Line Training in Stationary Environments
- (a)
- Order parameters
- (b)
- Recursions
- (c)
- Averages over the Model Data
- (d)
- Self-Averaging Properties
- (e)
- Continuous Time Limit and ODE
- (f)
- Generalization error
- (g)
- Learning curves
2.4. The Learning Dynamics Under Concept Drift
2.4.1. Virtual Drift
2.4.2. Real Drift
2.4.3. Weight Decay
3. Results and Discussion
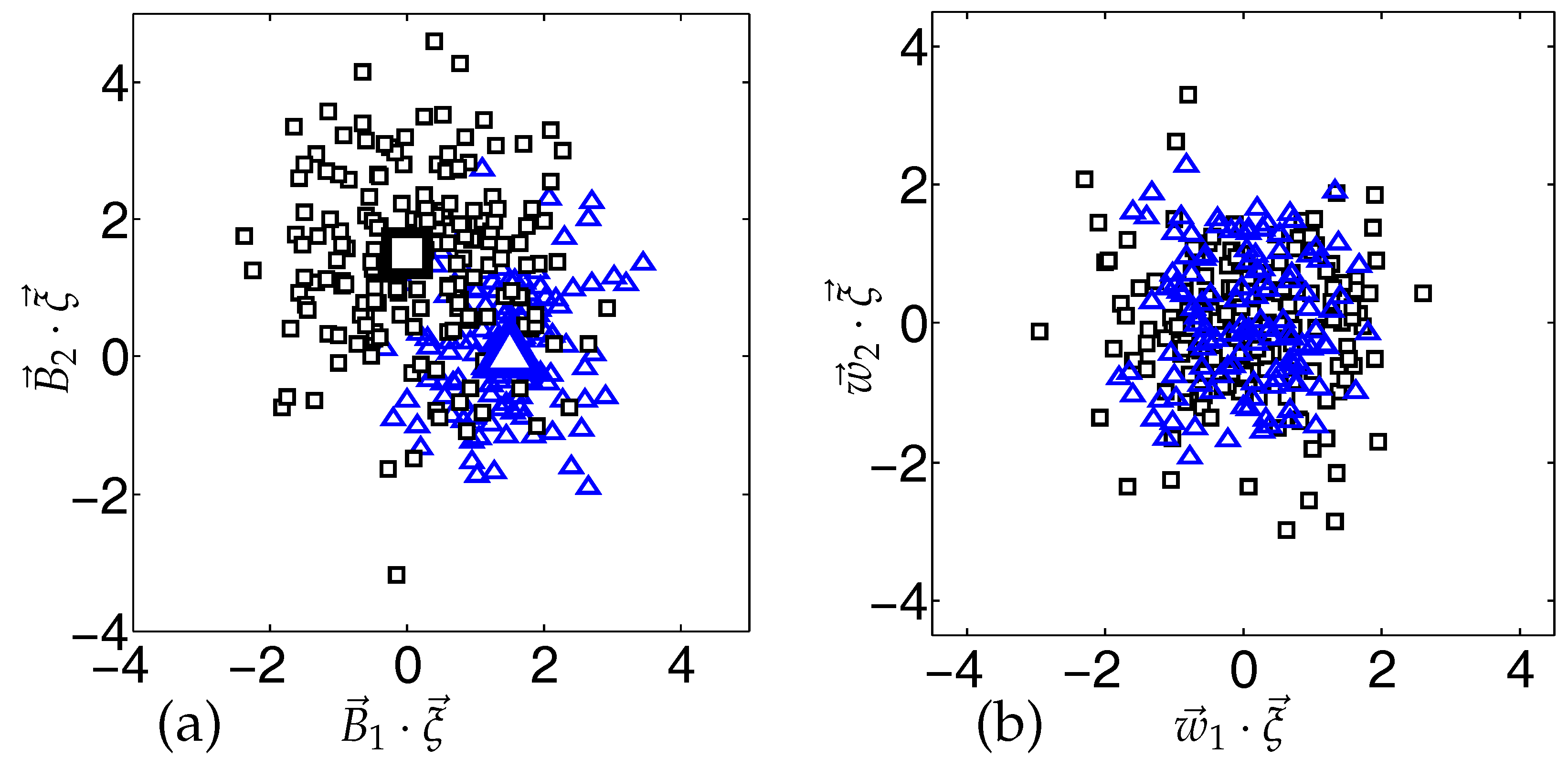
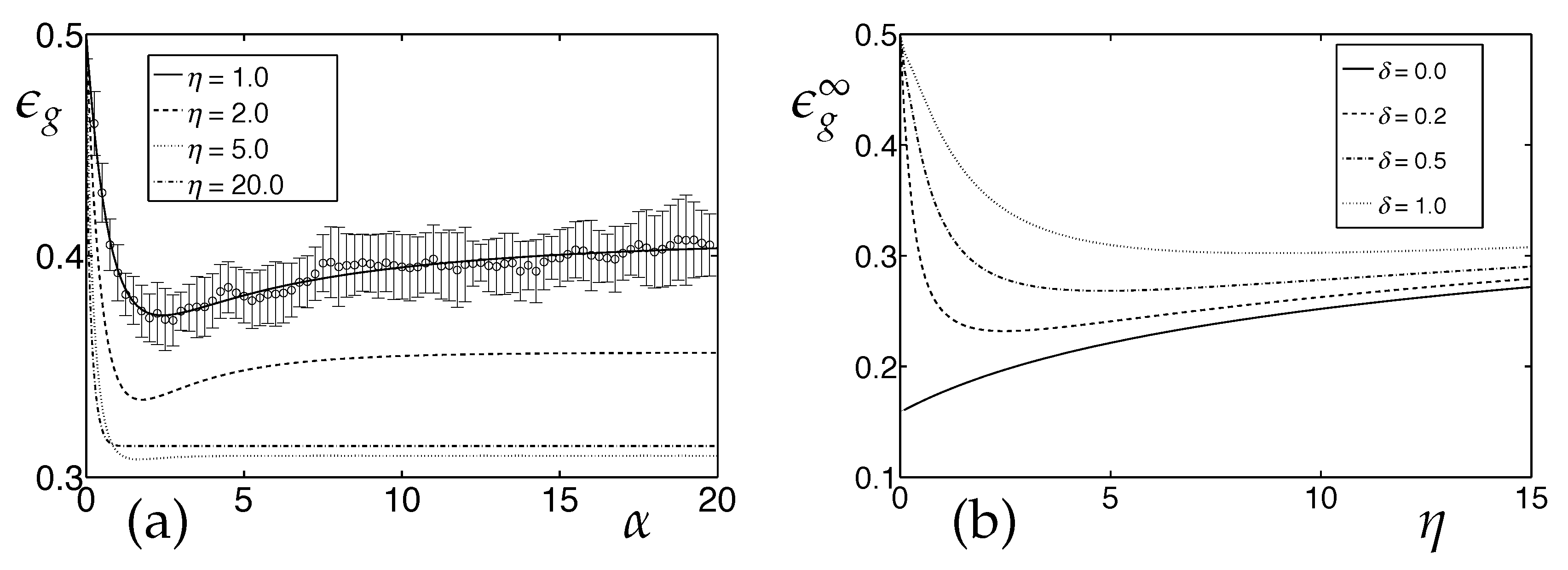
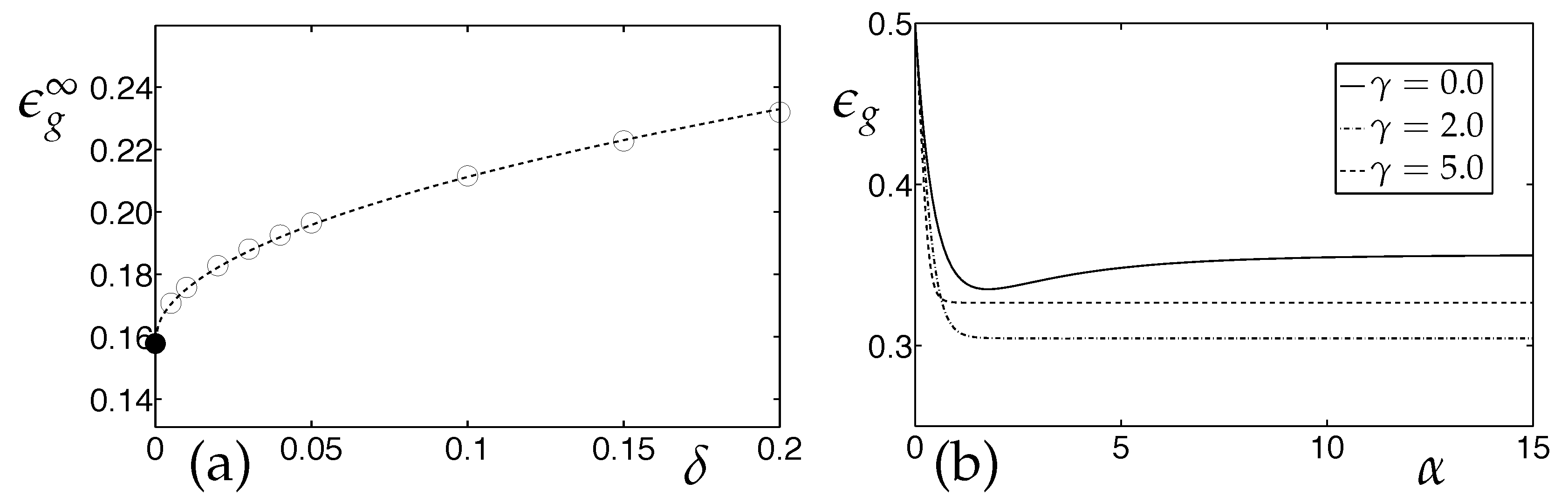
3.1. Learning Vector Quantization in the Presence of Real Concept Drift
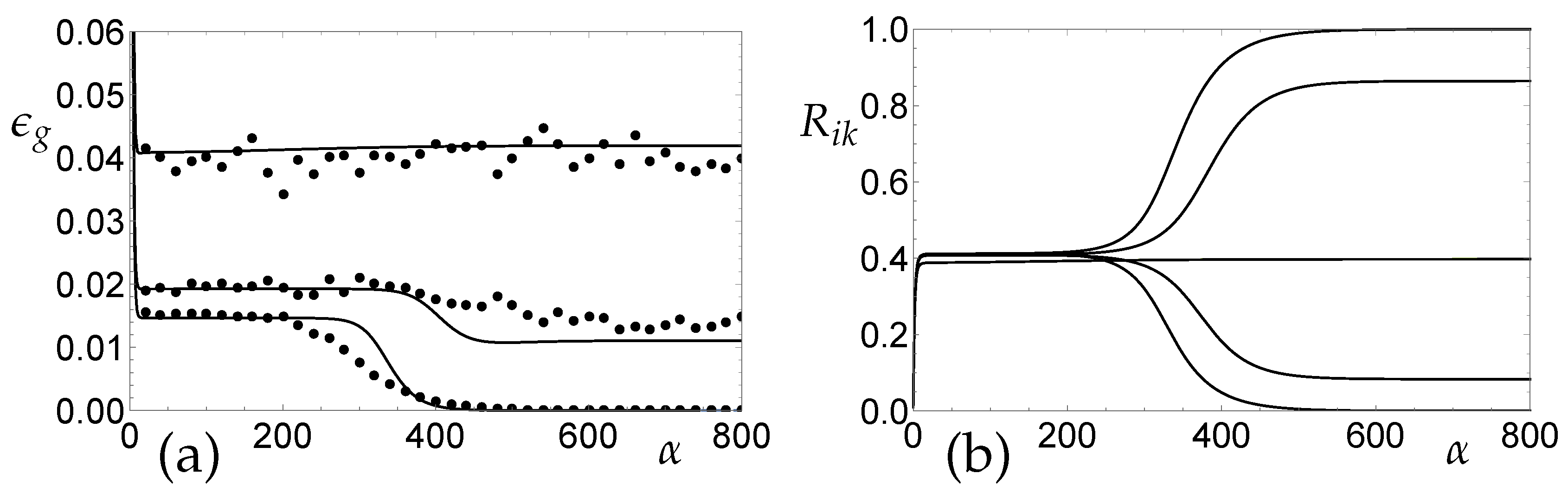
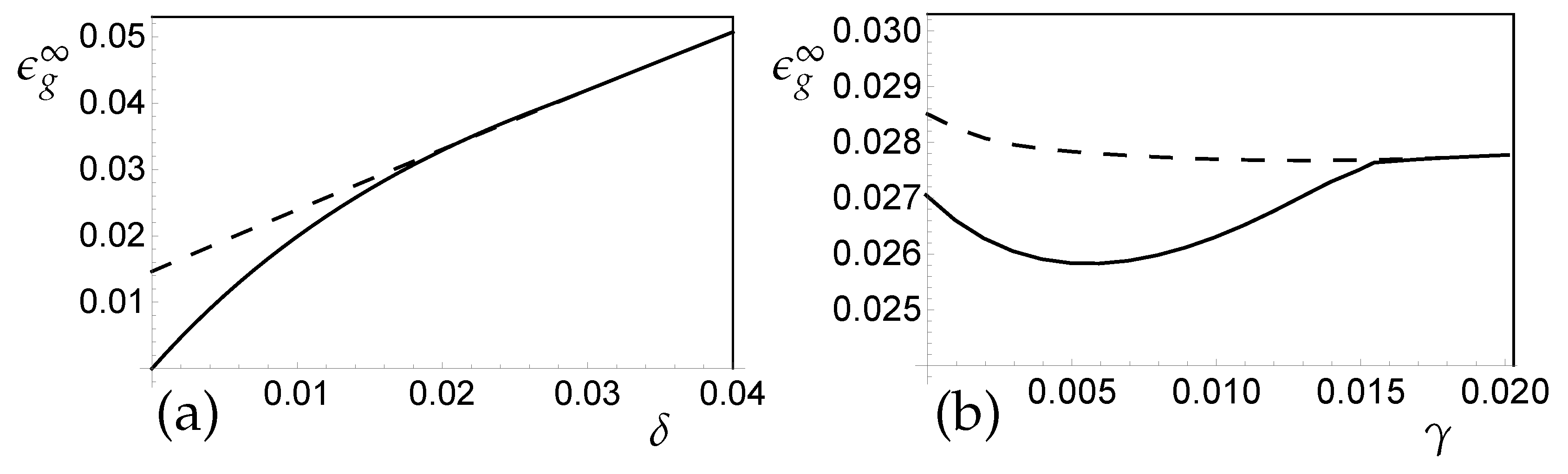
3.2. SCM Regression in the Presence of Real Concept Drift
4. Conclusions
4.1. Brief Summary
4.2. Future Work and Extensions
- The systematic investigation of virtual drifts as in, for instance, non-stationary label noise, prior weights or cluster separation is readily possible by consideration of explicitly time-dependent ODE.
- The restriction to LVQ systems with one prototype per class results, effectively, in the parameterization of linear class boundaries only. This limitation can be lifted by considering distances different from the simple Euclidean measure (see, e.g., [29]). Alternatively, systems with several prototypes per class correspond to non-linear (piece-wise linear) decision boundaries which has non-trivial effects on the training dynamics, as demonstrated for stationary environments in [49].
- Similarly, the investigation of SCM student–teacher scenarios with more general settings of K and M will provide insight into the interplay of concept drift with the larger number of possible plateau states for . Over- and under-fitting effects in mismatched situations with will be in the center of interest.
- The shallow SCM architectures studied here are limited to a single hidden layer of units. The important extension to deeper networks with several hidden layers will be addressed in forthcoming studies.
- It will be interesting to explore the extent to which the theoretically studied phenomena can be observed in practical situations. To this end, we will investigate the behavior of LVQ and SCM in realistic training set-ups with real world data streams.
4.3. Perspectives and Challenges
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CLT | Central Limit Theorem |
| LVQ | Learning Vector Quantization |
| NPC | Nearest Prototype Classification |
| ODE | Ordinary Differential Equations |
| r.h.s. | right hand side |
| SCM | Soft Committee Machine |
| WTA | Winner Takes All |
References
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: New York, NY, USA, 2001. [Google Scholar]
- Bishop, C. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Hertz, J.A.; Krogh, A.S.; Palmer, R.G. Introduction to the Theory of Neural Computation; Addison-Wesley: Redwood City, CA, USA, 1991. [Google Scholar]
- Engel, A.; van den Broeck, C. The Statistical Mechanics of Learning; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Seung, S.; Sompolinsky, H.; Tishby, N. Statistical mechanics of learning from examples. Phys. Rev. A 1992, 45, 6056–6091. [Google Scholar] [CrossRef] [PubMed]
- Watkin, T.L.H.; Rau, A.; Biehl, M. The statistical mechanics of learning a rule. Rev. Mod. Phys. 1993, 65, 499–556. [Google Scholar] [CrossRef]
- Biehl, M.; Caticha, N. The statistical mechanics of on-line learning and generalization. In The Handbook of Brain Theory and Neural Networks; Arbib, M.A., Ed.; MIT Press: Cambridge, MA, USA, 2003; pp. 1095–1098. [Google Scholar]
- Biehl, M.; Caticha, N.; Riegler, P. Statistical mechanics of on-line learning. In Similiarity Based Clustering; Lecture Notes in Artificial Intelligence; Biehl, M., Hammer, B., Verleysen, M., Villmann, T., Eds.; Springer: Cham, Switzerland, 2009; Volume 5400, pp. 1–22. [Google Scholar]
- Zliobaite, I.; Pechenizkiy, M.; Gama, J. An overview of concept drift applications. In Big Data Analysis: New Algorithms for a New Society; Big Data Analysis; Japkowicz, N., Stefanowski, J., Eds.; Springer: Cham, Switzerland, 2016; Volume 16. [Google Scholar]
- Losing, V.; Hammer, B.; Wersing, H. Incremental on-line learning: A review and comparison of state of the art algorithms. Neurocomputing 2017, 275, 1261–1274. [Google Scholar] [CrossRef]
- Ditzler, G.; Roveri, M.; Alippi, C.; Polikar, R. Learning in nonstationary environment: A survey. Comput. Intell. Mag. 2015, 10, 12–25. [Google Scholar] [CrossRef]
- Joshi, J.; Kulkarni, P. Incremental learning: areas and methods—A survey. Int. J. Data Min. Knowl. Manag. Process 2012, 2, 43–51. [Google Scholar] [CrossRef]
- Ade, R.; Desmukh, P. Methods for incremental learning: A survey. Int. J. Data Min. Knowl. Manag. Process. 2013, 3, 119–125. [Google Scholar]
- De Francisci Morales, G.; Bifet, A. SAMOA: Scalable advanced massive online analysis. J. Mach. Learn. Res. 2015, 16, 149–153. [Google Scholar]
- Grandinetti, L.; Lippert, T.; Petkov, N. (Eds.) Computing ternational Workshop BrainComp 2013; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2014; Volume 8603. [Google Scholar]
- Amunts, K.; Grandinetti, L.; Lippert, T.; Petkov, N. (Eds.) Brain-Inspired Computing. Second International Workshop BrainComp 2015; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2016; Volume 10087. [Google Scholar]
- Faria, E.R.; Gonçalves, I.J.C.R.; de Carvalho, A.C.P.L.F.; Gama, J. Novelty detection in data streams. Artif. Intell. Rev. 2016, 45, 235–269. [Google Scholar] [CrossRef]
- Krawczyk, B.; Minku, L.L.; Gama, J.; Stefanowski, J.; Wozniak, M. Ensemble learning for data stream analysis: A survey. Inf. Fusion 2017, 37, 132–156. [Google Scholar] [CrossRef]
- Gomes, H.M.; Bifet, A.; Read, J.; Barddal, J.P.; Enembreck, F.; Pfharinger, B.; Holmes, G.; Abdessalam, T. Adaptive random forests for evolving data stream classification. Mach. Learn. 2017, 106, 1469–1495. [Google Scholar] [CrossRef]
- Losing, V.; Hammer, B.; Wersing, H. Tackling heterogeneous concept drift with the Self-Adjusting Memory (SAM). Knowl. Inf. Syst. 2018, 54, 171–201. [Google Scholar] [CrossRef]
- Loeffel, P.-X.; Marsala, C.; Detyniecki, M. Classification with a reject option under Concept Drift: The Droplets algorithm. In Proceedings of the International Conference on Data Science and Advanced Analytics (DSAA 2015), Paris, France, 19–21 October 2015; IEEE: New York, NY, USA, 2015; pp. 1–9. [Google Scholar]
- Janakiraman, V.M.; Nguyen, X.; Assanis, D. Stochastic gradient based extreme learning machines for stable online learning of advanced combustion engines. Neurocomput 2016, 177, 304–316. [Google Scholar] [CrossRef]
- Benczúr, A.A.; Kocsis, L.; Pálovics, R.; Online machine learning in big data streams. arXiv 2018, arxiv:1802.05872. Available online: http://arxiv.org/abs/1802.05872 (accessed on 13 August 2018).
- Kohonen, T.; Barna, G.; Chrisley, R. Statistical pattern recognition with neural network: Benchmarking studies. In Proceedings of the IEEE second international conference on Neural Networks, San Diego, CA, USA, 24–27 July 1988; IEEE: New York, NY, USA, 1988; Volume 1, pp. 61–68. [Google Scholar]
- Kohonen, T. Self-Organizing Maps; Springer: New York, NY, USA, 2001. [Google Scholar]
- Kohonen, T. Improved versions of Learning Vector Quantization. In Proceedings of the 1990 IJCNN International Joint Conference on Neural Networks, San Diego, CA, USA, 17–21 June 1990; Volume 1, pp. 545–550. [Google Scholar]
- Nova, D.; Estevez, P.A. A review of Learning Vector Quantization classifiers. Neural Comput. Appl. 2014, 25, 511–524. [Google Scholar] [CrossRef]
- Biehl, M.; Hammer, B.; Villmann, T. Prototype-based models in machine learning. WIREs Cogn. Sci. 2016, 7, 92–111. [Google Scholar] [CrossRef] [PubMed]
- Biehl, M.; Schwarze, H. Learning by on-line gradient descent. J. Phys. A Math. Gen. 1995, 28, 643–656. [Google Scholar] [CrossRef]
- Saad, D.; Solla, S.A. Exact solution for on-line learning in multilayer neural. Phys. Rev. Lett. 1995, 74, 4337–4340. [Google Scholar] [CrossRef] [PubMed]
- Saad, D.; Solla, S.A. On-line learning in soft committee machines. Phys. Rev. E 1995, 52, 4225–4243. [Google Scholar] [CrossRef]
- Riegler, P.; Biehl, M. On-line backpropagation in two-layered neural networks. J. Phys. A Math. Gen. 1995, 28, L507–L513. [Google Scholar] [CrossRef]
- Biehl, M.; Riegler, P.; Wöhler, C. Transient dynamics of on-line learning in two-layered neural networks. J. Phys. A Math. Gen. 1996, 29, 4769–4780. [Google Scholar] [CrossRef]
- Vicente, R.; Caticha, N. Functional optimization of online algorithms in multilayer neural networks. J. Phys. A Math. Gen. 1997, 30, L599–L605. [Google Scholar] [CrossRef]
- Inoue, M.; Park, H.; Okada, M. On-line learning theory of soft committee machines with correlated hidden units-steepest gradient descent and natural gradient descent. J. Phys. Soc. Jpn. 2003, 72, 805–810. [Google Scholar] [CrossRef]
- Marcus, G. Deep learning: A critical appraisal. arXiv. 2018. arxiv:1801.00631. Available online: http://arxiv.org/abs/1801.00631 (accessed on 27 August 2018).
- Saad, D. (Ed.) On-Line Learning in Neural Networks; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Biehl, M.; Ghosh, A.; Hammer, B. Dynamics and generalization ability of LVQ algorithms. J. Mach. Learn. Res. 2007, 8, 323–360. [Google Scholar]
- Biehl, M.; Freking, A.; Reents, G. Dynamics of on-line competitive learning. Europhys. Lett. 1997, 38, 73–78. [Google Scholar] [CrossRef]
- Biehl, M.; Freking, A.; Reents, G.; Schlösser, E. Specialization processes in on-line unsupervised learning. Phil. Mag. B 1999, 77, 1487–1494. [Google Scholar] [CrossRef]
- Biehl, M.; Schlösser, E. The dynamics of on-line principal component analysis. J. Phys. A Math. Gen. 1998, 31, L97–L103. [Google Scholar] [CrossRef]
- Barkai, N.; Seung, H.S.; Sompolinksy, H. Scaling laws in learning of classification tasks. Phys. Rev. Lett. 1993, 70, 3167–3170. [Google Scholar] [CrossRef] [PubMed]
- Marangi, C.; Biehl, M.; Solla, S.A. Supervised learning from clustered input examples. Europhys. Lett. 1995, 30, 117–122. [Google Scholar] [CrossRef]
- Meir, R. Empirical risk minimization versus maximum-likelihood estimation: a case study. Neural Comput. 1995, 7, 144–157. [Google Scholar] [CrossRef]
- Ghosh, A.; Biehl, M.; Hammer, B. Performance analysis of LVQ algorithms: a statistical physics approach. Neural Netw. 2006, 19, 817–829. [Google Scholar] [CrossRef] [PubMed]
- Biehl, M.; Ghosh, A.; Hammer, B. The dynamics of Learning Vector Quantization. In Proceedings of the 13th European Symposium on Artificial Neural Networks (ESANN 2005), Bruges, Belgium, 27–29 April 2005; Verleysen, M., Ed.; D-Side: Evere, Belgium, 2005; pp. 13–18. [Google Scholar]
- Ghosh, A.; Biehl, M.; Hammer, B. Dynamical analysis of LVQ type learning rules. In Proceedings of the 5th Workshop on the Self-Organizing-Map (WSOM 2005), Paris, France, 5–8 September 2005; Cottrell, M., Ed.; Université de Paris: Paris, France, 2005. 6p. [Google Scholar]
- Witoelar, A.; Ghosh, A.; de Vries, J.J.G.; Hammer, B.; Biehl, M. Window-based example selection in learning vector quantization. Neural Comput. 2010, 22, 2924–2961. [Google Scholar] [CrossRef] [PubMed]
- Biehl, M.; Schwarze, H. On-line learning of a time-dependent rule. Europhys. Lett. 1992, 20, 733–738. [Google Scholar] [CrossRef]
- Biehl, M.; Schwarze, H. Learning drifting concepts with neural networks. J. Phys. A Math. Gen. 1993, 26, 2651–2665. [Google Scholar] [CrossRef]
- Kinouchi, O.; Caticha, N. Lower bounds on generalization errors for drifting rules. J. Phys. A Math. Gen. 1993, 26, 6161–6172. [Google Scholar] [CrossRef]
- Vicente, R.; Caticha, N. Statistical mechanics of online learning of drifting concepts: A variational approach. Mach. Learn. 1998, 32, 179–201. [Google Scholar] [CrossRef]
- Biehl, M.; Hammer, B.; Villmann, T. Distance measures for prototype based classification. In International Workshop on Brain-Inspired Computing; Springer: Cham, Switzerland, 2013; pp. 110–116. [Google Scholar]
- Biehl, M.; Schlösser, E.; Ahr, M. Phase transitions in soft-committee machines. Europhys. Lett. 1998, 44, 261–266. [Google Scholar] [CrossRef]
- Ahr, M.; Biehl, M.; Urbanczik, R. Statistical physics and practical training of soft-committee machines. Eur. Phys. J. B 1999, 10, 583–588. [Google Scholar] [CrossRef]
- Cybenko, G. Approximations by superpositions of sigmoidal functions. Math. Control Signals Syst. 1989, 2, 303–314. [Google Scholar] [CrossRef]
- Reents, G.; Urbanczik, R. Self-averaging and on-line learning. Phys. Rev. Lett. 1998, 80, 5445–5448. [Google Scholar] [CrossRef]
- Mezard, M.; Nadal, J.P.; Toulouse, G. Solvable models of working memories. J. Phys. 1986, 47, 1457–1462. [Google Scholar] [CrossRef]
- Van Hemmen, J.L.; Keller, G.; Kühn, R. Forgetful memories. Europhys. Lett. 1987, 5, 663–668. [Google Scholar] [CrossRef]
- Saad, D.; Solla, S.A. Learning with noise and regularizers in multilayer neural networks. In Advances in Neural Information Processing Systems; Mozer, M., Jordan, M.I., Petsche, T., Eds.; MIT Press: Cambridge, MA, USA, 1997; pp. 260–266. [Google Scholar]
- Saad, D.; Rattray, M. Learning with regularizers in multilayer neural networks. Phys. Rev. E 1998, 57, 2170–2176. [Google Scholar] [CrossRef]
- Dauphin, Y.N.; Pascanu, R.; Gulcehre, C.; Cho, K.; Ganguli, S.; Bengio, Y. Identifying and attacking the saddle point problem in high-dimensional non-convex optimization. In Proceedings of the Twenty-Eighth Conference on Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; Curran Associates: Red Hook, NY, USA, 2014; pp. 2933–2941. [Google Scholar]
- Tishby, N.; Zaslavsky, N. Deep Learning and the information bottleneck principle. In Proceedings of the 2015 IEEE Information Theory Workshop (ITW), Jerusalem, Israel, 26 April–1 May 2015; IEEE: New York, NY, USA, 2015; pp. 1–5. [Google Scholar]
- Fischer, L.; Hammer, B.; Wersing, H. Combining offline and online classifiers for life-long learning (OOL). In Proceedings of the International Joint Conference on Neural Networks (IJCNN 2015), Killarney, Ireland, 12–16 July 2015; IEEE: New York, NY, USA, 2015. 8p. [Google Scholar]
- Fischer, L.; Hammer, B.; Wersing, H. Online metric learning for an adaptation to confidence drift. In Proceedings of the International Joint Conference on Neural Networks (IJCNN 2016), Vancouver, BC, Canada, 24–29 July 2016; IEEE: New York, NY, USA, 2016; pp. 748–755. [Google Scholar]
- Göpfert, J.P.; Hammer, B.; Wersing, H. Mitigating concept drift via rejection. In Proceedings of the 27th International Conference on Artificial Neural Networks (ICANN 2018), Rhodes, Greece, 4–7 October 2018; Kurkova, V., Manolopoulos, Y., Hammer, B., Iliadis, L., Magogiannis, I., Eds.; Springer: New York, NY, USA, 2018; pp. 456–467. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Straat, M.; Abadi, F.; Göpfert, C.; Hammer, B.; Biehl, M. Statistical Mechanics of On-Line Learning Under Concept Drift. Entropy 2018, 20, 775. https://doi.org/10.3390/e20100775
Straat M, Abadi F, Göpfert C, Hammer B, Biehl M. Statistical Mechanics of On-Line Learning Under Concept Drift. Entropy. 2018; 20(10):775. https://doi.org/10.3390/e20100775
Chicago/Turabian StyleStraat, Michiel, Fthi Abadi, Christina Göpfert, Barbara Hammer, and Michael Biehl. 2018. "Statistical Mechanics of On-Line Learning Under Concept Drift" Entropy 20, no. 10: 775. https://doi.org/10.3390/e20100775
APA StyleStraat, M., Abadi, F., Göpfert, C., Hammer, B., & Biehl, M. (2018). Statistical Mechanics of On-Line Learning Under Concept Drift. Entropy, 20(10), 775. https://doi.org/10.3390/e20100775




