Information Transfer Among the Components in Multi-Dimensional Complex Dynamical Systems
Abstract
1. Introduction
2. Two-Dimensional Formalism of Information Transfer (the LK2005 Formalism [6])
2.1. Continuous Flows
2.2. Discrete Mappings
3. n-Dimensional Formalism of Information Transfer
3.1. Continuous Flows
3.2. Discrete Mappings
4. The Application of Multi-Dimensional Formalism of Information Transfer
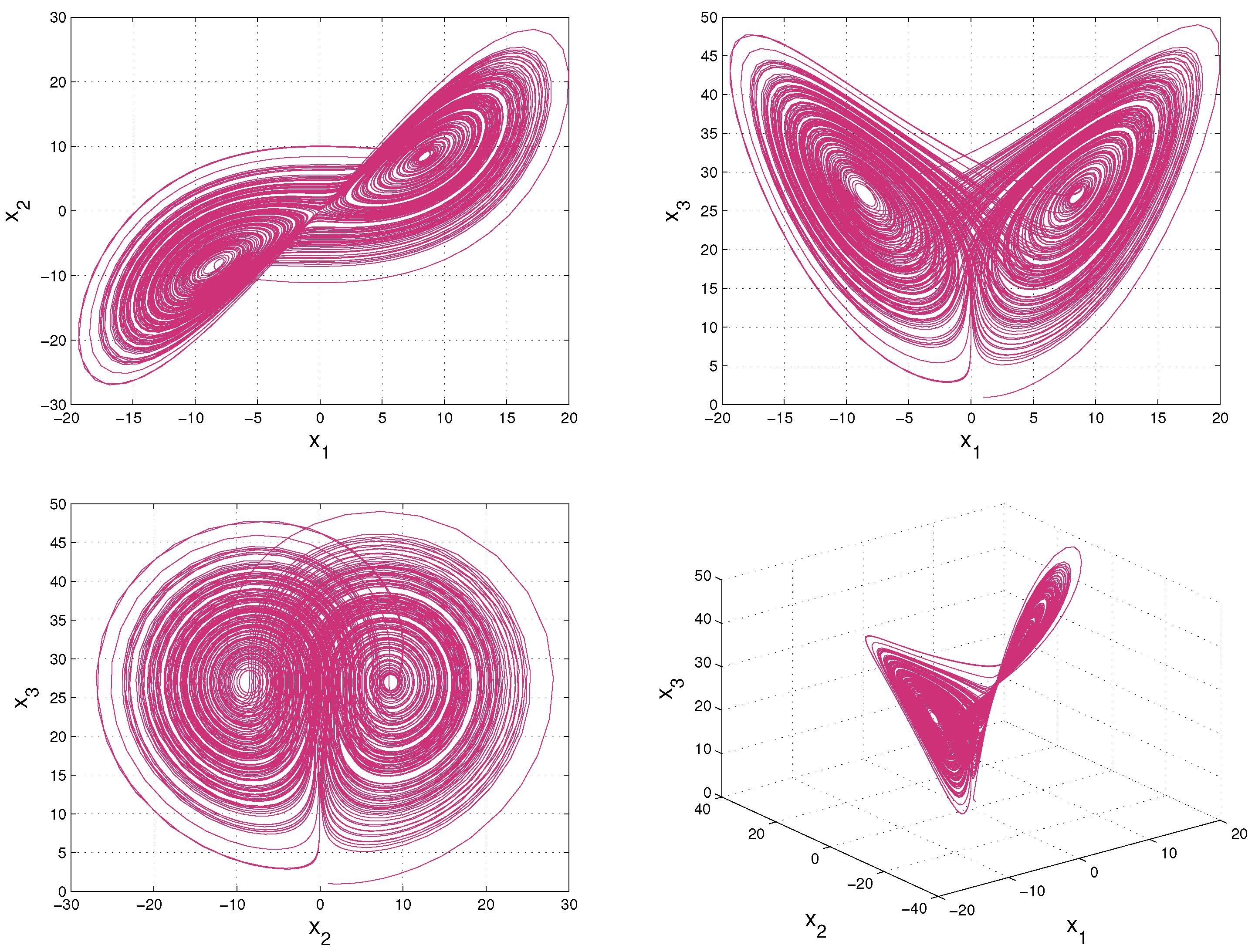
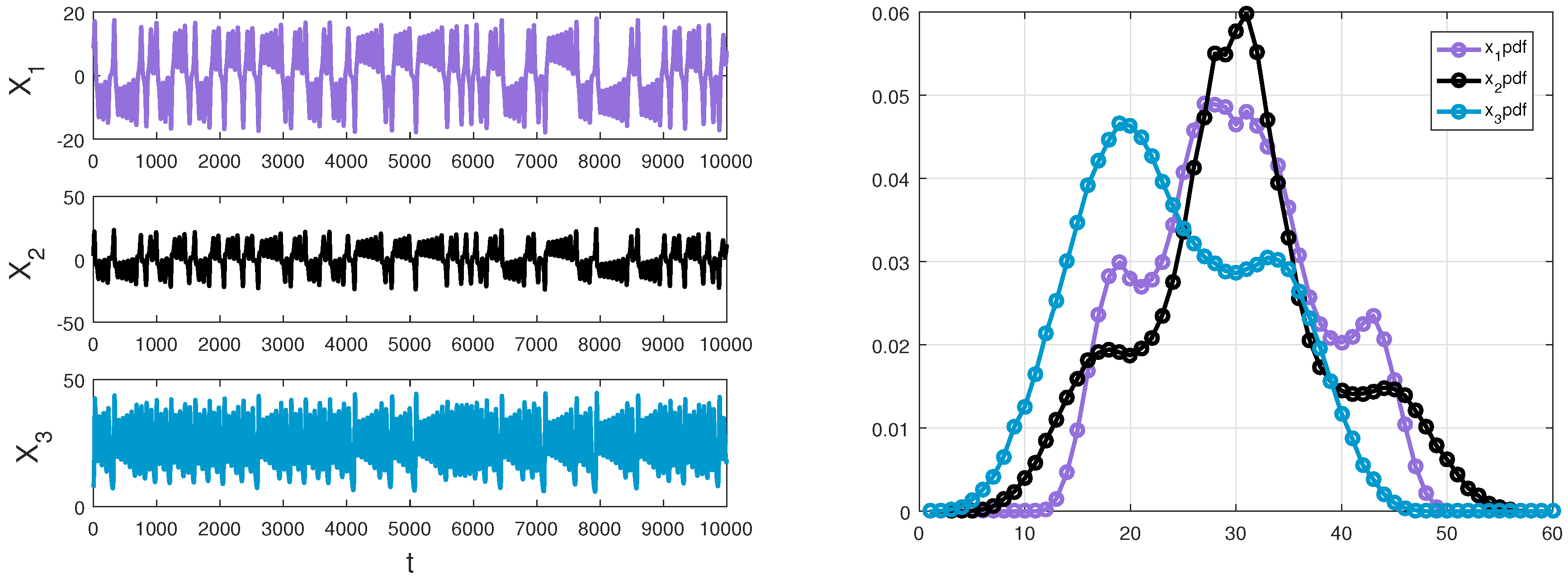
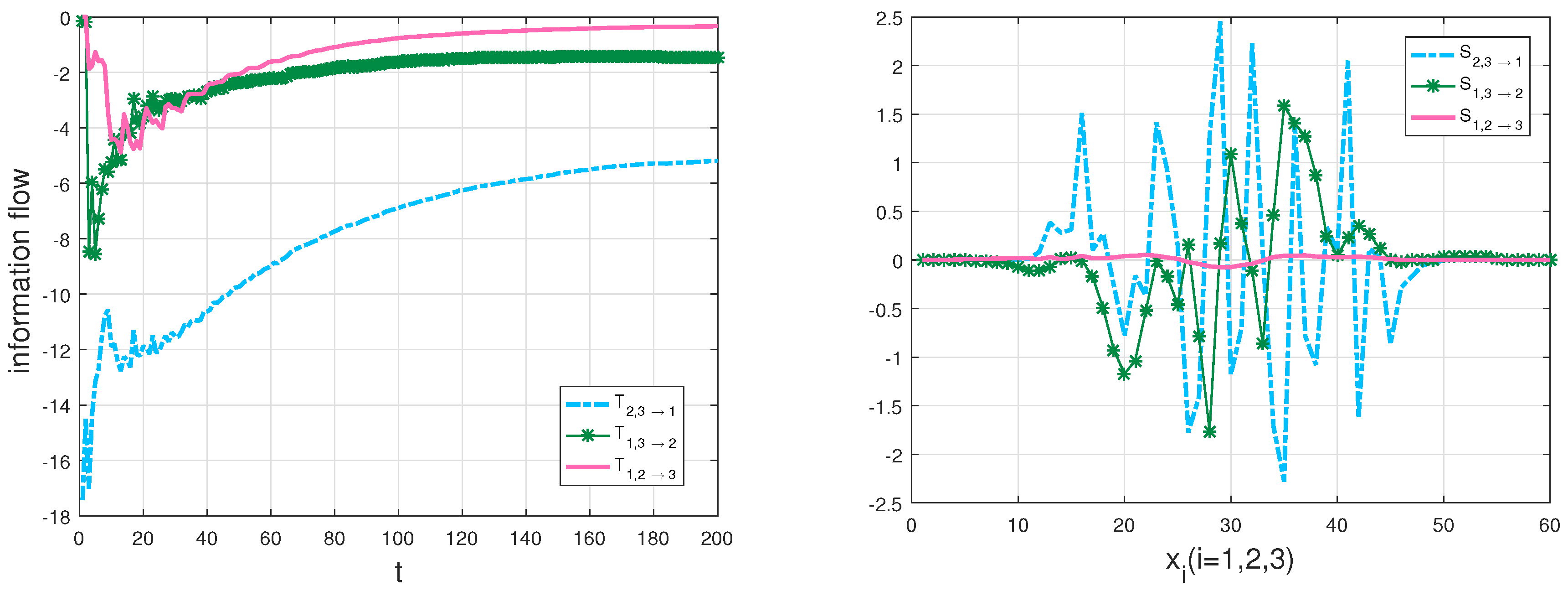
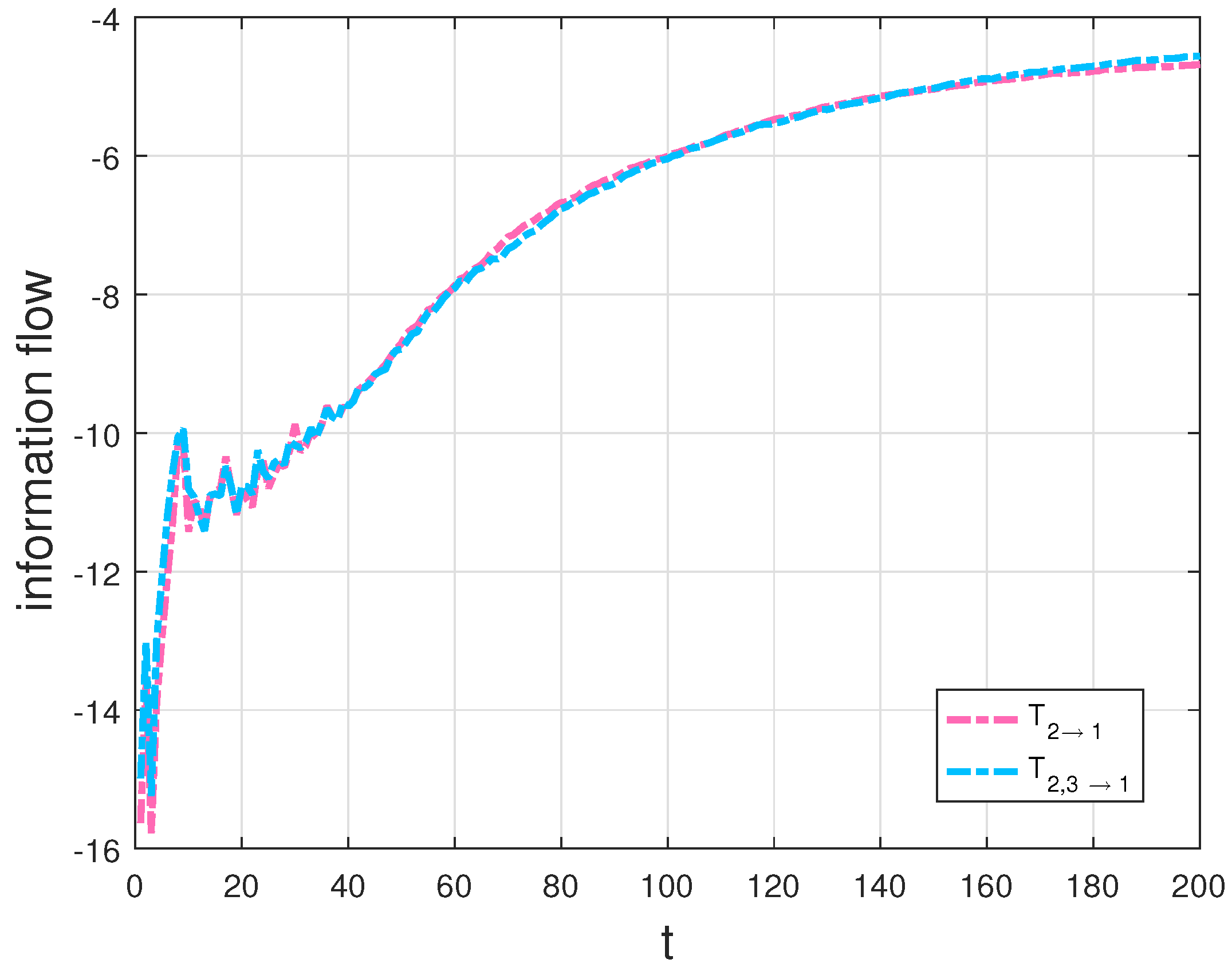
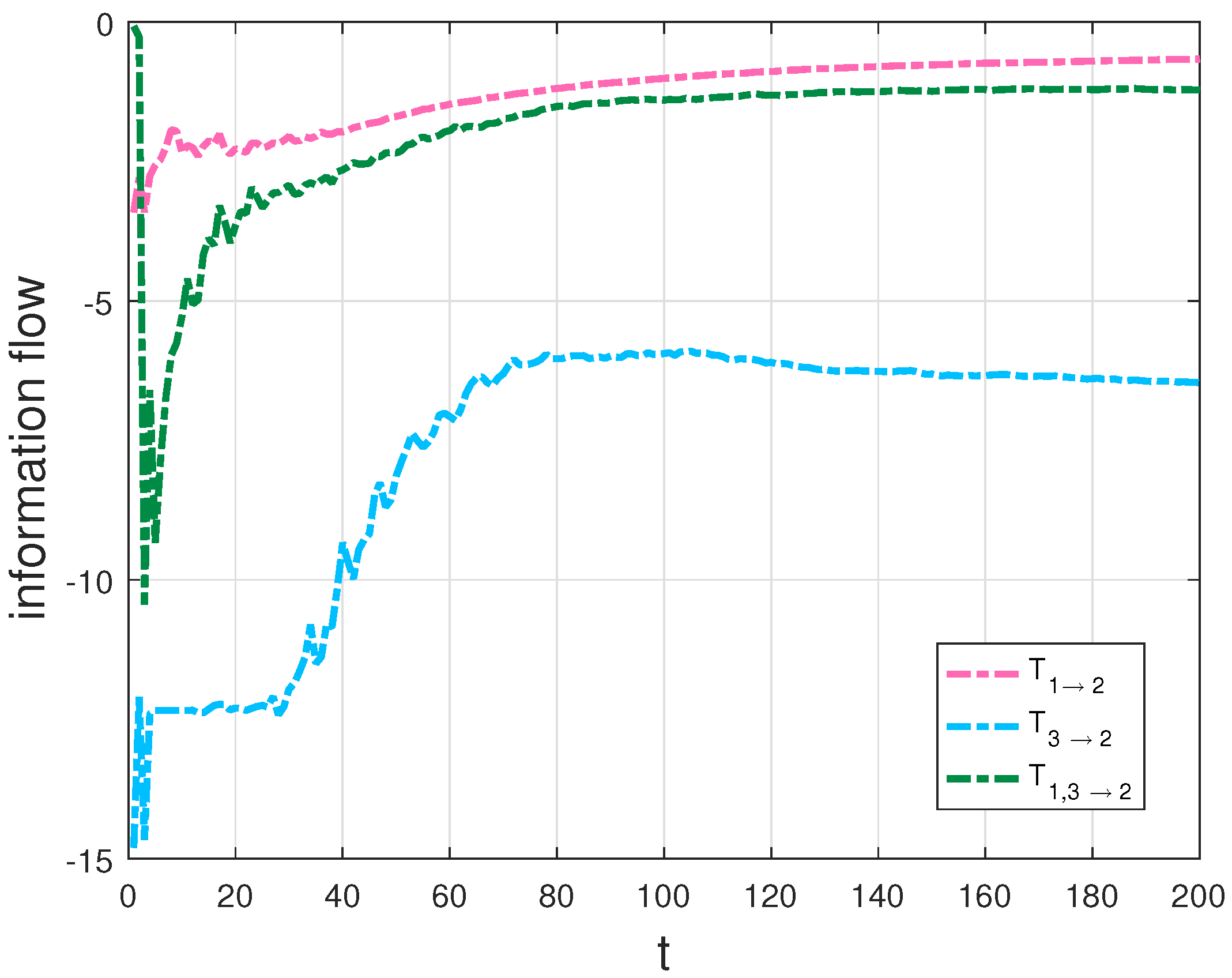
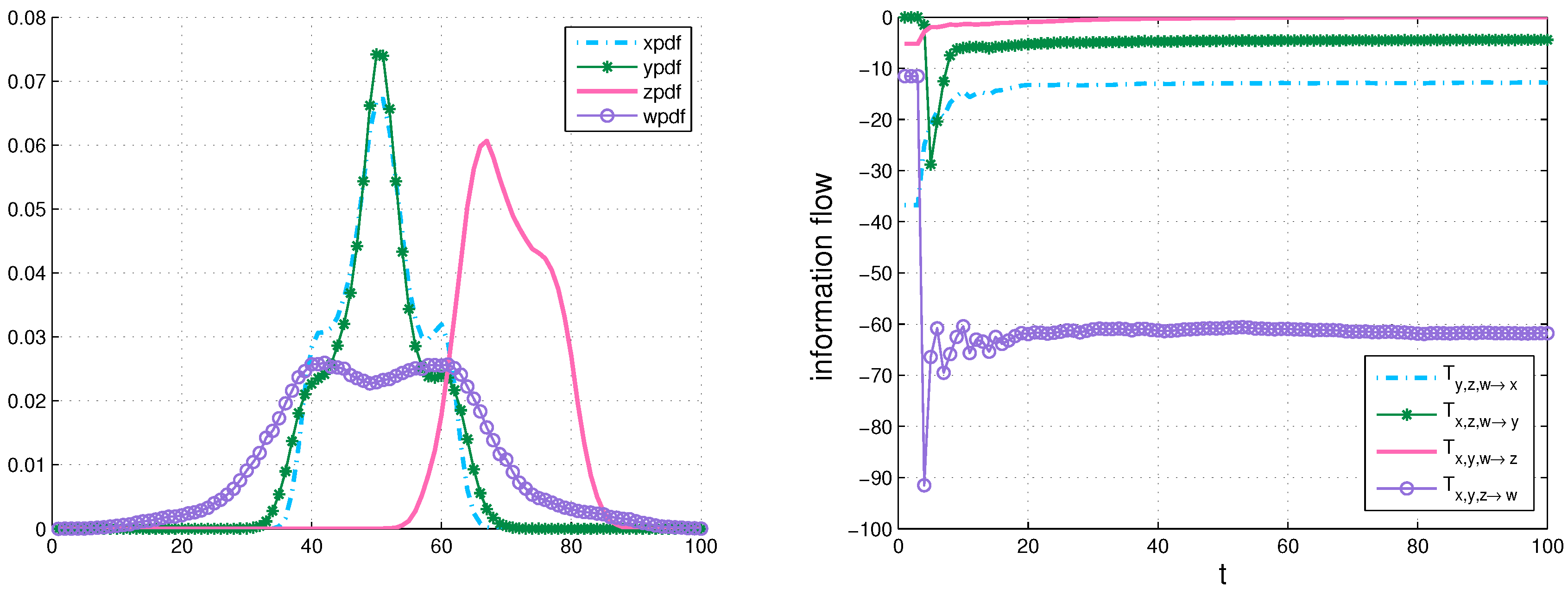
4.1. The Lorenz System
- Initialize the joint density with a preset distribution , then generate an ensemble through drawing samples randomly according to the initial distribution .
- Partition the sample space into “bins”.
- Obtain an ensemble prediction for the Lorenz system at every time step.
- Estimate the three-variable joint probability density function via bin counting at every time step.
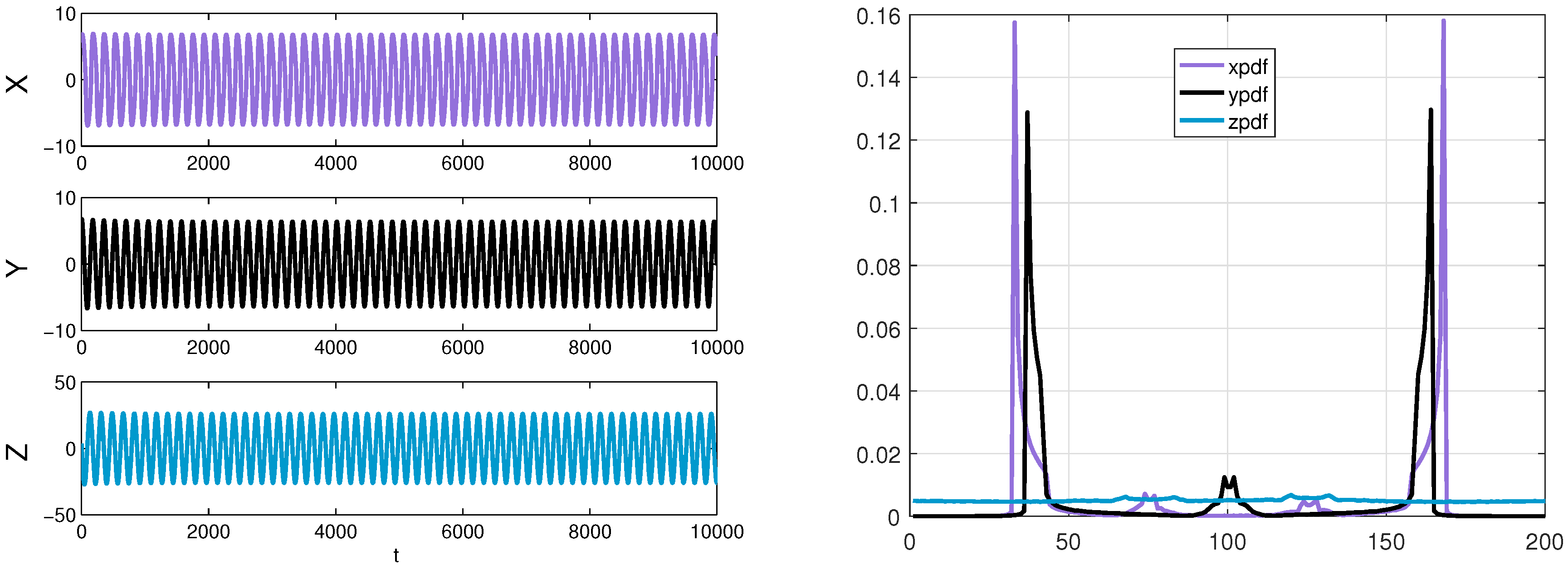
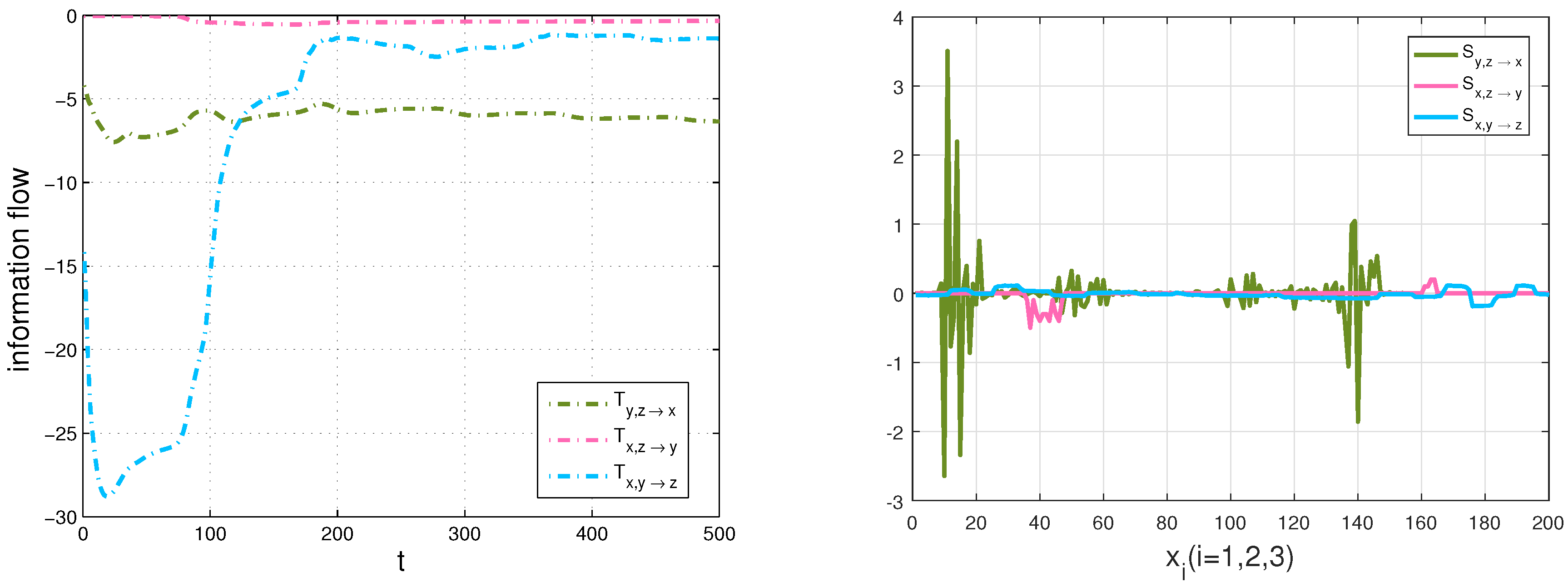
4.2. The Chua’s System
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Appendix A. Discrete Mappings
Appendix A.1.
References
- Schreiber, T. Measuring Information Transfer. Phys. Rev. Lett. 2000, 85, 461. [Google Scholar] [CrossRef] [PubMed]
- Horowitz, J.M.; Esposito, M. Thermodynamics with Continuous Information Flow. Phys. Rev. X 2014, 4, 031015. [Google Scholar] [CrossRef]
- Cafaro, C.; Ali, S.A.; Giffin, A. Thermodynamic aspects of information transfer in complex dynamical systems. Phys. Rev. E 2016, 93, 022114. [Google Scholar] [CrossRef] [PubMed]
- Gencaga, D.; Knuth, K.H.; Rossow, W.B. A Recipe for the Estimation of Information Flow in a Dynamical System. Entropy 2015, 17, 438–470. [Google Scholar] [CrossRef]
- Kwapien, J.; Drozdz, S. Physical approach to complex systems. Phys. Rep. 2012, 515, 115–226. [Google Scholar] [CrossRef]
- Liang, X.S.; Kleeman, R. Information Transfer between Dynamical Systems Components. Phys. Rev. Lett. 2005, 95, 244101. [Google Scholar] [CrossRef] [PubMed]
- Kleeman, R. Information flow in ensemble weather predictions. J. Atmos. Sci 2007, 6, 1005–1016. [Google Scholar] [CrossRef]
- Touchette, H.; Lloyd, S. Information-Theoretic Limits of Control. Phys. Rev. Lett. 2000, 84, 1156. [Google Scholar] [CrossRef] [PubMed]
- Touchette, H.; Lloyd, S. Information-theoretic approach to the study of control systems. Phys. A 2004, 331, 140. [Google Scholar] [CrossRef]
- Sun, J.; Cafaro, C.; Bollt, E.M. Identifying coupling structure in complex systems through the optimal causation entropy principle. Entropy 2014, 16, 3416–3433. [Google Scholar] [CrossRef]
- Cafaro, C.; Lord, W.M.; Sun, J.; Bollt, E.M. Causation entropy from symbolic representations of dynamical systems. CHAOS 2015, 25, 043106. [Google Scholar] [CrossRef] [PubMed]
- Majda, A.; Kleeman, R.; Cai, D. A Framework for Predictability through Relative Entropy. Methods Appl. Anal. 2002, 9, 425–444. [Google Scholar]
- Haven, K.; Majda, A.; Abramov, R. Quantifying predictability through information theory: Small-sample estimation in a non-Gaussian framework. J. Comp. Phys. 2005, 206, 334–362. [Google Scholar] [CrossRef]
- Abramov, R.V.; Majda, A.J. Quantifying Uncertainty for Non-Gaussian Ensembles in Complex Systems. SIAM J. Sci. Stat. Comp. 2004, 26, 411–447. [Google Scholar] [CrossRef]
- Kaiser, A.; Schreiber, T. Information transfer in continuous processes. Phys. D 2002, 166, 43–62. [Google Scholar] [CrossRef]
- Abarbanel, H.D.I.; Masuda, N.; Rabinovich, M.I.; Tumer, E. Distribution of Mutual Information. Phys. Lett. A 2001, 281, 368–373. [Google Scholar] [CrossRef]
- Wyner, A.D.; Mackey, M.C. A definition of conditional mutual information for arbitrary ensembles. Inf. Control 1978, 38, 51–59. [Google Scholar] [CrossRef]
- Lasota, A.; Mackey, M.C. Chaos, Fractals, and Noise: Stochastic Aspects of Dynamics; Springer: New York, NY, USA, 1994. [Google Scholar]
- Liang, X.S.; Kleeman, R. A rigorous formalism of information transfer between dynamical system components. I. Discrete mapping. Physica D 2007, 231, 1–9. [Google Scholar] [CrossRef]
- Liang, X.S.; Kleeman, R. A rigorous formalism of information transfer between dynamical system components. II. Continuous flow. Physica D 2007, 227, 173–182. [Google Scholar] [CrossRef]
- Liang, X.S. Information flow within stochastic dynamical systems. Phys. Rev. E 2008, 78, 031113. [Google Scholar] [CrossRef] [PubMed]
- Liang, X.S. Uncertainty generation in deterministic fluid flows: Theory and applications with an atmospheric stability model. Dyn. Atmos. Oceans 2011, 52, 51–79. [Google Scholar] [CrossRef]
- Liang, X.S. The Liang-Kleeman information flow: Theory and application. Entropy 2013, 15, 327–360. [Google Scholar] [CrossRef]
- Liang, X.S. Unraveling the cause-effect relation between time series. Phys. Rev. E 2014, 90, 052150. [Google Scholar] [CrossRef] [PubMed]
- Liang, X.S. Information flow and causality as rigorous notions ab initio. Phys. Rev. E 2016, 94, 052201. [Google Scholar] [CrossRef] [PubMed]
- Majda, A.J.; Harlim, J. Information flow between subspaces of complex dynamical systems. Proc. Natl. Acad. Sci. USA 2007, 104, 9558–9563. [Google Scholar] [CrossRef]
- Zhao, X.J.; Shang, P.J. Measuring the uncertainty of coupling. Europhys. Lett. 2015, 110, 60007. [Google Scholar] [CrossRef]
- Zhao, X.J.; Shang, P.J.; Huang, J.J. Permutation complexity and dependence measures of time series. Europhys. Lett. 2013, 102, 40005. [Google Scholar] [CrossRef]
- Iooss, B.; Lemaitre, P. A review on global sensitivity analysis methods. Oper. Res. Comput. Sci. Interfaces 2014, 59, 101–122. [Google Scholar]
- Borgonovo, E.; Plischke, E. Sensitivity analysis: A review of recent advances. Eur. J. Oper. Res. 2016, 248, 869–887. [Google Scholar] [CrossRef]
- Auder, B.; Crecy, A.D.; Iooss, B.; Marques, M. Screening and metamodeling of computer experiments with functional outputs. Application to thermal–hydraulic computations. Reliab. Eng. Syst. Safety 2012, 107, 122–131. [Google Scholar] [CrossRef]
- Zhao, X.J.; Shang, P.J.; Lin, A.J. Transfer mutual information: A new method for measuring information transfer to the interactions of time series. Physica A 2017, 467, 517–526. [Google Scholar] [CrossRef]
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Nepomuceno, E.G.; Mendes, E.M.A.M. On the analysis of pseudo-orbits of continuous chaotic nonlinear systems simulated using discretization schemes in a digital computer. Chaos Soliton Fract. 2017, 95, 21–32. [Google Scholar] [CrossRef]
- Brunton, S.L.; Brunton, B.W.; Proctor, J.L.; Kaiser, E.; Kutz, J.N. Chaos as an intermittently forced linear system. Nat. Commun. 2017. [Google Scholar] [CrossRef] [PubMed]
- Campbell, K.; McKay, M.D.; Williams, B.J. Sensitivity analysis when model outputs are functions. Reliab. Eng. Syst. Saf. 2006, 91, 1468–1472. [Google Scholar] [CrossRef]
- Lamboni, M.; Monod, H.; Makowski, D. Multivariate sensitivity analysis to measure global contribution of input factors in dynamic models. Reliab. Eng. Syst. Saf. 2011, 96, 450–459. [Google Scholar] [CrossRef]
- Marrel, A.; Iooss, B.; Jullien, M.; Laurent, B.; Volkova, E. Global sensitivity analysis for models with spatially dependent outputs. Environmetrics 2011, 22, 383–397. [Google Scholar] [CrossRef]
- Loonen, R.C.G.M.; Hensen, J.L.M. Dynamic sensitivity analysis for performance-based building design and operation. In Proceedings of the BS2013: 13th Conference of International Building Performance Simulation Association, Chambéry, France, 26– 28 August 2013; pp. 299–305. [Google Scholar]
- Richard, R.; Casas, J.; McCauley, E. Sensitivity analysis of continuous-time models for ecological and evolutionary theories. Theor. Ecol. 2015. [Google Scholar] [CrossRef]
- Chua, L.O.; Komuro, M.; Matsumoto, T. The double scroll family: Parts I and II. IEEE Trans. Circuits Syst. 1986, CAS-33(11), 1072–1118. [Google Scholar] [CrossRef]
- Chua, L.O. The genesis of Chua’s circuit. In Archiv fur Elektronik und Ubertragungstechnik; University of California: Berkeley, CA, USA, 1992; Volume 46, pp. 250–257. [Google Scholar]
- Chua, L.O. A zoo of strange attractor from the canonical Chua’s circuits. In Proceedings of the 35th Midwest Symposium on Circuits and Systems, Washington, DC, USA; 1992; pp. 916–926. [Google Scholar]
- Liao, X.X.; Yu, P.; Xie, S.L.; Fu, Y.L. Study on the global property of the smooth Chua’s system. Int. J. Bifurcat. Chaos Appl. Sci. Eng. 2006, 16, 2815–2841. [Google Scholar] [CrossRef]
- Zhou, G.P.; Huang, J.H.; Liao, X.X.; Cheng, S.J. Stability Analysis and Control of a New Smooth Chua’s System. Abstract Appl. Anal. 2013, 2013. 10 pages. [Google Scholar] [CrossRef]
- Bertacchini, F.; Bilotta, E.; Gabriele, L.; Pantano, P.; Tavernise, A. Toward the Use of Chua’s Circuit in Education, Art and Interdisciplinary Research: Some Implementation and Opportunities. LEONARDO 2013, 46, 456–463. [Google Scholar] [CrossRef]
- Bilotta, E.; Blasi, G.D.; Stranges, F.; Pantano, P. A Gallery of Chua Attractors. Part V. Int. J. Bifurcat. Chaos 2007, 17, 1383–1511. [Google Scholar] [CrossRef]
- Adamo, A.; Tavernise, A. Generation of Ego dynamics. In Proceedings of the VIII International Conference on Generative Art, Milan, Italy, 15–17 December 2007. [Google Scholar]
- Kingni, S.T.; Jafari, S.; Simo, H.; Woafo, P. Three-dimensional chaotic autonomous system with only one stable equilibrium: Analysis, circuit design, parameter estimation, control, synchronization and its fractional-order form. Eur. Phys. J. Plus 2014, 129. [Google Scholar] [CrossRef]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, Y.; Duan, X. Information Transfer Among the Components in Multi-Dimensional Complex Dynamical Systems. Entropy 2018, 20, 774. https://doi.org/10.3390/e20100774
Yin Y, Duan X. Information Transfer Among the Components in Multi-Dimensional Complex Dynamical Systems. Entropy. 2018; 20(10):774. https://doi.org/10.3390/e20100774
Chicago/Turabian StyleYin, Yimin, and Xiaojun Duan. 2018. "Information Transfer Among the Components in Multi-Dimensional Complex Dynamical Systems" Entropy 20, no. 10: 774. https://doi.org/10.3390/e20100774
APA StyleYin, Y., & Duan, X. (2018). Information Transfer Among the Components in Multi-Dimensional Complex Dynamical Systems. Entropy, 20(10), 774. https://doi.org/10.3390/e20100774



