Fractional Form of a Chaotic Map without Fixed Points: Chaos, Entropy and Control
Abstract
1. Introduction
2. The Fractional Map without Fixed Points
3. Chaotic Dynamics and Entropy Analysis
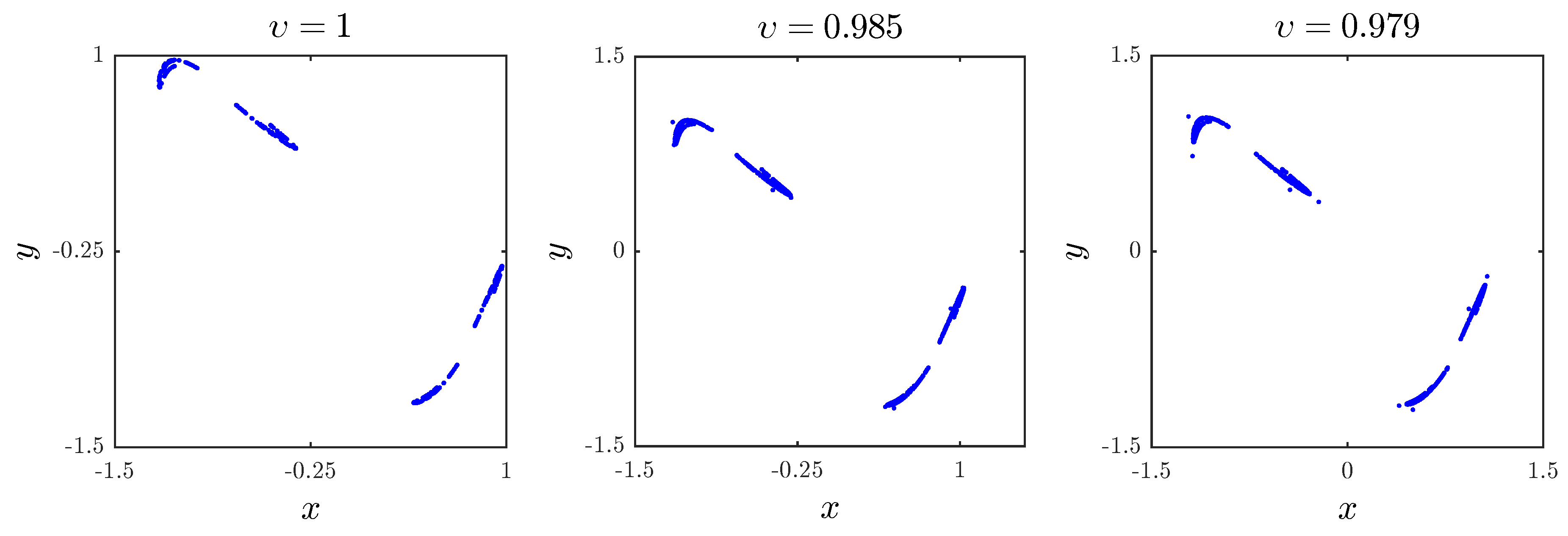
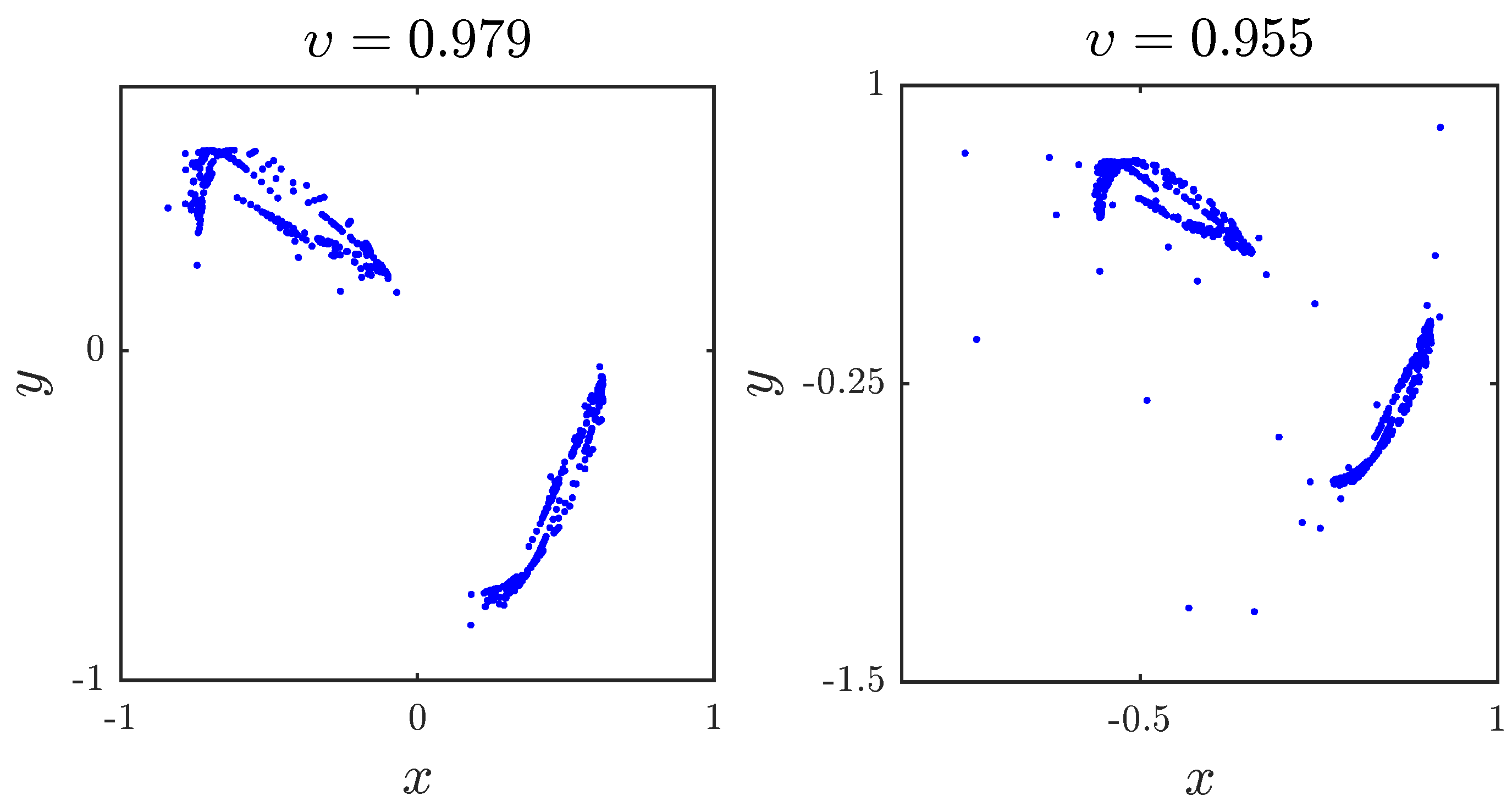
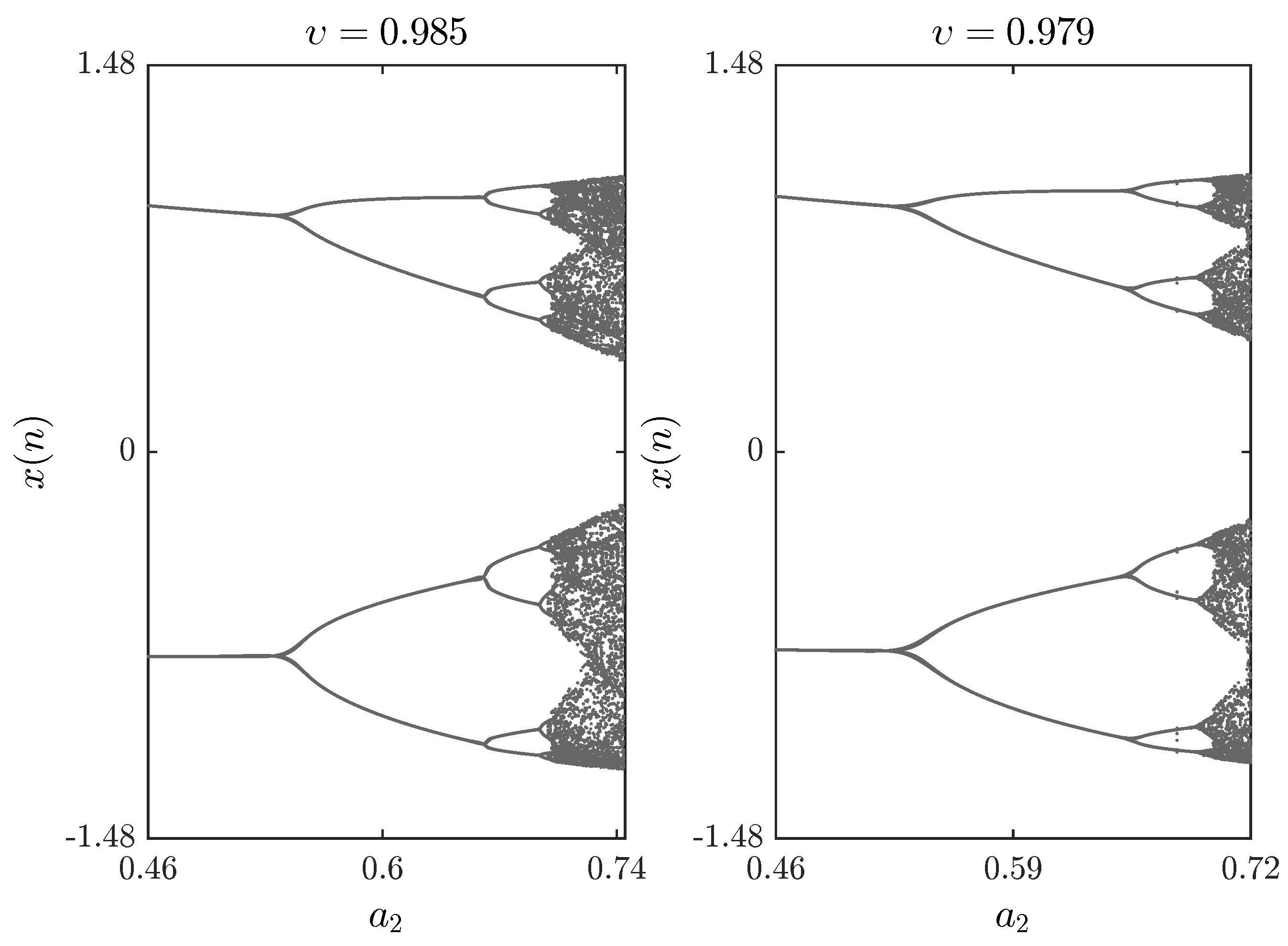
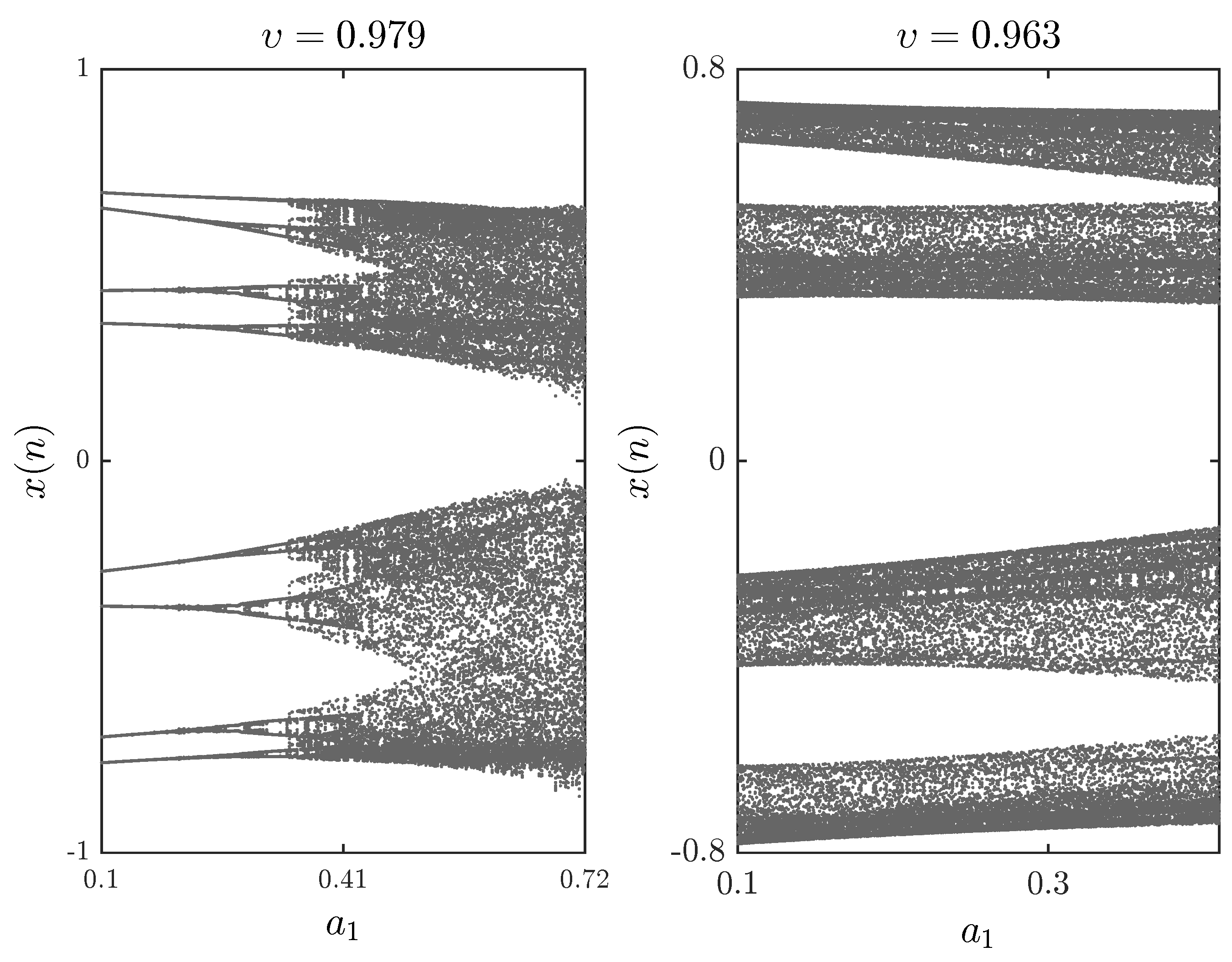
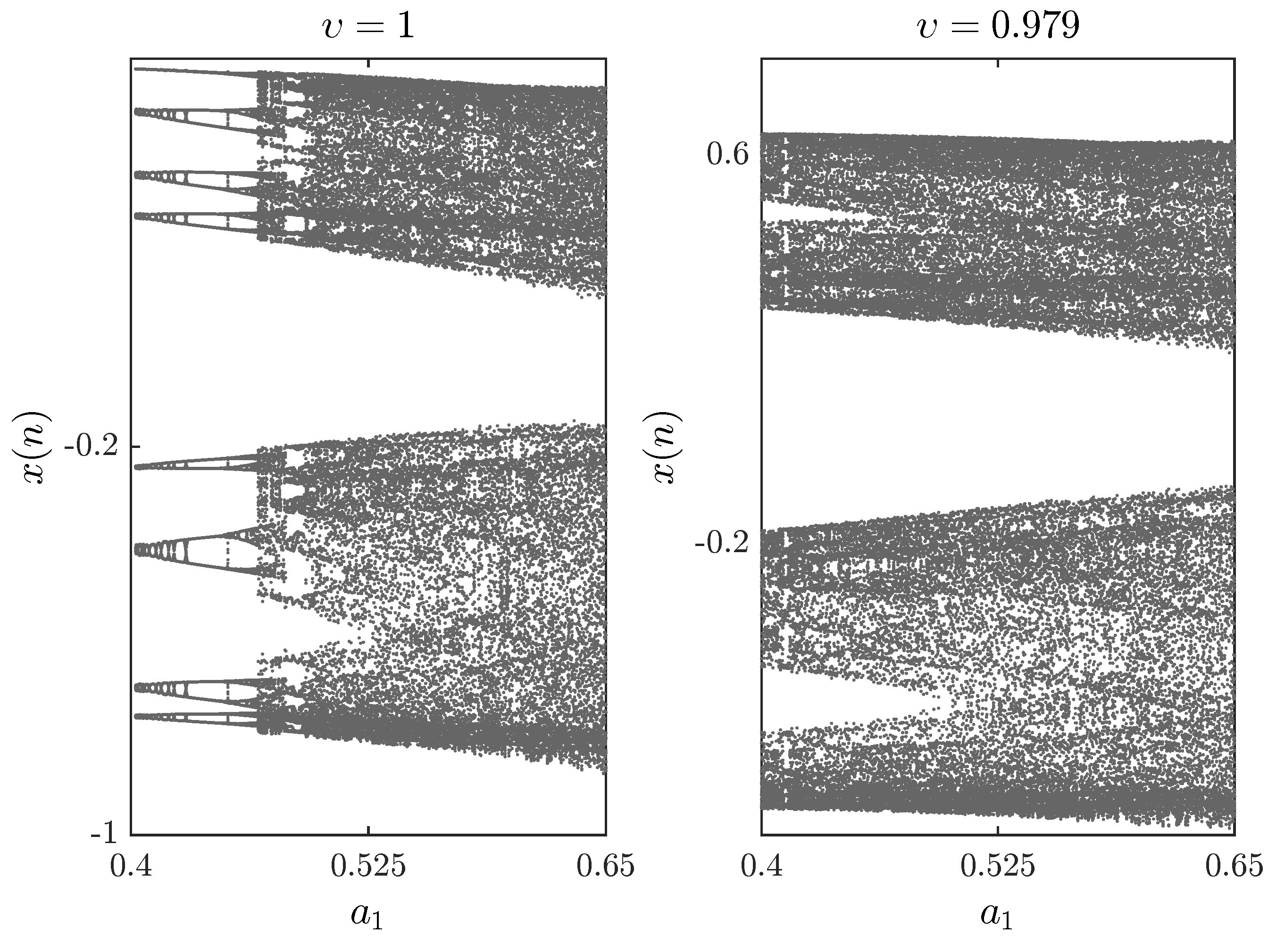
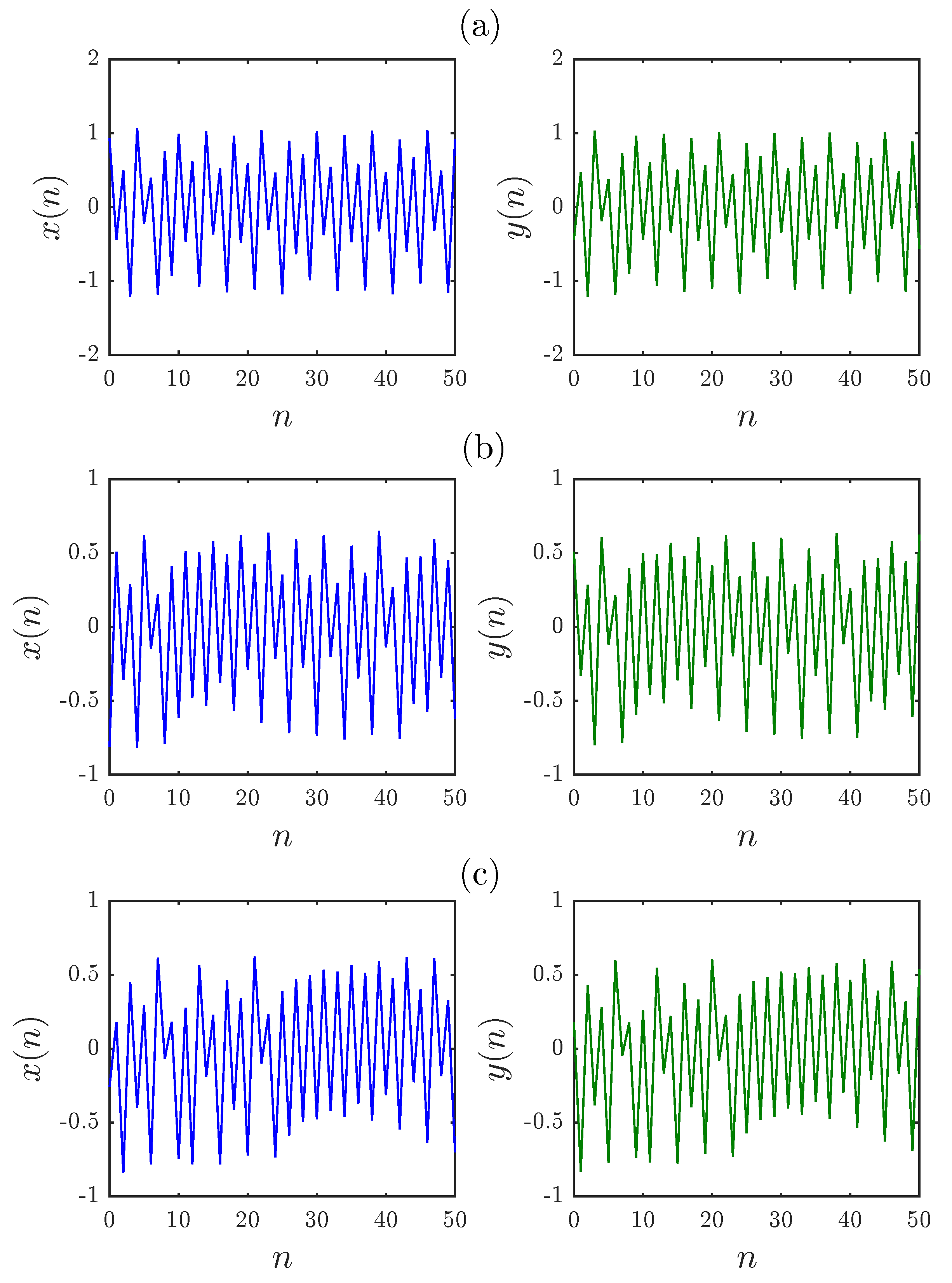
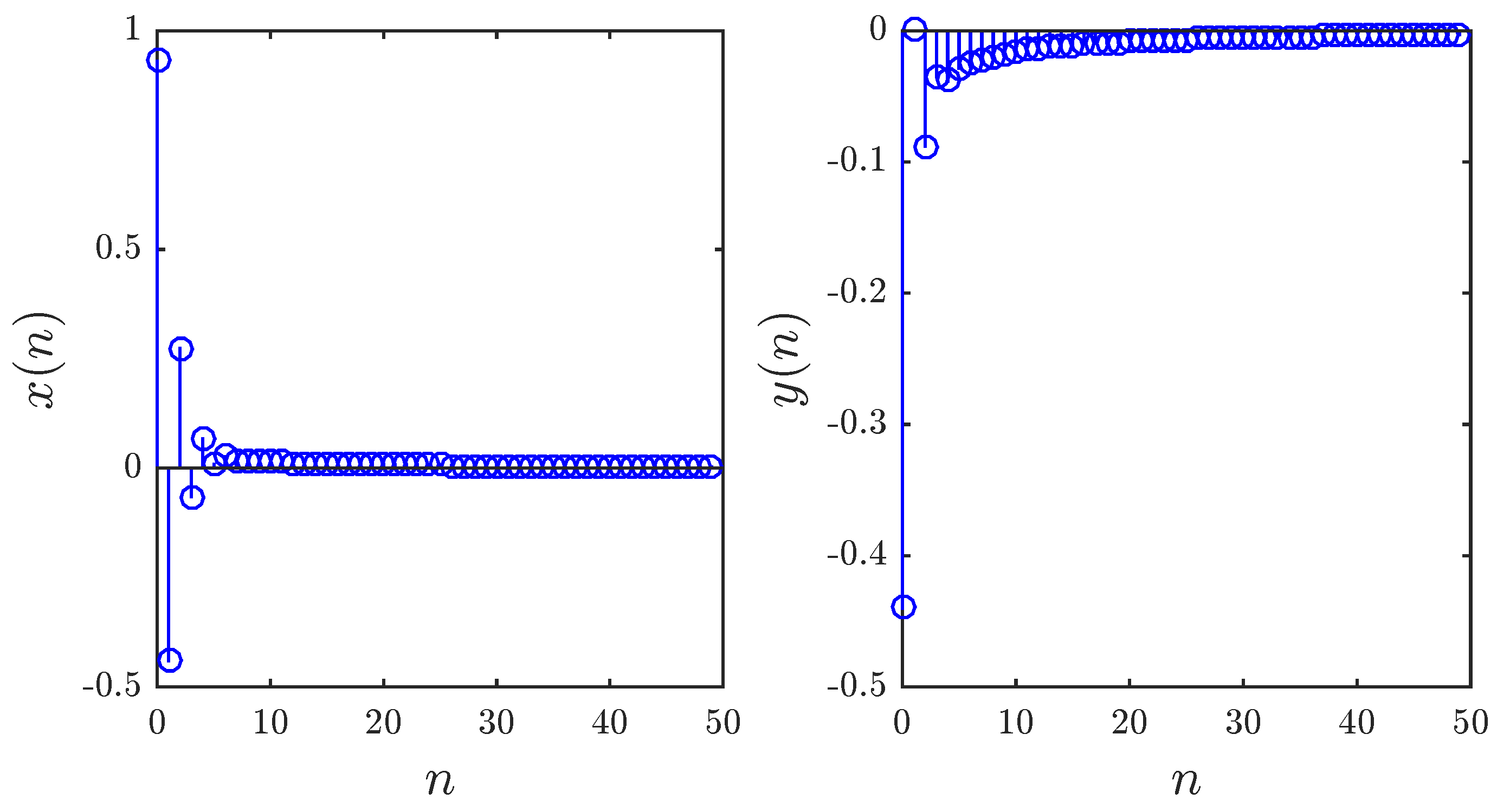
3.1. Chaotic Dynamics
3.2. Entropy Analysis
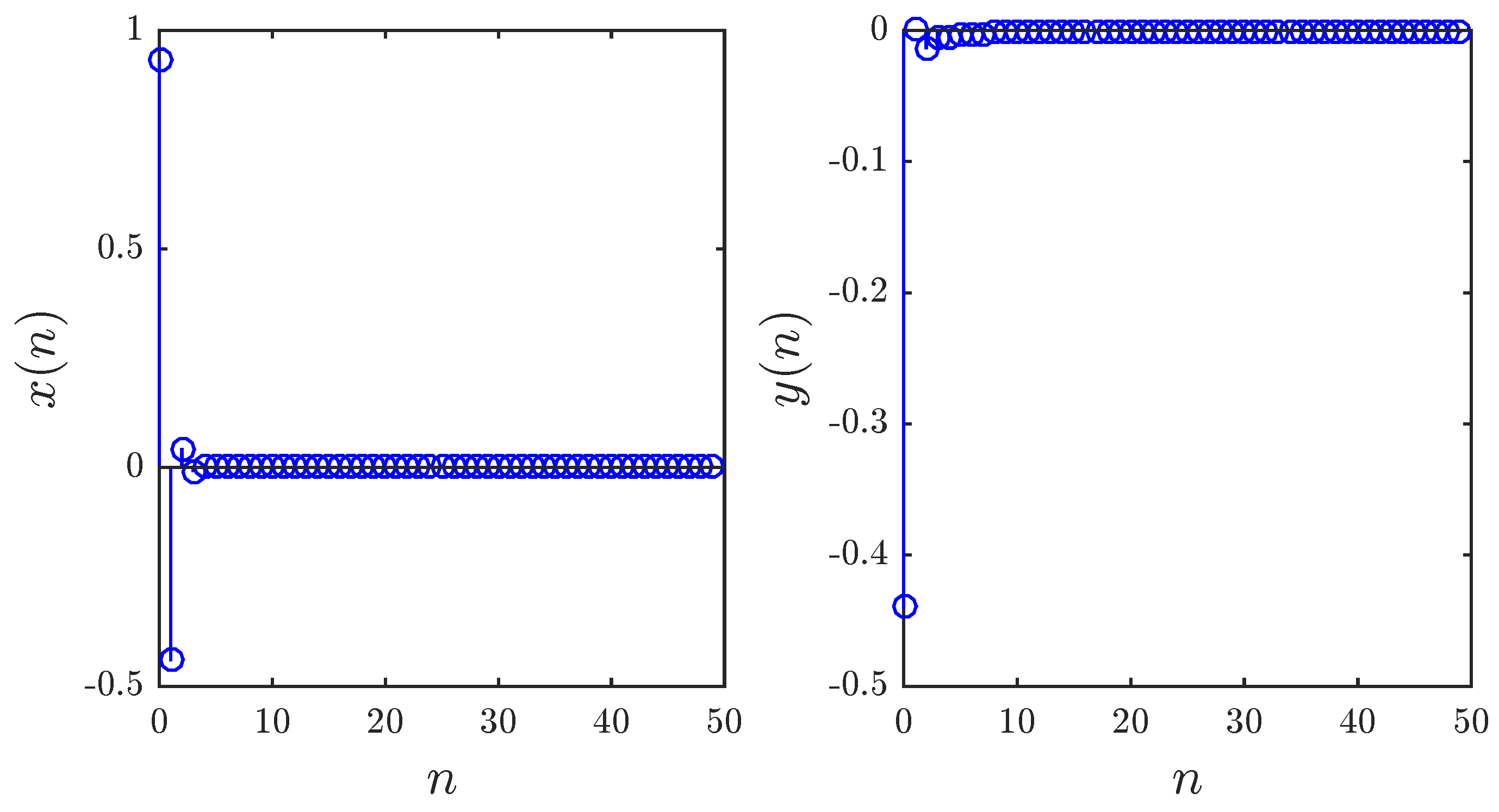
4. Stabilization Control
5. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hénon, M. A two-dimensional mapping with a strange attractor. Commun. Math. Phys. 1976, 50, 69–77. [Google Scholar] [CrossRef]
- Elaydi, S.N. Discrete Chaos: With Applications in Science and Engineering, 2nd ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2007. [Google Scholar]
- Lozi, R. Un atracteur étrange du type attracteur de Hénon. J. Phys. 1978, 39, 9–10. (In French) [Google Scholar]
- Hitzl, D.L.; Zele, F. An exploration of the Hénon quadratic map. Phys. D Nonlinear Phenom. 1985, 14, 305–326. [Google Scholar] [CrossRef]
- Baier, G.G.; Sahle, S. Design of hyperchaotic flows. Phys. Rev. E 1995, 51, 2712–2714. [Google Scholar] [CrossRef]
- Stefanski, K. Modelling chaos and hyperchaos with 3D maps. Chaos Solitons Fractals 1998, 9, 83–93. [Google Scholar] [CrossRef]
- Itoh, M.; Yang, T.; Chua, L.O. Conditions for impulsive synchronization of chaotic and hyperchaotic systems. Int. J. Bifurc. Chaos Appl. Sci. Eng. 2001, 11, 551–558. [Google Scholar] [CrossRef]
- Ouannas, A.; Grassi, G. Inverse full state hybrid projective synchronization for chaotic maps with different dimensions. Chin. Phys. B 2016, 25, 090503. [Google Scholar] [CrossRef]
- Ouannas, A.; Grassi, G.; Karouma, A.; Ziar, T.; Wang, X.; Pham, V.T. New type of chaos synchronization in discrete-time systems: The F-M synchronization. Open Phys. 2018, 16, 174–182. [Google Scholar] [CrossRef]
- Ouannas, A.; Obidat, Z.; Shawagfeh, N. Universal chaos synchronization control laws for general quadratic discrete-time systems. Appl. Theor. Model 2017, 45, 636–641. [Google Scholar] [CrossRef]
- Ouannas, A.; Obidat, Z.; Shawagfeh, N. A new synchronization result for discrete-time chaotic systems. Differ. Equ. Dyn. Syst. 2018, 26, 125. [Google Scholar] [CrossRef]
- Ouannas, A.; Al-Sawalha, M.M. A new approach to synchronize different dimensional chaotic maps using two scaling matrices. Nonlinear Dyn. Syst. Theory 2015, 15, 400–408. [Google Scholar]
- Ouannas, A.; Al-Sawalha, M.M. Synchronization of chaotic dynamical systems in discrete-time. In Advances in Chaos Theory and Intelligent Control: Studies in Fuziness and Soft Computing; Azar, A., Vaydiyanathan, S., Eds.; Springer: New York, NY, USA, 2017. [Google Scholar]
- Jiang, H.; Liu, Y.; Wei, Z.; Zhang, L. Hidden chaotic attractors in a class of two–dimensional maps. Nonlinear Dyn. 2016, 85, 2719–2727. [Google Scholar] [CrossRef]
- Leonov, G.; Kuznetsov, N.; Vagaitsev, V. Localization of hidden Chua’s attractors. Phys. Lett. A 2011, 375, 2230–2233. [Google Scholar] [CrossRef]
- Leonov, G.; Kuznetsov, N.; Vagaitsev, V. Hidden attractor in smooth Chua systems. Phys. D Nonlinear Phenom. 2012, 241, 1482–1486. [Google Scholar] [CrossRef]
- Leonov, G.A.; Kuznetsov, N.V. Hidden attractors in dynamical systems. Int. J. Bifurc. Chaos 2013, 23, 1330002. [Google Scholar] [CrossRef]
- Leonov, G.; Kuznetsov, N.; Kiseleva, M.; Solovyeva, E.; Zaretskiy, A. Hidden oscillations in mathematical model of drilling system actuated by induction motor with a wound rotor. Nonlinear Dyn. 2014, 77, 277–288. [Google Scholar] [CrossRef]
- Danca, M.-F.; Kuznetsov, N. Hidden chaotic sets in a Hopfield neural system. Chaos Solitons Fractals 2017, 103, 144–150. [Google Scholar] [CrossRef]
- Danca, M.-F.; Kuznetsov, N.; Chen, G. Unusual dynamics and hidden attractors of the Rabinovich–Fabrikant system. Nonlinear Dyn. 2017, 88, 791–805. [Google Scholar] [CrossRef]
- Kuznetsov, N.; Leonov, G.; Yuldashev, M.; Yuldashev, R. Hidden attractors in dynamical models of phase-locked loop circuits: Limitations of simulation in MATLAB and SPICE. Commun. Nonlinear Sci. Numer. Simul. 2017, 51, 39–49. [Google Scholar]
- Sharma, P.; Shrimali, M.; Prasad, A.; Kuznetsov, N.; Leonov, G. Control of multistability in hidden attractors. Eur. Phys. J. Spec. Top. 2015, 224, 1485–1491. [Google Scholar] [CrossRef]
- Sharma, P.R.; Shrimali, M.D.; Prasad, A.; Kuznetsov, N.; Leonov, G. Controlling dynamics of hidden attractors. Int. J. Bifurc. Chaos 2015, 25, 1550061. [Google Scholar] [CrossRef]
- Dudkowski, D.; Jafari, S.; Kapitaniak, T.; Kuznetsov, N.V.; Leonov, G.A.; Prasad, A. Hidden attractors in dynamical systems. Phys. Rep. 2016, 637, 1–50. [Google Scholar] [CrossRef]
- Wang, C.; Ding, Q. A new two–Dimensional map with hidden attractors. Entropy 2018, 20, 322. [Google Scholar] [CrossRef]
- Wu, G.C.; Baleanu, D. Discrete fractional logistic map and its chaos. Nonlinear Dyn. 2013, 75, 283–287. [Google Scholar] [CrossRef]
- Hu, T. Discrete Chaos in Fractional Henon Map. Appl. Math. 2014, 5, 2243–2248. [Google Scholar] [CrossRef]
- Wu, G.C.; Baleanu, D. Discrete chaos in fractional delayed logistic maps. Nonlinear Dyn. 2015, 80, 1697–1703. [Google Scholar] [CrossRef]
- Wu, G.; Baleanu, D. Chaos synchronization of the discrete fractional logistic map. Signal Process. 2014, 102, 96–99. [Google Scholar] [CrossRef]
- Wu, G.; Baleanu, D.; Xie, H.; Chen, F. Chaos synchronization of fractional chaotic maps based on the stability condition. Physica A 2016, 460, 374–383. [Google Scholar] [CrossRef]
- Xin, B.; Liu, L.; Hou, G.; Ma, Y. Chaos synchronization of nonlinear fractional discrete dynamical systems via linear control. Entropy 2017, 19, 351. [Google Scholar] [CrossRef]
- Shukla, M.K.; Sharma, B.B. Investigation of chaos in fractional order generalized hyperchaotic Henon map. Int. J. Electron. Commun. 2017, 78, 265–273. [Google Scholar] [CrossRef]
- Goodrich, C.; Peterson, A.C. Discrete Fractional Calculus; Springer: New York, NY, USA, 2015. [Google Scholar]
- Diaz, J.B.; Olser, T.J. Differences of fractional order. Math. Comput. 1974, 28, 185–202. [Google Scholar] [CrossRef]
- Atici, F.M.; Eloe, P.W. Discrete fractional calculus with the nabla operator. Electron. J. Qual. Theory Differ. Equ. 2009, 3, 1–12. [Google Scholar] [CrossRef]
- Abdeljawad, T. On Riemann and Caputo fractional differences. Comput. Math. Appl. 2011, 62, 1602–1611. [Google Scholar] [CrossRef]
- Cermak, J.; Gyori, I.; Nechvatal, L. On explicit stability conditions for a linear fractional difference system. Fract. Calc. Appl. Anal. 2015, 18, 651–672. [Google Scholar] [CrossRef]
- Baleanu, D.; Wu, G.; Bai, Y.; Chen, F. Stability analysis of Caputo–like discrete fractional systems. Commun. Nonlinear Sci. Numer. Simul. 2017, 48, 520–530. [Google Scholar] [CrossRef]
- Baleanu, D.; Jajarmi, A.; Asad, J.; Blaszczyk, T. The motion of a bead sliding on a wire in fractional sense. Acta Phys. Pol. A 2017, 131, 1561–1564. [Google Scholar] [CrossRef]
- Jajarmi, A.; Hajipour, M.; Mohammadzadeh, E.; Baleanu, D. A new approach for the nonlinear fractional optimal control problems with external persistent disturbances. J. Frankl. Inst. 2018, 335, 3938–3967. [Google Scholar] [CrossRef]
- Anastassiou, G.A. Principles of delta fractional calculus on time scales and inequalities. Math. Comput. Model. 2010, 52, 556–566. [Google Scholar] [CrossRef]
- Eckmann, J.P.; Ruelle, D. Ergodic theory of chaos and strange attractors. Rev. Mod. Phys. 2018, 57, 617. [Google Scholar] [CrossRef]
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef] [PubMed]
- Pincus, S. Approximate entropy (ApEn) as a complexity measure. Chaos Interdiscip. J. Nonlinear Sci. 1995, 5, 110–117. [Google Scholar] [CrossRef] [PubMed]
- Xu, G.H.; Shekofteh, Y.; Akgul, A.; Li, C.B.; Panahi, S. A new chaotic system with a self-excited attractor: Entropy measurement, signal encryption, and parameter estimation. Entropy 2018, 20, 86. [Google Scholar] [CrossRef]


© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ouannas, A.; Wang, X.; Khennaoui, A.-A.; Bendoukha, S.; Pham, V.-T.; Alsaadi, F.E. Fractional Form of a Chaotic Map without Fixed Points: Chaos, Entropy and Control. Entropy 2018, 20, 720. https://doi.org/10.3390/e20100720
Ouannas A, Wang X, Khennaoui A-A, Bendoukha S, Pham V-T, Alsaadi FE. Fractional Form of a Chaotic Map without Fixed Points: Chaos, Entropy and Control. Entropy. 2018; 20(10):720. https://doi.org/10.3390/e20100720
Chicago/Turabian StyleOuannas, Adel, Xiong Wang, Amina-Aicha Khennaoui, Samir Bendoukha, Viet-Thanh Pham, and Fawaz E. Alsaadi. 2018. "Fractional Form of a Chaotic Map without Fixed Points: Chaos, Entropy and Control" Entropy 20, no. 10: 720. https://doi.org/10.3390/e20100720
APA StyleOuannas, A., Wang, X., Khennaoui, A.-A., Bendoukha, S., Pham, V.-T., & Alsaadi, F. E. (2018). Fractional Form of a Chaotic Map without Fixed Points: Chaos, Entropy and Control. Entropy, 20(10), 720. https://doi.org/10.3390/e20100720





