Impact of Microgroove Shape on Flat Miniature Heat Pipe Efficiency
Abstract
:1. Introduction
2. Heat Pipe Analytical Model
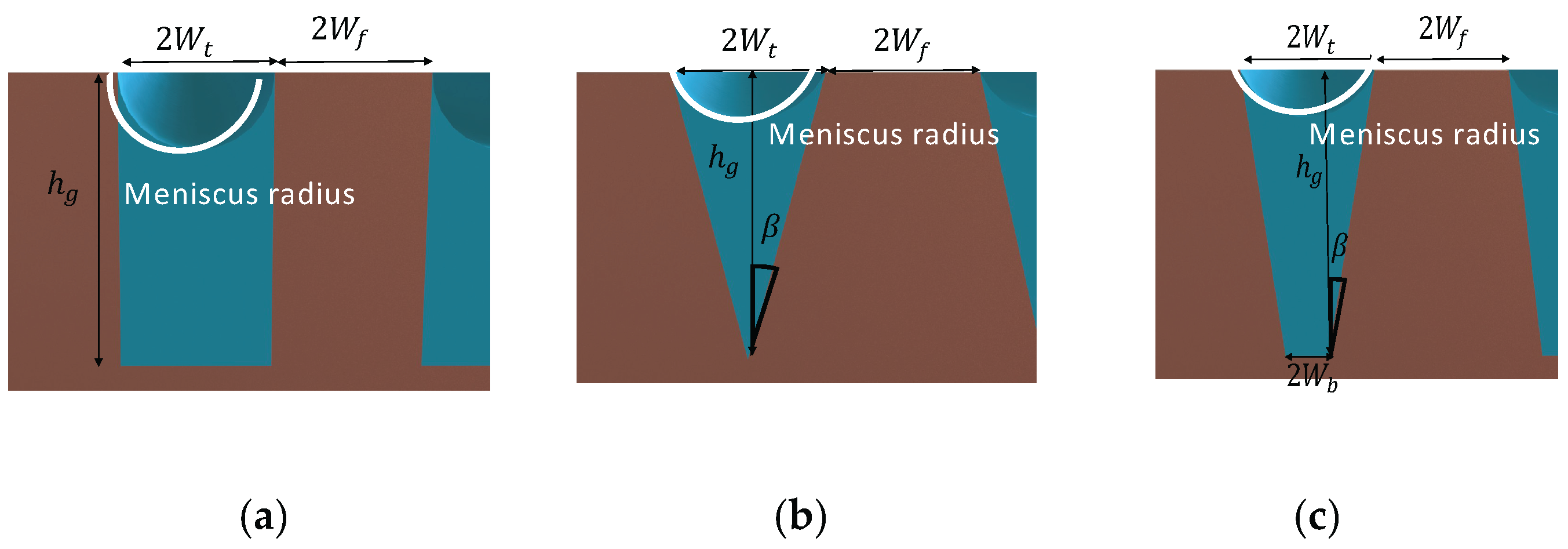
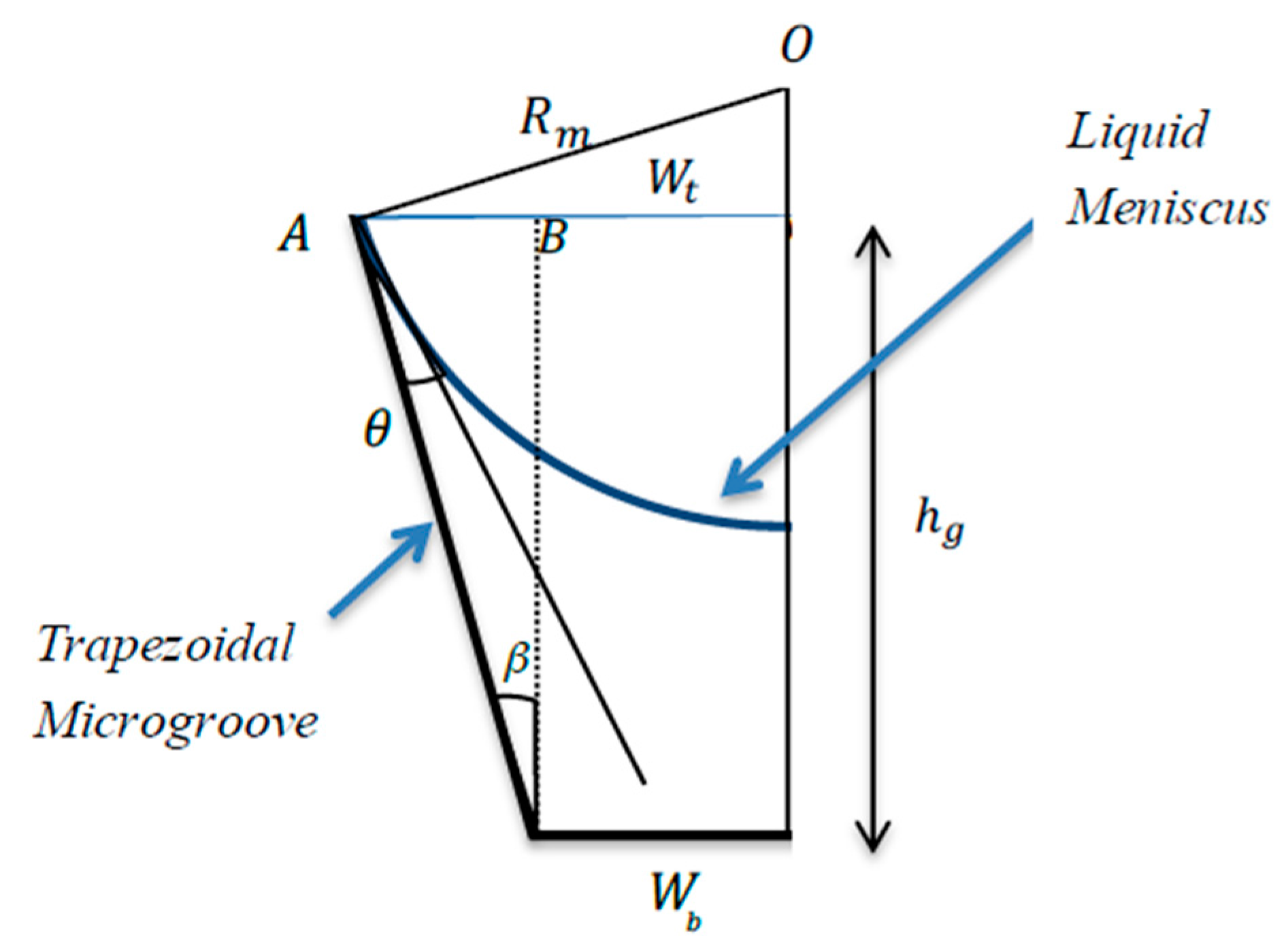
2.1. Meniscus Radius Expressions
2.2. Capillary Limit
2.2.1. Liquid Flow Pressure Loss
2.2.2. Vapor Flow Pressure Loss
2.3. Heat Pipe Effective Length and Maximum Heat
2.4. Solution Procedures
- Step 1: The input parameters are imposed, and the working fluid thermophysical properties are calculated. The saturation temperature is deduced from the pressure and the heat pipe size and orientation;
- Step 2: An initial value of the heat flux is given;
- Step 3: Selection of the microgroove number;
- Step 4: Calculation of the maximum heat flux;
- Step 5: Calculation of the heat transport limits;
- Step 6: Calculation of the hydraulic limits;
- Step 7: Calculation of the fluid velocities;
- Step 8: Calculation of the pressure differences;
- Step 9: Calculation of the boiling limitation;
- Step 10: Check the convergence criterion calculations. If this criterion is not satisfied, a new value will be estimated by the secant method, taking into account the difference obtained on the estimation of the new value of the heat flux and the value imposed at Step 2;
- Step 11: The calculation loop is repeated until the error is less than the imposed criterion.
3. Results
3.1. Determination of the Heat Pipe Design
3.1.1. Flat Heat Pipe with Rectangular Microgrooves
3.1.2. Flat Heat Pipe with Trapezoidal Microgrooves
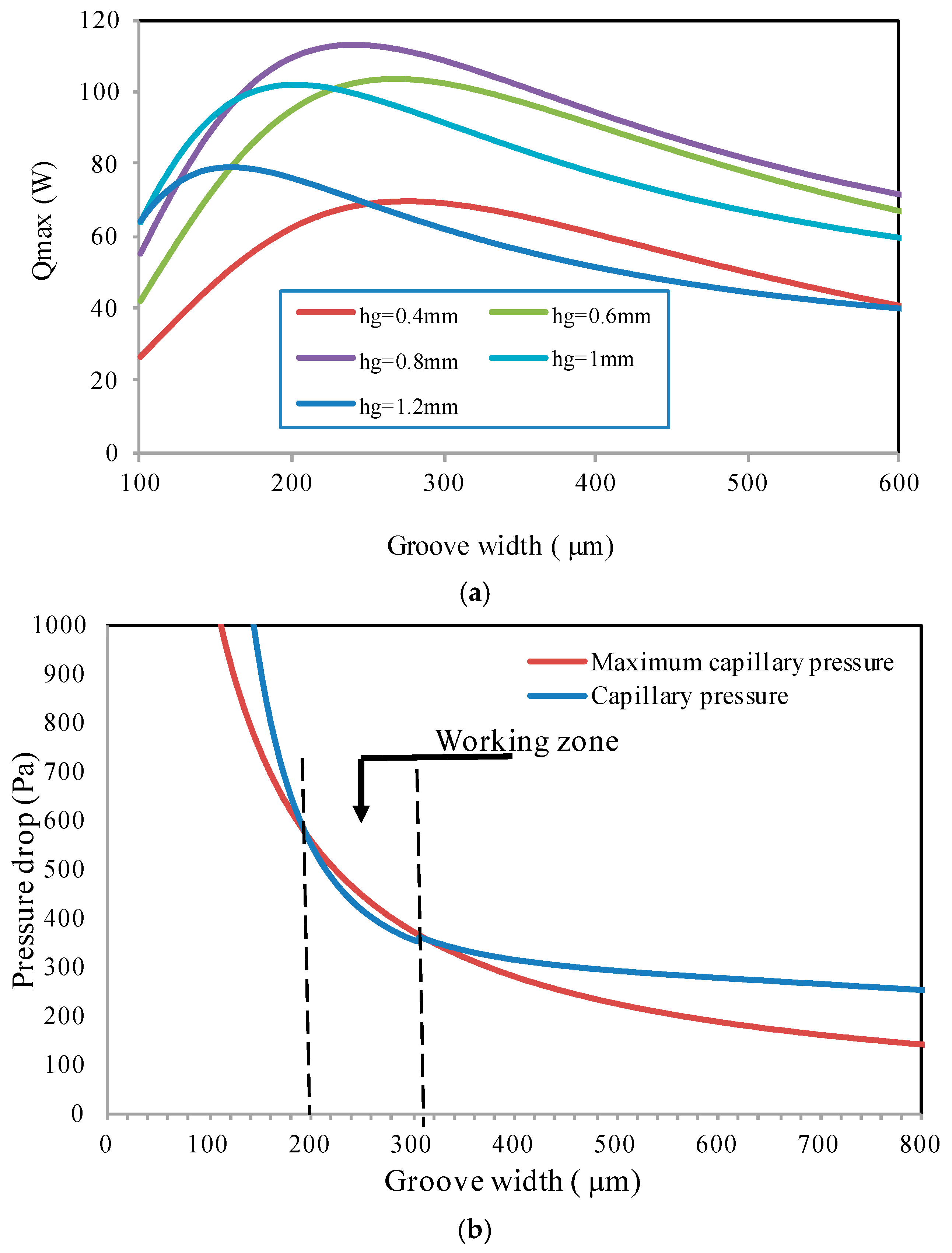
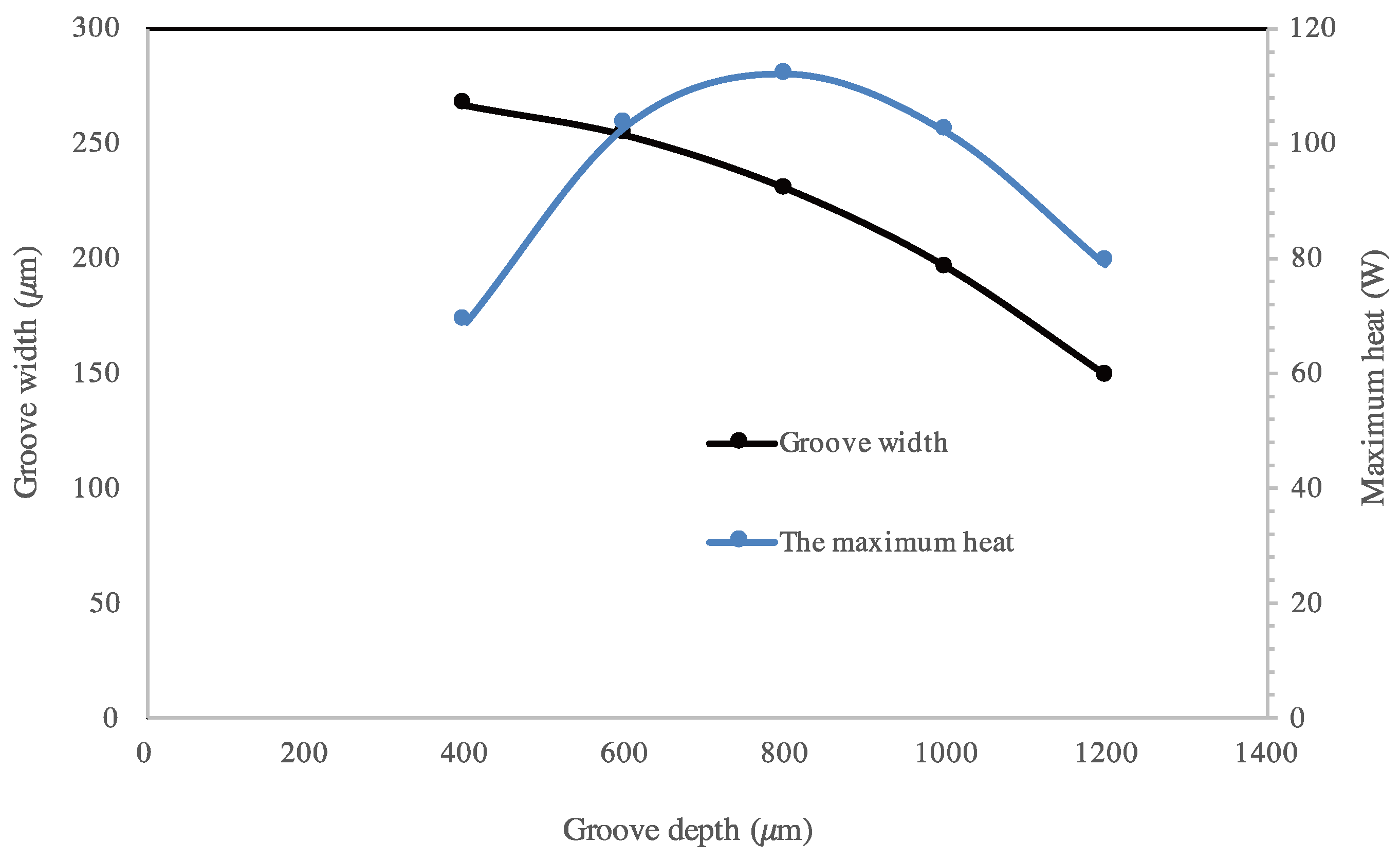
3.1.3. Influence of the Microgroove Shape on the Maximum Heat Flux
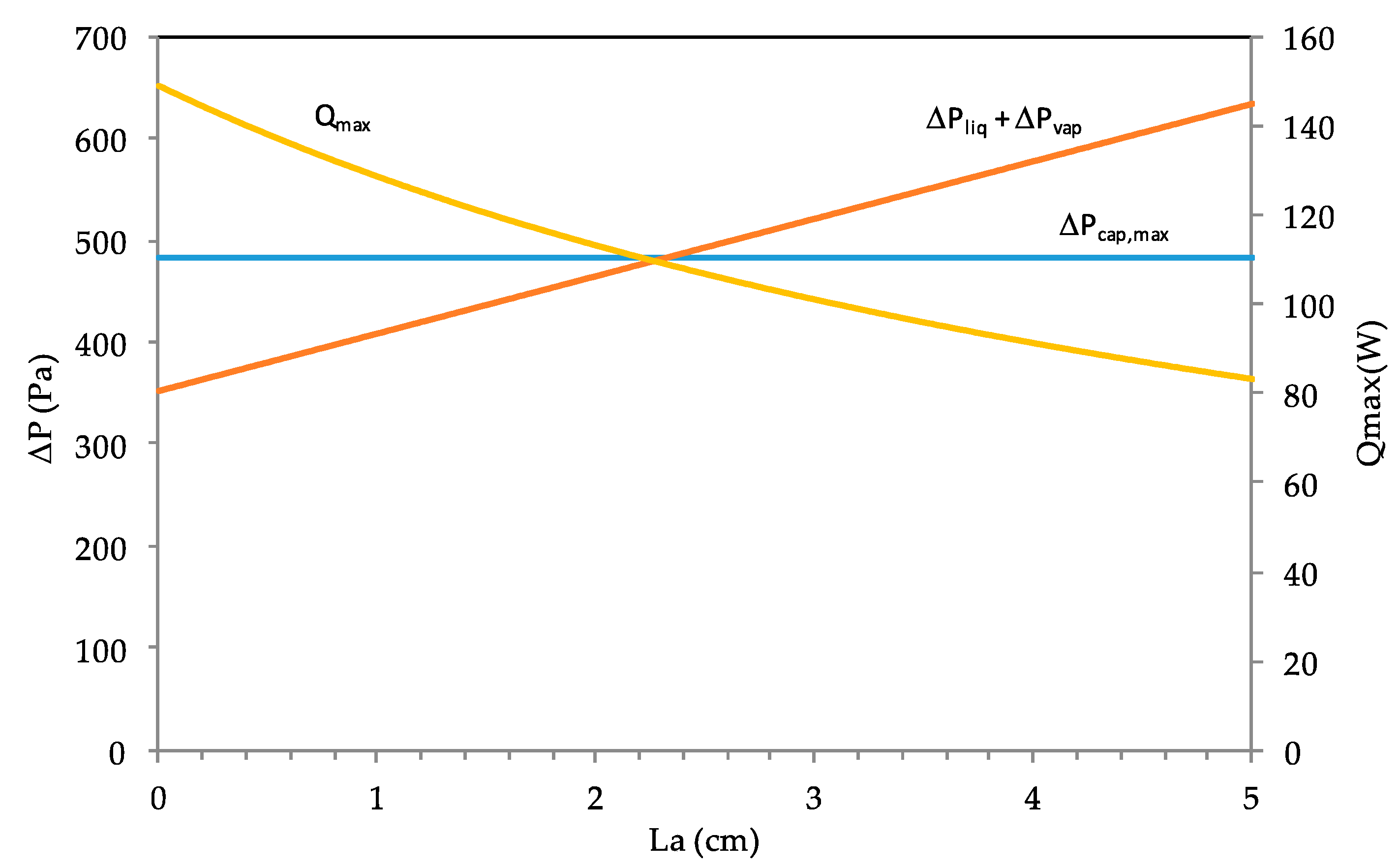
3.1.4. Influence of the Heat Pipe Length
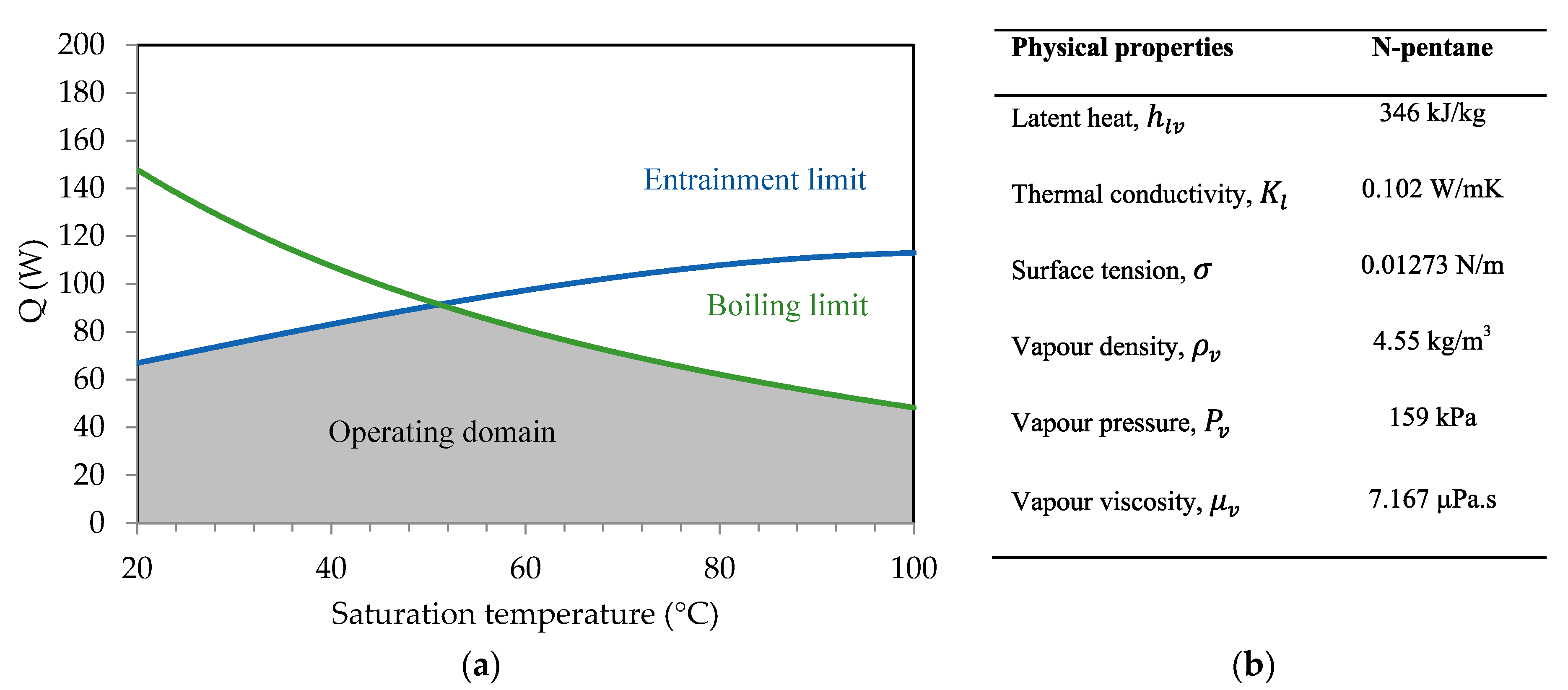
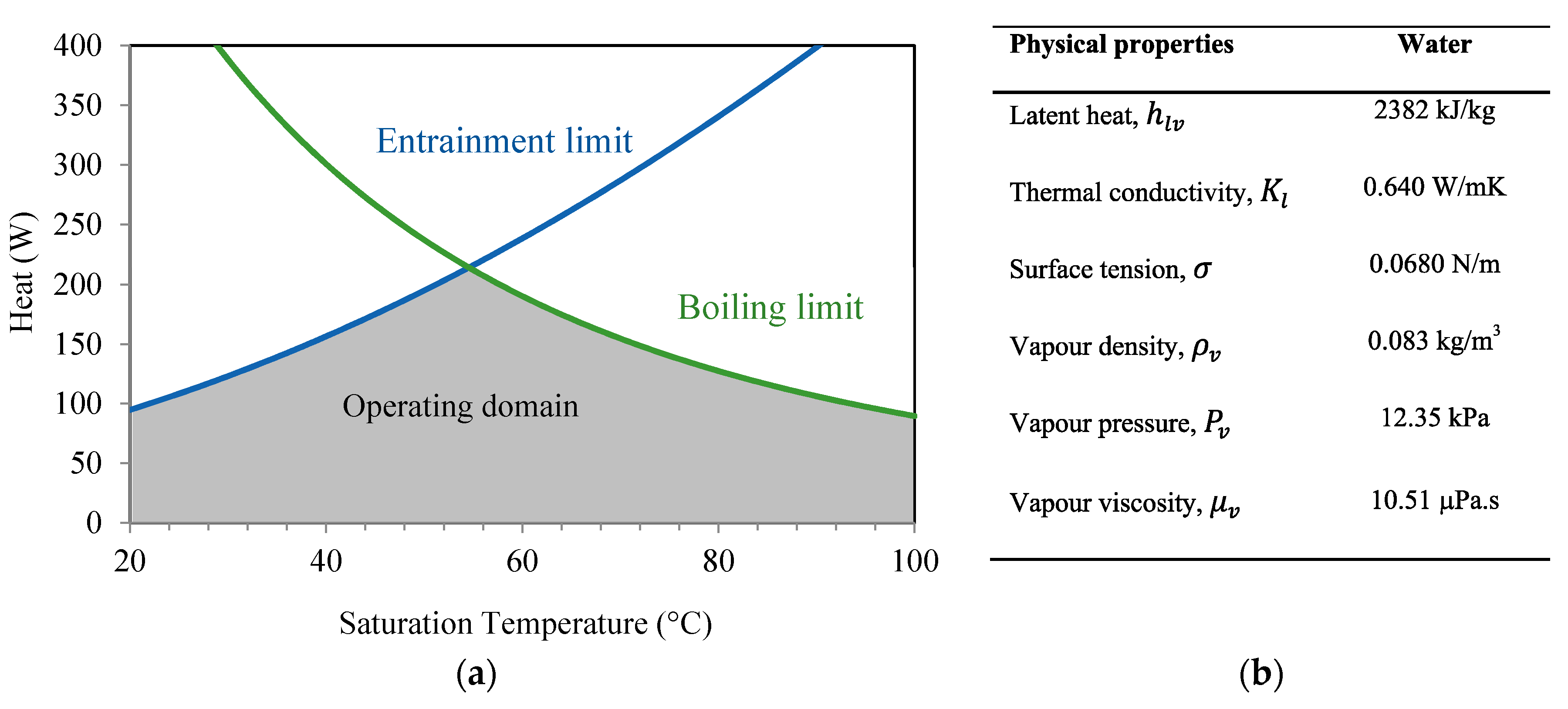
3.1.5. Heat Pipe Heat Transport Limitations
3.2. Experimental Tests on the Optimal Flat Heat Pipe
4. Conclusions
- (a)
- The effect of microgroove width and depth for a flat heat pipe was investigated. It can be seen that increasing microgroove width increases the maximum heat for low values of width and decreases it for high width values. An optimal width and depth were defined for the highest maximum heat.
- (b)
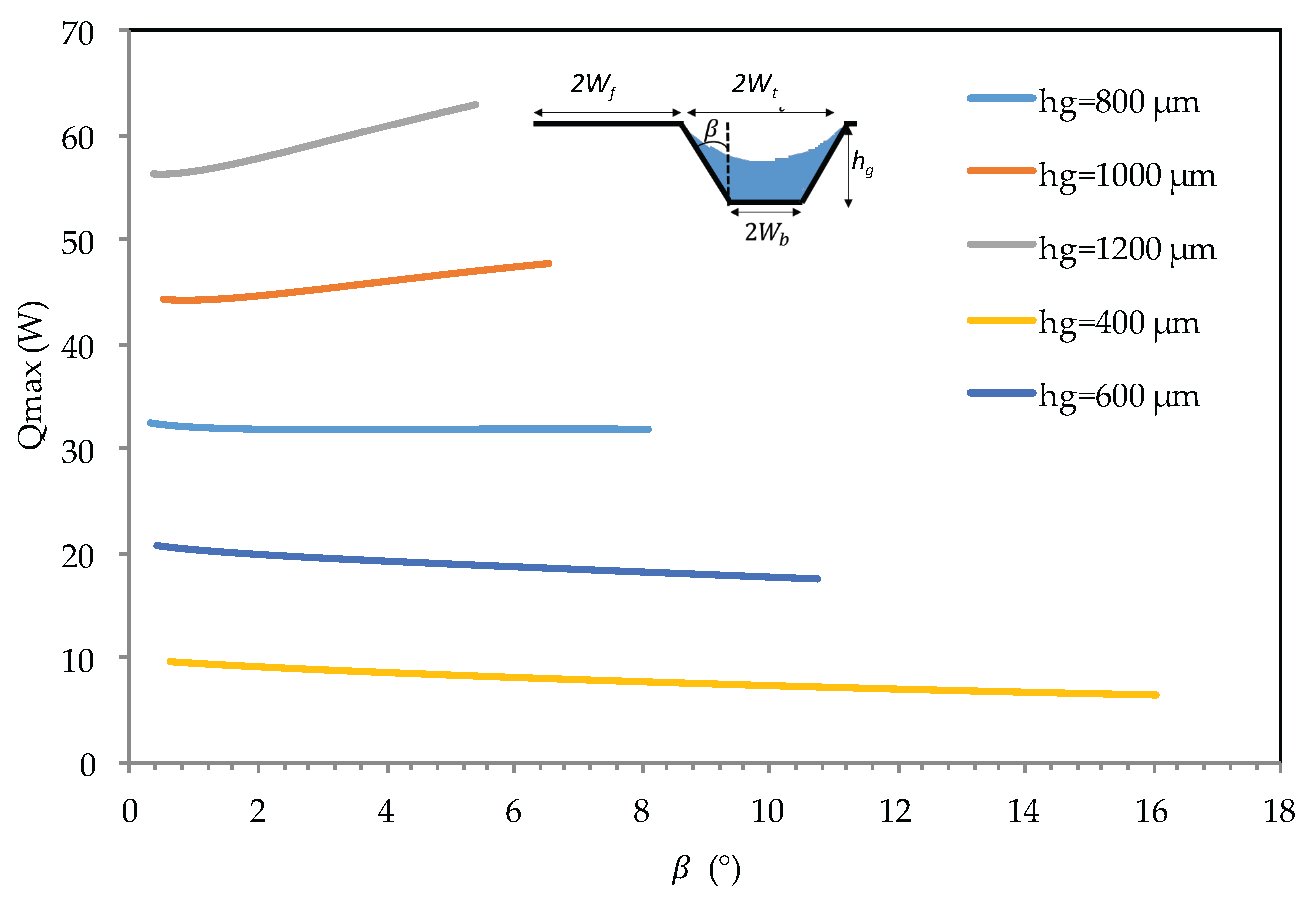
- For the flat heat pipe with trapezoidal microgrooves, the impact of the inclination angle () of the groove side slope was analyzed for different heat pipe depths. The maximum heat is influenced by for low values of the microgroove depth. For high values of hg (>800 ), the angle has no effect on the maximum heat flux.
- (c)
- The influence of microgroove shape on the heat pipe efficiency is highlighted by studying different architecture of grooves respecting the same cross-sectional area or the same hydraulic diameter. For the same microgroove cross sections, the lowest heat transfer was obtained by microgrooves with a triangular cross section. The highest maximum heat was obtained for the rectangular microgroove cross section. For the same hydraulic diameter, the best configuration is the trapezoidal cross section, for which the highest maximum heat was obtained.
- (d)
- Heat transport limitations were studied versus operating temperature, taking into account the hydrodynamic and thermal processes inside the heat pipe. Respecting the capillary limit, entrainment and boiling limits delimited the operating domain. The maximum heat is approximately 2 times higher for water than for n-pentane due to the water latent heat, which is 7 times higher than that of n-pentane.
- (e)
- Experiments were conducted using a flat heat pipe respecting the optimal geometrical parameters defined by the analytical model. DI water was used as the working fluid. Measurements of thermal resistances and temperatures were in accordance with the performance predicted by the model.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Odaymet, A.; Gualous, H.L. Experimental study of slug flow for condensation in a single square microchannel. Exp. Therm. Fluid Sci. 2012, 38, 1–13. [Google Scholar] [CrossRef]
- El Mghari, H.; Louahlia-Gualous, H. Experimental and numerical investigations of local heat transfer in a single square microchannel under variable heat flux. Int. Commun. Heat Mass Transf. 2016, 71, 197–207. [Google Scholar] [CrossRef]
- Falcucci, G.; Ubertini, S.; Chiappini, D.; Succi, S. Modern lattice Boltzmann methods for multiphase microflows. IMA J. Appl. Math. 2011, 76, 712–725. [Google Scholar] [CrossRef]
- Falcucci, G.; la Rocca, M.; Ansumali, S.; Succi, S. Three-Dimensional Lattice Pseudo-Potentials for Multiphase Flow Simulations at High Density Ratios. J. Stat. Phys. 2015, 161, 1404–1419. [Google Scholar]
- Gualous, H.L.; le Masson, S.; Chehade, A. An experimental study of evaporation and condensation heat transfer coefficients for looped thermosyphon. Appl. Therm. Eng. 2017, 110, 931–940. [Google Scholar] [CrossRef]
- Suman, B.; Kumar, P. An analytical model for fluid flow and heat transfer in a micro-heat pipe of polygonal shape. Int. J. Heat Mass Transf. 2005, 48, 4498–4509. [Google Scholar] [CrossRef]
- Chi, S.W. Heat Pipe, Theory and Practice; McGraw-Hill: New York, NY, USA, 1976. [Google Scholar]
- Cao, Y.; Gao, M.; Beam, J.E.; Donovan, B. Experiments and anaylyses of flat miniature Heat Pipes. J. Thermophys. Heat Transf. 1997, 11, 158–164. [Google Scholar] [CrossRef]
- Cotter, T. Principles and prospects of micro-heat pipes. In Proceedings of the 5th International Heat Pipe Conference, Tsubaka, Japan, 14–18 May 1984. [Google Scholar]
- Ma, H.B.; Peterson, G.; Lu, X. The influence of vapor-liquide interactions on the liquid pressure drop in triangular microgrooves. Int. J. Heat Mass Transf. 1994, 37, 2211–2219. [Google Scholar] [CrossRef]
- Jiao, A.; Ma, H.; Critser, J. Evaporation heat transfer characteristics of a grooved heat pipe with micro-trapezoidal grooves. Int. J. Heat Mass Transf. 2007, 50, 2905–2911. [Google Scholar] [CrossRef]
- Faghri, A.; Hopkins, R.; Khrustalev, D. Flat Miniature Heat Pipes with Micro Capillary Grooves. J. Heat Transf. 1999, 121, 102–109. [Google Scholar]
- Khrustalev, D.; Faghri, A. Thermal Characteristics of Conventional and Flat Miniature Axially Grooved Heat Pipes. J. Heat Transf. 1995, 117, 1048–1054. [Google Scholar] [CrossRef]
- Suh, J.-S.; Greif, R.; Grigoropoulos, C. Friction in micro-channel flows of a liquid and vapor in trapezoidal and sinusoidal grooves. Int. J. Heat Mass Transf. 2001, 44, 3103–3109. [Google Scholar] [CrossRef]
- Ayyaswamy, P.S.; Catton, I.; Edwards, D.K. Capillary flow in triangula grooves. J. Appl. Mech. 1974, 41, 332–336. [Google Scholar] [CrossRef]
- Faghri, A.; Thomas, S. Performance characteristics of a concentric annular heat pipe: Part I—Experimental prediction and analysis of the capillary limit. J. Heat Transf. 1989, 11, 844–850. [Google Scholar] [CrossRef]
- Busse, C.A. Theory of ultimate heat transfer limit of cylindrical heat pipes. Int. J. Heat. 1973, 16, 169–186. [Google Scholar] [CrossRef]
- Reay, D.A.; Kew, P. Heat Pipes: Theory Design and Applications; Butterworth-Heinemann: Oxford, UK, 2006. [Google Scholar]




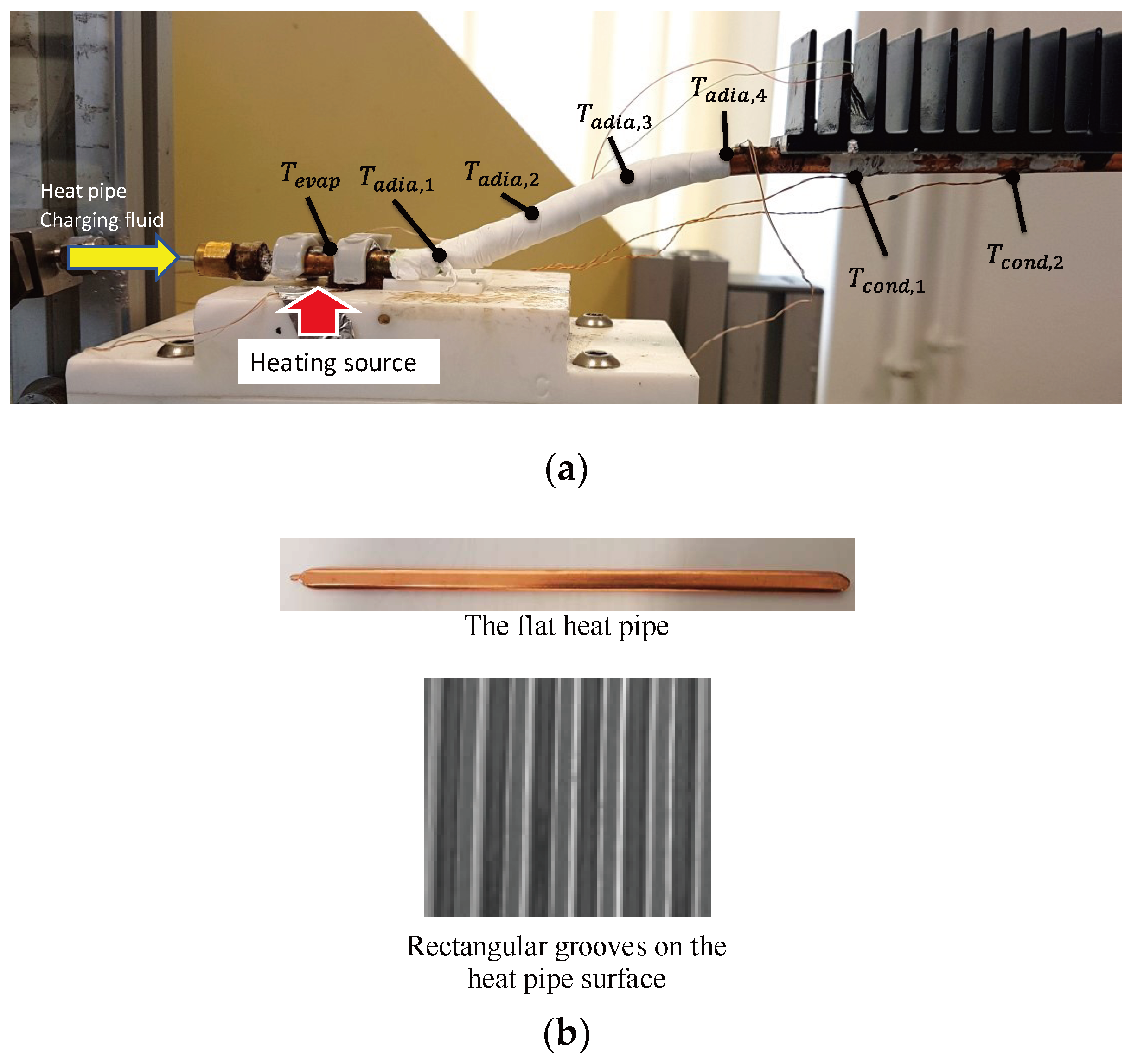
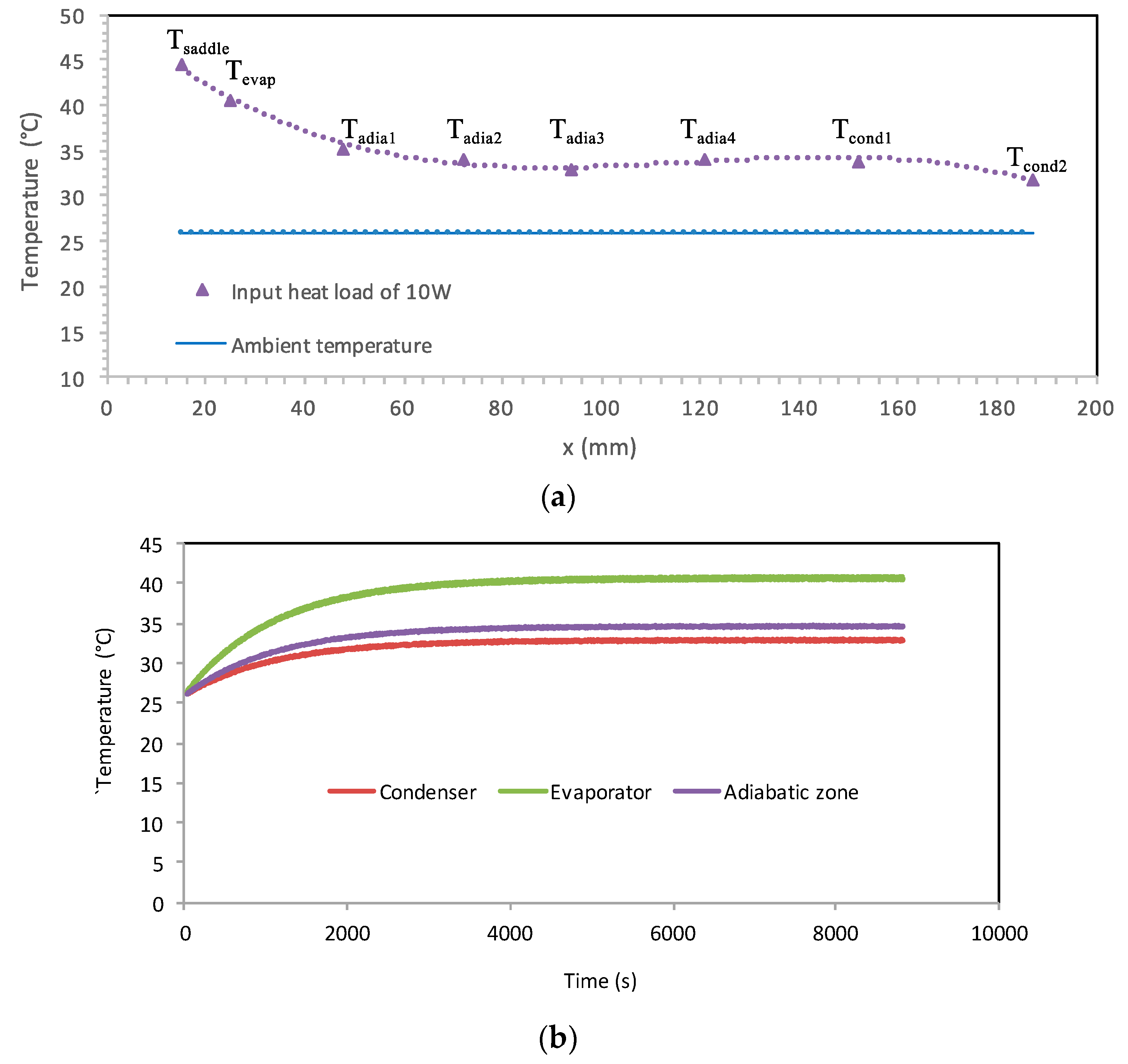
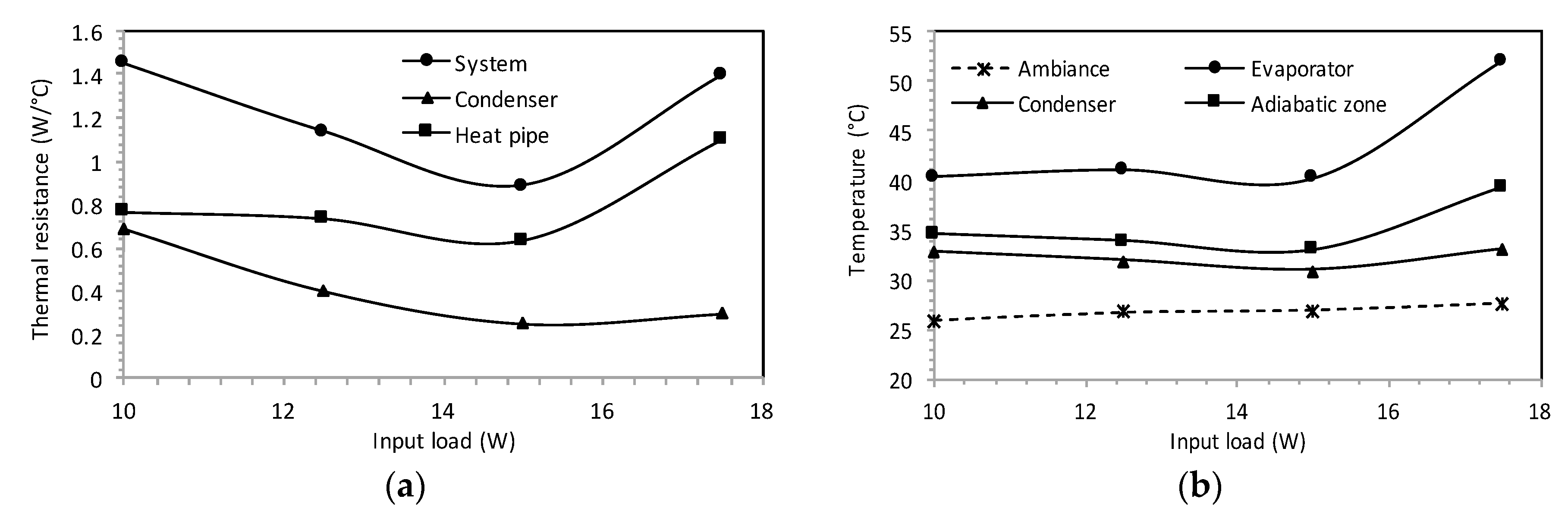
| Parameters | Values |
|---|---|
| Hydraulic vapor diameter, | |
| Effective length, | |
| Capillary radius, | |
| Nucleation radius, [18] | |
| Vapor flow cross section, | 2 |
| Width of vapor cross section, | m |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ternet, F.; Louahlia-Gualous, H.; Le Masson, S. Impact of Microgroove Shape on Flat Miniature Heat Pipe Efficiency. Entropy 2018, 20, 44. https://doi.org/10.3390/e20010044
Ternet F, Louahlia-Gualous H, Le Masson S. Impact of Microgroove Shape on Flat Miniature Heat Pipe Efficiency. Entropy. 2018; 20(1):44. https://doi.org/10.3390/e20010044
Chicago/Turabian StyleTernet, François, Hasna Louahlia-Gualous, and Stéphane Le Masson. 2018. "Impact of Microgroove Shape on Flat Miniature Heat Pipe Efficiency" Entropy 20, no. 1: 44. https://doi.org/10.3390/e20010044
APA StyleTernet, F., Louahlia-Gualous, H., & Le Masson, S. (2018). Impact of Microgroove Shape on Flat Miniature Heat Pipe Efficiency. Entropy, 20(1), 44. https://doi.org/10.3390/e20010044




