The Poincaré Half-Plane for Informationally-Complete POVMs
Abstract
:1. Introduction
Nulle parole ne trouve une branche où se poser (No words find a branch where to land [1]).
Pasch’s axiom (of plane geometry) was used by Hilbert to complete Euclid’s axioms. It is related to Pasch’s configuration of points and lines (in projective geometry). Incidence geometry, born at the time of Pappus of Alexandria, developed with Desargues (1591–1661), Jacob Steiner (1796–1863), Thomas Kirkman (1806–1895), Gino Fano (1871–1952), David Hilbert (1862–1943) and, more recently, with Jacques Tits (1930–) and Francis Buekenhout (1937–).I am also late in thanking you for sending your essay on non-Euclidean geometry from last year… I also agree with most of what you say in the last two pages of your essay. The content of the axioms comes from observations (intuition as an internal activity is based on remembering what has been observed); the concepts used in the axioms, however, are inexact, and thus so are the axioms themselves. These latter can, however, only be used purely logically if they are presented as being exact. By further working on the axioms and seeking geometric propositions, we commonly make use of figures, either by drawing them or by ‘imagining’ them… The consideration must be possible even without the figures, in other words: that which is derived from the figures must already be contained in the axioms, for otherwise the axioms are not complete.
2. Prolegomenon about and Its Relation to IC-POVMs
2.1. The Modular Group
2.2. Minimal Informationally-Complete POVMs and the Pauli Group
2.3. The Single Qubit SIC-POVM
2.4. The Kochen–Specker Theorem
3. Permutation Gates from , Fiducial States and Informationally-Complete Measurements
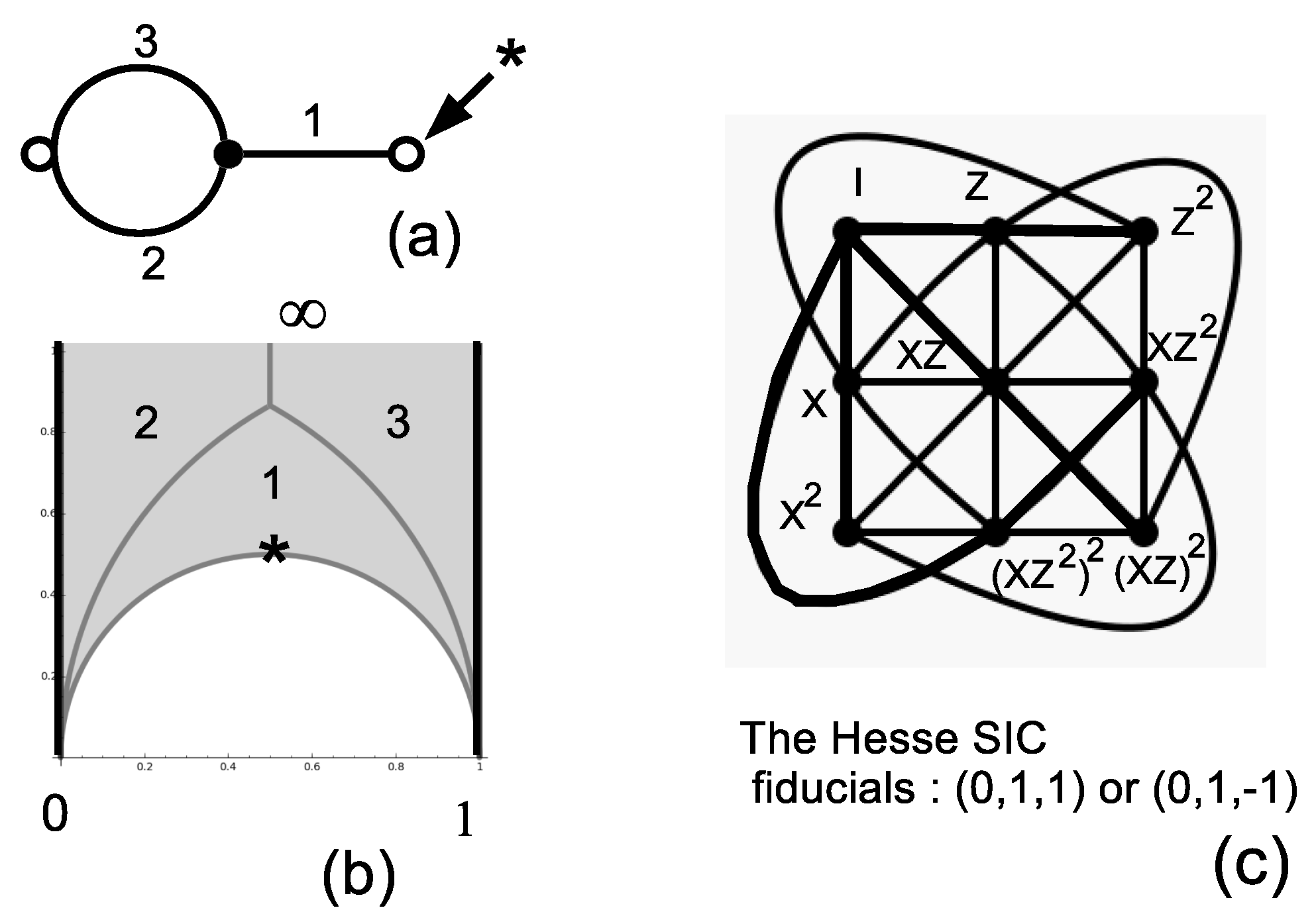
3.1. The Three-Dimensional Hesse SIC
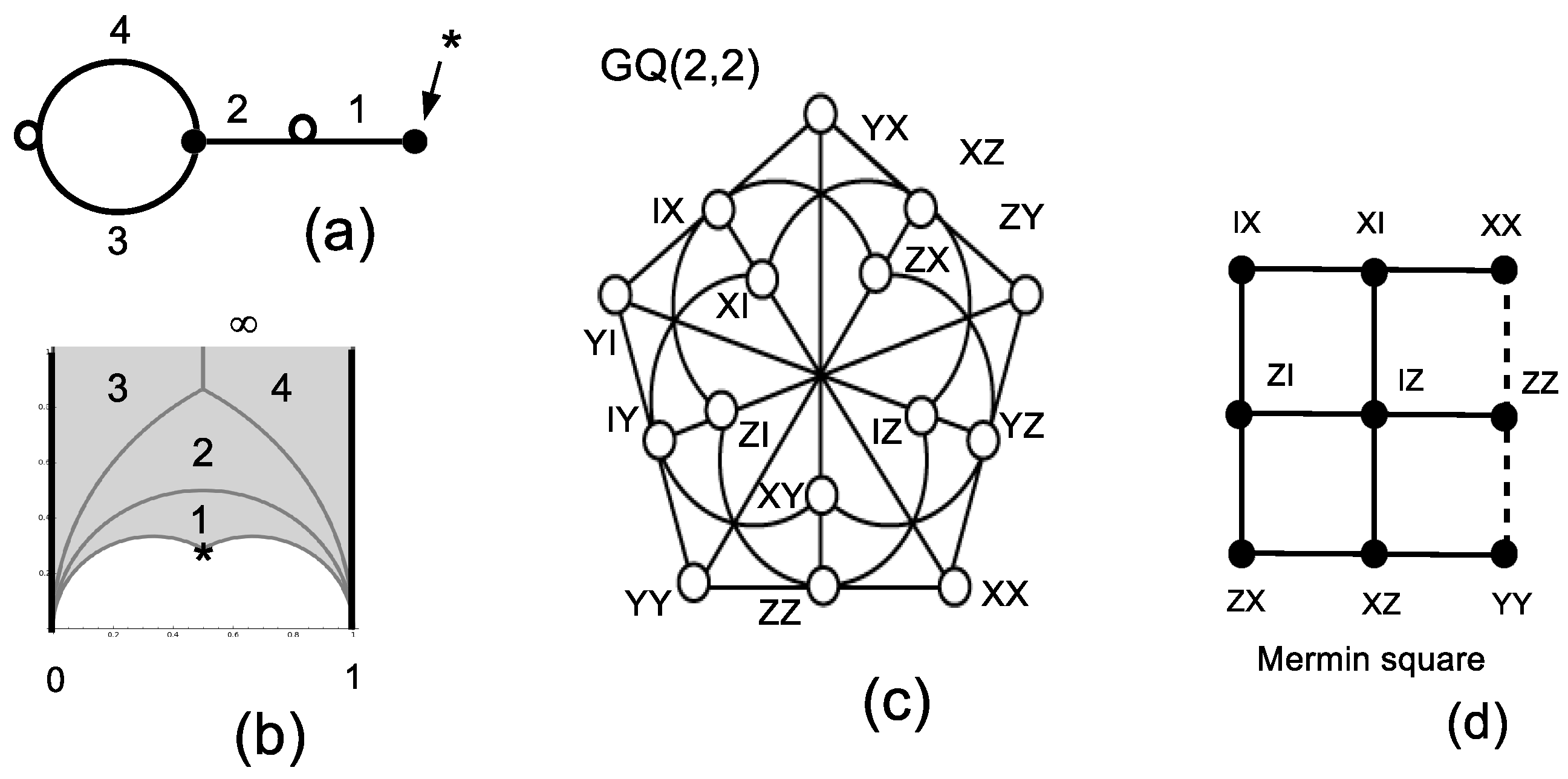
3.2. The Two-Qubit IC-POVM
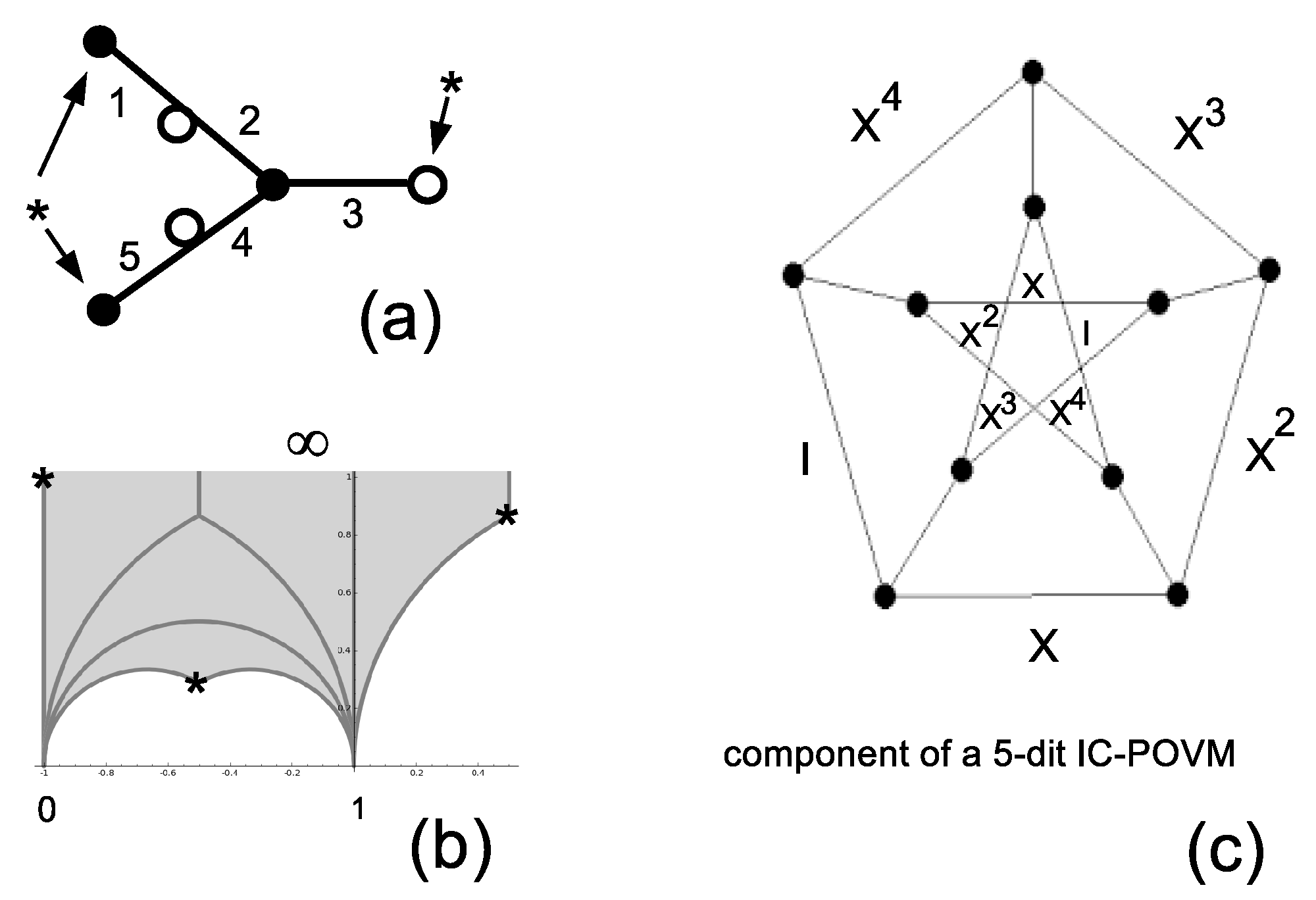
3.3. The Five-Dimensional Equiangular IC-POVM
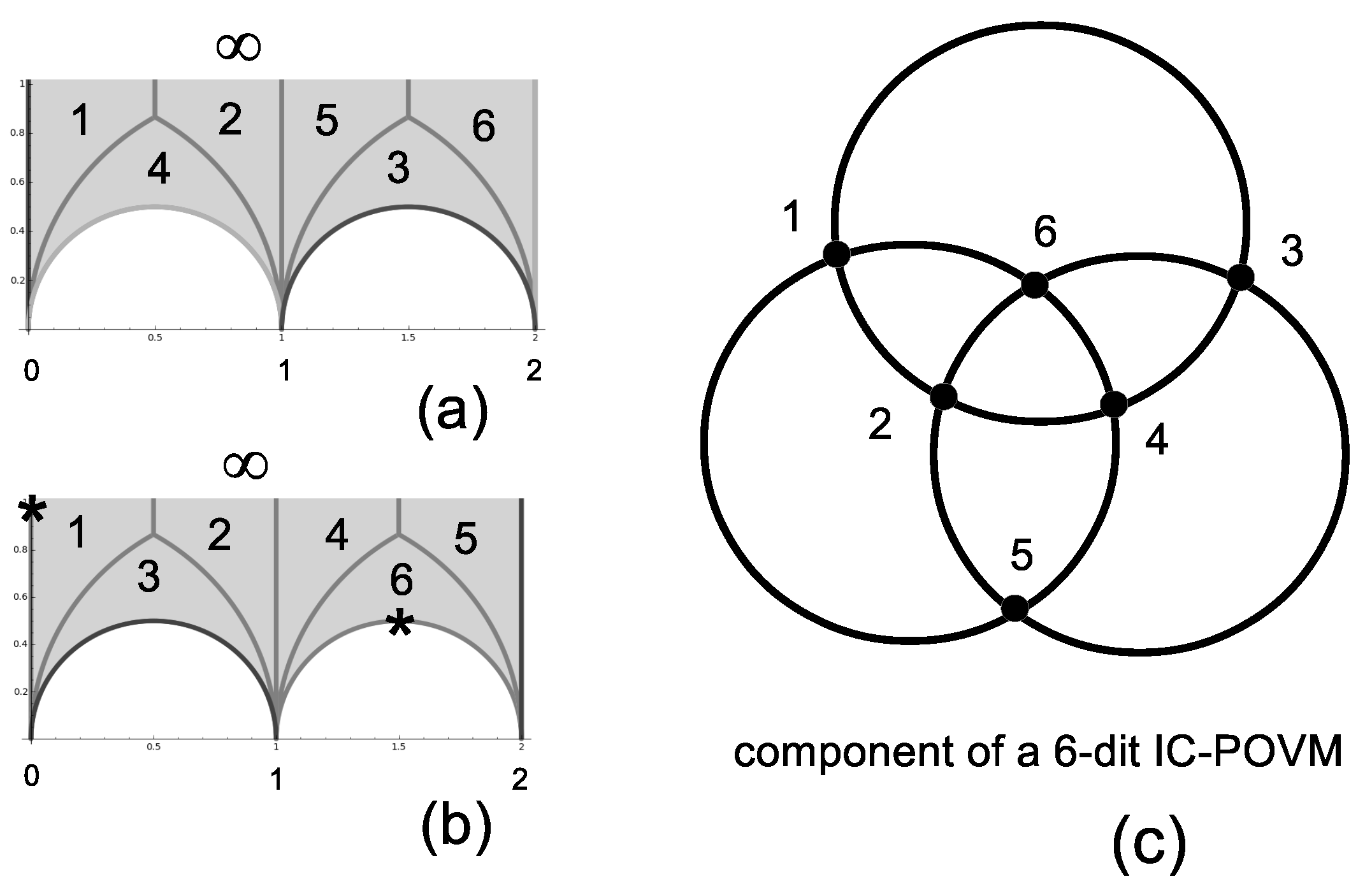
3.4. The Six-Dimensional IC-POVM
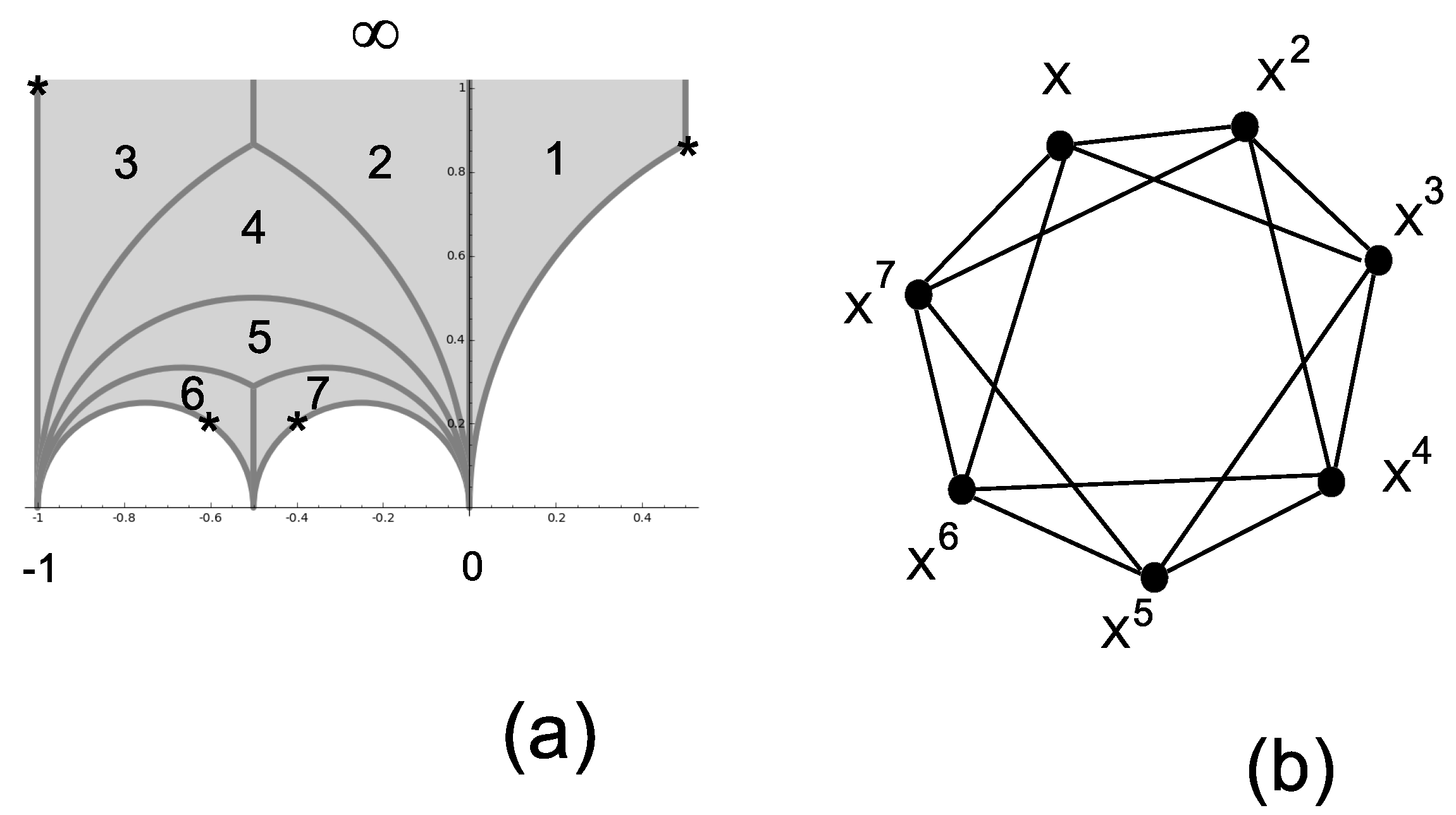
3.5. Seven-Dimensional IC-POVMs
3.6. The Three-Qubit Hoggar SIC
3.7. Nine-Dimensional IC-POVMs
3.8. Higher Dimensional IC-POVMs
4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Ghesquier, M.-F. A Hauteur d’Ombre; Cardère: Avignon, France, 2014; p. 57. [Google Scholar]
- Lobachevsky, N.I. Pangeometry; European Mathematical Society: Zurich, Switzerland, 2010; ISBN 9783037190876. [Google Scholar]
- Schlimm, D. The correspondence between Moritz Pasch and Felix Klein. Hist. Math. 2013, 40, 183–202. [Google Scholar] [CrossRef]
- Keller, K.J.; Papadopoulos, N.A.; Reyes-Lega, A.F. On the realizations of symmetries in quantum mechanics. arXiv, 2008; arXiv:0712.0997. [Google Scholar]
- Freed, D.S. On Wigner’s theorem. Geom. Topol. Monogr. 2012, 18, 83–89. [Google Scholar]
- Słomczyński, W.; Szymusiak, A. Highly symmetric POVMs and their informational power. Quant. Inf. Process. 2016, 15, 565–606. [Google Scholar] [CrossRef]
- Dang, H.B. Studies of Symmetries That Give Special Quantum States the “Right to Exist”. Ph.D. Thesis, University of Waterloo, Waterloo, ON, Canada, 11 August 2015. [Google Scholar]
- Chien, T.Y.; Waldron, S. Nice error frames, canonical abstract error groups and the construction of SICs. Linear Algebra Appl. 2017, 516, 93–117. [Google Scholar] [CrossRef]
- Planat, M.; Zainuddin, H. Zoology of Atlas-Groups: Dessins D’enfants, Finite Geometries and Quantum Commutation. Mathematics 2017, 5, 6. [Google Scholar] [CrossRef]
- Planat, M.; Ul Haq, R. The magic of universal quantum computing with permutations. Adv. Math. Phys. 2017, 217, 5287862. [Google Scholar] [CrossRef]
- Planat, M.; Gedik, Z. Magic informationally complete POVMs with permutations. R. Soc. Open Sci. 2017, 4, 170387. [Google Scholar] [CrossRef] [PubMed]
- Poincaré, H. La Valeur de la Science (The Value of Science); Flammarion: Paris, France, 1905; p. 214. (In French) [Google Scholar]
- Diamond, F.; Shurman, J. A First Course in Modular Forms; Springer: New York, NY, USA, 2005. [Google Scholar]
- Bravyi, S.; Kitaev, A. Universal quantum computation with ideal Clifford gates and noisy ancillas. Phys. Rev. A 2005, 71, 022316. [Google Scholar] [CrossRef]
- Bengtsson, I. From SIC’s and MUBs to Eddington. J. Phys. Conf. Ser. 2010, 254, 012007. [Google Scholar] [CrossRef]
- Stacey, B.C. Geometric and information-theoretic properties of the Hoggar lines. arxiv, 2016; arXiv:1609.03075. [Google Scholar]
- Kurth, C.A.; Long, L. Computations with finite index subgroups of PSL(2, ℤ) using Farey symbols. In Advances in Algebra and Combinatorics; Shum, K.P., Zelmanov, E., Zhang, J., Li, S., Eds.; World Scientific: Singapore, 2008; pp. 225–242. [Google Scholar]
- Cummins, C.J.; Pauli, S. Congruence Subgroups of PSL(2,Z) of Genus Less than or Equal to 24. Exp. Math. 2003, 12, 243–255. [Google Scholar] [CrossRef]
- Stein, W.A.; Abbott, T.; Abshoff, M.; Ajanki, A.; Albrecht, M.; Alexander, N.; Allombert, B.; Van Andel, E.; Andrus, I.; Angulo, P.; et al. Sage Mathematics Software; Version 6.4.1; The Sage Development Team: Washington, WA, USA, 2014; Available online: http://www.sagemath.org (accessed on 1 January 2017).
- DeBrota, J.B.; Fuchs, C.A. Negativity bounds for Weyl-Heisenberg quasiprobability representations. Found. Phys. 2017, 47, 1009–1030. [Google Scholar] [CrossRef]
- Renes, J.M.; Blume-Kohout, R.; Scott, A.J.; Caves, C.M. Symmetric informationally complete quantum measurements. J. Math. Phys. 2004, 45, 2171–2180. [Google Scholar] [CrossRef]
- Fuchs, C.A. On the quantumness of a Hibert space. Quant. Inf. Comput. 2004, 4, 467–478. [Google Scholar]
- Appleby, M.; Chien, T.Y.; Fammia, S.; Waldron, S. Constructing exact symmetric informationally complete measurements from numerical solutions. arxiv, 2017; arXiv:1703.05981. [Google Scholar]
- Bengtsson, I. The number behind the simplest SIC-POVM. Found Phys. 2017, 47, 1031–1041. [Google Scholar] [CrossRef]
- Cohen, H. A Course in Computational Algebraic Number Theory; Springer: New York, NY, USA, 1996. [Google Scholar]
- Queneau, R.; Le Lionnais, F. Wikimedia. Available online: https://en.wikipedia.org/wiki/oulipo (accessed on 1 January 2017).
- Cabello, A. A proof with 18 vectors of the Bell–Kochen–Specker theorem. In New Developments on Fundamental Problems in Quantum Physics; Ferrero, M., van der Merwe, A., Eds.; Kluwer Academic: Dordrecht, The Netherlands, 1997; pp. 59–62. [Google Scholar]
- Planat, M. On small proofs of Bell-Kochen–Specker theorem for two, three and four qubits. Eur. Phys. J. Plus 2012, 127, 86. [Google Scholar] [CrossRef]
- Pavic˘ić, M. Arbitrarily exhaustive hypergraph generation of 4-, 6-, 8-, 16-, and 32-dimensional quantum contextual sets. Phys. Rev. A 2017, 95, 062121. [Google Scholar] [CrossRef]
- Delfosse, N.; Guerin, P.A.; Bian, J.; Raussendorf, R. Wigner function negativity and contextuality in quantum computation on rebits. Phys. Rev. X 2015, 5, 021003. [Google Scholar] [CrossRef]
- De Silva, N. Logical paradoxes in quantum computation. arxiv, 2017; arXiv:1709.00013. [Google Scholar]
- Tabia, G.N.M.; Appleby, D.M. Exploring the geometry of qutrit space using symmetric informationally complete probabilities. Phys. Rev. A 2013, 88, 012131. [Google Scholar] [CrossRef]
- Planat, M. Pauli graphs when the Hilbert space dimension contains a square: Why the Dedekind psi function? J. Phys. A Math. Theor. 2011, 44, 045301. [Google Scholar] [CrossRef]
- Knuth, D. Π M & Epsilon J. S. Frame Talk, MathFest. Available online: http://sites.math.rutgers.edu/~zeilberg/quotes.html (accessed on 1 January 2017).

| Dim | Subgroups of Leading to an IC-POVM | PP | Geometry |
|---|---|---|---|
| 2 | none | 1 | tetrahedron [14] |
| 3 | 1 | Hesse SIC [15] | |
| 4 | under 2QB Pauli group | ||
| 2 | |||
| 5 | 1 | Petersen graph | |
| 6 | 2 | Borromean ring | |
| 7 | 2 | Figure 5b | |
| NC | 2 | ||
| none | 1 | [11] | |
| 8 | none under 3QB, 8-dit, 4-dit-QB Pauli group | 1 | Hoggar SIC [11,16] |
| 9 | under 2QT Pauli group | ||
| NC | 2 | -grid, Pappus | |
| NC | 3 | ||
| 10 | 5 | ||
| 11 | 3 | ||
| 12 | under 2QB-QT Pauli group | ||
| 5 | |||
| NC | 5 | Hesse () | |
| NC | 6 | ||
| 12 | under 12-dit Pauli group | ||
| , NC | 11,7 | ||
| 13 | NC | 4 | |
| 14 | , NC, | 12,5,6 | |
| 15 | , NC, , | 5,4,10,3 | |
| 16 | none under 4QB and 2 4-dit Pauli group | ||
| 18 | under 18-dit or 2QT-QB Pauli group | ||
| , NC | 7,5 | ||
| 19 | NC | 3 | |
| 21 | NC, NC | 4 | |
| NC, NC | 59,4 | ||
| 24 | none under 3QB-QT Pauli group | ||
| 24 | under 24-dit Pauli group | ||
| , NC, , | 40,56,40,30 | ||
| NC, NC | 8,7 | ||
| , | 23,60 | ||
| 25 | under 25-dit Pauli group | ||
| NC | 15 | ||
| 27 | under 3QT Pauli group | ||
| NC, NC | 4 | Pappus |
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Planat, M. The Poincaré Half-Plane for Informationally-Complete POVMs. Entropy 2018, 20, 16. https://doi.org/10.3390/e20010016
Planat M. The Poincaré Half-Plane for Informationally-Complete POVMs. Entropy. 2018; 20(1):16. https://doi.org/10.3390/e20010016
Chicago/Turabian StylePlanat, Michel. 2018. "The Poincaré Half-Plane for Informationally-Complete POVMs" Entropy 20, no. 1: 16. https://doi.org/10.3390/e20010016
APA StylePlanat, M. (2018). The Poincaré Half-Plane for Informationally-Complete POVMs. Entropy, 20(1), 16. https://doi.org/10.3390/e20010016





