1. Introduction
In recent years, we observed an increasing interest toward the use of quantum formalism in non-microscopic domains [
1,
2,
3,
4]. The idea is that the powerful predictive properties of quantum mechanics, used for describing the behavior of microscopic phenomena, turn out to be particularly beneficial also in non-microscopic domains. Indeed, the real power of quantum computing consists in exploiting the strength of particular quantum properties in order to implement algorithms which are much more efficient and faster than the respective classical counterpart. For this purpose, several non standard applications involving the quantum mechanical formalism have been proposed, in research fields such as game theory [
5], economics [
6], cognitive sciences [
7], signal processing [
8], and so on. Further, particular applications, interesting for the specific topics of the present paper, concern the areas of machine learning and pattern recognition.
Quantum machine learning aims at using quantum computation advantages in order to find new solutions to pattern recognition and image understanding problems. Regarding this, we can find several efforts exploiting quantum information properties for the resolution of pattern recognition problems in [
9], while a detailed overview concerning the application of quantum computing techniques to machine learning is presented in [
10].
In this context, there exist different approaches involving the use of quantum formalism in pattern recognition and machine learning. We can find, for instance, procedures that exploit quantum properties in order to reach advantages on a classical computer [
11,
12,
13] or techniques supposing the existence of a quantum computer in order to perform in an inherently parallel way all the required operations, taking advantage of quantum mechanical effects and providing high performance in terms of computational efficiency [
14,
15,
16].
One of the main aspects of pattern recognition is focused on the application of quantum information processing methods [
17] to solve classification and clustering problems [
18,
19].
The use of quantum states for representing patterns has a twofold motivation: as already discussed, first of all it permits the exploitation of quantum algorithms for enhancing the computational efficiency of the classification procedure. Secondly, it is possible to use quantum-inspired models in order to reach some benefits with respect to classical problems. With regards to the first motivation, in [
15,
16], it was proved that the computation of distances between
d-dimensional real vectors takes time
on a quantum computer, while the same operation on a classical computer is computationally much harder. Therefore, the introduction of a quantum algorithm for the purpose of classifying patterns based on our encoding gives potential advantages to rush the whole procedure.
Even if in literature we can find techniques proposing some kind of computational benefits [
20], the main problem to find a
more convenient encoding from classical to quantum objects is currently an open and interesting matter of debate [
9,
10]. Here, our contribution consists of constructing a quantum version of a minimum distance classifier in order to reach some convenience, in terms of the error in pattern classification, with respect to the corresponding classical model. We have already proposed this kind of approach in two previous works [
21,
22], where a “quantum counterpart” of the well known
Nearest Mean Classifier (NMC) has been presented.
In both cases, the model is based on the introduction of two main ingredients: first, an appropriate encoding of arbitrary patterns into density operators; second, a distance between density matrices, representing the quantum counterpart of the Euclidean metric in the “classical” NMC. The main difference between the two previous works is the following one:
(i) firstly [
21], we tested our quantum classifier on two-dimensional datasets and we proposed a purely theoretical generalization to an arbitrary dimension;
(ii) secondly [
22], a new encoding for arbitrary
n-dimensional patterns into quantum states has been proposed, and it was tested on different real-world and artificial two-class datasets. Anyway, in both cases we observed a significant improvement of the accuracy in the classification process. In addition, we found that, by using the encoding proposed in [
22] and for two-dimensional problems only, the classification accuracy of our quantum classifier can be further improved by performing a uniform rescaling of the original dataset.
In this work we propose a new encoding of arbitrary
n-dimensional patterns into quantum objects, extending both the theoretical model and the experimental results to multi-class problems, which preserves information about the norm of the original pattern. This idea has been inspired by recent debates on quantum machine learning [
9], according to which it is crucial to avoid loss of information when a particular encoding of real vectors into quantum states is considered. Such an approach turns out to be very promising in terms of classification performance compared to the NMC. Further, differing from the NMC, our quantum classifier is not invariant under uniform rescaling. In particular, the classification error provided by the QNMC changes by feature rescaling. As a consequence, we observe that, for several datasets, the new encoding exhibits a further advantage that can be gained by exploiting the non-invariance under rescaling, and also for
n-dimensional problems (conversely to the previous works). To this end, some experimental results have been presented.
The organization of this paper is as follows. In
Section 2, the classification process and the formal structure of the NMC for multi-class problems are described.
Section 3 is devoted to the definition of a new encoding of real patterns into quantum states. In
Section 4, we introduce the quantum version of the NMC, called
Quantum Nearest Mean Classifier (QNMC), based on the new encoding previously described. In
Section 5, we show experimental results related to the NMC and QNMC comparison which generally exhibit better performance of our quantum classifier (in terms of error and other meaningful classification parameters) with respect to the NMC. Further, starting from the fact that the QNMC is not invariant under uniform coordinate rescaling (contrary to the corresponding classical version), we also show that for some datasets it is possible to provide a benefit from this non-invariance property. Finally, the last section includes conclusions and probable future developments.
The present work is an extended version of the paper presented at the conference
Quantum and Beyond 2016, Vaxjo, 13–16 June 2016 [
23], significantly enlarged in theoretical discussion, experimental section and bibliography.
2. Minimum Distance Classification
Pattern recognition [
24,
25] is the machine learning branch whose purpose is to design algorithms able to automatically recognize “objects”.
Here, we deal with supervised learning, whose goal is to infer a map from labeled training objects. The purpose of pattern classification, which represents one of the main tasks in this context, consists in assigning input data to different classes.
Each object is univocally identified by a set of features; in other words, we represent a d-feature object as a d-dimensional vector , where is generally a subset of the d-dimensional real space representing the feature space. Consequently, any arbitrary object is represented by a vector associated with a given class of objects (but, in principle, we do not know which one). Let be the class label set. A pattern is represented by a pair , where is the feature vector representing an object and is the label of the class which is associated with. A classification procedure aims at attributing (with high accuracy) to any unlabeled object the corresponding label (where the label attached to an object represents the class which the object belongs to), by learning about the set of objects whose class is known. The training set is given by , where , (for ) and N is the number of patterns belonging to . Finally, let be the cardinality of the training set associated to the l-th class (for ) such that .
We now introduce the well known
Nearest Mean Classifier (NMC) [
24], which is a particular kind of minimum distance classifier widely used in pattern recognition. The strategy consists in computing the distances between an object
(to classify) and other objects chosen as prototypes of each class (called
centroids). Finally, the classifier associates to
the label of the closest centroid. So, we can resume the NMC algorithm as follows:
Computation of the
centroid (i.e., the sample mean [
26]) associated to each class, whose corresponding feature vector is given by:
where
l is the label of the class;
Classification of the object
, provided by:
where
is the standard Euclidean distance. In this framework,
argmin plays the role of classifier, i.e., a function that associates to any unlabeled object the correspondent label.
Generally, it could be that a pattern of a given class is closer to the centroid of another class. This fact can depend on the specific data distribution for instance. Consequently, if the algorithm would be applied to this pattern, it would fail. Hence, for an arbitrary object
which belongs to an
a priori not known class, the classification method output has the following four possibilities [
27]:
(i) True Positive (TP): pattern belonging to the
l-th class and correctly classified as
l;
(ii) True Negative (TN): pattern belonging to a class different than
l, and correctly classified as not
l;
(iii) False Positive (FP): pattern belonging to a class different than
l, and incorrectly classified as
l;
(iv) False Negative (FN): pattern belonging to the
l-th class, and incorrectly classified as not
l.
Generally, a given classification method is evaluated via a standard procedure which consists of dividing the original labeled dataset
of size
, into a set
of
N training patterns and a set
of
test patterns, i.e.,
where
is the
test set [
24], defined as
.
As a consequence, we can examine the classification algorithm performance by considering the following statistical measures associated to each class l depending on the quantities listed above:
True Positive Rate (TPR): ;
True Negative Rate (TNR): ;
False Positive Rate (FPR): ;
False Negative Rate (FNR): .
Further, other standard statistical coefficients [
27] used to establish the reliability of a classification algorithm are:
Classification error (E): ;
Precision (P): ;
Cohen’s Kappa (K): , where
, .
The classification error represents the percentage of misclassified patterns, the precision is a measure of the statistical variability of the considered model and the Cohen’s Kappa represents the degree of reliability and accuracy of a statistical classification and it can assume values ranging from to . In particular, if K (K), we correctly (incorrectly) classify all the test set patterns. Let us note that these statistical coefficients have to be computed for each class. Then, the final value of each statistical coefficient related to the classification algorithm is the weighted sum of the statistical coefficients of each class.
3. Mapping Real Patterns into Quantum States
As already discussed, quantum mechanical formalism seems to be promising in non-standard scenarios, in our case to solve for instance pattern classification tasks. To this end, in order to provide our quantum classification model, the first ingredient we have to introduce is an appropriate encoding of real patterns into quantum states. Quoting Schuld et al. [
9], “in order to use the strengths of quantum mechanics without being confined by classical ideas of data encoding, finding ‘genuinely quantum’ ways of representing and extracting information could become vital for the future of quantum machine learning.”
Generally, given a
d-dimensional feature vector, there exist different ways to encode it into a density operator [
9]. As already mentioned, finding the “best” encoding of real vectors into quantum states (i.e., outperforming all the possible encodings for any dataset) is still an open and intricate problem. This fact is not so surprising because, on the other hand, in pattern recognition is not possible to establish an absolute superiority of a given classification method with respect to the other ones, and the reason is that each dataset has unique and specific characteristics (this point will be deepened in the numerical section).
In [
21], the proposed encoding was based on the use of the stereographic projection [
28]. In particular, it uniquely maps a point
on the surface of a radius-one sphere
(except for the north pole) into a point
in
, i.e.,
whose image plane passes through the center of the sphere. The inverse of the stereographic projection is:
where
. By imposing that
, we consider
as Pauli components of the density operator
(where the space
of density operators for
d-dimensional systems consists of positive semidefinite matrices with unitary trace) associated to the pattern
, defined as:
The proposed encoding offers the advantage of visualizing a bi-dimensional vector on the Bloch sphere [
21]. In the same work, we also introduced a generalization of our encoding to the
d-dimensional case, which allows to represent
d-dimensional vectors as points on the hypersphere
by writing a density operator
as a linear combination of the
d-dimensional identity and
-matrices
(i.e.,
generalized Pauli matrices [
29,
30]).
To this end, we introduced the generalized stereographic projection [
31], which maps any point
into an arbitrary point
, i.e.,
However, even if it is possible to map points on the
d-hypersphere into
d-feature patterns, they are not density operators as a rule and the one-to-one correspondence between them and density matrices is guaranteed only on particular regions [
29,
32,
33].
An alternative encoding of a
d-feature vector
into a density operator was proposed in [
22]. It is obtained by:
(i) by mapping
into a (
)-dimensional vector
according to the generalized version of Equation (
4), i.e.,
where
;
(ii) by considering the projector
.
Here, a different kind of quantum minimum distance classifier is considered, based on a new encoding again and we show that it exhibits interesting improvements by also exploiting the non-invariance under feature rescaling. Accordingly with [
9,
15], when a real vector is encoded into a quantum state, in order to avoid a loss of information it is important that the quantum state keeps information on the original real vector norm. In light of this fact, we introduce the following alternative encoding.
Let be a d-dimensional vector.
We map the vector
into a vector
, whose first
d features are the components of the vector
and the
-th feature is the norm of
. Formally:
We obtain the vector
by dividing the first
d components of the vector
for
:
We compute the norm of the vector
, i.e.,
and we map the vector
into the normalized vector
as follows:
Now, we provide the following definition.
Definition 1 (Density Pattern).
Let be a d-dimensional vector and the corresponding pattern. Then, the density pattern
associated with is represented by the pair , where the matrix , corresponding to the feature vector , has the following form:where the vector is given by Equation (10) and y is the label of the original pattern. Hence, this encoding maps real d-dimensional vectors into -dimensional pure states . In this way, we obtain an encoding that takes into account the information about the initial real vector norm and, at the same time, allows to easily encode arbitrary real d-dimensional vectors.
Clearly, there exist different ways to encode patterns into quantum states by maintaining some information about the vector norm. However, the one we show has been inspired by simple considerations concerning the two-dimensional encoding on the Bloch sphere, naturally extended to the
d-dimensional case. To this end, in [
21] it was analytically proved that the encoding of
into the density operator
given by Equation (
5) can be exactly recovered if we consider as starting point the vector
and by applying the set of transformations given by Equations (
9)–(
11).
4. Density Pattern Classification
In this section, a quantum counterpart of the NMC is provided, named Quantum Nearest Mean Classifier (QNMC). It can be seen as a particular kind of minimum distance classifier between quantum objects (i.e., density patterns). First of all, the use of this new quantum formalism could provide potential advantages in reducing the computational complexity of the problem if we consider a possible implementation of our framework on a quantum computer (as already explained in the Introduction). Secondly, it permits to fully compare the NMC and the QNMC performance by using a classical computer only. About the second point, we reiterate that our aim is not to assert that the QNMC outperforms all the other supervised classical procedures, but to prove (as we will show by numerical simulations) that it performs better than its “natural” classical counterpart (i.e., the NMC).
In order to provide a quantum counterpart of the NMC, we need:
(i) an encoding from real patterns to quantum objects (defined above);
(ii) a quantum version of the classical centroid (i.e., a sort of quantum class prototype), that will be named
quantum centroid; and
(iii) an appropriate
quantum distance between density patterns, corresponding to the Euclidean metric for the NMC. In such a quantum framework, the quantum version
of the dataset
is given by:
where
is the density pattern associated to the pattern
. Consequently,
and
represent the quantum versions of the training and test set respectively, i.e., the sets of all the density patterns corresponding to the patterns in
and
. Now, we can naturally define the quantum version of the classical centroid
, given in Equation (
1).
Definition 2 (Quantum Centroid).
Let be a labeled dataset of density patterns such that is a training set composed of N density patterns. Further, let be the class label set. The quantum centroid
of the l-th class is given by:where is the number of density patterns of the l-th class in , such that . Let us stress that the quantum centroids are generally mixed states and we cannot get them by mapping the classical centroids
, i.e.,
Therefore, the quantum centroid has a completely new meaning because it is no longer a pure state and does not have any classical counterpart. This is the main reason that establishes the deep difference between both classifiers. At this purpose, it is easy to verify [
21] that, unlike the classical case, the expression of the quantum centroid is sensitive to the dataset dispersion.
Now, we recall the definition of trace distance between quantum states (see, e.g., [
34]), which can be considered as a suitable metric between density patterns.
Definition 3 (Trace Distance).
Let and be two arbitrary density operators belonging to the same dimensional Hilbert space. The trace distance
between and is:where . Clearly
, as the true metric for density operators, satisfies the standard properties of
positivity,
symmetry and
triangle inequality. The use of the trace distance in our quantum framework is naturally motivated by the fact that it is the simplest possible choice among other possible metrics in the density matrix space [
35]. Consequently, it can be seen as the “authentic” quantum counterpart of the Euclidean distance, which represents the simplest choice in the starting space. However, the trace distance exhibits some limitations and downsides (in particular, it is monotone but not Riemannian [
36]). On the other hand, the Euclidean distance in some pattern classification problems is not enough to fully capture for instance the dataset distribution. For this reason, other kinds of metrics in the classical space are adopted to avoid this limitation [
24]. To this end, as a future development of the present work, it could be interesting to compare different distances in both quantum and classical framework, able to treat more complex situations (we will deepen this point in the conclusions).
We are ready to introduce the QNMC procedure consisting, as the classical one, of the following steps:
Constructing the sets , by mapping each pattern of the sets , via the encoding introduced in Definition 1;
Calculating the quantum centroids (), by using the quantum training set , in accordance with Definition 2;
Classifying a density pattern
by means of the optimization problem:
where
is the trace distance introduced in Definition 3.
5. Experimental Results
This section is devoted to showing a comparison between the NMC and the QNMC performances in terms of the statistical coefficients introduced in
Section 2. We use both classifiers to analyze twenty-seven datasets, divided into two categories: artificial datasets (
Gaussian (I), Gaussian (II), Gaussian (III), Moon, Banana) and the remaining ones which are real-world datasets, extracted both from the UCI (UC Irvine Machine Learning Repository) [
37] and KEEL (Knowledge Extraction based on Evolutionary Learning) [
38] repositories. Further, among them we can find also imbalanced datasets, whose main characteristic is that the number of patterns in a given class is significantly lower than those belonging to the other classes. Let us note that, in real situations, we usually deal with data whose distribution is unknown, then the most interesting case is the one in which we use real-world datasets. However, the use of artificial datasets following known distribution, and in particular Gaussian distributions with specific parameters, can help to catch precious information.
5.1. Comparison between QNMC and NMC
In
Table 1 we summarize the characteristics of the datasets involved in our experiments. In particular, for each dataset we list the total number of patterns, the number of each class and the number of features. Let us note that, although we mostly confine our investigation to two-class datasets, our model can be easily extended to multi-class problems (as we show for the three-class datasets
Balance,
Gaussian (III),
Hayes-Roth,
Iris).
In order to make our results statistically significant, we apply the standard procedure which consists in randomly splitting each dataset into two parts, the training set (representing the of the original dataset) and the test set (representing the of the original dataset). Finally, we perform 10 runs for each dataset, with a random partition at each experiment. Let us stress that the results appear robust with respect to different partitions of the original dataset. Further, we consider only 10 runs because, for a greater number, the standard deviation of the classification error mean value is substantially the same.
In
Table 2, we report the QNMC and NMC performance for each dataset, evaluated in terms of mean value and standard deviation (computed on ten runs) of the statistical coefficients, discussed in the previous section. For the sake of simplicity, we omit the values of FPR and FNR because they can be easily obtained by TPR and TNR values (i.e., FPR = 1 − TNR, FNR = 1 − TPR).
We observe, by comparing QNMC and NMC performances (see
Table 2), that the first provides a significant improvement with respect to the standard NMC in terms of all the statistical parameters we have considered. In several cases, the difference between the classification error for both classifiers is very high, up to
(see
Mutagenesis-Bond). Further, the new encoding, for two-feature datasets, provides better performance than the one considered in [
21] (where the QNMC error with related standard deviation was
for
Moon and
for
Banana) and it generally exhibits a quite similar performance with respect to the one in [
22] for multi-dimension datasets or a classification improvement of about
, generally.
The artificial Gaussian datasets may deserve a brief comment. Let us discuss the way in which the three Gaussian datasets have been created.
Gaussian (I) [
39] is a perfectly balanced dataset (i.e., both classes have the same number of patterns), patterns have the same dispersion in both classes, and only some features are correlated [
40].
Gaussian (II) is an unbalanced dataset (i.e., classes have a very different number of patterns), patterns do not exhibit the same dispersion in both classes and features are not correlated.
Gaussian (III) is composed of three classes and it is an unbalanced dataset with different pattern dispersion in all the classes, where all the features are correlated.
For this kind of Gaussian data, we remark that the NMC does not offer the best performance in terms of pattern classification [
24] because of the particular characteristics of the class distribution. Indeed, the NMC does not keep into consideration the pattern dispersion. Conversely, by looking at
Table 2, the improvements of the QNMC seem to exhibit some kind of sensitivity of the classifier with respect to the data dispersion. A detailed description of this problem will be addressed in a future work.
Further, we can note that the QNMC performance is better also for imbalanced datasets (the most significant cases are
Balance,
Ilpd,
Segment,
Page,
Gaussian (III)), which are usually difficult to deal with standard classification models. At this purpose, we can note that the QNMC exhibits a classification error much lower than the NMC, up to a difference of about
. Another interesting and surprising result concerns the
Iris0 dataset, which represents the imbalanced version of the
Iris dataset: as we can observe looking at
Table 2, our quantum classifier is able to perfectly classify all the test set patterns, conversely to the NMC.
We remark that, even if it is possible to establish whether a classifier is “good” or “bad” for a given dataset by the evaluation of some a priori data characteristics, generally it is no possible to establish an absolute superiority of a given classifier for any dataset, thanks to the
No Free Lunch Theorem [
24]. In any case, the QNMC seems to be particularly convenient when the data distribution is difficult to treat with the standard NMC.
5.2. Non-Invariance Under Rescaling
The final experimental results that we present in this paper regard a significant difference between NMC and QNMC. Let us suppose that all the components of the feature vectors
(
) belonging to the original dataset
are multiplied by the same parameter
, i.e.,
. Then, the whole dataset is subjected to an increasing dispersion (for
) or a decreasing dispersion (for
) and the classical centroids change according to
(
). Therefore, pattern classification for the rescaled problem consists of solving:
For any value of the parameter
it can be proved [
22] that, while the NMC is invariant under rescaling, for the QNMC this invariance fails. Interestingly enough, it is possible to consider the failure of the invariance under rescaling as a resource for the classification problem. In other words, through a suitable choice of the rescaling factor is possible, in principle, to get a decreasing of the classification error. To this end, we have studied the variation of the QNMC performance (in particular of the classification error) in terms of the
free parameter
and in
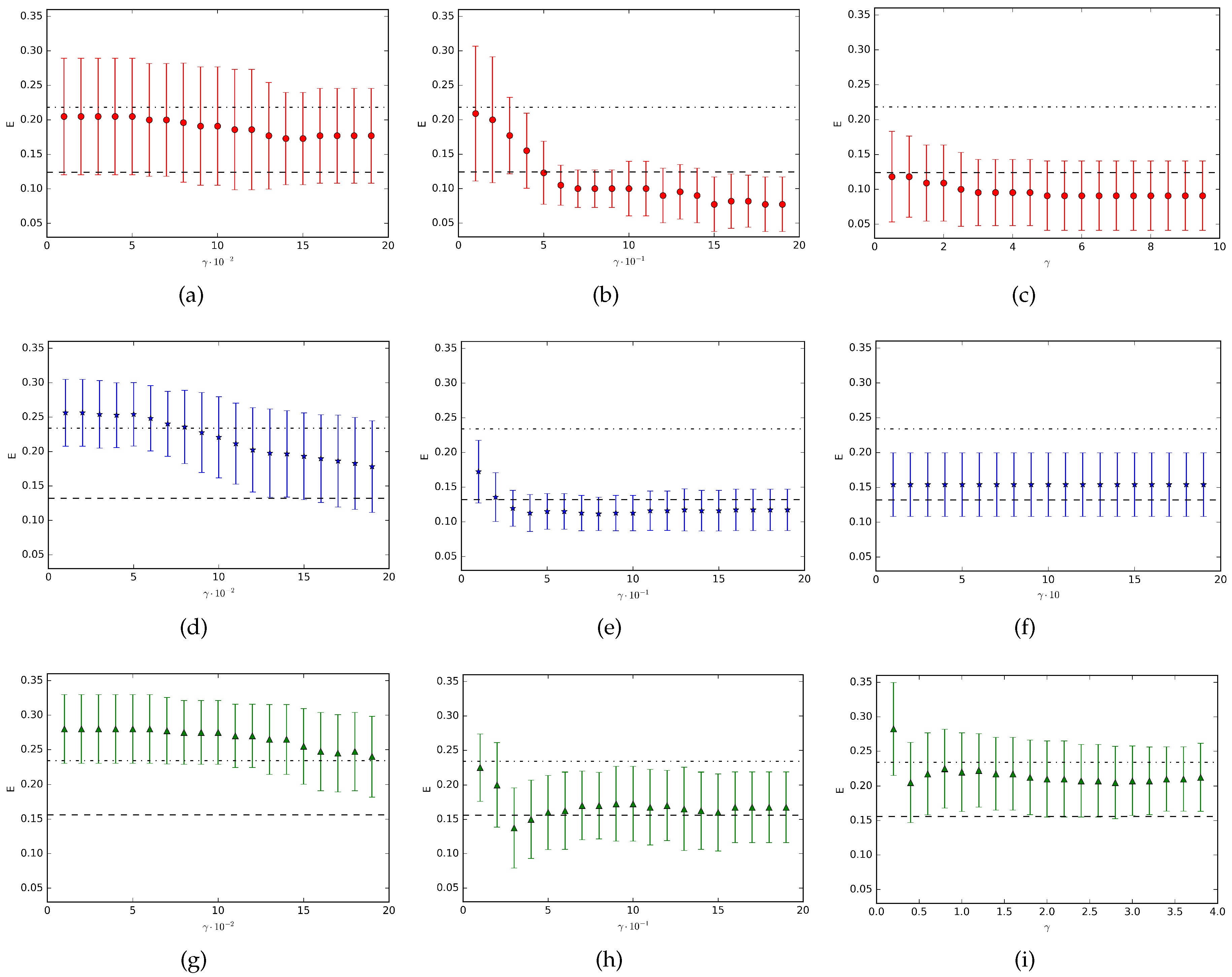
Figure 1 the results for the datasets
Appendicitis,
Monk and
Moon are shown. In the figure, each point represents the mean value (with corresponding standard deviation represented by the vertical bar) over ten runs of the experiments. Finally, we have considered, as an example, three different ranges of the rescaling parameter
for each dataset. We can observe that the resulting classification performance strongly depends on the
range. Indeed, in all the three cases we consider, we obtain completely different classification results based on different choices of the
values. As we can see, in some situations we observe an improvement of the QNMC performance with respect to the unrescaled problem (subfigures (b), (c), (e), (h)), in other cases we get worse classification results (subfigures (a), (d), (g), (i)) and sometimes the rescaling parameter does not offer any variation of the classification error (subfigure (f)).
In conclusion, the range of the parameter for which the QNMC performance improves, is generally not unique and strongly depends on the considered dataset. As a consequence, we do not generally get an improvement in the classification process for any ranges. On the contrary, there exist some intervals for the parameter where the QNMC classification performance is worse than the case without rescaling. Then, each dataset has specific and unique characteristics (in complete accord to the No Free Lunch Theorem) and the incidence of the non-invariance under rescaling in the decreasing of the error, in general, should be determined by empirical evidences.
6. Conclusions and Future Developments
In this work we have introduced a quantum minimum distance classifier, named Quantum Nearest Mean Classifier, which can be seen as a quantum version of the well known Nearest Mean Classifier. In particular, it is obtained by defining a suitable encoding of real patterns, i.e., density patterns, and by recovering the trace distance between density operators.
A new encoding of real patterns into a quantum objects have been proposed, suggested by recent debates on quantum machine learning according to which, in order to avoid a loss of information caused by encoding a real vector into a quantum state, we need to consider the normalized vector keeping some information about its norm simultaneously. Secondly, we have defined the quantum centroid, i.e., the pattern chosen as the prototype of each class, which is not invariant under uniform rescaling of the original dataset (unlike the NMC) and seems to exhibit a kind of sensitivity to the data dispersion.
In the experiments, both classifiers have been compared in terms of significant statistical coefficients. In particular, we have considered 27 different datasets having different nature (real-world and artificial). Further, the non-invariance under rescaling of the QNMC has suggested to study the variation of the classification error in terms of a free parameter , whose variation produces a modification of the data dispersion and, consequently, of the classifier performance. In particular we have showed as, in the most of cases, the QNMC exhibits a significant decreasing of the classification error (and of the other statistical coefficients) with respect to the NMC and, for some cases, the non-invariance under rescaling can provide a positive incidence in the classification process.
Let us remark that, even if there is not an absolute superiority of QNMC with respect to the NMC, the proposed technique leads to relevant improvements in terms of pattern classification when we deal with an a priori knowledge of the data distribution.
In light of such considerations, further developments of the present work will involve the study of:
(i) the
optimal encoding (mapping patterns to quantum states) which ensures a better classification accuracy (at least for a finite set of data);
(ii) a general method to find the suitable rescaling parameter range we can apply to a given dataset for further optimizing the classification process; and
(iii) the data distribution for which our quantum classifier outperforms the NMC. Further, as discussed in
Section 4, in some situations the standard NMC is not very useful as a classification model, especially when the dataset distribution is quite complex to deal with. In pattern recognition, in order to address such problems, other kinds of classification techniques are used instead of the NMC, for instance the well known
Linear Discriminant Analysis (LDA) or
Quadratic Discriminant Analysis (QDA) classifiers, where different distances between patterns are considered, taking the data distribution into account more precisely [
24]. To this end, an interesting development of the present work could regard the comparison between the LDA or QDA models and the QNMC based on the computation of more suitable and convenient distances between density patterns [
35].