Nonlinear Multiscale Entropy and Recurrence Quantification Analysis of Foreign Exchange Markets Efficiency
Abstract
:1. Introduction
2. Data Description and Processing
3. Methodologies
3.1. The MWPE Method
- (i)
- For a time series , its consecutive coarse-grained series, determined by the scale factor s, is constructed
- (ii)
- For , given an embedding dimension m and a time delay , an m-dimensional space is transformed from ,
- (iii)
- The components of are placed in an ascending orderWhen confronting an equality, e.g.,we consider the quantities y by the k values, namely if , we set . Thus, any vector has a permutation , which is one of the permutations of m distinct symbol set .
- (iv)
- Of every permutation , the relative frequency with weight for is given aswhere is the weighted value of and can be computedwhere is the arithmetic mean of . is the indicator function of for permutation , defined as if and if .
- (v)
- The MWPE is defined as the Shannon entropyWhen , then gets the maximum value , thus can be normalized through . The normalized MWPE is defined as .
3.2. The RQA Approach
4. Empirical Results of Price Returns
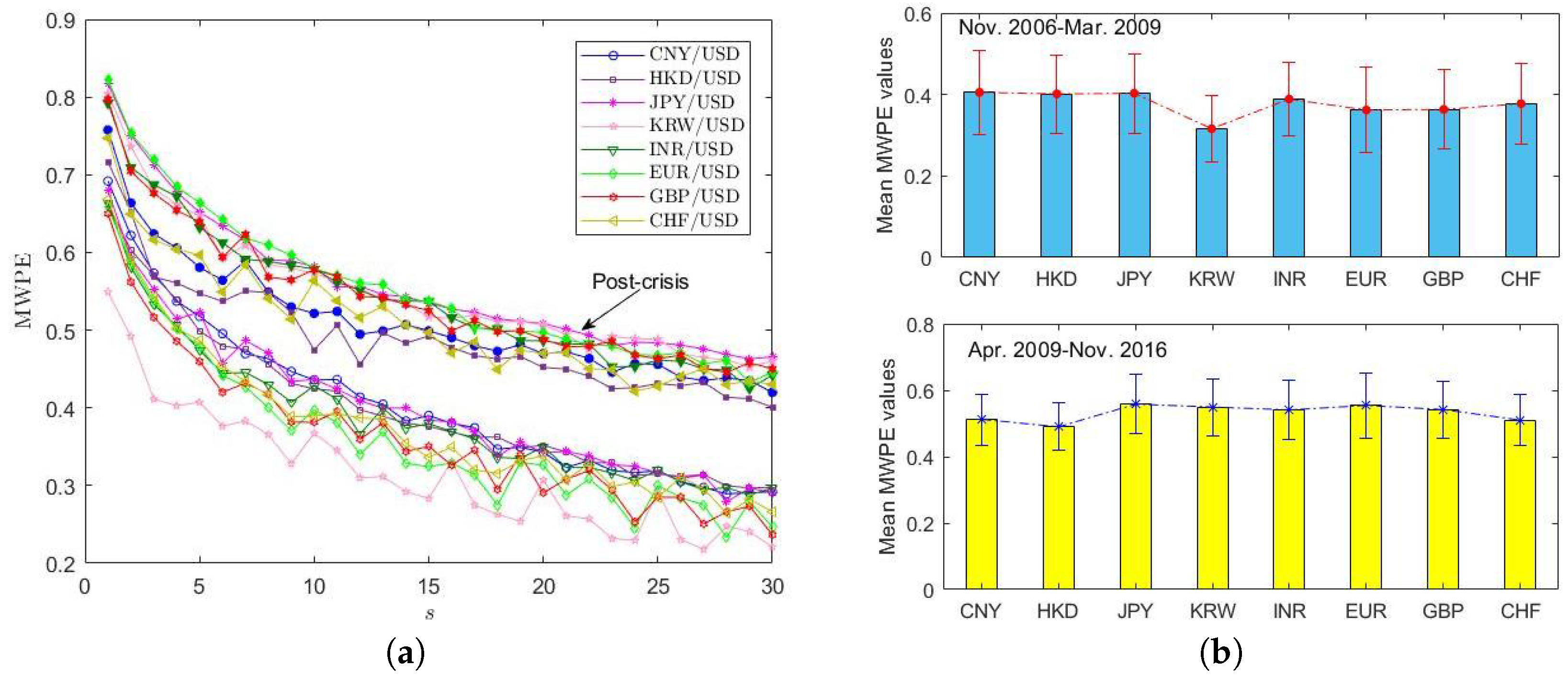
4.1. Complexity Analysis by the MWPE
4.2. Determinism Analysis by the RQA
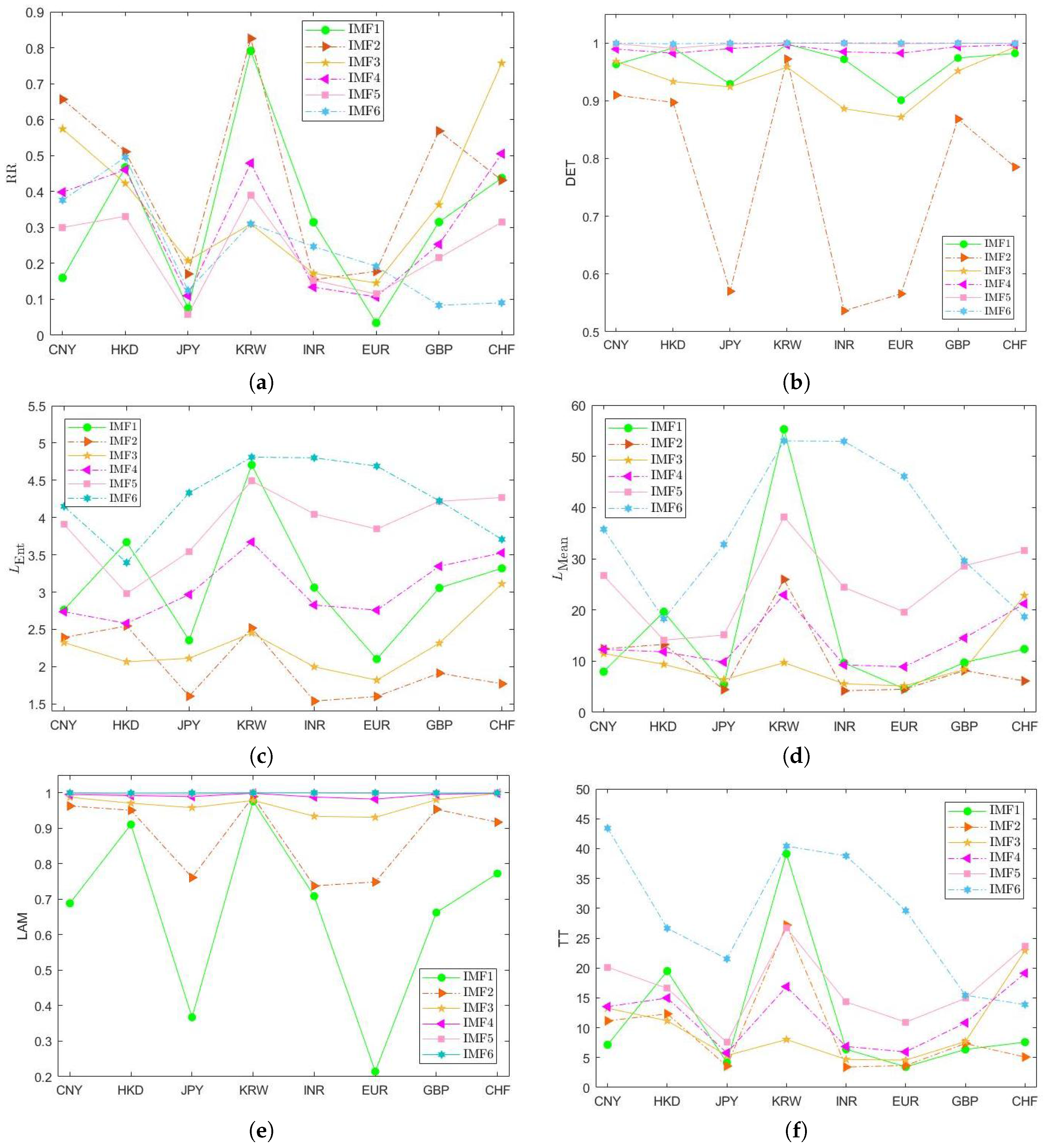
5. Complexity Study of EMD-Based IMF Series
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Calvet, L.E.; Fisher, A.J. Multifractal Volatility: Theory, Forecasting, and Pricing (Academic Press Advanced Finance); Academic Press: Cambridge, CA, USA, 2008. [Google Scholar]
- Fang, W.; Wang, J. Statistical properties and multifractal behaviors of market returns by Ising dynamic systems. Int. J. Mod. Phys. C 2012, 23, 1250023. [Google Scholar] [CrossRef]
- Gabaix, X.; Gopikrishnan, P.; Plerou, V.; Stanley, H.E. A theory of power-law distributions in financial market fluctuations. Nature 2003, 423, 267–270. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.F.; Wang, J.; Niu, H.L. Nonlinear multi-analysis of agent-based financial market dynamics by epidemic system. Chaos 2015, 25, 103103. [Google Scholar] [CrossRef] [PubMed]
- Lux, T. Financial Power Laws: Empirical Evidence, Models and Mechanisms; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Mandelbrot, B.B. Fractals and Scaling in Finance: Discontinuity, Concentration, Risks; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar]
- Mantegna, R.N.; Stanley, H.E. Scaling behaviour in the dynamics of an economic index. Nature 2002, 376, 46–49. [Google Scholar] [CrossRef]
- Niu, H.L.; Wang, J. Volatility clustering and long memory of financial time series and financial price model. Digit. Signal Process. 2013, 23, 489–498. [Google Scholar] [CrossRef]
- Niu, H.L.; Wang, J. Quantifying complexity of financial short-term time series by composite multiscale entropy measure. Commun. Nonlinear Sci. Numer. Simul. 2015, 22, 375–382. [Google Scholar] [CrossRef]
- Niu, H.L.; Wang, J.; Lu, Y.F. Fluctuation behaviors of financial return volatility duration. Physica A 2016, 448, 30–40. [Google Scholar] [CrossRef]
- Vodenska, I.; Becker, A.; Zhou, D.; Kenett, D.; Stanley, H.E.; Havlin, S. Community analysis of global financial markets. Risks 2016, 4, 13. [Google Scholar] [CrossRef]
- Junior, L.S.; Asher, M.; Kenett, D. Dependency relations among international stock market indices. J. Risk Financ. Manag. 2015, 8, 227–265. [Google Scholar] [CrossRef]
- Maasoumi, E.; Racine, J. Entropy and predictability of stock market returns. J. Econom. 2002, 107, 291–312. [Google Scholar] [CrossRef]
- Roman, H.E.; Porto, M.; Giovanardi, N. Anomalous scaling of stock price dynamics within ARCH-models. Eur. Phys. J. B 2001, 21, 155–158. [Google Scholar] [CrossRef]
- Stanley, H.E.; Mantegna, R. An Introduction to Econophysics; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Tang, L.H.; Huang, Z.F. Modelling high-frequency economic time series. Physica A 2000, 288, 444–450. [Google Scholar] [CrossRef]
- Tenreiro Machado, J.A. Entropy analysis of integer and fractional dynamical systems. Nonlinear Dyn. 2010, 62, 371–378. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Stosic, D.; Ludermir, T.; Oliveira, W.; Stosic, T. Foreign exchange rate entropy evolution during financial crises. Physica A 2016, 449, 233–239. [Google Scholar] [CrossRef]
- Benettin, G.; Galgani, L.; Strelcyn, J.M. Kolmogorov Entropy and Numerical Experiments. Phys. Rev. A 1976, 14, 2338–2345. [Google Scholar] [CrossRef]
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef] [PubMed]
- Richmann, J.S.; Moorman, J.R. Physiological time series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, 2039–2049. [Google Scholar] [CrossRef] [PubMed]
- Silva, L.E.V.; Cabella, B.C.T.; Nevesc, U.P.C.; Junior, L.O.M. Multiscale entropy-based methods for heart rate variability complexity analysis. Physica A 2015, 422, 143–152. [Google Scholar] [CrossRef]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Ouyang, G.; Li, D.; Li, X. Characterization of the causality between spike trains with permutation conditional mutual information. Phys. Rev. E 2011, 84, 021929. [Google Scholar] [CrossRef] [PubMed]
- Bruzzo, A.; Gesierich, B.; Santi, M.; Tassinari, C.; Birbaumer, N.; Rubboli, G. Permutation entropy to detect vigilance changes and preictal states from scalp EEG in epileptic patients. A preliminary study. Neurol. Sci. 2008, 29, 3–9. [Google Scholar] [CrossRef] [PubMed]
- Cao, Y.; Tung, W.W.; Gao, J.B.; Protopopescu, V.A.; Hively, L.M. Detecting dynamical changes in time series using the permutation entropy. Phys. Rev. E 2004, 70, 046217. [Google Scholar] [CrossRef] [PubMed]
- Graff, B.; Graff, G.; Kaczkowska, A. Entropy measures of heart rate variability for short ECG datasets in patients with congestive heart failure. Acta Phys. Pol. B 2012, 5, 153–157. [Google Scholar]
- Sacoa, P.M.; Carpia, L.C.; Figliolad, A.; Serranoe, E.; Rosso, O.A. Entropy analysis of the dynamics of El Nino/Southern Oscillation during the Holocene. Physica A 2010, 389, 5022–5027. [Google Scholar] [CrossRef]
- Zunino, L.; Zanin, M.; Tabak, B.; Perez, D.; Rosso, O.A. Forbidden patterns, permutation entropy and stock market inefficiency. Physica A 2009, 388, 2854–2864. [Google Scholar] [CrossRef]
- Fadlallah, B.; Principe, J.; Chen, B.; Keil, A. Weighted-permutation entropy: A complexity measure for time series incorporating amplitude information. Phys. Rev. E 2013, 87, 02291. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Jin, N.D.; Zhao, A.; Gao, Z.K.; Zhai, L.S.; Sun, B. The experimental signals analysis for bubbly oil-in-water flow using multi-scale weighted-permutation entropy. Physica A 2015, 417, 230–244. [Google Scholar] [CrossRef]
- Li, R.; Wang, J. Interacting price model and fluctuation behavior analysis from Lempel-Ziv complexity and multi-scale weighted-permutation entropy. Phys. Lett. A 2016, 380, 117–129. [Google Scholar] [CrossRef]
- Aparicio, T.; Pozo, E.F.; Saura, D. Detecting determinism using recurrence quantification analysis: Three test procedures. J. Econ. Behav. Organ. 2008, 65, 768–787. [Google Scholar] [CrossRef]
- Kwuimy, C.A.K.; Samadani, M.; Nataraj, C. Bifurcation analysis of a nonlinear pendulum using recurrence and statistical methods: Applications to fault diagnostics. Nonlinear Dyn. 2014, 76, 1963–1975. [Google Scholar] [CrossRef]
- Marwan, N.; Romano, M.C.; Thiel, M.; Kurths, J. Recurrence Plots for the Analysis of Complex Systems. Phys. Rep. 2007, 438, 237–329. [Google Scholar] [CrossRef]
- Zbilut, J.P.; Zaldivar-Comenges, J.M.; Strozzi, F. Recurrence quantification based on Lyapunov exponents for monitoring divergence in experimental data. Phys. Lett. A 2002, 297, 173–181. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.G.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and Hilbert spectrum for nonlinear and nonstationary time series analysis. Proc. R. Soc. Lond. A 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Ribeiro, H.V.; Zunino, L.; Mendes, R.S.; Lenzi, E.K. Complexity-entropy causality plane: A useful approach for distinguishing songs. Physica A 2012, 391, 1421–1428. [Google Scholar] [CrossRef]
- Hsieh, D.A. Chaos and nonlinear dynamics: Application to financial markets. J. Financ. 1991, 46, 1839–1877. [Google Scholar] [CrossRef]
- Frazer, A.M.; Swinney, H.L. Independent coordinates for strange attractors from mutual information. Phys. Rev. A 1986, 33, 1134–1140. [Google Scholar] [CrossRef]
- Kitamura, Y. Simple measures of market efficiency: A study in foreign exchange markets. Jpn. World Econ. 2017, 41, 1–16. [Google Scholar] [CrossRef]
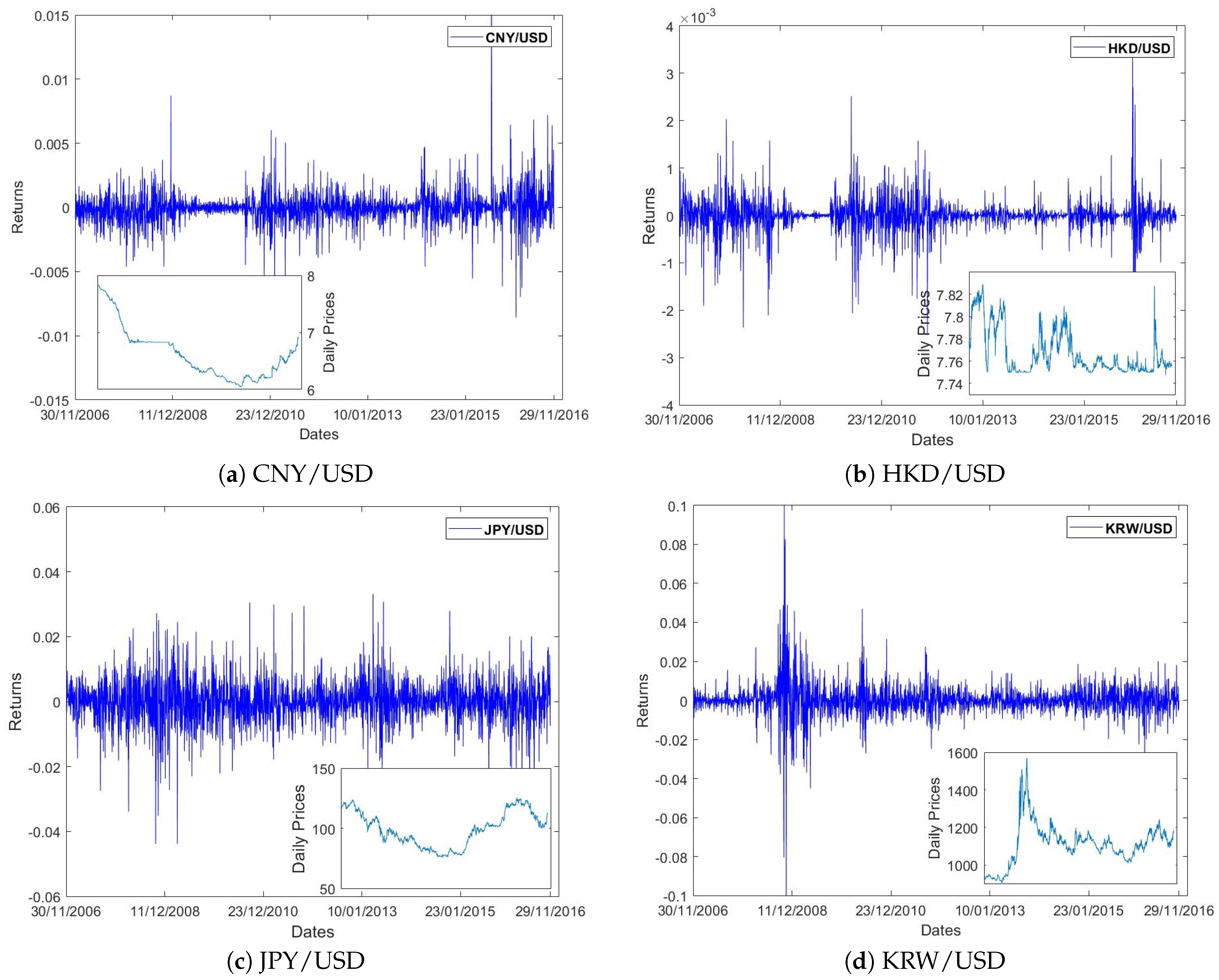



| Symbol | Mean | Std. | Min. | Median | Max. | Mode | Kur. | Skew. |
|---|---|---|---|---|---|---|---|---|
| CNY/USD | 6.6241 | 0.4487 | 6.0409 | 7.8346 | 6.8276 | 6.8276 | 3.3777 | 1.0076 |
| HKD/USD | 7.7677 | 0.0202 | 7.7474 | 7.8288 | 7.7501 | 7.7501 | 3.2079 | 1.1966 |
| JPY/USD | 99.5427 | 14.3627 | 75.7186 | 100.0821 | 125.5933 | 76.6822 | 1.8443 | 0.0441 |
| KRW/USD | 1111.5366 | 108.0174 | 903.8059 | 1111.5366 | 1570.0365 | 923.9899 | 4.8571 | 0.6416 |
| INR/USD | 52.7574 | 8.9675 | 39.1129 | 50.2955 | 68.8737 | 39.1667 | 1.6737 | 0.2335 |
| EUR/USD | 0.7682 | 0.0753 | 0.6246 | 0.7521 | 0.9503 | 0.7552 | 2.7133 | 0.6841 |
| GBP/USD | 0.6206 | 0.0669 | 0.4738 | 0.6288 | 0.8228 | 0.6240 | 3.4634 | −0.1852 |
| CHF/USD | 1.0042 | 0.1037 | 0.7299 | 0.9755 | 1.2535 | 0.9349 | 2.6815 | 0.6531 |
| 0.31337 | 0.70738 | 2.80653 | 16.02005 | 113.01158 | 928.67353 | 8421.36806 |
| CNY/USD | 0.7967 | 0.6696 | 0.6272 | 0.5962 | 0.5731 | 0.5682 | 0.5318 | 0.5145 | 0.5164 | 0.4932 |
| HKD/USD | 0.7645 | 0.6302 | 0.6258 | 0.5966 | 0.5280 | 0.5627 | 0.5301 | 0.5033 | 0.4960 | 0.4844 |
| JPY/USD | 0.8363 | 0.7298 | 0.6865 | 0.6467 | 0.6118 | 0.6008 | 0.5791 | 0.5638 | 0.5550 | 0.5207 |
| KRW/USD | 0.7316 | 0.5850 | 0.5818 | 0.5705 | 0.5016 | 0.5233 | 0.5138 | 0.4725 | 0.4767 | 0.5048 |
| INR/USD | 0.8161 | 0.7132 | 0.6486 | 0.6304 | 0.5970 | 0.5904 | 0.5778 | 0.5627 | 0.5486 | 0.5201 |
| EUR/USD | 0.8342 | 0.7286 | 0.6808 | 0.6255 | 0.5916 | 0.5895 | 0.5610 | 0.5377 | 0.5239 | 0.5204 |
| GBP/USD | 0.8114 | 0.6895 | 0.6508 | 0.6255 | 0.5874 | 0.5940 | 0.5679 | 0.5471 | 0.5348 | 0.5103 |
| CHF/USD | 0.7863 | 0.6622 | 0.6136 | 0.5816 | 0.5732 | 0.5777 | 0.5581 | 0.5237 | 0.5151 | 0.5160 |
| Gaussian | 0.8678 | 0.7618 | 0.6987 | 0.6571 | 0.6329 | 0.6099 | 0.5909 | 0.5759 | 0.5582 | 0.5423 |
| CNY/USD | HKD/USD | JPY/USD | KRW/USD | INR/USD | EUR/USD | GBP/USD | CHF/USD | |
|---|---|---|---|---|---|---|---|---|
| mean | 0.1069 | 0.0884 | 0.1549 | 0.2335 | 0.1520 | 0.1924 | 0.1783 | 0.1327 |
| 0.1270 | 0.1003 | 0.1661 | 0.1995 | 0.1364 | 0.1709 | 0.1975 | 0.1316 |
| Data | RR | DET | LAM | TT | |||||
|---|---|---|---|---|---|---|---|---|---|
| CNY/USD | 0.0030 | 0.3439 | 0.9665 | 2.9517 | 9.4494 | 0.8653 | 8.4481 | ||
| HKD/USD | 0.000852 | 0.4713 | 0.9842 | 3.4302 | 15.9962 | 0.9457 | 16.5285 | ||
| JPY/USD | 0.0104 | 0.0346 | 0.8471 | 1.8694 | 3.9859 | 0.4149 | 3.0828 | ||
| KRW/USD | 0.0280 | 0.7529 | 0.9955 | 4.2750 | 35.8296 | 0.9784 | 25.2570 | ||
| INR/USD | 0.0125 | 0.2467 | 0.9499 | 2.6748 | 7.0894 | 0.7608 | 5.3144 | ||
| EUR/USD | 0.0099 | 0.0319 | 0.8329 | 1.8931 | 4.0782 | 0.4170 | 3.1038 | ||
| GBP/USD | 0.0147 | 0.2094 | 0.9336 | 2.5286 | 6.3789 | 0.6928 | 4.6615 | ||
| CHF/USD | 0.0229 | 0.5309 | 0.9746 | 3.2140 | 11.6567 | 0.8779 | 7.9887 |
| Data | m | RR | DET | LAM | TT | ||||
|---|---|---|---|---|---|---|---|---|---|
| IMF1 | 8 | 1 | 0.0079 | 0.0347 | 0.9008 | 2.1014 | 4.6083 | 0.2144 | 3.4507 |
| IMF2 | 5 | 3 | 0.0047 | 0.1781 | 0.5657 | 1.5994 | 4.5146 | 0.7487 | 3.6681 |
| IMF3 | 4 | 4 | 0.0025 | 0.1454 | 0.8715 | 1.8186 | 5.1570 | 0.9308 | 4.5780 |
| IMF4 | 3 | 6 | 0.0016 | 0.1069 | 0.9823 | 2.7571 | 8.8940 | 0.9822 | 5.9583 |
| IMF5 | 3 | 9 | 0.0011 | 0.1148 | 0.9987 | 3.8455 | 19.6199 | 0.9982 | 10.9299 |
| IMF6 | 2 | 19 | 0.000708 | 0.1917 | 0.9999 | 4.6898 | 46.0817 | 0.9999 | 29.6150 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niu, H.; Zhang, L. Nonlinear Multiscale Entropy and Recurrence Quantification Analysis of Foreign Exchange Markets Efficiency. Entropy 2018, 20, 17. https://doi.org/10.3390/e20010017
Niu H, Zhang L. Nonlinear Multiscale Entropy and Recurrence Quantification Analysis of Foreign Exchange Markets Efficiency. Entropy. 2018; 20(1):17. https://doi.org/10.3390/e20010017
Chicago/Turabian StyleNiu, Hongli, and Lin Zhang. 2018. "Nonlinear Multiscale Entropy and Recurrence Quantification Analysis of Foreign Exchange Markets Efficiency" Entropy 20, no. 1: 17. https://doi.org/10.3390/e20010017
APA StyleNiu, H., & Zhang, L. (2018). Nonlinear Multiscale Entropy and Recurrence Quantification Analysis of Foreign Exchange Markets Efficiency. Entropy, 20(1), 17. https://doi.org/10.3390/e20010017




