Automated Diagnosis of Myocardial Infarction ECG Signals Using Sample Entropy in Flexible Analytic Wavelet Transform Framework
Abstract
:1. Introduction
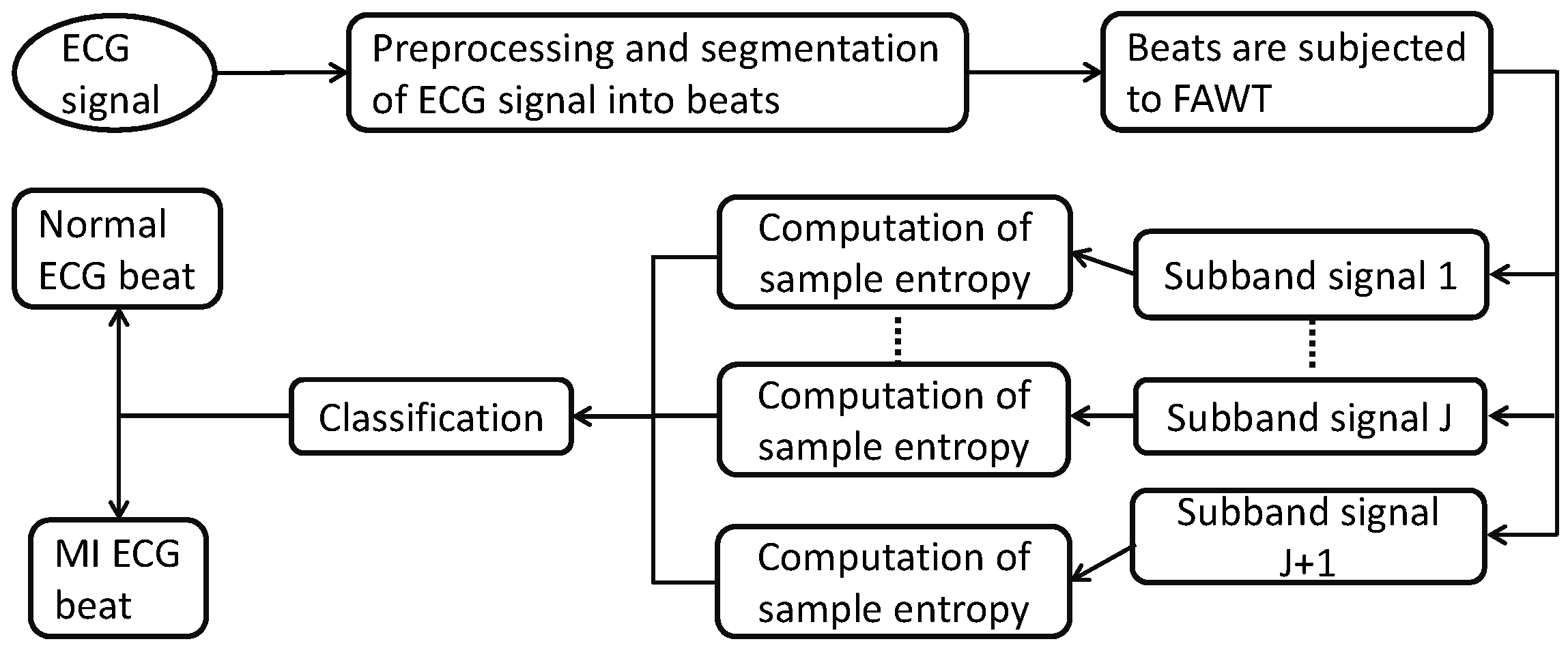
2. Methodology
2.1. Dataset Studied in This Work
2.2. Preprocessing and Segmentation of ECG Signals
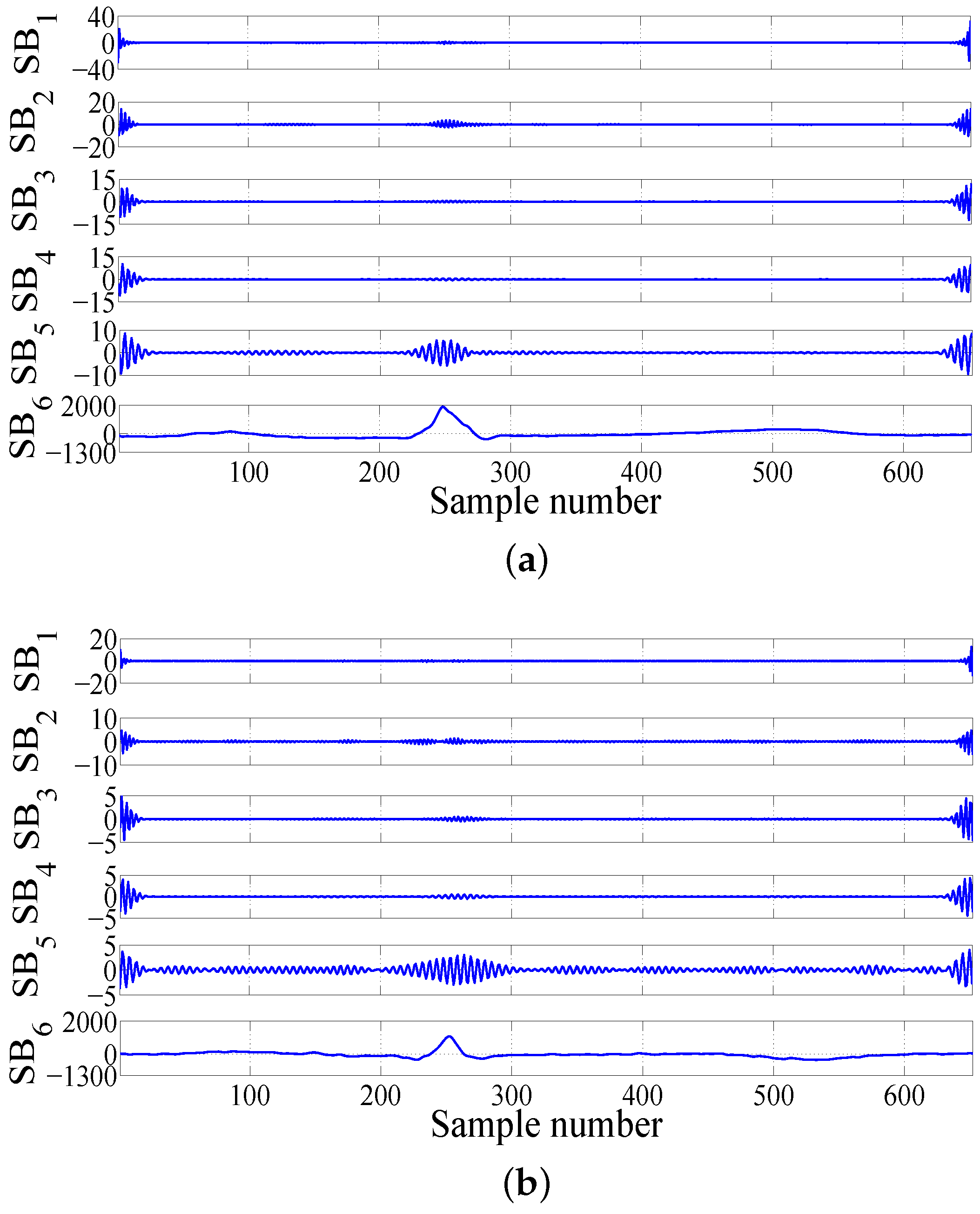
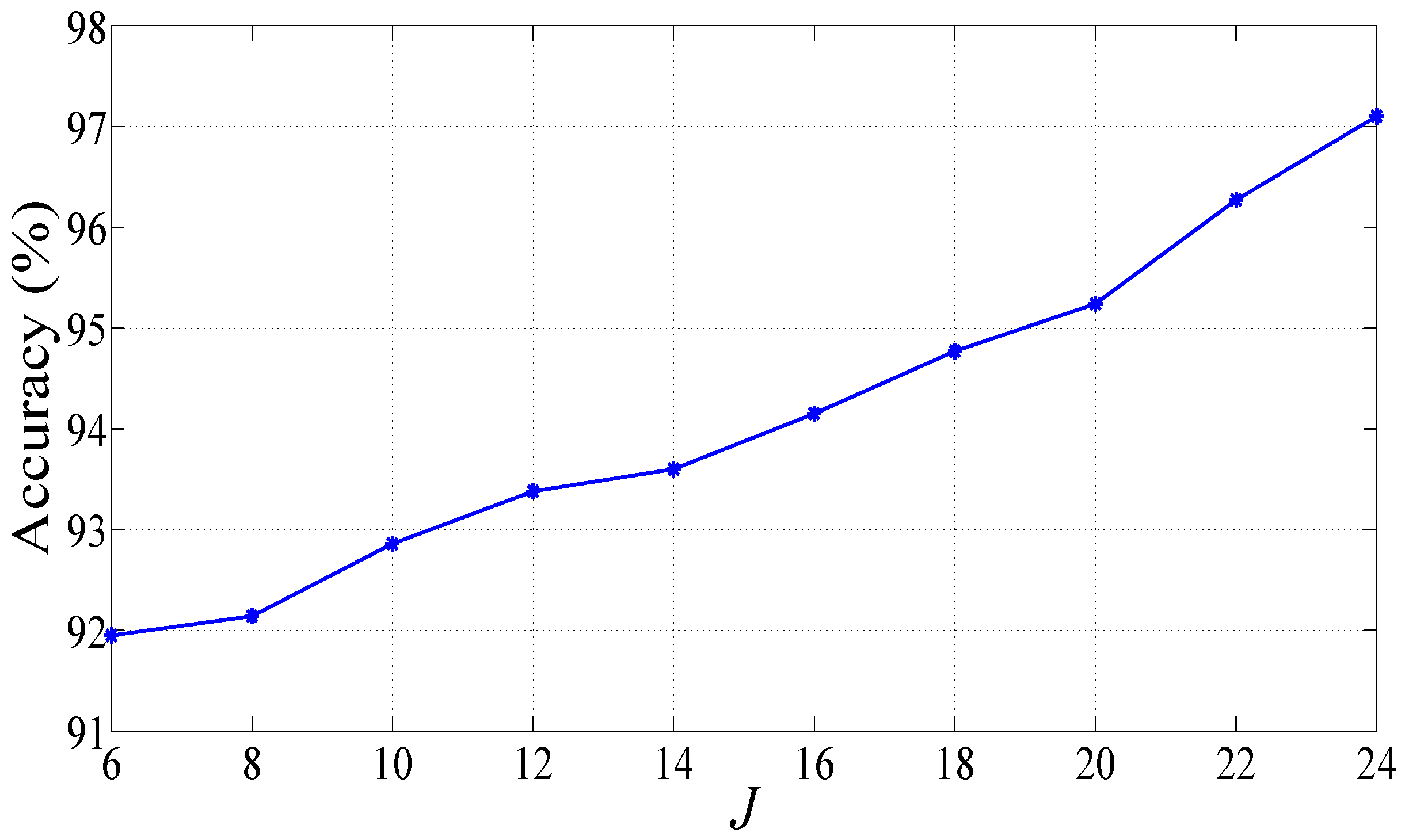
2.3. Computation of Features in FAWT Framework
• FAWT
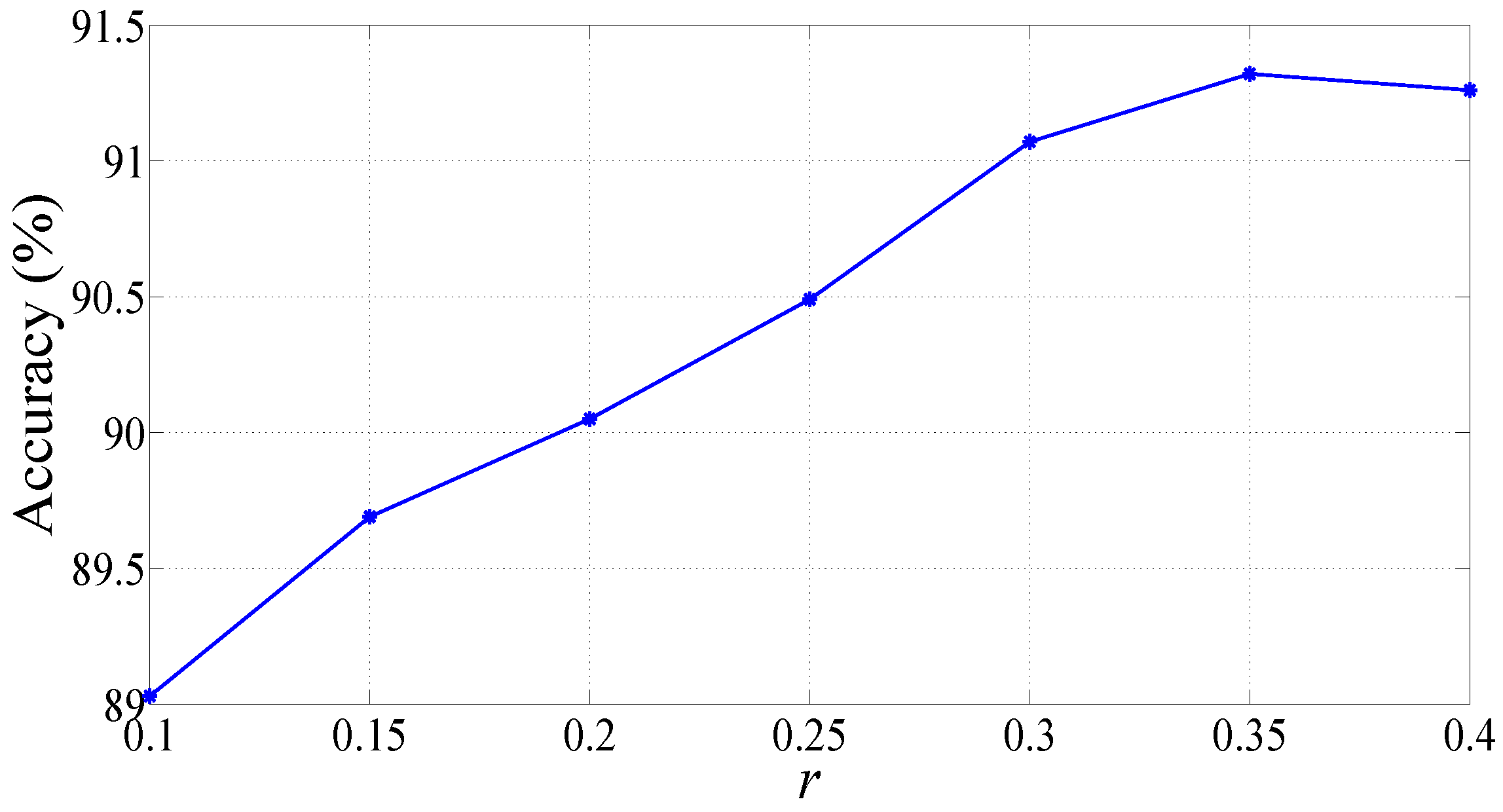
2.4. Sample Entropy
2.5. Studied Classification Techniques
3. Results
4. Discussions
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Thygesen, K.; Alpert, J.S.; Jaffe, A.S.; Simoons, M.L.; Chaitman, B.R.; White, H.D. Third universal definition of myocardial infarction. Eur. Heart J. 2012, 33, 2551–2567. [Google Scholar] [CrossRef] [PubMed]
- Sanchis-Gomar, F.; Perez-Quilis, C.; Leischik, R.; Lucia, A. Epidemiology of coronary heart disease and acute coronary syndrome. Ann. Transl. Med. 2016, 4, 256. [Google Scholar] [CrossRef] [PubMed]
- Acharya, U.R.; Fujita, H.; Sudarshan, V.K.; Oh, S.L.; Adam, M.; Koh, J.E.W.; Tan, J.H.; Ghista, D.N.; Martis, R.J.; Chua, C.K.; et al. Automated detection and localization of myocardial infarction using electrocardiogram: A comparative study of different leads. Knowl. Based Syst. 2016, 99, 146–156. [Google Scholar] [CrossRef]
- Lu, H.L.; Ong, K.; Chia, P. An automated ECG classification system based on a neuro-fuzzy system. Comput. Cardiol. 2000, 27, 387–390. [Google Scholar]
- Liu, B.; Liu, J.; Wang, G.; Huang, K.; Li, F.; Zheng, Y.; Luo, Y.; Zhou, F. A novel electrocardiogram parameterization algorithm and its application in myocardial infarction detection. Comput. Biol. Med. 2015, 61, 178–184. [Google Scholar] [CrossRef] [PubMed]
- Crippa, P.; Curzi, A.; Falaschetti, L.; Turchetti, C. Multi-class ECG beat classification based on a Gaussian mixture model of Karhunen-Loève transform. Int. J. Simul. Syst. Sci. Technol. 2015, 16. [Google Scholar] [CrossRef]
- Biagetti, G.; Crippa, P.; Curzi, A.; Orcioni, S.; Turchetti, C. A Multi-class ECG beat classifier based on the truncated KLT representation. In Proceedings of the European Modelling Symposium, Pisa, Italy, 21–23 October 2014; pp. 93–98. [Google Scholar]
- Li, H.; Liang, H.; Miao, C.; Cao, L.; Feng, X.; Tang, C.; Li, E. Novel ECG signal classification based on KICA nonlinear feature extraction. Circuits Syst. Signal Process. 2016, 35, 1187–1197. [Google Scholar] [CrossRef]
- Safdarian, N.; Dabanloo, N.J.; Attarodi, G. A new pattern recognition method for detection and localization of myocardial infarction using T-wave integral and total integral as extracted features from one cycle of ECG signal. J. Biomed. Sci. Eng. 2014, 7, 818–824. [Google Scholar] [CrossRef]
- Bozzola, P.; Bortolan, G.; Combi, C.; Pinciroli, F.; Brohet, C. A hybrid neuro-fuzzy system for ECG classification of myocardial infarction. In Proceedings of the Computers in Cardiology, Indianapolis, IN, USA, 8–11 September 1996; pp. 241–244. [Google Scholar]
- Sun, L.; Lu, Y.; Yang, K.; Li, S. ECG analysis using multiple instance learning for myocardial infarction detection. IEEE Trans. Biomed. Eng. 2012, 59, 3348–3356. [Google Scholar] [CrossRef] [PubMed]
- Haraldsson, H.; Edenbrandt, L.; Ohlsson, M. Detecting acute myocardial infarction in the 12-lead ECG using Hermite expansions and neural networks. Artif. Intell. Med. 2004, 32, 127–136. [Google Scholar] [CrossRef] [PubMed]
- Lahiri, T.; Kumar, U.; Mishra, H.; Sarkar, S.; Roy, A.D. Analysis of ECG signal by chaos principle to help automatic diagnosis of myocardial infarction. J. Sci. Ind. Res. 2009, 68, 866–870. [Google Scholar]
- Chang, P.C.; Hsieh, J.C.; Lin, J.J.; Chou, Y.H.; Liu, C.H. A hybrid system with hidden Markov models and Gaussian mixture models for myocardial infarction classification with 12-lead ECGs. In Proceedings of the 11th IEEE International Conference on High Performance Computing and Communications, Seoul, Korea, 25–27 June 2009; pp. 110–116. [Google Scholar]
- McDarby, G.; Celler, B.G.; Lovell, N.H. Characterising the discrete wavelet transform of an ECG signal with simple parameters for use in automated diagnosis. In Proceedings of the 2nd International Conference on Bioelectromagnetism, Melbourne, Australia, 15–18 February 1998; pp. 31–32. [Google Scholar]
- Banerjee, S.; Mitra, M. ECG feature extraction and classification of anteroseptal myocardial infarction and normal subjects using discrete wavelet transform. In Proceedings of the International Conference on Systems in Medicine and Biology, Kharagpur, India, 16–18 December 2010; pp. 55–60. [Google Scholar]
- Tripathy, R.K.; Dandapat, S. Detection of cardiac abnormalities from multilead ECG using multiscale phase alternation features. J. Med. Syst. 2016, 40, 143. [Google Scholar] [CrossRef] [PubMed]
- Acharya, U.R.; Fujita, H.; Adam, M.; Lih, O.S.; Sudarshan, V.K.; Hong, T.J.; Koh, J.E.W.; Hagiwara, Y.; Chua, C.K.; Poo, C.K.; et al. Automated characterization and classification of coronary artery disease and myocardial infarction by decomposition of ECG signals: A comparative study. Inf. Sci. 2017, 377, 17–29. [Google Scholar] [CrossRef]
- Acharya, U.R.; Fujita, H.; Sudarshan, V.K.; Oh, S.L.; Adam, M.; Tan, J.H.; Koo, J.H.; Jain, A.; Lim, C.M.; Chua, K.C. Automated characterization of coronary artery disease, myocardial infarction, and congestive heart failure using contourlet and shearlet transforms of electrocardiogram signal. Knowl. Based Syst. 2017, 132, 156–166. [Google Scholar] [CrossRef]
- Bayram, İ. An analytic wavelet transform with a flexible time-frequency covering. IEEE Trans. Signal Process. 2013, 61, 1131–1142. [Google Scholar]
- Zhang, C.; Li, B.; Chen, B.; Cao, H.; Zi, Y.; He, Z. Weak fault signature extraction of rotating machinery using flexible analytic wavelet transform. Mech. Syst. Signal Process. 2015, 64–65, 162–187. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Quinlan, J.R. Induction of decision trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar] [CrossRef]
- Quinlan, J.R. C4.5: Programs for Machine Learning; Morgan Kaufmann: San Francisco, CA, USA, 1993. [Google Scholar]
- Jang, J.S.R.; Sun, C.T.; Mizutani, E. Neuro-Fuzzy and Soft Computing: A Computational Approach to Learning and Machine Intelligence; Pearson: London, UK, 1997. [Google Scholar]
- Suykens, J.A.K.; Vandewalle, J. Least squares support vector machine classifiers. Neural Process. Lett. 1999, 9, 293–300. [Google Scholar] [CrossRef]
- Bousseljot, R.; Kreiseler, D.; Schnabel, A. Nutzung der EKG-Signaldatenbank CARDIODAT der PTB über das Internet. Biomed. Tech. Biomed. Eng. 1995, 40, 317–318. [Google Scholar] [CrossRef]
- Goldberger, A.L.; Amaral, L.A.; Glass, L.; Hausdorff, J.M.; Ivanov, P.C.; Mark, R.G.; Mietus, J.E.; Moody, G.B.; Peng, C.K.; Stanley, H.E. Physiobank, physiotoolkit, and physionet: Components of a new research resource for complex physiologic signals. Circulation 2000, 101, e215–e220. [Google Scholar] [CrossRef] [PubMed]
- Martis, R.J.; Acharya, U.R.; Min, L.C. ECG beat classification using PCA, LDA, ICA and discrete wavelet transform. Biomed. Signal Process. Control 2013, 8, 437–448. [Google Scholar] [CrossRef]
- Pan, J.; Tompkins, W.J. A real-time QRS detection algorithm. IEEE Trans. Biomed. Eng. 1985, 32, 230–236. [Google Scholar] [CrossRef] [PubMed]
- Kumar, M.; Pachori, R.B.; Acharya, U.R. An efficient automated technique for CAD diagnosis using flexible analytic wavelet transform and entropy features extracted from HRV signals. Expert Syst. Appl. 2016, 63, 165–172. [Google Scholar] [CrossRef]
- Kumar, M.; Pachori, R.B.; Acharya, U.R. Characterization of coronary artery disease using flexible analytic wavelet transform applied on ECG signals. Biomed. Signal Process. Control 2017, 31, 301–308. [Google Scholar] [CrossRef]
- Kumar, M.; Pachori, R.B.; Acharya, U.R. Use of accumulated entropies for automated detection of congestive heart failure in flexible analytic wavelet transform framework based on short-term HRV signals. Entropy 2017, 19, 92. [Google Scholar] [CrossRef]
- Gupta, V.; Priya, T.; Yadav, A.K.; Pachori, R.B.; Acharya, U.R. Automated detection of focal EEG signals using features extracted from flexible analytic wavelet transform. Pattern Recogn. Lett. 2017, 94, 180–188. [Google Scholar] [CrossRef]
- Bayram, İ. An Analytic Wavelet Transform with a Flexible Time-Frequency Covering. Available online: http://web.itu.edu.tr/ibayram/AnDWT/ (accessed on 11 June 2017).
- Richman, J.S.; Moorman, J.R. Physiological time–series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [PubMed]
- Sokunbi, M.O.; Fung, W.; Sawlani, V.; Choppin, S.; Linden, D.E.J.; Thome, J. Resting state fMRI entropy probes complexity of brain activity in adults with ADHD. Psychiatry Res. Neuroimaging 2013, 214, 341–348. [Google Scholar] [CrossRef] [PubMed]
- Hall, M.; Frank, E.; Holmes, G.; Pfahringer, B.; Reutemann, P.; Witten, I.H. The WEKA data mining software: An update. SIGKDD Explor. 2009, 11, 10–18. [Google Scholar] [CrossRef]
- Sharma, R.; Pachori, R.B.; Upadhyay, A. Automatic sleep stages classification based on iterative filtering of electroencephalogram signals. Neural Comput. Appl. 2017, 1–20. [Google Scholar] [CrossRef]
- Sharma, R.; Pachori, R.B.; Acharya, U.R. An integrated index for the identification of focal electroencephalogram signals using discrete wavelet transform and entropy measures. Entropy 2015, 17, 5218–5240. [Google Scholar]
- Pachori, R.B.; Kumar, M.; Avinash, P.; Shashank, K.; Acharya, U.R. An improved online paradigm for screening of diabetic patients using RR-interval signals. J. Mech. Med. Biol. 2016, 16, 1640003. [Google Scholar] [CrossRef]
- Sharma, R.; Pachori, R.B.; Acharya, U.R. Application of entropy measures on intrinsic mode functions for the automated identification of focal electroencephalogram signals. Entropy 2015, 17, 669–691. [Google Scholar] [CrossRef]
- Sharma, R.; Pachori, R.B. Classification of epileptic seizures in EEG signals based on phase space representation of intrinsic mode functions. Expert Syst. Appl. 2015, 42, 1106–1117. [Google Scholar] [CrossRef]
- Sharma, R.; Kumar, M.; Pachori, R.B.; Acharya, U.R. Decision support system for focal EEG signals using tunable-Q wavelet transform. J. Comput. Sci. 2017, 20, 52–60. [Google Scholar] [CrossRef]
- Azar, A.T.; El-Said, S.A. Performance analysis of support vector machines classifiers in breast cancer mammography recognition. Neural Comput. Appl. 2014, 24, 1163–1177. [Google Scholar] [CrossRef]
- Khandoker, A.H.; Lai, D.T.H.; Begg, R.K.; Palaniswami, M. Wavelet-based feature extraction for support vector machines for screening balance impairments in the elderly. IEEE Trans. Neural Syst. Rehabil. Eng. 2007, 15, 587–597. [Google Scholar] [CrossRef] [PubMed]
- Zavar, M.; Rahati, S.; Akbarzadeh-T, M.R.; Ghasemifard, H. Evolutionary model selection in a wavelet-based support vector machine for automated seizure detection. Expert Syst. Appl. 2011, 38, 10751–10758. [Google Scholar] [CrossRef]
- Bajaj, V.; Pachori, R.B. Classification of seizure and nonseizure EEG signals using empirical mode decomposition. IEEE Trans. Inf. Technol. Biomed. 2012, 16, 1135–1142. [Google Scholar]
- Kohavi, R. A study of cross-validation and bootstrap for accuracy estimation and model selection. In Proceedings of the 14th International Joint Conference on Artificial Intelligence, Montreal, QC, Canada, 20–25 August 1995; pp. 1137–1143. [Google Scholar]
- Derryberry, D.R.; Schou, S.B.; Conover, W.J. Teaching rank-based tests by emphasizing structural similarities to corresponding parametric tests. J. Stat. Educ. 2010, 18, 1–19. [Google Scholar]
- Theodoridis, S.; Koutroumbas, K. Feature Selection. In Pattern Recognition, 2nd ed.; Academic Press: San Diego, CA, USA, 2003; pp. 163–205. [Google Scholar]
- McKight, P.E.; Najab, J. Kruskal-Wallis Test. Corsini Encyclopedia of Psychology; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 2010. [Google Scholar]
- Pachori, R.B. Discrimination between ictal and seizure-free EEG signals using empirical mode decomposition. Res. Lett. Signal Process. 2008. [Google Scholar] [CrossRef]
- Pachori, R.B.; Avinash, P.; Shashank, K.; Sharma, R.; Acharya, U.R. Application of empirical mode decomposition for analysis of normal and diabetic RR-interval signals. Expert Syst. Appl. 2015, 42, 4567–4581. [Google Scholar] [CrossRef]
- Sood, S.; Kumar, M.; Pachori, R.B.; Acharya, U.R. Application of empirical mode decomposition-based features for analysis of normal and CAD heart rate signals. J. Mech. Med. Biol. 2016, 16, 1640002. [Google Scholar] [CrossRef]
- Arif, M.; Malagore, I.A.; Afsar, F.A. Automatic detection and localization of myocardial infarction using back propagation neural networks. In Proceedings of the 4th International Conference on Bioinformatics and Biomedical Engineering, Chengdu, China, 18–20 June 2010; pp. 1–4. [Google Scholar]
- Al-Kindi, S.G.; Ali, F.; Farghaly, A.; Nathani, M.; Tafreshi, R. Towards real-time detection of myocardial infarction by digital analysis of electrocardiograms. In Proceedings of the 1st Middle East Conference on Biomedical Engineering, Sharjah, UAE, 21–24 February 2011; pp. 454–457. [Google Scholar]
- Banerjee, S.; Mitra, M. Application of cross wavelet transform for ECG pattern analysis and classification. IEEE Trans. Instrum. Meas. 2014, 63, 326–333. [Google Scholar] [CrossRef]
- Sharma, L.N.; Tripathy, R.K.; Dandapat, S. Multiscale energy and eigenspace approach to detection and localization of myocardial infarction. IEEE Trans. Biomed. Eng. 2015, 62, 1827–1837. [Google Scholar] [CrossRef] [PubMed]
- Acharya, U.R.; Fujita, H.; Oh, S.L.; Hagiwara, Y.; Tan, J.H.; Adam, M. Application of deep convolutional neural network for automated detection of myocardial infarction using ECG signals. Inf. Sci. 2017, 415, 190–198. [Google Scholar] [CrossRef]
| Filters and Parameters | Mathematical Expressions |
|---|---|
| Used in FAWT | |
| Low pass filter [20] | |
| where, | |
| High pass filter [20] | |
| where, | |
| , | |
| Condition for perfect reconstruction [20] | |
| where, | |
| = |
| Kernel Functions | Mathematical Expressions |
|---|---|
| Linear [26] | |
| Polynomial [26] | |
| Radial basis function (RBF) [46] | |
| Morlet wavelet [47,48] |
| m⟶ | 2 | 3 | 4 | 5 |
|---|---|---|---|---|
| ↓ | ||||
| 1 | 87.716% | 89.353% | 89.353% | 89.629% |
| 2 | 88.92% | 89.128% | 89.32% | 89.075% |
| 3 | 89.126% | 88.84% | 88.739% | 88.84% |
| Kernel Function | Parameters | Accuracy (%) | Sensitivity (%) | Specificity (%) |
|---|---|---|---|---|
| Linear | 83.32 | 81.83 | 89.02 | |
| Polynomial | x = 2 | 96.30 | 96.01 | 97.43 |
| x = 3 | 96.74 | 96.44 | 97.92 | |
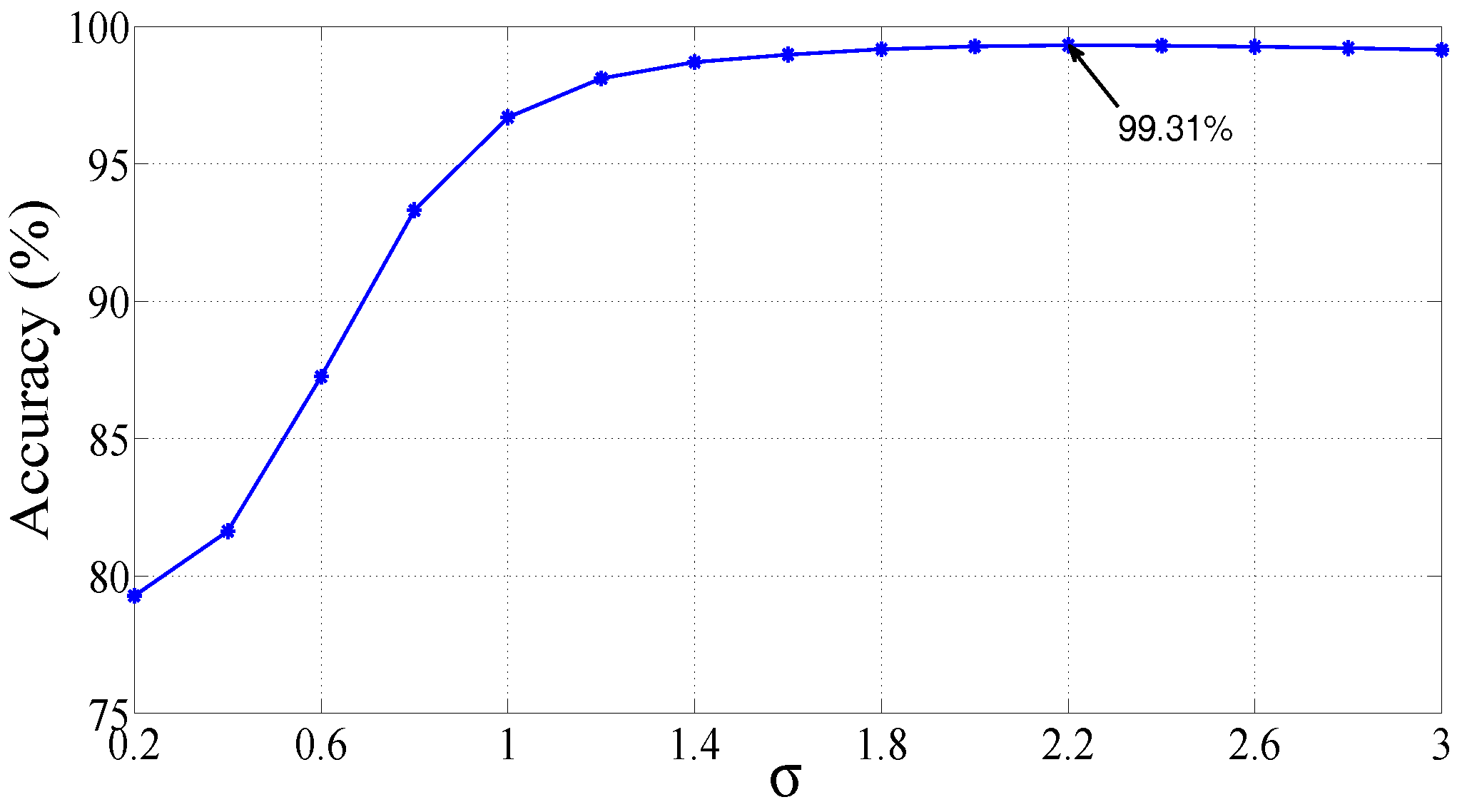
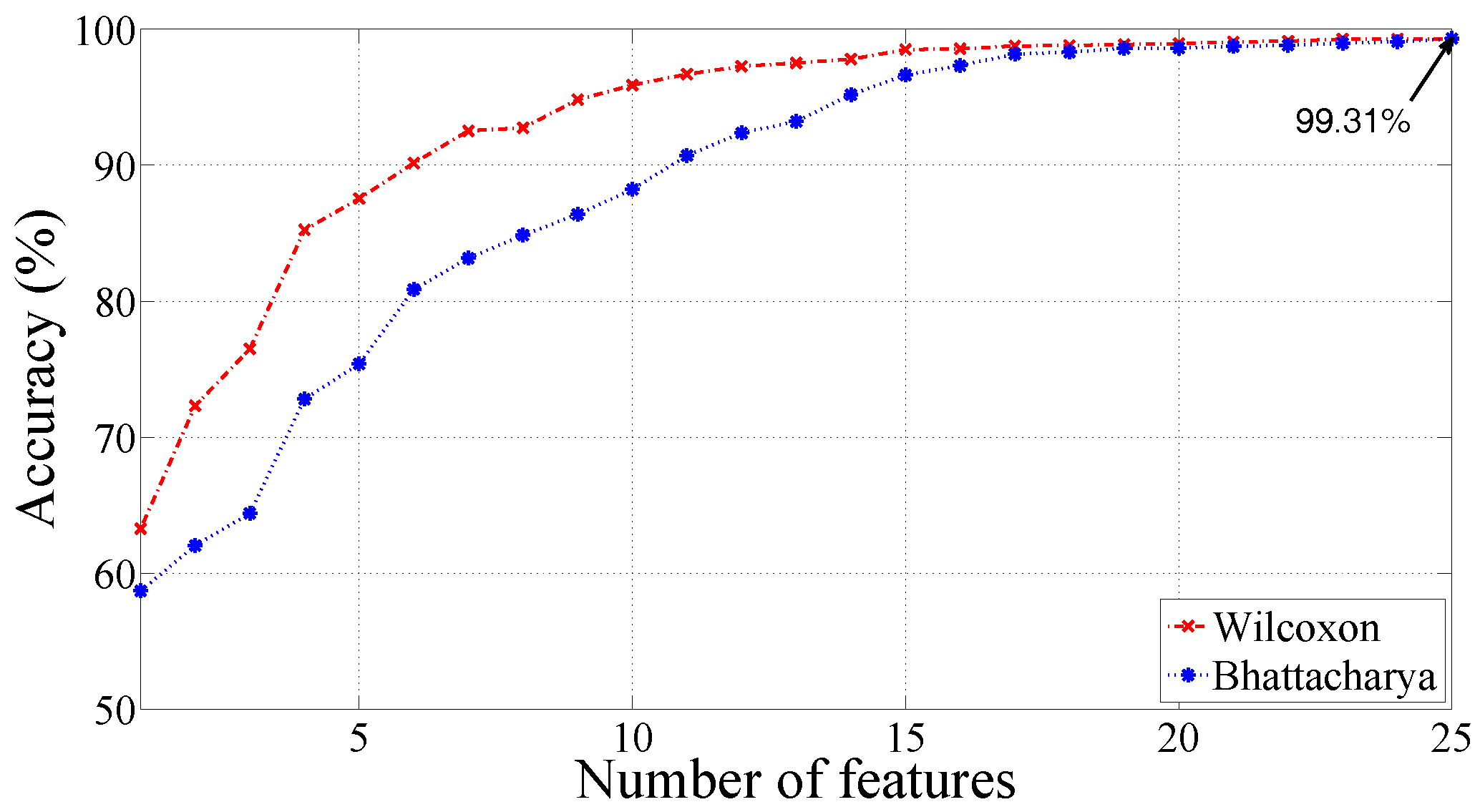
| RBF | = 2.2 | 99.31 | 99.62 | 98.12 |
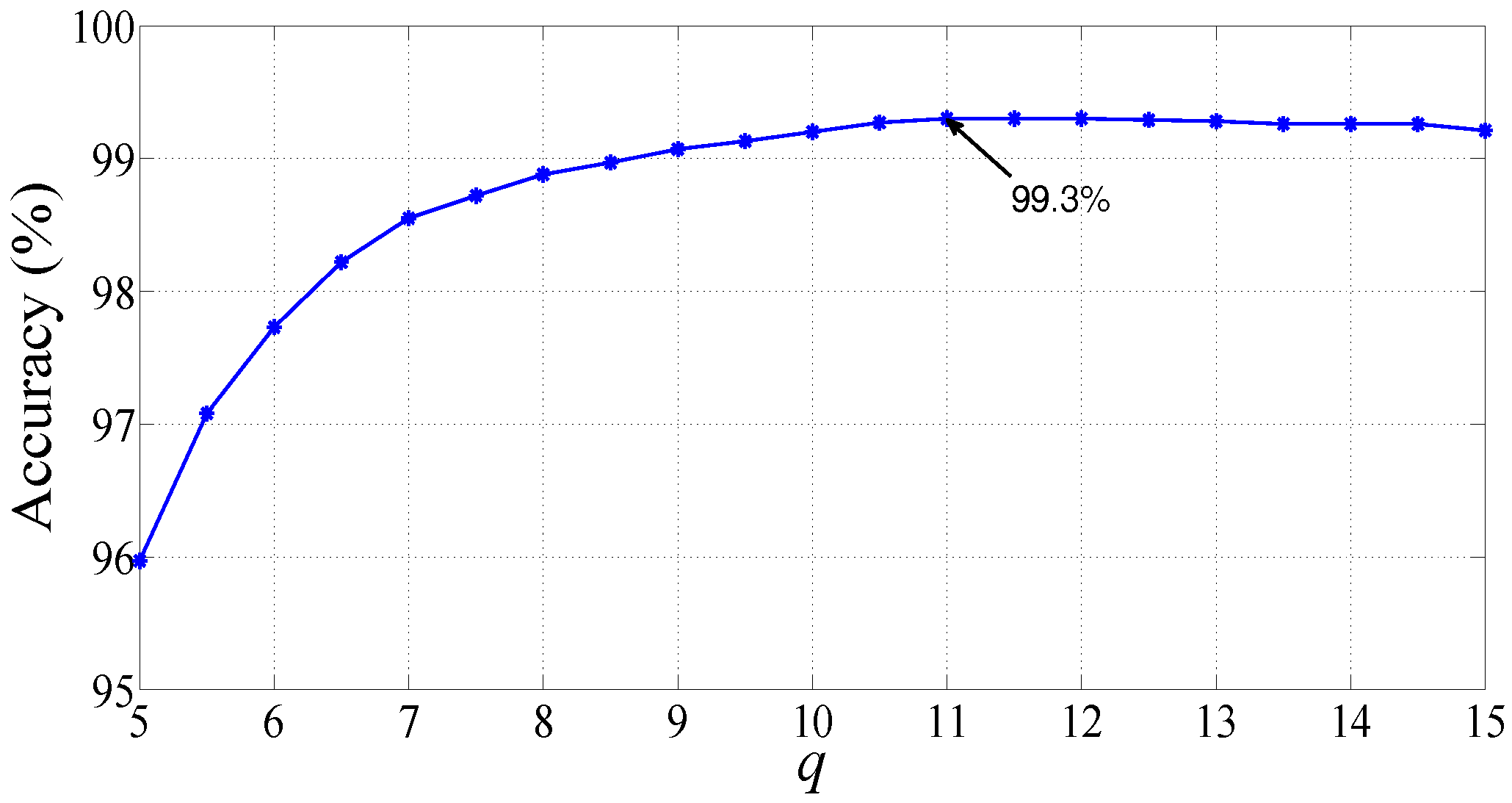
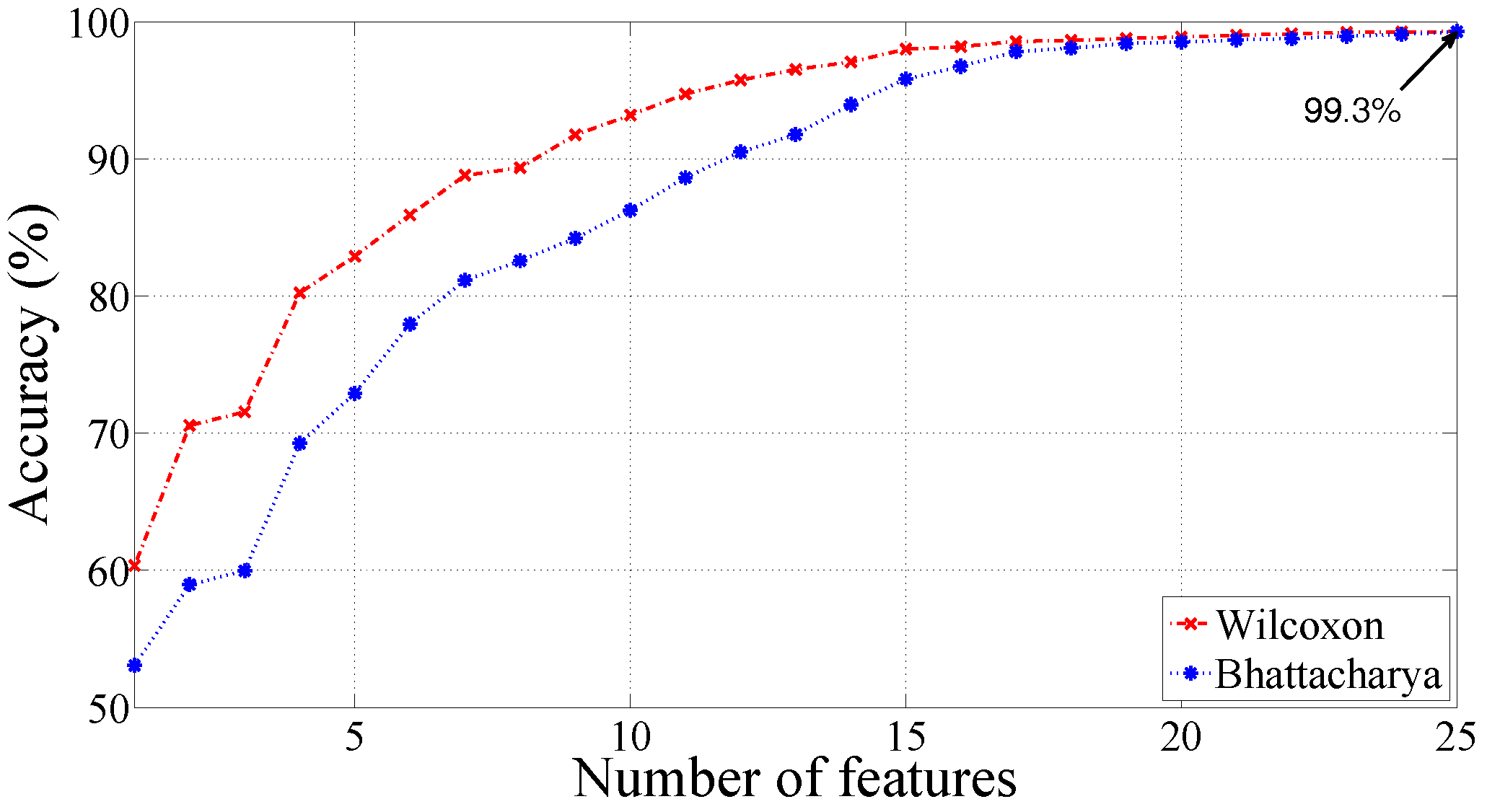
| Morlet wavelet | q = 11, = 0.25 | 99.30 | 99.64 | 97.92 |
| Feature | Normal Class () | MI Class () |
|---|---|---|
| SEnt | ||
| SEnt | ||
| SEnt | ||
| SEnt | ||
| SEnt | ||
| SEnt | ||
| SEnt | ||
| SEnt | ||
| SEnt | ||
| SEnt | ||
| SEnt | ||
| SEnt | ||
| SEnt | ||
| SEnt | ||
| SEnt | ||
| SEnt | ||
| SEnt | ||
| SEnt | ||
| SEnt | ||
| SEnt | ||
| SEnt | ||
| SEnt | ||
| SEnt | ||
| SEnt | ||
| SEnt |
| Kernel Function | Parameters | Accuracy (%) | Sensitivity (%) | Specificity (%) |
|---|---|---|---|---|
| Linear | ||||
| Polynomial | x = 2 | |||
| x = 3 | ||||
| RBF | = 2.2 | |||
| Morlet wavelet | q = 11, = 0.25 |
| Author | Year | Dataset | Analyzing | Number | Classification | 10-Fold Cross | Classification |
|---|---|---|---|---|---|---|---|
| Method | of Leads | Method Used | Validation | Performance (%) | |||
| Arif et al. [56] | 2010 | PTB diagnostic | Time-domain | 12-lead | BPNN | No | Sensitivity = 97.5 |
| ECG dtabase | method | ||||||
| Al-Kindi et al. [57] | 2011 | PTB diagnostic | Time-domain | 12-lead | - | No | Sensitivity = 85 |
| ECG dtabase | method | ||||||
| Banerjee et al. [58] | 2014 | PTB diagnostic | XWT based | 3-lead | Threshold based | No | Accuracy = 97.6 |
| ECG dtabase | method | classifier | |||||
| Liu et al. [5] | 2015 | PTB diagnostic | ECG polynomial | 12-lead | J48 | No | Accuracy = 94.4 |
| ECG dtabase | fitting | decision tree | |||||
| Sharma et al. [59] | 2015 | PTB diagnostic | MEES based | 12-lead | SVM with | No | Accuracy = 96.15 |
| ECG dtabase | method | RBF kernel | |||||
| Acharya et al. [3] | 2016 | PTB diagnostic | DWT, Nonlinear | One lead | k-NN | Yes | Accuracy = 98.8 |
| ECG dtabase | features | (lead-11) | |||||
| Acharya et al. [60] | 2017 | PTB diagnostic | No feature extraction | One lead | CNN | Yes | Accuracy = 95.22 |
| ECG dtabase | and selection | (lead-2) | |||||
| Present method | PTB diagnostic | FAWT and | One lead | LS-SVM | Yes | Accuracy = 99.31 | |
| ECG dtabase | SEnt | (lead-2) |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar, M.; Pachori, R.B.; Acharya, U.R. Automated Diagnosis of Myocardial Infarction ECG Signals Using Sample Entropy in Flexible Analytic Wavelet Transform Framework. Entropy 2017, 19, 488. https://doi.org/10.3390/e19090488
Kumar M, Pachori RB, Acharya UR. Automated Diagnosis of Myocardial Infarction ECG Signals Using Sample Entropy in Flexible Analytic Wavelet Transform Framework. Entropy. 2017; 19(9):488. https://doi.org/10.3390/e19090488
Chicago/Turabian StyleKumar, Mohit, Ram Bilas Pachori, and U. Rajendra Acharya. 2017. "Automated Diagnosis of Myocardial Infarction ECG Signals Using Sample Entropy in Flexible Analytic Wavelet Transform Framework" Entropy 19, no. 9: 488. https://doi.org/10.3390/e19090488
APA StyleKumar, M., Pachori, R. B., & Acharya, U. R. (2017). Automated Diagnosis of Myocardial Infarction ECG Signals Using Sample Entropy in Flexible Analytic Wavelet Transform Framework. Entropy, 19(9), 488. https://doi.org/10.3390/e19090488






