The Partial Information Decomposition of Generative Neural Network Models
Abstract
:1. Introduction
1.1. Why Information Theory?
1.2. Related Work
2. Methods
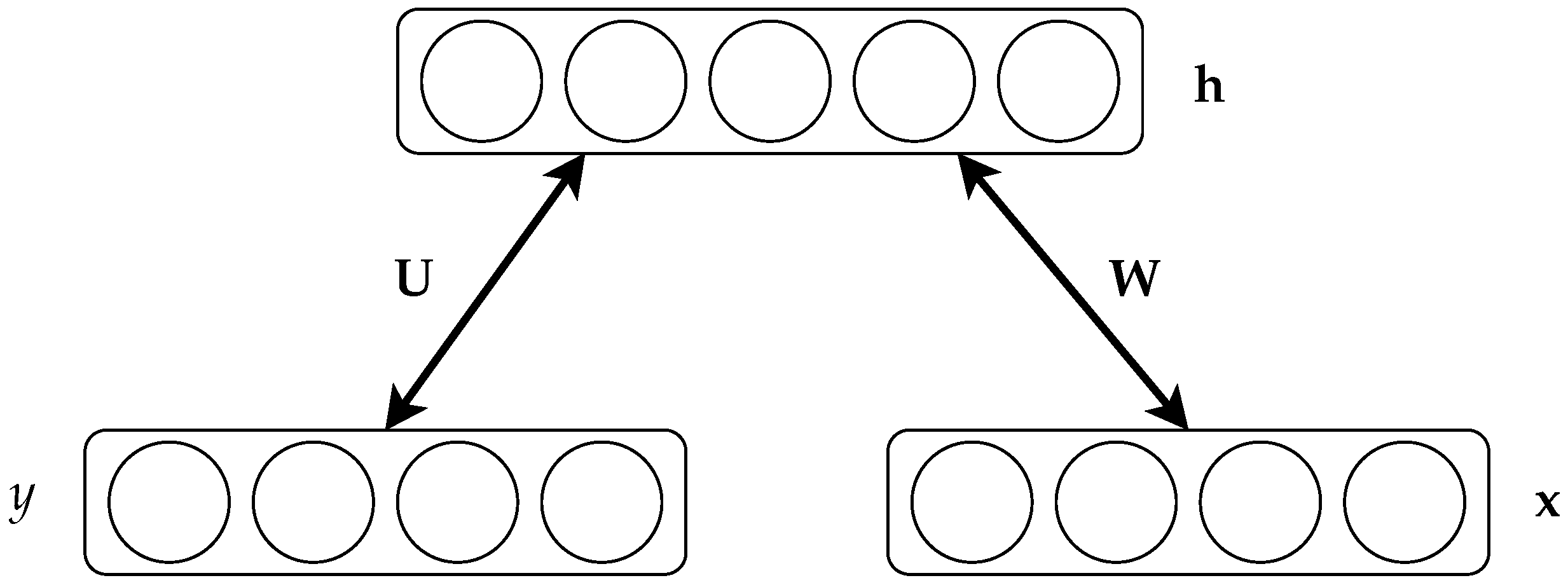
2.1. Restricted Boltzmann Machines
2.2. Information Theory
2.2.1. Non-Negative Decomposition of Multivariate Information
- Unique information U one of the sources provides and the other does not.
- Redundant information R both sources provide.
- Synergistic information S the sources provide jointly, which is not known when either of them is considered separately.
3. Results
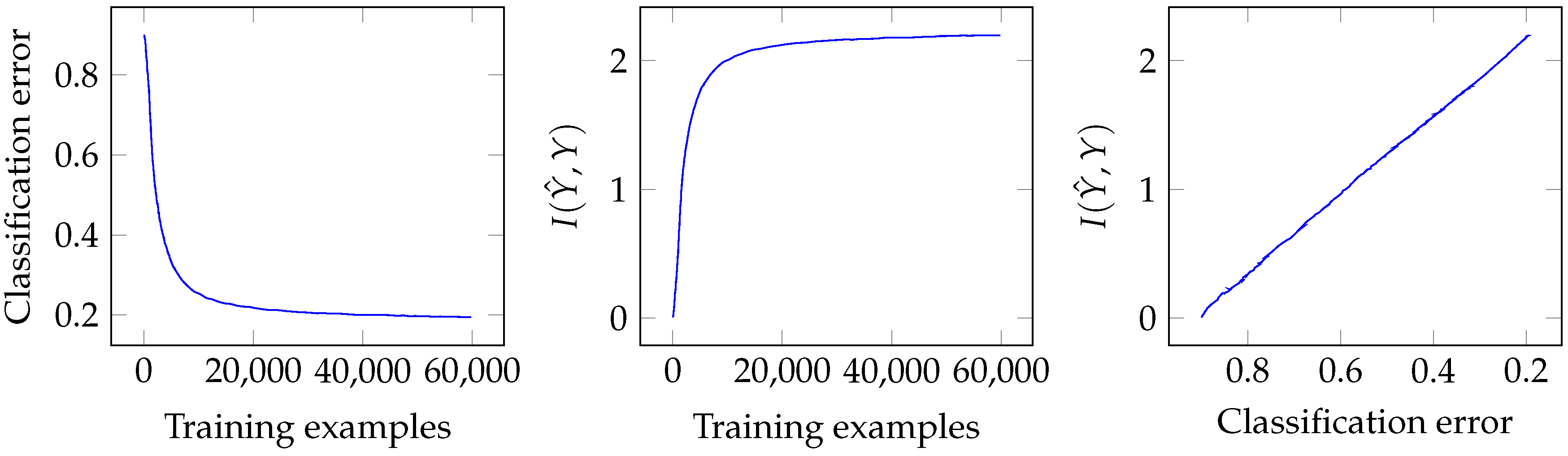
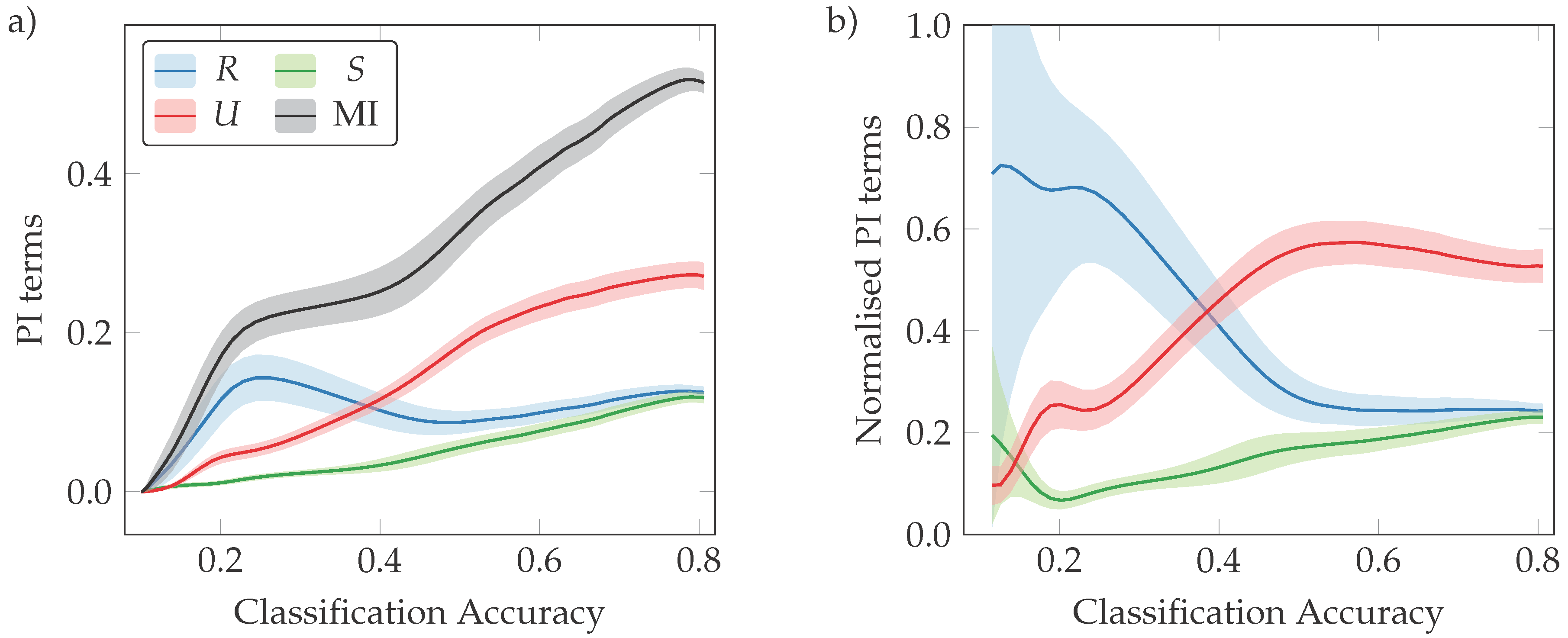
3.1. Classification Error and Mutual Information
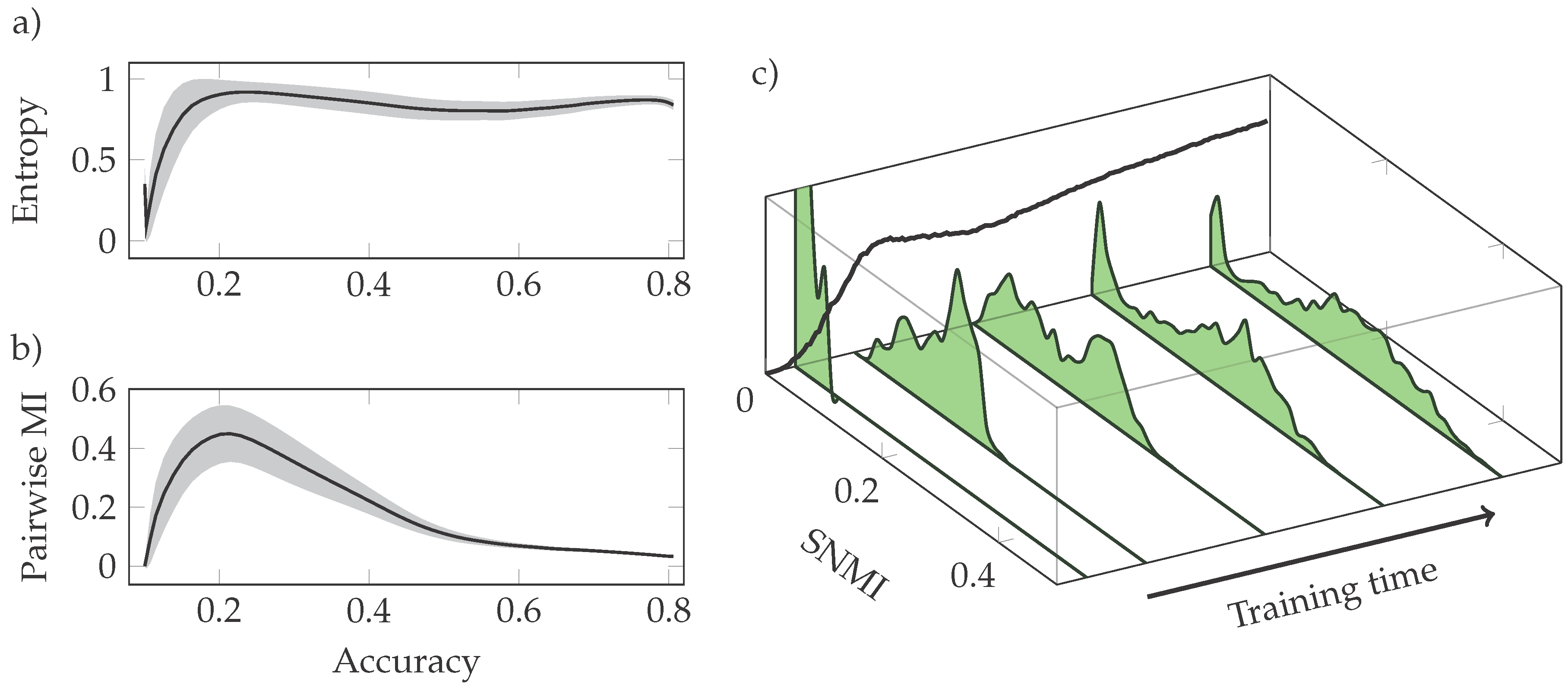
3.2. Phases of Learning
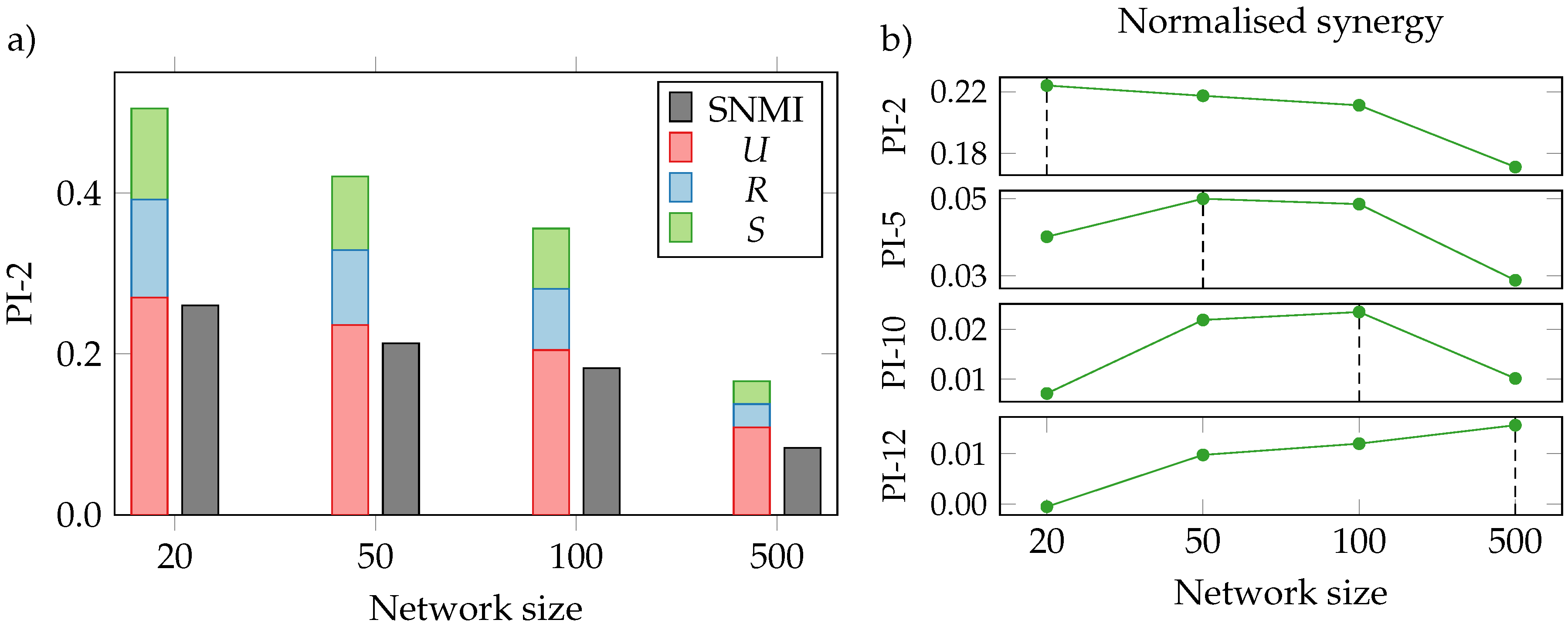
3.3. Neural Interactions
3.4. Limitations
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Gal, Y.; Ghahramani, Z. Dropout as a Bayesian Approximation: Representing Model Uncertainty in Deep Learning. arXiv 2015, arXiv:1206.5538. [Google Scholar]
- Bengio, Y.; Courville, A.; Vincent, P. Representation Learning: A Review and New Perspectives. arXiv 2012, arXiv:1206.5538. [Google Scholar] [CrossRef] [PubMed]
- Higgins, I.; Matthey, L.; Glorot, X.; Pal, A.; Uria, B.; Blundell, C.; Mohamed, S.; Lerchner, A. Early Visual Concept Learning with Unsupervised Deep Learning. arXiv 2016, arXiv:1606.05579. [Google Scholar]
- Mathieu, M.; Zhao, J.; Sprechmann, P.; Ramesh, A.; LeCun, Y. Disentangling Factors of Variation in Deep Representations Using Adversarial Training. arXiv 2016, arXiv:1611.03383. [Google Scholar]
- Siddharth, N.; Paige, B.; Van de Meent, J.W.; Desmaison, A.; Wood, F.; Goodman, N.D.; Kohli, P.; Torr, P.H.S. Learning Disentangled Representations with Semi-Supervised Deep Generative Models. arXiv 2017, arXiv:1706.00400. [Google Scholar]
- Lake, B.M.; Ullman, T.D.; Tenenbaum, J.B.; Gershman, S.J. Building Machines That Learn and Think Like People. arXiv 2016, arXiv:1604.00289. [Google Scholar] [CrossRef] [PubMed]
- Garnelo, M.; Arulkumaran, K.; Shanahan, M. Towards Deep Symbolic Reinforcement Learning. arXiv 2016, arXiv:1609.05518. [Google Scholar]
- Williams, P.L.; Beer, R.D. Nonnegative Decomposition of Multivariate Information. arXiv 2010, arXiv:1004.2515. [Google Scholar]
- Rieke, F.; Bialek, W.; Warland, D.; de Ruyter van Steveninck, R. Spikes: Exploring the Neural Code; MIT Press: Cambridge, MA, USA, 1997; p. 395. [Google Scholar]
- Le, Q.V.; Ranzato, M.; Monga, R.; Devin, M.; Chen, K.; Corrado, G.S.; Dean, J.; Ng, A.Y. Building High-Level Features Using Large Scale Unsupervised Learning. arXiv 2011, arXiv:1112.6209. [Google Scholar]
- Zeiler, M.D.; Fergus, R. Visualizing and Understanding Convolutional Networks. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; Springer: Berlin, Germany, 2014; pp. 818–833. [Google Scholar]
- Choromanska, A.; Henaff, M.; Mathieu, M.; Arous, G.B.; LeCun, Y. The Loss Surfaces of Multilayer Networks. arXiv 2014, arXiv:1412.0233. [Google Scholar]
- Kawaguchi, K. Deep Learning Without Poor Local Minima. arXiv 2016, arXiv:1605.07110. [Google Scholar]
- Sørngård, B. Information Theory for Analyzing Neural Networks. Master’s Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2014. [Google Scholar]
- Schwartz-Ziv, R.; Tishby, N. Opening the Black Box of Deep Neural Networks via Information. arXiv 2017, arXiv:1703.00810. [Google Scholar]
- Achille, A.; Soatto, S. On the Emergence of Invariance and Disentangling in Deep Representations. arXiv 2017, arXiv:1706.01350. [Google Scholar]
- Tishby, N.; Zaslavsky, N. Deep Learning and the Information Bottleneck Principle. arXiv 2015, arXiv:1503.02406. [Google Scholar]
- Berglund, M.; Raiko, T.; Cho, K. Measuring the Usefulness of Hidden Units in Boltzmann Machines with Mutual Information. Neural Netw. 2015, 64, 12–18. [Google Scholar] [CrossRef] [PubMed]
- Balduzzi, D.; Frean, M.; Leary, L.; Lewis, J.; Ma, K.W.D.; McWilliams, B. The Shattered Gradients Problem: If Resnets are the Answer, Then What is the Question? arXiv 2017, arXiv:1702.08591. [Google Scholar]
- Hinton, G.E.; van Camp, D. Keeping the Neural Networks Simple by Minimizing the Description Length of the Weights. In Proceedings of the Sixth Annual Conference on Computational Learning Theory (COLT), Santa Cruz, CA, USA, 26–28 July 1993; ACM: New York, NY, USA, 1993; pp. 5–13. [Google Scholar]
- Smolensky, P. Information Processing in Dynamical Systems: Foundations of Harmony Theory; Technical Report, DTIC Document; MIT Press: Cambridge, MA, USA, 1986. [Google Scholar]
- Larochelle, H.; Bengio, Y. Classification Using Discriminative Restricted Boltzmann Machines. In Proceedings of the 25th International Conference on Machine Learning, Helsinki, Finland, 5–9 July 2008; pp. 536–543. [Google Scholar]
- Hinton, G.E.; Osindero, S.; Teh, Y.W. A Fast Learning Algorithm for Deep Belief Nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef] [PubMed]
- Tieleman, T. Training Restricted Boltzmann Machines Using Approximations to the Likelihood Gradient. In Proceedings of the 25th International Conference on Machine Learning, Helsinki, Finland, 5–9 July 2008; ACM Press: New York, NY, USA, 2008; pp. 1064–1071. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley: Hoboken, NJ, USA, 2006. [Google Scholar]
- DeWeese, M.R.; Meister, M. How to Measure the Information Gained from one Symbol. Netw. Comput. Neural Syst. 1999, 12, 325–340. [Google Scholar] [CrossRef]
- Ince, R.A.A. Measuring Multivariate Redundant Information with Pointwise Common Change in Surprisal. Entropy 2017, 19. [Google Scholar] [CrossRef]
- Griffith, V.; Ho, T. Quantifying Redundant Information in Predicting a Target Random Variable. Entropy 2015, 17, 4644–4653. [Google Scholar] [CrossRef]
- Harder, M.; Salge, C.; Polani, D. Bivariate Measure of Redundant Information. Phys. Rev. E 2013, 87. [Google Scholar] [CrossRef] [PubMed]
- Bertschinger, N.; Rauh, J.; Olbrich, E.; Jost, J. Shared Information—New Insights and Problems in Decomposing Information in Complex Systems. In Proceedings of the European Conference on Complex Systems 2012; Gilbert, T., Kirkilionis, M., Nicolis, G., Eds.; Springer: Berlin, Germany, 2013; pp. 251–269. [Google Scholar]
- Williams, P.L. Information Dynamics: Its Theory and Application to EmbodiedCognitive Systems. Ph.D. Thesis, Indiana University, Bloomington, IN, USA, 2011. [Google Scholar]
- Lizier, J.T. The Local Information Dynamics of Distributed Computation in Complex Systems; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Timme, N.; Alford, W.; Flecker, B.; Beggs, J.M. Synergy, Redundancy, and Multivariate Information Measures: An Experimentalist’s Perspective. J. Comput. Neurosci. 2014, 36, 119–140. [Google Scholar] [CrossRef] [PubMed]
- Bertschinger, N.; Rauh, J.; Olbrich, E.; Jost, J.; Ay, N. Quantifying Unique Information. Entropy 2014, 16, 2161–2183. [Google Scholar] [CrossRef]
- Montúfar, G.; Ay, N.; Ghazi-Zahedi, K. Geometry and Expressive Power of Conditional Restricted Boltzmann Machines. J. Mach. Learn. Res. 2015, 16, 2405–2436. [Google Scholar]
- Kingma, D.P.; Welling, M. Auto-Encoding Variational Bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar]
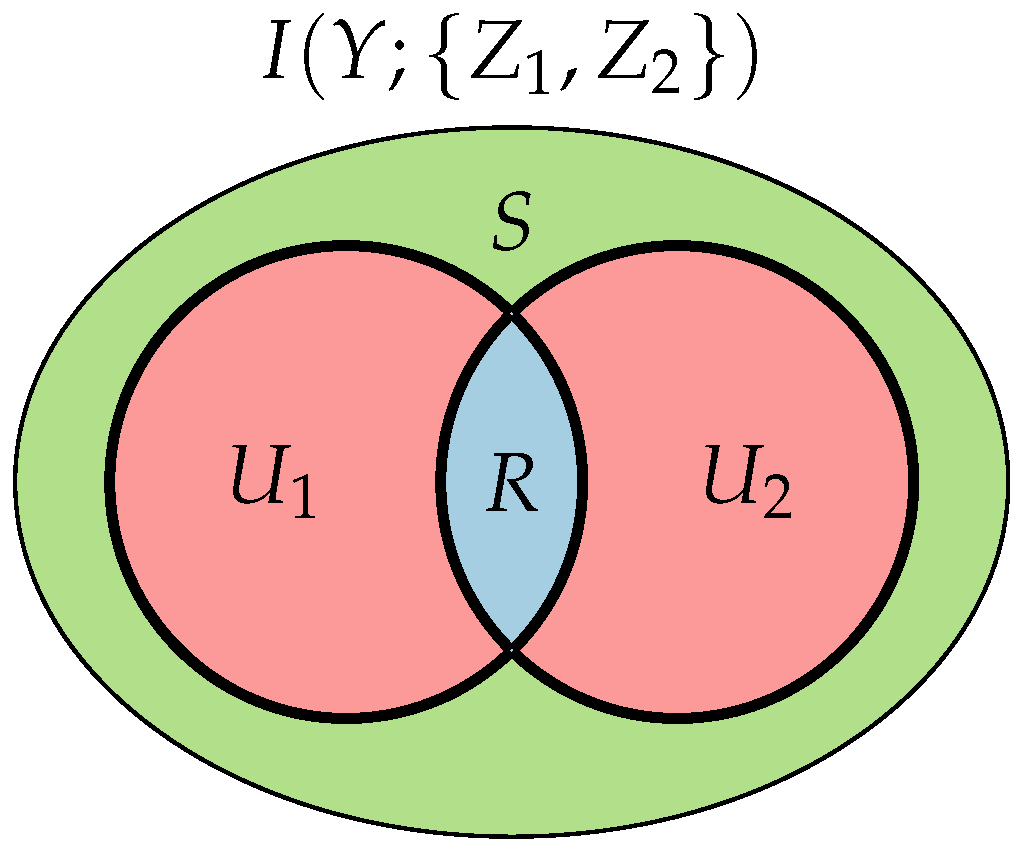
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tax, T.M.S.; Mediano, P.A.M.; Shanahan, M. The Partial Information Decomposition of Generative Neural Network Models. Entropy 2017, 19, 474. https://doi.org/10.3390/e19090474
Tax TMS, Mediano PAM, Shanahan M. The Partial Information Decomposition of Generative Neural Network Models. Entropy. 2017; 19(9):474. https://doi.org/10.3390/e19090474
Chicago/Turabian StyleTax, Tycho M.S., Pedro A.M. Mediano, and Murray Shanahan. 2017. "The Partial Information Decomposition of Generative Neural Network Models" Entropy 19, no. 9: 474. https://doi.org/10.3390/e19090474
APA StyleTax, T. M. S., Mediano, P. A. M., & Shanahan, M. (2017). The Partial Information Decomposition of Generative Neural Network Models. Entropy, 19(9), 474. https://doi.org/10.3390/e19090474




