Lifespan Development of the Human Brain Revealed by Large-Scale Network Eigen-Entropy
Abstract
1. Introduction
2. Materials and Methods
2.1. fMRI Data Acquisition
2.2. Data Preprocessing
2.3. Construction of Resting-State Functional Connectivity Network
2.4. Calculate Network Eigen-Entropy
2.5. Statistical Analyses
2.6. Test–Retest Reliability
3. Results
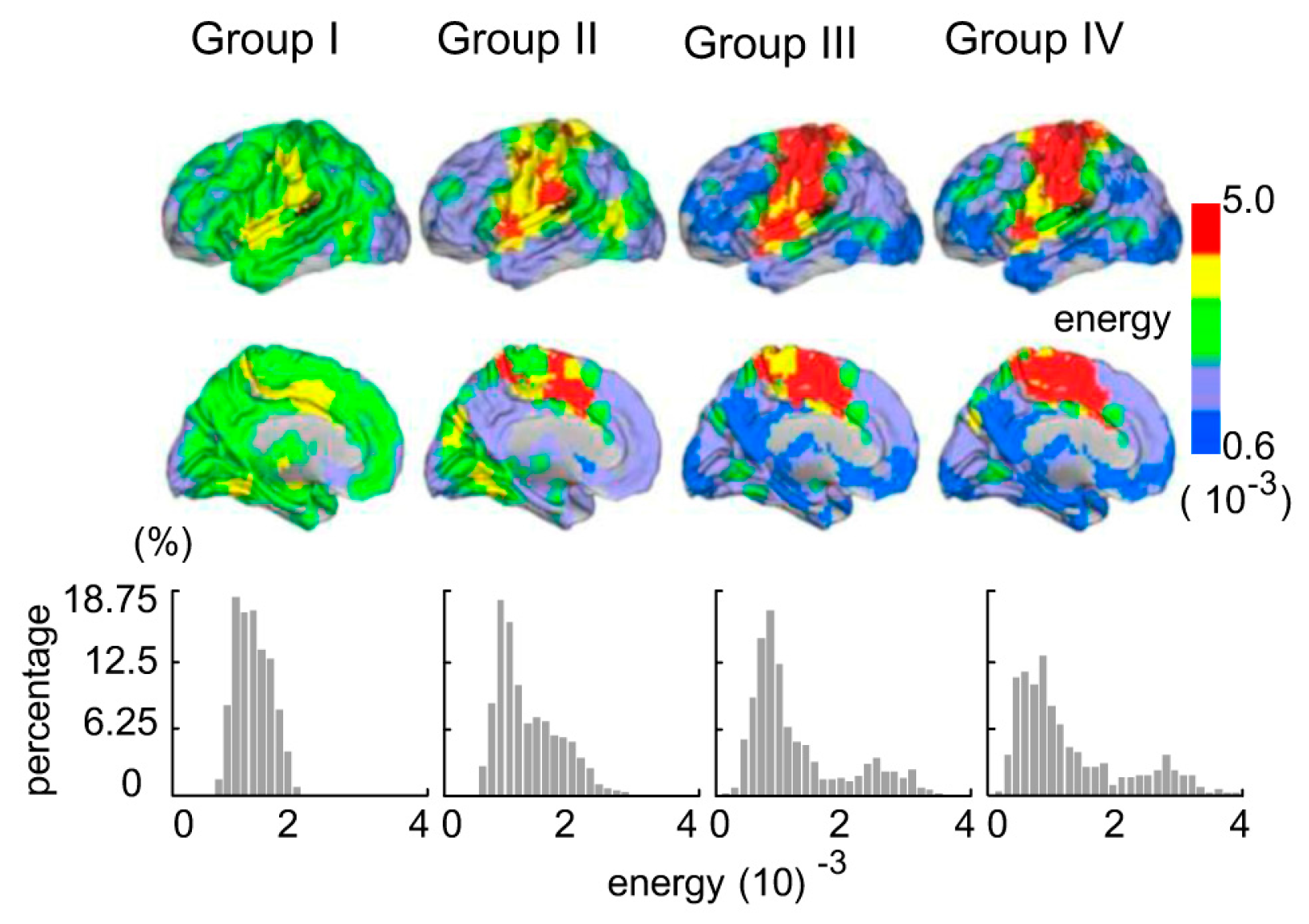
3.1. Age-Related Changes of Topologic Energy Probability Distribution and Energy Probability Histograms between Groups
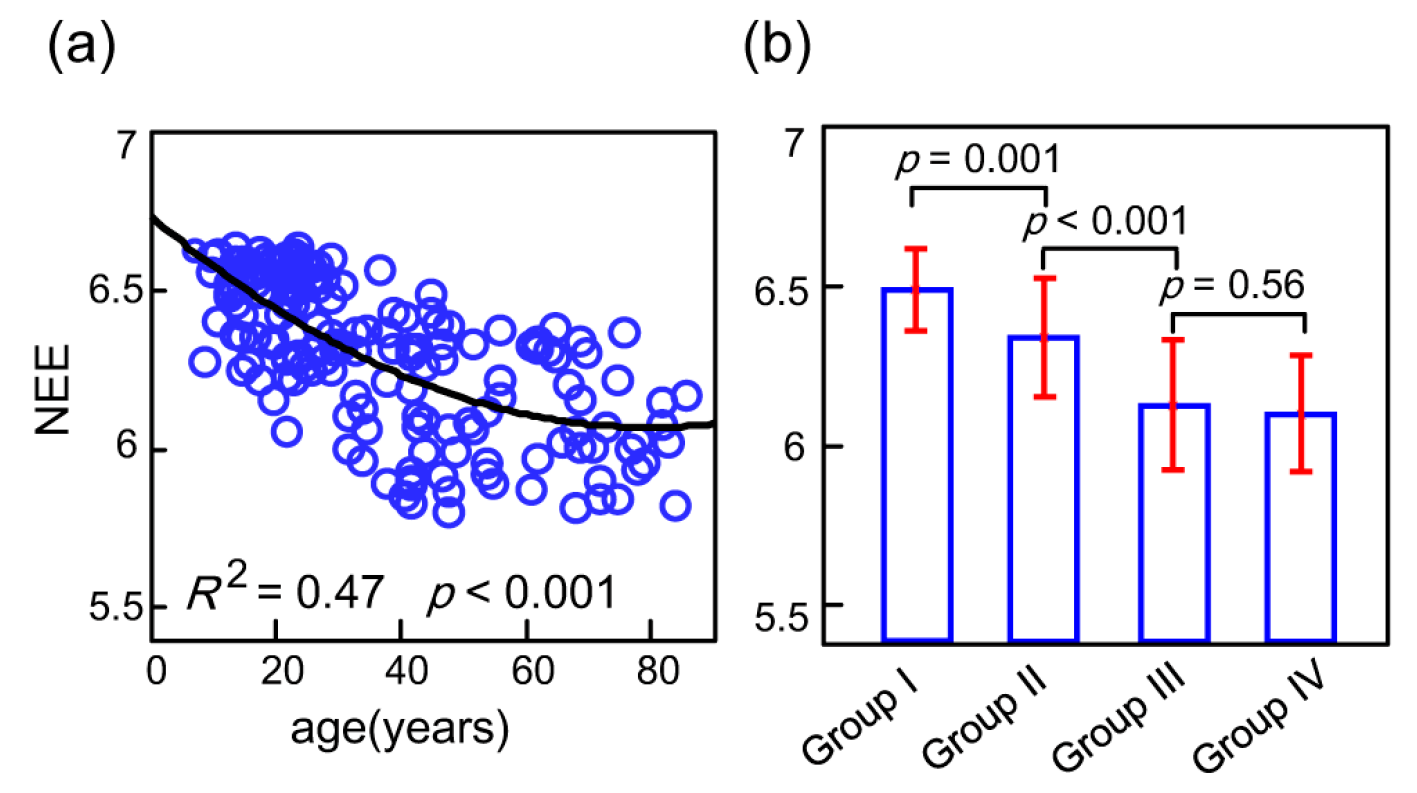
3.2. Age-Related Changes of the Whole-Brain Network Eigen-Entropy across Lifespan
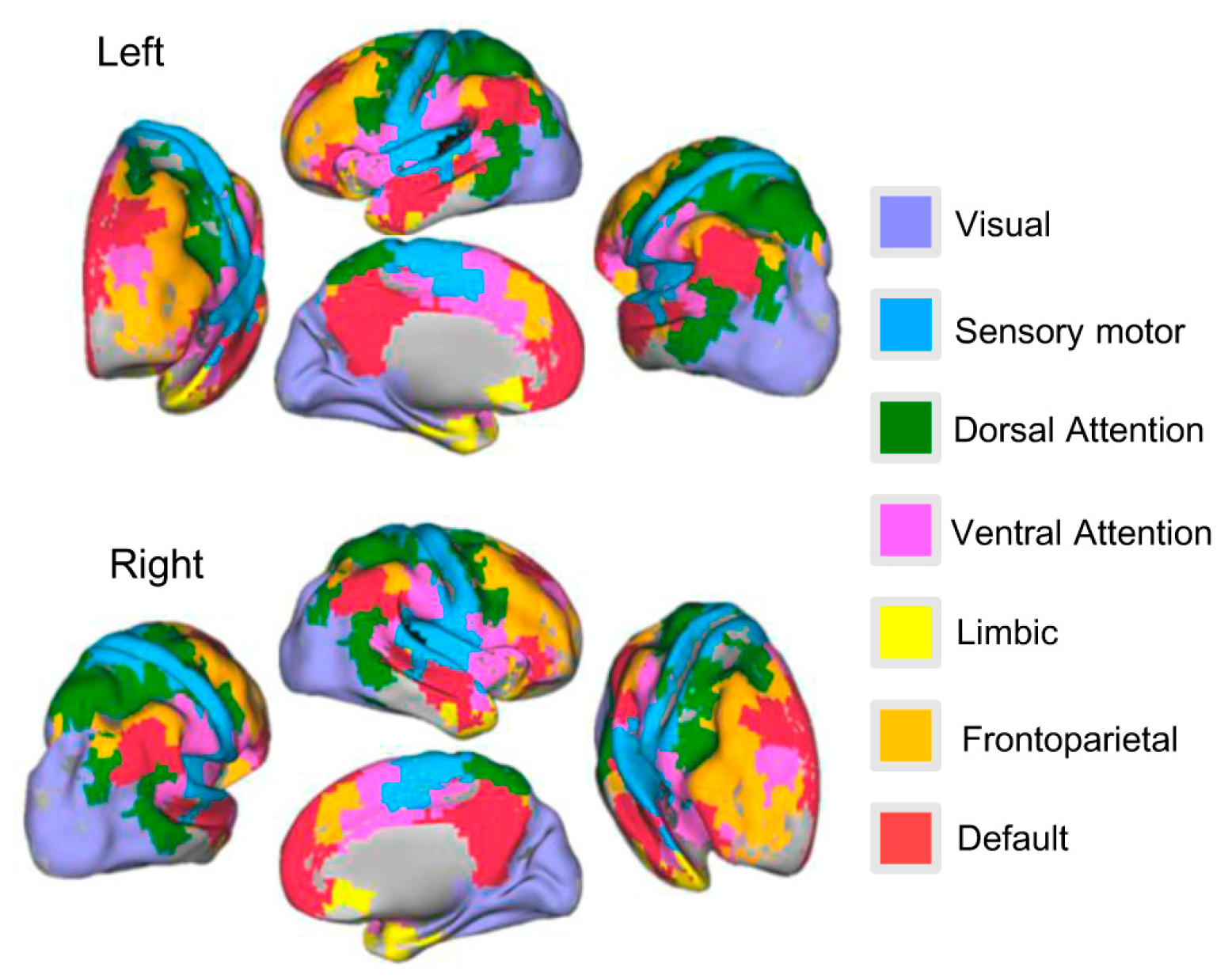
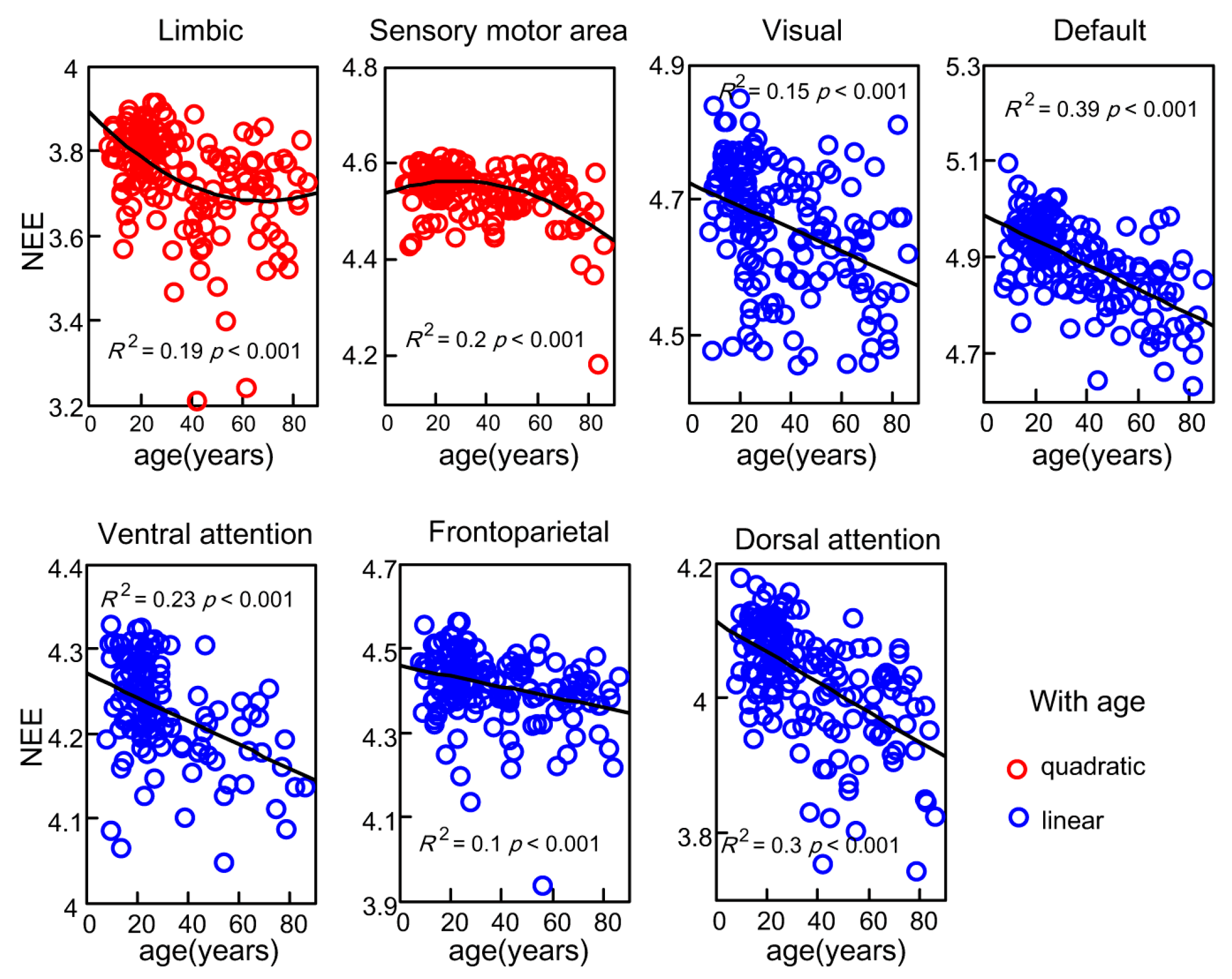
3.3. Age-Related Changes of Subsystems’ Network Eigen-Entropy across Lifespan
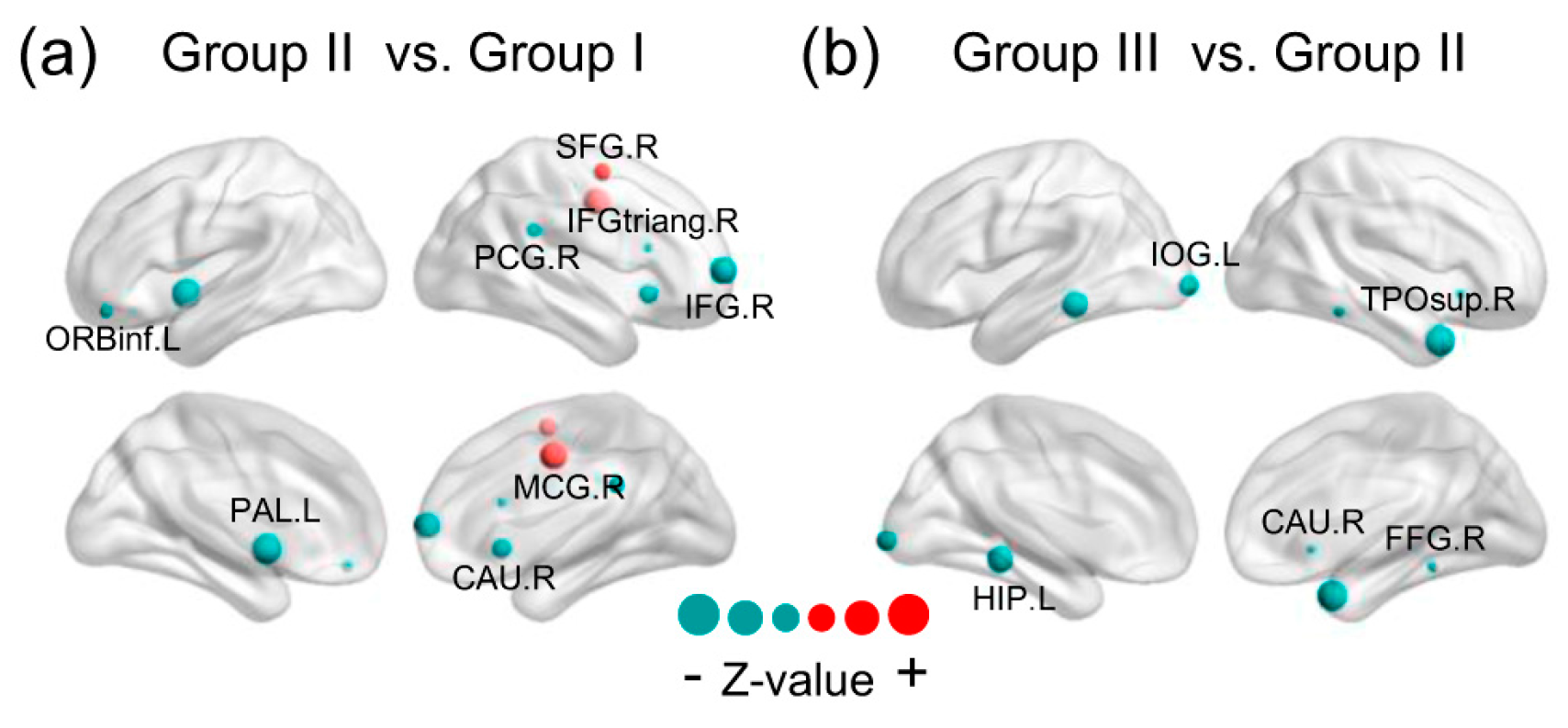
3.4. Brain Regions with Significant Energy Probablity Changes
3.5. Control Analyses
4. Discussion
4.1. The Orderness of the Functional Connectome Measured by the Network Eigen-Entropy
4.2. The Orderness Variability of the Whole-Brain with Age
4.3. The Orderness Variability of Functional Subsystems with Age
4.4. Brain Regions with Significant Energy Probablity Changing
4.5. Limitations and Future Directions
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wainwright, M.J.; Jordan, M.I. Graphical models, exponential families, and variational inference. Found. Trends Mach. Learn. 2008, 1, 1–305. [Google Scholar] [CrossRef]
- Buckner, R.L.; Krienen, F.M.; Yeo, B.T.T. Opportunities and limitations of intrinsic functional connectivity MRI. Nat. Neurosci. 2013, 16, 832–837. [Google Scholar] [CrossRef] [PubMed]
- Power, J.D.; Fair, D.A.; Schlaggar, B.L.; Petersen, S.E. The development of human functional brain networks. Neuron 2010, 67, 735–748. [Google Scholar] [CrossRef] [PubMed]
- Yeo, B.T.T.; Krienen, F.M.; Sepulcre, J.; Sabuncu, M.R.; Lashkari, D.; Hollinshead, M.; Roffman, J.L.; Smoller, J.W.; Zöllei, L.; Polimeni, J.R.; et al. The organization of the human cerebral cortex estimated by intrinsic functional connectivity. J. Neurophysiol. 2011, 106, 1125–1165. [Google Scholar] [PubMed]
- Betzel, R.F.; Byrge, L.; He, Y.; Goni, J.; Zuo, X.N.; Sporns, O. Changes in structural and functional connectivity among resting-state networks across the human lifespan. Neuroimage 2014, 102, 345–357. [Google Scholar] [CrossRef] [PubMed]
- Zuo, X.-N.; Kelly, C.; Martino, A.D.; Mennes, M.; Margulies, D.S.; Bangaru, S.; Grzadzinski, R.; Evans, A.C.; Zang, Y.-F.; Castellanos, F.X.; et al. Growing together and growing apart-regional and sex differences in the lifespan developmental trajectories of functional homotopy. J. Neurosci. 2010, 30, 15034–15043. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Su, L.; Shen, H.; Hu, D. Decoding lifespan changes of the human brain using resting-state functional connectivity mri. PLoS ONE 2012, 7, e44530. [Google Scholar] [CrossRef] [PubMed]
- Achard, S.; Bullmore, E. Efficiency and cost of economical brain functional networks. PLoS Comput. Biol. 2007, 3, e17. [Google Scholar] [CrossRef] [PubMed]
- Fair, D.A.; Cohen, A.L.; Power, J.D.; Dosenbach, N.U.; Church, J.A.; Miezin, F.M.; Schlaggar, B.L.; Petersen, S.E. Functional brain networks develop from a “local to distributed” organization. PLoS Comput. Biol. 2009, 5, e1000381. [Google Scholar] [CrossRef] [PubMed]
- Fransson, P.; Aden, U.; Blennow, M.; Lagercrantz, H. The functional architecture of the infant brain as revealed by resting-state fMRI. Cereb. Cortex 2011, 21, 145–154. [Google Scholar] [CrossRef] [PubMed]
- Uddin, L.Q.; Supekar, K.S.; Ryali, S.; Menon, V. Dynamic reconfiguration of structural and functional connectivity across core neurocognitive brain networks with development. J. Neurosci. 2011, 31, 18578–18589. [Google Scholar] [CrossRef] [PubMed]
- Supekar, K.; Musen, M.; Menon, V. Development of large-scale functional brain networks in children. PLoS Biol. 2009, 7, e1000157. [Google Scholar] [CrossRef] [PubMed]
- Gu, S.; Satterthwaite, T.D.; Medaglia, J.D.; Yang, M.; Gur, R.E.; Gur, R.C.; Bassett, D.S. Emergence of system roles in normative neurodevelopment. Proc. Natl. Acad. Sci. USA 2015, 112, 13681–13686. [Google Scholar] [CrossRef] [PubMed]
- Fair, D.A.; Cohen, A.L.; Dosenbach, N.U.F.; Church, J.A.; Miezin, F.M.; Barch, D.M.; Raichle, M.E.; Petersen, S.E.; Schlaggar, B.L. The maturing architecture of the brain’s default network. Proc. Natl. Acad. Sci. USA 2008, 105, 4028–4032. [Google Scholar] [CrossRef] [PubMed]
- Gao, W.; Zhu, H.; Giovanello, K.S.; Smith, J.K.; Shen, D.; Gilmore, J.H.; Lin, W. Evidence on the emergence of the brain’s default network from 2-week-old to 2-year-old healthy pediatric subjects. Proc. Natl. Acad. Sci. USA 2009, 106, 6790–6795. [Google Scholar] [CrossRef] [PubMed]
- Supekar, K.; Uddin, L.Q.; Prater, K.; Amin, H.; Greicius, M.D.; Menon, V. Development of functional and structural connectivity within the default mode network in young children. Neuroimage 2010, 52, 290–301. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.; Chang, C.; Xu, T.; Jiang, L.; Handwerker, D.A.; Castellanos, F.X.; Milham, M.P.; Bandettini, P.A.; Zuo, X.-N. Connectivity trajectory across lifespan differentiates the precuneus from the default network. Neuroimage 2014, 89, 45–56. [Google Scholar] [CrossRef] [PubMed]
- Fair, D.A.; Dosenbach, N.U.F.; Church, J.A.; Cohen, A.L.; Brahmbhatt, S.; Miezin, F.M.; Barch, D.M.; Raichle, M.E.; Petersen, S.E.; Schlaggar, B.L. Development of distinct control networks through segregation and integration. Proc. Natl. Acad. Sci. USA 2007, 104, 13507–13512. [Google Scholar] [CrossRef] [PubMed]
- Kilford, E.J.; Garrett, E.; Blakemore, S.J. The development of social cognition in adolescence: An integrated perspective. Neurosci. Biobehav. Rev. 2016, 70, 106–120. [Google Scholar] [CrossRef] [PubMed]
- Luna, B.; Padmanabhan, A.; O’Hearn, K. What has fmri told us about the development of cognitive control through adolescence? Brain Cogn. 2010, 72, 101–113. [Google Scholar] [CrossRef] [PubMed]
- Cao, M.; Wang, J.H.; Dai, Z.J.; Cao, X.Y.; Jiang, L.L.; Fan, F.M.; Song, X.W.; Xia, M.R.; Shu, N.; Dong, Q.; et al. Topological organization of the human brain functional connectome across the lifespan. Dev. Cogn. Neurosci. 2014, 7, 76–93. [Google Scholar] [CrossRef] [PubMed]
- Song, J.; Birn, R.M.; Boly, M.; Meier, T.B.; Nair, V.A.; Meyerand, M.E.; Prabhakaran, V. Age-related reorganizational changes in modularity and functional connectivity of human brain networks. Brain Connect. 2014, 4, 662–676. [Google Scholar] [CrossRef] [PubMed]
- Geerligs, L.; Renken, R.J.; Saliasi, E.; Maurits, N.M.; Lorist, M.M. A brain-wide study of age-related changes in functional connectivity. Cereb. Cortex 2015, 25, 1987–1999. [Google Scholar] [CrossRef] [PubMed]
- Meunier, D.; Achard, S.; Morcom, A.; Bullmore, E. Age-related changes in modular organization of human brain functional networks. Neuroimage 2009, 44, 715–723. [Google Scholar] [CrossRef] [PubMed]
- Joyce, K.E.; Laurienti, P.J.; Burdette, J.H.; Hayasaka, S. A new measure of centrality for brain networks. PLoS ONE 2010, 5, e12200. [Google Scholar] [CrossRef] [PubMed]
- Lohmann, G.; Margulies, D.S.; Horstmann, A.; Pleger, B.; Lepsien, J.; Goldhahn, D.; Schloegl, H.; Stumvoll, M.; Villringer, A.; Turner, R. Eigenvector centrality mapping for analyzing connectivity patterns in fmri data of the human brain. PLoS ONE 2010, 5, e10232. [Google Scholar] [CrossRef] [PubMed]
- He, Y.; Wang, J.; Wang, L.; Chen, Z.J.; Yan, C.; Yang, H.; Tang, H.; Zhu, C.; Gong, Q.; Zang, Y.; et al. Uncovering intrinsic modular organization of spontaneous brain activity in humans. PLoS ONE 2009, 4, e5226. [Google Scholar] [CrossRef] [PubMed]
- Power, J.D.; Schlaggar, B.L.; Lessov-Schlaggar, C.N.; Petersen, S.E. Evidence for hubs in human functional brain networks. Neuron 2013, 79, 798–813. [Google Scholar] [CrossRef] [PubMed]
- Cao, M.; Huang, H.; Peng, Y.; Dong, Q.; He, Y. Toward developmental connectomics of the human brain. Front. Neuroanat. 2016, 10, 25. [Google Scholar] [CrossRef] [PubMed]
- Van den Heuvel, M.P.; Sporns, O. Rich-club organization of the human connectome. J. Neurosci. 2011, 31, 15775–15786. [Google Scholar] [CrossRef] [PubMed]
- Nigam, S.; Shimono, M.; Ito, S.; Yeh, F.C.; Timme, N.; Myroshnychenko, M.; Lapish, C.C.; Tosi, Z.; Hottowy, P.; Smith, W.C. Rich-club organization in effective connectivity among cortical neurons. J. Neurosci. 2016, 36, 670–684. [Google Scholar] [CrossRef] [PubMed]
- Bullmore, E.; Sporns, O. Complex brain networks: Graph theoretical analysis of structural and functional systems. Nat. Rev. Neurosci. 2009, 10, 186–198. [Google Scholar] [CrossRef] [PubMed]
- Achard, S.; Salvador, R.; Whitcher, B.; Suckling, J.; Bullmore, E. A resilient, low-frequency, small-world human brain functional network with highly connected association cortical hubs. J. Neurosci. 2006, 26, 63–72. [Google Scholar] [CrossRef] [PubMed]
- Van, D.E.; Schoonheim, M.M.; Ijzerman, R.G.; Moll, A.C.; Landeirafernandez, J.; Klein, M.; Diamant, M.; Snoek, F.J.; Barkhof, F.; Wink, A.M. Altered eigenvector centrality is related to local resting-state network functional connectivity in patients with longstanding type 1 diabetes mellitus. Hum. Brain Mapp. 2017, 38, 3623–3636. [Google Scholar]
- Binnewijzend, M.; Adriaanse, S.; Flier, W.M.; Teunissen, C.E.; Munck, J.C.; Stam, C.J.; Scheltens, P.; Berckel, B.N.M.; Barkhof, F.; Wink, A.M. Brain network alterations in alzheimer’s disease measured by eigenvector centrality in fmri are related to cognition and csf biomarkers. Hum. Brain Mapp. 2014, 35, 2383–2393. [Google Scholar] [CrossRef] [PubMed]
- Zuo, X.N.; Ehmke, R.; Mennes, M.; Imperati, D.; Castellanos, F.X.; Sporns, O.; Milham, M.P. Network centrality in the human functional connectome. Cereb. Cortex 2012, 22, 1862–1875. [Google Scholar] [CrossRef] [PubMed]
- Wink, A.M.; de Munck, J.C.; Yd, V.D.W.; Oa, V.D.H.; Barkhof, F. Fast eigenvector centrality mapping of voxel-wise connectivity in functional magnetic resonance imaging: Implementation, validation, and interpretation. Brain Connect. 2012, 2, 265–274. [Google Scholar] [CrossRef] [PubMed]
- Smith, S.M.; Beckmann, C.F.; Andersson, J.; Auerbach, E.J.; Bijsterbosch, J.; Douaud, G.; Duff, E.; Feinberg, D.A.; Griffanti, L.; Harms, M.P. Resting-state fmri in the human connectome project. Neuroimage 2013, 80, 144–168. [Google Scholar] [CrossRef] [PubMed]
- Zeng, L.L.; Wang, D.; Fox, M.D.; Sabuncu, M.; Hu, D.; Ge, M.; Buckner, R.L.; Liu, H. Neurobiological basis of head motion in brain imaging. Proc. Natl. Acad. Sci. USA 2014, 111, 6058–6062. [Google Scholar] [CrossRef] [PubMed]
- Zeng, L.L.; Shen, H.; Liu, L.; Hu, D. Unsupervised classification of major depression using functional connectivity mri. Hum. Brain Mapp. 2014, 35, 1630–1641. [Google Scholar] [CrossRef] [PubMed]
- Craddock, R.C.; James, G.A.; Holtzheimer, P.E.; Hu, X.P.; Mayberg, H.S. A whole brain fmri atlas generated via spatially constrained spectral clustering. Hum. Brain Mapp. 2012, 33, 1914–1928. [Google Scholar] [CrossRef] [PubMed]
- Strang, G. Introduction to Linear Algebra, 5th ed.; Wellesley-Cambridge Press: Wellesley, MA, USA, 2016. [Google Scholar]
- Power, J.D.; Barnes, K.A.; Snyder, A.Z.; Schlaggar, B.L.; Petersen, S.E. Spurious but systematic correlations in functional connectivity mri networks arise from subject motion. Neuroimage 2012, 59, 2142–2154. [Google Scholar] [CrossRef] [PubMed]
- Van Dijk, K.R.; Sabuncu, M.R.; Buckner, R.L. The influence of head motion on intrinsic functional connectivity mri. Neuroimage 2012, 59, 431–438. [Google Scholar] [CrossRef] [PubMed]
- Zuo, X.N.; Xing, X.X. Test-retest reliabilities of resting-state fmri measurements in human brain functional connectomics: A systems neuroscience perspective. Neurosci. Biobehav. Rev. 2014, 45, 100–118. [Google Scholar] [CrossRef] [PubMed]
- Landis, J.R.; Koch, G.G. The measurement of observer agreement for categorical data. Biometrics 1977, 33, 159–174. [Google Scholar] [CrossRef] [PubMed]
- Vargha, P. A critical discussion of intraclass correlation coefficients. Stat. Med. 1997, 16, 821–823. [Google Scholar] [CrossRef]
- Allen, E.A.; Damaraju, E.; Plis, S.M.; Erhardt, E.B.; Eichele, T.; Calhoun, V.D. Tracking whole-brain connectivity dynamics in the resting state. Cereb. Cortex 2014, 24, 663–676. [Google Scholar] [CrossRef] [PubMed]
- Eguı´luz, V.M.; Chialvo, D.R.; Cecchi, G.A.; Baliki, M.; Apkarian, A.V. Scale-free brain functional networks. Phys. Rev. Lett. 2005, 94, 018102. [Google Scholar] [CrossRef] [PubMed]
- Liao, X.; Vasilakos, A.V.; Yong, H. Small-world human brain networks: Perspectives and challenges. Neurosci. Biobehav. Rev. 2017, 77, 286–300. [Google Scholar] [CrossRef] [PubMed]
- Yao, Y.; Lu, W.L.; Xu, B.; Li, C.B.; Lin, C.P.; Waxman, D.; Feng, J.F. The increase of the functional entropy of the human brain with age. Sci. Rep. 2013, 3, 2853. [Google Scholar] [CrossRef] [PubMed]
- Mcintosh, A.R.; Vakorin, V.; Kovacevic, N.; Wang, H.; Diaconescu, A.; Protzner, A.B. Spatiotemporal dependency of age-related changes in brain signal variability. Cereb. Cortex 2014, 24, 1806–1817. [Google Scholar] [CrossRef] [PubMed]
- Schrödinger, E. What is Life? University Press: Cambridge, UK, 1944. [Google Scholar]
- Tkacik, G.; Marre, O.; Mora, T.; Amodei, D.; Ii, M.J.B.; Bialek, W. The simplest maximum entropy model for collective behavior in a neural network. J. Stat. Mech. Theor. Exp. 2012, 2013, 829–837. [Google Scholar]
- Maren, A.J. The cluster variation method: A primer for neuroscientists. Brain Sci. 2016, 6, E44. [Google Scholar] [CrossRef] [PubMed]
- Tkačik’s, G.; Marre, O.; Amodei, D.; Schneidman, E.; Bialek, W.; Nd, B.M. Searching for collective behavior in a large network of sensory neurons. PLoS Comput. Biol. 2014, 10, e1003408. [Google Scholar] [CrossRef] [PubMed]
- Lin, W.; Zhu, Q.; Gao, W.; Chen, Y.; Toh, C.H.; Styner, M.; Gerig, G.; Smith, J.K.; Biswal, B.; Gilmore, J.H. Functional connectivity mr imaging reveals cortical functional connectivity in the developing brain. AJNR Am. J. Neuroradiol. 2008, 29, 1883–1889. [Google Scholar] [CrossRef] [PubMed]
- Miao, C.; Yong, H.; Dai, Z.; Liao, X.; Jeon, T.; Ouyang, M.; Chalak, L.; Bi, Y.; Rollins, N.; Qi, D. Early development of functional network segregation revealed by connectomic analysis of the preterm human brain. Cereb. Cortex 2016, 27, 1949–1963. [Google Scholar]
- Kaiser, M. Mechanisms of connectome development. Trends Cogn. Sci. 2017, 9, 703–717. [Google Scholar] [CrossRef] [PubMed]
- Fjell, A.M.; Sneve, M.H.; Grydeland, H.; Storsve, A.B.; Walhovd, K.B. The disconnected brain and executive function decline in aging. Cereb. Cortex 2017, 27, 2303–2317. [Google Scholar] [CrossRef] [PubMed]
- Sala-Llonch, R.; Bartres-Faz, D.; Junque, C. Reorganization of brain networks in aging: A review of functional connectivity studies. Front. Psychol. 2015, 6, 663. [Google Scholar] [CrossRef] [PubMed]
- Andrewshanna, J.R.; Snyder, A.Z.; Vincent, J.L.; Lustig, C.; Head, D.; Raichle, M.E.; Buckner, R.L. Disruption of large-scale brain systems in advanced aging. Neuron 2007, 56, 924–935. [Google Scholar] [CrossRef] [PubMed]
- Wu, T.; Zang, Y.; Wang, L.; Long, X.; Li, K.; Chan, P. Normal aging decreases regional homogeneity of the motor areas in the resting state. Neurosci. Lett. 2007, 423, 189–193. [Google Scholar] [CrossRef] [PubMed]
- Onoda, K.; Ishihara, M.; Yamaguchi, S. Decreased functional connectivity by aging is associated with cognitive decline. J. Cogn. Neurosci. 2012, 24, 2186–2198. [Google Scholar] [CrossRef] [PubMed]
- Tomasi, D.; Volkow, N.D. Aging and functional brain networks. Mol. Psychiatry 2012, 17, 471, 549–558. [Google Scholar] [CrossRef] [PubMed]
- West, R.L. An application of prefrontal cortex function theory to cognitive aging. Psychol. Bull. 1996, 120, 272–292. [Google Scholar] [CrossRef] [PubMed]
- Raz-Yaseef, N. Aging of the brain and its impact on cognitive performance: Integration of structural and functional findings. In Handbook of Aging and Cognition, 2nd ed.; Psychology Press: Hove, UK, 2000; pp. 1–90. [Google Scholar]
- Woodruff-Pak, D.S. The Neuropsychology of Aging; Blackwell: Hoboken, NJ, USA, 1997; p. 119. [Google Scholar]
- Albin, R.L.; Young, A.B.; Penney, J.B. The functional anatomy of basal ganglia disorders. Trends Neurosci. 1989, 12, 366–375. [Google Scholar] [CrossRef]
- Alexander, G.E.; Crutcher, M.D. Functional architecture of basal ganglia circuits: Neural substrates of parallel processing. Trends Neurosci. 1990, 13, 266–271. [Google Scholar] [CrossRef]
- Alexander, G.E.; DeLong, M.R.; Strick, P.L. Parallel organization of functionally segregated circuits linking basal ganglia and cortex. Annu. Rev. Neurosci. 1986, 9, 357–381. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Zeng, L.L.; Chen, Y.; Yin, H.; Tan, Q.; Hu, D. Evidence of a dissociation pattern in default mode subnetwork functional connectivity in schizophrenia. Sci. Rep. 2015, 5, 14655. [Google Scholar] [CrossRef] [PubMed]
- Zeng, L.L.; Shen, H.; Liu, L.; Wang, L.; Li, B.; Fang, P.; Zhou, Z.; Li, Y.; Hu, D. Identifying major depression using whole-brain functional connectivity: A multivariate pattern analysis. Brain 2012, 135, 1498–1507. [Google Scholar] [CrossRef] [PubMed]

| Groups | Classification | Age Range (years) | Number of Participants | Gender (M a/F b) |
|---|---|---|---|---|
| Group I | flourishing | 7–20 | 40 | 23/17 |
| Group II | youth period | 23–38 | 35 | 17/18 |
| Group III | middle age | 40–59 | 37 | 27/10 |
| Group IV | old age | 61–85 | 32 | 15/17 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, Y.; Zeng, L.-L.; Shen, H.; Qin, J.; Li, F.; Hu, D. Lifespan Development of the Human Brain Revealed by Large-Scale Network Eigen-Entropy. Entropy 2017, 19, 471. https://doi.org/10.3390/e19090471
Fan Y, Zeng L-L, Shen H, Qin J, Li F, Hu D. Lifespan Development of the Human Brain Revealed by Large-Scale Network Eigen-Entropy. Entropy. 2017; 19(9):471. https://doi.org/10.3390/e19090471
Chicago/Turabian StyleFan, Yiming, Ling-Li Zeng, Hui Shen, Jian Qin, Fuquan Li, and Dewen Hu. 2017. "Lifespan Development of the Human Brain Revealed by Large-Scale Network Eigen-Entropy" Entropy 19, no. 9: 471. https://doi.org/10.3390/e19090471
APA StyleFan, Y., Zeng, L.-L., Shen, H., Qin, J., Li, F., & Hu, D. (2017). Lifespan Development of the Human Brain Revealed by Large-Scale Network Eigen-Entropy. Entropy, 19(9), 471. https://doi.org/10.3390/e19090471




