The present Special-Issue contribution deals with the transition to turbulence in wall-bounded flows, an important case of systems driven far from equilibrium where patterns develop against a turbulent background. This active field of research is rapidly evolving, and important results have been obtained recently. To set the frame, in
Section 1, I will summarize a recent paper reviewing the subject from a more general standpoint [
1], enabling me to focus on a specific feature of this transition: the existence of a statistically well-organized laminar-turbulent patterning of flows along planar walls in some intermediate range of Reynolds numbers
. The Reynolds number is the main
control parameter of the problem. Its generic expression reads
, in which
V and
ℓ are typical velocity and length scales, and
the fluid’s kinematic viscosity.
R compares the typical shear rate
to the viscous diffusion rate over the same length scale
.
is a global stability threshold marking unconditional return to laminar flow and
some upper threshold beyond which turbulence is essentially uniform. After having taken the cylindrical shear configuration as an illustrating case in
Section 2, I will turn to strictly planar cases in
Section 3. The best understood part of the transition scenario, pattern decay at
is considered in
Section 4. How patterns emerge as
R is decreased from large values is next examined in
Section 5 before a discussion of perspectives and questions that, in my view, remain open in
Section 6. I have tried to limit the bibliography to contributions of specific significance, historical or physical, and to the most recent articles of which I am aware. The remaining plethoric literature on the subject can be accessed via the review articles or books quoted, which also introduce background prerequisites when necessary.
1. Context
Under weak forcing, close to thermodynamic equilibrium, fluid motion is
laminar, i.e., smoothly evolving in space and time with macroscopic transfer properties of microscopic origin (molecular dissipation). When driven sufficiently far from equilibrium, the flow generically becomes
turbulent, with irregular swirls on a wide continuum of spatiotemporal scales and enormously enhanced effective transport properties. The full Navier-Stokes system, i.e., the set formed by the equations governing the velocity and pressure fields
,
(
: density;
: dynamic viscosity;
: advection term) and the continuity equation that simply reads
for the incompressible flow of simple fluids, plus boundary and initial conditions, called the Navier-Stokes equation (NSE) for short in the following, governs the whole flow behavior. As the applied shear rate increases, its viscous (Stokes) part is overtaken by its nonlinear advection term that enables nontrivial solutions competing with the unique trivial
base state permitted near equilibrium. The transition from laminar to turbulent dynamics has been an important field of study, in view of deep theoretical issues relating to the nature of stochasticity and its important consequences on macroscopic transfer properties in applications (consult [
2] for an introduction). Basically two transition scenarios can be distinguished upon varying
R [
1].
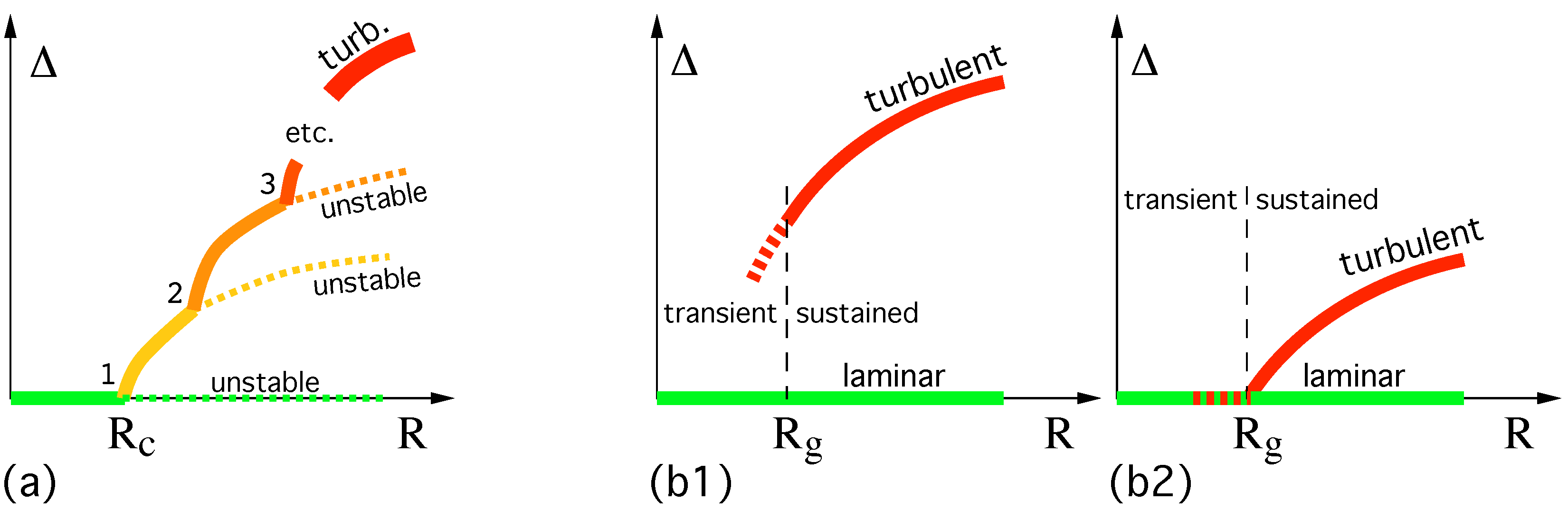
In the first scenario, at increasing
R, the base state is continuously changed into more and more complex flow regimes resulting from a cascade of instabilities ending in turbulence (
Figure 1a). Importantly, this scenario develops from a linear primary instability amplifying infinitesimal disturbances beyond some threshold
. The subsequent cascade involves a finite number of steps, while at each step, the bifurcated and bifurcating states exchange themselves as
R is varied. The cascade is essentially reversible with no (or very limited) hysteresis as
R is swept up and down, a property best conveyed by the expression
globally super-critical. A typical closed flow example is convection in a horizontal fluid layer originally at rest and heated from below with differential buoyancy playing the destabilizing role, see §3.2.2 in [
2]. This scenario is relevant every time the dynamics away from the base state can be analyzed using the standard tools of linear stability analysis and weakly nonlinear perturbation theory, at least in principle since technical difficulties can be insurmountable beyond the few first steps. This is of course the case for convection, but also for open flows with velocity profiles displaying inflection points (unstable according to Rayleigh’s inviscid criterion [
3]; see [
2,
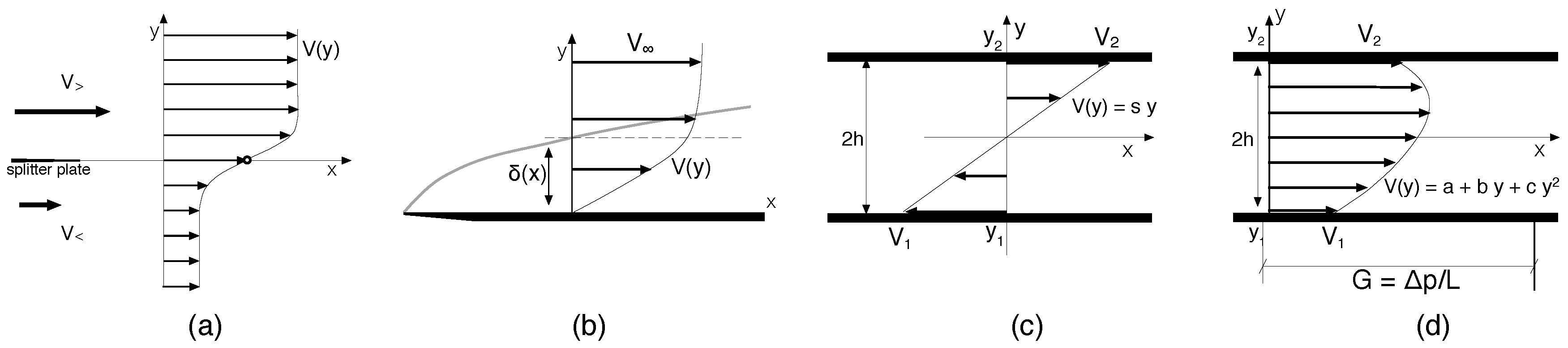
4]), e.g., a shear layer downstream a splitter plate (
Figure 2a) or a wake downstream a blunt obstacle, in which case primary destabilization arises from a Kelvin–Helmholtz instability, while viscosity plays its intuitive stabilizing role on a primary instability that develops at low Reynolds number (§7.2.2 in [
2]).
In this review, I will be concerned with the alternative
catastrophic scenario in which nonlinearity plays the essential role, while dissipative processes are less efficient in controlling the flow. (To my knowledge, the term ‘catastrophic’ was introduced by Coles [
5] who described the first scenario as ‘spectral evolution’, an expression that conveys the right idea, but is less nonlinearly connoted than ‘globally super-critical’.) Linearity is associated to uniqueness of solutions, namely the laminar base flow response to small driving away from equilibrium along the
thermodynamic solution branch. On the other hand, far from equilibrium, nonlinearity indeed permits a multiplicity of solutions to the NSE. The transition to turbulence is now much wilder, laminar flow directly competing with a turbulent regime and no stage of intermediate complexity in between (
Figure 1b). Coexistence of locally stable solutions being the mark of sub-criticality in elementary bifurcation theory, this scenario can legitimately be termed
globally sub-critical [
1,
6,
7]. It also displays strong hysteresis upon sweeping
R up and down and, on general grounds, a
global stability threshold can be defined, corresponding to the value of
R below which the base state is unconditionally stable. Sustained coexistence can accordingly be observed for
.
The
phase space interpretation of multi-stability is straightforward in
confined systems where lateral boundary effects enforce the spatial coherence of nonlinear modes (see §3.3.2–4 in [
2]). Confinement effects are appreciated through aspect ratios, viz.
where
L is a typical extrinsic scale of interest and
the intrinsic scale generated by the instability mechanism, i.e., ≈the number of cells in convection. Open flows through pipes or along plates are always extended at least in the streamwise direction. By placing artificial periodic boundary conditions at small distances, the ensuing
low-dimensional dynamical-system reduction undoubtedly helps one identifying locally relevant nontrivial solutions in
phase space [
8,
9], but does not provide any understanding of the coexistence of such local solutions with the laminar flow solution in different regions of
physical space, which, as earlier stressed by Pomeau [
10], is the prominent feature to explain: in the catastrophic case, chaos is
spatiotemporal in essence, and the whole system of interest is better viewed as a patchwork of subdomains filled with either laminar or turbulent flow separated by sharply-defined interfaces. Due to intrinsic stochasticity in the local nontrivial state, these interfaces permanently fluctuate, generically leading to a regime of spatiotemporal intermittency [
11]. Though still conceptually appealing, the phase-space picture, mostly valuable for confined systems, becomes unpractical and, possibly, even misleading. Natural observables are now statistically-defined quantities such as the
turbulent fraction, the mean fraction of space occupied by the turbulent state (spatial viewpoint) or the
intermittency factor, the mean fraction of time spend in the turbulent state (temporal viewpoint) and higher spatiotemporal statistical moments defined via the laminar/turbulent dichotomy.
I now turn to examples taken from planar configurations where a fluid flows along solid boundaries for which, controlled by viscosity, the velocity profile is deprived from inflection point, Rayleigh’s inviscid condition for linear stability [
3], and remains stable up to large Reynolds numbers (
Figure 2b–d). This is the case of the
channel flow between parallel plates under pressure gradient with the parabolic Poiseuille profile (PPF), of the
simple shear flow between counter-sliding parallel plates with linear Couette profile (PCF;
Figure 2c), of a mixture of the two with a more general quadratic profile called Couette–Poiseuille flow (CPF;
Figure 2d), of the plane
boundary layer flow in the absence of pressure gradient with Blasius profile (BBL;
Figure 2b), or its variant with permeation at the wall, the asymptotic suction boundary layer (ASBL). Flow under pressure gradient in
pipes of circular section with parabolic Poiseuille profile, the Hagen-Poiseuille flow (HPF), or nearly square section, also enter this category [
12].
In all of these cases, viscous effects do not play their simple, low-
R, damping role, but a more subtle part in a mechanism producing Tollmien–Schlichting (TS) waves, effective at high
R only [
4]. Among the cases mentioned above, PPF, BBL and ASBL, have finite, but high enough TS-threshold
, while PCF is known to be linearly stable for all
R and HPF believed to be so. These two, PCF and HPF, therefore come out as paradigms of systems controlled by mechanisms that do not rely on conventional linear stability analysis, such as the Kim–Hamilton–Waleffe self-sustainment process (SSP) [
7,
13,
14]. The SSP is a cyclic process where perturbations in the form of low-level
streamwise vortices induce by
lift-up large spanwise modulations of the base flow called streamwise
streaks. When sufficiently amplified, these streaks are themselves unstable via the development of locally inflectional velocity profiles, provoking their breakdown. In a third step breakdown products are filtered out to regenerate the streamwise vortices [
13,
14]. For an illustration, see Gibson’s video
Turbulent dynamics in a ‘minimal flow unit’ on
channelflow.org [
15], choosing tab ‘
movies’ among the headings. Nontrivial solutions brought about by such inherently nonlinear couplings can then be found away from the base flow in an intermediate
R range,
(possibly infinite). Scenarios resting on the presence of a linear instability (infinitesimal disturbances) are, in practice,
bypassed by the amplification of
finite-amplitude,
localized perturbations pushing the flow in the attraction basin of these nontrivial states living on the turbulent solution branch. As previously mentioned, this branch will be stable for
, but its states are only transient below. Now, on general grounds, a regime of spatially uniform or
featureless turbulence [
16], is expected at very large
R with turbulent fraction or intermittency factor saturating at one [
5,
17]. On the other hand, just above
, one may expect these quantities to be markedly smaller than one, characterizing the conspicuous laminar-turbulent alternation. How do they approach saturation as
R increases, either through a smooth crossover or at a well-defined upper threshold
, and more generally, how do they vary all along the
transitional range between
and the putative
are the questions of interest.
Before discussing the
two-dimensional (2D) transitional regime for flows along plates with laminar-turbulent patterns depending on two directions, streamwise and spanwise, I now briefly review the other paradigmatic case considered first by Reynolds in a transition perspective [
18], namely HPF, the flow along a straight pipe (hence
one-dimensional, 1D for short). This summary is just given for further reference since several extensive accounts can be found in the recent literature [
19,
20] and one can rely on the remarkable article by Barkley [
21] for a brilliant analysis of theoretical issues and associated modeling. First, the parabolic HPF profile is presumed to be linearly stable for all
R, whereas at moderate
R, once triggered, turbulence remains localized in isolated coherent chaotic
puffs with finite lifetimes that increase super-exponentially with
R [
22]. Transient turbulence happens to become sustained because, when
R gets larger, before decaying puffs can split and propagate localized chaotic disturbances further, thus contaminating the flow. The threshold
can be defined without ambiguity when decay is statistically compensated by splitting so that turbulence persists on average [
23]. Somewhat above
, turbulence inside the puffs becomes more aggressive and the puffs turn into turbulent plugs called
slugs that, when
R increases a bit, grow in the upstream direction despite downstream advection [
12]. As
R further increases, laminar-turbulent intermittency is progressively reduced to the benefit of featureless turbulence, hence a smooth crossover rather than a threshold at some well defined
. At the phenomenological level, a remarkably successful model covering the whole transitional regime has been developed by Barkley [
12,
21,
24]. The reaction-diffusion-advection process [
25] in terms of which this model is formulated will have some relevance to the discussion of the 2D organization of the laminar-turbulent coexistence (
Section 6).
At this stage, as a step toward the problem of 2D patterns proper, I should point out that the transition from 1D axial to 2D wall-parallel dependence of the turbulence intensity can be studied in a few experimental settings with straightforward numerical implementation. Annular Poiseuille flow, the flow between two coaxial cylinders driven by a pressure gradient, is a first example. When the radius ratio is small, despite the presence of the inner cylinder, the transition to/from turbulence basically follows the 1D scenario of pure HPF with no inner cylinder (puffs, slugs, etc.). On the other hand in the small gap limit, when this ratio tends to one and the curvature of the fluid layer tends to zero, a laminar-turbulent organization takes place in the form of turbulent helices translating in the gap, locally anticipating the oblique bands of the planar case. The crossover between the two regimes has been studied as a function of the radius ratio [
26,
27,
28]. In the same way, fluid motion induced by steadily counter-sliding the cylinders along their axis, yields annular Couette flow (more easily implemented numerically [
29] than approximated experimentally) that connects to PCF in the small gap limit in the same way as annular to plane Poiseuille flow. In the next section, I turn to the Couette case but when the two cylinders are differentially rotating around, rather than translating along, their common axis in the moderate-to-small gap range for which the local state, once bifurcated, depends on axial and azimuthal coordinates from the start, being thus genuinely 2D.
2. Cylindrical Couette Flow
Together with the flow through a pipe and thermal convection, cylindrical Couette flow (CCF), represents one of the most emblematic testbeds for studying hydrodynamic stability and the transition to turbulence [
30]. This rich experimental configuration is geometrically specified by the radii
of the cylinders (inner: 1, outer: 2), ratio
measuring curvature effects, the axial and circumferential aspect ratios,
and
,
being the gap between the cylinders and
L their length (usually fairly large when compared to
d), and the rotation rates
. By convention,
with
,
, or
for the outer cylinder at rest, co-rotating, or contra-rotating with respect to the inner cylinder, respectively. One usually defines the inner and outer Reynolds numbers as
, (
: kinematic viscosity), but other physics-motivated parameterizations are possible, such as the Taylor number [
31]. A definition referring to the mean shear,
, is particularly helpful for direct comparisons with other wall-bounded configurations [
32,
33,
34,
35], especially plane Couette flow in the limit
. The advantage of CCF is that most situations of interest can be spanned [
30], from temporal chaos (short cylinders, wide gap) to spatiotemporal chaos (gap small compared to perimeter), and from globally super-critical to globally sub-critical according to whether or not the dynamics is controlled by the centrifugal instability of the innermost fluid layer at the inner cylinder [
31,
36]. At this point, I want to stress that the present review is restricted to the globally sub-critical transitional regime where laminar-turbulent patterns form. I will not consider the fully developed regime much beyond the limit for featureless turbulence [
37] and, apart from a brief mention below, I will not consider the globally super-critical case in detail, leaving it to [
16,
30,
38].
CCF is entrained by the motion of the cylinders where no-slip conditions apply. All along the thermodynamic branch, the
base state displays a purely azimuthal velocity profile, entirely controlled by viscous effects. In the inviscid case,
, when the Rayleigh stability criterion is violated—here, when the angular momentum does not increase monotonically outwards [
36]—infinitesimal perturbations to the base flow are amplified through inertial effects while a finite viscosity delays the instability until a shearing threshold is reached. A super-critical instability then develops producing axisymmetric Taylor vortices [
31]. This is the case when the Rayleigh criterion for stability is violated all over the gap, i.e.,
. Taylor instability is then at the start of a globally super-critical sequence of bifurcations toward more and more complicated flow behavior up to a turbulent regime, a scenario termed ‘spectral evolution’ by Coles [
5] who early reported on it. Consult [
30,
38] for reviews and Figure 1 in [
16] for a detailed bifurcation diagram at
. The typical wavelength of Taylor rolls is twice the gap and when the axial aspect-ratio
is small enough, the setup accommodates a small number of rolls that remain highly coherent even when the flow enters the turbulent regime, then rather understood in terms of
temporal chaos within the theory of low-dimensional dissipative dynamical systems (see Chapter 4 in [
2]). When
is large, CCF can be studied using the
envelope and
phase formalisms, turbulence acquiring a more
spatiotemporal flavor [
39], still in a globally super-critical context.
When the two cylinders rotate in opposite directions,
, the Rayleigh criterion for stability is violated only in a fluid layer near the inner cylinder where unstable linear modes with non-axisymmetric structure can develop [
16]. Near the outer cylinder, the criterion is fulfilled so that the corresponding fluid layer is stable in the inviscid limit, right in the situation described above for globally sub-critical plane flows. Localized finite amplitude perturbations bursting from the inner unstable layer [
40] can now trigger the transition to turbulence. Bursting perturbations affect a network of interpenetrating spirals (IPS) [
16] generating
turbulent spots, at first intermittent and disseminated, but more and more persistent as the shear increases [
5,
17]. Turbulent spots further grow into turbulent patches and next into
spiral turbulence (ST regime), characterized by its helical,
barber pole, aspect first reported by Coles [
17], later scrutinized by Andereck et al. [
16] and others, e.g., [
41,
42]. Upon further increasing the shear, the helical arrangement disappears above some mean shear threshold
, translated as a line in the
parameter plane, beyond which the flow enters the featureless turbulent (FT) regime, thus saturating the turbulent fraction or equivalently the intermittency factor (line
in Figure 2a,b of [
5]; see also Figure 1 of [
16]). A direct collapse of turbulence to axisymmetric laminar flow can be observed for very fast counter-rotation as a direct transition in the ‘hysteresis region’ in Figure 2a of [
17] or Figure 3 of [
43], with features specific to transient temporal chaos when
is small, enforcing spatial coherence [
44]. At more moderate counter-rotation rate, decay happens via IPS in the shear range just before axisymmetric laminar flow is recovered (Figure 1 of [
16]).
In the experiments mentioned above, all with
(
) a single helical branch (
) was ordinarily obtained [
5,
16,
17]. Thinking in terms of a laminar-turbulent pattern, owing to azimuthal periodicity, a single helix branch corresponds to an oblique band and, accordingly, a streamwise wavelength
; not currently observing
-helices means
, which is confirmed by the fact that no pattern was found for
, i.e.,
. Patterns with wavelengths very large when compared to the gap
d are therefore observed. In order to approach the paradigmatic case of PCF, experimental configurations with
closer to 1 have been considered. Prigent [
45,
46] scrutinized the cases
and
, hence
and 358. Besides noting a continuous shift of the bifurcation diagram towards the
-line in the
-parameter plane as
approached the PCF limit
, he obtained helices with more branches and wavelengths
in agreement with those for
and
. A few supplementary features are worth mentioning. (i) In all cases, the spiral patterns appeared to be nearly at rest in a framework rotating at the mean angular speed
[
5,
17,
46]; (ii.a) The helical pattern emerged continuously from the FT regime with, close to
, domains of opposite-helicity modes separated by grain boundaries (Figure 9 in [
46]) seen to move so as to favor a single helicity farther from
. (ii.b) In the single-helicity regime, the azimuthal and axial wavelengths were seen to vary with the mean shear, with larger wavelengths close to decay at
(Figure 5 of [
46]); (iii) When the pattern was well established, the laminar-turbulent interfaces displayed
overhangs, that is, quiescent flow close to one cylinder facing turbulent flow near the other [
5,
17,
43,
47]. I will come back to the emergence of the spirals at
from the featureless regime and their characterization in
Section 5.
4. Decay at R as a Statistical Physics Problem: Directed Percolation
On general grounds, bifurcations in nonlinear dynamics and phase transitions in thermodynamics can be connected via dissipative dynamical systems defined in terms of gradients of a potential which, on one side, govern the most elementary bifurcations and, on the other side, the classical Landau theory. In Landau’s classification of phase transitions [
96], super-criticality maps onto continuous second-order phase transitions, e.g., ferromagnetic, and sub-criticality onto discontinuous first-order phase transitions, e.g., liquid-gas. The correspondence is strict in the mean-field approximation neglecting microscopic thermal fluctuations. Taking them into account implies deep corrections. Second-order transitions then come in with the notion of
universality linked to a scale-free power-law behavior of correlations at the transition point, introducing sets of critical exponents. Universality means that physically different systems macroscopically described using observables with identical symmetries behave in the same way at given physical-space dimension. For a compact self-contained overview of critical behavior and universality in phase transitions consult §1 of [
97]. As to first-order transitions, they experience the effect of fluctuations through the nucleation of germs that drive the phase change when they exceed some critical size.
Near equilibrium, thermodynamic systems fulfill micro-reversibility, a property that is lost sufficiently far from equilibrium, in hydrodynamic systems having experienced instabilities, and
a fortiori in turbulent flows. The globally sub-critical transition typical of wall-bounded flows is specific in that it sets a laminar flow stable against small perturbations in competition with a locally highly fluctuating, but statistically well-characterized turbulent regime. At given
R the laminar flow is locally attracting in the dynamical-system sense and is only submitted to extrinsic fluctuations of thermal origin, or due to residual imperfections, that are in themselves unable to drive the flow toward the turbulent state (at least for intermediate values of
R in the transitional range). In statistical physics of far-from-equilibrium systems, this property qualifies an
absorbing state [
97], where the word ‘state’ qualifies the system as a whole with a global (thermodynamic) meaning.
On the other hand, the turbulent flow is the seat of large fluctuations of intrinsic origin due to chaos. Furthermore, all over the coexistence range, this local stochasticity is only
transient, i.e., can be viewed as a memoryless process with a finite decay probability function of
R [
58]. Pomeau [
10] early suggested that, in view of these characteristics, the whole spatiotemporally intermittent arrangement of laminar-turbulent domains could be interpreted as the result of a purely stochastic process called
directed percolation (DP) in statistical physics [
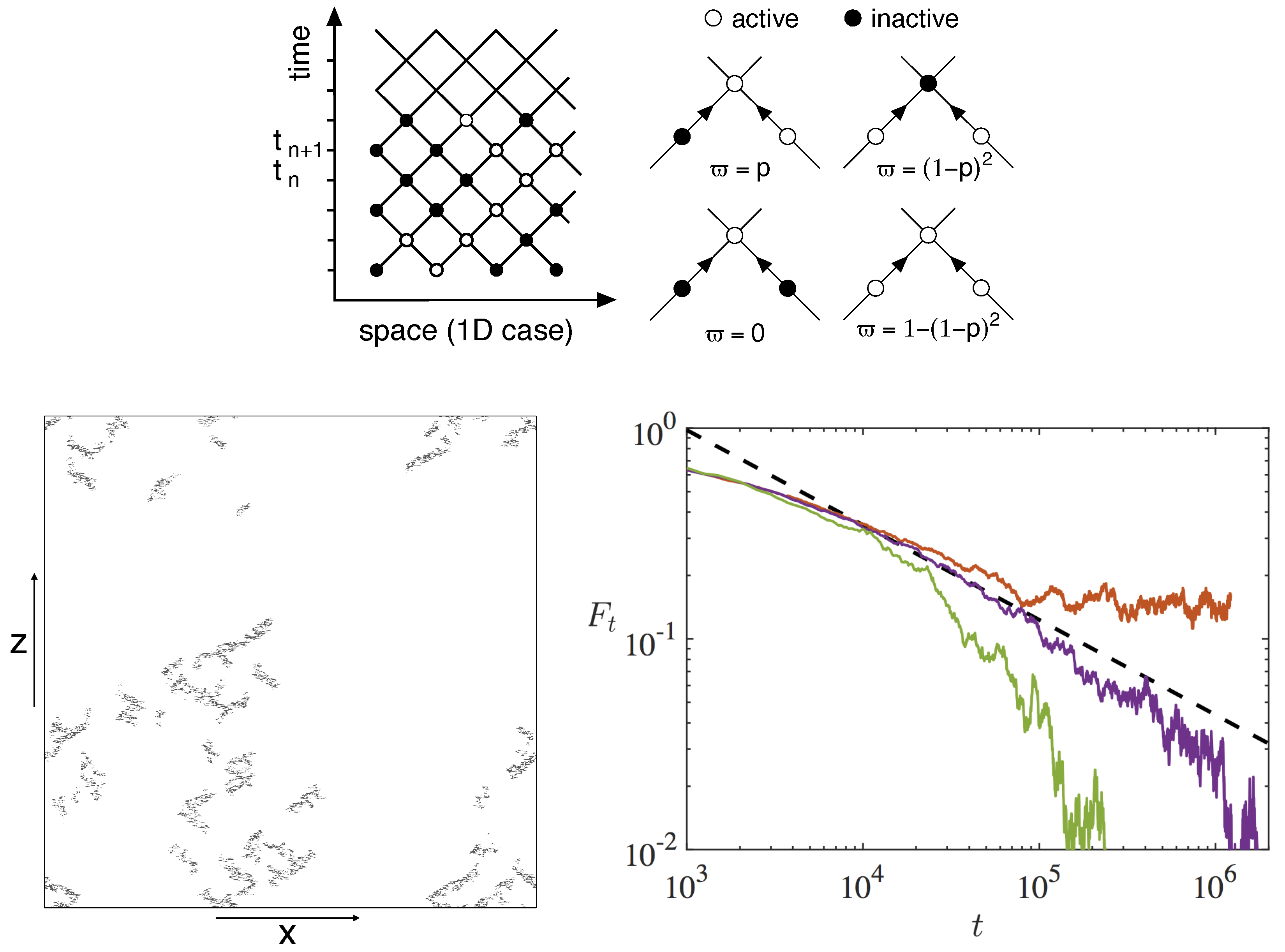
97]. This process can be described in terms of a probabilistic cellular automaton defined on a space-time lattice (
Figure 4, top left) of cells that can each be in one of two states,
active (turbulent) and
inactive (laminar). Here ‘state’ has an obvious local meaning, like for spins that can be ‘up’ or ‘down’ (‘active/inactive’ is also often termed ‘on/off’, even ‘alive/dead’). A given cell in the inactive state cannot become active by itself, but only by
contamination with some probability
p from one of its neighbors in the active state (
Figure 4, top right), as can be the case for trees in forest fires, or individuals in epidemics. Pomeau went further in conjecturing that the laminar-turbulent transition was in the DP universality class, i.e., had its main properties characterized by the same set of exponents as the abstract statistical-physics process, which triggered numerous studies of analogical models, numerical simulations of NSE, or laboratory experiments. As to universality, the Janssen–Grassberger conjecture [
97] stipulates that all systems with short-range interactions, characterized by a single order parameter, experiencing a continuous transition to a non-degenerated absorbing state, belong to the same class in the absence of additional symmetries or quenched disorder. The main corresponding critical exponents are
describing the variation of the turbulent fraction
, where
is the relative distance to threshold,
and
, accounting for the power-law distribution of absorbing (here, laminar) sequences at threshold,
either in space or in time,
ℓ being the mean size of inactive clusters at a typical time for
, or the mean duration of intermissions (period of inactivity) at a typical location for
. One gets
,
,
, and
,
,
, see §A.3.1 of [
97] for more information.
The study of critical properties of directed percolation comes in two ways, both statistical and requiring a large number of realizations, either (i) by triggering the active state in a germ, a (small set of contiguous) cell(s), or (ii) by observing the decay of a uniformly active state. The first procedure, which corresponds to the triggering of turbulent spots, has been followed since the early days [
49,
50,
79], though outside the DP framework. Numerical approaches devoted to the determination of germs able to drive the transition to sustained turbulence has comparatively received less systematic attention and, in view of reliable statistics, seem much more demanding in terms of analytical shapes to be tested than localized seeds in the 0/1 context of DP. The search for
edge states [
98], flow configurations that are sitting on the laminar-turbulent boundary in a phase-space perspective, is a step in that direction [
99]. The second procedure, the decay from a featureless turbulent state, is more easily implemented and has accordingly received more attention in the last few years.
As a first step, analogical models have been considered [
11]. They were expressed in terms of coupled map lattices where the local map implemented the active/inactive nature of the states at the lattice nodes. The coupling to neighbors was usually diffusive and 1D or 2D lattices were considered in view of their relevance to 1D pipe flow [
21,
24], or to 2D planar flows [
54] recently re-examined in §2 of [
75]. Considering these computationally light cases helps one better figure out the requirements of large aspect ratios and long simulation durations for a proper characterization of the critical behavior at
. These requirements turn out to be extremely demanding, which explains why early PCF experiments were inconclusive as to a 2D-DP critical behavior. That the DP framework be relevant for PCF was first obtained within the quasi-1D Barkley–Tuckerman framework [
63], which was quantitatively confirmed soon later [
100]. In addition to the numerical experiment, a quasi-1D CCF configuration was considered with
, hence
and very short cylinders,
, yielding exponents in excellent agreement with the theoretical values for 1D-DP.
In the 2D case, up to now, a single experiment in the PPF case has concluded to the relevance of the DP universality class [
87]. The observation rested on the decay of turbulence produced by a grid at the entrance of a wide (
) and long (
) channel and a detection of turbulent domains in the part of the channel closest to the exit. Exponents corresponding to 2D-DP have been found, but the critical point for DP,
, was clearly larger than
above which localized turbulent states are now known to be sustained [
83,
84,
85,
86]. Since by definition
is the threshold below which the base state is unconditionally stable in the long term, this could mean that initial conditions produced in the experiment belonged to the inset of a specific scenario with the flow staying outside the basin of attraction of the localized states mentioned above. As of today, I am not aware of numerical simulations of 2D-patterned PPF turbulence in systems with aspect ratios sufficiently large to conclude on its decay in a DP perspective, though the use of streamwise periodic boundary conditions should help solving the problem of streamwise advection and the associated experimental aspect ratio limitation (channel length).
Things are different for laminar-turbulent patterns in PCF, at least if one accepts some dose of modeling. As already mentioned, such a modeling has mainly been developed along two lines, controlled wall-normal under-resolution of the NSE with no-slip boundary conditions [
66], and consideration of stress-free boundary conditions with a subsequent reduction of the number of wall-normal modes [
55,
70]. In both cases the computational load is significantly decreased, thus allowing the consideration of larger aspect ratios in order to check the behavior. Along the first avenue, at reduced wall-normal resolution, the exponent
attached to the variation of the turbulent fraction close to the threshold for band decay in a
domain has recently be found to fit 2D-DP universality by Shimizu [
101] at a shifted
consistent previous studies [
66]. In the second modeling approach, spectacular results have been obtained by Chantry et al. [
75] within the framework of their stress-free reduced model that they simulated in huge domains up to
and
(
Figure 4, bottom). They measured all of the exponents of the 2D-DP universality class to extremely good accuracy and obtained excellent data collapse of scaling functions [
97] proving their claim. They also explained why laboratory or numerical experiments in too small domains [
53,
60,
67] could erroneously suggest a discontinuous transition as sketched in
Figure 1 (b1–b2). However, they also documented further that, within coupled-map-lattice modeling [
11,
54], the DP universality class is particularly fragile in 2D and thus prone to break down as a discontinuous transition (§2 of [
75]). Since modeling specificities, such as the bad account (under-resolution) or neglect (stress-free) of boundary layers close to the walls, could affect the properties of the transition, simulations of the realistic case with no-slip conditions at full resolution are underway [
101].
5. Emergence of Patterns from the Featureless Regime
Pattern formation is a standard problem in non-equilibrium dynamics [
2,
102]. Usually, e.g., in convection, the state of the considered system lies on the thermodynamic branch where the effects of noise, of thermal origin, are small and bifurcations away from this state are essentially governed by deterministic dynamics. On general grounds, one expects a super-critical bifurcation governed by an ordinary differential equation, viz. a
Landau equation:
where
r is a reduced control parameter.
, the amplitude of the deviation from the basic state, is a function of time
t. When a periodic pattern forms, amplitude
A is the intensity of corresponding Fourier mode, e.g., convection rolls with wavelength
. In large aspect-ratio systems, the spatial coherence induced by the local instability mechanism cannot be maintained by lateral boundary effects. The intensity of the developing structure get modulated with an expected tendency to relax toward the arrangement favored by the instability mechanism in a diffusive fashion. Typically
A becomes a function of time
and space,
, governed by a partial differential equation of
Ginzburg–Landau (GL) type:
, in which
is a Laplacian operator accounting for diffusion, in 1D or 2D depending on the geometry. This simplified description can be extended to deal with competing modes and associated amplitudes with specific symmetries. Such formulations can (at least in principle) be derived from the NSE via multi-scale expansions resting on scale separation, i.e.,
modulation scales, as discussed e.g., in Chapter 6 of [
2]. Weak extrinsic noise can be introduced as an additive perturbation.
The high degree of generality of this approach [
102] gives strong motivation to its use at a
phenomenological level when strict applicability conditions are not fulfilled, here in an overall globally-sub-critical context for an apparently continuous bifurcation which is super-critical-like, but at decreasing control parameter
and from a uniform turbulent background. Prigent et al. [
45,
46] introduced such a description of patterning in CCF, directly stemming from their observations with
, as summarized at the end of
Section 2. Introducing a set of two coupled GL equations for two amplitudes, one for each orientation, and adding a noise term to account for the intrinsic stochasticity in the turbulent background, they were able to fit all of the phenomenological coefficients introduced in their expressions against the experiments, including the effective noise intensity, and to account for the whole variation of the pattern’s amplitude with a reduced control parameter
. The fits used the amplitude of the dominant Fourier modes of the turbulence intensity in a plane containing the cylinders’ axes, with demodulation to separate the two possible helical pattern components. They showed that the amplitude followed the square-root behavior expected from GL theory, extrapolating to an apparent threshold
beyond the values of
R where the pattern becomes visible by eye. This observation was understood as an effect of high-level noise from the background turbulence implying strong orientation fluctuations and a subsequent reduction of the pattern’s amplitude. When transposed to PCF, this provides an explanation to the difference between the value
obtained in the Barkley–Tuckerman oblique domain [
64], and the value found consistently in the range 405–415 in experiments [
45,
46] or numerical simulations in streamwise-spanwise extended domains [
60,
103] that keep full track of orientation fluctuations.
Better understanding fluctuations around
should give insight in the nature of the transition to turbulence and the mechanisms presiding the emergence of a pattern. To this aim, I performed numerical simulations of PCF in domains of size ∼
hosting two to three turbulent bands (App.A of [
103]).
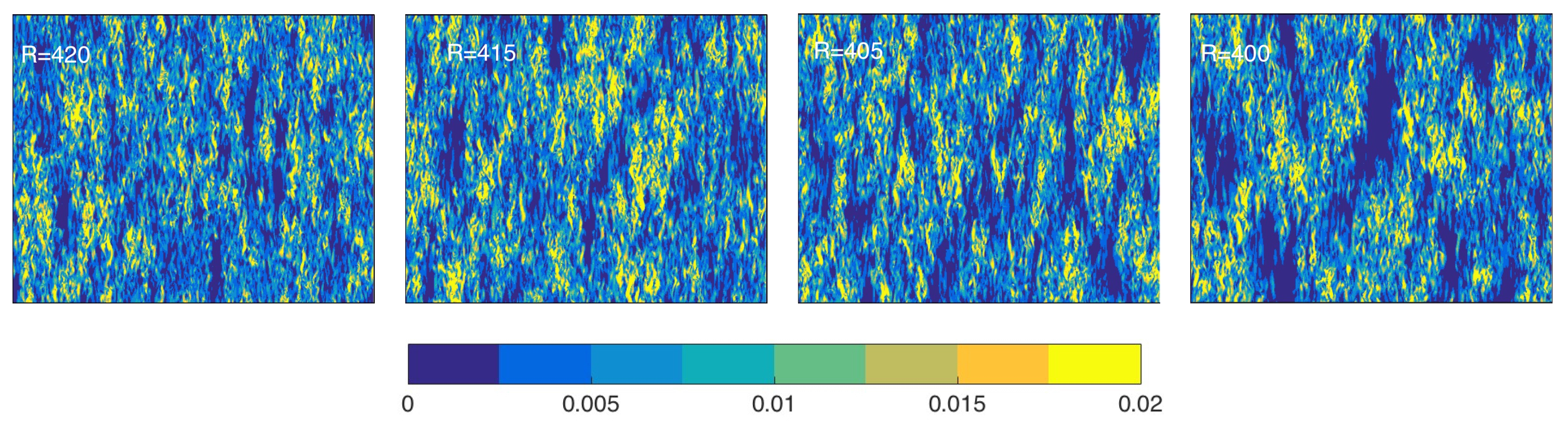
Figure 5 depicts typical snapshots from my simulations down to
that could however not be precisely located due to size effects and lack of statistics to deal with the high level of fluctuations. As a matter of fact, intermittent elongated laminar patches appear well above
in what remains predominantly featureless turbulence. They are small, short-lived, and mainly streamwise without any apparent ordering above
. For
, though still intermittent, they become bigger, occasionally oblique, with longer lifetime, and show a tendency to cluster, either with the same orientation or forming chevrons when the orientations were different. As
R is further lowered, the turbulent fraction decreases due to the widening of the laminar domains that seem to progressively percolate (in the ordinary, not directed, sense) through the remaining turbulent flow. Fourier characterization of this modulated turbulence warrants further scrutiny in view of a comparison with results from experiments in CCF [
45,
46] and the quasi-1D numerical approach [
64].
The origin of localized, short-lived, MFU-sized laminar patches can be traced back to the behavior of chaotic solutions to the NSE at the MFU scale, with their irregular alternations of bursting and low-activity excursions [
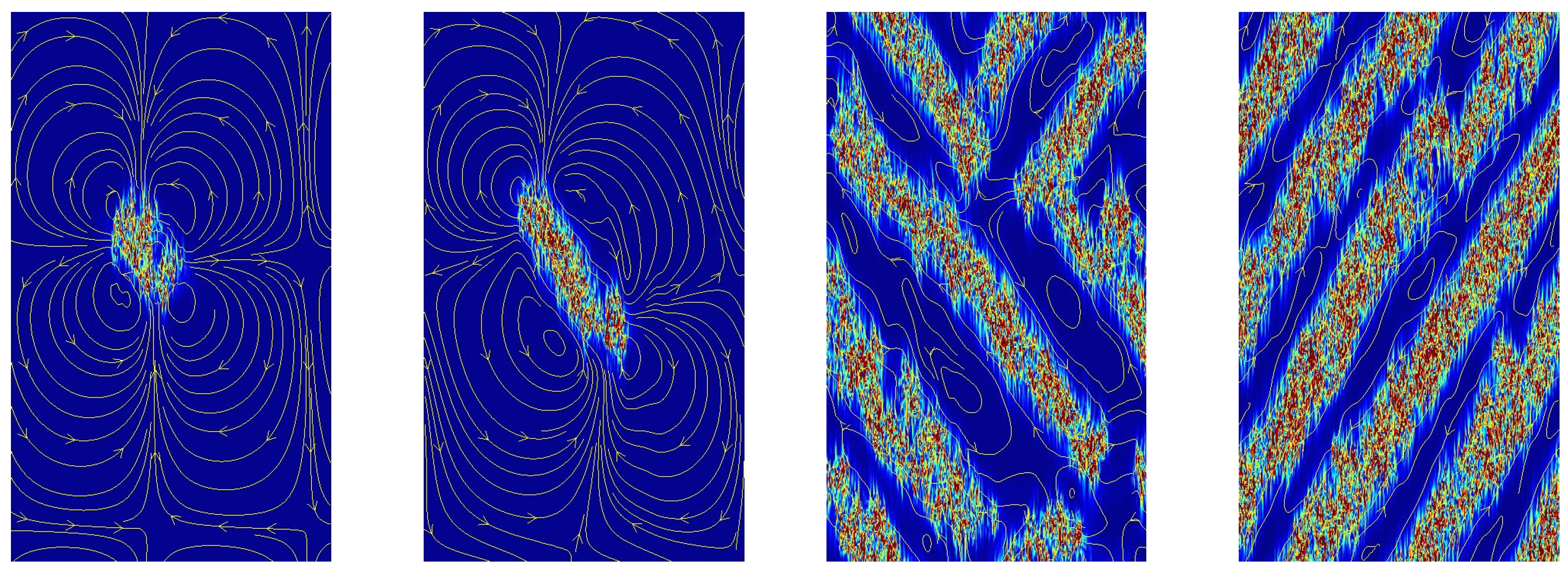
8], but the formation of more extended laminar domains remains to be elucidated. The nature of the flow inside laminar patches of intermediate size is of special interest since, on general grounds, it can be analyzed as a superposition of the laminar base flow and a large scale correction (the faint yellow lines on the blue background in
Figure 3). In the lower part of the transitional range
where the pattern is well established, the large-scale flow is easily extracted by time-averaging [
35] or by filtering out small scales around growing spots [
62,
95]. In systems bounded by plates in the wall-normal direction, PCF, PPF, etc., a non-vanishing 2D divergence-free component can be isolated out of the large-scale flow by averaging over that direction [
95]. This component might be crucial for the organization of laminar patches into regularly arranged bands since patterns disappear when large-scale flows are not constrained to stay 2D, but allowed to escape in the third direction as for ASBL [
68] or too weakly stratified Ekman layer [
90]. Unfortunately, in the upper transitional range around
this large-scale flow component is difficult to educe without a combination of averaging and filtering free from arbitrariness when laminar depressions are still small. If detected unambiguously, it could however serve to characterize the transition at
in much the same way as it was used to identify the transition from 1D to 2D in annular Poiseuille flow when curvature is decreased [
28]. How much does it contribute to the percolation of laminar patches into bands at
and the details of the laminar-turbulent organization, wavelength and angle, whether it is a cause or a consequence, are questions that directly leads to the discussion below.
6. Understanding Laminar-Turbulent Patterning: Theoretical Issues and Modeling Perspectives
Ideally, the physical explanation for patterning should derive from the NSE. Unfortunately this does not seem easy since, whereas the analytical solution for laminar flow can be straightforwardly obtained, neither locally turbulent flow nor the flow in the interface region can be obtained without some empirical averaging or modeling. Closure models that work in engineering conditions where turbulence is rather homogeneous and sufficiently developed do not provide appropriate solutions in the transitional regime where coexistence is the rule. This was shown in [
64] where a standard
K–
approach was used to treat the laminar-turbulent mixture without producing any modulation of the turbulence intensity. Other approaches must therefore be followed.
Working by analogy is the way followed by Barkley to obtain his model for HPF [
21,
24]. First identifying the similarity between puffs in a pipe (HPF) and nerve impulse propagation, he treated the pipe as a 1D reaction-diffusion (RD) system (Chapter 9–14 of [
25]). In the
excitable regime, the dynamics only produces localized concentration perturbations, pulses, followed by refractory stages during which the medium can recover the properties necessary for pulse propagation. Upon changing the reaction and diffusion rates, the RD system can enter a
bi-stable regime with locally homogeneous domains of reactants or reaction products generically separated by propagating fronts, e.g., flame fronts, the domain filled with the most stable state, e.g., burnt gases, invading that of the least stable one, i.e., fresh gases. Barkley [
24] introduced just two variables, one ‘
q’ measuring the local turbulence level and another one ‘
u’ characterizing the mean shear, coupled by two partial differential equations functions of the streamwise coordinate
x and time
t. An appropriate choice of the intrinsic dynamics for
q permitted the control of the
excitable vs.
bistable behavior by means of a single parameter playing the role of
R. A coupling of
u and
q mimicked empirical knowledge on the relaxation of
u. This led Barkley to the sought-after model [
24], allowing him to reproduce the overall behavior of HPF, from puff dynamics (excitable regime) to the transformation into slugs (bistable regime). The adjustment of a few coefficients allowed the quantitative reproduction of the different dynamical regimes observed and the model was simple enough to permit a detailed analytical treatment that really explains the behavior of HPF all along its transitional range [
21].
A support of the reduced description sketched above from the NSE would however be welcome. In that form, it can also not help us understand the 2D patterning typical of planar flows. As a first step in that direction, I proposed [
104] to keep the RD framework, but to exploit another of its features: the possibility of a Turing instability ending in a pattern when diffusivities of the reactants are of different orders of magnitude (Chapter 14 in [
25]). To be more specific, I chose to describe the local reaction using Waleffe’s implementation of the SSP [
14]. From its four variables, I enslaved two of them to the mean flow correction
m analogous to Barkley’s
u and to a second variable
w analogous to
q. Furthermore, I introduced diffusion along a fictitious space coordinate, slow for
m and fast for
w as guessed from the physical nature of these variables and, magically, patterning emerged. A beneficial aspect of my approach was that the nonlinear reaction part could be traced back to NSE by following Waleffe, but, while alleging that patterns might result from the interplay of effective diffusion and nonlinear reaction, by construction it could predict neither the wavelength nor the orientation of the so-obtained pattern. In an attempt to fix the wavelength in a 1D periodic domain, Hayot and Pomeau [
105] introduced a phenomenological feedback from large-scale secondary flows in a sub-critical GL formulation,
, where
expressed the pressure loss through Reynolds stresses in the turbulent fraction of the whole domain. While a variation of the turbulent fraction with
r could indeed be predicted, a single laminar-turbulent alternation was obtained, hence no nontrivial wavelength. Realistic, though simple enough, modeling leading to an explanation of pattern formation could hopefully come from a combination of the ingredients mentioned up to now, especially if one could make them stem from the NSE in some way.
A promising strategy follows from the remark that under-resolved numerical simulations of NSE give already precious qualitative information on the processes at work [
67], and even quantitative results [
101] once the systematic downward shift of
and
[
66] is taken into account. The most common simulations are based on spectral representations of the wall-normal dependence. The robustness of patterning against under-resolution stems from the fact that the dynamics seems controlled rather by the behavior of the ‘interior flow’ [
70] than by what happens close to the solid boundaries. Further, owing to the intermediate values of
R involved, neither too small nor too large, this behavior can be accounted for by the very first modes of the functional expansion of wall-normal space dependence that can be dealt with analytically rather than in the black-box fashion of a simulation software. This treatment is all the more feasible that the basis functions can be chosen for analytical simplicity rather than for computational efficiency. Trigonometric lines are appropriate to stress-free boundary conditions, as proposed by Rayleigh [
69] and exploited in [
14,
55,
70]. If no-slip boundary conditions are judged more realistic, simple polynomials [
72,
73,
74] can be preferred to Chebyshev polynomials generally used in simulations.
The standard Galerkin approximation procedure eliminates the explicit dependence on the wall-normal coordinate and replaces the 3D velocity and pressure fields by 2D mode amplitudes in the planar case [
70,
73] and even 1D for pipe flow [
70]. Simultaneously the NSE is replaced by a set of partial differential equations with reduced spatial dimensionality. Importantly, truncation of the expansion, retaining just a small number of amplitudes and equations, implements the dominant features of the dynamics, namely the SSP, while preserving the general structure of the NSE, notably its symmetries relevant to the case at hand and kinetic energy conservation by the advection term, as discussed in §3.2 of [
55]. Numerical simulations of so-obtained models show that realistic patterning in PCF is obtained by keeping just seven amplitudes [
70,
73], while the three lowest ones account locally for Waleffe’s implementation of the SSP [
55], and globally for large scale flows around a turbulent patch [
74].
The analytical approach in [
73] emphasizes the generic character of the such low order models where a particular coefficient set relates to a given system (flow geometry and boundary conditions, e.g., stress-free vs. no-slip, cf. Table 1 in [
72]), which can be tentatively changed to test the effect of specific coupling terms. Beyond plain simulations, the formulation can be the starting point for further modeling in view of building RD-like simplified models giving some foundation to the nonlinear interaction terms introduced on semi-empirical grounds for HPF [
24] or from purely phenomenological arguments for PCF [
45,
46]. This derivation should focus on slow and large scale properties relevant to patterning, therefore eliminating all spatiotemporally fast interaction terms at the MFU scale, as partially done in [
74], or in [
104,
105]. The problem lies in a realistic modeling of Reynolds stresses generated by the SSP as a local source driving the large scale flow, which might be achieved by completing Waleffe’s local approach [
14] with a closure assumption expressing the feedback of large scale flows on the turbulence level at MFU scales. Including such physical insight would help one skirt around the limitations of closures usually referred to in turbulence modeling, such as the
K–
scheme used in [
64].
The interest of such a modeling would not primarily be in view of appreciating/questioning universality at
when the pattern decays since, in very large systems, the turbulent fraction is so low that long range interactions associated to large scale flows are expected to be extremely weak (
Figure 4, bottom-left) and are not really suspected to violate the terms of the Janssen–Grassberger conjecture mentioned in
Section 4. On another hand, offering a reliable representation of the dynamics at scales somewhat larger than the MFU, it would provide indications about the dependence on
R of probabilities for turbulent patches to grow, recede, or branch, for turbulent bands to break and recover from laminar gaps, etc. [
67]. Besides giving a microscopic foundation to the macroscopic behavior at
, its main interest would certainly be to answer the question of patterning emergence from the FT regime when
R decreases from large values. In this respect, the goal would be to eliminate all irrelevant information and derive an effective GL formulation valid all along a large part of the transitional range, accounting for laminar-turbulent alternation with possible superposition of different orientations around
, for the selection of a given orientation somewhat below
, and for wavelength and orientation changes as
R decreases, since all of this can be contained in the coefficients of the effective GL model [
45,
46].
Another question is why does patterning occurs at all, and whether it achieves some sort of dynamical optimum (minimization of an effective potential with thermodynamic flavor), as would stem from the weakly nonlinear GL formalism with added noise [
46,
106]. It is however not clear how to apply this approach when working at decreasing
R from a turbulent state. In previous studies [
106] the bifurcating and bifurcated states were affected in the same way by weak additive noise. For example in convection, the bifurcation is super-critical and, near threshold, the rest state and the Bénard cells remain qualitatively and quantitatively close to each other in a phase-space perspective and are perturbed by small extrinsic imperfections and intrinsic low-amplitude thermal noise in the same way. In wall-bounded flows the branch of nontrivial states is qualitatively always far from the laminar flow branch in phase space, even when the distance is quantitatively evaluated as a vanishingly small turbulence fraction immediately above
as sketched in
Figure 1 (b2). Meanwhile, far above
the FT regime displays large, space-time localized, intrinsic fluctuations that make the flow ‘remember’ the presence of the laminar (absorbing) regime, far from a situation where detailed balance would hold. Any thermodynamic viewpoint about transitions consequently remains a challenge, at least compared to spin systems or other microscopic systems at equilibrium.
Beyond these formal considerations, I would like to conclude by first stressing that organized patterning is a common feature of transitional wall-bounded flows, with laminar-turbulent coexistence holding both in physical space and, usually, over some finite range of Reynolds numbers. Next global sub-criticality is linked to the absence of any relevant instability against infinitesimal perturbations to the laminar base flow in the whole series of systems that I have considered, PCF being just a paradigmatic case. In addition, the universal behavior of turbulence decay at
, much debated for a long time since Pomeau’s early conjecture [
10], is on the verge of being demonstrated. However, though conceptually satisfactory, this property concerns a narrow vicinity of
and appears to be much less important than the nature of physical processes involved at intermediate
R and large scales (i.e., ≫MFU), at the laminar-turbulent interface dynamics, especially in spot growth and pattern formation. Further study of these subjects, experimental, numerical, or theoretical
via simplified, but realistic modeling, seem particularly necessary in view of controlling the transition in less academic cases, a matter of great practical interest for applications.