Regularizing Neural Networks via Retaining Confident Connections
Abstract
:1. Introduction
2. Theoretical Foundation of IG
2.1. Parametric Coordinate Systems
2.2. The Fisher Information Matrix
2.3. The Fisher Information Distance
3. Motivation
3.1. Data-Independent Regularization
3.2. Data-Dependent Regularization
4. Model
4.1. Restricted Boltzmann Machine in IG
4.2. The Confidence of a Connection
4.3. ConfNet
| Algorithm 1: Data-dependent Regularization. |
 |
4.4. Stochastic ConfNet
4.5. Training with Back-Propagation
| Algorithm 2: Training with Back-propagation. | |
| Input: A fully connected layer of a DNN with input ; N input samples | |
| Output: weights W and biases b | |
| 1 | Initialize W and b |
| 2 | while classification error converges do |
| 3 | Calculate the mask M via Algorithm 1 |
| 4 | Reduce NN by |
| 5 | Feed-forward: |
| 6 | Differentiate loss with respect to W and b |
| 7 | Update W and b using the back-propagated gradients |
| 8 | end |
| 9 | returnW and b |
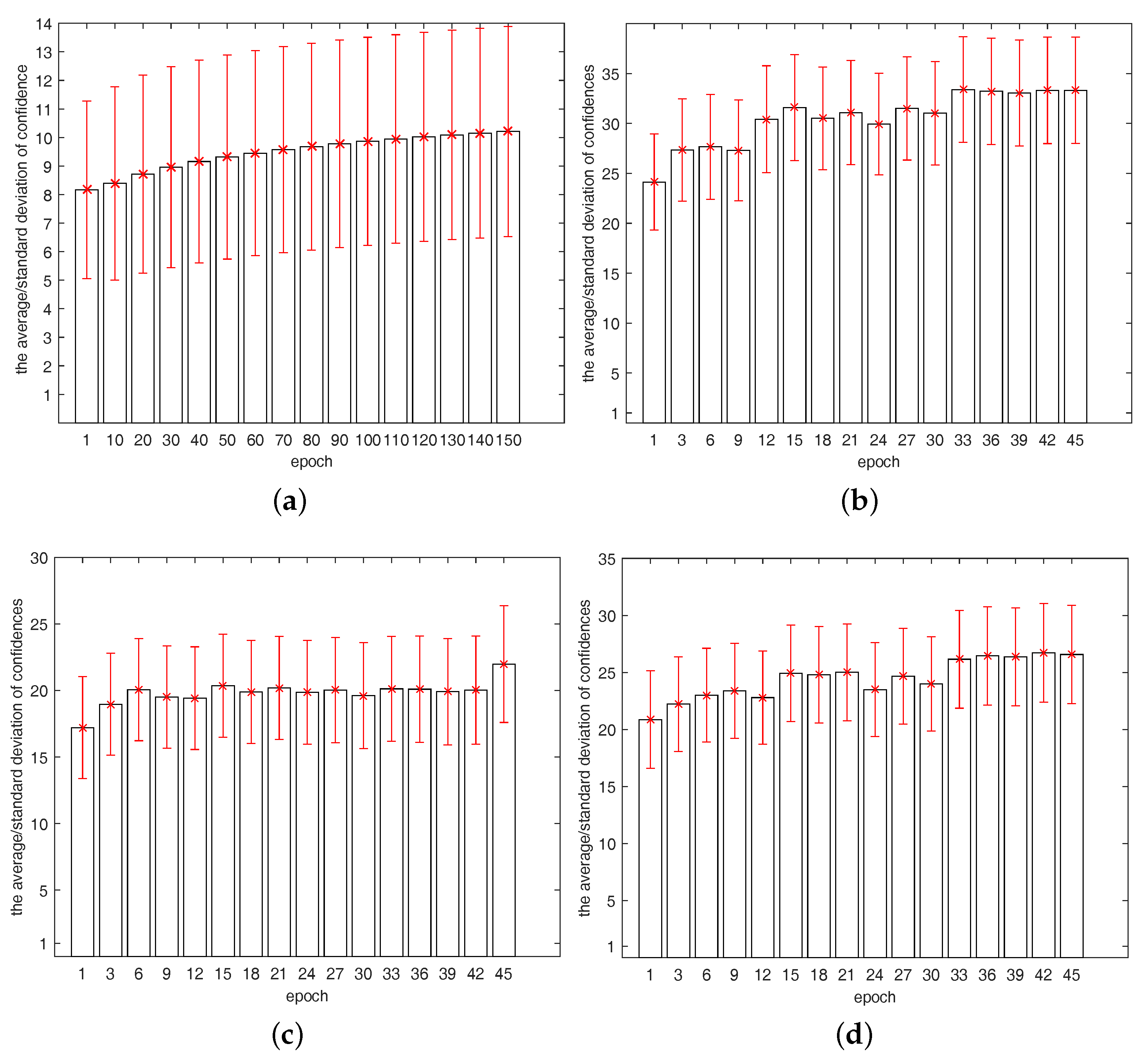
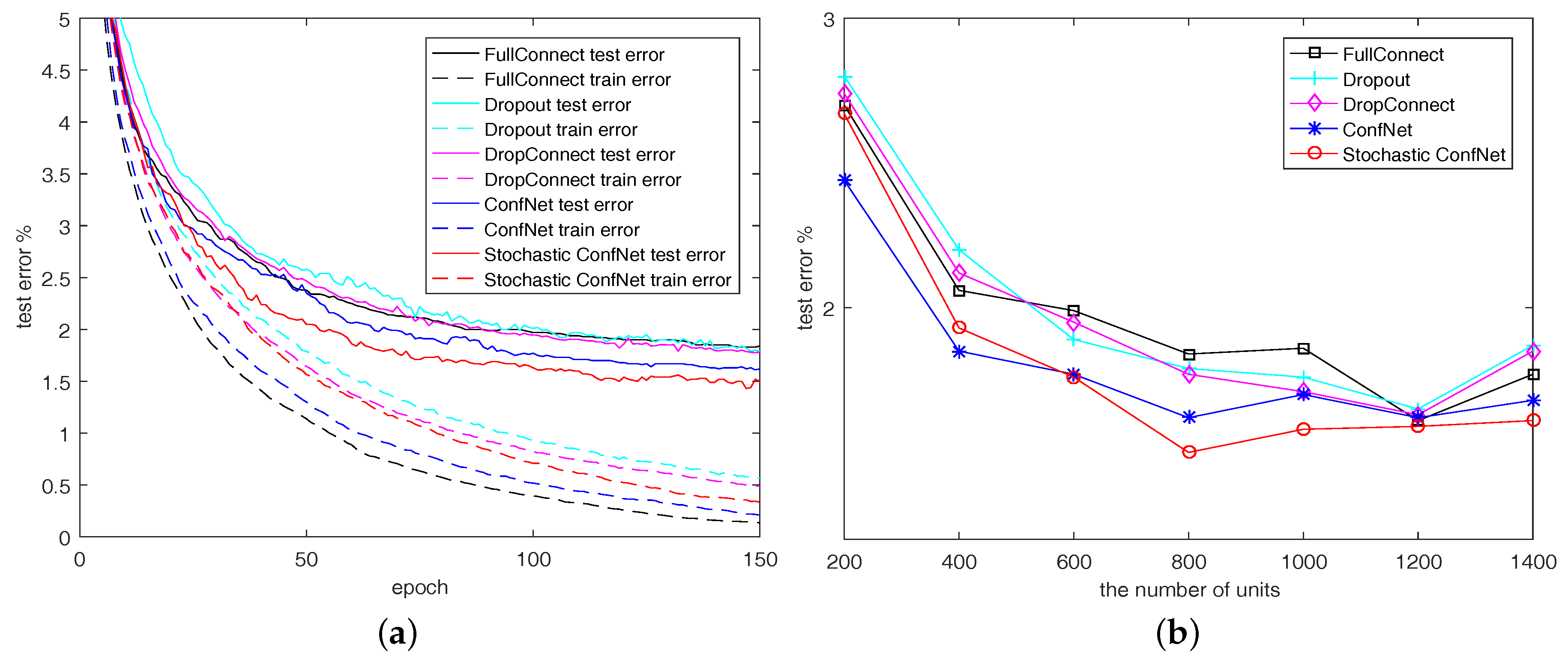
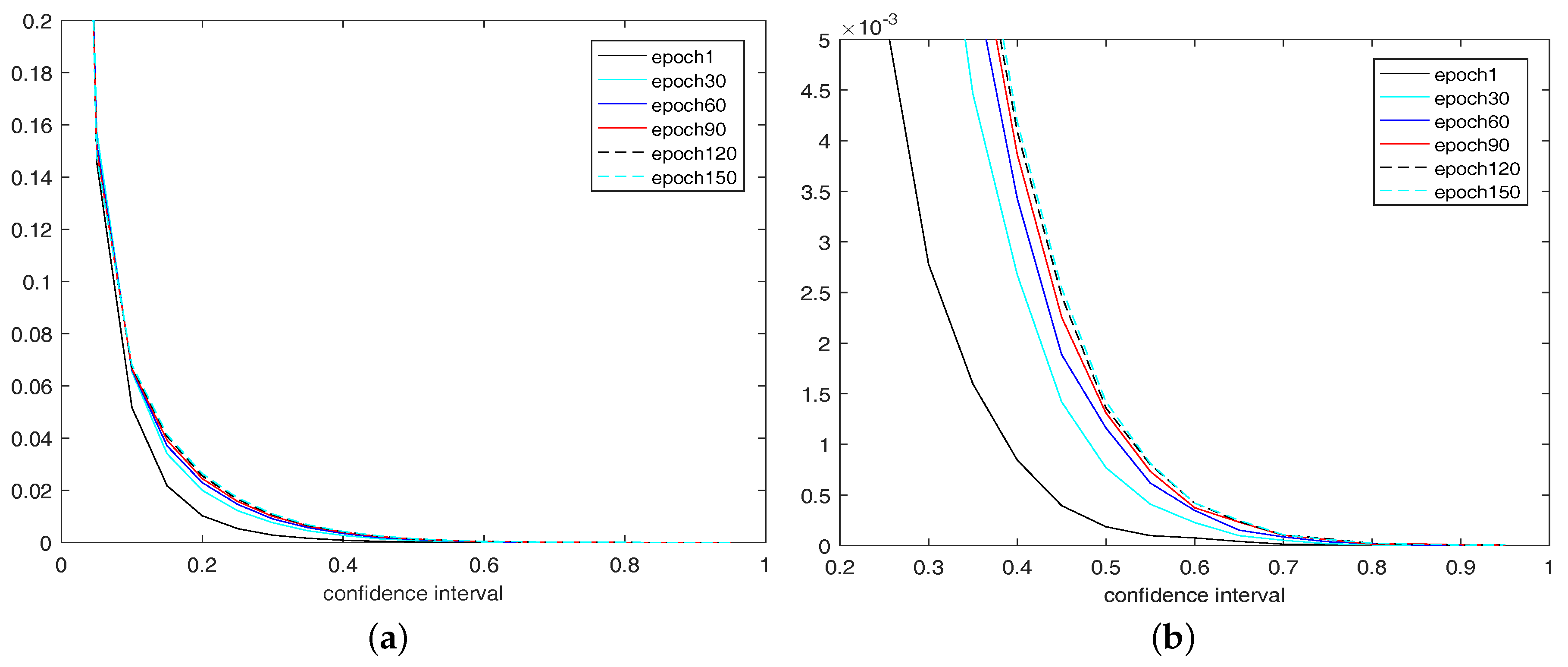
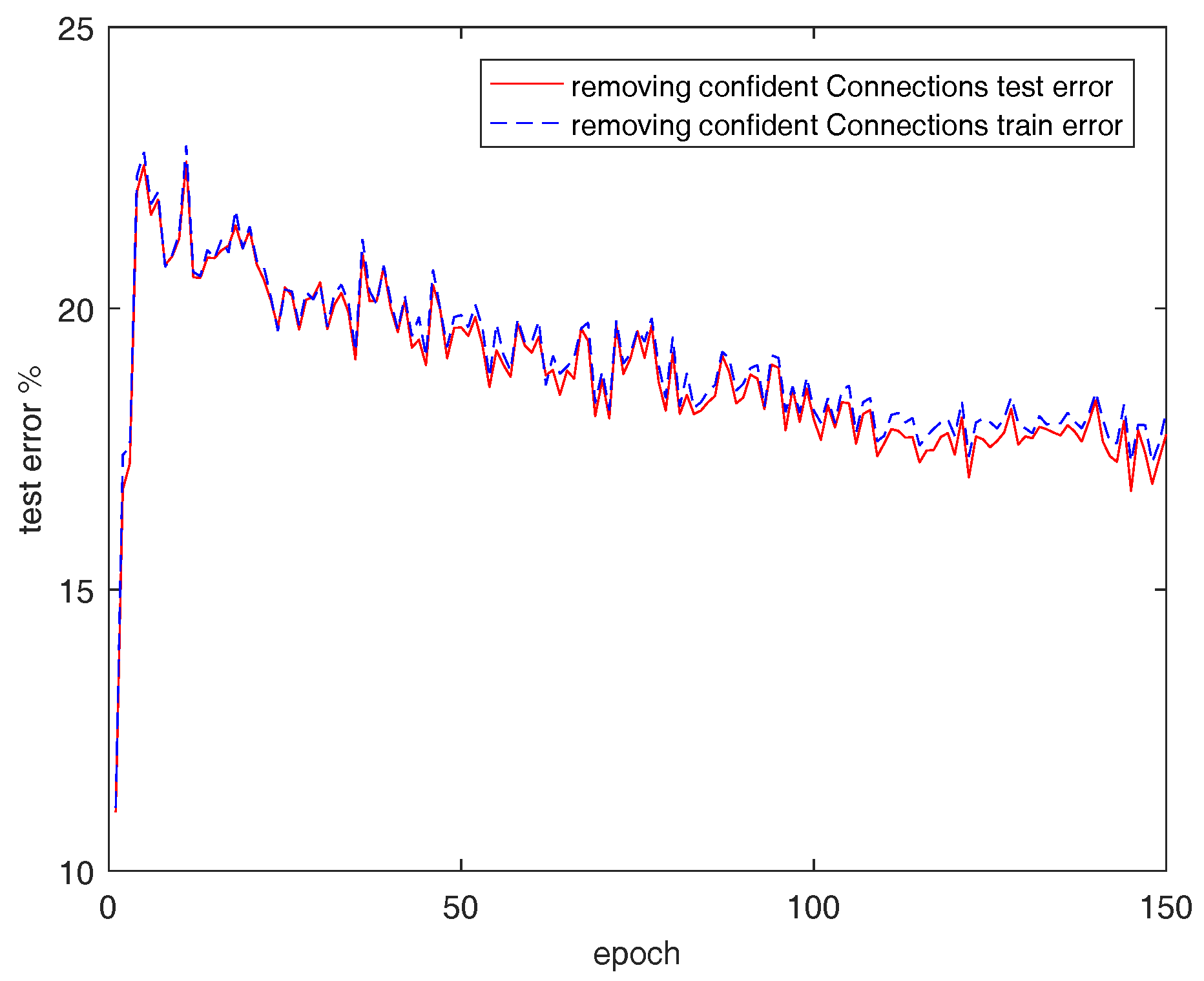
5. Experiments
5.1. Experimental Setup
5.2. Experimental Results
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hinton, G.; Deng, L.; Yu, D.; Dahl, G.E.; Mohamed, A.; Jaitly, N.; Senior, A.; Vanhoucke, V.; Nguyen, P.; Sainath, T.N. Deep Neural Networks for Acoustic Modeling in Speech Recognition. IEEE Signal Process. Mag. 2012, 29, 82–97. [Google Scholar] [CrossRef]
- Mikolov, T.; Deoras, A.; Povey, D.; Burget, L. Strategies for training large scale neural network language models. In Proceedings of the 2011 IEEE Workshop on Automatic Speech Recognition and Understanding (ASRU), Waikoloa, HI, USA, 11–15 December 2011; pp. 196–201. [Google Scholar]
- Sainath, T.N.; Mohamed, A.R.; Kingsbury, B.; Ramabhadran, B. Deep convolutional neural networks for LVCSR. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Vancouver, BC, Canada, 26–31 May 2013; pp. 8614–8618. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. Adv. Neural Inf. Process. Syst. 2012, 25, 2012. [Google Scholar] [CrossRef]
- Farabet, C.; Couprie, C.; Najman, L.; Lecun, Y. Learning Hierarchical Features for Scene Labeling. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1915–1929. [Google Scholar] [CrossRef] [PubMed]
- Tompson, J.; Jain, A.; Lecun, Y.; Bregler, C. Joint Training of a Convolutional Network and a Graphical Model for Human Pose Estimation. In Proceedings of the 27th International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; pp. 1799–1807. [Google Scholar]
- Collobert, R.; Weston, J. A unified architecture for natural language processing: Deep neural networks with multitask learning. In Proceedings of the 25th International Conference on Machine learning, Helsinki, Finland, 5–9 July 2008; pp. 160–167. [Google Scholar]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the dimensionality of data with neural networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef] [PubMed]
- Tanner, M.A.; Wong, W.H. The Calculation of Posterior Distributions by Data Augmentation. J. Am. Stat. Assoc. 1987, 82, 528–540. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Wan, L.; Zeiler, M.; Zhang, S.; Cun, Y.L.; Fergus, R. Regularization of neural networks using dropconnect. In Proceedings of the 30th International Conference on International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013; pp. 1058–1066. [Google Scholar]
- Specht, D.F. Probabilistic Neural Networks. Neural Netw. 1990, 3, 109–118. [Google Scholar] [CrossRef]
- Zhao, X.; Hou, Y.; Song, D.; Li, W. A Confident Information First Principle for Parameter Reduction and Model Selection of Boltzmann Machines. IEEE Trans. Neural Netw. Learn. Syst. 2017. [Google Scholar] [CrossRef] [PubMed]
- Amari, S.; Kurata, K.; Nagaoka, H. Information geometry of Boltzmann machines. IEEE Trans. Neural Netw. 1992, 3, 260–271. [Google Scholar] [CrossRef] [PubMed]
- Hinton, G.E.; Osindero, S.; Teh, Y.W. A fast learning algorithm for deep belief nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef] [PubMed]
- Hou, Y.; Zhao, X.; Song, D.; Li, W. Mining pure high-order word associations via information geometry for information retrieval. ACM Trans. Inf. Syst. 2013, 31, 293–314. [Google Scholar] [CrossRef]
- Amari, S.; Nagaoka, H. Methods of Information Geometry (Translations of Mathematical Monographs); American Mathematical Society: Providence, RI, USA, 2007. [Google Scholar]
- Rao, C.R. Information and the Accuracy Attainable in the Estimation of Statistical Parameters; Springer: New York, NY, USA, 1945; pp. 235–247. [Google Scholar]
- Kass, R.E. The Geometry of Asymptotic Inference. Stat. Sci. 1989, 4, 188–219. [Google Scholar] [CrossRef]
- Zhao, X.; Hou, Y.; Song, D.; Li, W. Extending the extreme physical information to universal cognitive models via a confident information first principle. Entropy 2014, 16, 3670–3688. [Google Scholar] [CrossRef]
- Gibilisco, P.; Riccomagno, E.; Rogantin, M.P.; Wynn, H.P. Algebraic and Geometric Methods in Statistics; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Cencov, N.N. Statistical Decision Rules and Optimal Inference; American Mathematical Society: Providence, RI, USA, 1982. [Google Scholar]
- Hinton, G.E.; Srivastava, N.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R.R. Improving neural networks by preventing co-adaptation of feature detectors. arXiv, 2012; arXiv:1207.0580. [Google Scholar]
- Amari, S.I. Information geometry on hierarchy of probability distributions. IEEE Trans. Inf. Theory 2001, 47, 1701–1711. [Google Scholar] [CrossRef]
- Akaike, H. IEEE Xplore Abstract—A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Bozdogan, H. Model selection and Akaike’s Information Criterion (AIC): The general theory and its analytical extensions. Psychometrika 1987, 52, 345–370. [Google Scholar] [CrossRef]
- Nakahara, H.; Amari, S.I. Information-geometric measure for neural spikes. Neural Comput. 2002, 14, 2269–2316. [Google Scholar] [CrossRef]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Hinton, G. Learning Multiple Layers of Features from Tiny Images. Available online: http://www.cs.utoronto.ca/kriz/learning-features-2009-TR.pdf (accessed on 26 June 2017).

| Model | MNIST | CIFAR-10 | CIFAR-100 | |||
|---|---|---|---|---|---|---|
| Top-1 ➀ | Top-1 ➁ | Top-1 | Top-5 | Top-1 | Top-5 | |
| FullConnect | 1.84 | 1.56 | 20.09 | 1.32 | 52.02 | 23.26 |
| Dropout | 1.79 | 1.43 | 19.87 | 1.24 | 51.18 | 23.02 |
| DropConnect | 1.77 | 1.59 | 18.53 | 1.19 | 50.87 | 22.79 |
| Confnet | 1.62 | 1.19 | 19.48 | 1.31 | 50.06 | 22.74 |
| Stochastic ConfNet | 1.50 | 1.19 | 18.25 | 1.12 | 48.39 | 19.96 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Hou, Y.; Wang, B.; Song, D. Regularizing Neural Networks via Retaining Confident Connections. Entropy 2017, 19, 313. https://doi.org/10.3390/e19070313
Zhang S, Hou Y, Wang B, Song D. Regularizing Neural Networks via Retaining Confident Connections. Entropy. 2017; 19(7):313. https://doi.org/10.3390/e19070313
Chicago/Turabian StyleZhang, Shengnan, Yuexian Hou, Benyou Wang, and Dawei Song. 2017. "Regularizing Neural Networks via Retaining Confident Connections" Entropy 19, no. 7: 313. https://doi.org/10.3390/e19070313
APA StyleZhang, S., Hou, Y., Wang, B., & Song, D. (2017). Regularizing Neural Networks via Retaining Confident Connections. Entropy, 19(7), 313. https://doi.org/10.3390/e19070313





